Abstract
Tight gas reservoirs present unique forecasting challenges due to steep decline rates, nonlinear production dynamics, and sensitivity to operational conditions. Conventional decline-curve methods and reservoir simulations are limited either by oversimplifying assumptions or by the need for extensive input data, although univariate deep learning models fail to fully capture external influences on well performance. To address these limitations, this study develops a transfer learning–enhanced N-BEATSx (Neural Basis Expansion Analysis Time Series with exogenous variables) framework for multivariate forecasting of tight gas well production. The model integrates exogenous variables, particularly casing pressure, with production histories to jointly represent reservoir behavior and operational effects. A pretraining dataset, comprising more than 100,000-day records from Block S of the Sulige Gas Field, was used to initialize the model, which was subsequently applied in a zero-shot setting to wells A1 and A2. Comparative analysis with the transfer learning-enhanced N-BEATS model demonstrates that N-BEATSx achieves consistently higher accuracy, with RMSE reductions of 23.9%, 39.1%, and 33.1% for Well A1 in short-, medium-, and long-term forecasts, respectively. These advances establish N-BEATSx as a robust tool for multivariate production forecasting, with direct industrial value in optimizing resource allocation, guiding development strategies, and enhancing operational decision-making in unconventional gas fields.
1. Introduction
Tight sandstone gas, commonly referred to as tight gas, is an unconventional natural gas resource that occurs in reservoirs with very low permeability (typically less than 0.1 mD) and low porosity [1,2,3]. As one of the largest unconventional gas categories, tight gas is geologically distinct from shale gas and coalbed methane, yet together these resources form an increasingly important component of the global natural gas supply system [4,5,6,7]. For instance, in 2024, China’s total natural gas production reached 246.37 billion cubic meters, of which shale gas and tight gas accounted for 25.4 and 62.0 billion cubic meters, respectively. Tight gas alone represented more than one quarter of national output, underscoring its strategic importance [8]. Within this category, the Sulige Gas Field accounts for nearly half of China’s tight gas production, offering a large-scale real-world dataset for forecasting studies. Its scale and strategic importance make reliable production forecasting both a scientific challenge and an industrial priority [9,10].
Accurate forecasting of tight gas well production is therefore a critical task in the energy industry, underpinning strategic, economic, and operational decisions throughout the entire lifecycle of a well, from initial investment to final abandonment. Despite its importance, forecasting in unconventional reservoirs such as tight gas remains highly challenging. Tight gas wells are characterized by steep decline rates, nonlinear production dynamics, and strong sensitivity to operational conditions such as wellhead pressure and water production [11]. Traditional approaches in petroleum engineering have largely relied on decline-curve analysis and reservoir simulation. Decline-curve analysis is computationally efficient and requires only limited data, but it depends on strong curve-fitting assumptions that frequently fail for unconventional wells [12,13,14]. Reservoir simulation can incorporate multiphase flow physics and geological heterogeneity, but it demands extensive input data and high computational costs, restricting its applicability in large-scale forecasting scenarios [15,16].
The remainder of this paper is structured as follows. Section 2 reviews related works and highlights the original contributions of this study. Section 3 introduces the study area, dataset, and preprocessing steps. Section 4 presents the methodology, including the N-BEATS and N-BEATSx architectures, transfer learning strategy, and evaluation metrics. Section 5 reports experimental results and comparative analysis. Finally, Section 6 concludes the paper and outlines possible directions for future research.
2. Related Works
These limitations have motivated growing interest in the application of deep learning models for time-series forecasting. Architectures such as recurrent neural networks (RNNs), attention-based long short-term memory networks (A-LSTMs), and temporal convolutional networks (TCNs) have shown strong capability in capturing nonlinear dependencies and long-range temporal correlations in production data [17,18,19,20,21,22]. For example, RNNs and LSTMs have been successfully applied to forecast oil and gas production declines, outperforming classical decline-curve analysis by directly learning from historical well trajectories [17,18,19]. A-LSTM further improves upon traditional LSTM by incorporating an attention mechanism that dynamically assigns weights to past time steps, thereby enhancing its predictive accuracy [20]. More recently, a Dual-Stage Attention TCN (DA-TCN) model has been developed to improve the accuracy and efficiency of gas production forecasting, particularly for wells in tight sandstone reservoirs. By integrating both feature-level and temporal attention within the TCN framework, DA-TCN strengthens the ability to capture complex temporal dependencies and highlight key operational features, ultimately achieving robust forecasting performance across multiple time horizons [21].
Despite recent progress in deep learning, recurrent and convolutional models remain limited by long-horizon generalization, training instability, and interpretability, particularly in unconventional reservoirs. To overcome these issues, the Neural Basis Expansion Analysis for Time Series (N-BEATS) model was developed, which represents trend and seasonality through a fully connected basis-expansion framework. Unlike RNNs and LSTMs that process sequences sequentially and suffer from vanishing gradients, N-BEATS captures long-range dependencies without recurrence, yielding improved efficiency, stability, and scalability for extended horizons [22,23]. Building on this foundation, N-BEATSx extends the architecture to handle multivariate inputs, enabling production to be modeled jointly with operational covariates such as wellhead and casing pressures. Compared to attention-based LSTMs, which rely on explicit attention mechanisms, N-BEATSx implicitly learns temporal structure through backcast–forecast decomposition, reducing architectural complexity while remaining well suited for forecasting nonlinear dynamics in tight gas production [24,25].
Although N-BEATSx enhances accuracy through multivariate learning, its effectiveness is still constrained by the limited historical data typical of unconventional reservoirs. Transfer learning provides a natural solution by leveraging pretrained models from large external or domain-specific datasets to improve generalization and mitigate overfitting [26,27]. In our previous work, we developed a transfer learning framework based on univariate N-BEATS, which outperformed attention-based LSTMs in tight gas forecasting [28]. However, that approach could not incorporate auxiliary information, despite the fact that well performance is strongly shaped by operational factors such as pressures, choke settings, and water production.
This study addresses the above gaps and advances production forecasting in unconventional reservoirs in three ways:
- It presents the first application of the N-BEATSx framework with transfer learning for multivariate forecasting of tight gas wells.
- By incorporating operational covariates such as casing pressure, the model captures reservoir–operation interactions that univariate methods cannot represent.
- The model is evaluated in a zero-shot setting on wells from the Sulige Gas Field, demonstrating strong predictive accuracy across short-, medium-, and long-term horizons, with substantial improvements over the univariate N-BEATS transfer model.
These contributions establish N-BEATSx as a scalable and data-efficient tool for forecasting in unconventional reservoirs. The following section introduces the study area, dataset, and preprocessing steps that support the empirical evaluation of the proposed forecasting framework.
3. Study Area and Dataset Preparation
To evaluate the proposed forecasting framework, we focus on Block S of the Sulige Gas Field, a representative tight sandstone reservoir. This section provides an overview of the study area, describes the production and operational dataset, and outlines the preprocessing steps applied to ensure data quality and reliability.
3.1. Overview of the Study Area
The study area, known as S block, located in the central region of the Sulige Gas Field and adjacent to Wushenqi on the east, lies structurally within the Yishan Slope in the northwestern Ordos Basin, as shown in Figure 1.
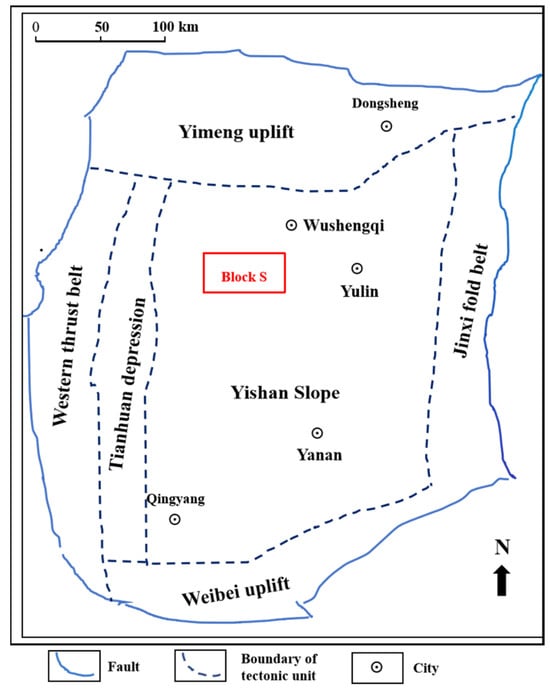
Figure 1.
Location of Block S in the Sulige Gas Field.
Covering an area of approximately 850 km2, this block represents a typical tight sandstone gas reservoir characterized by low permeability, low abundance, low productivity, and pronounced formation heterogeneity [29]. These geological and production conditions make it an ideal case study for evaluating advanced machine learning-based forecasting frameworks under highly heterogeneous formation. The average matrix porosity of the block is 6.2%, and the porosity of the gas-bearing intervals ranges from 5% to 15%. The average permeability is 0.14 mD [30]. Since its initial development in 2006, the S Block has gradually expanded into large-scale production through the adoption of advanced technologies such as horizontal drilling and multi-stage hydraulic fracturing. By the end of 2014, it became the first production area in the Sulige Gas Field to surpass a cumulative output of 10 billion cubic meters, confirming the viability of its development model. By 2023, more than 1000 wells had been brought online, with vertical wells accounting for over 80% of all fractured completions. This extensive and diverse well set provides a rich dataset for evaluating production forecasting models, encompassing variations in well types, completion strategies, and production behaviors [9].
3.2. Data Description
Building on this overview of the study area, the subsection describes the production and operational dataset used for forecasting. The dataset consists of production and operational records from fractured wells in Block S of the Sulige Gas Field. The primary target variable is the daily gas production rate, supplemented with exogenous variables such as wellhead pressure, casing pressure, and water production. To provide a statistical overview, Table 1 summarizes the descriptive measures of daily gas production and casing pressure for one of analyzed wells.

Table 1.
Descriptive statistics of the target (daily gas production) and main exogenous variable (casing pressure) for the Sulige dataset.
In daily gas rate forecasting, relying solely on production history often fails to capture the complex physical and operational variations that influence reservoir performance. The inclusion of covariates provides a means to improve predictive accuracy by revealing underlying environmental and operational factors, as well as by helping to model complex phenomena such as seasonal fluctuations, abrupt interventions, and long-term decline trends. Within the N-BEATSx framework, covariates are incorporated as an external feature matrix concatenated with lagged production data. This design allows the model to condition forecasts on both historical production trajectories and operational factors, thereby enhancing its ability to represent long-term trends while adapting to short-term production dynamics [24].
Preliminary analysis revealed that casing pressure exhibits a stronger correlation with daily gas production than other operational variables and contains fewer missing values, making it a stable and reliable covariate. Physically, time-dependent casing pressure reflects subsurface conditions like reservoir pressure, liquid loading, and gas–liquid distribution, and is captured in near real-time. This choice is consistent with findings in the literature; for instance, casing pressure is used as an important input in coalbed methane production forecasting models [31]. In contrast, wellhead pressure and daily water production proved less reliable, being prone to noise and discontinuities due to factors such as equipment aging, multiphase flow, aquifer influx, and well maintenance, increasing the risk of predictive uncertainty. As a result, casing pressure because of its physical relevance, temporal stability, and empirical validation, was selected as the most informative covariate to enhance the predictive accuracy and robustness of data-driven models like N-BEATSx.
If casing pressure is unavailable, the model can incorporate alternatives such as wellhead pressure, choke settings, or water production. However, these variables are typically noisier and subject to discontinuities from operational interventions, which may reduce model accuracy. In such cases, additional preprocessing (e.g., smoothing, outlier removal, or imputation) would be required to mitigate data instability. Alternatively, combining multiple auxiliary variables may partially compensate for the absence of casing pressure by capturing complementary aspects of reservoir and operational dynamics. Future research should systematically evaluate the model’s sensitivity to different covariates across diverse fields to further strengthen its robustness under varying data availability conditions.
3.3. Data Preprocessing
Following the dataset description, the subsection outlines the preprocessing steps applied to ensure data quality and reliability prior to model training. Data preprocessing is a crucial step for ensuring the accuracy and reliability of subsequent analysis and modeling. In practice, raw production data from gas wells frequently contain missing values, outliers, and noise, all of which can adversely impact the performance and stability of forecasting models. Effective preprocessing enhances data quality, standardizes input formats, improves usability, and reduces computational complexity. These steps not only increase predictive accuracy but also improve the efficiency and robustness of model training, making preprocessing an essential component of the forecasting workflow.
3.3.1. Missing Value Handling
Missing values in gas well production data may arise from equipment malfunctions, human error during data logging, or adverse environmental conditions that disrupt measurement devices. If left untreated, these gaps reduce data completeness, break time-series continuity, and introduce bias into model training, ultimately degrading forecasting accuracy and reliability. Therefore, missing value treatment is a critical step in the preprocessing workflow.
To address missing values in the S block production dataset, a three-step strategy was adopted based on the extent and duration of missing records:
- 1.
- Short-term gaps (≤3 consecutive days):
- Filled using linear interpolation to preserve time-series continuity and minimize distortions that could adversely affect model training.
- 2.
- Long-term gaps (>3 consecutive days):
- Imputed using the average production from comparable production stages of the same well, thereby ensuring consistency with reservoir dynamics and restoring data completeness.
- 3.
- High missing rates:
- Wells with ≥10% missing production data were excluded from analysis to maintain dataset reliability.
The missing value handling strategy in this study combining linear interpolation for short gaps, stage-based averaging for longer gaps, and exclusion of wells with excessive missing was designed to ensure data continuity and reliability under heterogeneous reservoir conditions. This pragmatic, domain-informed approach is computationally efficient and well suited to data-scarce unconventional reservoirs, where missing values often arise from equipment failures, logging errors, or harsh operating environments. Although advanced imputation methods such as RNN-based model [32], GAN-based model [33], and graph-based imputer [34] have shown promise in broader time-series applications, they generally require large, high-quality datasets and incur higher computational costs, making them less practical for petroleum production data, which are often sparse, noisy, and heterogeneous. Future work may combine domain knowledge with transfer learning and AI-based imputation to better exploit cross-well correlations while maintaining robustness.
3.3.2. Outlier Detection and Treatment
Outlier detection was performed using a moving median-based approach, chosen for its robustness and interpretability under the approximately normal distribution of the dataset with localized fluctuations. A threshold factor of 3.0 was adopted to balance sensitivity and false detection rate. A 30-day sliding window was selected after testing 7- and 90-day windows, as it aligns with monthly operational practices and effectively captures periodic production patterns. Outliers were treated through linear interpolation rather than deletion to ensure continuity and preserve smooth temporal dynamics. Although advanced anomaly detection methods such as isolation forests [35], autoencoders [36], and LSTM-based models [37] can capture more complex nonlinear patterns, they require larger, cleaner datasets and extensive parameter tuning. Given the sparse and heterogeneous nature of petroleum production data, the rule-based strategy was preferred for its robustness and reproducibility. The complete procedure is summarized in Table 2.

Table 2.
Summary of Outlier Detection and Treatment Strategy.
Furthermore, all continuous variables were normalized using min–max scaling to facilitate efficient training.
4. Methodology
After describing the study area, dataset, and preprocessing steps in Section 3, This section introduces the proposed forecasting methodology. This section details the problem formulation, the N-BEATS and N-BEATSx architectures, the transfer learning strategy, and the evaluation metrics.
This section outlines the modeling framework developed for tight gas production forecasting. An overview of the proposed workflow, including pretraining on long-history wells and zero-shot forecasting on newly drilled wells, is illustrated in Figure 2. We formulate tight gas forecasting as a multivariate time-series task, where future production is predicted from historical rates and operational covariates. The framework builds on the N-BEATS architecture, which models trend and seasonality through backcast–forecast decomposition, and extends it to N-BEATSx to incorporate exogenous variables via basis expansion. To handle newly drilled wells with short or incomplete histories, we adopt a zero-shot transfer learning strategy: the model is pretrained on wells with long production records and applied directly to new wells without fine-tuning. This approach lowers training costs, avoids overfitting, and enables accurate forecasting in data-scarce environments.
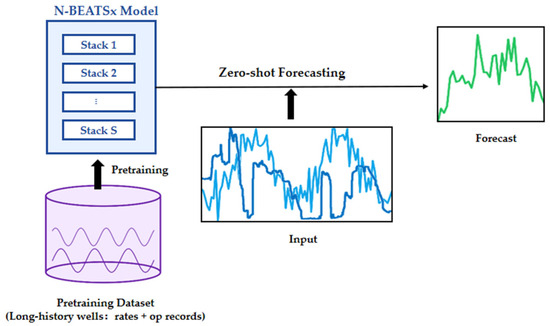
Figure 2.
Workflow of the transfer learning-enhanced N-BEATSx framework. The model is pretrained on wells with long production histories and operational records, then applied directly in a zero-shot setting to new wells with limited data for accurate forecasting.
4.1. Problem Formulation
Forecasting daily gas production in tight reservoirs is inherently challenging due to reservoir heterogeneity, operational variability, and limited historical records. Traditional univariate models rely solely on past production rates, which cannot adequately capture the influence of external factors such as well pressures, water cut, and seasonal variations. To address this, we formulate the task as a multivariate time-series forecasting problem. Let yt denote the daily gas production at time t, xt represent a vector of d exogenous covariates (e.g., casing pressure, wellhead pressure, water cut). Given a historical input window of length L, consisting of past production values {yt−L+1, …, yt} and corresponding covariates {xt−L+1, …, xt}, the objective is to learn a mapping:
where H is the forecast horizon, denotes
the predicted gas production, and θ represents the model parameters. Within the
N-BEATSx framework, this mapping is achieved by jointly processing lagged
production values and exogenous features through a basis-expansion
architecture, enabling the model to capture both long-term trends and
short-term dynamics. The ultimate goal is to minimize the prediction error:
thereby improving forecasting accuracy and robustness in tight gas reservoirs. In this study, the lookback window length was fixed at 5 days, consistent with our previous work [28], and determined through a 10-fold cross-validation strategy to balance model complexity with predictive accuracy. The forecast horizon was set to a single time step (H = 1), such that the model produced one-step ahead predictions at each point in the series. This configuration was applied uniformly across short-, medium-, and long-term evaluations, defined by partitioning the dataset into the final 10%, subsequent 20%, and following 30% of production records, respectively.
4.2. N-BEATS Architecture Overview
The N-BEATS is a deep learning architecture tailored for time-series forecasting. Unlike recurrent or convolutional models, N-BEATS is a fully connected, stack-based architecture that models trend and seasonality through backcast–forecast decomposition. It avoids recurrence and convolution, offering stability and scalability for long-horizon forecasting.
Nevertheless, N-BEATS is limited to univariate inputs, restricting its use in settings such as petroleum production, where exogenous variables (e.g., well pressures, operational factors) are critical. This limitation motivates the multivariate extension, N-BEATSx, introduced in the next subsection.
4.3. N-BEATSx: Multivariate Extension
Olivares et al. (2023) [24] introduced N-BEATSx, a multivariate extension that integrates exogenous variables into the forecasting process. In this architecture, production data are modeled jointly with operational and contextual inputs such as casing pressure, wellhead pressure, water cut, and temporal indicators by concatenating lagged target values with an external feature matrix. This design allows the network to capture not only intrinsic temporal patterns in production, but also auxiliary effects driven by operational dynamics and reservoir conditions.
As illustrated in Figure 3, the N-BEATSx workflow begins with the ingestion of historical production data and covariates. Given a lookback window of length L, the model input is defined as
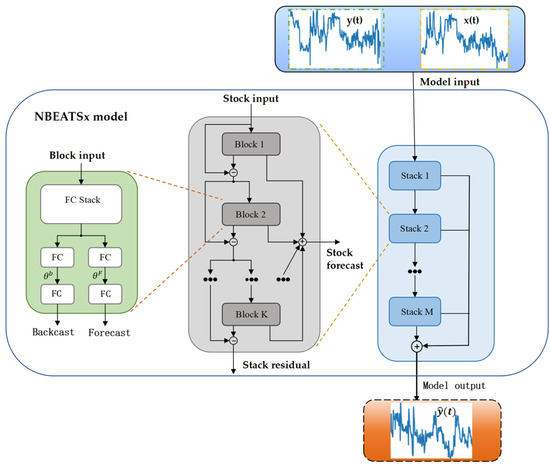
Figure 3.
Schematic of the N-BEATSx prediction approach applied to gas production forecasting.
Each block within the architecture maps this input to a backcast–forecast pair:
with the backcast refining residuals of past observations and the forecast contributing to the forward prediction. Forecasts across all stacks and blocks are aggregated as
Importantly, each forecast is further decomposed into interpretable trend, seasonality, and exogenous components through basis expansion:
Here, T, S, and X denote the basis matrices corresponding to trend, seasonality, and exogenous effects, respectively, and , , and are the learned coefficient vectors. This formulation allows the forecast to be expressed
as a linear combination of basis functions, thereby linking predictions to
physically interpretable components.
With this design, daily gas production is represented as the sum of long-term depletion trends, seasonality, and exogenous influences. The joint modeling of reservoir dynamics and operational drivers ensures robustness under nonstationary conditions. At the same time, the model remains interpretable, making it well suited for tight gas forecasting.
4.4. Transfer Learning Strategy
Newly drilled wells in tight gas reservoirs often
provide only short or incomplete production histories, making reliable
forecasting particularly challenging. Nevertheless, accurate prediction of
future production for these wells is crucial, as it directly informs field
development planning, resource allocation, and operational decision-making. To
address the limitations imposed by sparse data, this study employs a zero-shot
transfer learning strategy within the N-BEATSx framework. The model is
pretrained on wells with long production histories and high-quality operational
records from Block S, enabling it to capture generalizable temporal patterns
and operational dependencies. The pretrained weights are then applied directly
to newly drilled wells without further fine-tuning, allowing immediate
forecasting in data-scarce settings. This zero-shot design not only reduces
training costs and complexity, but it also mitigates overfitting while still
delivering accurate and robust forecasts for tight gas wells with limited
production histories.
4.5. Evaluation Metrics
Accuracy was assessed using four complementary metrics: MAE, RMSE, MAPE, and R2. Together, these capture scale-dependent errors, percentage error, and variance explained, providing a balanced evaluation of forecasting performance.
represents the total number of data samples, denotes the true value at the position, represents the predicted value at the position, and is the
mean of the true values.
5. Results and Discussion
After establishing the study area, dataset, and methodological framework, this section presents experimental results. We first report the pretraining outcomes of the N-BEATSx model, followed by comparative analyses with the baseline N-BEATS model across short-, medium-, and long-term horizons. The discussion highlights both numerical performance and industrial implications.
We extend our previous analysis of Wells A1 and A2 in Block S of the Sulige Gas Field, which were also examined in our earlier work using the transfer learning-enhanced N-BEATS framework. Figure 4 shows the normalized daily gas production rates for Wells A1 and A2, where production values have been linearly scaled to the range [0, 1]. Clear seasonal fluctuations can be observed, with lower production levels in summer and higher output in winter, reflecting demand-driven patterns in the Sulige Gas Field. A two-sample t-test comparing winter and summer daily production confirmed that these seasonal differences are statistically significant (p < 0.05), consistent with operational adjustments to match consumption levels.
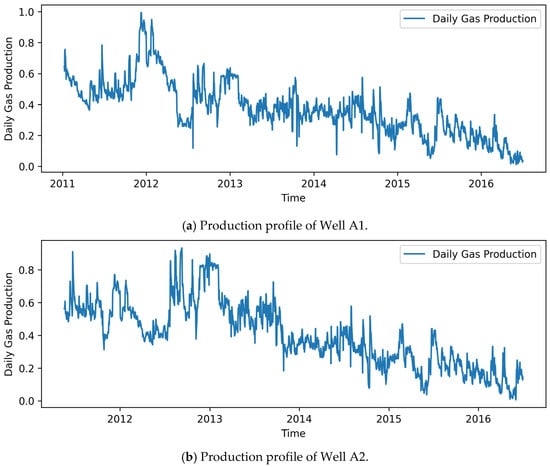
Figure 4.
Normalized production profiles of Wells A1 and A2.
Here, we apply both the N-BEATS transfer model and the newly proposed N-BEATSx transfer model to forecast daily gas production rates across three horizons: short-term, medium-term, and long-term. For evaluation, the final 10% production records were reserved for short-term prediction, the subsequent 20% for medium-term forecasting, and the following 30% for long-term forecasting. This partitioning strategy follows our previously published work [28], ensuring methodological consistency and enabling direct comparison with the earlier N-BEATS framework. At the same time, dividing the dataset into progressively longer horizons provides a systematic means of evaluating each model’s robustness in capturing both near-term fluctuations and longer-term depletion trends. The production characteristics of Wells A1 and A2, together with the dataset partitions for each horizon, are summarized in Table 3. This design allows for a direct head-to-head comparison between the two transfer learning models, thereby highlighting the incremental benefits of incorporating exogenous variables through N-BEATSx.

Table 3.
Dataset partitioning of production histories into short-, medium- and long-term evaluation periods for Wells A1 and A2.
5.1. Pretraining of the N-BEATSx Model
To construct the pretraining dataset for the N-BEATSx model, 23 wells with high-quality production data were selected from Block S of the Sulige Gas Field. For each well, daily gas production rates were collected as the target variable. Although casing pressure was included as a covariate, reflecting the intrinsic relationship between reservoir pressure and production dynamics. The data was preprocessed using the methods described in Section 3.3, including imputation of missing values through interpolation and stage-based averaging, and detection and removal of anomalous records using robust statistical techniques. This process ensured that the final dataset achieved both high completeness and strong representativeness. For model development, 90% of the wells were used for training and the remaining 10% were reserved for testing, thereby ensuring a fair evaluation of predictive performance.
The pretraining dataset ultimately comprised over 100,000 daily production records paired with corresponding casing pressure measurements. This dataset spans multiple development phases of the gas field, thereby capturing the transition from early high-output production to late-stage decline, while also reflecting the influence of external operational conditions on well performance. By pretraining on this dataset, the N-BEATSx model was able to learn the nonlinear dependencies between production and pressure, automatically extract latent production dynamics, and store the resulting optimal weights. The values of the model parameters were kept the same as those used in the N-BEATS training to ensure consistency and comparability, and the detailed parameters adopted for pretraining are summarized in Table 4.

Table 4.
Key parameters of the N-BEATSx pretraining model.
As shown in Table 5, the N-BEATSx model achieved consistently low RMSE and MAPE values on both the training and testing sets during pretraining. These results demonstrate that the model not only fits historical data with high accuracy but also generalizes well to unseen samples. This strong pretraining performance provides a solid foundation for applying the model in a zero-shot forecasting setting, where it can be directly transferred to new wells without additional fine-tuning.

Table 5.
Training and testing performance of the N-BEATSx pretraining model.
Figure 5 further illustrates the model’s capability, showing that the predicted daily gas production curves for the test wells closely track the observed values, with no significant deviations. Across different time periods, the forecasts remain highly consistent with actual production, and the statistical indicators confirm the model’s strong fitting and generalization ability. These findings underscore the accuracy and robustness of the N-BEATSx model in gas well production forecasting and establish it as an effective foundation for transfer learning. Building on this, the subsequent analysis applies the pretrained N-BEATSx model in a zero-shot setting to wells A1 and A2, enabling a direct comparison with the previously developed N-BEATS framework.
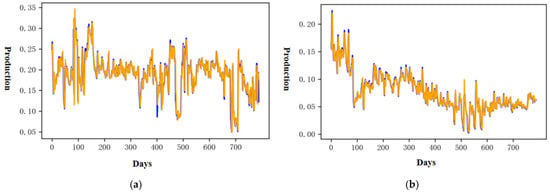
Figure 5.
Comparison of predicted and observed normalized daily production for the two test wells. The yellow curve denotes the predicted values, while the blue curve denotes the observed values. All production values are presented in normalized form. (a) Well one; (b) Well two.
5.2. Comparative Analysis
To further evaluate its generalization capability, the pretrained N-BEATSx model was applied in a zero-shot forecasting setting to two representative wells, A1 and A2, from Block S of the Sulige Gas Field. These wells were also analyzed in our previous study using the transfer learning-enhanced N-BEATS model, providing a consistent benchmark for comparison. Forecasting experiments were conducted across short-term, medium-term, and long-term horizons, following the same partitioning strategy as before. The performance of N-BEATSx was compared directly against the univariate N-BEATS model to assess the benefits of incorporating exogenous variables. The results, summarized in Table 6, highlight the predictive accuracy of both models and provide insights into their relative strengths across different time horizons. RMSE and MAE values are reported in normalized units.

Table 6.
Performance Comparison of N-BEATSx and N-BEATS Transfer Models Across Three Forecast Horizons.
As shown in Table 6, the N-BEATSx transfer model consistently outperforms the N-BEATS transfer model across long-term, medium-term, and short-term forecasts for both Wells A1 and A2. For Well A1, the RMSE was reduced by 33.1%, 39.1%, and 23.8%, respectively, across the three forecasting horizons. The effectiveness of this approach is clearly reflected in the residual analysis. The effectiveness of this approach is clearly reflected in the residual analysis. To provide further transparency, Appendix A includes the figures: Figure A1, Figure A2 and Figure A3 show observed and forecasted values of Wells A1 for short-, medium-, and long-term horizons, while Figure A4 zooms into a representative 100-day window. These figures confirm the robustness of the N-BEATSx model at both full-dataset and sample-level scales. Figure 6, Figure 7 and Figure 8 show the residuals between the actual daily gas production rates of Well A1 and the predicted values across the three forecast horizons. The patterns observed in these figures align closely with the results reported in Table 6, confirming that the N-BEATSx transfer model achieves superior forecasting accuracy compared to the N-BEATS transfer model. In particular, the residuals from N-BEATSx are smaller and more evenly distributed, demonstrating its greater ability to capture nonlinear depletion trends, seasonal fluctuations, and operational effects. To further assess the robustness of these improvements, paired t-tests were conducted on the residuals of N-BEATSx and N-BEATS across the forecast horizons. For example, in the long-term forecast for Well A1, the paired t-test yielded p = 0.933, indicating that the observed RMSE reduction was not statistically significant at the 5% level. Similar tests for the medium- and short-term horizons also showed no significant differences, despite consistently lower RMSE values for N-BEATSx. These results highlight the importance of complementing descriptive error metrics with hypothesis testing when evaluating forecasting models.
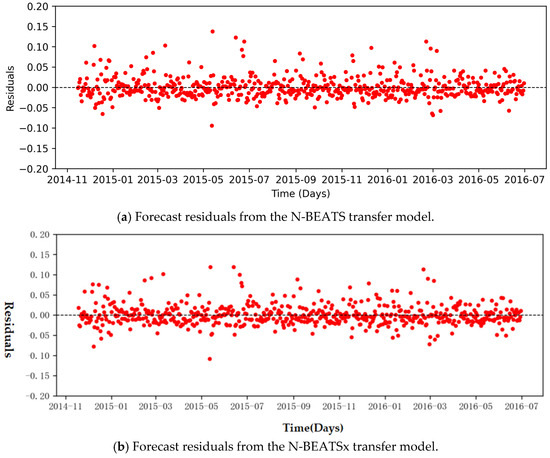
Figure 6.
Residual analysis of long-term forecasts for Well A1. Residual values are shown in normalized form.
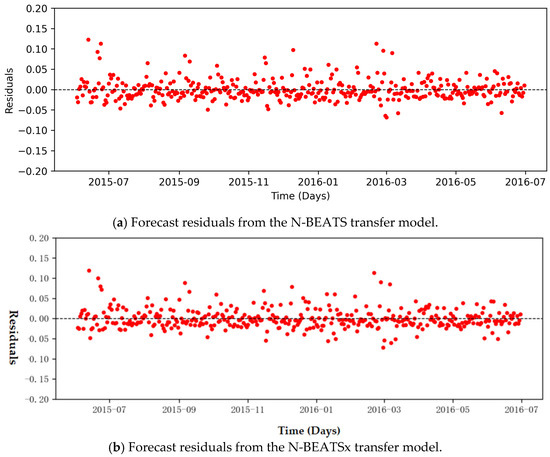
Figure 7.
Residual Analysis of Medium-Term Forecasts for Well A1. Residual values are shown in normalized form.
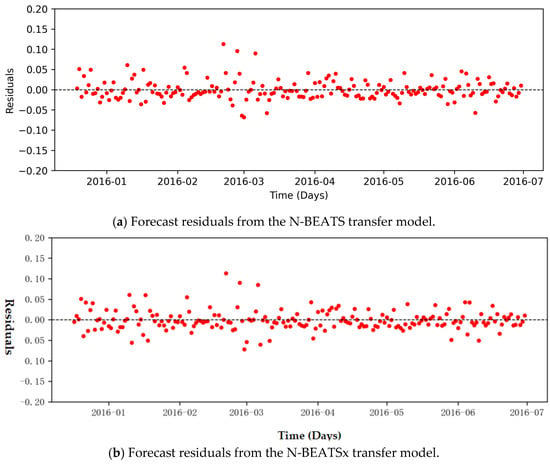
Figure 8.
Residual Analysis of Short-Term Forecasts for Well A1. Residual values are shown in normalized form.
These comparative analyses further demonstrate that the N-BEATSx transfer model consistently outperforms the original N-BEATS transfer model in forecasting tight gas production. Although the univariate N-BEATS framework captures temporal patterns through trend and seasonality decomposition, it is constrained to learning solely from historical production data. In our previous work, the N-BEATS transfer model was pretrained on the generic M4 dataset. We acknowledge that it could also be pretrained on domain-specific production data or even a combination of generic and domain-specific datasets. Nonetheless, because the original N-BEATS architecture does not incorporate covariates, its capacity to fully exploit such datasets remains limited, as it can only learn from the production series alone. By contrast, N-BEATSx explicitly integrates exogenous covariates such as casing pressure, enabling the model to jointly capture reservoir dynamics and operational influences. This design substantially improves forecasting performance, particularly in medium- and long-term horizons where external factors exert stronger effects.
Compared to univariate forecasting approaches, the multivariate N-BEATSx framework offers several advantages. By jointly modeling production with operational covariates, it captures reservoir-operation interactions that shape well performance. This multivariate design improves predictive accuracy under nonstationary conditions, where production dynamics are strongly influenced by pressure and operational changes. It also provides greater robustness when only short production histories are available, as exogenous variables supply additional information. Moreover, multivariate models enable scenario analysis, where forecasts can be conditioned on alternative operational settings, offering practical value for field management and decision-making.
These improvements have clear industrial value. Accurate forecasts across different horizons support resource allocation, production scheduling, and risk management. Medium- and long-term predictions inform strategic decisions such as infill drilling, stimulation planning, and investments, while short-term accuracy helps guide daily operations. Nevertheless, several limitations remain. The performance of N-BEATSx is sensitive to the availability and quality of exogenous data, and the inclusion of multiple covariates introduces greater architectural complexity compared to N-BEATS. Future work could extend this comparison by pretraining both N-BEATS and N-BEATSx on hybrid datasets that combine generic and domain-specific information, thereby providing deeper insight into the relative advantages of incorporating exogenous variables. Moreover, incorporating physics-informed priors could further improve interpretability and robustness.
Although the empirical validation in this study was carried out exclusively using data from the Sulige Gas Field, the proposed N-BEATSx transfer learning framework has broader applicability. Reservoirs with higher degrees of heterogeneity may exhibit more abrupt production fluctuations and stronger nonstationary behavior. In such cases, the model’s multivariate structure and backcast–forecast decomposition remain advantageous, but predictive accuracy will depend on the availability of informative covariates (e.g., bottom-hole pressure, water cut, or operational interventions). Operating practices also play an important role. Fields with frequent choke adjustments or enhanced recovery measures introduce operational signatures distinct from those observed in Sulige. These can be effectively incorporated into the model by treating them as exogenous variables, but their inclusion requires careful preprocessing and domain-informed selection.
Overall, while the present results establish a proof-of-concept for tight sandstone reservoirs, future research should extend the validation to datasets from other geological settings and operational regimes. Pretraining on multi-field datasets and transfer across different formations would provide a more comprehensive assessment of generalizability and robustness, ensuring wider industrial adoption.
6. Conclusions
This study proposed a transfer learning-enhanced N-BEATSx framework for multivariate forecasting of tight gas production. Based on the empirical results from the Sulige Gas Field, the following conclusions can be drawn:
- The study introduces, for the first time in petroleum engineering, a transfer learning enhanced N-BEATSx model that integrates operational covariates with production data, enabling robust multivariate forecasting in data-scarce unconventional reservoirs.
- Comparative experiments on Wells A1 and A2 demonstrate that the N-BEATSx transfer model consistently outperforms the univariate N-BEATS transfer model, achieving RMSE reductions of 23.9%, 39.1%, and 33.1% for short-, medium-, and long-term forecasts of Well A1, respectively.
- The improved forecasting accuracy across multiple horizons provides practical value for field development planning, resource allocation, and operational optimization. In particular, enhanced medium- and long-term predictions can support decisions on infill drilling, stimulation design, and investment strategies.
- Future work should expand empirical validation to multiple fields with diverse geological and operational characteristics, incorporate additional covariates when casing pressure is unavailable, and explore hybrid frameworks that combine domain knowledge, physics-informed priors, and explainable AI techniques to further improve generalizability and interpretability.
Author Contributions
Conceptualization, Y.S. and X.M.; methodology, Y.S. and X.M.; validation, S.C., W.X. and Z.Z.; formal analysis, X.M. and W.X.; investigation, W.X. and J.W.; data curation, S.C. and Z.Z.; writing—original draft preparation, Y.S. and X.M.; writing—review and editing, Y.S., J.J. and J.W.; visualization, S.C. and Z.Z.; funding acquisition, Y.S. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Basic Research Program of Shaanxi (Grant No. 2025JC-YBQN-648) and National Science and Technology Major Project: Mechanisms and New Technologies for Enhancing Tight Gas Recovery (Grant No. 2025ZD1404300).
Data Availability Statement
The datasets presented in this article are not readily available due to technical limitations. Requests to access the datasets should be directed to the corresponding author.
Conflicts of Interest
Author Yangnan Shangguan, Junhong Jia, Weiliang Xiong and Jinghua Wang were employed by the company Changqing Oilfield Branch Company, PetroChina. Author Shilong Chang was employed by the company PipeChina Energy Storage Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
The following figures provide supplementary visualizations of observed and forecasted daily production values across the long-, medium-, and short-term forecasting horizons, as well as a sample-level perspective that complements the main text results. As the observed and forecasted values are nearly overlapping, readers are referring to the residual plots for a clearer comparison.
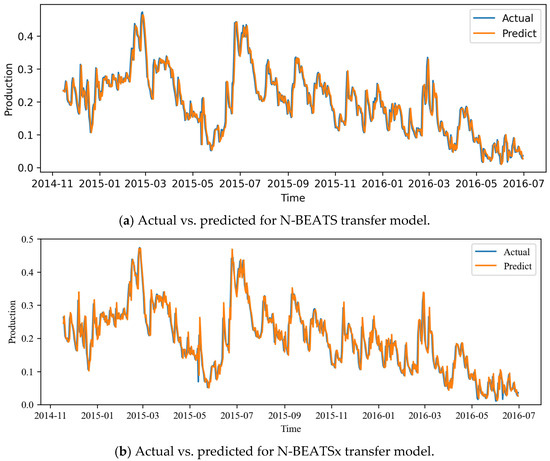
Figure A1.
Observed and forecasted daily production values over the long-term horizon for Well A1 using N-BEATS and N-BEATSx models.
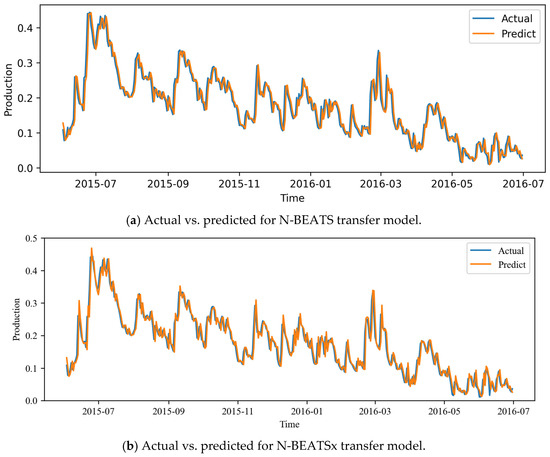
Figure A2.
Observed and forecasted daily production values over medium-term horizons for Well A1 using N-BEATS and N-BEATSx models.
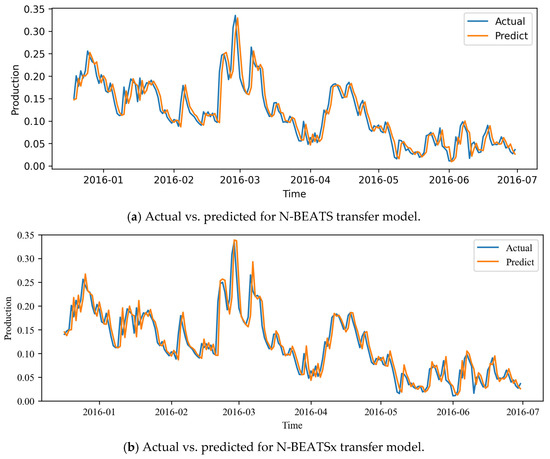
Figure A3.
Observed and forecasted daily production values over short-term horizons for Well A1 using N-BEATS and N-BEATSx models.
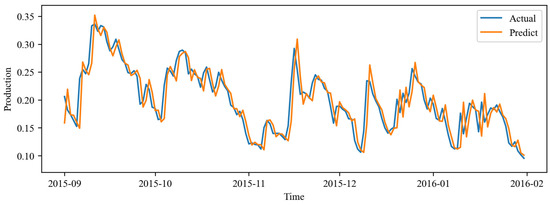
Figure A4.
Zoomed-in comparison of observed and forecasted values for a representative 150-day sample window using N-BEATS and N-BEATSx models.
References
- Holditch, S.A. Tight Gas Sands. J. Pet. Technol. 2006, 58, 86–93. [Google Scholar] [CrossRef]
- He, D.; Jia, C.; Wei, Y.; Guo, J.L.; Ji, G.; Li, Y.L. Current Situation and Development Trend of World Natural Gas Industry. Nat. Gas Ind. 2022, 42, 1–12. [Google Scholar]
- Jia, A.; Wei, Y.; Guo, Z.; Wang, G.; Meng, D.; Huang, S. Development Status and Prospect of Tight Sandstone Gas in China. Nat. Gas Ind. B 2022, 9, 467–476. [Google Scholar] [CrossRef]
- BP. bp Energy Outlook; BP: London, UK, 2024. [Google Scholar]
- Li, G.; Lei, Z.; Dong, W.; Wang, H.; Zheng, X.; Tan, J. Progress, challenges and prospects of unconventional oil and gas development of CNPC. China Pet. Explor. 2022, 27, 1–11. [Google Scholar]
- Jiao, F. Rerecognition of “unconventional” in unconventional oil and gas. Pet. Explor. Dev. 2019, 46, 803–810. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.; Jha, A.N.; Rogers, H. Natural gas from shale formation-The evolution, evidences and challenges of shale gas revolution in United States. Renew. Sustain. Energy Rev. 2014, 30, 1–28. [Google Scholar] [CrossRef]
- Jia, A.; Wang, G.; Li, Y. Natural Gas Development in China: Present Situation and Prospect. Nat. Gas Ind. 2025, 45, 31–42. [Google Scholar]
- Wu, Z.; Jiang, Q.; Zhou, Y.; He, Y.; Sun, Y.; Tian, W.; Zhou, C.; An, W. Key Technologies And Orientation of EGR for the Sulige Tight Sandstone Gas Field in the Ordos Basin. Nat. Gas Ind. 2023, 43, 66–75. [Google Scholar] [CrossRef]
- Cheng, M.; Lei, D.; Zhang, L.; Liu, L.; Zhao, M. Technical Strategy for Beneficial Development of Tight Sand Gas in Sulige Gas Field. Pet. Reserv. Eval. Dev. 2024, 14, 475–483. [Google Scholar]
- Wang, J.; Zhang, C.; Li, J.; Li, Y.; Li, X.; Liu, P.; Lu, J. Tight sandstone gas reservoirs in the Sulige Gas Field: Development understandings and stable-production proposals. Nat. Gas Ind. 2021, 41, 100. [Google Scholar]
- Arps, J.J. Analysis of Decline Curves. Trans. AIME 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Yehia, T.; Abdelhafiz, M.; Hegazy, G.; Elnekhaily, S.; Mahmoud, O. A Comprehensive Review of Deterministic Decline Curve Analysis for Oil and Gas Reservoirs. Geoenergy Sci. Eng. 2023, 226, 211775. [Google Scholar] [CrossRef]
- Gupta, I.; Rai, C.; Sondergeld, C.; Devegowda, D. Variable exponential decline: Modified Arps to characterize unconventional-shale production performance. SPE Reserv. Eval. Eng. 2018, 21, 1045–1057. [Google Scholar] [CrossRef]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Applied Science Publishers: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Wang, L.; Wang, S.; Zhang, R.; Wang, C.; Xiong, Y.; Zheng, X.; Li, S.; Jin, K.; Rui, Z. Review of Multi-Scale and Multi-Physical Simulation Technologies for Shale and Tight Gas Reservoirs. J. Nat. Gas Sci. Eng. 2017, 37, 560–578. [Google Scholar] [CrossRef]
- Huang, R.; Wei, C.; Wang, B.; Yang, J.; Xu, X.; Wu, S.; Huang, S. Well performance prediction based on Long Short-Term Memory (LSTM) neural network. J. Pet. Sci. Eng. 2022, 208 Pt D, 109686. [Google Scholar] [CrossRef]
- Chaikine, I.A.; Gates, I.D. A Machine Learning Model for Predicting Multi-Stage Horizontal Well Production. J. Pet. Sci. Eng. 2021, 198, 108133. [Google Scholar] [CrossRef]
- Schuetter, J.; Mishra, S.; Zhong, M.; Ret, R.L. A Data-Analytics Tutorial: Building Predictive Models for Oil Production in an Unconventional Shale Reservoir. SPE J. 2018, 23, 1075–1089. [Google Scholar] [CrossRef]
- Kumar, I.; Tripathi, B.K.; Singh, A. Attention-Based LSTM Network-Assisted Time Series Forecasting Models for Petroleum Production. Eng. Appl. Artif. Intell. 2023, 123, 106440. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, L.; Zhan, J.; Chang, S. Application of Dual-Stage Attention Temporal Convolutional Networks in Gas Well Production Prediction. Mathematics 2024, 12, 3896. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Yi, C.; Xu, X.; Wang, J.; Zhang, Y. EcoForecast: An interpretable data-driven approach for short-term macroeconomic forecasting using N-BEATS neural network. Eng. Appl. Artif. Intell. 2022, 114, 105072. [Google Scholar] [CrossRef]
- Olivares, K.G.; Challu, C.; Marcjasz, G.; Weron, R.; Dubrawski, A. Neural Basis Expansion Analysis with Exogenous Variables: Forecasting Electricity Prices with NBEATSx. Int. J. Forecast. 2023, 39, 884–900. [Google Scholar] [CrossRef]
- Souto, H.G.; Amir Moradi, A. Introducing NBEATSx to realized volatility forecasting. Expert Syst. Appl. 2024, 242, 122802. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Yu, F.; Xiu, X.; Li, Y. A Survey on Deep Transfer Learning and Beyond. Mathematics 2022, 10, 3619. [Google Scholar] [CrossRef]
- Ma, X.; Chang, S.; Zhan, J.; Zhang, L. Advanced Predictive Modeling of Tight Gas Production Leveraging Transfer Learning Techniques. Electronics 2024, 13, 4750. [Google Scholar] [CrossRef]
- Jia, A.; Wang, G.; Meng, D.; Guo, Z.; Ji, G.; Cheng, L. Well Pattern Infilling Strategy to Enhance Oil Recovery of Giant LowPermeability Tight Gasfield: A Case Study of Sulige Gasfield, Ordos Basin. Acta Pet. Sin. 2018, 39, 802–813. [Google Scholar]
- Wei, Q.; Yang, S.; Shi, K.; Wang, G.H.; Chen, A.Q.; Ou, J.G.; Chen, L.Y.; Diao, Y.B.; Zhou, H.L. Second Member of Shanxi Formation Tight Gas Reservoir in Su-14 Well Block of Sulige Gas Field. Mineral. Petrol. 2022, 42, 78–88. [Google Scholar] [CrossRef]
- Shi, J.; Jia, Y.; Wu, J.; Xu, F.; Sun, Z.; Liu, C.; Meng, Y.; Xiong, X.; Liu, C. Dynamic performance prediction of coalbed methane wells under the control of bottom-hole pressure and casing pressure. J. Pet. Sci. Eng. 2021, 196, 107799. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed]
- Qin, R.; Wang, Y. ImputeGAN: Generative Adversarial Network for Multivariate Time Series Imputation. Entropy 2023, 25, 137. [Google Scholar] [CrossRef] [PubMed]
- Lai, X.; Zhang, Z.; Zhang, L.; Lu, W.; Li, Z. Dynamic Graph-Based Bilateral Recurrent Imputation Network for Multivariate Time Series. Neural Netw. 2025, 186, 107298. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar] [CrossRef]
- Sakurada, M.; Yairi, T. Anomaly Detection Using Autoencoders with Nonlinear Dimensionality Reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, Gold Coast, QLD, Australia, 2 December 2014; pp. 4–11. [Google Scholar] [CrossRef]
- Saha, S.; Sarkar, J.; Dhavala, S.S.; Mota, P.; Sarkar, S. quantile-Long Short Term Memory: A Robust, Time Series Anomaly Detection Method. IEEE Trans. Artif. Intell. 2024, 5, 3939–3950. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).