A Safe In-Flight Reconfiguration Solution for UAV Swarms Based on Attraction/Repulsion Principles

Abstract

The increasing use of UAV swarms for collaborative autonomous missions presents significant challenges in coordination, safety, and scalability, especially during dynamic formation reconfigurations. This study introduces the Magnetic Swarm Reconfiguration (MSR) protocol, a fully distributed navigation method that enables UAV swarms to transition smoothly and safely between geometric formations. MSR achieves this by combining two main components: first, it employs the Hungarian algorithm to compute an optimal assignment of UAVs to target positions within the new formation, thereby minimizing trajectory overlap and interference; second, it utilizes virtual magnetic attraction and repulsion forces for real-time navigation, drawing each UAV toward its assigned destination while dynamically repelling nearby agents to avoid collisions. To evaluate the performance of the MSR protocol, six representative formation transitions were simulated across swarm sizes of up to 100 UAVs. Results show that MSR reduces reconfiguration time significantly compared to existing methods, maintains strict safety standards by achieving minimal to zero collisions, and supports fully decentralized and simultaneous maneuvering. The scalability and robustness of the MSR protocol make it suitable for complex, large-scale swarm operations requiring rapid and reliable formation changes.

1. Introduction

Unmanned Aerial Vehicles (UAVs) have witnessed significant growth in recent years, supporting a diverse array of applications that extend human capabilities in aerial monitoring and operations. While initially popular for recreational purposes such as photography, filmmaking, and content creation, UAVs are now increasingly used in commercial and industrial domains, including agriculture, topographic surveying, package delivery, thermal inspections, railway infrastructure monitoring, and search and rescue operations [1,2,3].

The growing deployment of UAVs, especially in urban environments, introduces new challenges and risks. Systems operating in such contexts must prioritize the safety of both the public and the UAVs, necessitating stringent regulations and robust collision avoidance mechanisms. Achieving the vision of a sky populated by UAVs cannot rely solely on individual units, which are limited by payload capacity, autonomy, and fault tolerance. Instead, coordinated groups of autonomous UAVs—commonly referred to as UAV swarms—offer improved resilience, adaptability, and operational efficiency for complex missions [4].

However, managing UAV swarms presents several technical challenges, including formation definition, coordinated takeoff, in-flight navigation, inter-UAV communication, swarm reconfiguration, failure recovery, and controlled landing [5]. Among these, the efficient and safe in-flight reconfiguration of swarm layouts is particularly critical, as collisions during this phase can jeopardize mission success and pose significant safety risks. A key limitation in many existing reconfiguration protocols is their reliance on vertical displacement, which increases both mission duration and energy consumption [6,7].

While reducing vertical movement improves efficiency, it also increases the likelihood of horizontal trajectory conflicts. To address this trade-off, this work builds upon the Directional Force Field Protocol (D-FFP), developed by the Computer Networks Group (GRC) at Universitat Politècnica de València, which resolves UAV trajectory conflicts using localized repulsion and attraction forces [8]. We introduce the Magnetic Swarm Reconfiguration (MSR) protocol, an adaptation of these virtual magnetic force vectors that eliminates vertical displacement during reconfiguration while maintaining robust collision avoidance. Unlike D-FFP, which focuses on independent flight paths, MSR integrates a pre-planning phase using the Hungarian algorithm to ensure an optimal assignment of UAVs to their new positions. This strategic planning minimizes overall flight distance and reduces trajectory crossings, a key innovation that complements the protocol’s distributed force fields to enable efficient and collision-free reconfiguration. MSR is designed to enable a fast, fully distributed, and collision-free reconfiguration of UAV formations.

In summary, this study presents and evaluates the MSR protocol, a novel approach that redefines swarm reconfiguration. The core contributions are twofold: (1) the strategic application of the Hungarian algorithm to achieve optimal UAV-to-target assignments, thereby minimizing trajectory interference, and (2) the adaptation of virtual magnetic attraction and repulsion forces to enable collision-free navigation without relying on vertical displacement. Extensive simulations demonstrate the effectiveness of MSR in optimizing UAV swarm reconfiguration by significantly reducing transition time, upholding stringent safety standards, and ensuring robust scalability for large swarm sizes.

The remainder of this paper is organized as follows: in the next section we present and discuss different related works. Our UAV simulation environments, ArduSim, is then presented in Section 3. Section 4 discusses previous solutions that leveraged the ArduSim framework to propose different field force protocols for collision avoidance targeting UAVs performing independent missions. Our proposed MSR protocol is presented in Section 5, including all the required technical details to gain an in-depth understanding of the protocol. Performance results are then presented in Section 6. Finally, Section 7 concludes the paper and refers to future work.

2. Related Work

UAVs have evolved from primarily military tools to widely adopted platforms in civilian domains such as logistics, agriculture, and emergency response [9]. Despite their expanding use, significant challenges persist in safely integrating UAVs into dense and dynamic environments—particularly urban airspace—due to regulatory gaps and public concerns related to privacy, security, and collision risks [10].

UAV swarms offer a promising solution by providing robust, scalable, and efficient multi-agent coordination that enhances fault tolerance and mission adaptability [11]. A critical capability currently under active research is formation reconfiguration, which involves the autonomous adjustment of swarm layouts in response to environmental or operational changes. Building upon existing coordination frameworks, this work proposes a novel approach to address these reconfiguration challenges.

Bu et al. (2024) [12] categorize UAV swarm control architectures into three main models: centralized, in which a master node directs the entire swarm; decentralized, where each UAV independently determines its position; and distributed, which emphasizes collaborative decision-making among agents during formation transitions. They further classify formation strategies into conventional and AI-based methods. Conventional techniques include leader-follower models—which are simple but susceptible to single-point failure—consensus-based methods that iteratively synchronize UAV states, and Artificial Potential Fields (APFs), which apply simulated attractive and repulsive forces for collision avoidance, and are particularly relevant to the approach in this study [13]. AI-based methods, such as Artificial Neural Networks and Deep Reinforcement Learning, provide greater adaptability to dynamic environments but often suffer from scalability limitations due to high computational requirements.

Recent advancements have specifically addressed the self-reconfiguration of modular systems in response to component failures. For instance, Gandhi et al. (2020) [14] present a technique that allows a modular flying platform to mitigate the impact of rotor failures by adapting its configuration. Their methodology, which utilizes a mixed-integer linear program and a dynamic programming algorithm, is shown to substantially increase the system’s robustness while efficiently utilizing resources. Building on this concept, Huang et al. (2025) [15] addressed a critical gap in previous research by focusing not just on the final reconfigured state, but on the practical controllability of the intermediate structures during the reassembly process. Their proposed algorithm is designed to maximize the controllability margin at each stage, leading to significant improvements in both controllability and trajectory tracking. Together, these works highlight a progressive effort to move beyond basic reconfiguration and towards more sophisticated, dynamically aware, and fault-tolerant systems.

Alqudsi and Makaraci (2025) [16] propose the Swarm Allocation and Route Generation (SARG) framework, which jointly optimizes task allocation and trajectory planning, improving upon traditional decoupled approaches. By representing each UAV as a state vector comprising position, velocity, and orientation, SARG employs the Hungarian algorithm to optimize flight distance, trajectory smoothness, and collision risk, a similar approach to the optimal assignment strategy in our proposed MSR protocol. Trajectories are further refined using minimum snap optimization, minimizing abrupt movements while respecting the UAVs’ physical constraints. Robust collision avoidance is achieved through two components: Detection to Obstacle (D2Obs), which introduces intermediate waypoints near obstacles, and Detection to Drone (D2D), a priority-based system that prevents UAV-to-UAV collisions. Combined, they are able to ensure safe mission execution.

Expanding on foundational coordination strategies, Abro et al. (2025) [17] reviewed adaptive control and route planning methods for UAV swarms, particularly in precision-critical applications such as search and rescue. Their work highlights enhancements to the leader–follower model, including the use of multiple or virtual leaders to improve fault tolerance, as well as the virtual structure approach, where UAV positions are rigidly maintained to enhance stability. More advanced strategies involve vector-based behavioral models that support individual UAV adaptability, a paradigm that underpins force-field-based navigation approaches like our proposed MSR protocol, though these approaches introduce significant challenges in mathematical modeling. For route planning, swarm members can be subdivided into subgroups coordinated using Ant Colony Optimization (ACO) and Multi-Agent Systems (MAS), with dynamic leadership mechanisms enabling rapid response to environmental changes.

Ma et al. (2025) [13] address common limitations of APF methods in multi-UAV formations—such as instability and magnetic loop entrapment—particularly in large-scale swarms. Their Distributed Swarm Architecture—Adaptive Artificial Potential Field (DSA-AAPF) framework—combines a distributed leader–follower architecture with graph theory to enable dynamic and scalable coordination. By assigning fixed offsets to follower UAVs relative to a leader, the framework achieves smooth reconfiguration without requiring global knowledge. An added inertia term reduces oscillations to enhance trajectory smoothness, while an adaptive attraction force modulates UAV speed based on target proximity and obstacle density, thereby balancing safety and efficiency.

These studies collectively illustrate the progressive refinement of UAV swarm coordination through integrated control architectures, optimization techniques, and adaptive behaviors for complex environments. Despite these significant advances, achieving highly effective and adaptable collision avoidance in dense UAV swarms, particularly without reliance on vertical maneuvers, remains a substantial challenge. While foundational force-field-based approaches, such as the Force Field Protocol (FFP) [18], offer a basis for collision prevention through omnidirectional repulsion, they often exhibit limitations in responsiveness and can lead to inefficient evasive actions. The D-FFP protocol [19] significantly improved upon this by incorporating UAV heading and velocity into its calculations, enabling earlier conflict detection, and more precise evasive maneuvers. However, applying these existing force-field methods to dense, large-scale reconfigurations still presents challenges related to inducing undesirable oscillations or their inherent reliance on vertical displacement for conflict resolution. A more detailed background on the principles of FFP and D-FFP is provided in Section 4.

Building upon these established foundations, we propose the MSR protocol, which specifically addresses these limitations by optimizing in-flight formation transitions while ensuring collision-free operation exclusively in the horizontal plane. MSR leverages a dynamic formation placement strategy (as detailed in Section 5.1), and it employs the Hungarian algorithm to compute optimal UAV-to-position assignments, minimizing both travel distance and trajectory conflicts. Its core lies in a refined collision avoidance layer, which is derived from and significantly enhanced over D-FFP’s original design, particularly through its emphasis on mobility slowdown and minimal repulsion for in-path obstacles (see Section 5.2). This integrated approach, coupled with an adaptive magnetic attraction mechanism (see Section 5.3), enables a fast, reliable, and scalable reconfiguration of large UAV swarms. In doing so, MSR represents a novel advancement in autonomous UAV swarm coordination for complex and constrained environments.

3. ArduSim Simulator

To develop, validate and assess the performance of the MSR protocol, we employed the ArduSim simulator [20], developed by the Computer Networks Group at the Universitat Politècnica de València, Spain. ArduSim provides a physics-based and realistic UAV simulation environment, incorporating key factors such as communication delays, UAV inertia, collision detection, and environmental influences including wind. It supports a variety of wireless communication models, ranging from idealized channels to realistic IEEE 802.11-based models [21], calibrated using real UAV data, and thereby enabling a comprehensive evaluation under diverse network conditions.

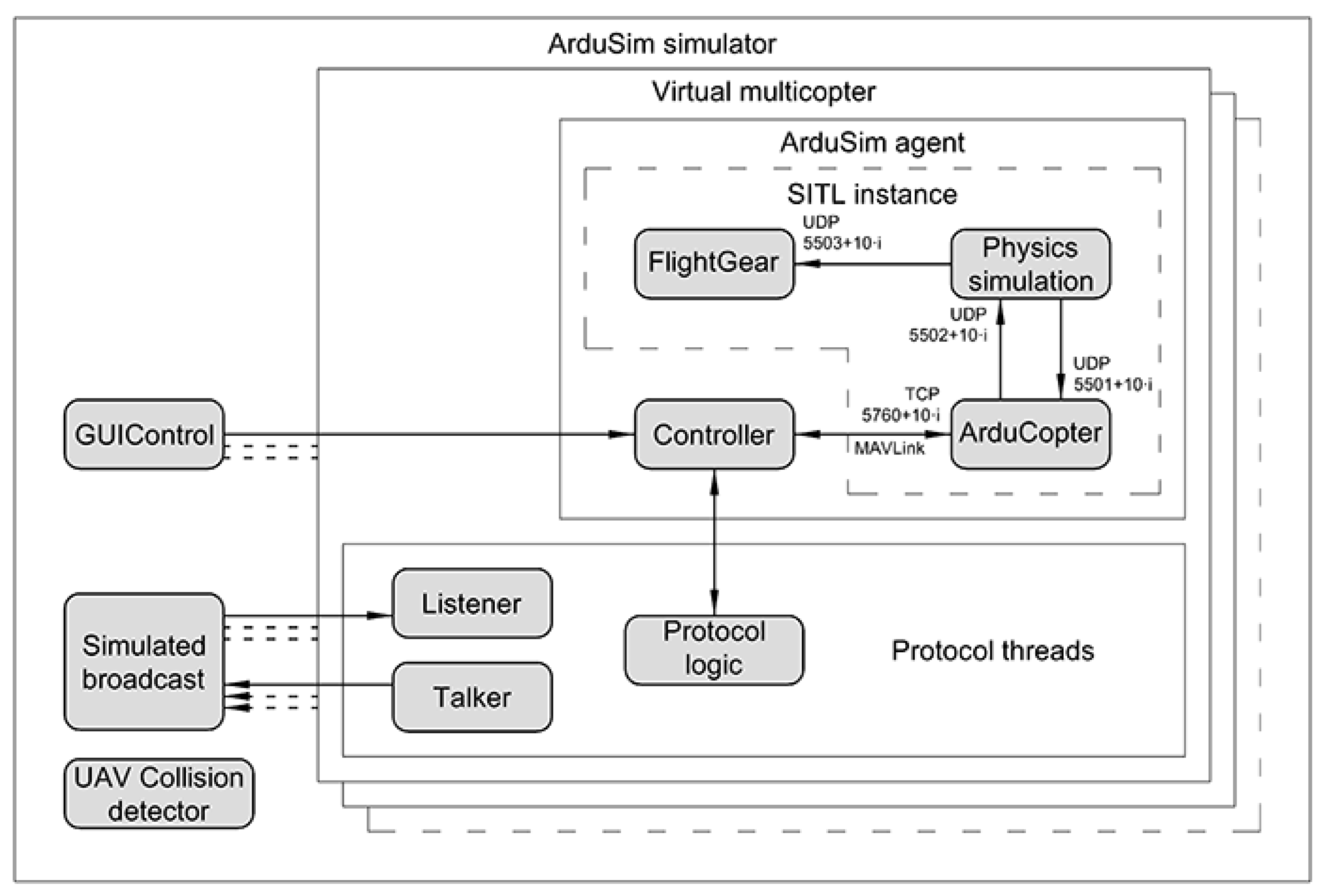
ArduSim’s modular and scalable architecture runs independent ArduCopter firmware instances for each UAV, managed through dedicated threads. This design supports the simulation of swarms of up to 256 UAVs (depending on hardware capabilities), facilitating the robust testing of scalability and coordination protocols. Additionally, ArduSim offers extensive data logging features, exporting detailed mission data—including UAV trajectories, network states, collision events, and computational performance metrics, being compatible with detailed wireless simulation tools such as OMNeT++ and NS2. A critical advantage of ArduSim is its support for seamless transition from simulation to real-world deployment: the same protocol code tested in simulation can be directly executed on physical UAVs equipped with Pixhawk controllers merely by adjusting a runtime parameter. This capability eliminates the need for code rewriting and significantly accelerates swarm mission development and validation.

Architecture Overview

ArduSim employs a modular architecture designed to support realistic and scalable UAV swarm simulation. At its core lies the SITL (Software In The Loop) component from the ArduPilot ecosystem [22], which runs the ArduCopterfirmware [23] version 3.5.7 to emulate real-world UAV dynamics. Since each SITL instance simulates a single UAV, multiple parallel processes must be launched to simulate a swarm, thus introducing challenges for implementing inter-UAV communication.

To address this, ArduSim integrates a distributed multi-agent control layer. Each UAV is managed by an agent composed of several concurrent threads: the Talker and Listener threads manage outbound and inbound communication, respectively; the Protocol Logic thread executes swarm coordination rules; and the Controller thread interfaces with SITL to issue control commands and retrieve telemetry data.

This architecture enables efficient simulation of swarm protocols, including collision avoidance, inter-agent communication, and dynamic path adaptation. Simulations can be configured and managed either through a graphical user interface (GUI) or a command-line interface, the latter of which supports automated testing workflows.

Figure 1 illustrates ArduSim’s multi-agent system architecture and its interaction with SITL processes to enable coordinated swarm behavior.

4. Background on Force Field Methods and Optimal Assignment

The MSR protocol builds upon established concepts in swarm robotics, particularly those derived from the FFP [18] and its successor, the D-FFP [19]. These protocols introduce the concept of virtual magnetic fields as a decentralized and reactive mechanism for UAV swarm navigation and collision avoidance.

4.1. Force Field Protocol (FFP)

Introduced by Wubben et al. [18], FFP operates on the principle of artificial potential fields, where each UAV navigates by responding to two primary types of virtual forces:

• Attraction Force: Guides the UAV towards its assigned target waypoint. Its magnitude dynamically decreases as the UAV approaches the target, ensuring a smooth and controlled arrival without overshooting.
• Repulsion Force: Pushes the UAV away from potential obstacles, including other UAVs. Each nearby obstacle generates a repulsive force inversely proportional to distance, intensifying significantly as collision proximity increases. In FFP, repulsion is weighted more heavily than attraction to prioritize safety.

At each time step, these attraction and repulsion vectors are combined to form a resultant motion vector, dictating the UAV’s immediate direction and speed. FFP operates without centralized control, with each drone making autonomous decisions based on local information from nearby swarm members. A key characteristic of the original FFP is its omnidirectional repulsion, meaning UAVs react to obstacles solely based on distance, irrespective of their relative velocity or collision course. This can sometimes lead to unnecessary evasive maneuvers.

4.2. Directional Force Field Protocol (D-FFP)

As an evolution of FFP, D-FFP was introduced by Arenillas et al. [19] to enhance collision avoidance by incorporating a directional component into the repulsion field. Unlike FFP’s omnidirectional approach, D-FFP focuses the repulsive forces primarily along a UAV’s intended direction of movement. Key improvements include the following:

• Directional Repulsion: Repulsion strength is calculated based on both distance and the obstacle’s angular position relative to the UAV’s heading, ensuring stronger forces for obstacles directly in the path or on a collision course.
• Relative Threat Assessment: D-FFP considers the relative orientations of both the drone and the obstacle to ensure robust mutual avoidance.
• Refined Repulsion Function: The repulsion vector combines distance-based scaling with an angle-based directional modifier, minimizing unnecessary evasive maneuvers for obstacles outside a defined cone of influence.
• Short-Range Safety Override: A minimal, short-range omnidirectional repulsion is retained as a critical last-resort safeguard for extremely close encounters.
• Vertical Maneuver Dampening: A correction to the vertical repulsion component helps to maintain the desired altitudes and prevent erratic vertical movements.

By being directionally aware, D-FFP significantly reduces unnecessary evasive actions, leading to smoother trajectories, improved efficiency, and enhanced scalability for UAV swarms compared to its predecessor. However, fully leveraging this directional capability to maximize efficiency and minimize mission time while completely eliminating vertical maneuvers during complex in-flight reconfigurations introduces additional complexity and, hence, represents a challenge to be addressed by the MSR protocol.

4.3. Optimal Position Assignment: The Hungarian Algorithm

Beyond the reactive force field mechanisms, optimal planning is crucial for efficient swarm reconfiguration, especially in assigning target positions to individual UAVs. For this purpose, the MSR protocol leverages the Hungarian Algorithm [24]. This is a combinatorial optimization algorithm that solves the assignment problem in polynomial time. By design, the Hungarian Algorithm guarantees a globally optimal solution for the linear assignment problem. In the context of UAV swarm reconfiguration, it is used to determine the most efficient one-to-one mapping between the current positions of the UAVs and their designated target positions within the new formation.

The algorithm works by minimizing the total cost of the assignment, where the cost between a UAV and a target position is typically defined as the Euclidean distance. By computing this optimal assignment prior to initiating movement, the Hungarian Algorithm significantly reduces the aggregate travel distance for the entire swarm. Hence, this strategic pre-planning seeks to minimize the total displacement for the entire swarm, which is the primary objective of the algorithm in our study. As an additional advantage, the strategic pre-planning also minimizes unnecessary trajectory crossings and potential conflicts, thereby enhancing the overall efficiency and safety of the reconfiguration process before the dynamic force field interactions even begin.

5. The Magnetic Swarm Reconfiguration (MSR) Protocol

Building upon the foundational principles of virtual force fields, the MSR protocol is a distributed and real-time framework engineered for the autonomous control and dynamic repositioning of UAV swarms. Its objective is to efficiently and safely guide a collection of UAVs from a flight formation to another. MSR distinguishes itself by empowering each UAV to autonomously plan its movement and react to its immediate environment, eliminating the need for centralized control. This decentralized architecture enhances scalability and robustness in complex operational scenarios. The protocol orchestrates each UAV’s mission through a clearly defined sequence of operational states: Initialization, Moving, Hovering, and Landing. While the complete protocol includes takeoff and landing sequences, this paper focuses specifically on the in-flight reconfiguration process. Following the initial assignment of a target position, UAVs transition into the MOVING state, which is the core of the reconfiguration process. In this state, each drone continuously calculates and applies its resultant movement vector. This vector is dynamically derived from two primary, interacting forces: repulsion forces for collision avoidance and attraction forces pulling the UAV towards its assigned target. This phase integrates a sophisticated adaptive collision avoidance system that reduces a UAV’s forward speed when threats are detected, prioritizing safety. Upon reaching its final position, a UAV transitions to the HOVERING state, communicating a ready status. The entire swarm waits for all members to reach this state, ensuring collective synchronization for the new formation’s integrity.

5.1. Formation Creation and Optimal Position Assignment

The initial phase of MSR’s detailed operation focuses on intelligently defining the new formation and optimally assigning each UAV to a specific target position within it. This process is a cornerstone of the protocol, ensuring an efficient and coordinated transition from an arbitrary initial arrangement to the desired user-defined configuration.

5.1.1. Formation Definition and Instantiation

The process begins with each UAV accessing user-defined parameters that specify the desired formation type (e.g., LINEAR, MATRIX, or CIRCLE), and the precise spacing required between individual drones. Based on these parameters, an internal Formation object is instantiated. This object essentially generates a geometric blueprint of the new desired shape, complete with placeholder coordinates for each drone that will comprise the swarm’s final arrangement.

5.1.2. Dynamic Formation Placement

To optimize overall movement efficiency and minimize displacement, the new formation is not placed at a fixed, predetermined point in space. Instead, MSR implements a dynamic placement strategy: the geographic center of the new formation is intelligently calculated as the average coordinates of all UAVs in their current positions. Specifically, the center of the new formation is computed as the average of the individual coordinates of all UAVs in the swarm. This ensures that the reconfiguration effectively happens around the existing swarm, significantly reducing the total distance the drones need to travel. This calculated center then serves as the anchor point from which the exact target coordinates for each individual drone within the new formation are generated.

5.1.3. Optimal Drone-to-Position Assignment

Perhaps the most critical aspect of the reconfiguration process is deciding precisely which drone goes to which specific spot in the new formation. MSR addresses this as an optimal assignment problem, employing the renowned Hungarian algorithm to find the minimum-cost matching between the set of available UAVs and the set of target positions. The cost function for this assignment is ingeniously defined to ensure both efficiency and smooth trajectories. It includes two primary components. First, the Euclidean distance accounts for the direct spatial distance between the UAV’s current position and its potential target position. Second, an angular penalty is applied if the UAV’s current heading significantly deviates from the ideal direction needed to reach that target. This component ensures that the algorithm prioritizes assignments that facilitate smoother, more natural flight paths, thereby minimizing awkward turns and sudden directional changes. A configurable parameter, angleWeight, allows for tuning the influence of this angular prioritization.

For a UAV i at current position $P_i=(x_i,y_i,z_i)$ with a current heading (yaw) angle ${\theta }_i$, and a target position $T_j=(t_x,t_y,t_z)$, the assignment cost $C_{ij}$ is computed as follows:

$$C_{ij}=D(P_i,T_j)+W_A·A(P_i,T_j,{\theta }_i)$$

(1)

where

• $D(P_i,T_j)$ is the 3D Euclidean distance between $P_i$ and $T_j$:

  $$D(P_i,T_j)=\sqrt{{(t_x-x_i)}^2+{(t_y-y_i)}^2+{(t_z-z_i)}^2}$$

  (2)
• $W_A$ is the angular weighting factor (corresponding to the angleWeight parameter in the implementation).
• $A(P_i,T_j,{\theta }_i)$ is the angular penalty (in radians), representing the angle between the UAV’s current 2D heading vector $(cos{\theta }_i,sin{\theta }_i)$ and the 2D vector from $P_i$ to $T_j$. Let $dx=t_x-x_i$ and $dy=t_y-y_i$. The angular penalty is calculated as follows:

  $$A(P_i,T_j,{\theta }_i)=arccos\left({\displaystyle \frac{dx·cos{\theta }_i+dy·sin{\theta }_i}{\sqrt{d{x}^2+d{y}^2}}}\right)$$

  (3)
  The result is clamped between $-1$ and 1 to prevent numerical errors.

The algorithm constructs a cost matrix incorporating these combined distance and angular costs for every possible UAV-to-target pair. It then iteratively processes this matrix to identify and establish the optimal assignments, ensuring the lowest possible total reorganization cost for the entire swarm.

5.1.4. Waypoint Generation

Once the Hungarian algorithm has provided the optimal assignment—specifying which target position each drone should aim for—this assignment is translated into a sequence of waypoints for each individual UAV to follow. The strategy for generating these waypoints depends on the geometry of the selected formation:

• For LINEAR formations, a two-waypoint strategy is utilized. Each UAV is directed first to an intermediate waypoint, and then directly to the final target. Specifically, for a UAV i at $(x_i,y_i,z_i)$ assigned to a final target position $T_j=(t_x,t_y,t_z)$, the intermediate waypoint $W_{int}$ is calculated as $(t_x,y_i,Z_{target\_altitude})$. This approach causes the UAV to first align its X-coordinate with the target before moving towards its final Y- and Z-coordinates, promoting predictable, perpendicular movements that reduce collision risks.
• For non-LINEAR formations (e.g., MATRIX, CIRCLE), a simpler single-waypoint strategy is generally employed, where the UAV proceeds directly to its assigned final position. This is based on the assumption that positions in such formations are typically sufficiently spaced to not require complex intermediate paths.

It is important to note that for all formation types, UAVs reconfigure to a common target altitude ($Z_{target\_altitude}$) defined for the new formation, which simplifies vertical coordination.

The use of waypoints, rather than simply commanding a direct flight to the final destination, offers finer control over movement and provides discrete targets that the real-time collision avoidance system can use for navigation. This decentralized planning allows each UAV to move towards its destination without the need for explicit, continuous coordination regarding its assignment, simplifying the protocol’s architecture and enhancing its scalability.

5.2. Collision Avoidance in MSR

During swarm reconfiguration, ensuring collision-free navigation is paramount, especially in dense environments, or when transitioning into compact formations. The MSR protocol addresses this challenge with a sophisticated, distributed collision avoidance mechanism built upon a virtual magnetic force system that dynamically adjusts each UAV’s movement. This system extends the principles of the Directional Force Field Protocol (D-FFP) by integrating and refining two types of repulsion forces, complemented by a unique adaptive slowdown factor.

5.2.1. Dual Repulsion Fields

The Multi-Swarm Reconfiguration (MSR) protocol employs a nuanced repulsion mechanism that differentiates between general containment and specific in-path threat mitigation. This is achieved through the use of a dual-repulsion field system. The first component is an omnidirectional magnetic field, which functions as a primary, strong containment barrier for dangerously close encounters. It applies a robust, quadratically decaying repulsive force whenever any obstacle, such as another UAV, comes within a defined radius. The purpose of this omnidirectional repulsion is to prevent collisions by pushing drones away irrespective of their relative orientation to the obstacle. The force magnitude is at its maximum when the obstacle is at or below the minimum safety distance, and it smoothly diminishes to zero as the distance approaches the outer boundary of its effective range.

The magnitude of this omnidirectional repulsive force $F_{\mathrm{omni}}$ between a UAV and an obstacle, based on their current distance d, is defined as follows:

$$F_{\mathrm{omni}}\left(d\right)=\left\{\begin{array}{cc}{F}_{\max }\hfill & \mathrm{if}d\le d_{min}\hfill \\ F_{\max }·\left(1-{\left({\displaystyle \frac{d-d_{min}}{d_{\mathrm{omni}}-d_{min}}}\right)}^2\right)\hfill & \mathrm{if}{d}_{min}<d\le d_{\mathrm{omni}}\hfill \\ 0\hfill & \mathrm{if}d>d_{\mathrm{omni}}\hfill \end{array}\right.$$

(4)

where

• d: current distance between the UAV and the obstacle.
• $d_{min}$: minimum safety distance.
• $d_{\mathrm{omni}}$: maximum omnidirectional repulsion radius.
• $F_{\max }$: maximum repulsion intensity.

Directional Magnetic Field (MSR’s Adaptation)

In contrast to the omnidirectional field, the directional magnetic field specifically targets obstacles located in the UAV’s forward path. A crucial distinction in MSR, unlike prior D-FFP implementations, is that this field applies no direct repulsion when obstacles are at or below the minimum safe distance. Its primary role is to subtly influence the UAV’s path and, more importantly, to trigger a speed reduction (slowdown) when an obstacle is within its detection range and angular cone of influence. This modification is critical for dense swarm operations, as strong/abrupt evasive maneuvers could, otherwise, cause detrimental rebound effects or a cascading chain of deflections, disrupting the overall formation transition, thereby reducing efficiency. The strength of the directional force is sensitive to both the distance to the obstacle and its angular position relative to the UAV’s heading, exerting its strongest influence when an obstacle is directly ahead, and smoothly decaying as the angle increases.

The magnitude of this directional repulsive force $F_{\mathrm{dir}}$ between a UAV and an obstacle, based on their current distance d, and the angle $\theta$ between the UAV’s heading and the vector towards the obstacle, is defined as follows:

$$F_{\mathrm{dir}}(d,\theta )=\left\{\begin{array}{cc}0\hfill & \mathrm{if}d>d_{\mathrm{dir}}\hfill \\ 0\hfill & \mathrm{if}cos\left(k·\theta \right)\le 0\hfill \\ F_{\max \_\mathrm{dir}}·\left(1-{\left({\displaystyle \frac{d-d_{min}}{d_{\mathrm{dir}}-d_{min}}}\right)}^2\right)·cos\left(k·\theta \right)\hfill & \mathrm{if}{d}_{min}<d\le d_{\mathrm{dir}}\mathrm{and}cos\left(k·\theta \right)>0\hfill \\ 0\hfill & \mathrm{if}d\le d_{min}\hfill \end{array}\right.$$

(5)

where

• d: current distance between the UAV and the obstacle.
• $\theta$: angle between the UAV’s current heading and the vector from the UAV towards the obstacle.
• $F_{\max \_\mathrm{dir}}$: maximum intensity of the directional force.
• $d_{\mathrm{dir}}$: maximum range of the directional field.
• $d_{min}$: minimum safe distance.
• k: angular amplification parameter.

5.2.2. Adaptive Slowdown Mechanism

Working in tandem with the direct repulsion forces, MSR incorporates an adaptive slowdown mechanism that progressively reduces the UAV’s forward speed. This slowdown factor is dynamically calculated based on the obstacle’s proximity and its alignment with the UAV’s heading, exerting its strongest effect when obstacles are close and directly in front. The purpose of this anticipatory braking is to enable smooth, controlled deceleration, allowing the UAV to reduce speed before entering a high-risk zone. This preemptive response provides more time and room to act for the repulsion forces if a direct collision becomes unavoidable, thereby ensuring smoother and safer evasive maneuvers.

For each detected obstacle, the current slowdown factor is updated multiplicatively. The reduction in speed is inversely proportional to the obstacle’s distance and directly proportional to its angular alignment with the UAV’s heading, ensuring that threats directly in front and closer by cause a more significant speed reduction. The slowdown update rule for each obstacle is given by the following:

$${\mathrm{slowdown}}_{\mathrm{new}}={\mathrm{slowdown}}_{\mathrm{current}}·\left(1-0.5·\left(1-{\displaystyle \frac{d}{d_{\mathrm{dir}}}}\right)·cos\left(\theta \right)\right)$$

(6)

where

• ${\mathrm{slowdown}}_{\mathrm{current}}$: The current accumulated slowdown factor from previously evaluated obstacles (initial value is 1.0).
• d: The distance to the current obstacle.
• $d_{\mathrm{dir}}$: The radius of the directional field.
• $\theta$: The angle between the UAV’s direction of movement and the vector toward the current obstacle.
• $S_k$: A scaling constant (usually 0.5) that determines the aggressiveness of the slowdown.

This iterative reduction ensures that the UAV’s speed is prudently managed based on the cumulative threat landscape, allowing for smoother and safer reconfigurations, especially in densely populated scenarios.

5.2.3. Local Calculation and Finalization of Forces

All repulsion and slowdown calculations are performed locally by each UAV. This decentralized computation utilizes real-time information about neighboring drones, obtained through the communication thread, ensuring reactive, distributed, and robust control within dynamic environments.

Once calculated, the summed repulsion vector undergoes two final adjustments:

• Scaling: The combined repulsion vector is scaled by a weightRepulsion parameter, allowing for the global tuning of the overall influence of the repulsion field relative to other forces in the protocol.
• Magnitude Limit: A critical upper limit is applied to the magnitude of the total repulsion vector. This threshold is typically defined as a percentage of the UAV’s maxSpeed, preventing the force from exceeding a safe boundary. This procedure ensures that the repulsion force does not cause overly abrupt movements or excessive accelerations that could destabilize the UAV.

Finally, the result of these computations is both the processed total accumulated repulsion vector and the refined slowdown factor (with a minimum bound to ensure the UAV never completely stops due to slowdown alone). In essence, MSR’s collision avoidance is a sophisticated, multi-layered system that judiciously balances aggressive repulsion for immediate threats with subtle, anticipatory speed adjustments for forward-facing obstacles. This distributed, adaptive approach is paramount for achieving safe, smooth, and efficient reconfigurations in dynamic, dense UAV swarm environments.

5.3. Magnetic Attraction in MSR

Beyond merely avoiding obstacles, the MSR protocol incorporates a robust magnetic attraction component responsible for precisely guiding each UAV towards its assigned target position within the new formation. This mechanism is not simply about defining a direction; it intelligently modulates the UAV’s speed to ensure both efficient movement and continuous safety throughout the reconfiguration process.

5.3.1. Target Direction: The Attraction Vector Base

The initial step in generating the attraction force involves determining the precise direction of movement. Each UAV calculates a vector pointing directly from its current geographical position to its immediate target waypoint (the next point in its planned trajectory towards the final formation position). This vector is then normalized to obtain only its direction, establishing the fundamental axis of movement without yet specifying a speed magnitude. This ensures the UAV consistently orientates itself towards its objective.

If a UAV is at the current position ${\overrightarrow{P}}_{\mathrm{current}}$, and its immediate target waypoint is ${\overrightarrow{W}}_{\mathrm{target}}$, the normalized attraction vector ${\widehat{V}}_{\mathrm{attraction}}$ is calculated as follows:

$${\widehat{V}}_{\mathrm{attraction}}={\displaystyle \frac{{\overrightarrow{W}}_{\mathrm{target}}-{\overrightarrow{P}}_{\mathrm{current}}}{\parallel {\overrightarrow{W}}_{\mathrm{target}}-{\overrightarrow{P}}_{\mathrm{current}}\parallel }}$$

(7)

5.3.2. Adaptive Speed Calculation

The UAV’s forward speed is not a fixed value but is rather dynamically adjusted based on the prevailing environmental conditions and its proximity to the target. This adaptive approach ensures optimal performance in diverse scenarios, involving a sequence of adjustments:

1.

Counting nearby neighbors: The protocol continuously monitors the number of neighboring UAVs (n) within a defined radius, which provides an estimate of the local density.

2.

Adaptive maximum speed ($V_{\mathrm{adapt}}$): If there are no nearby obstacles ($n=0$) and the target is far away (e.g., beyond a predefined threshold $D_{\mathrm{far}\_\mathrm{target}}$), the UAV is allowed to slightly exceed the configured maximum speed ($V_{\max }$) by 20% to speed up the transition. This adaptive speed is calculated as follows:

$$V_{\mathrm{adapt}}=\left\{\begin{array}{cc}1.2·V_{\max }\hfill & \mathrm{if}n=0\mathrm{and}d>D_{\mathrm{far}\_\mathrm{target}}\hfill \\ V_{\max }\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

where d is the current distance to the target waypoint, and $D_{\mathrm{far}\_\mathrm{target}}$ represents a distance threshold defining a ’far’ target.

3.

Adjustment based on the number of neighbors ($V_{\mathrm{neighbors}}$): The higher the local drone density, the lower the fraction of adaptive speed allowed. This adjustment helps reduce local congestion and prevent abrupt movements, being calculated as follows:

$$V_{\mathrm{neighbors}}=\left\{\begin{array}{cc}{V}_{\mathrm{adapt}}\hfill & \mathrm{if}n=0\hfill \\ 0.75·V_{\mathrm{adapt}}\hfill & \mathrm{if}1\le n\le 4\hfill \\ 0.5·V_{\mathrm{adapt}}\hfill & \mathrm{if}5\le n\le 8\hfill \\ 0.3·V_{\mathrm{adapt}}\hfill & \mathrm{if}n>8\hfill \end{array}\right.$$

(9)

The selection of thresholds in the $V_{neighbors}$ equation is based on empirical observations of swarm behavior under various formation patterns. During simulation experiments in ArduSim, it was noted that drones typically have a small number of neighbors (1 to 4) in sparse formations such as lines or circles, allowing for relatively high speeds without increasing the risk of collision. However, in denser configurations like matrices, the number of nearby drones increases, requiring a more cautious speed profile. As a result, the selected ranges reflect three levels of local density: low (1–4 neighbors), medium (5–8), and high (>8), with progressively stricter speed limitations (0.75, 0.5, and 0.3 times the adaptive speed, respectively). These thresholds were not chosen arbitrarily but rather tuned through extensive testing to strike a balance between smooth navigation and overall reconfiguration efficiency.

4.

Final distance-based limit ($V_{\mathrm{distance}\_\mathrm{limit}}$): Even if there are not many neighbors, if the target is close, the protocol limits the speed to avoid abrupt arrivals. This limitation acts as a final smoothing, ensuring precise arrival:

$$V_{\mathrm{distance}\_\mathrm{limit}}=\left\{\begin{array}{cc}0.05·V_{\mathrm{adapt}}\hfill & \mathrm{if}d\le 7\mathrm{m}\hfill \\ 0.10·V_{\mathrm{adapt}}\hfill & \mathrm{if}7<d\le 15\mathrm{m}\hfill \\ 0.15·V_{\mathrm{adapt}}\hfill & \mathrm{if}15<d\le 30\mathrm{m}\hfill \\ 0.30·V_{\mathrm{adapt}}\hfill & \mathrm{if}30<d\le 50\mathrm{m}\hfill \\ V_{\mathrm{neighbors}}\hfill & \mathrm{if}d>50\mathrm{m}\hfill \end{array}\right.$$

(10)

Here, d is the current distance to the target waypoint.

The distance thresholds defined in the $V_{distance\_limit}$ function were derived from dynamic patterns observed during simulation testing. The 7-meter threshold marks a critical settling zone, whereby any abrupt movement can lead to overshooting or oscillatory corrections. For this reason, a minimal speed (5% of $V_{adapt}$) is enforced. The intermediate zones (30–50 m, 15–30 m, and 7–15 m) represent progressively slower approach stages, designed to anticipate braking and ensure smooth convergence to the final destination. These values emerged from repeated observations in which UAVs tended to decelerate too late or exhibit unstable adjustments, particularly in high-density conditions. Beyond 50 m, the UAV is still considered in the cruise phase, and its speed is governed solely by the local density control (as defined in Equation (3)). This hybrid mechanism ensures both global efficiency and local precision in the final stages of swarm reconfiguration.

5.3.3. Final Speed Adjustments

Before the final movement command is issued, two additional critical adjustments are applied to the calculated speed to further enhance trajectory smoothness and safety:

• Slowdown due to Directional Repulsion: The slowdownFactor, computed by the collision avoidance system based on the presence of frontal obstacles, is directly applied to the UAV’s current speed. This provides an anticipatory braking response to potential head-on collisions, effectively reducing the UAV’s forward velocity when a threat is detected in its path. If $V_{\mathrm{current}}$ is the speed from previous calculations, the speed after this adjustment is $V_{\mathrm{current}}·\mathtt{slowdownFactor}$.
• Smoothing by Proximity to the Target: When the UAV is very close to its destination—specifically, when the current distance to the target d is less than a defined threshold—its speed is reduced proportionally to the remaining distance. This is achieved by scaling the current speed $V_{\mathrm{current}}$ by the ratio of d to a smoothingRadius, defined as $1.5\times \mathrm{threshold}$. This mechanism ensures a progressive deceleration during the final approach, enabling a gentle and precise arrival:

  $$V_{\mathrm{smoothed}}=\left\{\begin{array}{cc}{V}_{\mathrm{current}}·\left({\displaystyle \frac{d}{1.5·\mathrm{threshold}}}\right),\hfill & \mathrm{if}d<\mathrm{threshold},\hfill \\ V_{\mathrm{current}},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

  (11)
  A minimum speed of 0.05 is typically enforced to prevent complete stoppage until the target is reached.

The magnetic attraction system of the MSR protocol serves as a sophisticated, multi-layered speed controller, ensuring UAVs move purposefully towards their targets. It dynamically accelerates when paths are clear and gracefully decelerates when congested or approaching the destination. Critically, as a final safety check, MSR employs an Attraction–Repulsion Balancing mechanism: if the total calculated repulsion force indicates an immediate collision risk, the UAV’s attraction towards its target is actively penalized or reduced. This strategic override prioritizes safety by preventing UAVs from pushing through high-repulsion zones, effectively balancing goal-seeking behavior with robust collision prevention for safe, smooth, and efficient reconfigurations in dynamic, dense swarm environments.

6. Results and Analysis

6.1. Scenarios and Metrics

This section validates the MSR protocol, evaluating its capacity to guide UAV swarms through formation transitions efficiently, scalably, and without collisions. Experiments involved diverse geometric reconfigurations and varying swarm sizes (10 to 100 UAVs) to assess scalability. The six distinct reconfiguration scenarios for 50 UAVs are graphically represented in Figure 2, where blue dots indicate initial UAV positions, red dots mark final positions, and grey lines show individual planned trajectories computed via optimal assignment to minimize interference. Key performance metrics include the following: (i) total reconfiguration time, defined as the duration from the moment the first UAV begins its movement until the last UAV reaches its assigned target position and stabilizes within the new formation, and (ii) detected collisions. The analysis also examines the influence of the MSR protocol parameters and presents comparisons with previous versions of the protocol.

6.2. Tuning and Optimal Parameters

To ensure optimal performance and safe operation across diverse reconfiguration scenarios, the core parameters of the MSR protocol were carefully tuned. This iterative process aimed to balance the efficiency of movement towards targets with robust collision avoidance, specifically by minimizing the total reconfiguration time while rigorously ensuring zero or minimal detected collisions. This multi-objective approach allowed us to adapt the parameters to the unique challenges of each formation transition. The optimal parameter values determined for each of the six evaluated scenarios following a thorough experimentation are summarized in

Table 1. Optimal MSR protocol parameters for each reconfiguration scenario.

Scenario	Attraction Weight	Repulsion Weight	Dir. Field Det. Radius (m)	Dir. Force Magnitude	Omni. Field Trigger (m)	Omni. Force Magnitude	Dir. Factor	General Det. Radius (m)	Base Speed (m/s)
CIRCLE → LINEAR	1.0	1.1	N/A	0.5	N/A	N/A	2	40	10
CIRCLE → MATRIX	0.6	1.4	60	0.85	30	3.2	2	58	8
LINEAR → CIRCLE	0.75	1.2	55	0.7	30	2.8	2	52	12
LINEAR → MATRIX	0.70	1.5	55	0.85	28	3.2	2	58	8
MATRIX → CIRCLE	0.8	1.2	50	0.7	25	3.0	3	25	15
MATRIX → LINEAR	0.75	1.2	55	0.7	30	2.8	2	55	12

, along with their rationale.

• where

• Attraction Weight: Scalar multiplier for the magnetic attraction force, influencing movement towards the target.
• Repulsion Weight: Scalar multiplier for the magnetic repulsion force, influencing collision avoidance.
• Dir. Field Det. Radius (m): (Directional Field Detection Radius)—Distance at which directional repulsion starts to apply.
• Dir. Force Mag.: (Directional Force Magnitude)—Strength of the directional repulsion force.
• Omni. Field Trigger (m): (Omnidirectional Field Trigger)—Distance at which omnidirectional repulsion is activated for immediate threats.
• Omni. Force Mag.: (Omnidirectional Force Magnitude)—Strength of the omnidirectional repulsion force.
• Dir. Factor: (Directional Factor)—Parameter influencing the shape or intensity distribution of the directional field.
• General Det. Radius (m): (General Detection Radius)—Overall maximum distance for detecting other UAVs.
• Base Speed (m/s): The nominal flight speed of the UAVs in meters per second.

6.3. Performance Analysis

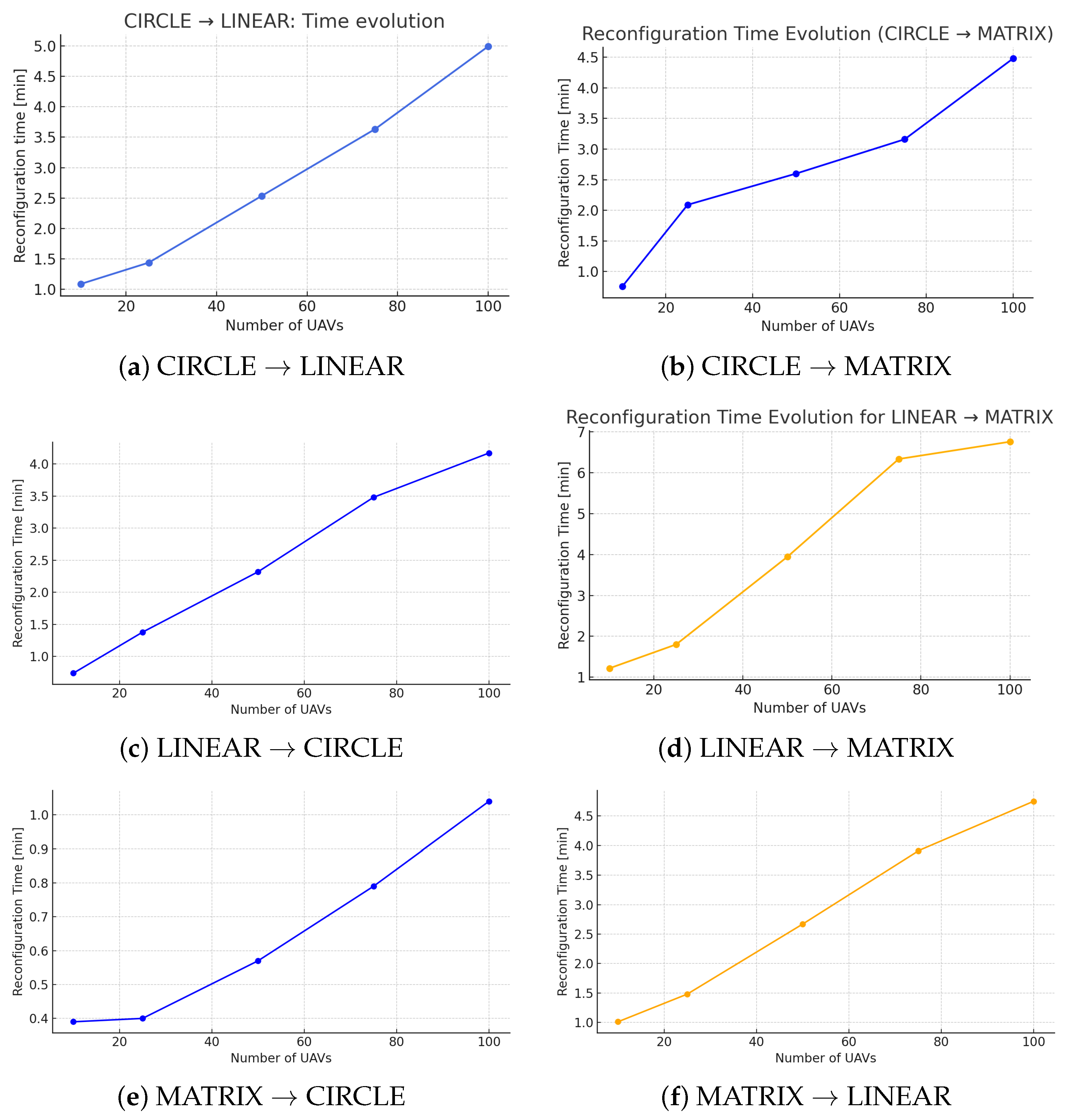
This section presents a comprehensive analysis of the MSR protocol’s performance across all evaluated scenarios and swarm sizes, focusing on reconfiguration time. Instead of individual figures for each transition, Figure 3 consolidates the reconfiguration time data, allowing for a direct comparison of scalability and efficiency across all six geometric transformations.

The results consistently demonstrate the scalable and efficient behavior of the MSR protocol across various formation reconfiguration scenarios. A clear upward trend in reconfiguration time is observed as the number of UAVs increases. While most scenarios exhibit a moderately linear progression, transitions like LINEAR → MATRIX show a more pronounced non-linear growth, particularly beyond 50 UAVs. This non-linearity is attributed to the higher trajectory density and increased coordination complexity when converging towards compact formations, demanding careful reorganization in the final phase. It is important to note that the core optimal assignment problem within the MSR protocol, solved by the Hungarian algorithm, has a well-established computational complexity of $O\left(N^3\right)$, where N is the number of UAVs. This theoretical cubic growth aligns with the observed non-linear trends in high-density scenarios, indicating that the assignment phase would become the primary computational bottleneck for swarms significantly larger than 100 UAVs. Future research could explore parallelizable assignment algorithms to push the scalability limits beyond this point.

Analyzing the specific transitions, scenarios involving expansion from dense formations, such as MATRIX → CIRCLE, consistently achieve the lowest reconfiguration times, showing an almost linear growth even up to 100 UAVs. This efficiency is due to the natural dispersion of UAVs, which inherently reduces conflict zones and allows for simultaneous, bottleneck-free execution. Conversely, transitions leading to more compact or constrained formations, like LINEAR → MATRIX, generally require longer reconfiguration times due to increased trajectory overlap and the need for intricate avoidance maneuvers. The MATRIX → LINEAR transition, despite its high initial density and convergence towards a single axis, maintains a moderately linear progression owing to a double waypoint strategy that aids in temporal and spatial spacing, thereby reducing interference.

A critical aspect of multi-UAV system performance is collision avoidance. As detailed in Section 6.1, simulations were configured to terminate upon the first detected collision to provide a conservative assessment of the MSR protocol’s safety mechanisms.

Table 2. Summary of detected collisions per scenario and swarm size.

Scenario	10 UAVs	25 UAVs	50 UAVs	75 UAVs	100 UAVs
CIRCLE → LINEAR	0	0	0	0	0
CIRCLE → MATRIX	0	0	0	0	0
LINEAR → CIRCLE	0	0	1	0	0
LINEAR → MATRIX	0	0	0	0	0
MATRIX → CIRCLE	0	0	0	0	0
MATRIX → LINEAR	0	0	0	1	1

presents a comprehensive summary of detected collisions for all evaluated scenarios across various swarm sizes.

The effectiveness of MSR’s magnetic collision avoidance mechanism is robustly confirmed. Across the large majority of simulated cases, the number of collisions remained at zero, confirming the effectiveness of the magnetic repulsion even in scenarios with high trajectory density or converging paths. The few instances of recorded collisions (one for 50 UAVs in LINEAR → CIRCLE, and one each for 75 and 100 UAVs in MATRIX → LINEAR) were minimal relative to the total number of trajectories. These isolated incidents occurred in complex convergence situations involving high initial density or high risk of trajectory overlap, highlighting inherent challenges rather than systemic failures. This remarkable collision-free performance, achieved without relying on vertical separation or angular sectorization, underscores MSR’s capability to safely manage complex swarm movements. The judicious selection of MSR’s tuning parameters, as detailed in Section 6.2, was instrumental in balancing efficient movement with robust collision avoidance, adapting the magnetic field magnitudes and detection radii to the specific demands of each transition type.

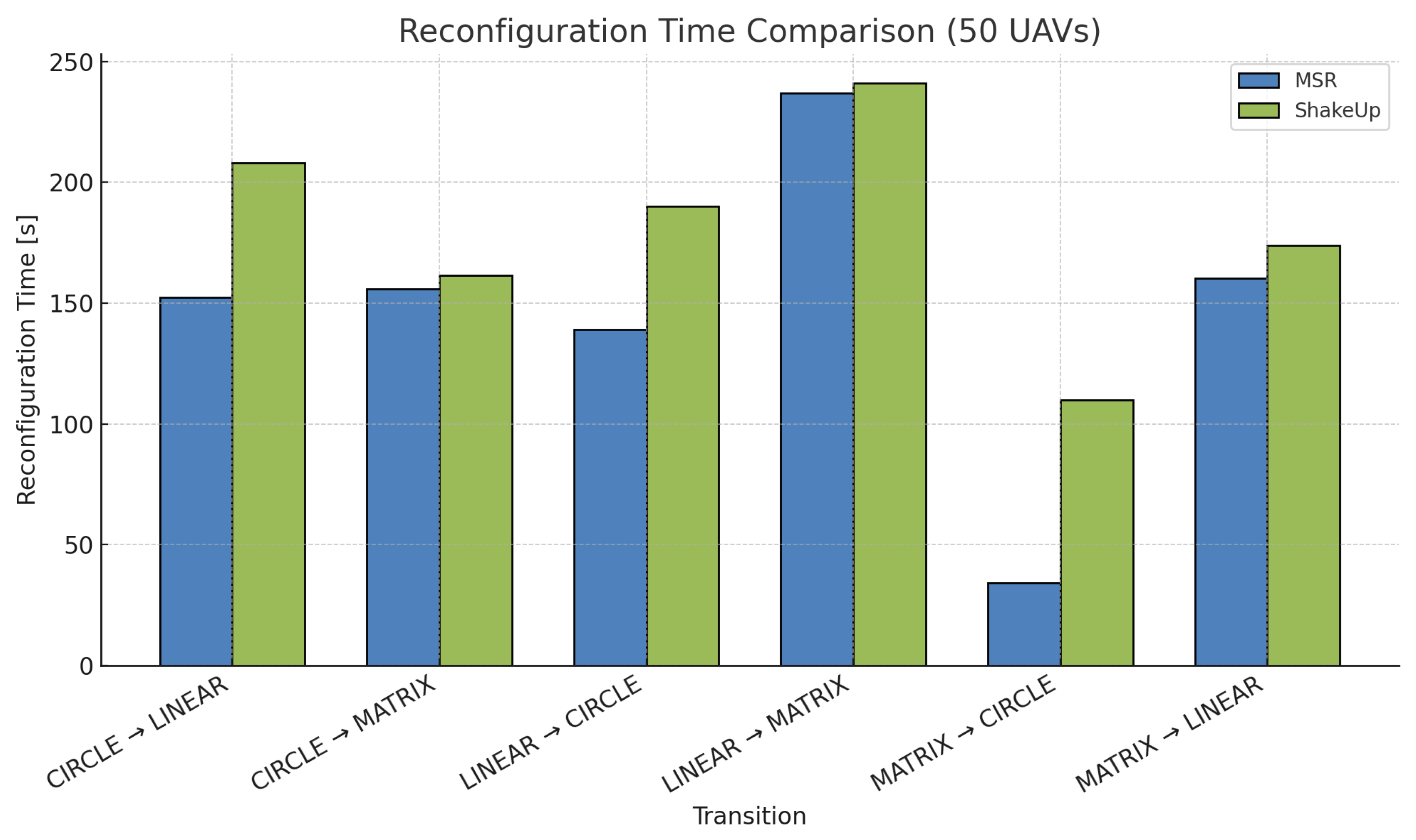
6.4. MSR vs. ShakeUp Comparison

To contextualize the MSR protocol’s performance, a comparative evaluation was conducted against the well-established ShakeUp [25] protocol. This comparison, primarily focusing on 50 UAVs across all six transitions, highlights MSR’s significant advantages in both efficiency and safety. The results are visually represented in Figure 4 and detailed in

Table 3. Comparative performance: MSR vs. ShakeUp (50 UAVs).

Scenario	Reconfiguration Time (min)		Collisions
	MSR	ShakeUp	MSR	ShakeUp
CIRCLE → LINEAR	2.54	3.47	0	1+
CIRCLE → MATRIX	2.60	2.69	0	1+
LINEAR → CIRCLE	2.32	3.17	0	1+
LINEAR → MATRIX	3.95	4.02	0	1+
MATRIX → CIRCLE	0.57	1.83	0	1+
MATRIX → LINEAR	2.67	2.90	0	1+

.

The data in Table 3 unequivocally demonstrates the superior efficiency and robustness of our MSR protocol. Across all tested transitions with 50 UAVs, MSR consistently achieves lower or comparable reconfiguration times. Notably, in the MATRIX → CIRCLE transition, MSR completes the task more than three times faster than ShakeUp (0.57 min vs. 1.83 min), showcasing its exceptional efficiency in expansive movements. While reconfiguration time differences are smaller in some other transitions (e.g., LINEAR → MATRIX, CIRCLE → MATRIX), MSR consistently maintains an edge.

The most compelling advantage of MSR, however, lies in its collision avoidance capability. MSR completes all analyzed transitions entirely without collisions, in stark contrast to ShakeUp, which consistently registers at least one collision in every compared scenario despite employing vertical sectorization and altitude separation. This fundamental difference underscores MSR’s superior safety and reliability in managing complex swarm dynamics.

The inherent design principles of MSR contribute to these performance advantages. Its decentralized architecture, combined with real-time trajectory computation, the innovative magnetic collision avoidance model, and optimal assignment strategy, enables UAVs to follow smooth, interference-free paths. It is worth pointing out that MSR achieves this superior safety while operating entirely in two dimensions, eliminating the need for complex vertical layering that, as shown by the results of the ShakeUp protocol, does not guarantee collision-free transitions, and can even lead to trajectory overlaps within sectors. This confirms the suitability of the MSR protocol for dynamic and densely populated UAV swarm scenarios where both efficiency and uncompromising safety are paramount.

7. Conclusions and Future Work

This study introduces the MSR protocol, a novel distributed approach enabling UAV swarms to dynamically transition between formations while ensuring safety and operational efficiency. MSR leverages local interactions, real-time trajectory generation combining attraction and repulsion forces, and an optimal assignment algorithm, eliminating the need for centralized control during reconfiguration.

Compared to prior methods, MSR offers several key advantages. Firstly, it enables the simultaneous movement of all UAVs, which significantly reduces overall reconfiguration time. Secondly, its strict adherence to two-dimensional maneuvers simplifies real-world execution. Thirdly, the protocol employs a novel magnetic repulsion-based mechanism for collision avoidance, thereby enhancing both safety and autonomy. Finally, an optimal assignment strategy is integrated to minimize travel distance and reduce trajectory crossings.

Simulations in six different formation transitions (CIRCLE, LINEAR, MATRIX formations and their combinations) demonstrate the scalability of MSR up to 100 UAVs, with consistently low reconfiguration times and zero collisions in most of the cases, thoroughly validating its robustness and efficiency.

While the simulations demonstrate a perfect collision-free record for the tested scenarios, it is important to acknowledge the potential for trajectory conflicts under more extreme or unpredictable conditions. For instance, in scenarios with much higher UAV speeds, sudden external disturbances, or near-instantaneous changes in formation, the reactive force-field mechanism could be momentarily overwhelmed. To address these theoretical possibilities, future work will explore advanced mitigation strategies. This includes the integration of a multi-layered repulsion system with predictive capabilities, a more sophisticated velocity-limiting model, and the incorporation of communication-based consensus mechanisms to prevent collisions in high-density, high-speed situations.

While the MSR protocol demonstrates robust performance in simulation, its transition to real-world deployment presents unique challenges that will be the focus of future work. First, the simulation environment assumes perfect state information, but in practice, UAVs are subject to significant sensor noise and GPS drift. These inaccuracies can compromise the precision of the force field calculations and the integrity of the inter-UAV distances. Future research will focus on integrating state estimation filters, such as an Extended Kalman Filter, to fuse sensor data and provide more robust positional awareness. Second, communication delays and packet loss can introduce lag in the local information exchange between UAVs. This could cause the real-time collision avoidance mechanism to react to outdated information, potentially leading to trajectory conflicts. We plan to investigate distributed predictive models and more resilient communication protocols to mitigate these effects. Finally, while the protocol’s two-dimensional nature simplifies maneuvers, environmental disturbances like wind gusts are a significant factor. Future work will explore the integration of a reactive force component that directly counters these external forces, ensuring that the swarm can maintain formation integrity even when facing turbulent conditions.