RIS-Assisted Backscatter V2I Communication System: Spectral-Energy Efficient Trade-Off
Abstract
1. Introduction
- To attain a balance between EE and SE for the distributed RIS-assisted backscatter V2I system, a novel multi-objective optimization framework is established for the first time using the linear weighting method. The optimization problem is transformed into a strictly convex problem by quadratic transformation. Then, an AO approach is applied to partition the original problem into two independent subproblems. The weighted minimization mean-square error (WMMSE) algorithm and the Riemannian conjugate gradient (RCG) algorithm are, respectively, used for the BS beamforming vectors and RIS phase shift matrices and converge rapidly through iterative optimization.
- Existing research predominantly overlooks the critical impact of the BD power reflection coefficient on RIS-assisted backscatter V2I system performance. To address this gap, this paper presents, to the best of our knowledge, the first investigation of its impact on both EE and SE performance in such systems. By jointly designing the beamforming for the BS and RIS, the BD power reflection coefficients are dynamically optimized subject to their activation requirements and the vehicle minimum QoS, thereby further enhancing the EE-SE trade-off performance.
- Unlike the conventional single RIS-assisted backscatter V2I communication system, distributed RIS is used in this paper to provide a high-quality link between the BS and BD, which overcomes the limitations of single RIS, such as high channel correlation and restricted beam steering range. It enables more parallel transmissions, thereby supporting a greater number of BDs and boosting the overall EE and SE performance of the backscatter V2I system. This distributed architecture also facilitates continuous signal transmission, which is crucial for the dynamic and mobile nature of V2I communication.
2. System Model
3. Optimization Problem Formulation
4. Optimization Scheme
4.1. BS Beamforming Optimization
| Algorithm 1 WMMSE-based algorithm. |
| Step 1. Initialize to feasible values, the iteration number t = 0. |
| Iterate repeatedly |
| Step 2. Equivalently transform (P3) into an equivalent convex form by introducing auxiliary variables , and . |
| Step 3. Obtain the closed-form expression for the optimal values of and by problem (P6). |
| Step 4. Rewrite and problem (P7). |
| Step 5. Optimize by standard convex optimization algorithms. |
| Step 6. = + 1 |
| Until the value of the objective function P7 converges |
4.2. Phase Shift Optimization of RIS
- 1.
- Riemannian Gradient Computation: This key operation involves projecting the Euclidean gradient onto the complex circle manifold to obtain the Riemannian gradient:where the symbol ∘ denotes the Hadamard product (element-wise multiplication) between two tensors of identical dimensions. The Euclidean gradient iswith parameters
- 2.
- Determine the Search Direction: The search direction is given by a tangent vector which is conjugate to :where is the conjugate gradient update parameter and denotes the vector transport function, which is defined aswhere denotes the previous search direction.
- 3.
- Retraction: Apply the retraction operation to map the tangent vector back onto the complex circle manifold:where refers to the Armijo step size.
| Algorithm 2 RCG-based algorithm. |
| Step 1. Initialize to feasible values, the iteration number = 0, iteration search direction |
| Iterate repeatedly |
| Step 2. Update Euclidean gradient of the objective function by (37). |
| Step 3. Calculate Riemannian conjugate gradient by (36). |
| Step 4. Updating the search direction by (39). |
| Step 5. Select the Armijo step size which satisfy |
| Step 6. Retraction by (41) |
| Step 7. = + 1 |
| Until the value of the objective function (36) converges |
4.3. BD Power Reflection Coefficient Optimization
4.3.1. The Range of the BD Power Reflection Coefficient
4.3.2. Determination of the Optimal BD Power Reflection Coefficient
| Algorithm 3 AO algorithm. |
| Step 1. Equivalently transform expression of (P1) into (P3) by quadratic transform. |
| Step 2. Initialize , and to feasible values. And set the iteration number ite = 0. |
| Iterate repeatedly |
| Step 3. Optimize by WMMSE algorithm. |
| Step 4. Optimize by RCG algorithm. |
| Step 5. Calculate of the feasible range (42) and (43) for the . |
| Step 6. Optimize by (44). |
| Step 7. = + 1 |
| Step 8. Update , and . |
| Until the value of the objective function P1 converges |
| Step 9. Output , and . |
5. Simulations
5.1. Simulation Scenario Settings
- S-RIS-phaserand: Only the BS beamforming vector is optimized by the WMMSE algorithm while the single RIS has random phase shift matrices .
- D-RIS-phaserand: Only the BS beamforming vector is optimized by the WMMSE algorithm while distributed RIS has random phase shift matrices .
- S-RIS-WMMSE + RCG: The BS beamforming vector and RIS phase shift matrices undergo alternating optimization by WMMSE and RCG with single RIS assistance.
- D-RIS-WMMSE + RCG: The BS beamforming vector and RIS phase shift matrices undergo alternating optimization by WMMSE and RCG with distributed RIS assistance.
- without-RIS: The BS beamforming vector is optimized by the WMMSE algorithm without RIS assistance.
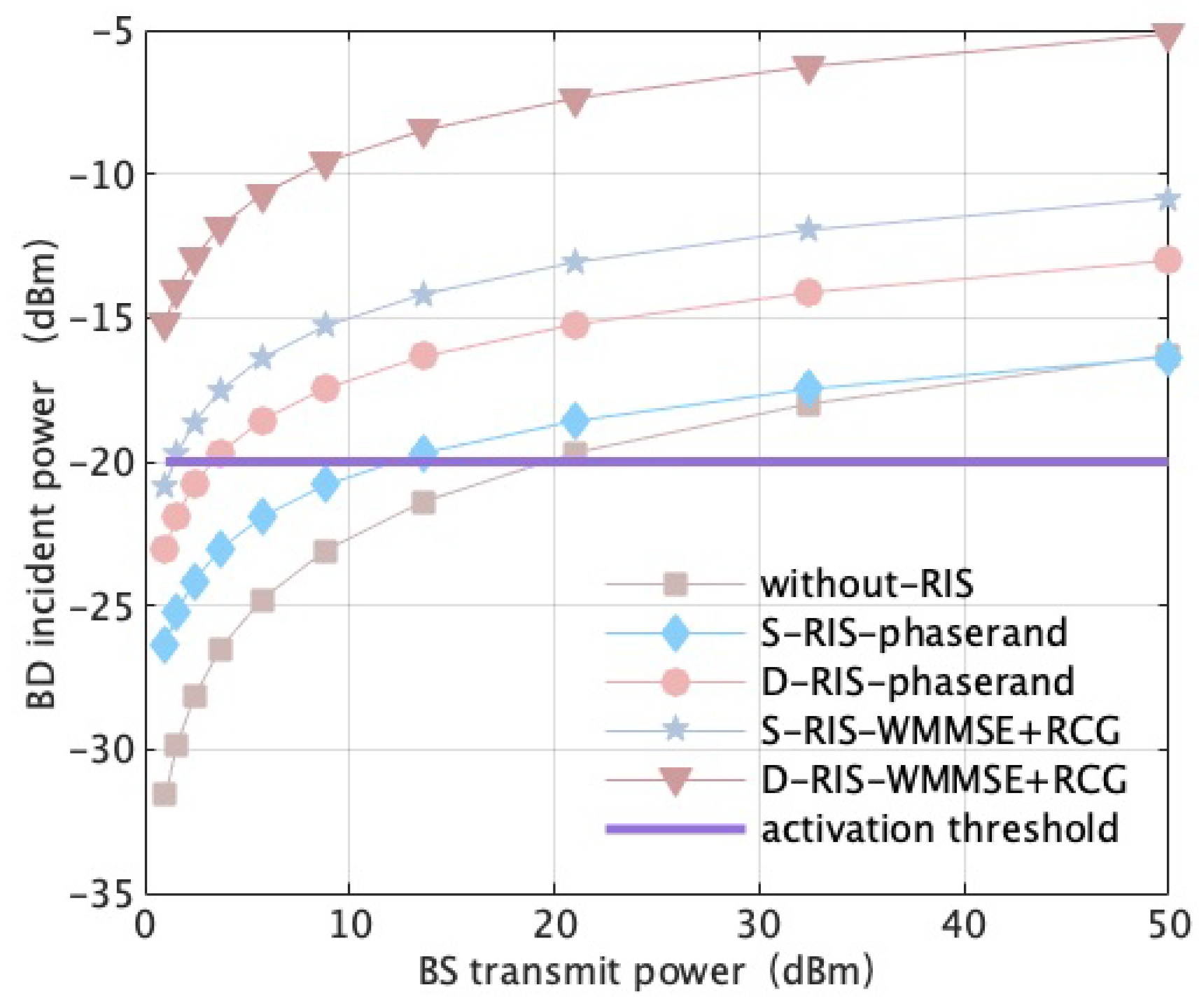
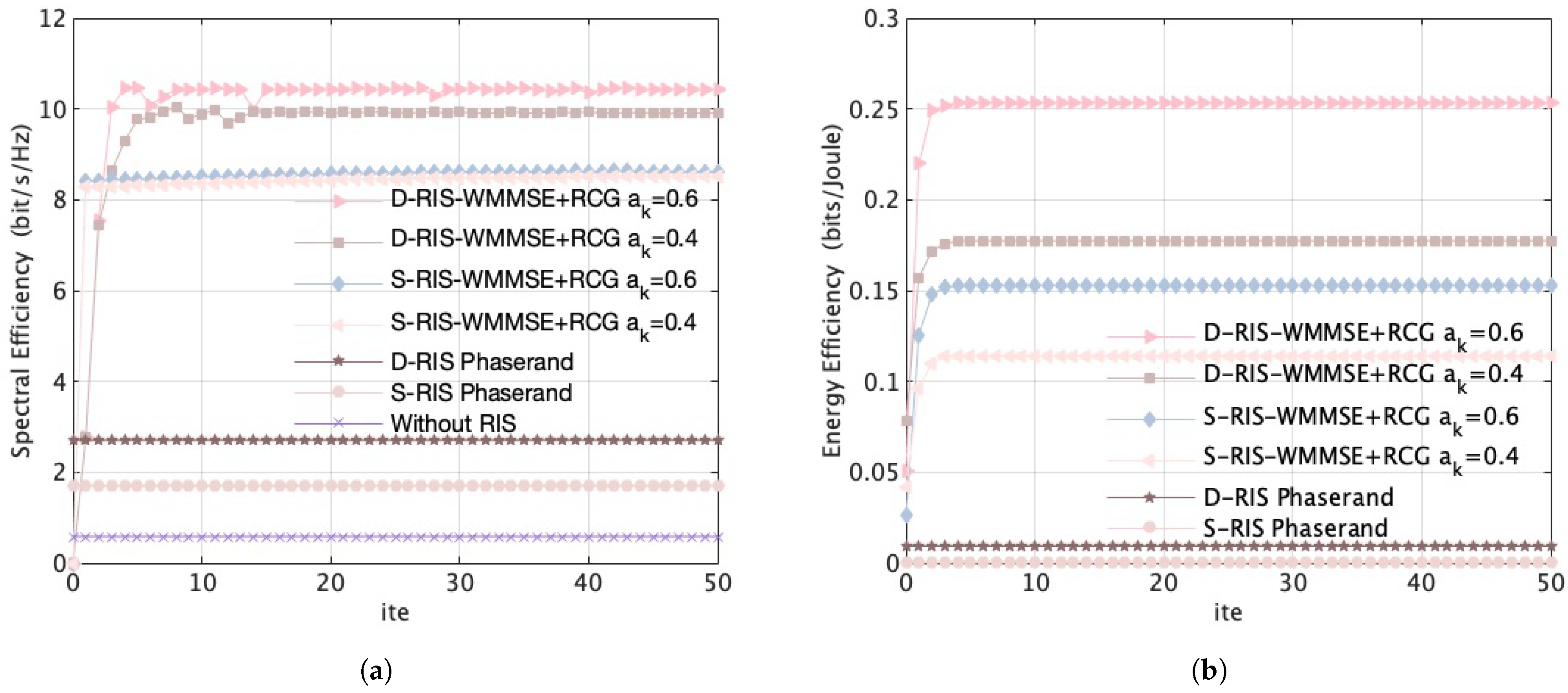
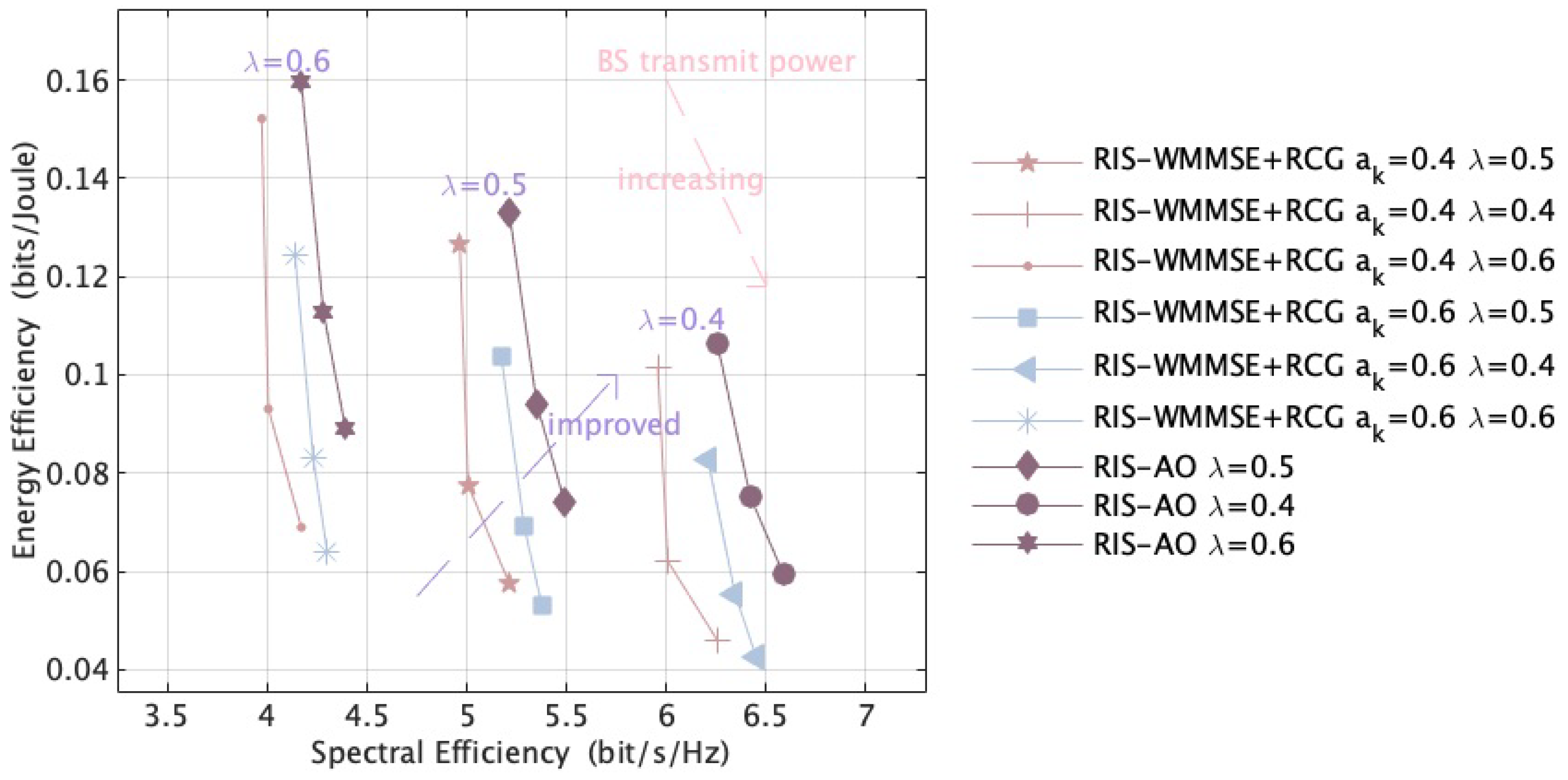
5.2. Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, J.; Lee, J.-H.; Noh, S. Position-Based Adaptive Beamforming and Roadside Unit Sectorization for V2I Communications. IEEE Trans. Veh. Technol. 2024, 73, 2960–2965. [Google Scholar] [CrossRef]
- Hong, M.; Choi, W.; Choi, S. Event Information Delivery Method Using Location Information for Route Replanning in V2I Local Environment. In Proceedings of the 2025 27th International Conference on Advanced Communications Technology (ICACT), Pyeong Chang, Republic of Korea, 16–19 February 2025; pp. 297–300. [Google Scholar]
- Qiao, Y.; Niu, Y.; Su, L.; Mao, S.; Wang, N.; Zhang, Z.; Ai, B. Deep Reinforcement Learning-Based mmWave Beam Alignment for V2I Communications. IEEE Trans. Mach. Learn. Commun. Netw. 2024, 2, 1216–1228. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, M.; Sun, Y.; Wang, K. Mobility-Aware Power Control and User Scheduling for Downlink V2I Networks. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 7–10 October 2024; pp. 1–5. [Google Scholar]
- Choi, P.; Kim, J.; Kwak, J. Joint Task Offloading and Resource Allocation for Integrated V2V and V2I Communication. In Proceedings of the 2024 15th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 16–18 October 2024; pp. 609–610. [Google Scholar]
- Zhao, R.; Mishra, D.; Seneviratne, A. Securing V2I Backscattering from Eavesdropper. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 2179–2184. [Google Scholar]
- Rastogi, A.; Yadav, S.; Gour, R.; Purohit, N.; Gurjar, D.S. Ergodic Capacity Analysis of AmBC-Assisted V2V Communications Over Cascaded Rayleigh Fading. In Proceedings of the 2024 IEEE 8th International Conference on Information and Communication Technology (CICT), Prayagraj, India, 6–8 December 2024; pp. 1–5. [Google Scholar]
- Asiedu, D.K.P.; Ofori-Amanfo, K.A.; Benjillali, M.; Yun, J.-H.; Saoudi, S. Sum-Rate Maximization of Symbiotic Multi-V2X MISO and Multi-RIS BackCom with Imperfections. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 7–10 October 2024; pp. 1–5. [Google Scholar]
- Khan, W.U.; Jameel, F.; Kumar, N.; Jäntti, R.; Guizani, M. Backscatter-Enabled Efficient V2X Communication with Non-Orthogonal Multiple Access. IEEE Trans. Veh. Technol. 2021, 70, 1724–1735. [Google Scholar] [CrossRef]
- Khan, W.U.; Jamshed, M.A.; Lagunas, E.; Chatzinotas, S.; Li, X.; Ottersten, B. Energy Efficiency Optimization for Backscatter Enhanced NOMA Cooperative V2X Communications Under Imperfect CSI. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12961–12972. [Google Scholar] [CrossRef]
- Loku Galappaththige, D.A.; Rezaei, F.; Tellambura, C.; Herath, S. Link Budget Analysis for Backscatter-Based Passive IoT. IEEE Access 2022, 10, 128890–128922. [Google Scholar] [CrossRef]
- Rezaei, F.; Galappaththige, D.; Tellambura, C.; Herath, S. Coding Techniques for Backscatter Communications—A Contemporary Survey. IEEE Commun. Surv. Tutor. 2023, 25, 1020–1058. [Google Scholar] [CrossRef]
- Pinuela, M.; Mitcheson, P.D.; Lucyszyn, S. Ambient RF Energy Harvesting in Urban and Semi-Urban Environments. IEEE Trans. Microw. Theory Tech. 2013, 61, 2715–2726. [Google Scholar] [CrossRef]
- Song, C.; Huang, Y.; Zhou, J.; Zhang, J.; Yuan, S.; Carter, P. A High-Efficiency Broadband Rectenna for Ambient Wireless Energy Harvesting. IEEE Trans. Antennas Propag. 2015, 63, 3486–3495. [Google Scholar] [CrossRef]
- Palazzi, V.; Hester, J.; Bito, J.; Alimenti, F.; Kalialakis, C.; Collado, A.; Mezzanotte, P.; Georgiadis, A.; Roselli, L.; Tentzeris, M.M. A Novel Ultra-Lightweight Multiband Rectenna on Paper for RF Energy Harvesting in the Next Generation LTE Bands. IEEE Trans. Microw. Theory Tech. 2018, 66, 366–379. [Google Scholar] [CrossRef]
- Shen, S.; Zhang, Y.; Chiu, C.-Y.; Murch, R. A Triple-Band High-Gain Multibeam Ambient RF Energy Harvesting System Utilizing Hybrid Combining. IEEE Trans. Ind. Electron. 2020, 67, 9215–9226. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Jiang, T. Joint Energy Harvest and Information Transfer for Energy Beamforming in Backscatter Multiuser Networks. IEEE Trans. Commun. 2021, 69, 1317–1328. [Google Scholar] [CrossRef]
- Long, R.; Yang, G.; Pei, Y.; Zhang, R. Transmit Beamforming for Cooperative Ambient Backscatter Communication Systems. In Proceedings of the 2017 IEEE Global Communications Conference (GLOBECOM), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Gong, S.; Huang, X.; Xu, J.; Liu, W.; Wang, P.; Niyato, D. Backscatter Relay Communications Powered by Wireless Energy Beamforming. IEEE Trans. Commun. 2018, 66, 3187–3200. [Google Scholar] [CrossRef]
- Yang, G.; Ho, C.K.; Guan, Y.L. Multi-Antenna Wireless Energy Transfer for Backscatter Communication Systems. IEEE J. Sel. Areas Commun. 2015, 33, 2974–2987. [Google Scholar] [CrossRef]
- Clerckx, B.; Bayguzina, E. Waveform Design for Wireless Power Transfer. IEEE Trans. Signal Process. 2016, 64, 6313–6328. [Google Scholar] [CrossRef]
- Liang, Y.-C.; Zhang, Q.; Wang, J.; Long, R.; Zhou, H.; Yang, G. Backscatter Communication Assisted by Reconfigurable Intelligent Surfaces. Proc. IEEE 2022, 110, 1339–1357. [Google Scholar] [CrossRef]
- Samir, A.; Ibrahim, A.S.; Ismail, M.H.; ElHalawany, B.M.; Elsayed, M. Outage Performance of RIS-Assisted AmBC-NOMA Cooperative V2I Communications. IEEE Open J. Commun. Soc. 2024, 5, 4371–4382. [Google Scholar] [CrossRef]
- Wang, J.; Han, S.; Li, C.; Meng, W. Efficient Data Collection Scheme for IRS-Based V2I Backscatter Communications. IEEE Wirel. Commun. Lett. 2024, 13, 1128–1132. [Google Scholar] [CrossRef]
- Wang, J.; Han, S.; Li, J.; Li, C. IRS-Enabled Monostatic Backscatter MIMO Communication Design for V2I Networks. IEEE Trans. Veh. Technol. 2024, 73, 19287–19298. [Google Scholar] [CrossRef]
- Han, S.; Wang, J.; Li, J.; Li, C. IRS-Enabled Secure Backscatter Communication Design for V2I MIMO Networks. IEEE Wirel. Commun. Lett. 2024, 13, 2591–2595. [Google Scholar] [CrossRef]
- Galappaththige, D.; Rezaei, F.; Tellambura, C.; Herath, S. Optimizing Passive Tag Performance with Reconfigurable Intelligent Surfaces in Bistatic Backscatter Networks. IEEE Trans. Veh. Technol. 2024, 73, 12917–12933. [Google Scholar] [CrossRef]
- Galappaththige, D.L.; Rezaei, F.; Tellambura, C.; Herath, S. RIS-Empowered Ambient Backscatter Communication Systems. IEEE Wirel. Commun. Lett. 2023, 12, 173–177. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, M.; Li, W.; Xie, J.; Kadoch, M. RIS-Assisted Ambient Backscatter Communication for SAGIN IoT. IEEE Internet Things J. 2023, 10, 9375–9384. [Google Scholar] [CrossRef]
- Zhang, M.; Tan, L.; Huang, K.; You, L. On the Trade-Off between Energy Efficiency and Spectral Efficiency in RIS-Aided Multi-User MISO Downlink. Electronics 2021, 10, 1307. [Google Scholar] [CrossRef]
- Wan, J.; Guan, Y.; Song, J.; Song, Q.; Guo, L. Energy Efficiency and Spectral Efficiency Tradeoff in Multi-BD Symbiotic Radio Systems. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China (ICCC), Dalian, China, 10–12 August 2023; pp. 1–6. [Google Scholar]
- You, L.; Xiong, J.; Ng, D.W.K.; Yuen, C.; Wang, W.; Gao, X. Energy Efficiency and Spectral Efficiency Tradeoff in RIS-Aided Multiuser MIMO Uplink Transmission. IEEE Trans. Signal Process. 2021, 69, 1407–1421. [Google Scholar] [CrossRef]
- Faisal, A.; Al-Nahhal, I.; Dobre, O.A.; Ngatched, T.M.N. Deep Reinforcement Learning for RIS-Assisted FD Systems: Single or Distributed RIS? IEEE Commun. Lett. 2022, 26, 1563–1567. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.-X.; Gao, X.; You, X.; Zhang, M. A General 3D Non-Stationary Wireless Channel Model for 5G and Beyond. IEEE Trans. Wirel. Commun. 2021, 20, 3211–3224. [Google Scholar] [CrossRef]
- Yang, H.; Ye, Y.; Chu, X. Max-Min Energy-Efficient Resource Allocation for Wireless Powered Backscatter Networks. IEEE Wirel. Commun. Lett. 2020, 9, 688–692. [Google Scholar] [CrossRef]
- Shi, Q.; Razaviyayn, M.; Luo, Z.-Q.; He, C. An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 3060–3063. [Google Scholar]
- Guo, H.; Liang, Y.-C.; Chen, J.; Larsson, E.G. Weighted Sum-Rate Maximization for Reconfigurable Intelligent Surface Aided Wireless Networks. IEEE Trans. Wirel. Commun. 2020, 19, 3064–3076. [Google Scholar] [CrossRef]
- Yu, X.; Xu, D.; Schober, R. MISO Wireless Communication Systems via Intelligent Reflecting Surfaces: (Invited Paper). In Proceedings of the 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 11–13 August 2019; pp. 735–740. [Google Scholar]



| Parameters | Value |
|---|---|
| Number of BS antennas () | 128 |
| Number of RIS reflection elements () | 100 |
| Number of BDs with single antennas () | 4 |
| Carrier frequency | 28 GHz |
| Transmission bandwidth | 100 MHz |
| BD-BR sub-channel path loss | 22.55 + 35.3lg + 20g dB |
| Backscattering period () | 4 s |
| Noise power spectral density | −174 dBm/Hz |
| Sampling frequency | 1 × 104 Hz |
| BR moving speed | 2 m/s |
| Width and height of the RIS elements | 0.234 times the wavelength |
| RIS pose | [[0, 0, −1]; [−0.7071, 0.7071, 0]; [0.7071, 0.7071, 0]] |
| Passive BD activation threshold () | −20 dBm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Xu, P.; Lan, X.; Wang, Y.; Li, Y. RIS-Assisted Backscatter V2I Communication System: Spectral-Energy Efficient Trade-Off. Electronics 2025, 14, 3800. https://doi.org/10.3390/electronics14193800
Dong Y, Xu P, Lan X, Wang Y, Li Y. RIS-Assisted Backscatter V2I Communication System: Spectral-Energy Efficient Trade-Off. Electronics. 2025; 14(19):3800. https://doi.org/10.3390/electronics14193800
Chicago/Turabian StyleDong, Yi, Peng Xu, Xiaoyu Lan, Yupeng Wang, and Yufeng Li. 2025. "RIS-Assisted Backscatter V2I Communication System: Spectral-Energy Efficient Trade-Off" Electronics 14, no. 19: 3800. https://doi.org/10.3390/electronics14193800
APA StyleDong, Y., Xu, P., Lan, X., Wang, Y., & Li, Y. (2025). RIS-Assisted Backscatter V2I Communication System: Spectral-Energy Efficient Trade-Off. Electronics, 14(19), 3800. https://doi.org/10.3390/electronics14193800





