Bayesian–Geometric Fusion: A Probabilistic Framework for Robust Line Feature Matching
Abstract
1. Introduction
- (i)
- It would be rude to “hard filter” based on the distance metric between the binary descriptors of the line feature to obtain the line feature matching pair. This can result in the loss of potentially correct line feature matching pairs. It is also unfriendly for low-texture, illuminated image pairs, as well as image pairs with rotation components.
- (ii)
- Relying on jointly constructed point–line invariants imposes significant limitations. Firstly, the accuracy of matching decreases in regions lacking texture and sparse point features. Secondly, the resultant computational complexity prohibits real-time deployment in time-sensitive applications.
- We propose a novel line feature matching algorithm that directly utilizes feature descriptors, eliminating the need for mismatch filtering based on rough geometric constraint condition or the computationally intensive process of computing homography matrix. Importantly, our approach achieves complete line feature matching without requiring supplementary point feature correspondences.
- This work introduces, to our knowledge, the first posterior probability distribution model specifically designed for line feature matching by exploiting intrinsic geometric properties. The proposed model synergistically combines spatial distance (endpoint and midpoint distances) and angular consistency through uniform distribution modeling, to optimize line feature correspondence determination in a unified probabilistic framework.
- We conducted extensive evaluations across challenging visual scenarios including low-texture environments, significant viewpoint rotations, and variable lighting conditions. Quantitative and qualitative comparisons with state-of-the-art methods demonstrate our algorithm’s superior performance. Comprehensive ablation studies further validate the robustness and effectiveness of the proposed approach.
2. Related Works
2.1. Single Line Feature Matching
2.2. Line Matching in Group
2.3. Line Feature Matching Using Deep Learning Techniques
3. Proposed Methodology
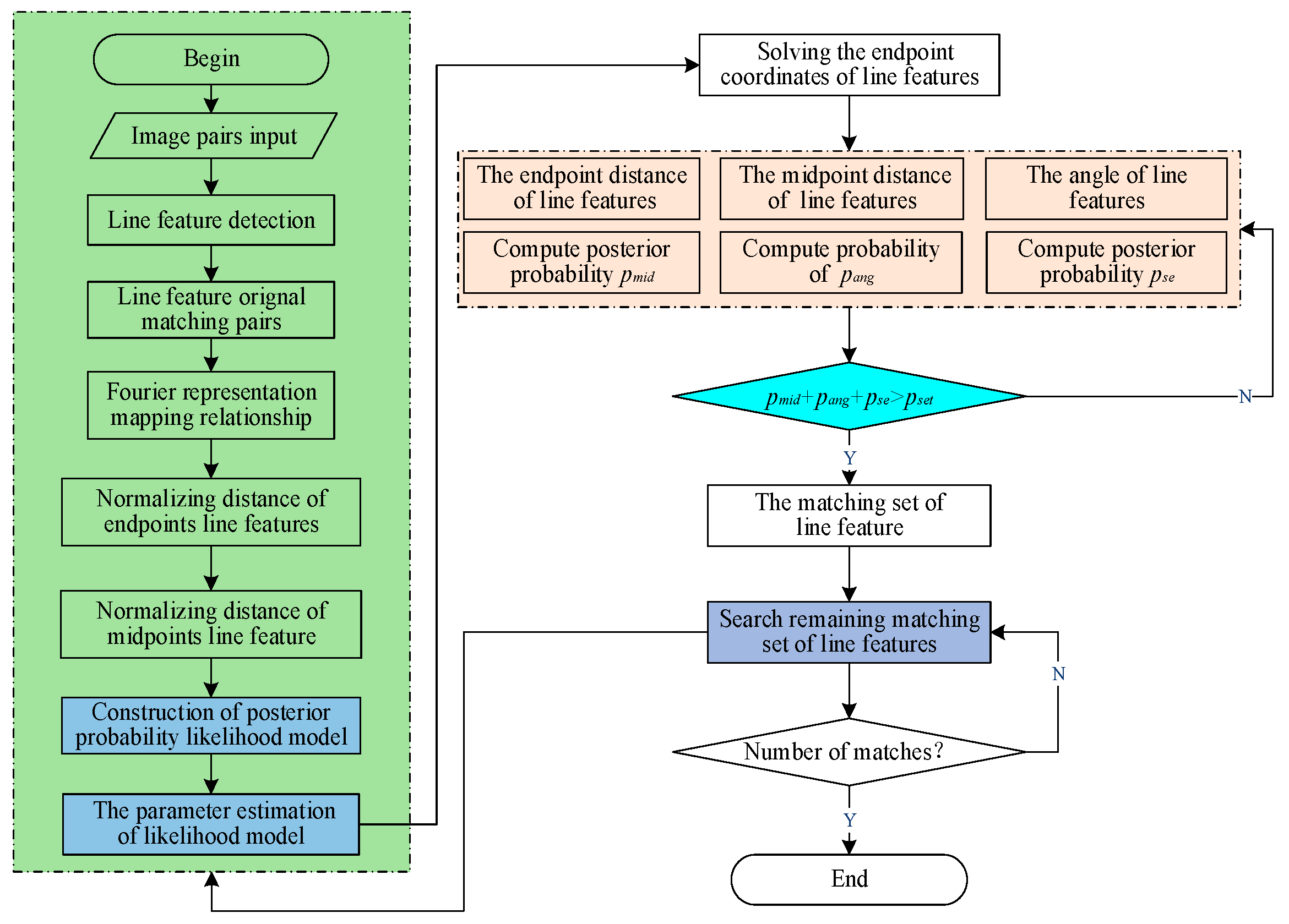
3.1. Algorithm Architecture and Workflow
- Line Feature Extraction and Descriptor Computation: Line features are detected and extracted from each image pair using the LSD algorithm [48] via the OpenCV library interface, followed by the computation of LBD binary descriptors.
- Initial Line Matching Set: Preliminary correspondences between line features are established by comparing their binary descriptors using Hamming distance, resulting in an initial set of potential matches.
- Mapping Relationship Representation: The geometric correspondence between pairs of line features is mathematically represented using a compact Fourier series, capturing the transformation between matched features.
- Posterior Probabilistic Matching Model: Our likelihood model includes normalizing the distances between endpoints and midpoints of matched line features, an angular condition characterized by a uniform distribution, and the initial parameterization of the maximum posteriori estimation framework.
- Iterative Model Optimization: Our probabilistic model iteratively determines optimal parameters through progressive refinement of line matching, inverse normalization of endpoint coordinates, and continuous evaluation of geometric constraints (endpoint/midpoint distances and angles) until parameter convergence is achieved.
- Final Line Match Set: The algorithm systematically processes remaining unmatched features by reapplying the matching criteria, resulting in a complete set of accurate and robust line correspondences.
| Algorithm 1: Line feature matching framework algorithm based on posterior probability model | |
| Input: | Image pairs Ia, Ib, The parameters of posterior probability model: λ, δ, s, γ, u |
| Output: | The final matching set of line features LineSet |
| 1: keyline1, keyline2, dsc1, dsc2: [keyline1,dsc1] → LsdAndCompute(Ia), [keyline2,dsc2]→LsdAndCompute(Ib); | |
| 2: intial line feature matches LineSetinitial → BinaryMatch (dsc1,dsc2); | |
| 3: (1) Fourier representation between candidate line features: X’ → f(X); (2) LineEquationi→Fitting(keylinei),(d1,d2,dm) → compute(keyline,LineEquation). | |
| 4: (1) Presetting these parameter value of λ γ s; While: (2) Normalize (d1, d2, dmid) to [0, 1] → Normalize(); (3) Establishing a posterior likelyhood probability model p; (4) Solving the variance δ, the mean value u of likelihood model:(u,δ) → EM(p); (5) Inverse normalization line endpoint coordinates:(keyline′) → InverseNormalize(keyline); (6) Calculating the probability pse(d1,d2), pmid(dm); (7) Calculating the angle β based on keylinei’; (8) Establishing an uniform distribution model pang, and calculating pang(β); (9) Updating the weight coefficient λ, γ, s. | |
| 5: (1) The final probability of LineSetinitial: p → (pse(d1,d2) + pmid(dm) + pang(β)); (2) Preset threshold pset: if p > pset, accept, otherwise, remove and obtaining MatchLine1; (3) Searching the unmatched line MatchLine2 → LineSetinitial MatchLine1; (4) Matching the remaining line: MatchLine3 → BinaryMatch(dsci1,dscj2), (dsci1,dscj2) MacthLine2; (5) LineSetnew → (MatchLine1MatchLine3); | |
| 6: Return 4, iterate through 4 to 6 until LineSetnew, convergence: LineSet → LineSetnew. | |
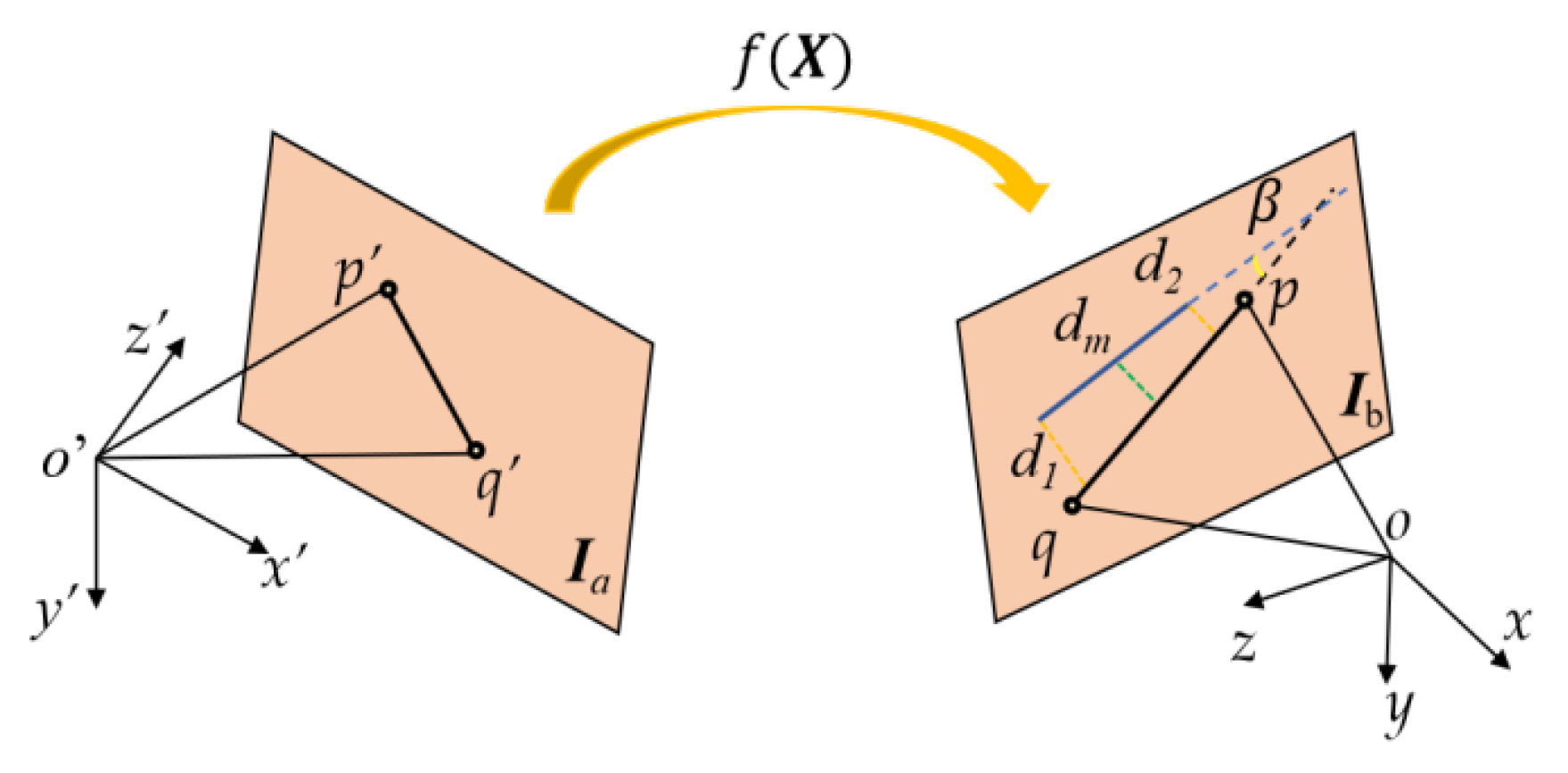
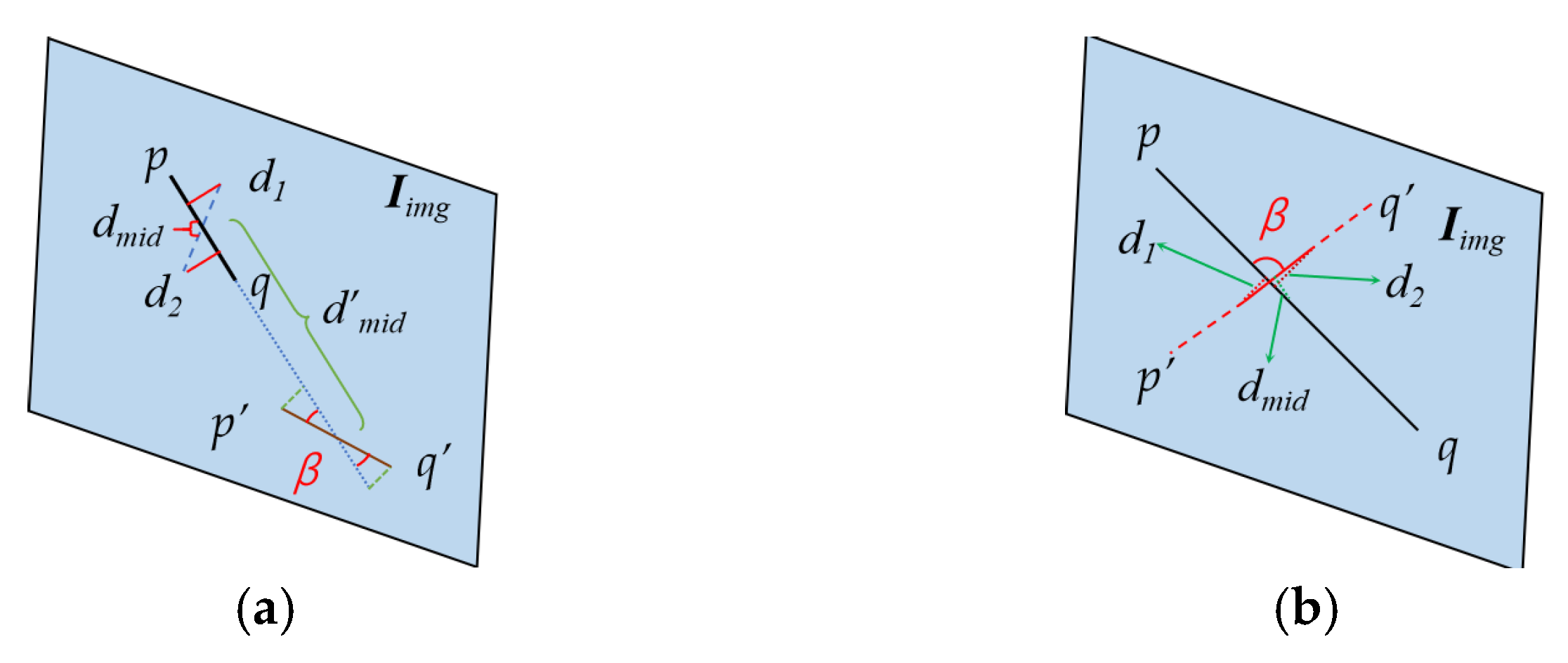
3.2. Fourier-Based Representation with Geometric Constraints for Robust Line Matching
3.3. Posterior Probability Estimation via Expectation–Maximization Algorithm
4. Experimental Verification and Performance Analysis
4.1. Experimental Parameter Configuration
- (i)
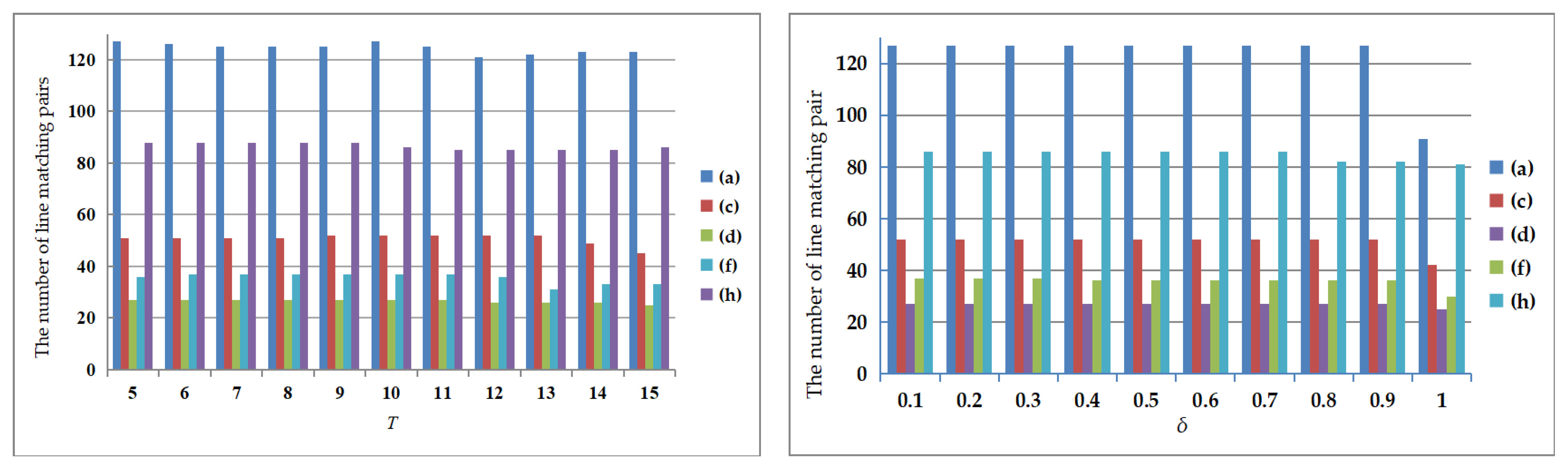
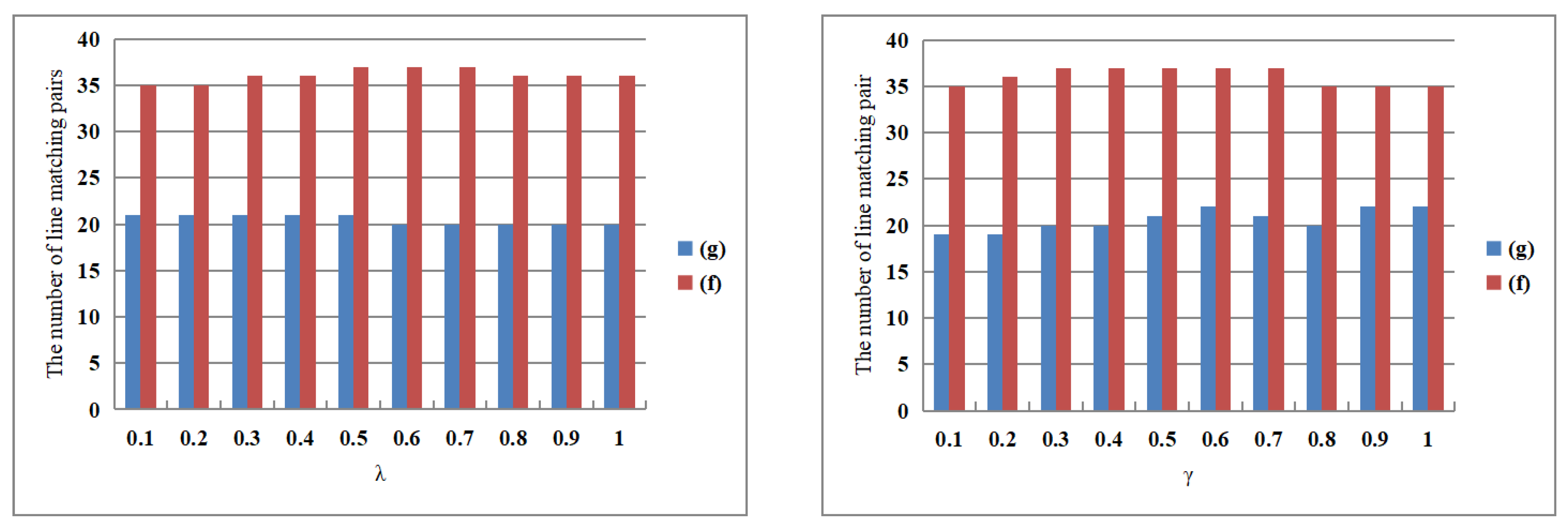
- T is the number of basis functions in Equation (1); we determine the optimal parameter by evaluating image pairs (a), (c), (d), (f), and (h) individually. Through our experimental observations, it was established that an insufficient number of basis functions (T < 5) compromises the robustness of representing relationships between image pairs, while an excessive number (T > 15) may lead to overfitting, catering to only specific cases of image matching pairs. Consequently, T was constrained to a range of 5 to 15. The outcomes depicted in Figure 5 revealed that T between 11 and 15 yielded a relatively low number of matching pairs, whereas T between 5 and 9 showed an increase in line matching pairs. Notably, setting T to 10 nearly maximized the selection of image line matching pairs. Considering the collective findings from our experiments, a final decision was made to set T at 10.
- (ii)
- The parameter (including , , here, we will synchronize the two with incremental increases, using to represent both) is the initial distance variance of the line feature matching pair. Based on the image pairs (a), (c), (d), (f) and (h), range from 0.1 to 1.0. By comparing the line feature matching results across different in Figure 5, it is observed that setting to 0.3 yields the maximum number of line feature matches for the selected image pair under a fixed T value. Therefore, the parameter is set to 0.3 in our study.
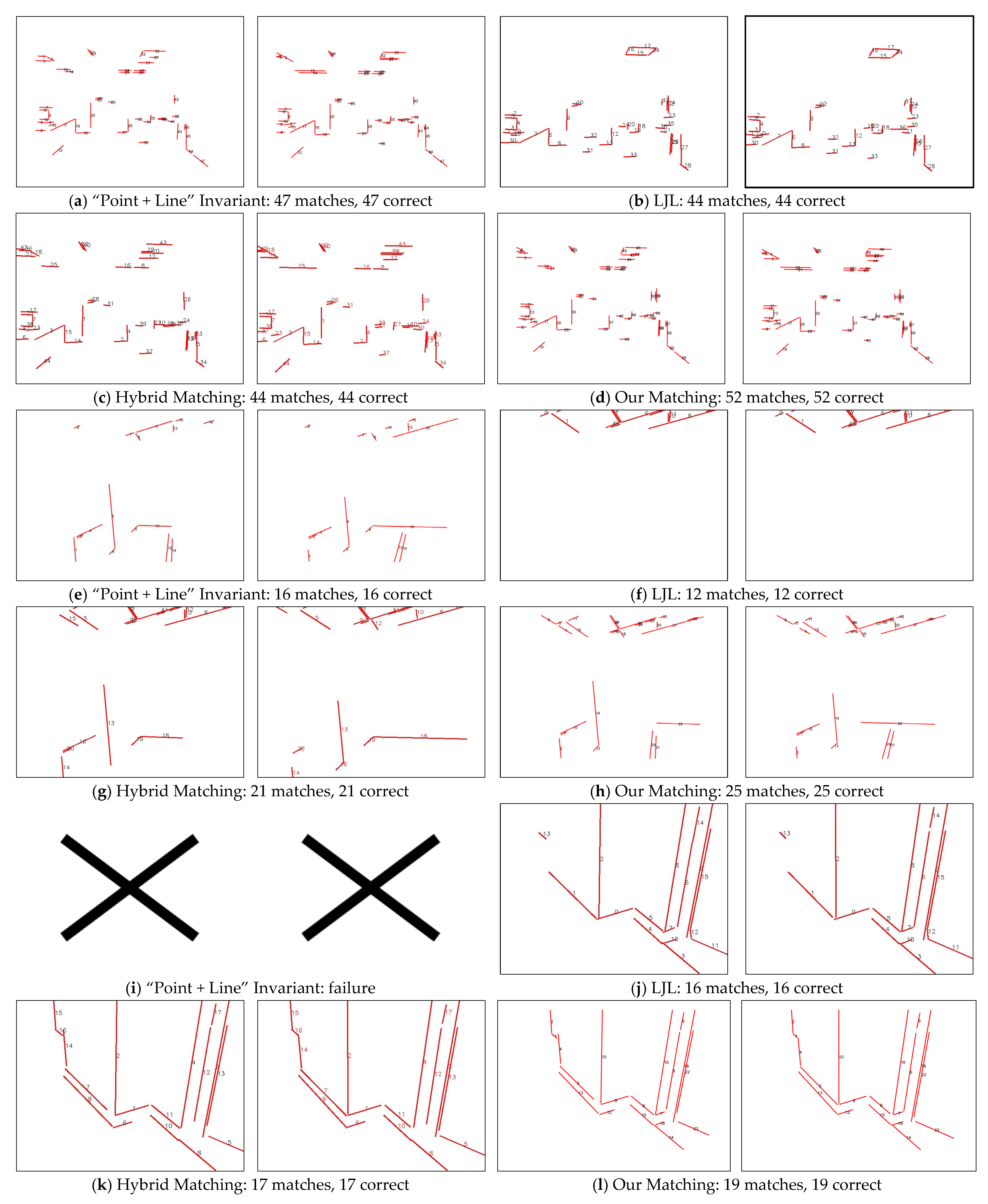
4.2. Line Feature Matching Comparison Among Our and Other Algorithms
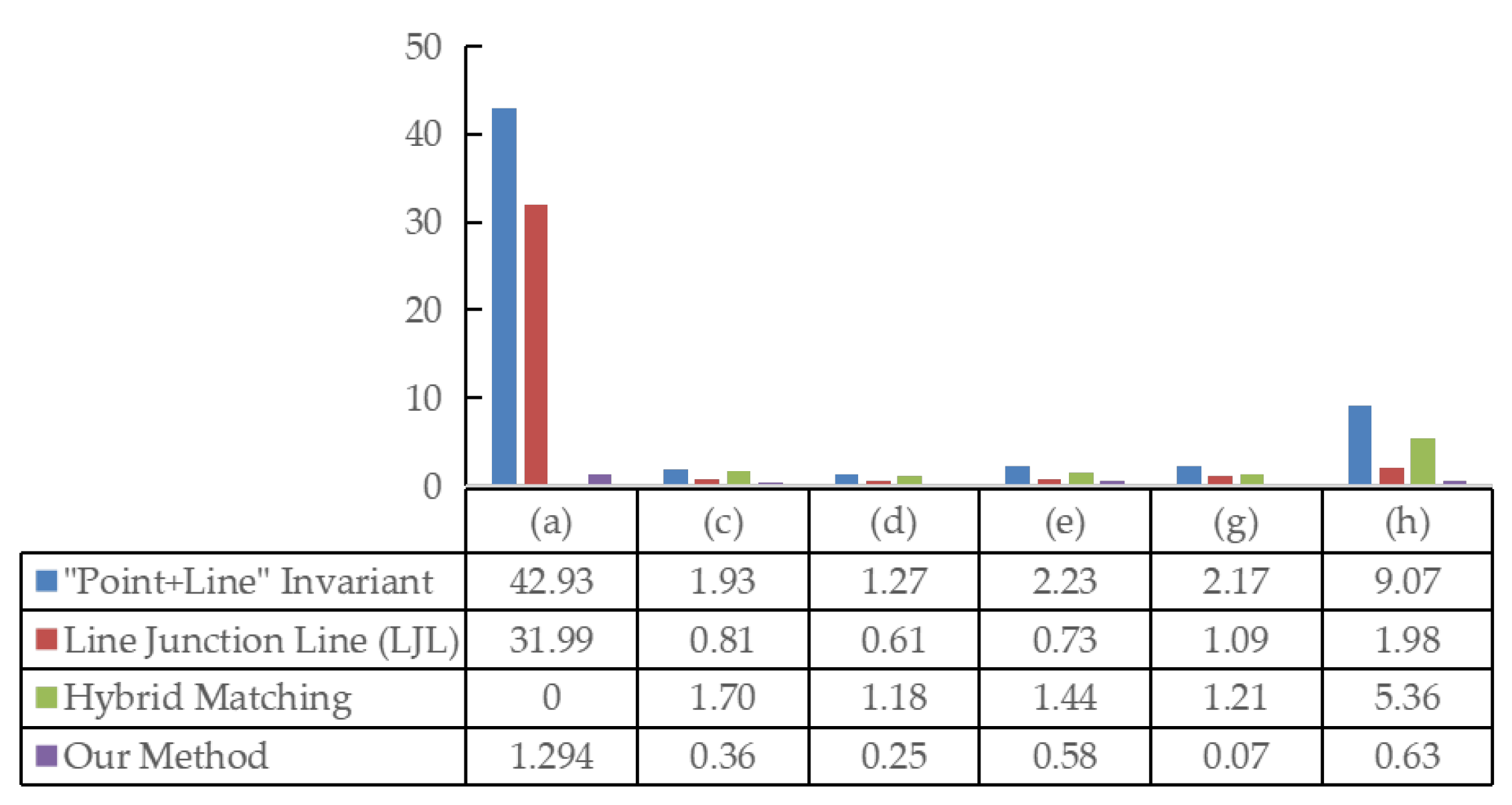
4.3. Ablation Study and Component Analysis
4.4. Comparative Analysis of Deep Learning-Based Line Feature Matching
4.5. Comparative Verification of Line Feature Matching Based on Descriptor
4.6. Line Feature Matching in Illumination-Sensitive Scenes
4.7. Sparse 3D Reconstruction Using Our Line Feature Matching Results
4.8. Comparative Time Efficiency Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, Y.; Yang, J.; Ponce, J.; Kong, H. Homography-Based Minimal-Case Relative Pose Estimation with Known Gravity Direction. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 196–210. [Google Scholar] [CrossRef]
- Jiang, H.; Dang, Z.; Gu, S.; Xie, J.; Salzmann, M.; Yang, J. Center-Based Decoupled Point Cloud Registration for 6D Object Pose Estimation. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 3404–3414. [Google Scholar]
- Schönberger, J.L.; Frahm, J.-M. Structure-from-Motion Revisited. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar]
- Agarwal, S.; Furukawa, Y.; Snavely, N.; Simon, I.; Curless, B.; Seitz, S.M.; Szeliski, R. Building rome in a day. Commun. ACM 2011, 54, 105–112. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z. RGB Line Pattern-Based Stereo Vision Matching for Single-Shot 3-D Measurement. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Kong, C.; Luo, A.; Wang, S.; Li, H.; Rocha, A.; Kot, A.C. Pixel-Inconsistency Modeling for Image Manipulation Localization. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 4455–4472. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Gu, S.; Li, X.; Deng, J.; Jin, S. VID-SLAM: A New Visual Inertial SLAM algorithm Coupling an RGB-D camera and IMU Based on Adaptive Point and Line Features. IEEE Sens. J. 2024, 44, 41548–41562. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, R.; Jin, S.; Yi, X. PFD-SLAM: A New RGB-D SLAM for Dynamic Indoor Environments Based on Non-Prior Semantic Segmentation. Remote Sens. 2022, 14, 2445. [Google Scholar] [CrossRef]
- Shen, Y.; Hui, L.; Xie, J.; Yang, J. Self-Supervised 3D Scene Flow Estimation Guided by Superpoints. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 5271–5280. [Google Scholar]
- Wu, M.; Zeng, W.; Fu, C.-W. FloorLevel-Net: Recognizing Floor-Level Lines with Height-Attention-Guided Multi-Task Learning. IEEE Trans. Image Process. 2021, 30, 6686–6699. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, T.; Li, H.; Wu, X.J.; Zhu, X.; Kittler, J. Exploring fusion strategies for accurate RGBT visual object tracking. Inf. Fusion 2023, 99, 101881. [Google Scholar] [CrossRef]
- Peng, Z.; Ma, Y.; Zhang, Y.; Li, H.; Fan, F.; Mei, X. Seamless UAV Hyperspectral Image Stitching Using Optimal Seamline Detection via Graph Cuts. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5512213. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, H.; Zhao, J.; Gao, Y.; Jiang, J.; Tian, J. Robust Feature Matching for Remote Sensing Image Registration via Locally Linear Transforming. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6469–6481. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, H.; Huang, W. Building Outline Delineation from VHR Remote Sensing Images Using the Convolutional Recurrent Neural Network Embedded with Line Segment Information. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Li, R.; Yuan, X.; Gan, S.; Bi, R.; Luo, W.; Chen, C.; Zhu, Z. Automatic Coarse Registration of Urban Point Clouds Using Line-Planar Semantic Structural Features. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5707824. [Google Scholar] [CrossRef]
- Xu, S.; Chen, S.; Xu, R.; Wang, C.; Lu, P.; Guo, L. Local feature matching using deep learning: A survey. Inf. Fusion 2024, 107, 102344. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Tian, J.; Yuille, A.L.; Tu, Z. Robust Point Matching via Vector Field Consensus. IEEE Trans. Image Process. 2014, 23, 1706–1721. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Bian, J.; Lin, W.Y.; Matsushita, Y.; Yeung, S.K.; Nguyen, T.D.; Cheng, M.M. GMS: Grid-Based Motion Statistics for Fast, Ultra-Robust Feature Correspondence. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2828–2837. [Google Scholar]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching with Graph Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 4937–4946. [Google Scholar]
- Wei, D.; Zhang, Y.; Liu, X.; Li, C.; Li, Z. Robust line segment matching across views via ranking the line-point graph. ISPRS J. Photogramm. Remote Sens. 2021, 171, 49–62. [Google Scholar] [CrossRef]
- Jin, Y.; Mishkin, D.; Mishchuk, A.; Matas, J.; Fua, P.; Yi, K.M.; Trulls, E. Image Matching Across Wide Baselines: From Paper to Practice. Int. J. Comput. Vis. 2021, 129, 517–547. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Xiao, G.; Shao, Z.; Guo, X. A review of multi-modal image matching: Methods and applications. Inf. Fusion 2021, 73, 22–71. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, L.; Cheng, L.; Koch, R. Pose Estimation from Line Correspondences: A Complete Analysis and a Series of Solutions. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1209–1222. [Google Scholar] [CrossRef]
- Lin, X.; Zhou, Y.; Liu, Y.; Zhu, C. A Comprehensive Review of Image Line Segment Detection and Description: Taxonomies, Comparisons, and Challenges. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 8074–8093. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Liu, S.; Wang, W. Robust line feature matching based on pair-wise geometric constraints and matching redundancy. ISPRS J. Photogramm. Remote Sens. 2021, 172, 41–58. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Hu, Z. MSLD: A robust descriptor for line matching. Pattern Recognit. 2009, 42, 941–953. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Liu, X. A line matching method based on local and global appearance. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; pp. 1381–1385. [Google Scholar]
- Zhang, L.; Koch, R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency. J. Vis. Commun. Image Represent. 2013, 24, 794–805. [Google Scholar] [CrossRef]
- Bay, H.; Ferraris, V.; Van Gool, L. Wide-baseline stereo matching with line segments. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 329–336. [Google Scholar]
- Verhagen, B.; Timofte, R.; Van Gool, L. Scale-invariant line descriptors for wide baseline matching. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Steamboat Springs, CO, USA, 24–26 March 2014; pp. 493–500. [Google Scholar]
- Li, K.; Yao, J.; Lu, X.; Li, L.; Zhang, Z. Hierarchical line matching based on line junction line structure descriptor and local homography estimation. Neurocomputing 2016, 184, 207–220. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale- invariant keypoints. Int. J. Comp. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Lin, X.; Zhou, Y.; Liu, Y.; Zhu, C. Illumination-Insensitive Line Binary Descriptor Based on Hierarchical Band Difference. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2680–2684. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X. Multiple Homography Estimation via Stereo Line Matching for Textureless Indoor Scenes. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 628–632. [Google Scholar]
- Wang, L.; Neumann, U.; You, S. Wide-baseline image matching using Line Signatures. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 1311–1318. [Google Scholar]
- López, J.; Santos, R.; Fdez-Vidal, X.R.; Pardo, X.M. Two-view line matching algorithm based on context and appearance in low-textured images. Pattern Recognit. 2015, 48, 2164–2184. [Google Scholar] [CrossRef]
- Fan, B.; Wu, F.; Hu, Z. Robust line matching through line point invariants. Pattern Recognit. 2012, 45, 794–805. [Google Scholar] [CrossRef]
- Fan, B.; Wu, F.; Hu, Z. Line matching leveraged by point correspondences. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 390–397. [Google Scholar]
- Jia, Q.; Gao, X.; Fan, X.; Luo, Z.; Li, H.; Chen, Z. Novel coplanar line points invariants for robust line matching across views. In Proceedings of the 2016 Computer Vision ECCV 2016, Amsterdam, The Netherlands, 11–14 October 2016; pp. 599–611. [Google Scholar]
- Zhang, C.; Xiang, Y.; Wang, Q.; Gu, S.; Deng, J.; Zhang, R. Robust Line Feature Matching via Point-Line Invariants and Geometric Constraints. Sensors 2025, 25, 2980. [Google Scholar] [CrossRef]
- OoYang, H.; Fan, D.; Ji, S.; Lei, R. Line Matching Based on Discrete Description and Conjugate Point Constraint. Acta Geod. Cartogr. Sin. 2018, 47, 1363–1371. [Google Scholar]
- Song, W.; Zhu, H.; Wang, J.; Liu, Y. Line feature matching method based on multiple constraints for close-range images. J. Image Graph. 2016, 21, 764–770. [Google Scholar]
- Pautrat, R.; Lin, J.T.; Larsson, V.; Oswald, M.R.; Pollefeys, M. SOLD2: Self-supervised Occlusion-aware Line Description and Detection. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 11363–11373. [Google Scholar]
- Yoon, S.; Kim, A. Line as a Visual Sentence: Context-Aware Line Descriptor for Visual Localization. IEEE Robot. Autom. Lett. 2021, 6, 8726–8733. [Google Scholar] [CrossRef]
- Lange, M.; Schweinfurth, F.; Schilling, A. Dld: A deep learning based line descriptor for line feature matching. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 5910–5915. [Google Scholar]
- Lange, M.; Raisch, C.; Schilling, A. Wld: A wavelet and learning based line descriptor for line feature matching. In Proceedings of the VMV 2020, Tübingen, Germany, 28 September–1 October 2020. [Google Scholar]
- von Gioi, R.G.; Jakubowicz, J.; Morel, J.-M.; Randall, G. LSD: A Fast Line Segment Detector with a False Detection Control. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 722–732. [Google Scholar] [CrossRef]
- Fan, A.; Jiang, X.; Ma, Y.; Mei, X.; Ma, J. Smoothness-Driven Consensus Based on Compact Representation for Robust Feature Matching. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4460–4472. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Jiang, J.; Lu, Y.; Liu, W.; Ma, J. Robust feature matching via progressive smoothness consensus. ISPRS J. Photogramm. Remote Sens. 2023, 196, 502–513. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Li, K.; Yao, J.; Lu, M.; Heng, Y.; Wu, T.; Li, Y. Line segment matching: A benchmark. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016; pp. 1–9. [Google Scholar]
- Handa, A.; Whelan, T.; McDonald, J.; Davison, A.J. A benchmark for RGB-D visual odometry, 3D reconstruction and SLAM. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1524–1531. [Google Scholar]
- Strecha, C.; Hansen, W.V.; Gool, L.V.; Fua, P.; Thoennessen, U. On benchmarking camera calibration and multi-view stereo for high resolution imagery. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 6, 381–395. [Google Scholar] [CrossRef]





| “Point + Line” Invariant | Line Junction Line (LJL) | Hybrid Matching | Our Method | |||||
|---|---|---|---|---|---|---|---|---|
| (I1-line, I2-line)/M | MC/MP | (I1-line, I2-line)/M | MC/MP | (I1-line, I2-line)/M | MC/MP | (I1-line, I2-line)/M | MC/MP | |
| (a) | [210, 213]/166 | 166/1.0 | [218, 214]/167 | 167/1.0 | —/— | —/— | [210, 213]/127 | 125/0.98 |
| (b) | [291, 291]/0 | —/— | [481, 421]/337 | 337/1.0 | —/— | —/— | [485, 429]/362 | 362/1.0 |
| (c) | [70, 63]/47 | 47/1.0 | [69, 61]/38 | 38/1.0 | [70, 63]/47 | 44/1.0 | [70, 63]/52 | 52/1.0 |
| (d) | [34, 34]/16 | 16/1.0 | [35, 27]/12 | 12/1.0 | [34, 34]/21 | 21/1.0 | [34, 34]/25 | 25/1.0 |
| (e) | [139, 113]/92 | —/— | [24, 27]/16 | 16/1.0 | [23, 24]/17 | 17/1.0 | [23, 24]/19 | 19/1.0 |
| (f) | [196, 59]/45 | 45/1.0 | [196, 59]/24 | 24/1.0 | [196, 59]/36 | 30/0.83 | [196, 59]/34 | 37/1.0 |
| (g) | [37, 36]/6 | 6/1.0 | [40, 38]/17 | 17/1.0 | [37, 36]/19 | 16/0.84 | [37, 36]/21 | 20/0.95 |
| (h) | [139, 113]/92 | 92/1.0 | [136, 119]/89 | 89/1.0 | [139, 113]/75 | 75/1.0 | [139, 113]/84 | 84/1.0 |
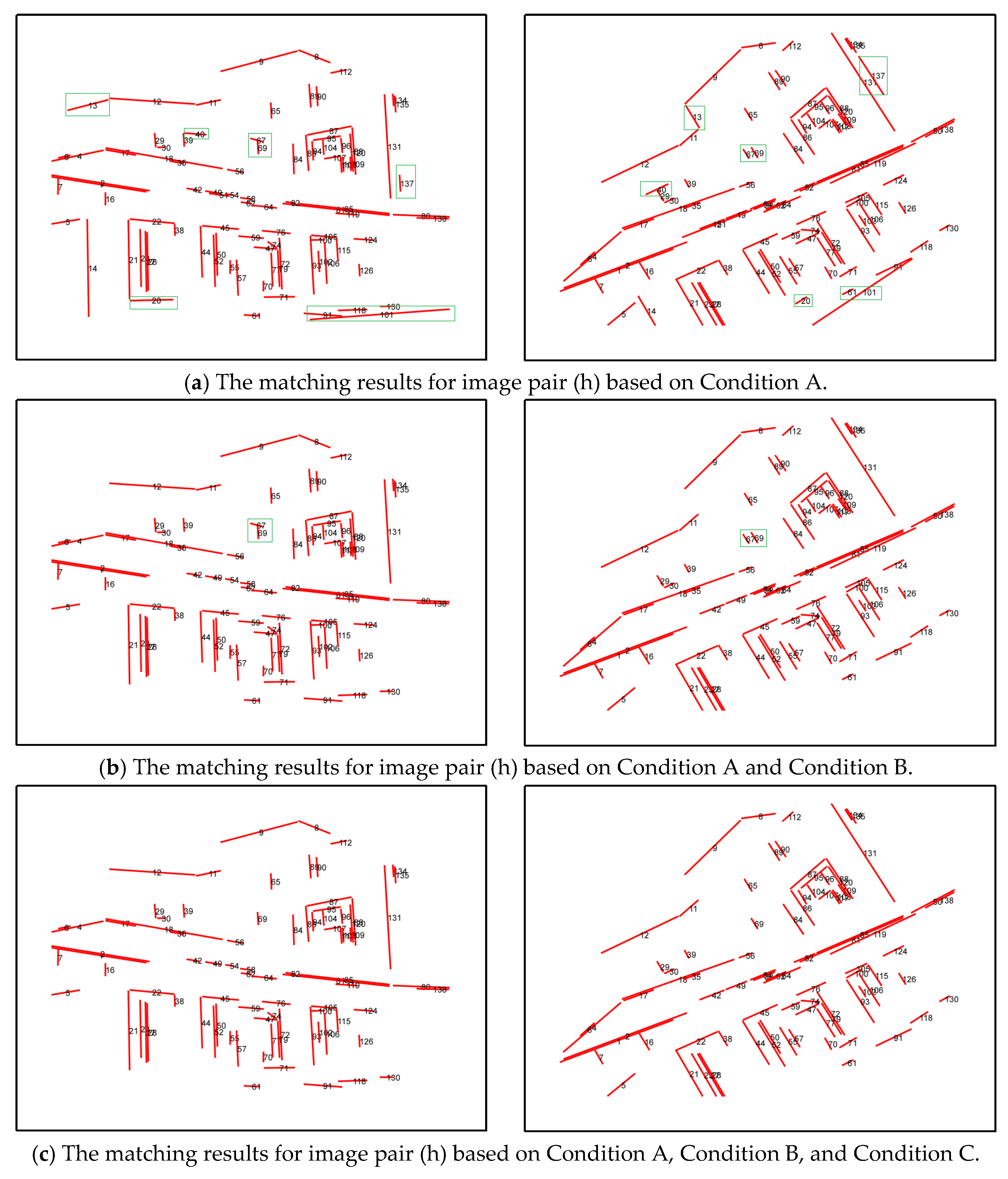
| Condition A: (MC/M/MP) | Condition A + B: (MC/M/MP) | Condition A + B + C: (MC/M/MP) | |
|---|---|---|---|
| (c) | 52/53/0.98 | 52/52/1.0 | 52/52/1.0 |
| (d) | 25/27/0.93 | 25/26/0.96 | 25/25/1.0 |
| (h) | 82/92/0.89 | 84/85/0.99 | 84/84/1.0 |
| LineTR (LSD) | SOLD2 | WLD (LSD) | Our Method (LSD) | |
|---|---|---|---|---|
| M/MC/MP | M/MC/MP | M/MC/MP | M/MC/MP | |
| (a) | 156/144/0.92 | 245/—/× | 253/—/× | 256/255/0.99 |
| (b) | 368/364/0.99 | 212/—/× | 413/—/× | 681/681/1.0 |
| (c) | 172/170/0.98 | 281/279/0.99 | 113/107/0.95 | 189/189/1.0 |
| (d) | 54/54/1.0 | 66/64/0.97 | 54/48/0.89 | 68/67/0.99 |
| (e) | 38/38/1.0 | 72/72/1.0 | 44/30/0.68 | 71/71/1.0 |
| (f) | 153/151/0.99 | 245/243/0.99 | 231/—/× | 130/129/0.99 |
| (g) | 18/18/1.0 | 48/36/0.75 | 57/—/× | 37/34/0.92 |
| (h) | 78/73/0.94 | 324/310/0.96 | 216/—/× | 278/278/1.0 |
| LBDfloat + FLANN | LBDbinary + FLANN | IILB + FLANN | Our Method | |||||
|---|---|---|---|---|---|---|---|---|
| (I1-line, I2-line)/M | MC/MP | (I1-line, I2-line)/M | MC/MP | (I1-line, I2-line)/M | MC/MP | (I1-line, I2-line)/M | MC/MP | |
| (a) | [220, 213]/63 | 63/1.0 | [220, 213]/114 | 108/0.95 | [220, 213]/37 | 35/0.94 | [220, 214]/126 | 126/1.0 |
| (b) | [380, 380]/0 | 0/0.0 | [380, 380]/304 | 298/0.98 | [380, 380]/5 | 0/0.0 | [380, 380]/307 | 307/1.0 |
| (c) | [70, 63]/51 | 51/1.0 | [70, 63]/46 | 46/1.0 | [70, 63]/39 | 39/1.0 | [70, 63]/52 | 52/1.0 |
| (d) | [34, 34]/25 | 25/1.0 | [34, 34]/22 | 22/1.0 | [34, 34]/17 | 17/1.0 | [34, 34]/25 | 25/1.0 |
| (e) | [23, 24]/21 | 21/1.0 | [23, 24]/18 | 18/1.0 | [23, 24]/11 | 11/1.0 | [23, 24]/19 | 19/1.0 |
| (f) | [35, 34]/0 | 0/0 | [35, 34]/10 | 7/0.7 | [35, 34]/0 | 0/0 | [35, 34]/13 | 12/0.92 |
| (g) | [37, 36]/14 | 13/0.93 | [37, 36]/16 | 15/0.94 | [37, 36]/10 | 9/0.9 | [37, 36]/19 | 18/0.95 |
| (h) | [139, 113]/32 | 32/1.0 | [139, 113]/56 | 53/0.95 | [139, 113]/22 | 21/0.95 | [139, 113]/84 | 84/1.0 |
| IILB + FLANN | Our Method | |||
|---|---|---|---|---|
| The Total Number of Line /The Total Matches (M) | MC/MP | The Total Number of Line /The Total Matches (M) | MC/MP | |
| (a–b) | [291, 250]/175 | 80/0.46 | [337, 304]/220 | 220/1.0 |
| (a–c) | [291, 224]/145 | 59/0.41 | [337, 279]/199 | 199/1.0 |
| (a–d) | [291, 210]/138 | 28/0.20 | [337, 244]/151 | 151/1.0 |
| (a–e) | [291, 177]/144 | 37/0.26 | [337, 222]/134 | 134/1.0 |
| (a–f) | [291, 174]/121 | 14/0.12 | [337, 189]/92 | 92/1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Ge, Y.; Gu, S. Bayesian–Geometric Fusion: A Probabilistic Framework for Robust Line Feature Matching. Electronics 2025, 14, 3783. https://doi.org/10.3390/electronics14193783
Zhang C, Ge Y, Gu S. Bayesian–Geometric Fusion: A Probabilistic Framework for Robust Line Feature Matching. Electronics. 2025; 14(19):3783. https://doi.org/10.3390/electronics14193783
Chicago/Turabian StyleZhang, Chenyang, Yufan Ge, and Shuo Gu. 2025. "Bayesian–Geometric Fusion: A Probabilistic Framework for Robust Line Feature Matching" Electronics 14, no. 19: 3783. https://doi.org/10.3390/electronics14193783
APA StyleZhang, C., Ge, Y., & Gu, S. (2025). Bayesian–Geometric Fusion: A Probabilistic Framework for Robust Line Feature Matching. Electronics, 14(19), 3783. https://doi.org/10.3390/electronics14193783






