Integrated FCS-MPC with Synchronous Optimal Pulse-Width Modulation for Enhanced Dynamic Performance in Two-Level Voltage-Source Inverters
Abstract
1. Introduction
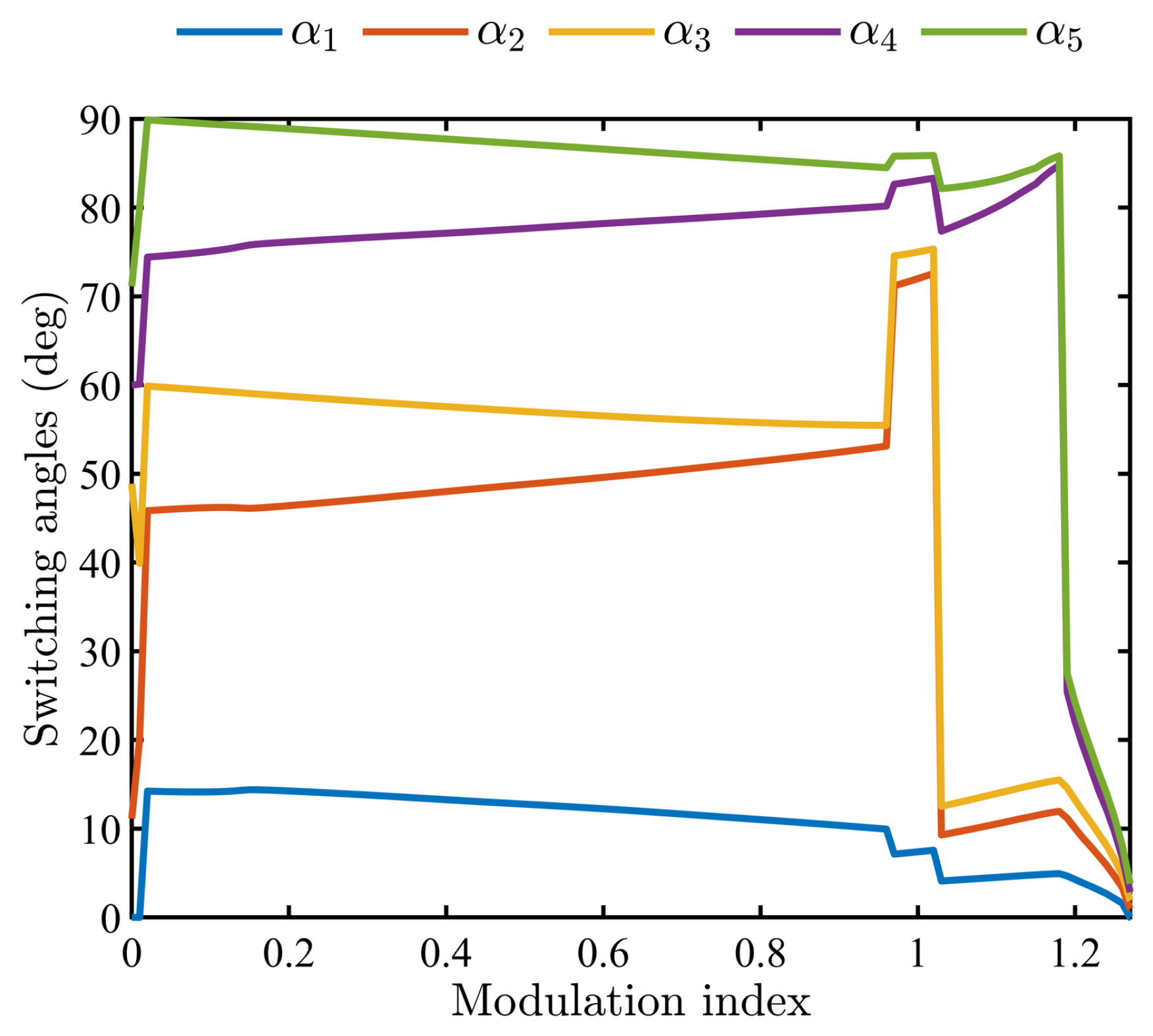
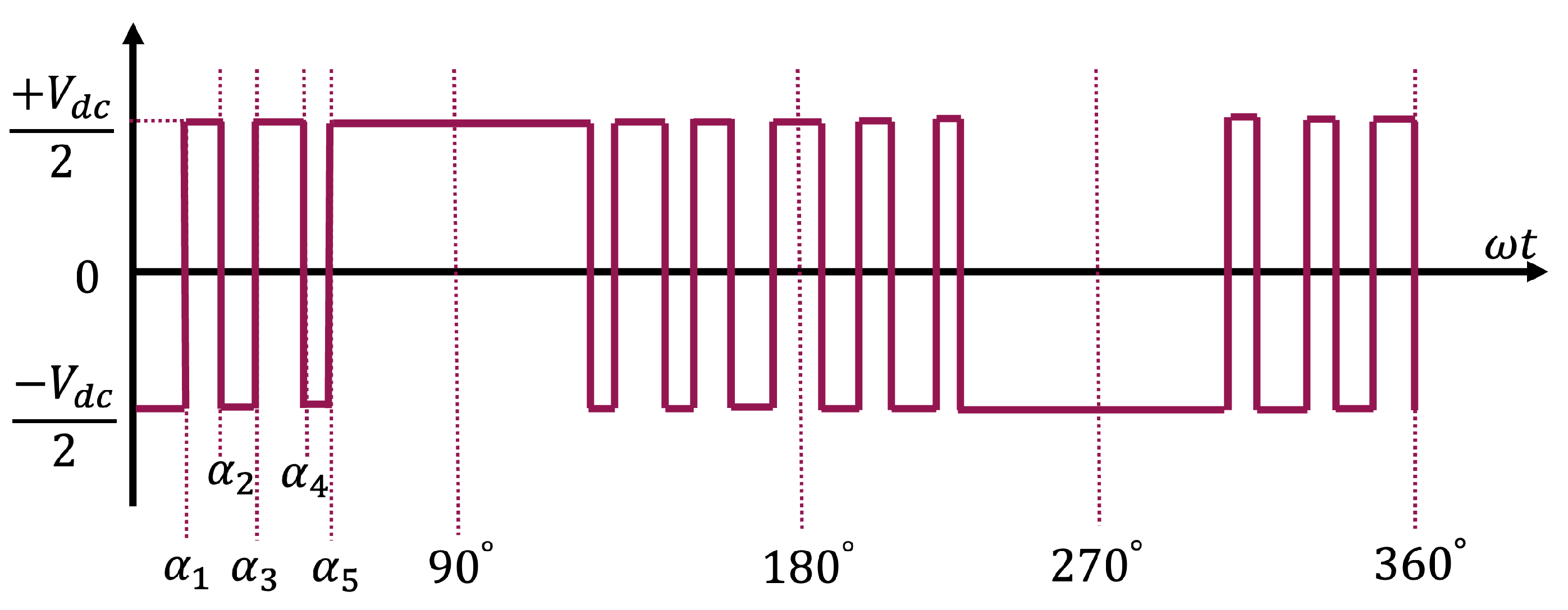
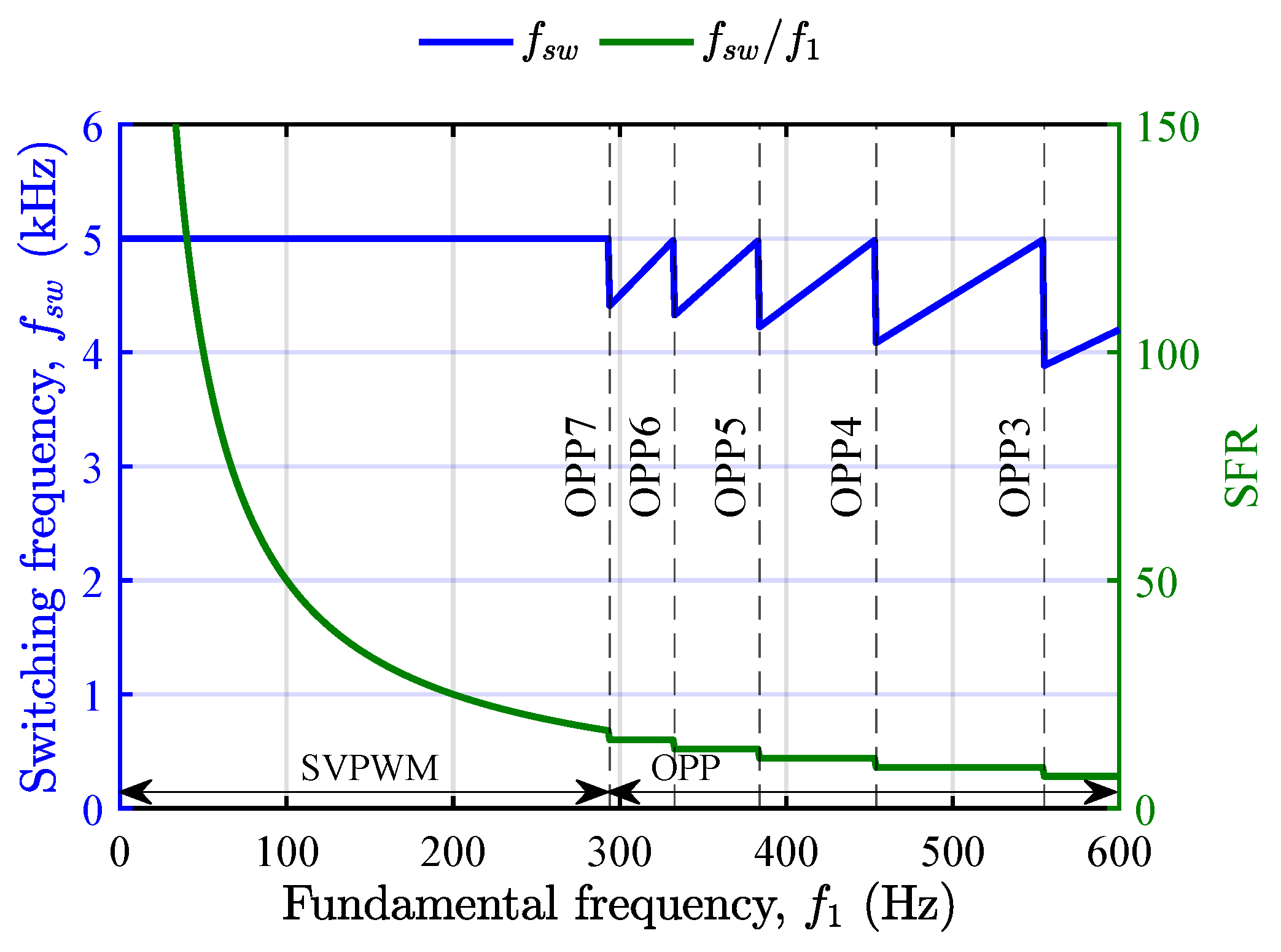
2. SOPWM Technique for 2L-VSI
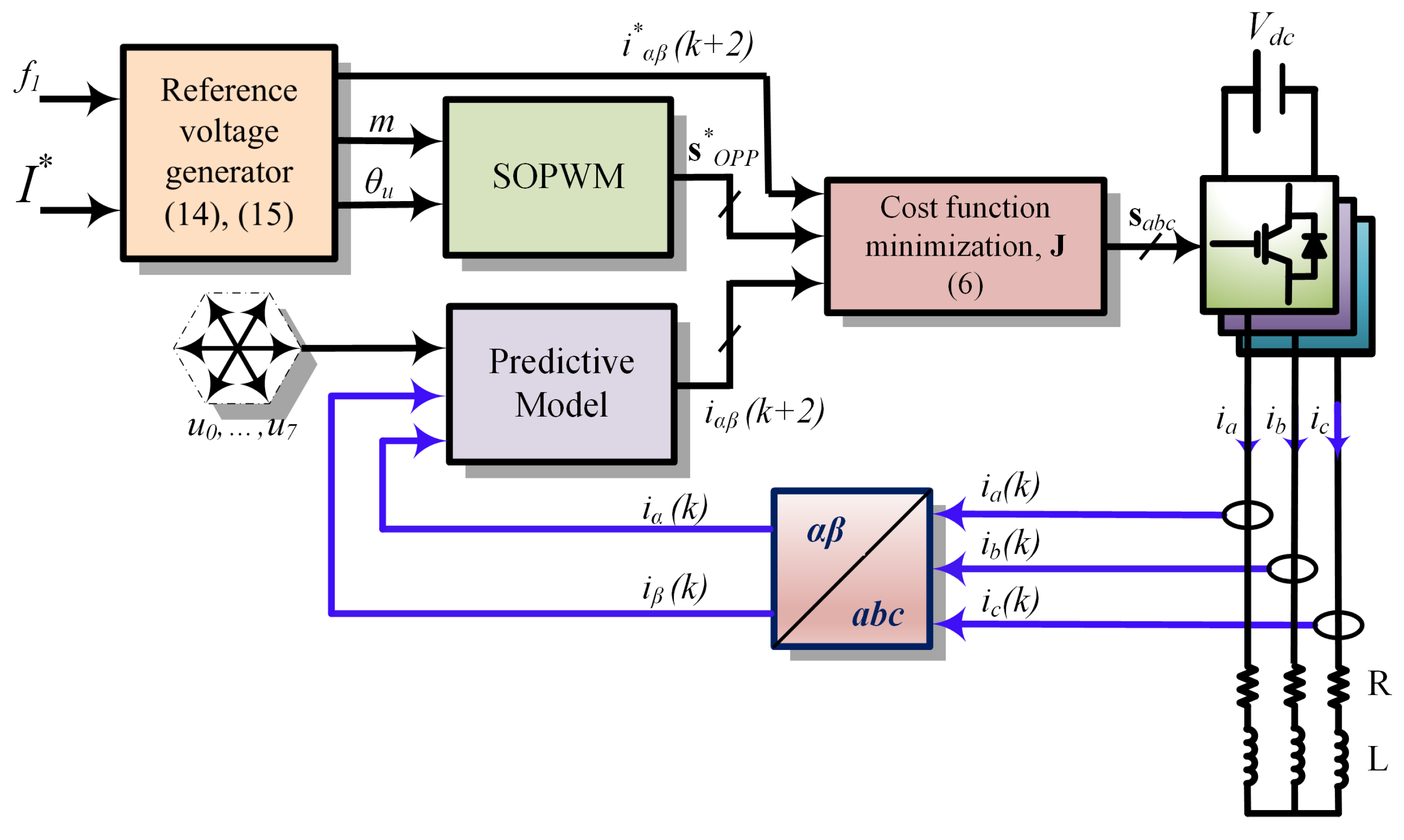
3. Simplified FCS-MPC with SOPWM
3.1. Cost Function Formulation
3.2. Current Tracking
3.3. SOPWM Pulse Pattern Tracking
3.4. Consecutive Switching Constraint
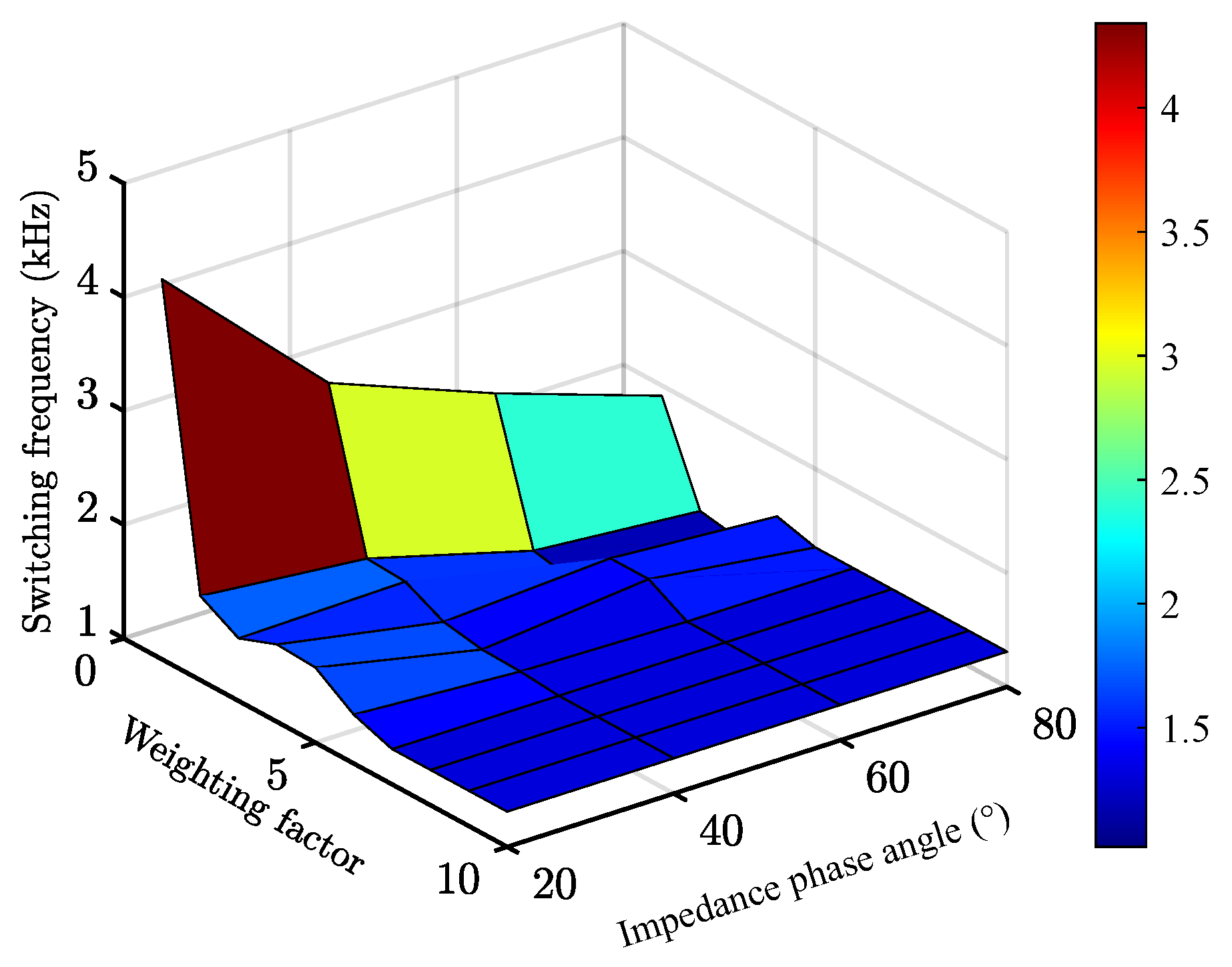
3.5. Proposed Weighting Factor Calculation
3.6. Proposed FCS-MPC with Variable Switching Strategy
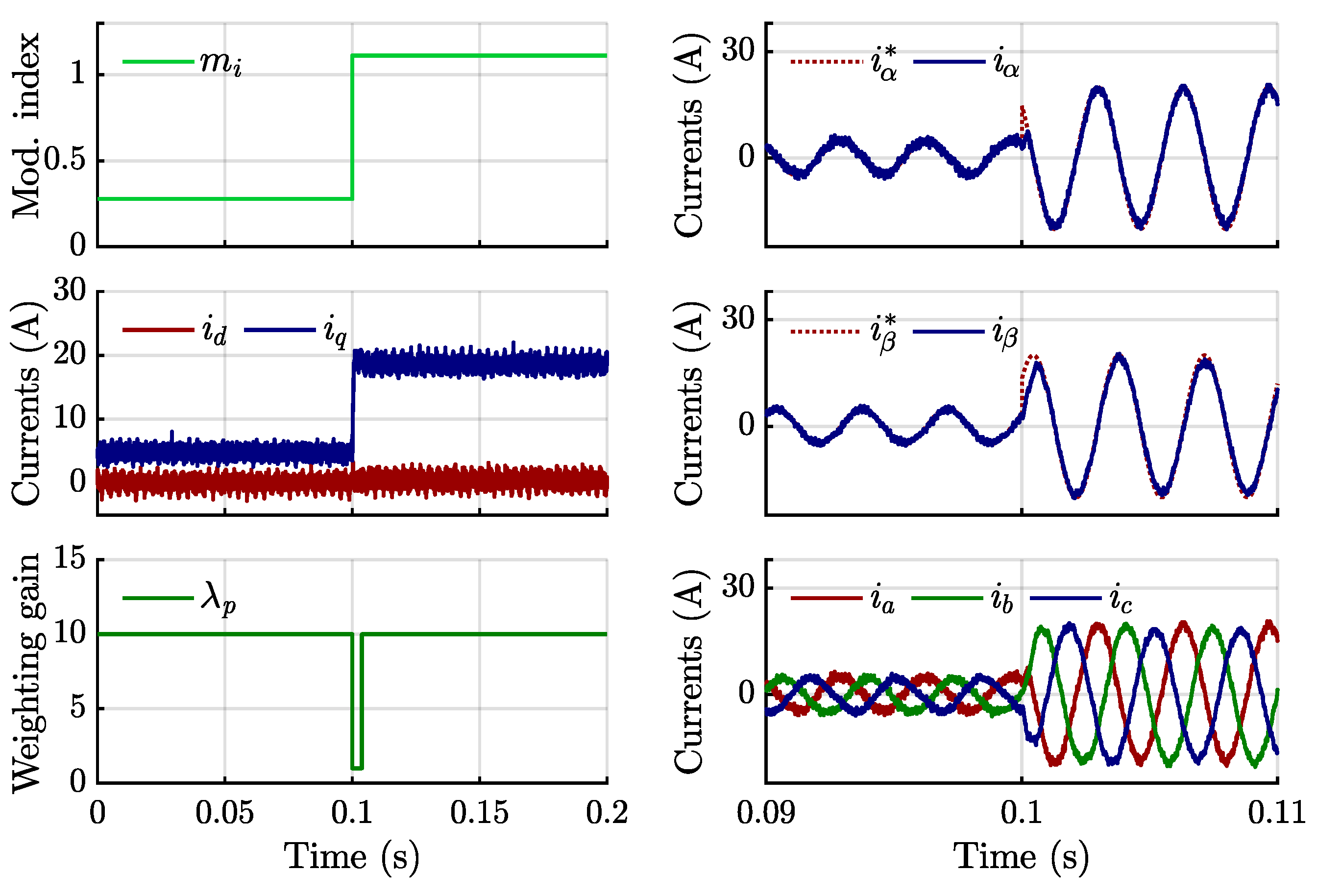
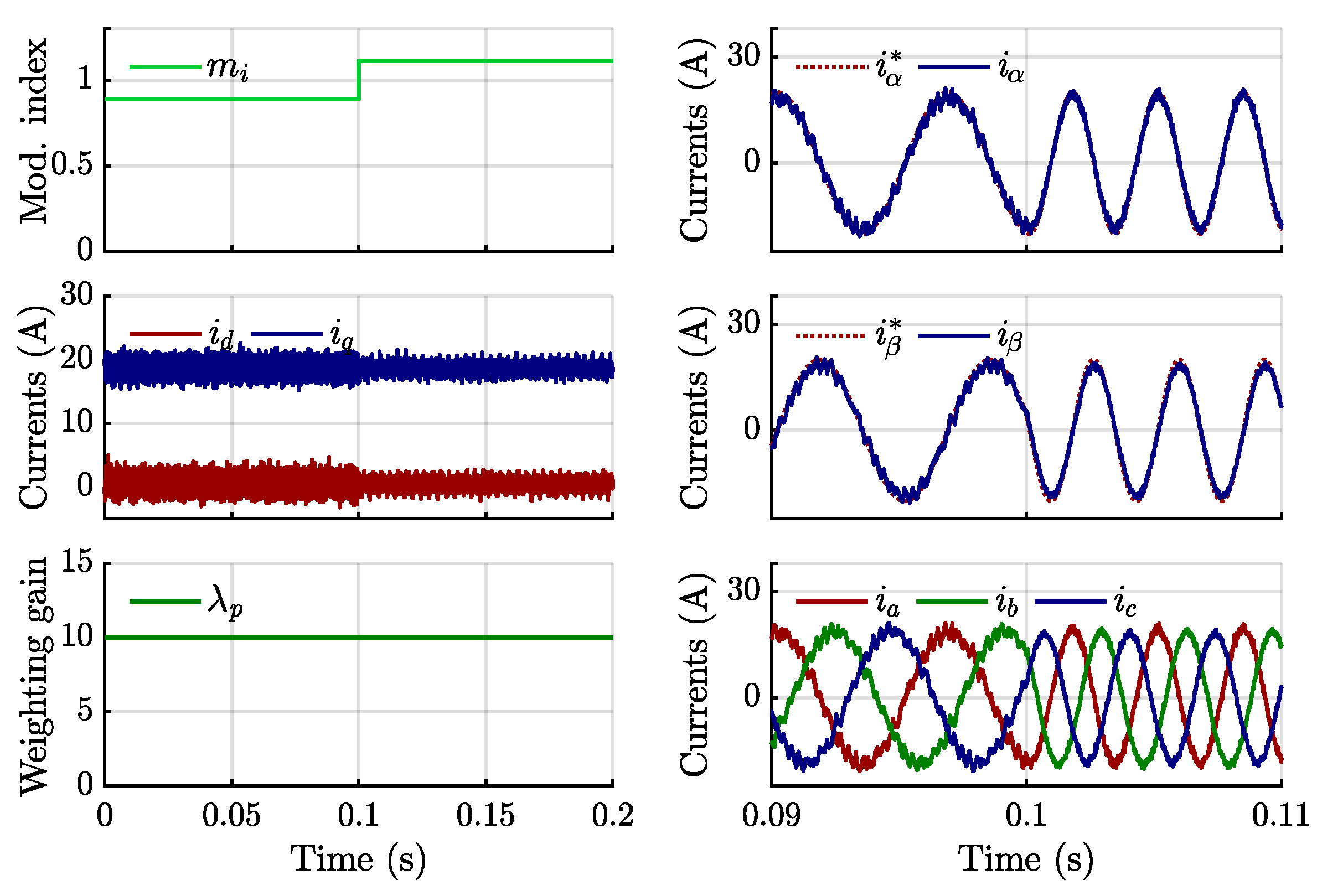
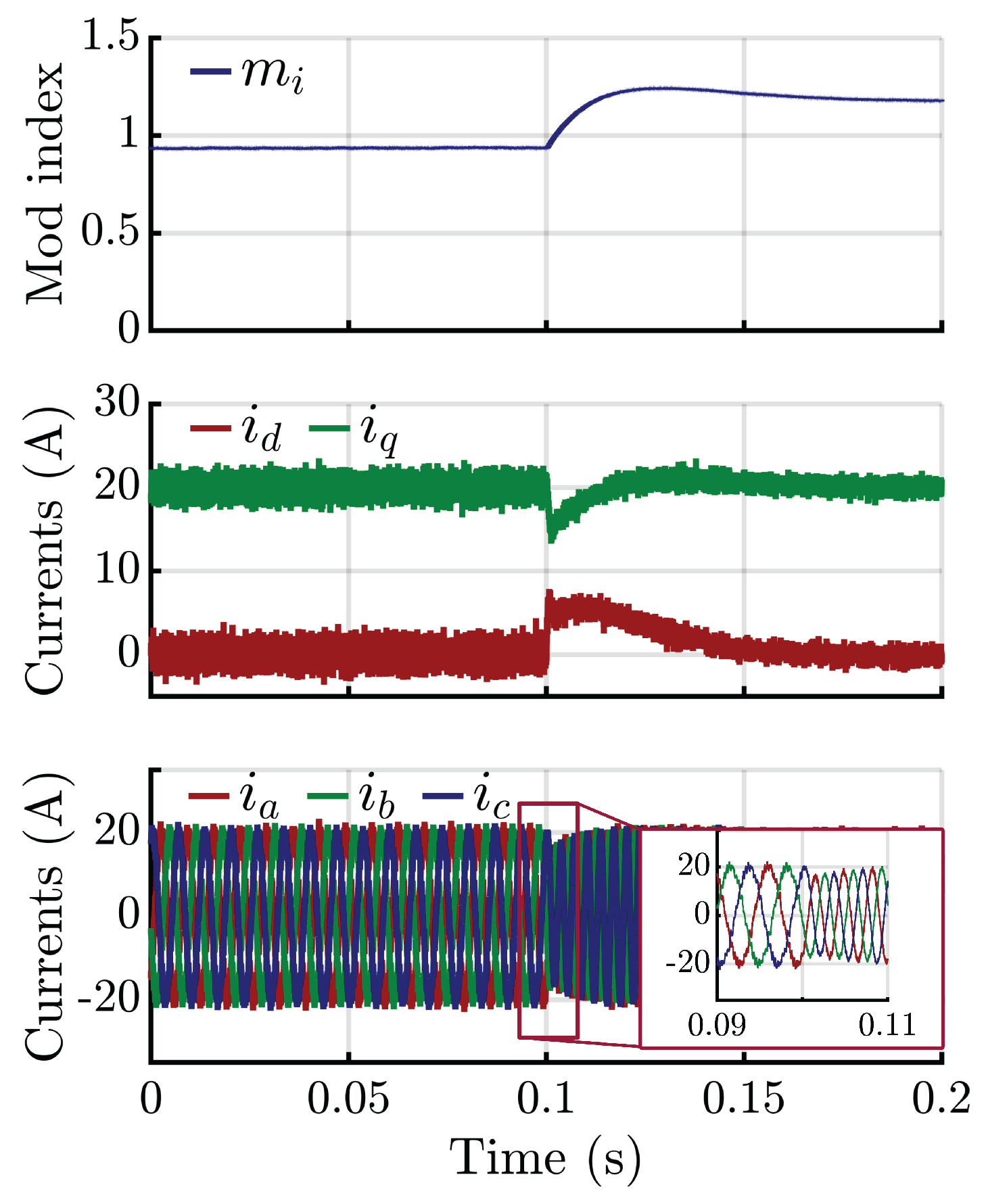
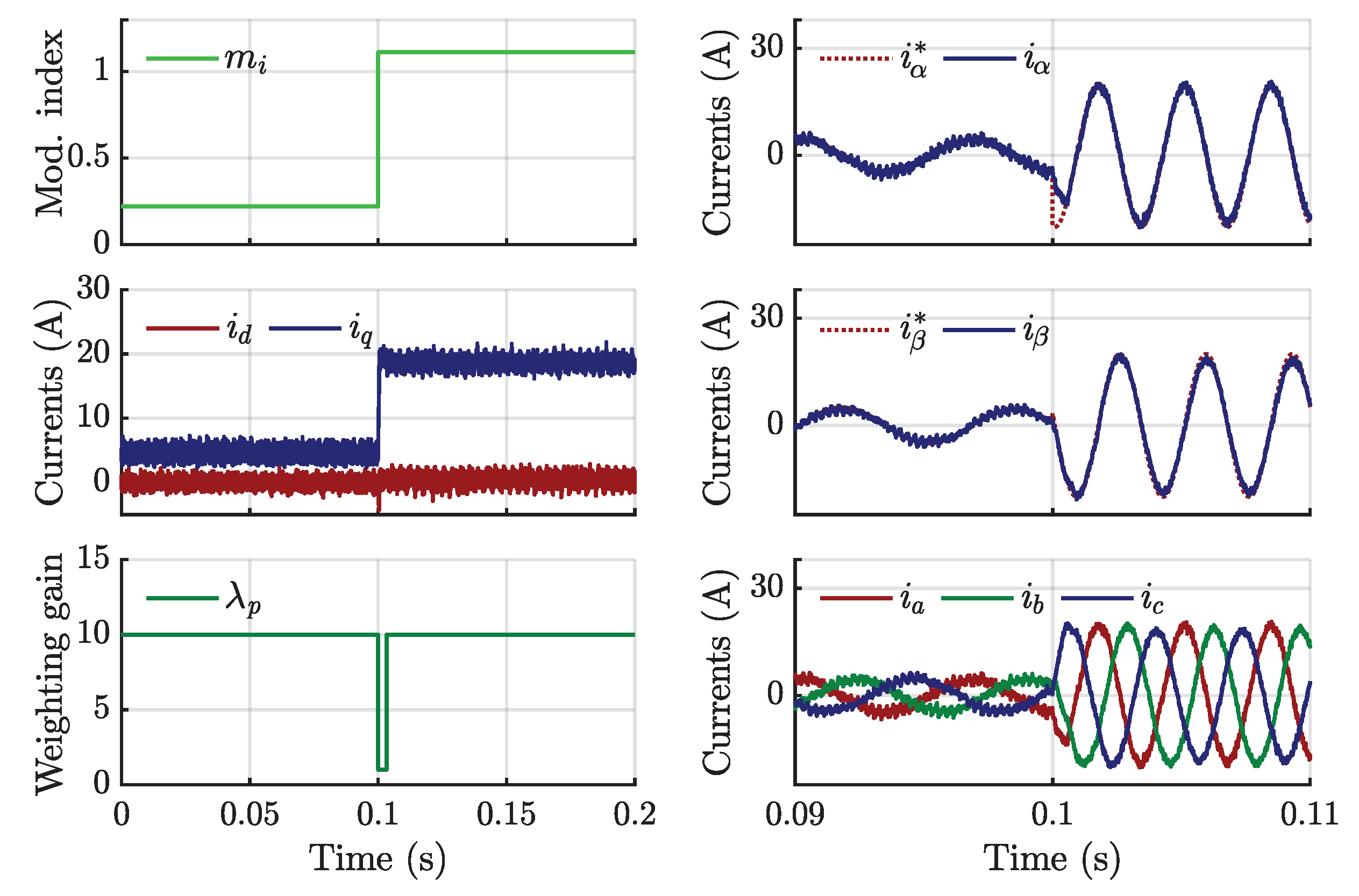
4. Simulation and Experimental Results
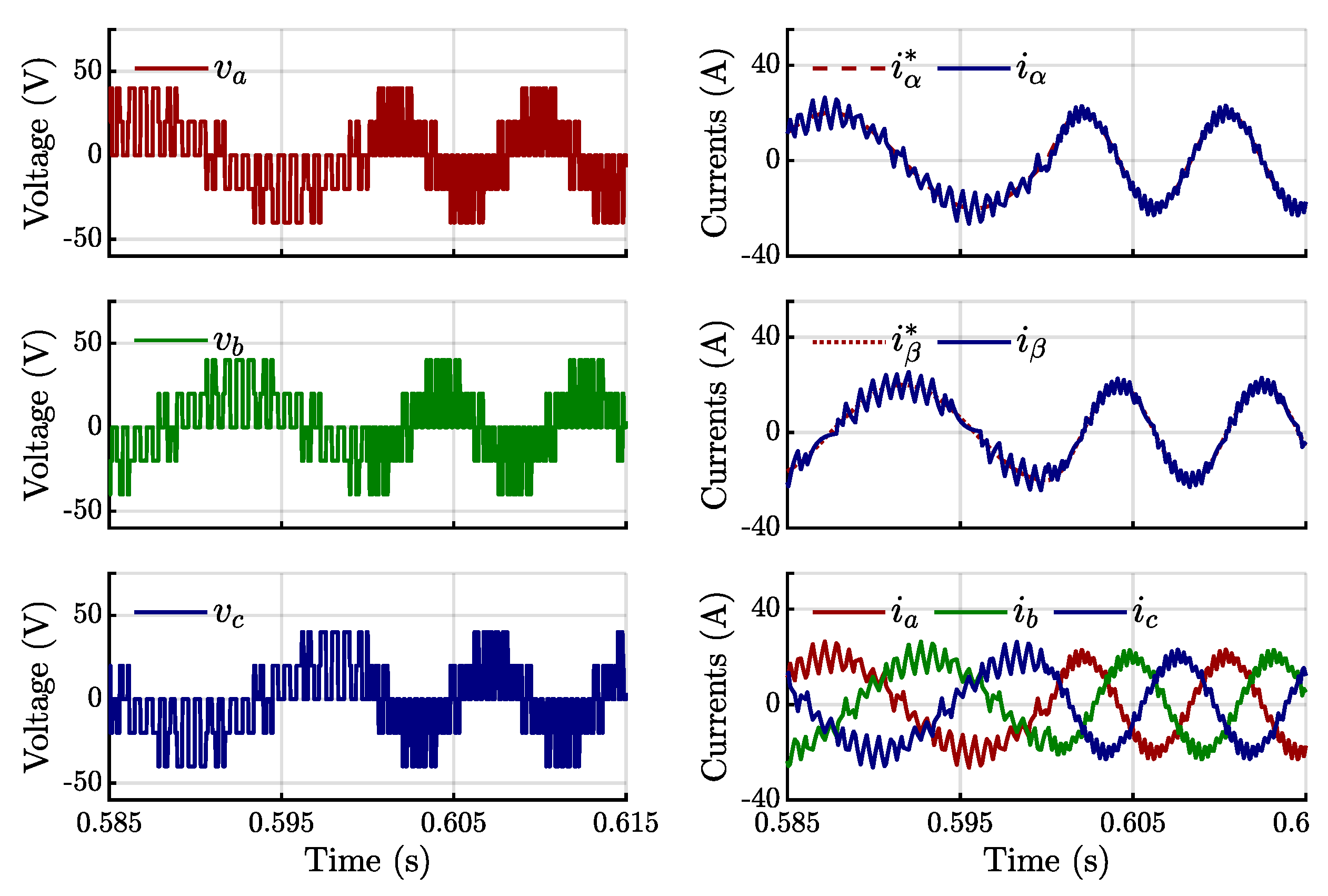
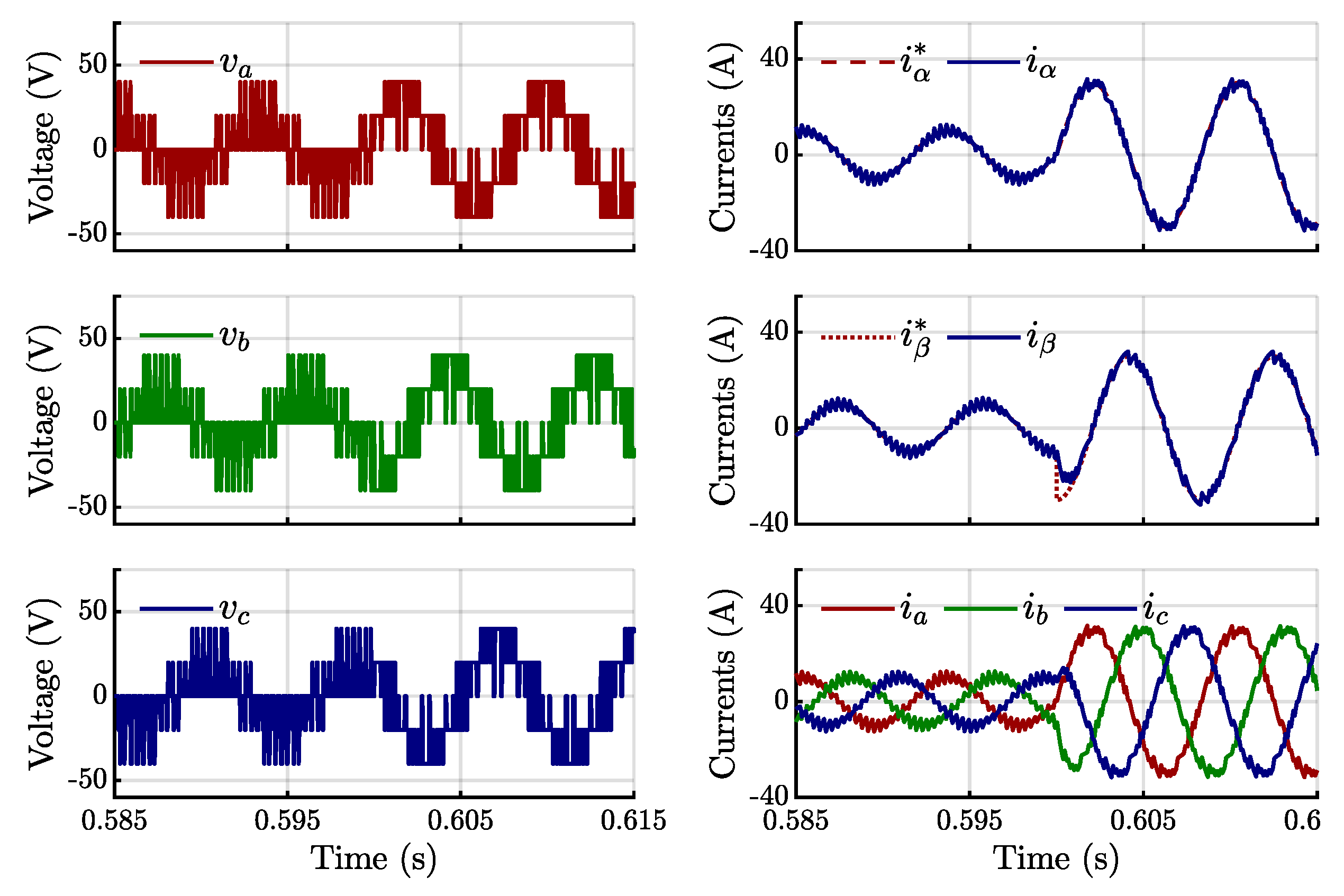
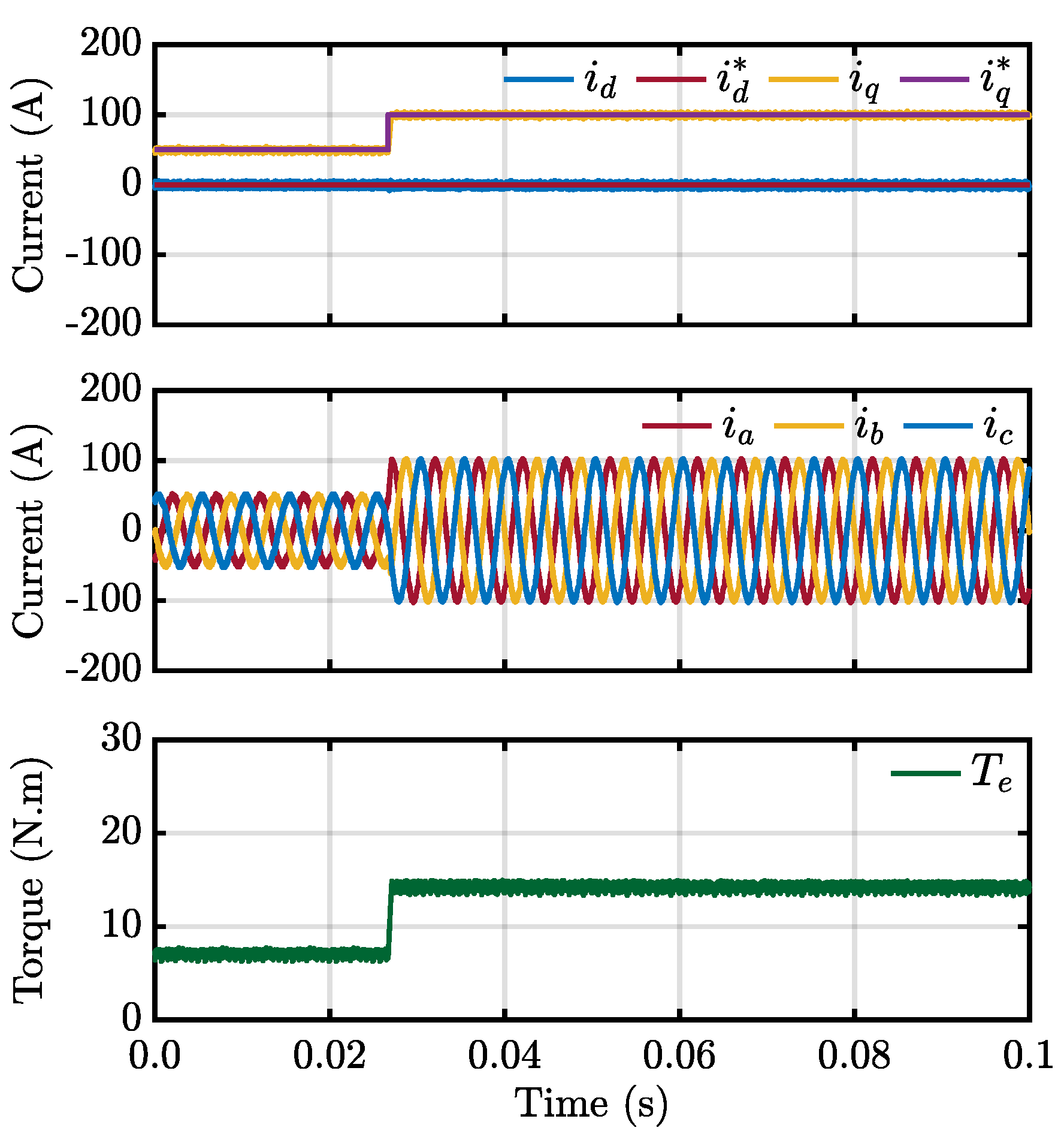
4.1. Simulation Results
4.2. Experimental Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2L | Two-level |
| FCS | Finite control set |
| MPC | Model predictive control |
| OPP | Optimal pulse pattern |
| PMSM | Permanent-magnet synchronous motor |
| QWS | Quarter-wave symmetry |
| SFR | Switching-to-fundamental frequency ratio |
| SHE | Selective harmonic elimination |
| SHM | Selective harmonic mitigation |
| SOPWM | Synchronous optimal pulse-width modulation |
| SVM | Space vector modulation |
| VSI | Voltage source inverter |
| WF | Weighting factor |
References
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Kouro, S.; Perez, M.A.; Rodriguez, J.; Llor, A.M.; Young, H.A. Model Predictive Control: MPC’s Role in the Evolution of Power Electronics. IEEE Ind. Electron. Mag. 2015, 9, 8–21. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Stellato, B.; Geyer, T.; Goulart, P.J. High-Speed Finite Control Set Model Predictive Control for Power Electronics. IEEE Trans. Power Electron. 2017, 32, 4007–4020. [Google Scholar] [CrossRef]
- Elmorshedy, M.F.; Xu, W.; El-Sousy, F.F.; Islam, M.R.; Ahmed, A.A. Recent achievements in model predictive control techniques for industrial motor: A comprehensive state-of-the-art. IEEE Access 2021, 9, 58170–58191. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest advances of model predictive control in electrical drives—Part I: Basic concepts and advanced strategies. IEEE Trans. Power Electron. 2022, 37, 3927–3942. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, S.A.; Rodas, J.; Valencia, D.F.; Elmorshedy, M.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest advances of model predictive control in electrical drives—Part II: Applications and benchmarking with classical control methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Lei, G.; Guo, Y.; Yang, Z.; Zhu, J. Finite-Control-Set Model Predictive Control of Permanent Magnet Synchronous Motor Drive Systems—An Overview. IEEE/CAA J. Autom. Sin. 2022, 9, 2087–2105. [Google Scholar] [CrossRef]
- Zafra, E.; Vazquez, S.; Geyer, T.; Aguilera, R.P.; Franquelo, L.G. Long Prediction Horizon FCS-MPC for Power Converters and Drives. IEEE Open J. Ind. Electron. Soc. 2023, 4, 159–175. [Google Scholar] [CrossRef]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model predictive control of power electronic systems: Methods, results, and challenges. IEEE Open J. Ind. Appl. 2020, 1, 95–114. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M.; Rossi, M.; Abdelrahem, M.; Trabelsi, M.; Ahmed, M.; et al. Model-Predictive Control of Multilevel Inverters: Challenges, Recent Advances, and Trends. IEEE Trans. Power Electron. 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Gonçalves, P.; Cruz, S.; Mendes, A. Finite control set model predictive control of six-phase asymmetrical machines—An overview. Energies 2019, 12, 4693. [Google Scholar]
- Zafra, E.; Vazquez, S.; Geyer, T.; Aguilera, R.P.; Freire, E.; Franquelo, L.G. Computational Analysis of the Long Horizon FCS-MPC Problem for Power Converters. IEEE Trans. Power Electron. 2024, 39, 12762–12773. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the design of finite control set model predictive controllers. IEEE Trans. Power Electron. 2020, 35, 7434–7450. [Google Scholar]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Vazquez, S. Enhanced Switching Frequency Control in FCS-MPC for Power Converters. IEEE Trans. Ind. Electron. 2021, 68, 2470–2479. [Google Scholar] [CrossRef]
- Keusch, R.; Loeliger, H.A.; Geyer, T. Long-Horizon Direct Model Predictive Control for Power Converters With State Constraints. IEEE Trans. Control Syst. Technol. 2024, 32, 340–350. [Google Scholar]
- Zafra, E.; Vazquez, S.; Dragičević, T.; Alcaide, A.M.; Leon, J.I.; Franquelo, L.G. Prediction Window Selection in FCS-MPC for Two-Level VSI Applications. IEEE Trans. Power Electron. 2024, 39, 3135–3143. [Google Scholar]
- Carrillo-Ríos, J.; González-Prieto, A.; González-Prieto, I.; Aciego, J.J.; Lara-López, R.; Mora-Moreno, P.; Durán, M.J. Reevaluating the Role of Single-Vector FCS-MPC for Multiphase Electric Drives. IEEE Trans. Power Electron. 2025, 40, 3419–3429. [Google Scholar]
- Yang, L.; Li, H.; Yang, J.; Li, S.; Meng, Q.; Zhang, M. Finite Control Set Model Predictive Current Control with Constant Switching Frequency Regulation for PMSM Drives. IEEJ Trans. Electr. Electron. Eng. 2025, 20, 1649–1659. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Yang, K.; Guo, Y.; Saeed, M.S.R. A Computationally Efficient Finite Control Set Model Predictive Control for Multiphase PMSM Drives. IEEE Trans. Ind. Electron. 2022, 69, 12066–12076. [Google Scholar] [CrossRef]
- Sun, J.; Yang, Y.; Chen, R.; Zhang, X.; Lim, C.S.; Rodriguez, J. An Efficient Multi-Vector-Based Model Predictive Current Control for PMSM Drive. CPSS Trans. Power Electron. Appl. 2024, 9, 79–89. [Google Scholar] [CrossRef]
- González-Prieto, I.; Duran, M.J.; Gonzalez-Prieto, A.; Aciego, J.J. A Simple Multistep Solution for Model Predictive Control in Multiphase Electric Drives. IEEE Trans. Ind. Electron. 2024, 71, 1158–1169. [Google Scholar] [CrossRef]
- Vazquez, S.; Marino, D.; Zafra, E.; Peña, M.D.V.; Rodríguez-Andina, J.J.; Franquelo, L.G.; Manic, M. An artificial intelligence approach for real-time tuning of weighting factors in FCS-MPC for power converters. IEEE Trans. Ind. Electron. 2022, 69, 11987–11998. [Google Scholar] [CrossRef]
- Yang, X.; Li, J.; Wang, K.; Kim, U.; Zhang, Z.; Park, K.B. A Weighting Factor Design Approach for FCS-MPC Techniques Based on PSO and K-Means Algorithm. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar]
- Notash, F.Y.; Luckett, B.; He, J. A Simplified Fixed Switching Frequency Model Predictive Control for an AFPM Motor Drive in a Distributed Electric Aircraft Propulsion System. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 4690–4697. [Google Scholar]
- Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. A Fuzzy Approximation for FCS-MPC in Power Converters. IEEE Trans. Power Electron. 2022, 37, 9153–9163. [Google Scholar] [CrossRef]
- Zerdali, E.; Rivera, M.; Wheeler, P. A Review on Weighting Factor Design of Finite Control Set Model Predictive Control Strategies for AC Electric Drives. IEEE Trans. Power Electron. 2024, 39, 9967–9981. [Google Scholar] [CrossRef]
- Wang, F.; Xie, H.; Chen, Q.; Davari, S.A.; Rodríguez, J.; Kennel, R. Parallel predictive torque control for induction machines without weighting factors. IEEE Trans. Power Electron. 2020, 35, 1779–1788. [Google Scholar] [CrossRef]
- Yan, S.; Li, C.; Cui, Y.; Zhang, H.; Yang, Q. A Low Computing FCS-MPC Based on Voltage Vector Tracking Algorithm With CMVs Suppression and Capacitor Charging Balance Algorithm Without Weight Factors for ANPC 3P-5L Converters. IEEE Trans. Power Electron. 2024, 39, 5361–5370. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Wu, D.; Zhao, J.; Hu, Y. Model predictive current control with lower switching frequency for permanent magnet synchronous motor drives. IET Electr. Power Appl. 2022, 16, 267–276. [Google Scholar] [CrossRef]
- He, K.; Li, J.; Xiao, L.; Lu, Y.; Wu, L.; Chen, H. Synchronous Optimal PWM With Continuous Switching-to-Fundamental Frequency Ratio. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1466–1476. [Google Scholar] [CrossRef]
- Han, Y.; Gong, C.; Yan, L.; Wen, H.; Wang, Y.; Shen, K. Multiobjective Finite Control Set Model Predictive Control Using Novel Delay Compensation Technique for PMSM. IEEE Trans. Power Electron. 2020, 35, 11193–11204. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z. Multi-Stage Series Model Predictive Control for PMSM Drives. IEEE Trans. Veh. Technol. 2021, 70, 6591–6600. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Z.; Hua, W.; Wang, Z.; Cheng, M. A Hybrid Dual-Mode Control for Permanent-Magnet Synchronous Motor Drives. IEEE Access 2020, 8, 105864–105873. [Google Scholar] [CrossRef]
- Geyer, T. Model Predictive Control of High Power Converters and Industrial Drives, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Batkhishig, B.; Gonçalves, P.F.D.C.; Pietrini, G.; Nahid-Mobarakeh, B.; Emadi, A. PWM Techniques for Two-Level Voltage Source Inverters: A Comparative Study. IEEE Access 2025, 13, 86235–86255. [Google Scholar] [CrossRef]
- Rosado, L.; Samanes, J.; Gubia, E.; Lopez, J. Selective Harmonic Mitigation: Limitations of Classical Control Strategies and Benefits of Model Predictive Control. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar]
- Subramanian, N.; Stonier, A.A. A Comprehensive Review on Selective Harmonic Elimination Techniques and Its Permissible Standards in Electrical Systems. IEEE Access 2024, 12, 141966–141998. [Google Scholar] [CrossRef]
- Rosado, L.; Samanes, J.; Gubia, E.; Lopez, J. Selective Harmonic Mitigation: Limitations of Classical Control Strategies and Benefits of Model Predictive Control. IEEE Trans. Ind. Appl. 2023, 59, 6082–6094. [Google Scholar] [CrossRef]
- Vijayan, A.K.; Batkhishig, B.; Gonçalves, P.F.d.C.; Pietrini, G.; Baranwal, R.; Nahid-Mobarakeh, B.; Emadi, A. Torque Harmonic Minimization Optimal Pulse Pattern Modulation Technique for Permanent-Magnet Synchronous Motors. IEEE Trans. Transp. Electrif. 2025, 11, 8115–8127. [Google Scholar] [CrossRef]
- Geyer, T. A Comparison of Control and Modulation Schemes for Medium-Voltage Drives: Emerging Predictive Control Concepts Versus PWM-Based Schemes. IEEE Trans. Ind. Appl. 2011, 47, 1380–1389. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Acuña, P.; Lezana, P.; Konstantinou, G.; Wu, B.; Bernet, S.; Agelidis, V.G. Selective Harmonic Elimination Model Predictive Control for Multilevel Power Converters. IEEE Trans. Power Electron. 2017, 32, 2416–2426. [Google Scholar] [CrossRef]
- Karuvaril Vijayan, A.; Xiao, D.; Nahid-Mobarakeh, B.; Emadi, A. Synchronous Optimal Pulsewidth Modulation for High-Power AC Motor Drives: A Review. IEEE Trans. Transp. Electrif. 2024, 10, 3976–3990. [Google Scholar] [CrossRef]
- Rathore, A.K.; Holtz, J.; Boller, T. Synchronous Optimal Pulsewidth Modulation for Low-Switching-Frequency Control of Medium-Voltage Multilevel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2374–2381. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Model Predictive Control of Wing Energy Conversion Systems, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2016. [Google Scholar]
- Yang, H.; Zhang, Y.; Yuan, G.; Walker, P.D.; Zhang, N. Hybrid Synchronized PWM Schemes for Closed-Loop Current Control of High-Power Motor Drives. IEEE Trans. Ind. Electron. 2017, 64, 6920–6929. [Google Scholar] [CrossRef]
- Wang, Y.; Wen, X.; Guo, X.; Zhao, F.; Cong, W. Vector control of induction motor based on selective harmonic elimination PWM in medium voltage high power propulsion system. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 6351–6354. [Google Scholar]
- Batkhishig, B.; Gonçalves, P.F.d.C.; Pietrini, G.; Nahid-Mobarakeh, B.; Baranwal, R.; Emadi, A. Enhanced Hybrid PWM for the Closed-Loop Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Transp. Electrif. 2024, 11, 3785–3795. [Google Scholar] [CrossRef]




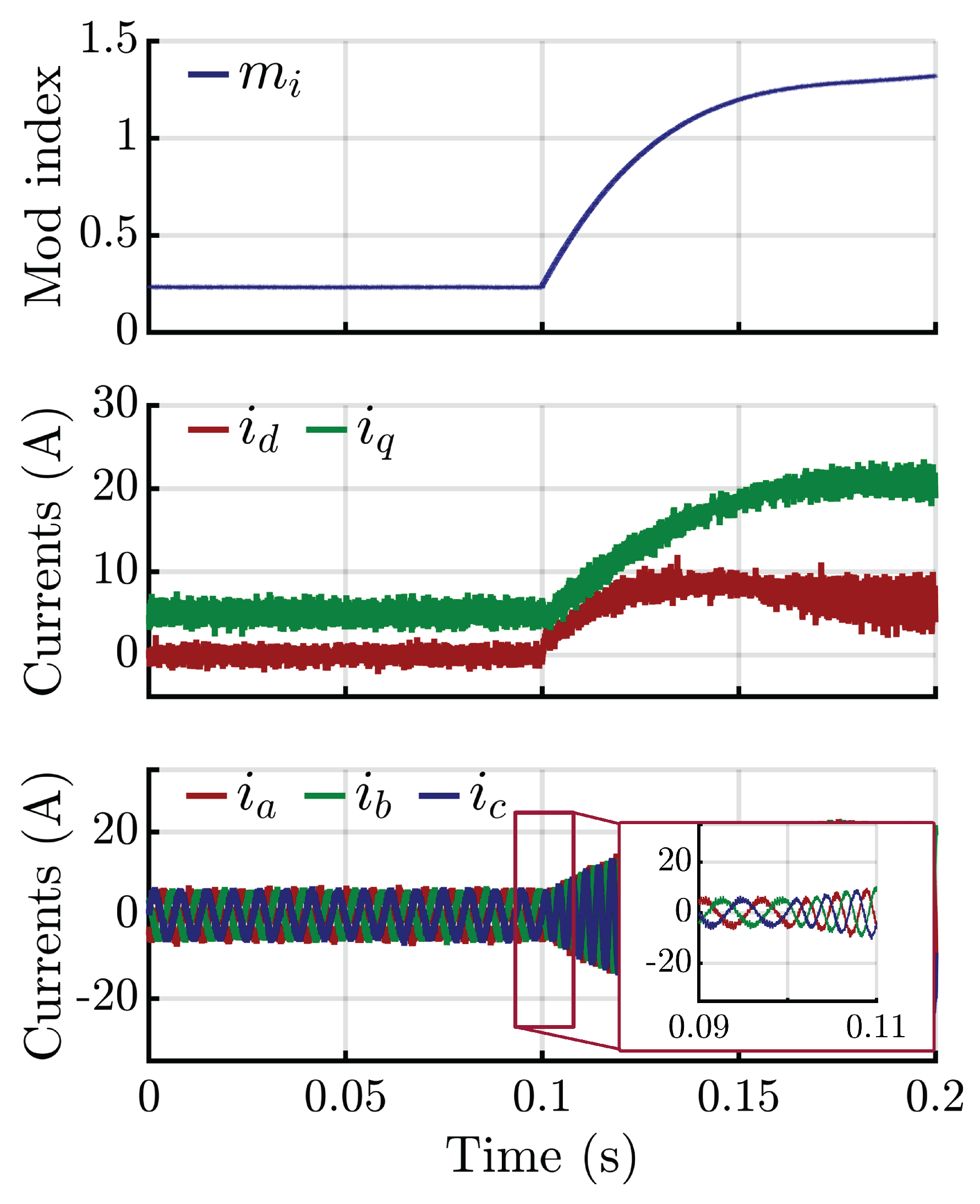
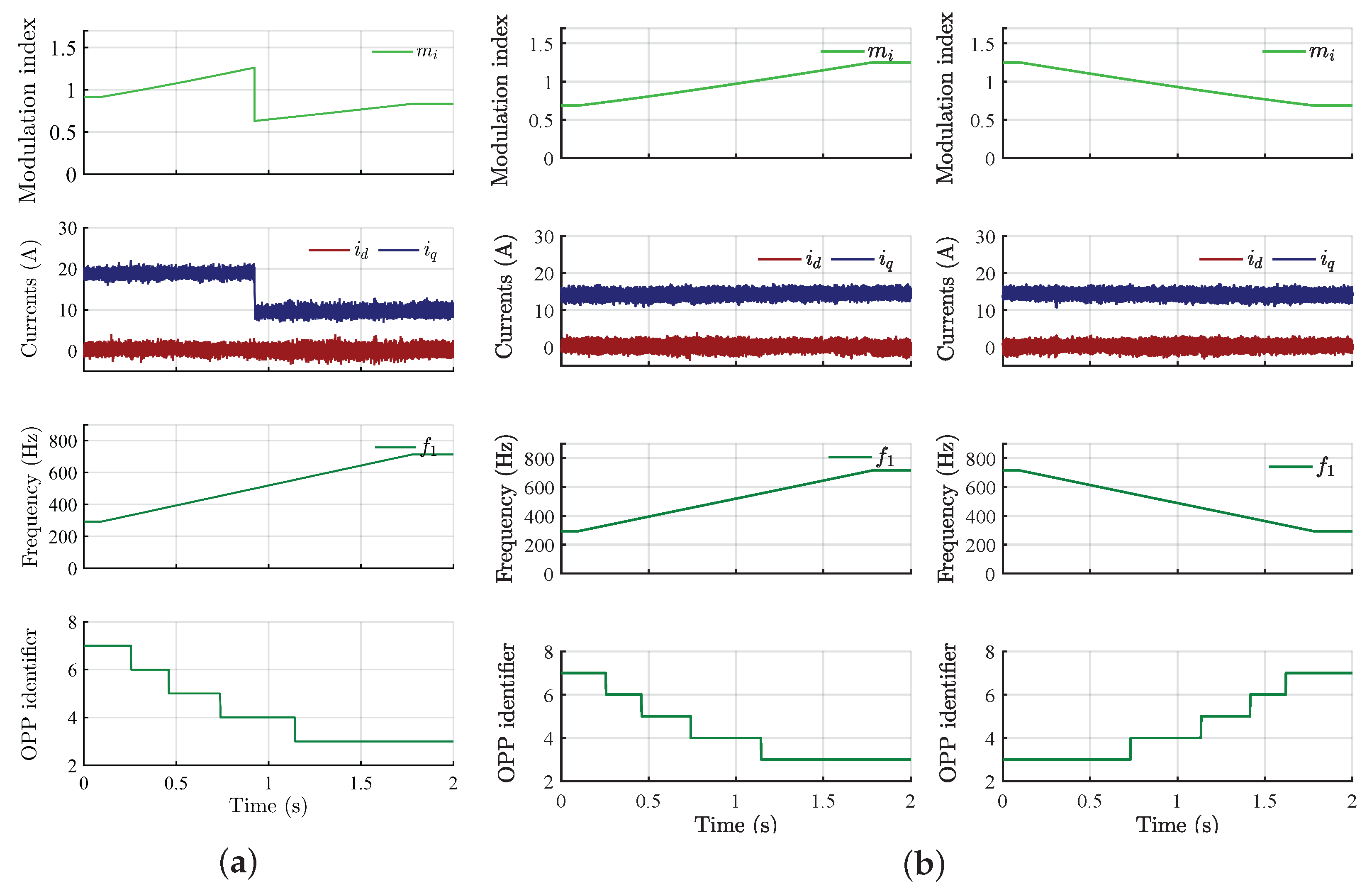
| Parameter | Value |
|---|---|
| DC-link voltage () | 50 V |
| Load resistor (R) | 1 |
| Load inductor (L) | 516 μH |
| Sampling frequency | 20 kHz |
| Controller setting () | 1 (transient) or 10 (steady state) |
| Controller setting () | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vijayan, A.K.; da Costa Gonçalves, P.F.; Batkhishig, B.; Nahid-Mobarakeh, B.; Emadi, A. Integrated FCS-MPC with Synchronous Optimal Pulse-Width Modulation for Enhanced Dynamic Performance in Two-Level Voltage-Source Inverters. Electronics 2025, 14, 3757. https://doi.org/10.3390/electronics14193757
Vijayan AK, da Costa Gonçalves PF, Batkhishig B, Nahid-Mobarakeh B, Emadi A. Integrated FCS-MPC with Synchronous Optimal Pulse-Width Modulation for Enhanced Dynamic Performance in Two-Level Voltage-Source Inverters. Electronics. 2025; 14(19):3757. https://doi.org/10.3390/electronics14193757
Chicago/Turabian StyleVijayan, Aathira Karuvaril, Pedro F. da Costa Gonçalves, Battur Batkhishig, Babak Nahid-Mobarakeh, and Ali Emadi. 2025. "Integrated FCS-MPC with Synchronous Optimal Pulse-Width Modulation for Enhanced Dynamic Performance in Two-Level Voltage-Source Inverters" Electronics 14, no. 19: 3757. https://doi.org/10.3390/electronics14193757
APA StyleVijayan, A. K., da Costa Gonçalves, P. F., Batkhishig, B., Nahid-Mobarakeh, B., & Emadi, A. (2025). Integrated FCS-MPC with Synchronous Optimal Pulse-Width Modulation for Enhanced Dynamic Performance in Two-Level Voltage-Source Inverters. Electronics, 14(19), 3757. https://doi.org/10.3390/electronics14193757







