Multi-Branch Knowledge-Assisted Proximal Policy Optimization for Design of MS-to-MS Vertical Transition with Multi-Layer Pixel Structures
Abstract
1. Introduction
2. Proposed Structure
3. The Proposed Design Method
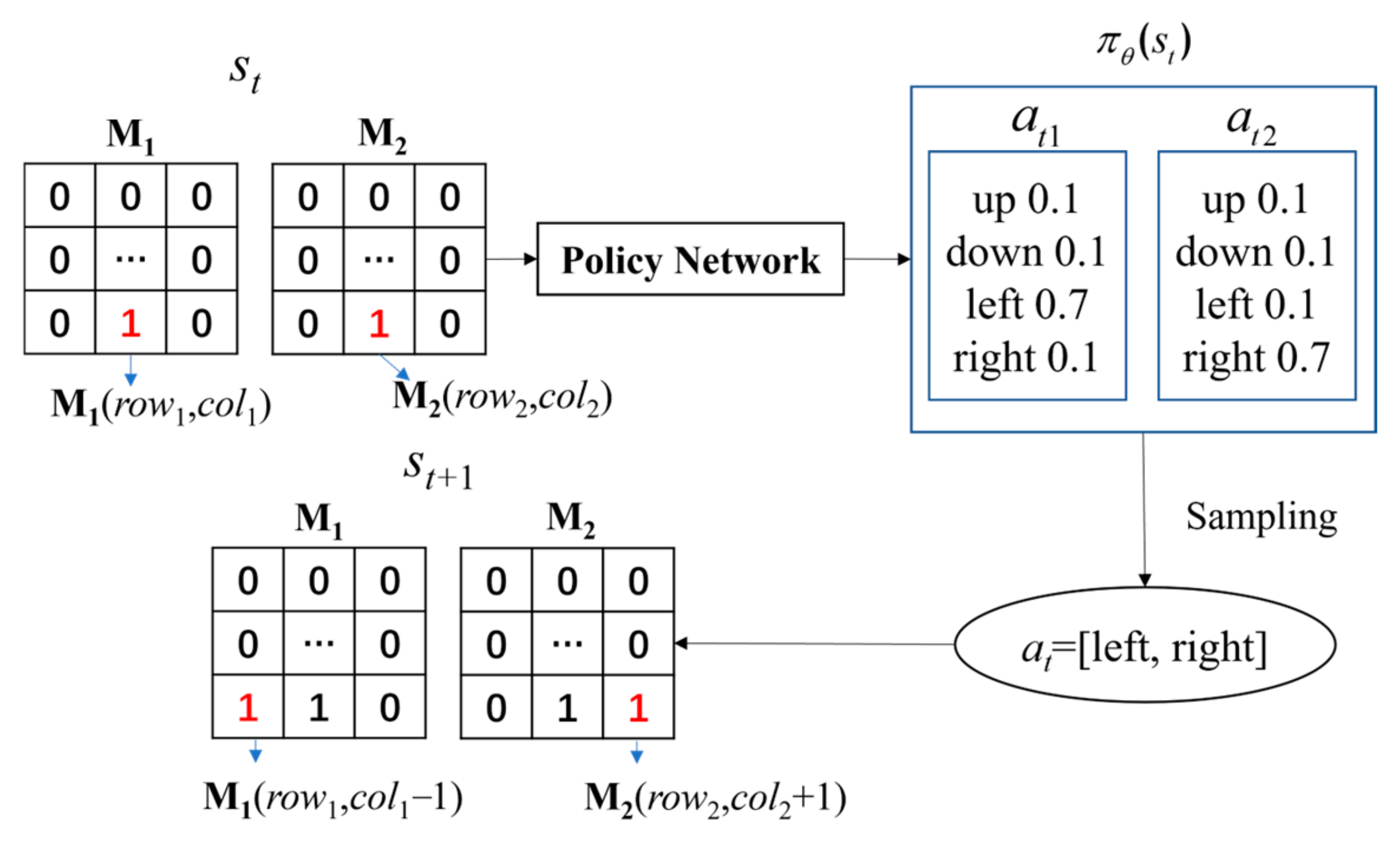
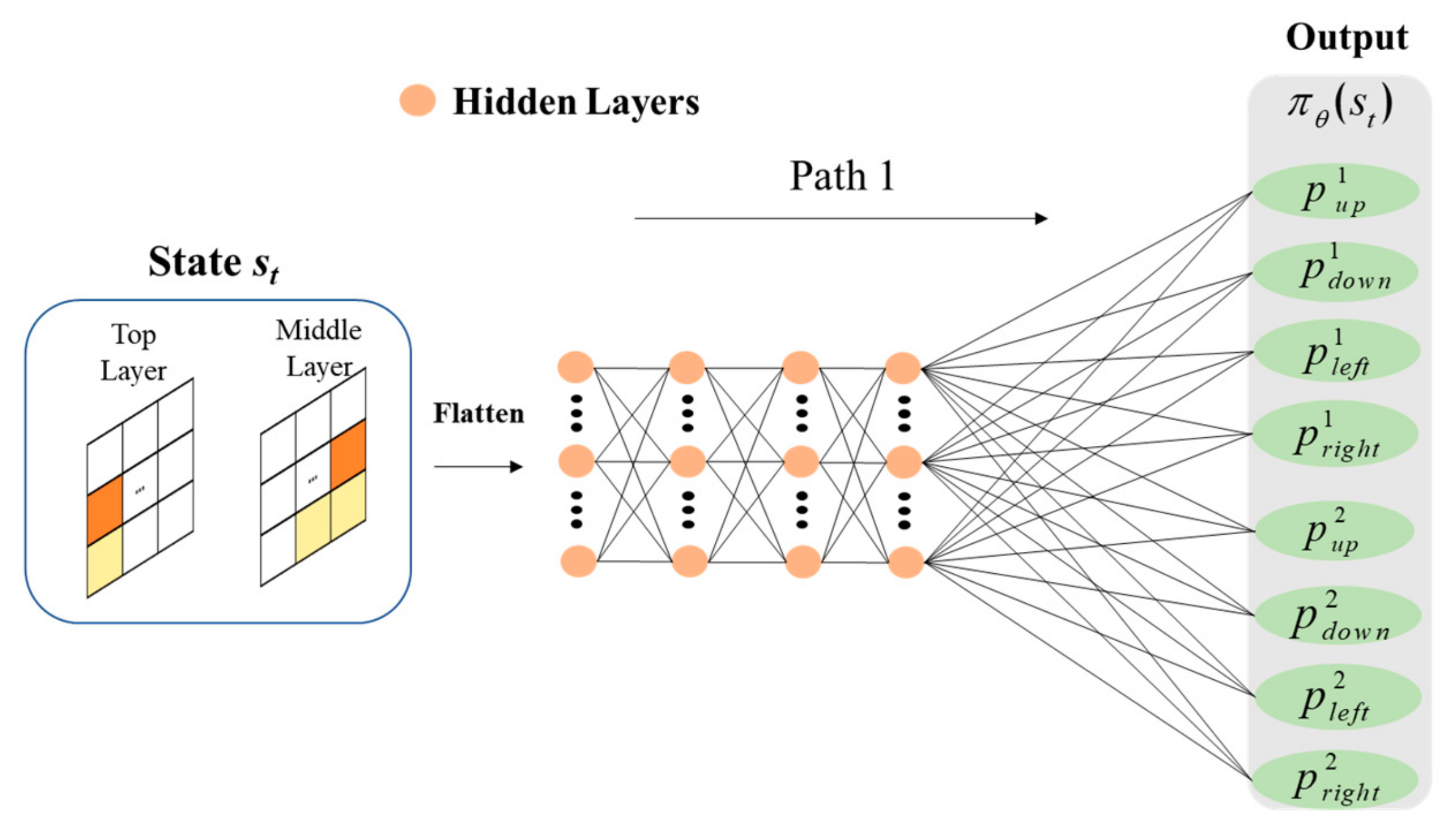
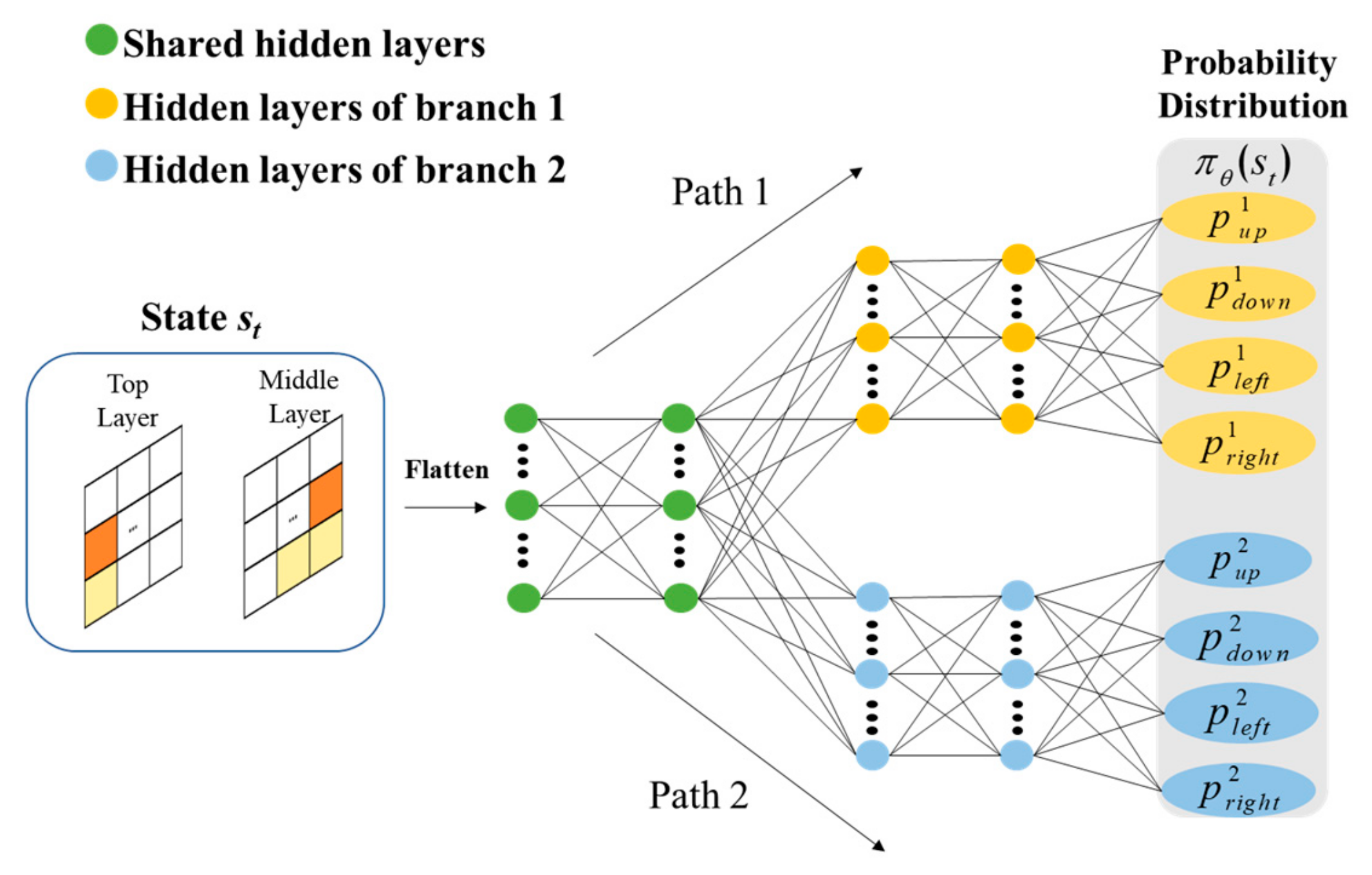
3.1. The Proposed MB-KPPO
3.2. The Design Process of MB-KPPO
| Algorithm 1: MB-KPPO method | |
| Input: and , two random m/2 × n matrices T, the preset total number of “1” in r, the termination reward | |
| 1 | Zero and , empty B |
| 2 | Initialize |
| 3 | Obtain at from the multi-branch policy network given |
| 4 | Execute the action to obtain |
| 5 | Obtain from the value network given . |
| 6 | Store {, , } in Buffer B |
| 7 | Update |
| 8 | Repeat 3–7 until sum () = T |
| 9 | Sent the and to HFSS using HFSS VBS |
| 10 | Compute the reward using (3) |
| 11 | Store in buffer B |
| 12 | Update and by maximizing (11) |
| 13 | Repeat 1–12 until |
| Output: The optimal M1 and M2 | |
4. Experiment
4.1. Design Setup and Process
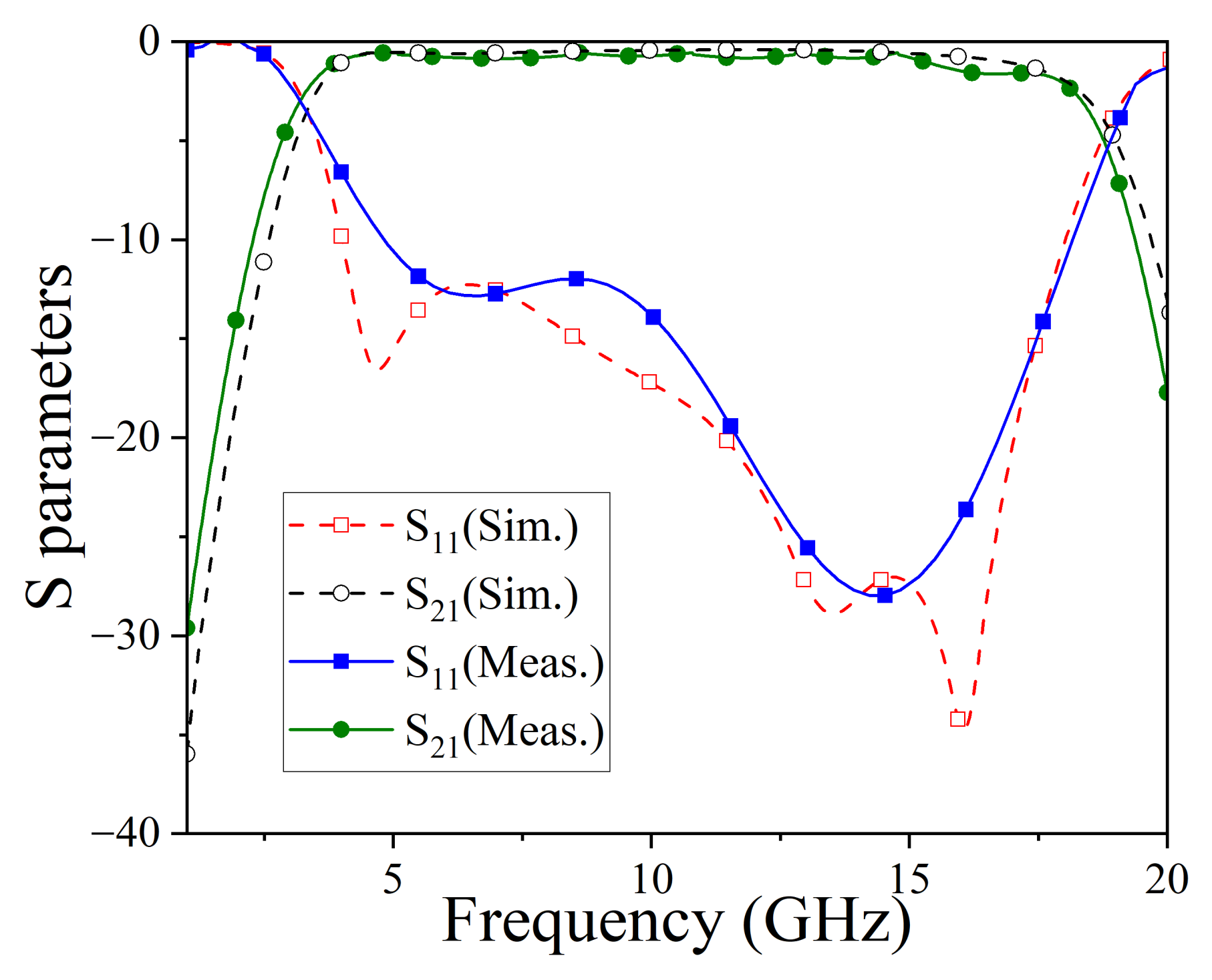
4.2. Measurement Results
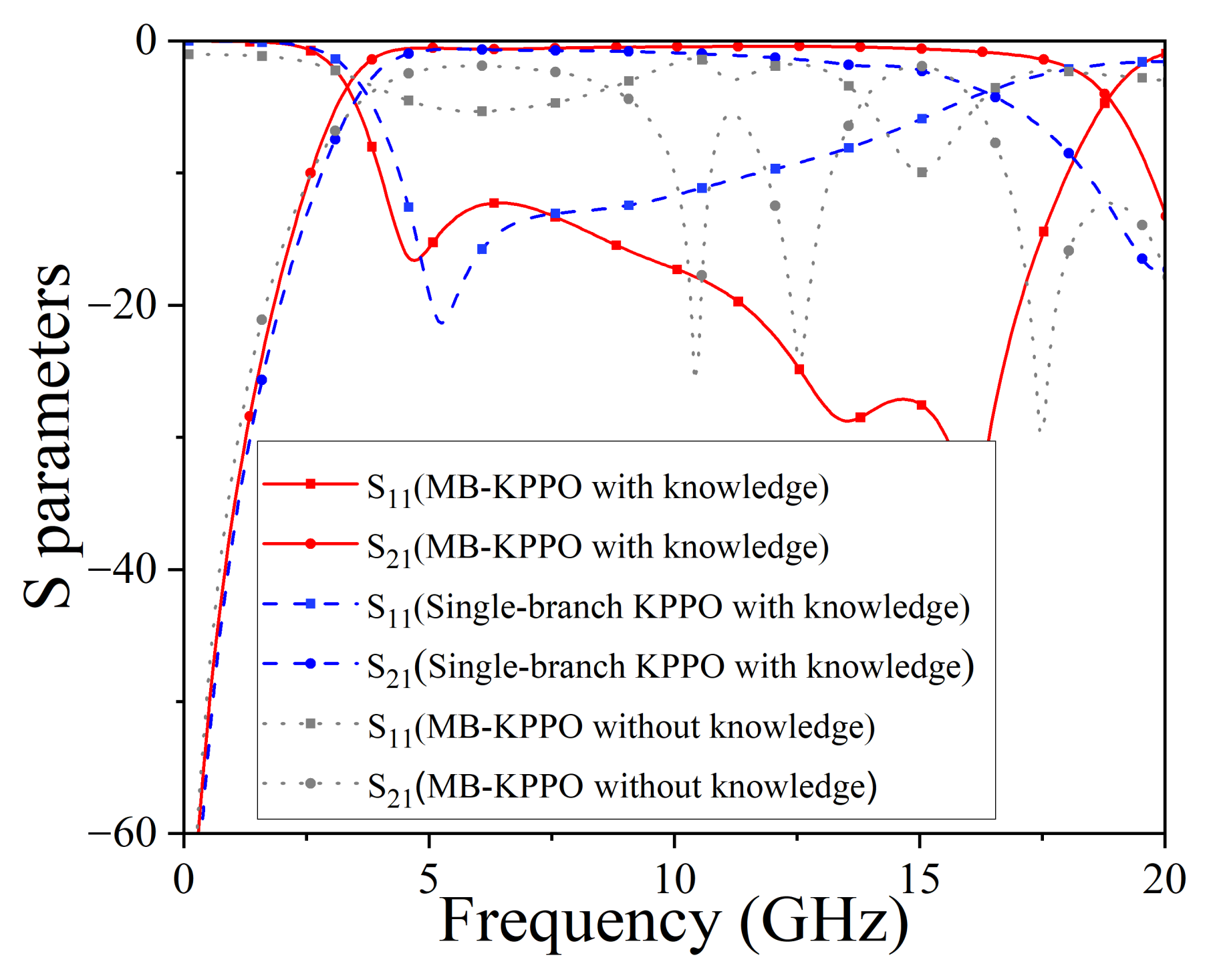
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Casares-Miranda, F.P.; Viereck, C.; Camacho-Penalosa, C.; Caloz, C. Vertical microstrip transition for multilayer microwave circuits with decoupled passive and active layers. IEEE Microw. Wirel. Compon. Lett. 2006, 16, 401–403. [Google Scholar] [CrossRef]
- Daneshmand, M.; Mansour, R.R.; Mousavi, P.; Choi, S.; Yassini, B.; Zybura, A.; Yu, M. Integrated interconnect networks for RF switch matrix applications. IEEE Trans. Microw. Theory Tech. 2005, 53, 12–21. [Google Scholar] [CrossRef]
- Yang, L.; Gómez-García, R. Transitioning to RF Filtering. IEEE Microw. Mag. 2024, 25, 52–67. [Google Scholar] [CrossRef]
- Li, E.S.; Cheng, J.-C.; Lai, C.C. Designs for broad-band microstrip vertical transitions using cavity couplers. IEEE Trans. Microw. Theory Tech. 2006, 54, 464–472. [Google Scholar] [CrossRef]
- Tao, Z.; Zhu, J.; Zuo, T.; Pan, L.; Yu, Y. Broadband Microstrip-to-Microstrip Vertical Transition Design. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 660–662. [Google Scholar] [CrossRef]
- Feng, L.; Zhu, H.; Feng, W.; Chen, H.; Shi, W.; Che, W.; Xue, Q. A New Class of Wideband MS-to-MS Vialess Vertical Transition with Function of Filtering Performance. IEEE Trans. Circuits Syst. II Exp. Briefs 2021, 68, 1877–1881. [Google Scholar] [CrossRef]
- Huang, X.; Wu, K.-L. A Broadband and Vialess Vertical Microstrip-to-Microstrip Transition. IEEE Trans. Microw. Theory Tech. 2012, 60, 938–944. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, L.; Choi, W.-W.; Tam, K.-W. Analysis and Design of Wideband Microstrip-to-Microstrip Equal Ripple Vertical Transitions and Their Application to Bandpass Filters. IEEE Trans. Microw. Theory Tech. 2017, 65, 2866–2877. [Google Scholar] [CrossRef]
- Zhu, L.; Wu, K. Ultra broadband vertical transition for multilayer integrated circuits. IEEE Microw. Guid. Wave Lett. 1999, 9, 453–455. [Google Scholar] [CrossRef]
- Tao, Z. Microstrip Vertical Transition Design with Ultra-Broadband Passband. IEEE Microw. Wirel. Technol. Lett. 2025, 35, 638–641. [Google Scholar] [CrossRef]
- Ma, J.; Dang, S.; Li, P.; Watkins, G.T.; Morris, K.; Beach, M. A Learning-Based Methodology for Microwave Passive Component Design. IEEE Trans. Microw. Theory Tech. 2023, 71, 3037–3050. [Google Scholar] [CrossRef]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications in engineering design. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN′95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Chen, S.; Sun, G.-H.; Wang, K. Inverse Design of Microstrip Antennas Based on Deep Learning. Electronics 2025, 14, 2510. [Google Scholar] [CrossRef]
- Wang, L.; Wang, G.; Sidén, J. Design of High-Directivity Wideband Microstrip Directional Coupler with Fragment-Type Structure. IEEE Trans. Microw. Theory Tech. 2015, 63, 3962–3970. [Google Scholar] [CrossRef]
- Huang, C.-P.; Ma, Y.-H.; Liu, Q.Q.; Zhao, W.-S.; You, B.; Wang, X.; Yu, C.-H.; Wang, D.-W. PPO Algorithm-Assisted Design of Absorptive Common-Mode Suppression Filters. IEEE Trans. Electromagn. Compat. 2024, 66, 2039–2047. [Google Scholar] [CrossRef]
- Zhang, Z.-C.; Hou, F.; Wang, D.-W.; Liu, J.; Zhao, W.-S. PSO-Algorithm-Assisted Design of Compact SSPP Transmission Line. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 247–250. [Google Scholar] [CrossRef]
- Liu, Z.-X.; Shao, W.; Ding, X.; Wang, B.-Z.; Peng, L.; Chen, Z.N. Equivalent circuit-guided GAN sample generation of metasurface for low-RCS scanning array. IEEE Trans. Antennas Propag. 2024, 72, 7201–7210. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets; Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Fang, X.; Li, H.; Cao, Q. Design of reconfigurable periodic structures based on machine learning. IEEE Trans. Microw. Theory Tech. 2023, 71, 3341–3351. [Google Scholar] [CrossRef]
- Liu, P.; Chen, L.; Chen, Z.N. Prior-knowledge-guided deep-learning-enabled synthesis for broadband and large phase shift range metacells in metalens antenna. IEEE Trans. Antennas Propag. 2022, 70, 5024–5034. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Wu, Z.-M.; Chen, H.-B.; Zhang, R.; Li, Z.; Wu, Y.-H.; Li, X.-C. Design of a Triple-Band and Ultra-Thin Absorber with Pixel structures Based on Reinforcement Learning. In Proceedings of the 2024 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Chengdu, China, 28–30 August 2024; pp. 1–3. [Google Scholar]
- Pan, J.-H.; Liu, Q.Q.; Zhao, W.-S.; Hu, X.; You, B.; Hu, Y.; Wang, J.; Yu, C.; Wang, D.-W. Proximal Policy Optimization-Based Optimization of Microwave Planar Resonators. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 2339–2347. [Google Scholar] [CrossRef]
- Chen, H.; Li, S.; Wu, Z.; Wang, L.; Li, X.-C.; Liu, Q.H. Multi-Head Discrete Action Calibration Proximal Policy Optimization Method for Pixel Antennas with High Degrees of Freedom. IEEE Trans. Antennas Propag. 2025, 73, 2881–2894. [Google Scholar] [CrossRef]
- Wu, Z.-M.; Li, Z.; Chen, H.-B.; Li, X.-C.; Zhan, H.-B.; Ning, K. Design of Wideband Microstrip-to-Microstrip Vertical Transition with Pixel structures Based on Reinforcement Learning. IEEE Microw. Wirel. Technol. Lett. 2025, 35, 274–277. [Google Scholar] [CrossRef]
- Naseri, P.; Hum, S.V. A Generative Machine Learning-Based Approach for Inverse Design of Multilayer Metasurfaces. IEEE Trans. Antennas Propag. 2021, 69, 5725–5739. [Google Scholar] [CrossRef]
- Liu, S.; Pei, C.; Khan, L.; Wang, H.; Tao, S. Multiobjective Optimization of Coding Metamaterial for Low-Profile and Broadband Microwave Absorber. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 379–383. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, F.; Liu, T.; Tao, D. Why ResNet works? Residuals generalize. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5349–5362. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 30. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
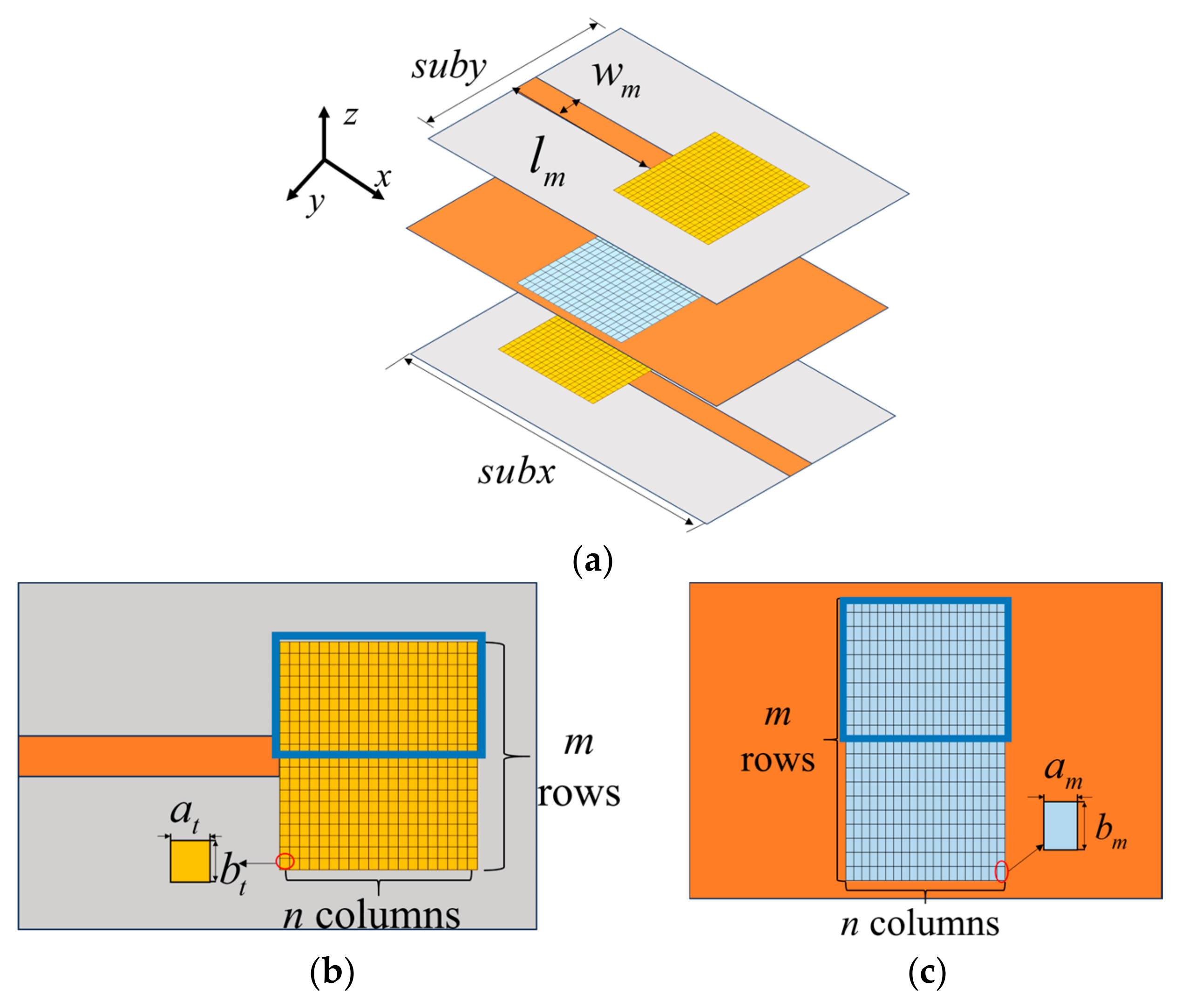


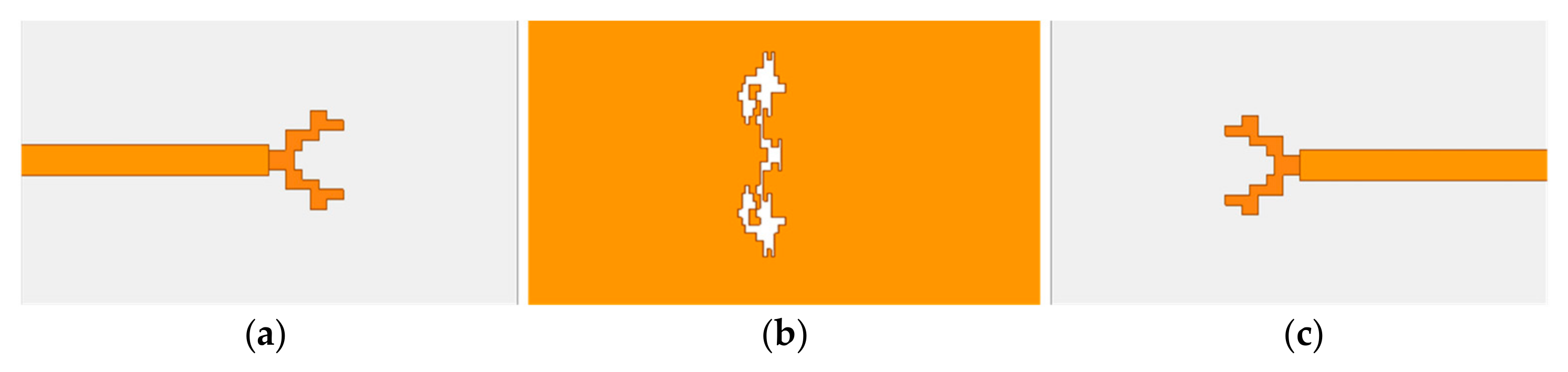

| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| subx | 30 mm | suby | 20 mm | 1.55 mm | |
| 15 mm | 0.25 mm | 0.25 mm | |||
| 0.15 mm | 0.4 mm | m | 40 | ||
| n | 20 |
| Hyper-Parameters | Value |
|---|---|
| Discount factor γ | 0.9 |
| Smoothing factor λ | 0.95 |
| Number of shared hidden layers of | 3 |
| Number of neurons in shared hidden layers of | 64 |
| Number of hidden layers in branch 1 of | 3 |
| Number of hidden neurons in branch 2 of | 64 |
| Learning rate of | 0.001 |
| Number of hidden layers of | 5 |
| Number of hidden neurons of | 64 |
| Learning rate of | 0.01 |
| T | 60 |
| r | 280 |
| T | 50 | 55 | 60 | 65 | 70 |
|---|---|---|---|---|---|
| The Highest Reward | 216 | 268 | 289 | 274 | 227 |
| Ref. | Type | Band (GHz) | FBW | Return Loss (dB) | Insertion Loss (dB) | Automated Design? |
|---|---|---|---|---|---|---|
| [4] | Cavity | 2.7–7.5 | 94% | 15 | <1 | No |
| [5] | Patch | 5.8–8.5 | 38% | 10 | <2.1 | No |
| [6] | CPW | 1–2.6 | 89% | 16.4 | <0.4 | No |
| [7] | U-slot | 3.1–11.5 | 115% | 15 | <1.7 | No |
| [8] | Folded Slot | 3.1–11.3 | 115% | 14.9 | 0.43–2 | No |
| [27] | Single Layer Pixel | 3.4–14.8 | 125% | 14.5 | 0.48–1.8 | Yes |
| This work | Multi-Layer Pixel | 3.5–17.8 | 134% | 13.5 | 0.55–2 | Yes |
| Ref. | Device | Variable Dimension | Dataset Required | Algorithm | Simultaneously Design Matrix | Used Prior Knowledge |
|---|---|---|---|---|---|---|
| [17] | SSPP transmission line | 23 × 9 | 80 | PSO | 1 | None |
| [19] | Frequency select surface | 8 × 8 | 2200 | GAN + GA | 1 | None |
| [18] | Meta-surface | 75 × 75 | 1400 | GAN | 1 | Equivalent Circuit |
| [28] | Meta-surface | 2 × 52 × 52 | 10,500 | VAE+PSO | 2 | None |
| [29] | Absorber | 2 × 10 × 10 | 2500 | GA | 2 | None |
| [24] | Absorber | 16 × 16 | 359 | PPO | 1 | None |
| [26] | Antenna | 20 × 20 | 238 | PPO | 1 | None |
| [27] | MS-to-MS vertical transition | 20 × 20 | 71 | KPPO | 1 | Fully connected shape generation mechanism |
| This work | MS-to-MS vertical transition | 2 × 20 × 20 | 289 | MB-KPPO | 2 | Fully connected shape generation mechanism |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.-M.; Li, Z.; Liang, R.-Y.; Li, X.-C.; Ning, K.; Mao, J.-F. Multi-Branch Knowledge-Assisted Proximal Policy Optimization for Design of MS-to-MS Vertical Transition with Multi-Layer Pixel Structures. Electronics 2025, 14, 3723. https://doi.org/10.3390/electronics14183723
Wu Z-M, Li Z, Liang R-Y, Li X-C, Ning K, Mao J-F. Multi-Branch Knowledge-Assisted Proximal Policy Optimization for Design of MS-to-MS Vertical Transition with Multi-Layer Pixel Structures. Electronics. 2025; 14(18):3723. https://doi.org/10.3390/electronics14183723
Chicago/Turabian StyleWu, Ze-Ming, Zheng Li, Ruo-Yu Liang, Xiao-Chun Li, Ken Ning, and Jun-Fa Mao. 2025. "Multi-Branch Knowledge-Assisted Proximal Policy Optimization for Design of MS-to-MS Vertical Transition with Multi-Layer Pixel Structures" Electronics 14, no. 18: 3723. https://doi.org/10.3390/electronics14183723
APA StyleWu, Z.-M., Li, Z., Liang, R.-Y., Li, X.-C., Ning, K., & Mao, J.-F. (2025). Multi-Branch Knowledge-Assisted Proximal Policy Optimization for Design of MS-to-MS Vertical Transition with Multi-Layer Pixel Structures. Electronics, 14(18), 3723. https://doi.org/10.3390/electronics14183723






