Heuristic-Based Computing-Aware Routing for Dynamic Networks

Abstract

The development of the computing power network has brought about a revolutionary effect on network routing architecture. As a result, the computing-aware network routing problem has been raised to explore routing various computational tasks to appropriate computing resources in the dynamic network. In this study, we propose a heuristic-based computing-aware routing algorithm to achieve the optimal routing path by considering the dynamic network performance and computing resource status simultaneously. Our proposed approach models the dynamic network using time-varying node and edge weights, which are obtained by mapping basic performance indicators to weights according to quality-of-service requirements. This allows us to improve the user’s experience more effectively during the routing process. Moreover, a novel heuristic-based algorithm, which creatively transforms the computing-aware routing problem into a single-source shortest path problem, has been designed to achieve the comprehensive optimal routing path. The experimental results, based on both simulated networks and a real dedicated network in Zhejiang, demonstrate that our proposed method can obtain the comprehensive optimal routing path with a lower computing time cost than enumerating search. Furthermore, our proposed computing-aware routing method has been proven to be robust to the dynamics of the network, computing resources, and service load changes.

1. Introduction

The development of 5G and artificial intelligence has led to the emergence of new computing demands, resulting in explosive growth of the data transmitted in the network. In addition, users are increasingly seeking stable, high-speed, and high-quality network responses while putting forth differentiated quality-of-service (QoS) requirements. Cloud computing and edge computing provide users with the ability to conveniently access various sizes of computing resources in distributed locations [1]. Edge computing emerges as a solution to address low-latency requirements and alleviate the congestion problem caused by large amounts of data in the backbone network [2]. On the other hand, it becomes crucial to achieve coordinated scheduling of multiple distributed resources and flexible deployment of applications to improve user experience.

The computing power network (CPN) is proposed for the integration of network and computing, which disseminates computing information to network devices [3]. By performing unified management, the CPN connects and schedules a large number of idle resources via ubiquitous networking to meet users’ computing demands. The development of software-defined networking (SDN) [4] and internet protocol version 6 (IPv6) [5] technologies enables more flexible computing-aware routing strategies in the network layer to be applied in the CPN. Therefore, computing-aware network routing has been proposed recently [6], improving the network efficiency and users’ experience.

However, distributed heterogeneous resources and diverse task requirements introduce distinct challenges to computing-aware routing. First, the CPN status changes dynamically, and the routing mechanism must integrate various metrics to enable real-time, multi-constraint optimization decisions that jointly consider the task distribution, computing resource utilization, and network performance. Second, user tasks may originate from multiple network access points (NAPs) and have numerous candidate computing service nodes, making the routing process considerably more time-consuming and complex than traditional point-to-point routing. Conventional methods typically emphasize static network metrics, such as latency or hop count, which are inadequate for dynamic modern CPNs. Specifically, classical routing algorithms like Dijkstra and A-Star often prioritize geographically proximate computing services, resulting in unexpected hotspot effects on resource-constrained platforms [7]. Therefore, an accurate and fast routing strategy [8,9] is desired for CPN routing mechanisms.

Driven by the aforementioned challenges, we propose a heuristic-based computing-aware routing mechanism designed to enhance resource utilization and elevate user experience. The end-to-end process of computing-aware network routing is illustrated in Figure 1. A single client task can be accessed through multiple network access points and computing service nodes. The core challenge lies in identifying a pair of $\{NAP,servicenode\}$ that minimizes both the computational load and latency accordingly. Overall, the contributions of this manuscript are summarized as follows:

• A study on computing-aware routing for the dynamic CPN environment, which considers seven-dimensional QoS attributes of the network resource and the computing resource. These attributes are transformed into two-dimensional comprehensive attribute priorities, enabling a holistic optimization of the computation and transmission processes.
• The proposal of a novel landmark-based A-star algorithm to solve the computing-aware routing problem in the dynamic network environment. This algorithm first transforms the computing-aware routing problem into a single-source shortest path problem and solves it under QoS constraints.
• Extensive experiments on both scalable simulation networks and a real dedicated network in Zhejiang province. The results demonstrate that the proposed heuristic-based computing-aware routing algorithm improves routing accuracy compared to traditional shortest path routing. It also reduces the path planning time by over 40 times while maintaining routing accuracy.

The rest of this manuscript is organized as follows. Section 2 summarizes related studies. Section 3 proposes a dynamic network and computing resource modeling method, along with the weight set mapping policy. The computing-aware routing problem is formulated in Section 4, and the landmark-based A-star algorithm is presented for routing path planning. In Section 5, we analyze the simulation experiment results and the current network test results on the dedicated network in Zhejiang to demonstrate the significance of our proposed method. Finally, we present a brief conclusion in Section 6.

Figure 1. Overall architecture. Clients submit computational tasks with QoS requirements, which are collected by the SDN controller. The SDN controller collects the real-time network and cloud resource data and invokes the proposed computing-aware routing strategy to determine the optimal routing path and resource node through dynamic network modeling, edge and node weighting, and routing path searching. The optimal route is translated into IPv6-compatible segment lists and deployed across the network, enabling tasks to flow from the user-side NAPs (CE) to the optimal computing service node (v) via provider-edge (PE) and core network (P) devices. This system ensures efficient task delivery, balancing QoS requirements with network and resource performance.

Figure 1. Overall architecture. Clients submit computational tasks with QoS requirements, which are collected by the SDN controller. The SDN controller collects the real-time network and cloud resource data and invokes the proposed computing-aware routing strategy to determine the optimal routing path and resource node through dynamic network modeling, edge and node weighting, and routing path searching. The optimal route is translated into IPv6-compatible segment lists and deployed across the network, enabling tasks to flow from the user-side NAPs (CE) to the optimal computing service node (v) via provider-edge (PE) and core network (P) devices. This system ensures efficient task delivery, balancing QoS requirements with network and resource performance.

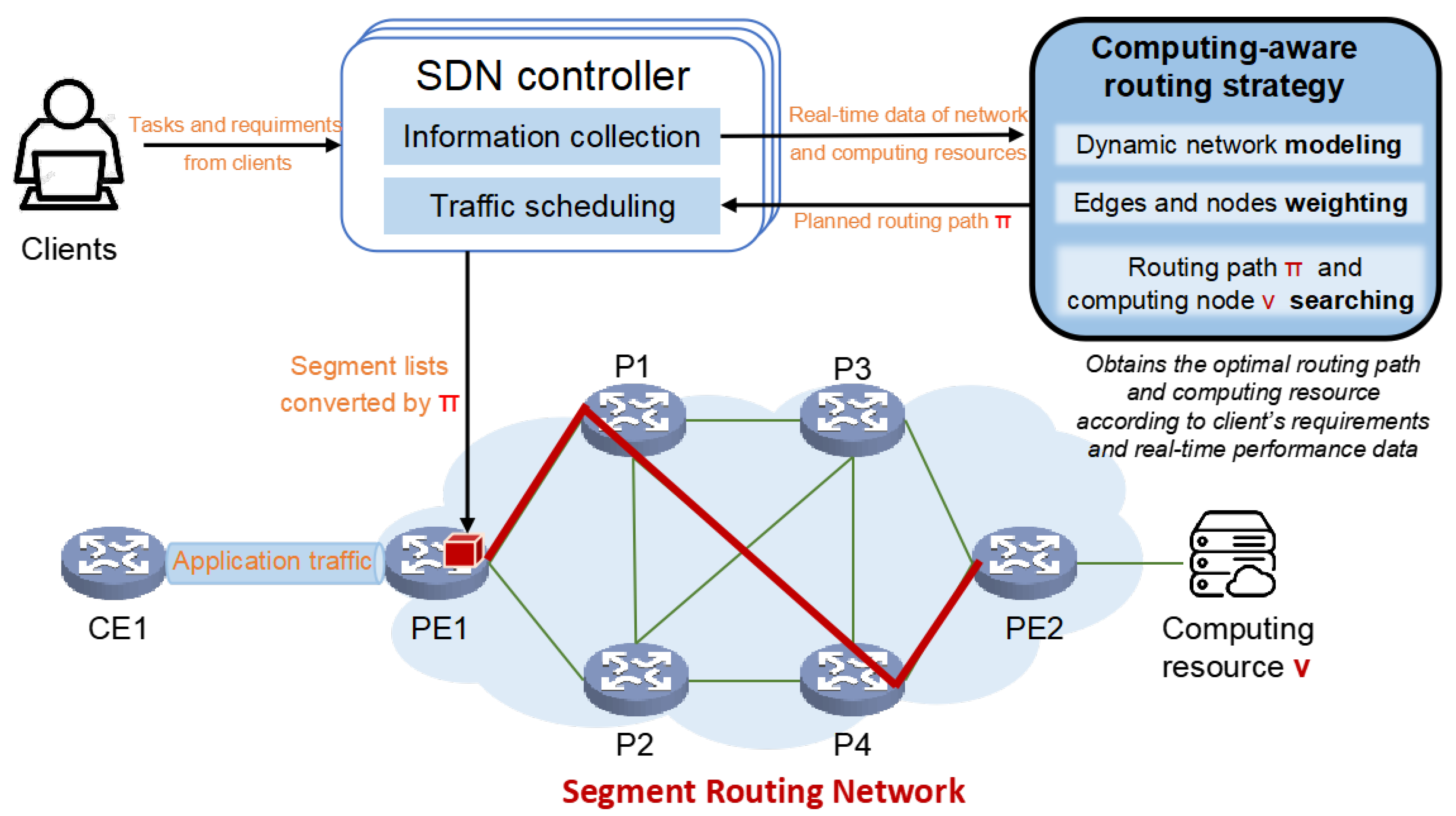
2. Related Work

With the rapid development of network technologies and applications, numerous studies have been conducted on various network routing protocols and network optimization strategies. In this section, several relevant works are introduced.

To cope with different challenges in the network, several improved routing strategies and protocols have been investigated [10,11,12,13,14]. Some scholars have proposed a cluster-based energy-aware routing algorithm for Wireless Sensor Networks (WSNs) [15] to solve the problem of the limited power of source nodes in order to balance the energy consumption. The authors in [16] improved the routing algorithm with a clever strategy for cluster head selection and cluster formation. In addition, an environment-fusion multi-path routing protocol for WSNs was demonstrated in [17], which ensured routing survivability under harsh environments. Routing strategies for satellite networks also raise great concern for researchers. The primary challenge for Earth orbit satellite networks is the constant dynamics in the network topology. Some existing works have proposed graph-based dynamic routing strategies and snapshot-based modeling methods, such as contact graph routing and a virtual topology model [18].

For a computing power network (CPN), one of the major challenges is realizing the joint scheduling of “network + computing”. In terms of the routing mechanism, computing resource constraints such as the computing capability and available memory should be considered based on the current network routing mechanism. A computing-aware routing protocol (CARP) architecture was first illustrated in [3], which emphasized the logic function of the CAPR system. Several frameworks for computing-aware traffic steering (CATS) were drafted after the Internet Engineering Task Force (IETF) created a working group (CATS-WG) to guide building a computing-aware system [19,20]. The authors in [21] developed a dynamic anycast (Dyncast) routing protocol to determine the best service instance and ensure service affinity. However, these protocols focused on the awareness and announcement mechanisms of multi-dimensional resources but simplified the modeling of the dynamic network and the algorithm of computing-aware routing. In addition, QoS-based constraints have not been considered in the existing work.

To improve the overall performance of the network and computing resources, some studies have discussed task scheduling mechanisms and resource allocation approaches. Load balancing is the most commonly used resource scheduling scheme, where tasks are assigned evenly to available computing resources [22]. An in-network computing architecture was proposed to allocate tasks for computing servers distributed over the network [23]. The authors in [24] discussed the computing resource allocation in a two-tier device-cloud network, where tasks could be processed locally, in the edge cloud, or both. However, existing methods solved the computing resource scheduling problem and the routing path planning problem separately.

In this manuscript, we propose a heuristic-based algorithm to jointly optimize the computing resources and routing paths by modeling the dynamic network with QoS constraints.

3. Dynamic Network and Computing Resource Modeling

The core goal of computing-aware network routing is to achieve appropriate integration of the network and computing resource information and ultimately improve the computing and network coordination performance. To overcome the limitations of existing static network routing models, a dynamic network and computing resource modeling method is proposed in this section. First, the dynamics of the network and computing resources are addressed. We propose a graph-based method to depict the topology dynamics. Then, we propose a method of mapping basic key performance indicators (KPIs) to weights based on the QoS. The significance of the proposed network and computing resource modeling is also summarized in this section.

3.1. Definition of Dynamic Network Model

The proposed graph-based dynamic network model defines the nodes and edges based on physical network elements and the computing resource topology. The major difference between the dynamic network model and the static physical topology is the weight set of the edges and nodes. The weight of an edge represents real-time network performance metrics such as latency, jitter, and cost, while the weight of a node represents the time-varying computing performance, such as the type of resource, capacity and current load, etc. The proposed model provides a holistic view of the entire network and resource topology dynamics, which is a basis for network routing design. The dynamic network model is defined as $G\left(t\right)=(\mathbf{V},\mathbf{E}\left(t\right),{\mathbf{W}}_{\mathbf{V}}\left(t\right),{\mathbf{W}}_{\mathbf{E}}\left(t\right))$, where $\mathbf{V}=\left\{v_1,v_2,\dots ,v_n\right\}(n=\left|\mathbf{V}\right|)$ is the set of nodes, and $\mathbf{E}\left(t\right)=\left\{e_1,e_2,\dots ,e_{m\left(t\right)}\right\}(m=\left|\mathbf{E}\left(t\right)\right|)$ is the set of edges. An edge can be represented as $e=(u,v)$ when u is the head of edge e and v is the tail of e. Time t is the instant at which the network and computing information is collected. ${\mathbf{W}}_{\mathbf{V}}\left(t\right)=\left\{w_{v_1}\left(t\right),w_{v_2}\left(t\right),\dots ,w_{v_n}\left(t\right)\right\}$ is the weight set of nodes, and ${\mathbf{W}}_{\mathbf{E}}\left(t\right)=\left\{w_{e_1}\left(t\right),w_{e_2}\left(t\right),\dots ,w_{e_{m\left(t\right)}}\left(t\right)\right\}$ is the weight set of edges. Since the computing-aware routing scheme takes both the transmission stage and the computation stage into account, our proposed model defines both edge weights and node weights. Note that the weights in ${\mathbf{W}}_{\mathbf{V}}\left(t\right),{\mathbf{W}}_{\mathbf{E}}\left(t\right)$ are task-related, which will be illustrated in the following subsection.

3.2. Time-Varying Network and Computing Resource Modeling

Considering the dynamics of the network environment, the limited computing resources, and the diversity of service applications, the computing-aware routing process is affected by several factors. Some critical factors are monitored as key performance indicators (KPIs) and used to evaluate quality of service (QoS), as highlighted in Figure 2. Generally, these influencing factors can be classified into three distinct categories: network link state, network element port state, and computing node state. While routing, the network link state and the network element port state are related to the transmission process, whereas the computing node state is related to the computation process. Taking real-time cloud rendering as an example, the transmission performance impacts the video stream stutter rate and resolution, while the computing process affects rendering accuracy. These KPI metrics contribute significantly to the overall QoS.

Therefore, the edge weights and node weights are modeled accordingly to optimize the transmission and computation process jointly. The definitions of the impact factor set of edges and nodes are elaborated below.

The impact factor set of edges ${\Lambda }_{\mathbf{E}}=\left\{\mathbb{D},\mathbb{DV},\mathbb{L},\mathbb{B}\right\}$. Here, the link propagation delay matrix is denoted as $\mathbb{D}=\left\{D_e\left(t\right),e\in \mathbf{E}\right\}$, the delay variation matrix is denoted as $\mathbb{DV}=\left\{D{V}_e\left(t\right),e\in \mathbf{E}\right\}$, and the packet loss rate matrix is denoted as $\mathbb{L}=\left\{L_e\left(t\right),u,v\in \mathbf{E}\right\}$, where $D_e\left(t\right),D{V}_e\left(t\right),L_e\left(t\right)$ are the propagation delay in $ms$, the delay variations in $us$, and the packet loss rate in % of edge e at instant t, respectively. $\mathbb{B}=\left\{B_e\left(t\right),e\in \mathbf{E}\right\}$ presents the available bandwidth matrix of links, where $B_e\left(t\right)$ is the available bandwidth in $bps$ of edge e at instant t. Therefore, $R_e\left(t\right)=\delta \ast B_e\left(t\right)$ presents the available data transmission rate for edge e at instant t, and it is proportional to the available bandwidth $B_e\left(t\right)$.

The impact factor set of nodes ${\Lambda }_{\mathbf{V}}=\left\{\mathbb{C},\mathbb{S},\mathbb{P}\right\}$. Here, the available computing capability matrix is represented as $\mathbb{C}=\left\{C_u\left(t\right),u\in \mathbf{V}\right\}$, the available memory matrix is defined as $\mathbb{S}=\left\{S_u\left(t\right),u\in \mathbf{V}\right\}$, and the resource pricing matrix is defined as $\mathbb{P}=\left\{P_u\left(t\right),u\in \mathbf{V}\right\}$. $C_u\left(t\right),S_u\left(t\right)$ and $P_u\left(t\right)$ represent the available computing capability in FLOPS, memory resources in GB, and resource pricing in RMB of computing node u at instant t, respectively.

The KPIs defined above are collected by the computing and network resource awareness architecture and updated regularly when the network and computing resources change. Nevertheless, to avoid routing fluctuations, the computing-aware routing path might be refreshed only when a new task is arriving, the Service-Level Agreement (SLA) is violated, or the updating timer runs out. The architecture of resource awareness and updates is out of the scope of this manuscript.

3.3. Basic KPIs for Weight Set Mapping

Different tasks tend to show concern for different specific performance indicators. For instance, video surveillance services require clear end-to-end delays, while game players are more sensitive to packet loss rate deterioration. Therefore, a significant benefit of computing-aware routing is comprehensively considering multi-dimensional performance indicators in the routing process, which can maintain a high service quality and achieve a satisfactory user experience. The mapping relationship from KPIs to the QoS is shown in Figure 2. The QoS is evaluated by both the transmission process and the computation process, which are related to the edge weights and the node weights, respectively. Since the weight sets are task-related, we define the task model and the mapping equations for the weight sets as follows.

Denote the $k^{th}$ computation task arriving at node i as ${\tau }_{i,k}$. To simplify the model, the task in this manuscript is independent and defined as the smallest unit of transmission and computation. Generally, there are five variables used to depict a task ${\tau }_{i,k}$, denoted as ${\Lambda }_{{\tau }_{i,k}}=(C_{i,k},S_{i,k},N_{i,k},{\vartheta }_{i,k},t_{i,k})$, where $C_{i,k},S_{i,k},N_{i,k},{\vartheta }_{i,k}$ are the computation capability requirement in FLOPS (i.e., CPU cycles, GPU cycles), the memory requirement in gigabytes (GB), the data volume of task ${\tau }_{i,k}$ in GB, and the delay threshold to process task ${\tau }_{i,k}$ in seconds, respectively. $t_{i,k}$ denotes the time at which task ${\tau }_{i,k}$ arrives.

According to the task model, the transmission delay and the computation delay of task ${\tau }_{i,k}$ on edge e starting from instant t can be deduced. In dynamic networks, the transmission delay $T_{trans}^{\tau }\left(t\right)$ is determined by the equation $N_{i,k}={\int }_t^{t+T_{trans}^{\tau }\left(t\right)}{R}_e\left(t\right)dt$, where $R_e\left(t\right)$ is the available data transmission rate and is equal to or less than $B_e\left(t\right)$. Similarly, the computation delay $T_{comp}^{\tau }\left(t\right)$ is determined by the equation $C_{i,k}={\int }_t^{t+T_{comp}^{\tau }\left(t\right)}{C}_u\left(t\right)dt$, where $C_u\left(t\right)$ is the available computing capability that node u can provide at instant t.

The set of edge weights. ${\mathbf{W}}_{\mathbf{E}}\left(t\right)=\left\{w_e^{{\tau }_{i,k}}\left(t\right)\mid e\in \mathbf{E}\left(t\right),i\in \mathbf{V}\right\}$ is the set of edge weights, and $w_e^{{\tau }_{i,k}}\left(t\right)$ is the weight of edge $e=(u,v)$ corresponding to task ${\tau }_{i,k}$ and instant t. By introducing the weight set $\omega =({\omega }_1,{\omega }_2,{\omega }_3)$ of task ${\tau }_{i,k}$, $w_e^{{\tau }_{i,k}}\left(t\right)$ can be mathematically defined following Equation (1):

$$w_e^{{\tau }_{i,k}}\left(t\right)=\left\{\begin{array}{cc}{\sum }_{j=1}^3{\omega }_j\ast {\Lambda }_{e,j},\hfill & {\zeta }_{\tau }\le {\vartheta }_{i,k}\&{\Lambda }_{e,j}\le {{\rm Y}}_{\tau }\left(t\right),\hfill \\ \infty ,\hfill & otherwise,\hfill \end{array}\right.$$

(1)

in which ${\zeta }_{\tau }$ is the sum of the transmission delay $T_{trans}^{\tau }\left(t\right)$ and the propagation delay $D_e\left(t\right)$ of task ${\tau }_{i,k}$ on edge e starting from instant t, ${\Lambda }_e$ represents the impact factor set of the edges mentioned in Section 3.2, and ${{\rm Y}}_{\tau }\left(t\right)$ denotes the task-related delay variation and packet loss rate thresholds, if present. It can be concluded that task ${\tau }_{i,k}$ cannot be transmitted through edge e successfully at t when any indicator in ${\Lambda }_e$ conflicts with the task requirements. The weight set $\omega$ is obtained through the sample statistics method based on information entropy and our sample dataset of network performance indicators annotated by task-related users, as shown in

Table 1. Sample dataset of network performance indicators annotated by task-related users. The table presents the sample dataset used to calculate the weight set $\omega$ through the sample statistics method based on information entropy. The task-related user labels d ($\langle \mathrm{True},\mathrm{False}\rangle$) serve as a reference to quantify the significance of each indicator to the task performance.

Collected Sample e	Delay De	Delay Variation DVe	Packet Loss Rate Le	Users Label d = <True, False>
1	$d_1$	$d{v}_1$	$l_1$	$d_1$
2	$d_2$	$d{v}_2$	$l_2$	$d_2$
3	$d_3$	$d{v}_3$	$l_3$	$d_3$
…	…	…	…	…
n	$d_n$	$d{v}_n$	$l_n$	$d_n$

.

The set of node weights. ${\mathbf{W}}_{\mathbf{V}}\left(t\right)=\left\{{\mathbf{w}}_j^{{\tau }_{i,k}}\left(t\right)\mid j\in \mathbf{V}\right\}$ is the set of node weights, where $w_j^{{\tau }_{i,k}}\left(t\right)$ is the weight of node j corresponding to task ${\tau }_{i,k}$ and instant t. $w_j^{{\tau }_{i,k}}\left(t\right)$ is mathematically defined as follows:

$$w_j^{{\tau }_{i,k}}\left(t\right)=\left\{\begin{array}{cc}{T}_{comp}^{\tau }\left(t\right)\ast P_j\left(t\right),\hfill & S_j\left(t\right)\ge S_{i,k}\&C_j\left(t\right)\ge C_{i,k},\hfill \\ 0,\hfill & j\in forwarding node set,\hfill \\ \infty ,\hfill & otherwise,\hfill \end{array}\right.$$

(2)

in which $T_{comp}^{\tau }\left(t\right)$ is the computation delay overhead of ${\tau }_{i,k}$ at node j from instant t, and $P_j\left(t\right)$ is the resource pricing of node j at instant t. $S_j\left(t\right)$ and $C_j\left(t\right)$ are the available memory and computing capability that node j can provide at instant t. For forwarding nodes without a computing capability in the path, the weights are equal to 0, as defined. It can be concluded that the weight $w_j^{{\tau }_{i,k}}\left(t\right)$ of a computing node j equals ∞ when $S_j\left(t\right)\le S_{i,k}$ or $C_j\left(t\right)\le C_{i,k}$, which means the computation requirement of task ${\tau }_{i,k}$ cannot be completed by node j at instant t with insufficient memory or computing resources.

Based on the definition above, our proposed dynamic network model has two important characteristics compared with the traditional static network model. Firstly, both the edges and nodes of the proposed dynamic network model are weighted. For computing-aware network routing, the computing node selection and the routing path selection are correlated and interactive. Hence, the computing-aware routing cost should take the node and edge weights into account and jointly optimize the path. The weights are determined by the task requirements, which makes the chosen routing path more suitable. Secondly, both the edge weights and node weights are time-varying. Not only the network service quality but also the available resources of the distributed computing nodes vary in real time. The dynamics defined above are closely related to the routing path selection. With consideration of the routing overall delay, the edge and node weights are updated frequently to select the most appropriate routing path, as well as the computing node.

4. Problem Formulation

In this section, we first introduce a typical routing problem. We then formulate the computing-aware network routing problem and propose a heuristic-based routing algorithm to address it.

4.1. Shortest Path Problem

The kernel of the routing problem lies in searching for an optimal path from a source node to a destination node in a network topology. The definition of “optimal” can be evaluated with multi-dimensional indicators and varies according to different requirements. It can denote less time delay or a lower packet loss rate, among other things. When the path cost is well defined, the routing problem becomes a shortest path problem. In the previous section, we formulate the dynamic network topology as a graph and assign task-related weights to nodes and edges. The routing problem can be defined as finding the shortest path ${\pi }_{u,v,t}=\left\{(u_1,v_1),(u_2,v_2),\dots ,(u_p,v_p)\right\}(u_p=v_{(p-1)},p\in \mathbb{N}+1)$ and its corresponding path length $L_t^{{\pi }_{u,v}}$ from a given source node $u_1$ to destination node $v_p$ at time t. The length of path ${\pi }_{u,v,t}$ at instant $t_1$ is computed as $L_{t_1}^{{\pi }_{u,v}}=\omega (e_1,t_1)+\omega (e_2,t_2)+\dots +\omega (e_p,t_p)$, where $t_p=t_{p-1}+D_{e_{p-1}}\left(t_{p-1}\right),p\in \mathbb{N}+1$.

The shortest path problem has been extensively studied, with dynamic programming methods like the Dijkstra algorithm widely applied to solving single-source routing in static networks [25,26]. For dynamic networks, the dynamic shortest path (DSP) problem becomes NP-hard, so it is computationally prohibitive to find the optimal solution. To solve the DSP problem, an intuitive approach is to take snapshots of the dynamic graph and apply dynamic programming algorithms or heuristic algorithms, such as a genetic algorithm (GA) or ant colony optimization (ACO) [27,28,29]. However, due to the network dynamics and complexity, conventional shortest path algorithms are inefficient for the DSP problem. Conventional algorithms need to recompute the entire routing path from snapshots frequently after network status updates, without reusing prior knowledge from previous executions.

4.2. Computing-Aware Network Routing Problem

For the computing-aware routing problem, there are typically multiple pairs of candidate source and destination nodes to consider, as mentioned in Section 1. In practice, each task often involves several alternative source nodes (candidate NAPs between the backbone network and the access network) and destination nodes (candidate computing resources) in the computing-aware routing problem. These candidates can form multiple source–destination node pairs. The primary objective of computing-aware routing is to identify the most suitable computing resource and select the optimal path for each task within the dynamic network $G\left(t\right)$, while minimizing the overall cost. The presence of multiple ambiguous source–destination node pairs adds complexity to the computing-aware routing problem, making it even more challenging than the DSP problem discussed earlier.

To simplify the problem, a snapshot of the dynamic network will be taken when a new computing-aware routing problem arrives. We consider the dynamic network as a discrete-time network and assume a fixed topology during the solving process [30]. The computing-aware routing problem is solved at each snapshot based on the updated data in real time. The computing-aware routing problem in $G\left(t\right)$ is then formulated as follows:

$$\begin{array}{cc}\hfill \underset{\Pi }{min}& (\Psi (\Pi )),\Pi =\left\{{\pi }_{u_1,v_q},\{u_1,v_q\}\right\}\hfill \\ \hfill s.t.& u_1,v_q\in \mathbf{V}\hfill \\ \hfill & w_{v_q}\ne 0or\infty \hfill \end{array}$$

(3)

Here, $\Psi (·)$ maps the path and the pair of source–destination nodes to the path length. The objective is to find an optimal pair of source–destination nodes $\{u_1,v_q\}$ and a path ${\pi }_{u_1,v_q}$ that can achieve the minimum path length $L^{{\pi }_{u,v_q}}$ accordingly. The candidate destination node $v_q$, i.e., the computing node, should satisfy the constraint $w_{v_q}\ne 0or\infty$ as defined in Equation (2). It is worth noting that both the edge and node weights are considered in calculating the computing-aware routing path length, as shown in Equation (4).

$$L_t^{{\pi }_{u,v_q}}=\sum _{e_{i,j}\in {\pi }_{u,v_q}}{w}_{e_{i,j}}+w_{v_q}$$

(4)

As mentioned earlier, due to the inefficiency of the traditional Dijkstra method in path searching, this manuscript proposes a heuristic-based computing-aware network routing algorithm (H-CAR). The core heuristic function H is constructed from the shortest paths between network nodes. The function is used to enhance the A-star algorithm, increasing the search efficiency in computing-aware routing. The strategy is presented in Algorithms 1 and 2.

Algorithm 1 Heuristic-based computing-aware routing (H-CAR) algorithm

Require: The snapshot of the dynamic network model $G\left(t\right)$, including the node set V, edge set E, impact factor set of nodes ${\Lambda }_E$, impact factor set of edges ${\Lambda }_V$, and the shortest path matrix between nodes P Require: Task $\tau$’s parameter set ${\Lambda }_{\tau }=(C_{\tau },S_{\tau },N_{\tau },{\vartheta }_{\tau },{\alpha }_{\tau },{\beta }_{\tau },t_{\tau })$ Ensure: The optimal computing-aware routing path $\Pi =\left\{{\pi }^{\ast },{\{u_1,v_q\}}^{\ast }\right\}$ and the overall cost $L^{\ast }$   1: Initialize ${\pi }^{\ast }\leftarrow \varnothing ,v_q^{\ast }\leftarrow \varnothing ,L^{\ast }\leftarrow \infty$;   2: Calculate $W_E^{\tau },W_V^{\tau }$ based on ${\Lambda }_E,{\Lambda }_V$, and ${\Lambda }_{\tau }$ with Equations (1) and (2);   3: Select the source node set $V_u$ for task $\tau$ based on the location information ${\alpha }_{\tau },{\beta }_{\tau }$ in ${\Lambda }_{\tau }$;   4: if$num\left(V_u\right)>1$ then   5:      V ← Add a virtual source node $\tilde{u}$   6:      E ← Add virtual edges $E_{vsrc}$ $\{e\in {\mathbf{E}}_{vsrc}$ links $\tilde{u}$ and all actual candidate source nodes}   7: end if   8: Select the potential computing node set $V_q$ for task $\tau$ based on the requirements $C_{\tau },S_{\tau }$ in ${\Lambda }_{\tau }$;   9: if$num\left(V_q\right)>1$  then 10:    V ← Add a virtual destination node $\widetilde{v_q}$ 11:    E ← Add virtual edges $E_{vtg}$ $\{e\in {\mathbf{E}}_{vtg}$ links $\widetilde{v_q}$ and all actual candidate destination nodes} 12: end if 13: SET $G\leftarrow \left(\mathbf{V},\mathbf{E},{\mathbf{W}}_{\mathbf{V}},{\mathbf{W}}_{\mathbf{E}}\right)$ 14: ${\pi }^{\ast },{\{u_1,v_q\}}^{\ast },L^{\ast }\leftarrow$ Landmark-based $A-STAR(G,u_1,v_q,P)$

As shown in Algorithm 1, the first step of our proposed H-CAR is to generate a snapshot of the dynamic network model and the task parameter set, which are used as the input data. The algorithm then outputs a set of the optimal real routing path and the computing node, denoted by $\Pi =\left\{{\pi }^{\ast },{\{u_1,v_q\}}^{\ast }\right\}$, along with the overall cost $L^{\ast }$.

After initialization, Algorithm 1 is composed of two parts. The first part is graph generation (line 2 to line 13). The algorithm assigns weights to edges and nodes based on physical constraints using Equations (1) and (2). Then, the pair of the source node and the destination node should be specified for the routing search. Enumerating all pairs to solve the routing problem through graph traversal can be time-consuming. To avoid the duplicated searches incurred by enumerating search and graph traversal methods, the virtual nodes $\tilde{u}$ and $\widetilde{v_q}$ and virtual edge sets ${\mathbf{E}}_{\mathit{vsrc}}$ and ${\mathbf{E}}_{\mathit{vtg}}$ are generated and introduced into the graph. Hence, the computing-aware network routing problem can be converted into a single-source shortest path problem, where the candidate computing nodes are contained as the penultimate points in the path.

Algorithm 2 Landmark-based A-STAR{$G,\tilde{u},\widetilde{v_q},P$}

1:  Initialize $OpenList\leftarrow \varnothing ,ClosedList\leftarrow \varnothing ,u.f=0$   2:  $OpenList\leftarrow$ Add $\tilde{u}$   3:  while$OpenList$ is not empty do   4:       $CurrentNode\leftarrow$ node $\in OpenList$ with min$\left(f\right)$   5:       $OpenList\leftarrow$ Remove $CurrentNode$   6:       $ClosedList\leftarrow$ Add $CurrentNode$   7:       if $CurrentNode=\widetilde{v_q}$ then   8:           Return   ${\pi }^{\ast },{\{u_1,v_q\}}^{\ast },L^{\ast }$   9:       end if 10:       $children\leftarrow G.adj\left(CurrentNode\right)$ {list of nodes adjacent to Current node} 11:       for all$child\in children$ do 12:           if $child\in ClosedList$ then 13:              continue 14:           end if 15:           $child.g=CurrentNode.g+L^{e_{child}}$ 16:           $child.h=H(child,P)$ 17:           $child.f=child.g+child.h$ 18:           if $child$.position is in $OpenList$’s nodes position then 19:               if $child.g>OpenList$ node’s g then 20:                  continue 21:               end if 22:           end if 23:           $OpenList\leftarrow$ Add $child$ 24:        end for 25:  end while

The second part of the algorithm involves the search for the optimal path, with inputs including a snapshot of the dynamic network G, the virtual source node $\tilde{u}$, the virtual destination node $\widetilde{v_q}$ and the shortest path matrix P, where P contains the shortest paths between nodes computed using the historical edge state. As defined in Equation (3), the overhead of the computing nodes is taken into account in the routing process, converting the optimization problem into a minimum cost problem. To solve the problem, we propose the landmark-based A-star algorithm, as presented in Algorithm 2. The algorithm updates the optimal path ${\pi }^{\ast }$, the optimal computing node $v_q^{\ast }$, and the minimum overall cost $L^{\ast }$ during the iteration process (line 10). The overall cost is evaluated using $L^e$ in line 15, which is calculated using Equation (4) and takes into account both the edge weights and node weights. The key feature of our proposed A-star algorithm is the well-designed heuristic function $H(n,P)$ in line 16, which is defined as follows:

$$H(n,P)=\underset{v_q}{min}(\sum _{i,j\in {\pi }_{n,v_q,t_0}^{\ast }}{w}_{i,j}^{Norm}+w_{v_q}^{Norm}),v_q\in V_q$$

(5)

$$w_{i,j}^{Norm}={\displaystyle \frac{w_{i,j}}{cos{t}_E}}$$

(6)

$$w_{v_q}^{Norm}={\displaystyle \frac{w_{v_q}}{cos{t}_Q}}$$

(7)

In Equation (5), $H(n,P)$ estimates the minimum cost for task $\tau$ from the current node n to the potential computing node set $V_q$; ${\pi }_{n,v_q,t_0}^{\ast }$ is the historical shortest path from the current node n to each potential computing node $v_q$, which are pre-calculated using the Dijkstra method at time $t_0$ and stored in a dedicated matrix for fast lookup. The feasible computing nodes in $V_q$ are considered landmarks during the routing process and are included in the matrix P. The computational complexity of constructing the landmark table depends on the complexity of the network topology, typically $\mathcal{O}\left(\right|E|log|V\left|\right)$. In practice, as the network topology is feasible to implement and relatively stable and network performance fluctuations are periodic, the landmark table does not need to be updated in real time. Instead, it only requires updates when there are significant changes in the network performance. Therefore, the precomputation time can be considered negligible during the routing search process.

To enhance the accuracy of the heuristic function $H(n,P)$, the historical edge weight $w_{i,j}$ and real-time node weight $w_{v_q}$ are normalized separately. The term $w_{i,j}^{Norm}$ is normalized by the average cost $Cos{t}_E$ among all paths in ${\pi }_{n,v_q,t_0}^{\ast }$, and $w_{v_q}^{Norm}$ is then obtained by normalizing with the average computational node cost $Cos{t}_Q$. By integrating the weights of candidate computing nodes into the routing process, the nodes along the path that are closer to the candidate computing nodes are prioritized for exploration.

It is worth noting that the candidate computing resources are not mutually exclusive but rather complementary in our proposed computing-aware routing scheme. If computing resources on the current node are insufficient, tasks can be offloaded to another candidate server for computation. Combining computing information with routing significantly reduces the search space and improves the search efficiency. The performance of our proposed algorithm will be illustrated in the next section.

5. Experiments and Evaluations

A series of simulation scenarios and field experiments are conducted to evaluate the effectiveness of the proposed H-CAR. The experiments focus on scheduling tasks to suitable computing nodes in changing environments with our landmark-based A-star algorithm, which combines computing node information in the routing path search.

5.1. Experimental Settings

Based on the different scenarios, the experiments are divided into two parts: simulation scenarios and field experiments. The simulation uses randomly generated networks to evaluate the effectiveness and robustness of H-CAR, while field experiments leverage real-world data and cases to assess its practical application value. In the simulated networks, nodes are connected with a probability $p=0.2$, and link weights w are randomly assigned within $[w_{\min },w_{\max }]$. The initialized simulation network is $G_n$, where n represents the number of network nodes and is also randomly selected within a predefined range. The normalization in the heuristic function Equations (6) and (7) ensures that the path selection depends only on the relative, not absolute, link weights. As an example, a randomly generated network topology with $n=30$ is presented in Figure 3.

To adequately test the feasibility of the proposed routing algorithm, the available computing nodes in the network are randomly specified and the task can be initiated by any node in the network. The critical shortest path matrix P is searched using the Dijkstra method with full enumeration in $G_n$. To simulate the dynamic network state, edge weights are appended with a random percentage fluctuation to characterize the real-time changes in the network. Node weights are then given randomly, which is consistent with the differences between different nodes in a real-world network.

The real-world experimental scenario is shown in Figure 4. A dedicated network that connects distributed cloud computing resources located in Zhejiang province, East China, is selected for the experiments. The edge cloud computing resources are allocated across all 11 cities in Zhejiang, and each cloud can deploy various service instances on demand. The computing requirements of a client connect to one of the Service Routers (SRs) in the task area and are then routed to an edge cloud according to the proposed computing-aware network routing algorithm.

In order to provide a clearer representation of the dedicated network, the topology was extracted separately and supplemented with details, as shown in Figure 5. The blue nodes represent SR devices and serve as the source points in routing paths, while the yellow and brown nodes represent provider-edge (PE) or provider (P) devices, which are connected directly to edge cloud computing resources. All devices in this network are routers. The edges denote direct connections between devices. The node location information also corresponds to the actual location of the device, as shown in Figure 4. Specifically, nodes 0 and 1 correspond to PE devices in Hangzhou, while nodes 30 to 53 correspond to SR devices in Hangzhou. From Figure 5, it can be observed that the dedicated network in Zhejiang is physically connected as a star topology. The total topology includes 167 nodes and 263 edges.

To address the issue of multiple source–destination node pairs during the computing-aware routing process, virtual nodes and edges are incorporated into the graph, as discussed in the previous section. These elements are also shown in Figure 5, where the green nodes represent the virtual source nodes, and the red node represents the virtual target node that connects with all candidate computing nodes. The proposed H-CAR is applied to this graph.

All simulation experiments in this section are conducted on a machine equipped with an AMD Ryzen 5 PRO 3500U processor with Radeon Vega Mobile Graphics (2.10 GHz) and 8 GB of RAM (manufacturer: Advanced Micro Devices, Inc. [AMD], Santa Clara, CA, USA).

5.2. Simulation Experiments and Performance Evaluation

In the simulation experiments, the performance of the proposed method is investigated under different simulation networks and computational states, and the accuracy of the routing paths and the time cost of path planning are analyzed further. The accuracy metric demonstrates that H-CAR achieves near-optimal solutions for computing-aware routing, while the time cost metric highlights its efficiency, proving the algorithm’s effectiveness and practicality in dynamic CPN networks.

5.2.1. Accuracy of Path Routing Under Fluctuating Networks

The routing path accuracy is first measured over different fluctuation ranges of edge weights. The number of network nodes is fixed to 60, and the experimental results are shown in Figure 6. The globally optimal path was found through complete enumeration to minimize the overall cost L. When the routing nodes are exactly the same as the optimal path, the generated path is considered correct. The method considering the shortest edge cost and the minimum computing cost is also tested separately to verify the advancement of the proposed method.

As shown in Figure 6, the proposed H-CAR algorithm demonstrates a significant advantage over both the load balancing strategy (minimum computing cost) and the shortest path strategy (shortest routing path) within the defined fluctuation ranges. Notably, when the fluctuation range is below 70%, H-CAR maintains an accuracy rate exceeding 90%. In contrast, the shortest path strategy exhibits larger errors due to its inability to account for the state of computing nodes. Although the load balancing strategy improves upon the shortest path approach by leveraging historical shortest paths and real-time node states, H-CAR outperforms it by effectively integrating historical path information with real-time network conditions, enabling more accurate path routing.

Simulated networks with varying numbers of nodes are also tested, with the maximum fluctuation range of the edge weights fixed at 50%. The results, shown in Figure 7, exhibit variability due to the randomness of the network structure and node connections. However, in all network sizes, the proposed H-CAR consistently achieves the highest path accuracy compared to that of the shortest path strategy and the load balancing strategy.

In addition to verifying the time efficiency of computing-aware routing, experiments are conducted to compare the time cost of H-CAR with that of a traditional enumerating search algorithm under the same network topology. The network is configured with 60 fixed nodes, and the maximum edge weight fluctuation is set to 50%. The time cost for both H-CAR and the enumeration method is measured by randomly selecting task source and target nodes. The results, based on 1000 experimental repetitions, are presented in Figure 8.

The enumeration method identifies the optimal path and computing nodes by exhaustively traversing all possible options. However, this results in an average path planning time of 5.78 ms with significant fluctuations, which is nearly 40 times higher than that of the proposed H-CAR method (0.13 ms).

Combined with the above experimental results, it can be concluded that the proposed method in this paper demonstrates a significant improvement in the path search efficiency across networks of varying sizes while maintaining high accuracy under normal network fluctuation conditions.

5.2.2. Network Load Testing

Achieving efficient task routing requires consideration of both the dynamic network conditions and computational performance. To further evaluate the proposed computing-aware routing (H-CAR) method, we simulate scenarios with varying numbers of clients connecting to a dedicated network and sending computing requests to candidate edge clouds. Each client generates an average of 5 to 10 tasks, with the task intervals following a Poisson distribution (default $\lambda =5$ ms). The computation task involves floating-point matrix multiplication $100\times 100$ in size. We record the average search space and the average task completion time, as shown in

Table 2. Results of multiple task scheduling in the simulated network. The table summarizes the performance of H-CAR, the Kubernetes-based load balancing strategy, and the shortest path strategy under varying task loads in a simulated network. Metrics include the average search space and average task completion time. H-CAR demonstrates a superior performance by significantly reducing the search space through its heuristic-driven approach and achieves lower task completion times compared to those of the other strategies, which experience substantial performance degradation as the task loads increase. These results highlight H-CAR’s ability to efficiently balance dynamic network and compute resources, ensuring scalability and adaptability in high-demand scenarios. Boldface indicates, within each experimental scenario, the algorithm and corresponding results that are the best-performing.

Number of Tasks	Load Balancing		Shortest Path		H-CAR
	Avg. Search Space	Avg. Time (ms)	Avg. Search Space	Avg. Time (ms)	Avg. Search Space	Avg. Time (ms)
10	16.39	21.5	21.85	23.58	4.15	16.97
50	16.31	22.52	23.04	23.81	4.18	20.95
100	17.01	25.39	23.61	28.21	4.30	26.12
200	16.57	52.82	24.33	78.88	4.33	38.15

, and compare H-CAR with two baseline methods: a traditional Kubernetes-based load balancing strategy [22] and a shortest path strategy.

The load balancing strategy distributes tasks evenly across all candidate compute nodes without considering the dynamic network or computational performance, while the shortest path strategy focuses solely on minimizing the routing path costs. The average search space is defined as the ratio of the total nodes in $OpenList$ to the number of nodes in the optimal routing path.

From the results, it can be seen that H-CAR is much better than the above two approaches in terms of both the average search space and average task completion time. Specifically, since both load balancing and shortest path policies require searching the entire network, the open list of computationally aware routing policies contains only forward nodes and their neighbors due to the heuristic function, which significantly reduces the search space, and the task completion time increases by 146%, 235%, and 125% with an increase in the number of tasks, respectively. These results show that computationally aware routing policies are able to adapt to dynamic service load changes and jointly optimize the network and computing resources better.

The results demonstrate that H-CAR significantly outperforms both baseline approaches in terms of the average search space and task completion time. Unlike the load balancing and shortest path strategies, which require searching the entire network, H-CAR leverages a heuristic function to limit $OpenList$ to forward nodes and their neighbors, substantially reducing the search space. Furthermore, as the number of tasks increases, the task completion time for the load balancing strategy, the shortest path strategy, and H-CAR grows by 146%, 235%, and 125%, respectively. These results highlight that H-CAR is able to adapt to dynamic service load changes and optimize the network and computational resources simultaneously.

5.3. Real-World Experiments and Case Study

In this subsection, real computation-aware information (including computational power, memory, and resource prices) along with the network topology are used to test the performance of H-CAR, and a case study is presented to illustrate the feasibility of the approach. Specifically, we consume Kubernetes (K8s) and Prometheus APIs to collect the real-time computing capacity at each computing node [31] and exploit the two-way active measurement protocol (TWAMP) to update the network performance information [32].

5.3.1. Routing with Computing-Aware Information

In the same network topology, the routing paths generated by the shortest path routing policy and H-CAR are presented in Figure 9a and Figure 9b, respectively. Among the available computational resources, Jiaxing node 4 has the minimum path cost and is therefore selected as a computation node in Figure 9a, while under the computation-aware routing policy, Taizhou node 17 has a better performance in terms of both the network and computational resources and is chosen by H-CAR. This experiment demonstrates the significance of considering the network and computing information comprehensively.

5.3.2. Routing with Varying Network and Computing Resource Status

In real-world network environments, both the network performance and the status of computing resources can fluctuate dynamically and influence the effectiveness of computing-aware routing significantly. In previous experiments conducted in a simulated environment, we validate the effectiveness of the proposed algorithm in dynamic and changing network conditions. Based on this, we further evaluate H-CAR’s performance in a real-world network topology. Using historical data on real-world network traffic fluctuations, link performance variations, and computational node load changes, we design experiments to assess the algorithm’s ability to adapt and perform effectively in realistic scenarios.

Based on the example in Section 5.3.1, we apply H-CAR in scenarios where the network service performance deteriorates. Using the same computing-aware information as that in Figure 9, the proposed algorithm automatically reroutes tasks to an alternative path when the link between nodes 23 and 17 becomes congested, as illustrated in Figure 10a.

Additionally, we simulate a scenario where the availability of computing resources changes. For instance, when the service load at Taizhou node 17 increases rapidly, H-CAR dynamically redirects the task to another suitable computing node, such as node 2 in Huzhou, as shown in Figure 10b. These results demonstrate H-CAR’s ability to adapt to both network and computational resource dynamics effectively.

6. Conclusions

In this study, we propose a heuristic-based computationally aware network routing algorithm (H-CAR) to efficiently find the optimal routing path in dynamic networks. H-CAR considers the status of the computing resources, network performance, and QoS requirements simultaneously to select the best computing node and routing path in real-time. A landmark table is pre-calculated for searching guidance, which improves the solving efficiency. We evaluate our proposed method on a variable simulation network and the dedicated network topology in Zhejiang, demonstrating that it achieves a better time efficiency performance than that of the traditional enumerating search method. The easy implementation of our proposed heuristic-based algorithm gives it good application prospects in real-time computing-aware routing.

On the other hand, there are still some promising directions for future research. First, the stability of the computing-aware routing protocol should be investigated as the dynamic network environment changes frequently. Second, obtaining sufficient high-quality data for computing-aware routing and QoS improvements remains challenging due to latency, noise, and aggregation issues. Future work will also focus on cross-domain resource discovery, state perception mechanisms, and predictive modeling for computing and network resources. Finally, deep reinforcement learning methods could be explored as a promising solution for computing-aware routing, as they can iteratively improve the routing policy based on user feedback.