Real-Time-Sensing-Assisted Intelligent Communication for Internet of Things
Abstract
1. Introduction
- A self-interference suppression architecture based on the NYFR is proposed, enabling real-time wideband spectrum sensing and communication at sub-Nyquist rates.
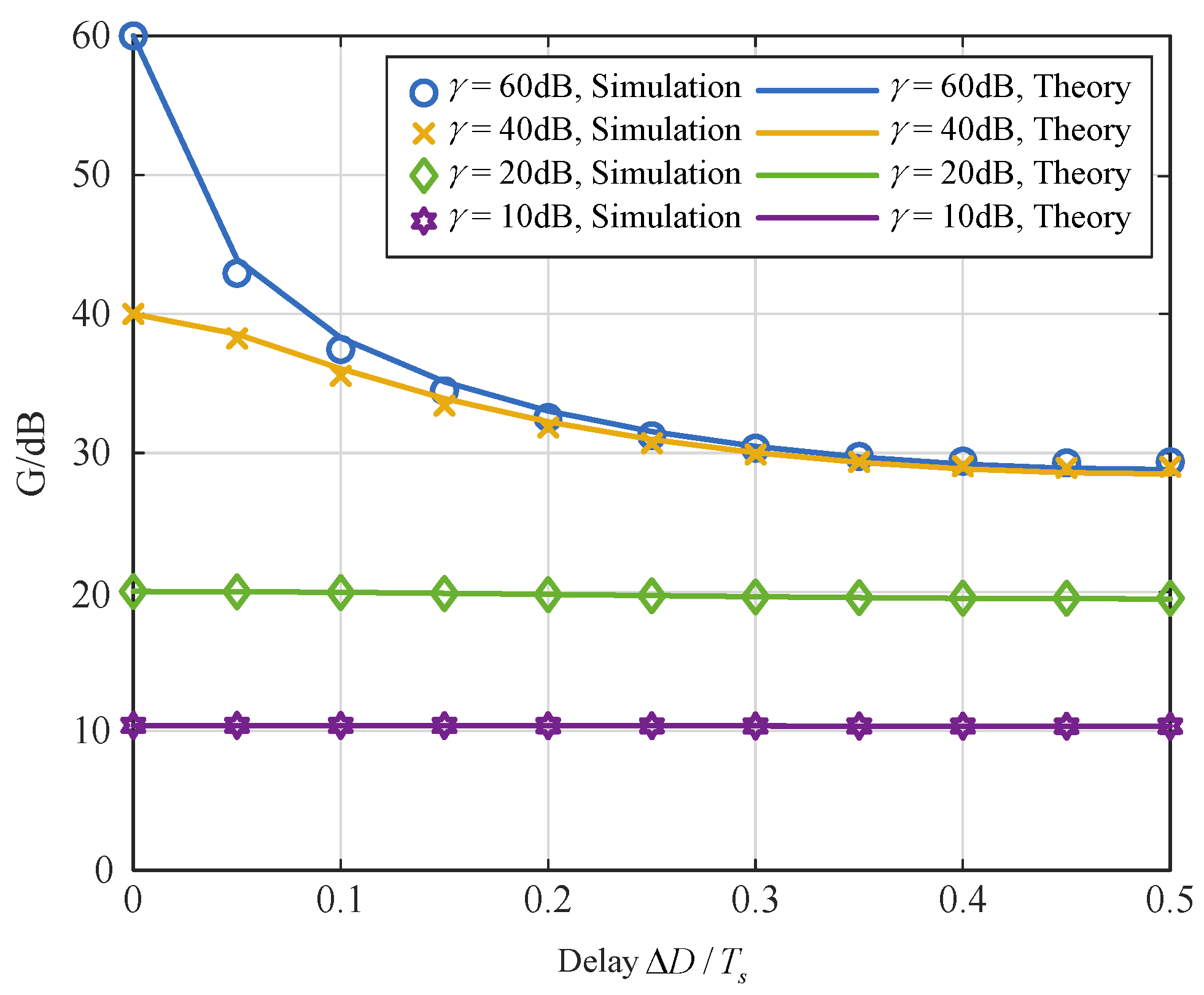
- A theoretical model is developed to quantify the effect of time synchronization errors on suppression performance in the compressed domain, with a closed-form expression derived under fractional delay.
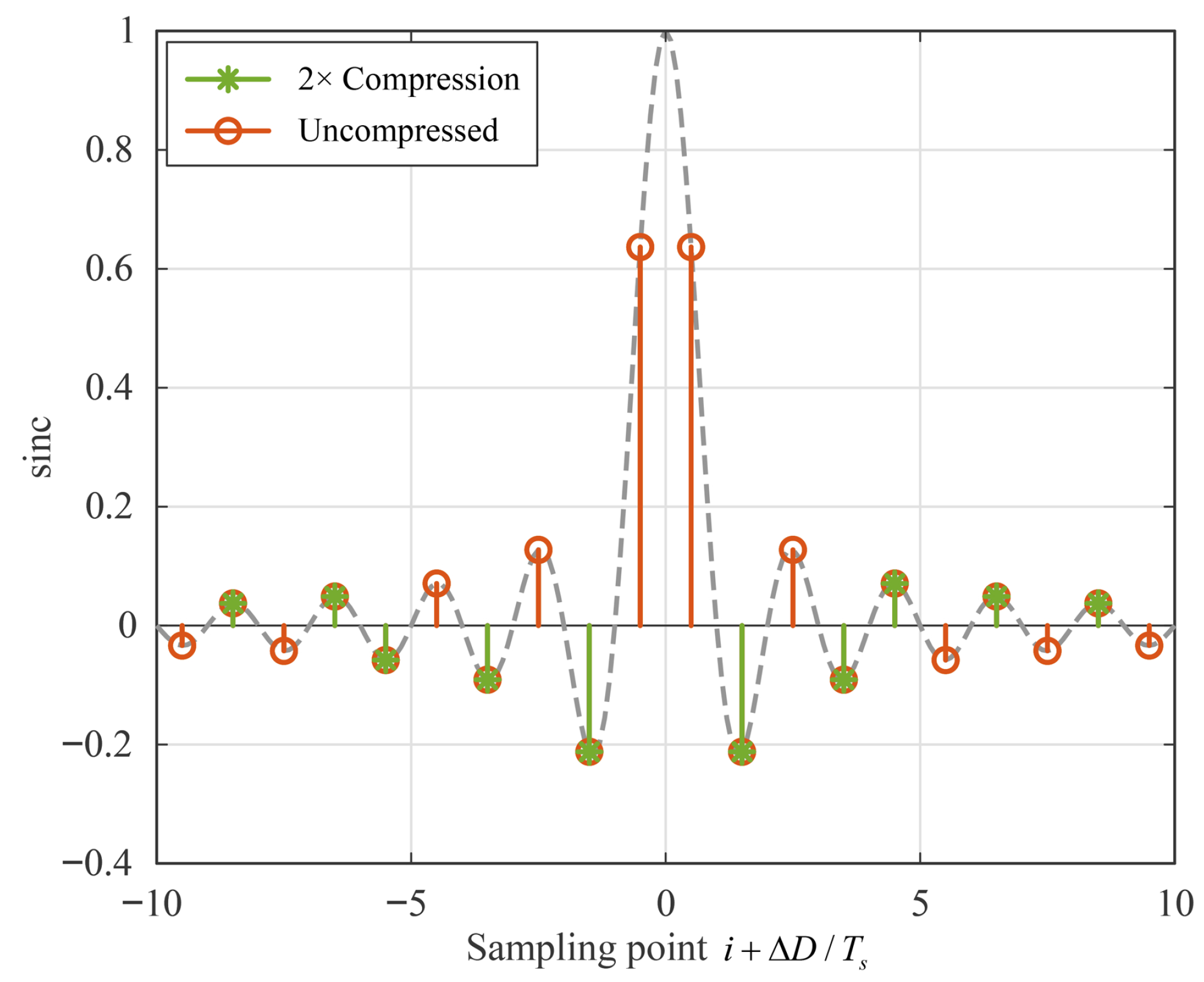
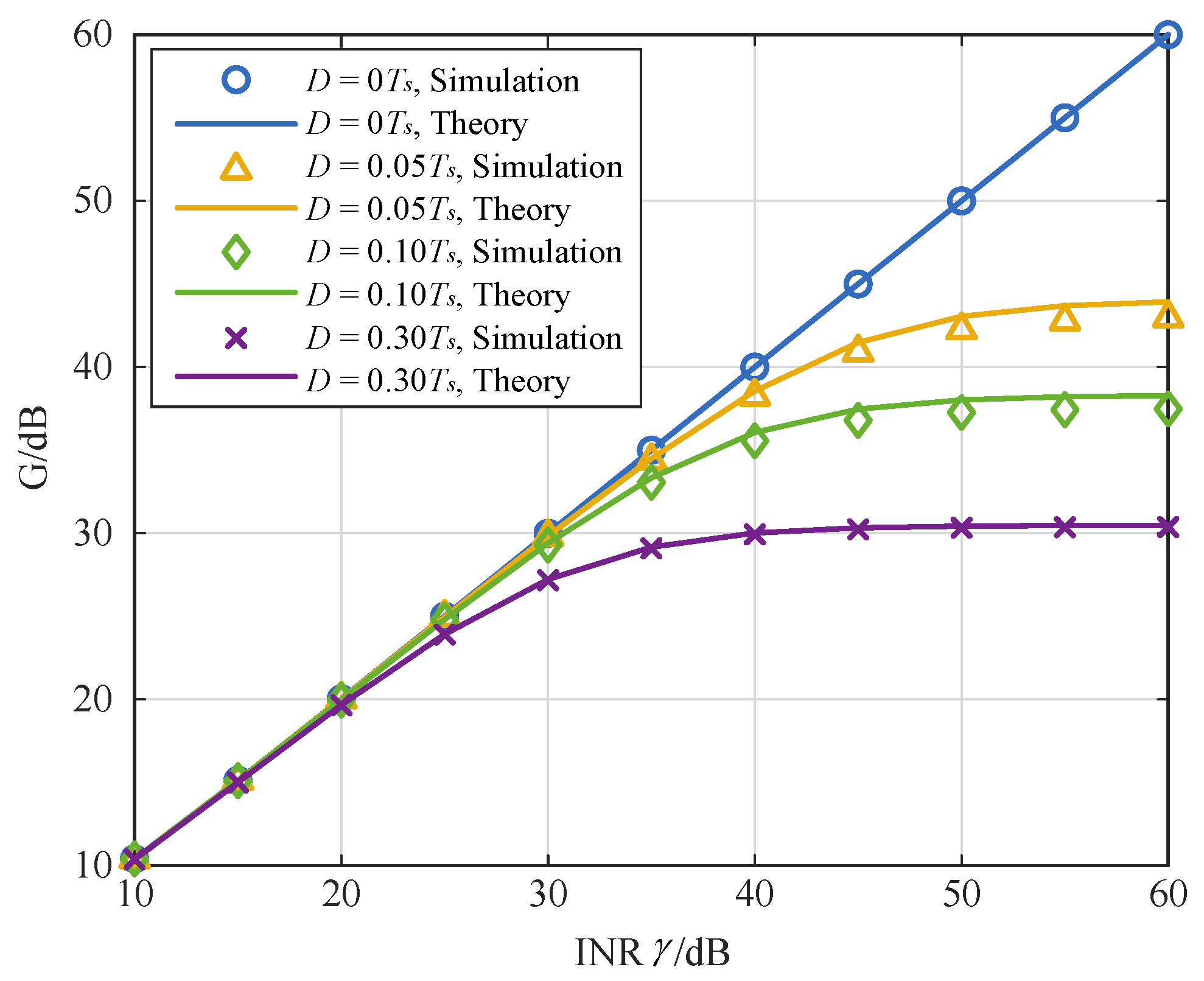
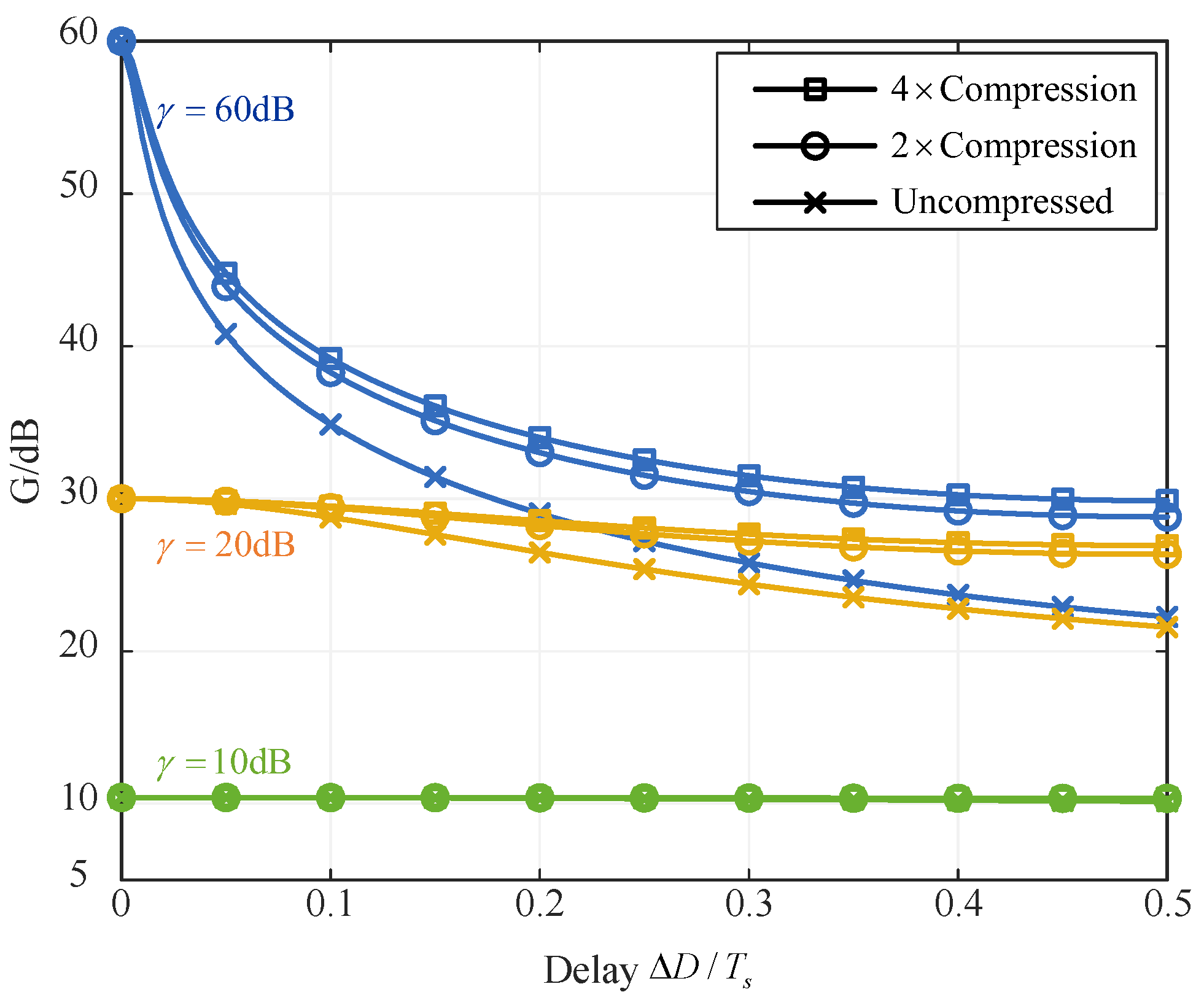
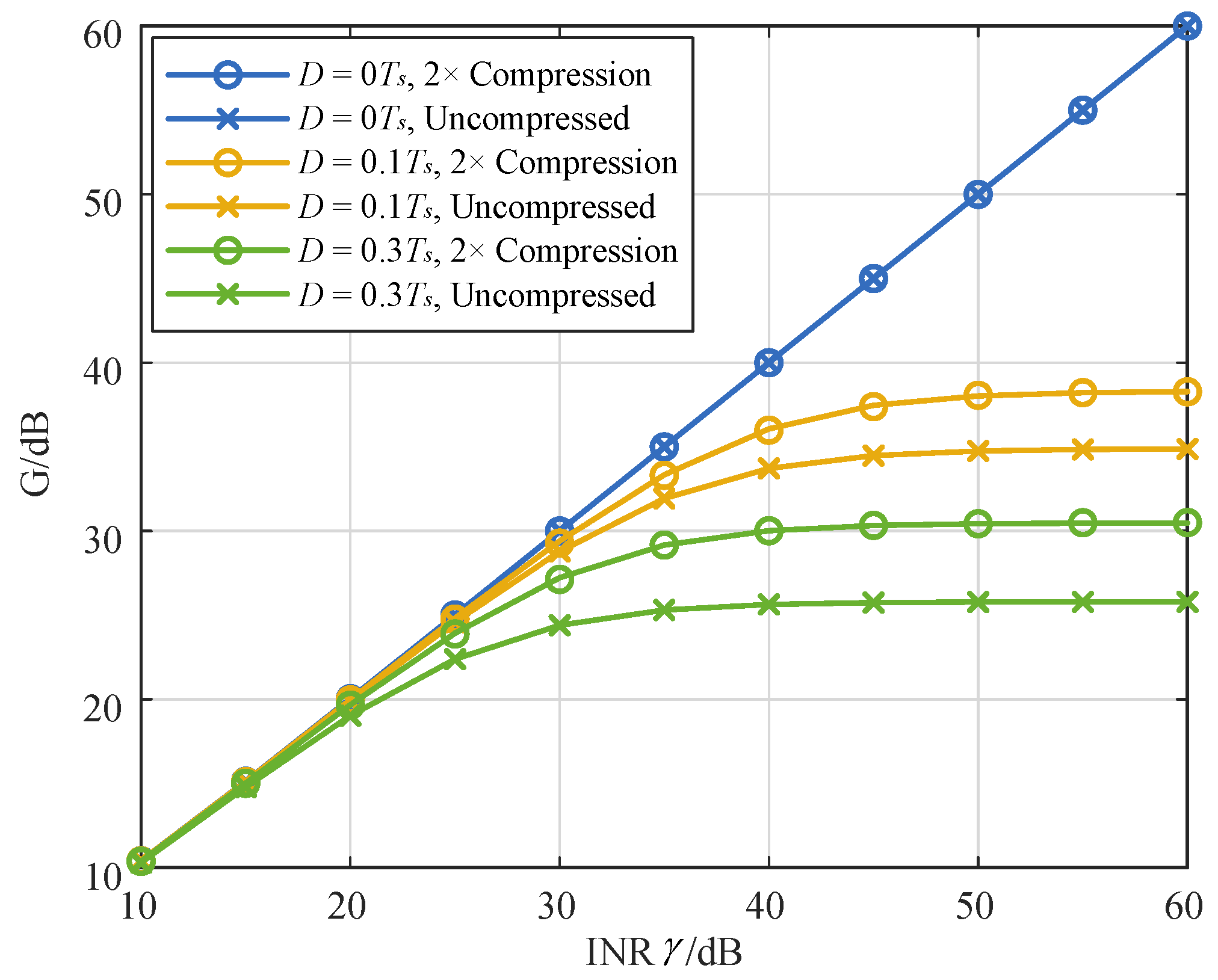
- Simulations validate the theoretical analysis, showing that under a normalized delay of 0.5, the 2-fold compressed receiver achieves 6.9 dB better suppression than the uncompressed receiver.
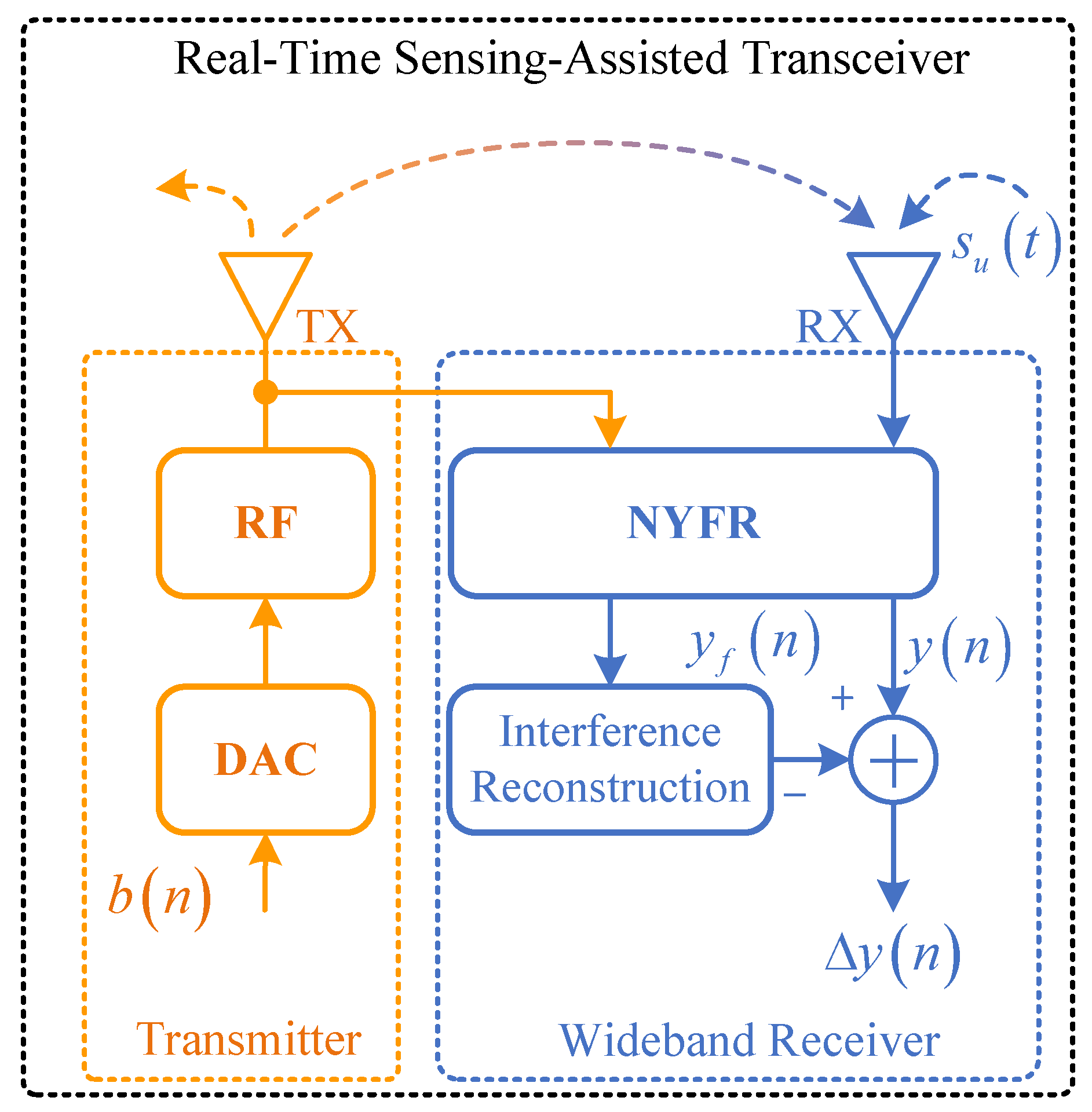
2. System Model
2.1. Transmitter
2.2. Channel
2.3. Wideband Receiver
3. CS-Based Wideband Receiver
3.1. NYFR-Based Signal Folding
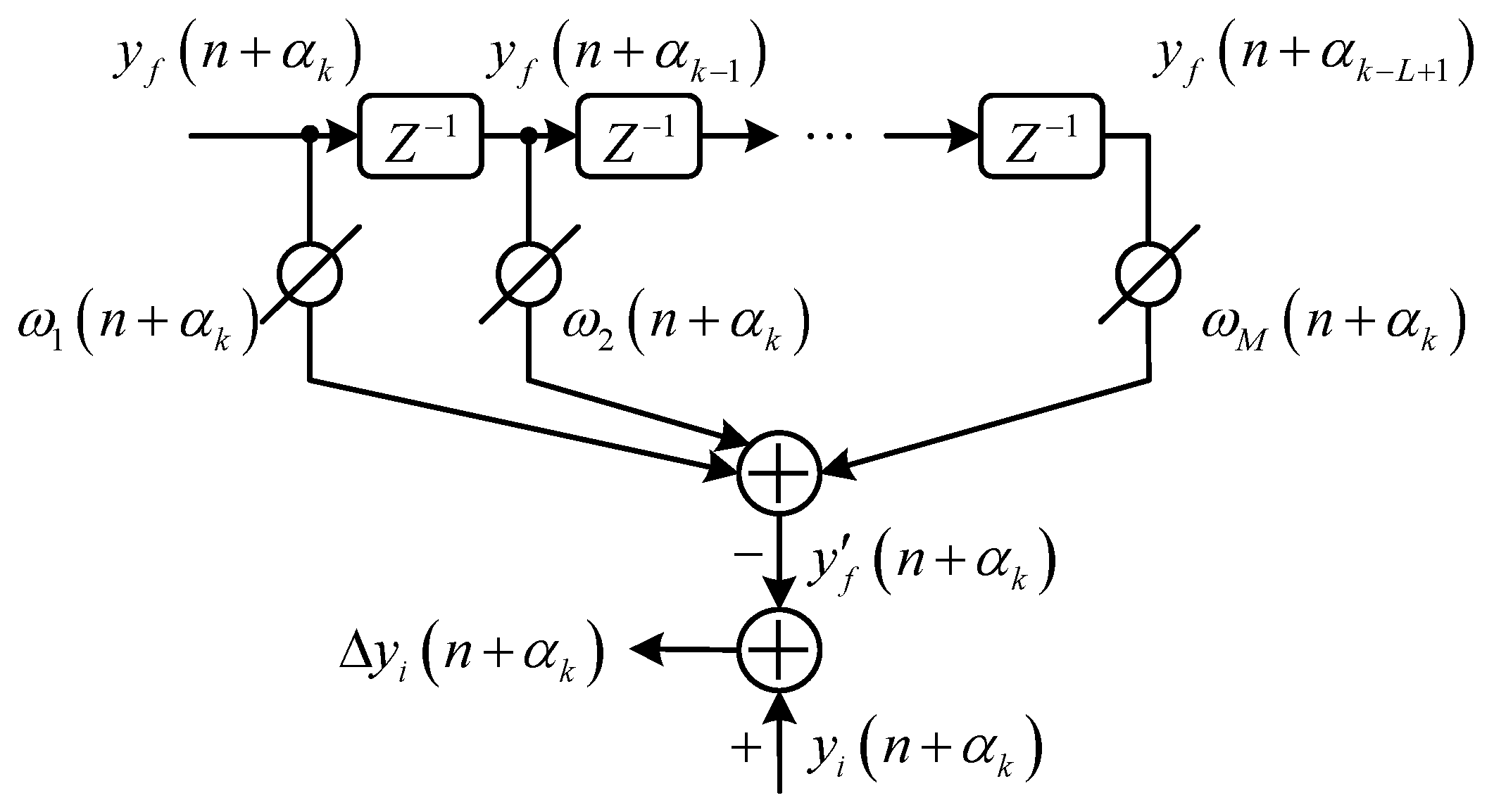
3.2. Self-Interference Suppression
3.3. SOI Reconstruction
4. Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CS | Compressive sensing |
| NYFR | Nyquist folding receiver |
| ADC | Analog-to-digital converter |
| DAC | Digital-to-analog converter |
| RF | Radio frequency |
| ISI | Inter-symbol interference |
| INR | Interference-to-noise ratio |
| SNR | Signal-to-noise ratio |
| SOI | Signal of interest |
References
- Garg, H.; Dave, M. Securing IoT Devices and SecurelyConnecting the Dots Using REST API and Middleware. In Proceedings of the 2019 4th International Conference on Internet of Things: Smart Innovation and Usages (IoT-SIU), Ghaziabad, India, 18–19 April 2019; pp. 1–6. [Google Scholar]
- Ramsudhan, G.; Hrudaya, G.; Krishnan, R. Blockchain Enabled IoT Security for Smart Home Network. In Proceedings of the 2025 13th International Conference on Smart Grid (icSmartGrid), Glasgow, UK, 27–29 May 2025; pp. 1–6. [Google Scholar]
- Zhou, Z.; Li, X.; He, J.; Bi, X.; Chen, Y.; Wang, G.; Zhu, P. 6G Integrated Sensing and Communication—Sensing Assisted Environmental Reconstruction and Communication. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Jiang, K.; Tian, K.; Feng, H.; Zhao, Y.; Wang, D.; Gao, J.; Cao, S.; Zhang, X.; Li, Y.; Yuan, J.; et al. Distributed UAV Swarm Augmented Wideband Spectrum Sensing Using Nyquist Folding Receiver. IEEE Trans. Wirel. Commun. 2024, 23, 14171–14184. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, M.; Gao, Y.; Liu, S. Efficient Millimeter-Wave Beam Prediction: A Wi-Fi Sensing-Assisted Deep Learning Approach. IEEE Sens. J. 2024, 24, 42210–42218. [Google Scholar] [CrossRef]
- Maleh, R.; Fudge, G.L.; Boyle, F.A.; Pace, P.E. Analog-to-information and the Nyquist folding receiver. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 564–578. [Google Scholar] [CrossRef]
- Sui, J.; Liu, Z.; Wei, X.; Li, X.; Peng, B.; Liao, D. Velocity false target identification in random pulse initial phase radar based on compressed sensing. In Proceedings of the 2015 3rd International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Pisa, Italy, 17–19 June 2015; pp. 179–183. [Google Scholar]
- Tang, J.; Qiu, Z.; Cao, B.; Yuan, Z. Parameter Estimation of Multiple Linear Frequency Modulation Signals Sensed by Nyquist Folding Receiver Using Periodic Linear Frequency Modulation Local Oscillator. IEEE Sens. J. 2025, 25, 31120–31134. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, P.; Zhu, J.; Tang, B. Estimation of both Nyquist zone index and code rate for BPSK radar signal intercepted by Nyquist folding receiver. IET Radar Sonar Navig. 2017, 11, 1652–1663. [Google Scholar] [CrossRef]
- Akama, C.; Nunoo, S.; Lee, K.J.; Annan, J.K. Optimal Beamforming for Full-Duplex Integrated Sensing, Communication and Computation Systems. IEEE Access 2025, 13, 152335–152345. [Google Scholar] [CrossRef]
- Liu, G.; Yu, F.R.; Ji, H.; Leung, V.C.; Li, X. In-band full-duplex relaying: A survey, research issues and challenges. IEEE Commun. Surv. Tutor. 2015, 17, 500–524. [Google Scholar] [CrossRef]
- Deo, P.; Mirshekar-Syahkal, D.; Zheng, G.; Pal, A.; Mehta, A. Broadband antenna for passive self-interference suppression in full-duplex communications. In Proceedings of the IEEE Radio and Wireless Symposium, Anaheim, CA, USA, 15–18 January 2018; pp. 243–245. [Google Scholar]
- Ju, H.; Xu, Y.; He, D.; Yang, N.; Li, H.; Zhang, W.; Wu, Y. An RF Self-Interference Cancellation method for In-Band Distribution Link in ATSC 3.0. In Proceedings of the 2024 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Toronto, ON, Canada, 19–21 June 2024; pp. 1–5. [Google Scholar]
- Liu, Y.; Quan, X.; Pan, W.; Tang, Y. Digitally assisted analog interference cancellation for in-band full-duplex radios. IEEE Commun. Lett. 2017, 21, 1079–1082. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, C.; Ding, W.; Zhao, N.; Liu, C. Nonlinear characteristic and its suppression for cosite interference cancellation system. In Proceedings of the 2017 7th IEEE International Conference on Electronics Information and Emergency Communication (ICEIEC), Macau, China, 21–23 July 2017; pp. 591–594. [Google Scholar]
- Guo, W.; Song, C.; Xia, X.; Hu, F.; Zhao, H.; Shao, S.; Tang, Y. Analysis of cooperative jamming cancellation with imperfect time synchronization in physical layer security. IEEE Wirel. Commun. Lett. 2020, 10, 335–338. [Google Scholar] [CrossRef]
- Guo, W.; Hu, H.; He, Y.; Yan, M.; Zhao, H.; Shao, S. Impacts of Clock Jitter on Cooperative Jamming Cancellation. In Proceedings of the IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 4142–4147. [Google Scholar]
- Jing, W.; Tang, J.; Cao, S.; Liu, P. Time synchronization with delay estimation and joint clock skew and offset estimation for UAV networks. In Proceedings of the International Conference on Communication Technology, Wuxi, China, 20–22 October 2023; pp. 1662–1667. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- He, Y.; Zhao, H.; Guo, W.; Shao, S.; Tang, Y. A Time-Robust Digital Self-Interference Cancellation in Full-Duplex Radios: Receiver Design and Performance Analysis. IEEE Access 2020, 8, 185021–185031. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Original Sampling Rate | 100 MHz |
| Compressed Sampling Rate | 50 MHz |
| Carrier Frequency | 2.4 GHz |
| Bandwidth of SOI | 1 MHz |
| Interference Signal Bandwidth | 5 MHz |
| Fractional Delay Range | 0∼0.5 |
| Interference-to-Noise Ratio | 10∼60 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Qin, L.; Sheng, W. Real-Time-Sensing-Assisted Intelligent Communication for Internet of Things. Electronics 2025, 14, 3707. https://doi.org/10.3390/electronics14183707
Zhang S, Qin L, Sheng W. Real-Time-Sensing-Assisted Intelligent Communication for Internet of Things. Electronics. 2025; 14(18):3707. https://doi.org/10.3390/electronics14183707
Chicago/Turabian StyleZhang, Shengfeng, Lizhi Qin, and Weixing Sheng. 2025. "Real-Time-Sensing-Assisted Intelligent Communication for Internet of Things" Electronics 14, no. 18: 3707. https://doi.org/10.3390/electronics14183707
APA StyleZhang, S., Qin, L., & Sheng, W. (2025). Real-Time-Sensing-Assisted Intelligent Communication for Internet of Things. Electronics, 14(18), 3707. https://doi.org/10.3390/electronics14183707






