Abstract
Spectrum prediction is essential for cognitive radio, enabling dynamic management and enhanced utilization, particularly in multi-band environments. Yet, its complex spatiotemporal nature and non-stationarity pose significant challenges for achieving high accuracy. Motivated by this, we propose a multi-scale Mamba-based multi-band spectrum prediction method. The core Mamba module combines Bidirectional Selective State Space Models (SSMs) for long-range dependencies and dynamic convolution for local features, efficiently extracting spatiotemporal characteristics. A multi-scale pyramid and adaptive prediction head select appropriate feature levels per prediction step, avoiding full-sequence processing to ensure accuracy while reducing computational cost. Experiments on real-world datasets across multiple frequency bands demonstrate effective handling of spectrum non-stationarity. Compared to baseline models, the method reduces root mean square error (RMSE) by 14.9% (indoor) and 7.9% (outdoor) while cutting GPU memory by 17%.
1. Introduction
The continuous advancement of wireless communication technologies, coupled with the proliferation of new applications and the surge in connected users, has intensified the challenge of spectrum scarcity. Traditional static spectrum management allocates fixed frequency bands to Primary User (PU) based on predefined rules. While granting exclusive access rights, this rigid approach suffers from inherent inflexibility in spectrum usage, hindering efficient resource utilization.
Dynamic Spectrum Access (DSA), a key component of Cognitive Radio (CR), enhances spectrum utilization by enabling Secondary Users (SUs) to detect and opportunistically access idle licensed bands without interfering with Primary Users (PUs) [1,2,3,4]. This capability is particularly valuable in massive machine-type communications (mMTC) scenarios—one of the core use cases in 5G and beyond—where numerous low-power devices generate sporadic uplink traffic unsuited to static allocation. By dynamically assigning spectrum based on real-time availability, DSA mitigates congestion and reduces latency [5]. However, traditional CR systems face challenges such as high sensing energy costs, hardware limitations, and unreliable detection, which may cause harmful interference [6,7]. Forecasting spectrum availability, therefore, is vital for intelligent decision-making and efficient dynamic spectrum management.
Functioning as a complementary technique to spectrum sensing, spectrum prediction analyzes historical spectrum monitoring data to uncover temporal occupancy patterns and inter-channel correlations within wireless channels, thereby forecasting critical parameters including future channel states, duty cycles, and power spectral density (PSD). By rapidly identifying spectrum holes—that is, frequency bands assigned to PUs but temporarily unoccupied in time or space, this methodology guides real-time sensing operations and subsequent access decisions, ultimately enhancing spectrum utilization efficiencies [8,9,10,11,12]. Existing spectrum prediction approaches fall into two paradigms: model-driven and data-driven. Model-driven methods, such as regression analysis [13,14] and Hidden Markov Models (HMM) [15,16] primarily rely on statistical frameworks with predefined structures. However, their rigid parameterization impedes adaptation to dynamic radio environments, resulting in limited prediction accuracy in practical deployments. Furthermore, current research predominantly focuses on short-term forecasting. In contrast, data-driven approaches leveraging deep learning have emerged as the predominant research frontier. Deep learning eliminates the need for explicit model assumptions, autonomously extracting intricate nonlinear features from raw data. The inherent flexibility of deep neural networks confers superior generalization capabilities while capturing long-range temporal and spatial dependencies in spectrum data, enabling significantly improved prediction accuracy. These compelling advantages drive extensive research on deep learning-based prediction algorithms, exemplified by employing Recurrent Neural Network (RNN) to model temporal dynamics and utilizing Convolutional Neural Network (CNN) to identify spectral correlations or spatial features.
However, increasingly scarce spectrum resources necessitate accurate long-term predictions spanning hours to days. Current prediction methodologies exhibit limited performance in extended forecasting horizons, while single-band approaches fail to meet the growing demand for coordinated multi-band utilization. Critically, deep learning models deployed for multi-band long-term prediction characterized by complex architectures and massive parameters incur prohibitive computational overhead during both training and inference phases. This fundamentally contradicts the core objective of spectrum prediction: reducing system energy consumption by minimizing spectrum sensing operations. Consequently, designing lightweight prediction algorithms that maintain accuracy while achieving low computational complexity and minimal resource requirements presents a pivotal research challenge demanding urgent resolution.
Fundamentally, spectrum prediction can be viewed as a challenging multivariate time-series forecasting problem characterized by high spectral non-stationarity due to dynamic channel occupancy, irregular interference, and heterogeneous band properties. Recent advances in enhanced Transformer architectures [17], including In-former [18], Autoformer [19], and iTransformer [20], have delivered promising results for temporal forecasting by leveraging attention’s ability to model long-range dependencies and positional encodings’ refinement of temporal representations. However, their quadratic growth in computational complexity with sequence length poses significant challenges for large-scale or real-time spectrum monitoring, particularly in multi-band scenarios with rapid changes in spectral characteristics. In contrast, the Mamba architecture, built upon selective State Space Models (SSM), achieves linear-time computational complexity through hardware-aware parallelization while preserving its strong capacity for long-sequence modeling [21]. Recent Mamba-based adaptations for time-series forecasting, such as MambaTS proposed by Cai et al. [22] and S-Mamba introduced by Wang et al. [23], have demonstrated remarkable performance in general application domains including electrical load prediction, traffic flow analysis, environmental monitoring, and meteorological forecasting. Nevertheless, these approaches are not explicitly tailored to address the multi-scale structure and frequency-domain dynamics that are intrinsic to spectrum data.
To overcome these limitations, we introduce a novel multi-scale Mamba framework for spectrum prediction. On one hand, it is designed to capture long-term temporal dependencies while integrating fine-grained local features; on the other, it enhances the modeling of spectral variations in the frequency domain. This work represents the first application of the Mamba model to spectrum prediction, fully leveraging its high prediction accuracy and low complexity in time-series analysis. Furthermore, we design a cooperative mechanism between a multi-scale feature pyramid and adaptive prediction heads, thereby strengthening the framework’s capacity to handle non-stationary characteristics and adapt to different forecasting horizons. As a result, our method delivers both high predictive accuracy and computational efficiency under diverse spectral conditions, while maintaining excellent scalability for long-sequence inputs. The key innovations of this work are as follows:
- Dual-SSM Mamba module with gated convolutional fusion: We design a Mamba module based on dual selective SSMs for core feature extraction, where a gated convolutional fusion mechanism integrates Mamba’s strength in long-term dependency modeling with dynamic convolution’s advantage in local feature extraction. This enables efficient extraction of multidimensional spatiotemporal–spectral features from spectrum data for precise forecasting.
- Multi-scale feature pyramid with adaptive prediction heads: We construct a feature pyramid that adapts to forecasting horizons and cooperates with prediction heads to improve both short- and long-term prediction accuracy. The pyramid dynamically matches each prediction head with appropriate levels of abstract features, effectively mitigating the adverse impact of non-stationary characteristics. A staged prediction scheme is further applied to avoid computational redundancy in reprocessing full sequences, thereby reducing resource consumption.
- Comprehensive experimental evaluation using real-world spectrum monitoring data, demonstrating significant advantages over benchmark models in both prediction accuracy and computational efficiency.
The remainder of this paper is organized as follows. Section 2 reviews the current research related to spectrum prediction. Section 3 clarifies the essence of spectrum prediction and its modeling, and provides an in-depth analysis of dataset characteristics, including correlations and non-stationarity. Section 4 presents the proposed model in detail, covering both its underlying principles and implementation process. Section 5 reports extensive simulation studies to validate the effectiveness of the approach. Finally, Section 6 concludes the paper with a summary of the main contributions.
2. Related Work
This section systematically reviews current research on spectrum prediction employing autoregressive models (AR), hidden Markov models (HMM), and deep learning architectures.
2.1. Autoregressive Model-Based Spectrum Prediction
Early research in spectrum prediction was dominated by autoregressive (AR) models based on time-series analysis. This is because the time-series data of spectrum usage, arising from user behavior and radio device activities, typically exhibit pronounced periodicity and trends. Researchers utilized parametrically estimated autoregressive (AR) and moving average (MA) models to capture underlying temporal dependencies within historical spectrum data, enabling predictions of the current spectrum state [24]. The later development of the Autoregressive Integrated Moving Average (ARIMA) model substantially improved modeling accuracy and prediction performance by incorporating differencing to eliminate periodic trends [25]. Despite offering good mathematical interpretability, these approaches fundamentally rely on the assumption of a linear relationship between historical and future spectrum values. This inherent limitation impedes the modeling of nonlinear dynamics and frequency correlations within the spectrum. Consequently, such linear approaches are generally confined to single-step or short-term prediction and are fundamentally incapable of achieving reliable long-term spectrum forecasting.
2.2. Hidden Markov Model-Based Spectrum Prediction
HMM characterize spectrum occupancy as stochastic processes through state transitions, making them applicable for spectrum prediction in DSA scenarios [26,27,28]. Nevertheless, first-order HMMs suffer from constrained contextual modeling capabilities due to their Markov property, the assumption that current states depend solely on immediate predecessors, which hinders comprehensive exploitation of historical spectrum states. To address this limitation, Chen et al. [29] developed higher-order HMMs incorporating multi-step historical states for enhanced prediction. However, their approach maintains the stationary process assumption for spectrum state transitions, contradicting empirical non-stationarity induced by time-varying conditions, user mobility, and random access behaviors. Furthermore, HMM-based frameworks typically require prior knowledge of spectrum states, which is rarely fully obtainable in operational communication systems. Consequently, HMM-based methodologies remain fundamentally unsuitable for reliable long-term spectrum forecasting in practical wireless environments.
2.3. Deep Learning-Based Spectrum Prediction
In recent years, deep learning techniques have driven significant progress in spectrum prediction, demonstrating exceptional capability in representing complex, multidimensional, and nonlinear patterns. Architectures such as convolutional neural networks (CNNs) and long short-term memory (LSTM) networks have been widely employed to jointly model spectral dependencies and temporal correlations. For example, to address the highly bursty characteristics of ISM bands, Wang et al. [30] designed a K-LSTM framework incorporating autocorrelation-based clustering. This method applies K-means analysis to identify spectral autocorrelation patterns and allocates specialized predictors to dynamically matched categories, thereby improving forecasting accuracy. To alleviate error accumulation over extended prediction horizons, Shawel et al. [31] proposed an encoder–decoder ConvLSTM model that explicitly integrates spatio-spectro-temporal dependencies, enabling more robust long-term spectrum prediction. Similarly, aiming to mitigate both error propagation and underutilization of inter-channel correlations, Gao et al. [32] developed an attention-augmented multi-channel architecture within a Seq-to-Seq framework, which allocates higher weights to essential channel features while preserving spatiotemporal relational structures via LSTM modeling.
Further, Pan et al. [33] utilized stacked autoencoders (SAE) to extract latent spectral representations, minimizing the reliance on handcrafted features. By integrating bidirectional LSTM (Bi-LSTM) to exploit dependencies in both temporal directions with CNN to capture localized spatiotemporal features, their model achieves enriched time–frequency–space representation suitable for improved long-term forecasts. Zhang et al. [34] advanced multi-band long-range prediction by applying graph convolutional networks (GCNs) to extract inter-band frequency relationships and gated recurrent units (GRUs) to capture intra-band temporal dynamics.
While Transformer-based frameworks and their derivatives have enhanced long-horizon spectral forecasting, their quadratic computational complexity presents a scalability bottleneck in large-scale, long-sequence applications. For instance, Pan et al. [16] incorporated 3D Patch Merging with a hierarchical Transformer to attain high-accuracy long-term predictions. However, this architecture improves accuracy primarily by increasing model complexity, which raises computational demands, and it exhibits limited responsiveness to short-term spectral variations. As a result, its predictive performance diminishes when the forecasting horizon is small, potentially restricting its deployment in latency-sensitive, real-time scenarios.
In the aforementioned related works, methods based on autoregressive (AR) models feature simple implementation but are limited in both prediction accuracy and horizon, making it difficult to capture the long-term dependencies of non-stationary spectrum data. Prediction approaches based on hidden Markov models (HMMs) rely on prior knowledge of spectrum states, which is often difficult to obtain comprehensively in practical communication scenarios. Although deep learning-based methods have achieved promising results in long-term forecasting, current deep learning architectures are generally complex and fail to balance computational demands with prediction accuracy. To address these limitations, this paper proposes a multi-scale Mamba framework that embeds a multi-scale feature pyramid structure while maintaining linear computational complexity. Through dynamic hierarchical modeling in the multi-scale feature pyramid, the framework enables simultaneous capture of local rapid fluctuations and global slow-varying patterns in the spectrum, significantly enhancing robustness to non-stationary spectral characteristics. Compared with state-of-the-art methods, it exhibits clear advantages, achieving high-accuracy prediction while effectively reducing computational complexity, thereby laying the foundation for practical deployment in real-world communication scenarios.
3. Problem Formulation and Dataset Characterization
3.1. Problem Formulation
Fundamentally, spectrum prediction constitutes a time-series forecasting task that infers future spectral occupancy from historical observations. We employ power spectral density (PSD) as the prediction dataset, inherently capturing inter-band correlations and temporal dependencies. To exploit latent spectral usage patterns and enable multi-scale multi-step forecasting, we construct a sliding-window dataset incorporating multi-scale prediction targets. In this study, the input data is PSD observations within a fixed time window.
where S is the input step size, denotes PSD data at time T on F frequency points. The frequency dimension constitutes the feature space, with the spectral occupancy state at each timestep characterized by an F-dimensional vector. This representation inherently incorporates spectral correlations across bands, reformulating multi-band prediction as an F-variate time-series forecasting problem. Consequently, the spectrum prediction task is defined as:
where denotes the predicted output of the i-th target sequence (i = 1, 2, …, n), with Li being the corresponding sequence length. The proposed multi-scale predictive framework jointly processes historical spectral states to simultaneously forecast spectral occupancy rates at multiple time horizons.
3.2. Dataset Characterization
To validate the applicability of prediction methods in practical wireless scenarios, the highly bursty and non-stationary nature of real-world spectrum data must be addressed. Consequently, this study employs authentic spectrum monitoring data collected from physical deployments, as opposed to model-generated datasets that inherently embody mathematical regularity inconsistent with operational complexities. The experimental dataset is sourced from the Electrosense open API, you can acquire it from https://electrosense.org/ (22 January 2024) Comprising aggregated spectral measurements across the 600–800 MHz band. This data was empirically gathered by two heterogeneous sensors (indoor/outdoor) deployed within a 6 km radius of central Madrid, Spain. With 2 MHz resolution bandwidth per spectral channel and 1 min temporal resolution, continuous received signal power measurements were recorded from 1 to 8 June 2021. To assess the viability of deep learning for long-term forecasting, we conduct dependency analysis through Pearson correlation coefficients to quantify linear interdependencies across temporal and spectral dimensions. Specifically, for random variables X and Y, the Pearson correlation coefficient r is defined as:
For two random variables X and Y, the i-th observations are denoted as xi and yi, with sample means and , and sample standard deviations and , respectively. quantifies the strength and direction of linear dependence.
Spectrum data were segmented into 1000 samples at 10 min intervals for temporal and frequency correlation analysis. The results indicate that temporal dependencies remain stable within this duration, whereas shorter sampling intervals provide only marginal correlation gains at the expense of increased data volume and processing overhead. For each frequency sub-band, outliers in the power spectral density (PSD) values were detected using the three-sigma criterion and replaced with the median of adjacent valid measurements to prevent distortion in correlation statistics. Missing values, primarily caused by temporary sensing interruptions, were filled via linear interpolation along the time axis to maintain continuity in temporal correlation analysis.
This study further conducts a detailed assessment of data availability and analytical challenges from four aspects. As shown in Figure 1a,b, the 610–630 MHz band exhibits higher user activity, containing richer information on user-induced spectrum occupancy patterns. Furthermore, this band is recognized as a potential segment of TV white space, which provides a theoretical basis for its use in cognitive radio spectrum prediction experiments and studies. In addition, as illustrated in Figure 1c,e, correlation coefficients exceeding 0.75 for both indoor and outdoor measurements indicate a pronounced temporal correlation. Such correlation persists across extended time scales, confirming the presence of long-term dependencies in spectrum data. Finally, frequency correlation is found to be substantially weaker than temporal correlation, as shown in Figure 1d,f. In heavily utilized frequency ranges (e.g., 610–630 MHz), high-correlation regions appear as clustered blocks, reflecting spectrum occupancy patterns driven by user behavior. These intrinsic patterns constitute important information for prediction algorithms. The inherent temporal dependency and latent occupancy characteristics of spectrum data form a solid foundation for deep learning-based spectrum prediction.
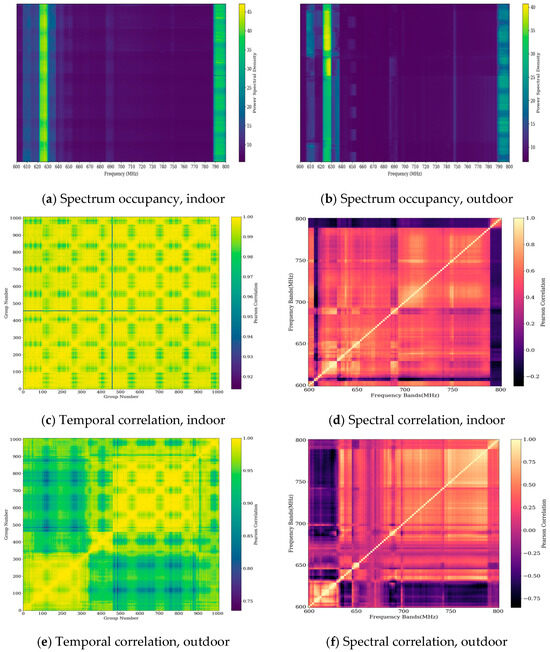
Figure 1.
Two-dimensional correlation of indoor and outdoor spectrum data.
Nevertheless, real-world data exhibit pronounced non-stationarity alongside predictive features. Daily segmentation of 7-day data in the 620–630 MHz band enabled mean and variance calculations. Figure 2 demonstrates measurable fluctuations in these statistics during the observation window. Figure 2b shows marked variance surges during days 2–3 and 5–6, caused by abrupt user population dynamics. Such non-stationary behavior imposes significant challenges for prediction.
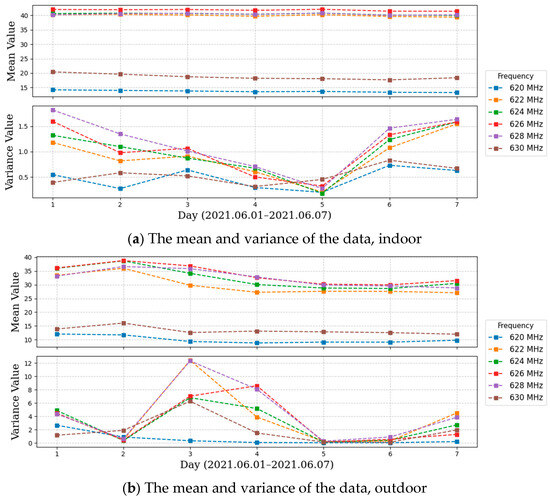
Figure 2.
Analysis of Non-stationary Characteristics in the 620−630 MHz Frequency Band Data.
4. Multi-Scale Mamba Model
4.1. Description of the MS-Mamba Model
Figure 3 illustrates the MS-Mamba architecture comprising three key components: a spatiotemporal embedding layer, a Mamba block with dual selective SSM, and a multi-scale prediction feature pyramid. Initially, temporal positional encoding projects raw features into high-dimensional space while preserving sequential properties of spectral data. The Mamba module subsequently captures long-range dependencies through dual selective SSMs, complemented by hierarchical feature extraction via the multi-scale pyramid. Ultimately, an adaptive prediction head with learned weighting coefficients enables precise multi-step forecasting.
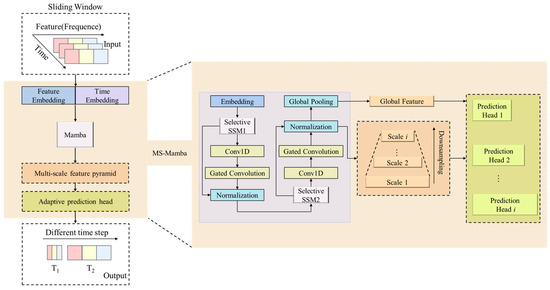
Figure 3.
Schematic diagram of the MS-Mamba model.
4.2. Spatiotemporal Embedding Layer
Spatiotemporal embedding layers are commonly utilized in time-series analysis applications such as financial forecasting and environmental monitoring. These components learn spatiotemporal feature interdependencies while dynamically adjusting prediction weights through temporal position encoding mechanisms. Essentially, they establish time-stamped feature representations. In this study, we effectively address two critical issues in spectral data processing, suboptimal feature discriminability and implicit temporal dependencies, achieved by integrating temporal positioning with cross-spectral correlations. Preprocessed spectral data is fed into this layer as standardized time-series matrices. Through feature embedding, low-dimensional spectral inputs are mapped to a high-dimensional latent space, significantly enhancing spectral correlation modeling capabilities. The mathematical representation of feature embedding is expressed as:
where denotes the learnable embedding matrix, B the batch size, and H the hidden dimension. Subsequently, temporal position encoding injects sequential ordering information into spectral data through a trainable position lookup table that assigns unique temporal index t for each time-step. The position encoding is mathematically defined as:
Here, Pos[t] is learnable position encoding table facilitates the model’s learning of both long-term dependencies and short-term fluctuations. The spatiotemporal embedding layer employs additive fusion to integrate data features and temporal position information, thereby enhancing the model’s precision in capturing temporal dependencies. The fused output is denoted as:
4.3. The Mamba Module Composed of Dual-Selective SSM
The Mamba module employs a selective SSM as its core component, which captures both long- and short-term temporal dependencies in data. This design achieves lower computational complexity than Transformer architectures while maintaining model efficacy and efficiency. The proposed dual selective SSM architecture integrates state space modeling with dynamic convolution, thereby enhancing feature extraction capabilities. Conceptually, SSM operates as a linear time-invariant system. It characterizes system behavior through state variables and predicts state evolution based on input signals. Its continuous-time formulation is expressed as:
where denotes the current state, represents the previous state, X is the input time-series matrix, and indicates the SSM output at time t. Here, A (state transition matrix), B (input matrix), C (output matrix), and D (residual matrix) are trainable parameters, A modulates historical state contributions, B governs input effects, C projects hidden states to outputs, and D enables direct input-output connections.
The SSM framework aims to predict outputs via state and observation equations based on system inputs and state vectors. To adapt SSM for discrete-time applications (e.g., spectrum prediction), it introduces dynamic discretization. Two linear layers generate data-dependent time steps , enabling adaptive state update intervals. This data-driven approach optimizes discretization parameters while permitting automatic time-scale adjustment across segments. Consequently, it mitigates the inherent trade-off in fixed-step SSMs between capturing short-term fluctuations and long-term temporal dependencies.
where and are weight matrices of the two linear layers, and denotes the Sigmoid activation function. Leveraging the adaptive time step, SSM parameters undergo discretization through a zero-order hold (ZOH) scheme.
This update mechanism preserves computational efficiency while substantially improving complex temporal pattern modeling. The formal discretization process follows:
where I represents identity matrix. Combining Equation (7) with Equation (9), the discretized SSM can be expressed as:
The fused output is first processed through depthwise separable convolution for local feature extraction, then fused with gated convolution outputs. Although SSM effectively capture long-range dependencies, they demonstrate limited local temporal pattern modeling capacity. Dynamic convolution addresses this gap by adaptively tuning the receptive field size via the input-dependent parameter.
These complementary mechanisms are integrated through gated convolution, which dynamically modulates the fusion ratio between long/short-term features based on instantaneous inputs. The resultant adaptive representation enables high-precision multi-scale forecasting. The fused Selective SSM output is expressed as:
Within this architecture, Ga is a gating mechanism, implemented as a tensor whose values are dynamically correlated with the input and lie within the interval (0, 1). Its purpose is to facilitate a weighted fusion of the outputs from the SSM path and the convolutional path. is a trainable gating weight matrix, represents the output from one-dimensional dynamic convolution, and designates the Selective SSM output. In its formulation, both A and B are dynamically varying parameters; however, in essence, these two parameters also change with the temporal step size . Therefore, the fundamental factor directly influencing the receptive field of the convolution is the dynamically varying temporal step size.
Initial spectrum inputs undergo dual Selective SSM processing, with feature enhancement via layer normalization, yielding the Mamba module’s final output. This output subsequently enters a multi-scale feature pyramid to hierarchically extract features across scales. The complete workflow is formalized as:
Here, represents the feature sequence output generated by the Mamba module through feature extraction and refinement of the input data.
4.4. Multi-Scale Predictive Feature Pyramid Module
Comprising a multi-scale feature pyramid and adaptive prediction head, this module employs hierarchical-scale matching: bottom-level features for short-term predictions, top-level for long-term horizons. Prediction-length-adaptive feature selection eliminates redundant full-sequence processing, enabling simultaneous multi-scale forecasting without retraining while maintaining computational efficiency. The pyramid hierarchically downsamples the Mamba output : lower layers preserve local spectral details, upper layers abstract global dynamics. Each level contains two convolutional layers with ReLU activation, formally expressed as:
Within this framework, designates the pyramid layer index: denotes the Mamba module’s output feature sequence when , while represents the k-th pyramid layer output for . indicate 1D convolutions of stride 2 and 1. This architecture adopts a 5-level pyramidal hierarchy, with downsampling factors exponentially scaled as across successive layers, with reducing feature sequence length via downsampling and maintaining scale invariance.
Serving as the output layer, the adaptive prediction head incorporates dedicated branches per prediction length to capture scale-specific temporal dynamics. Integration of global context and local temporal positioning balances long short-term dependencies. The full workflow is formalized as:
The workflow initiates with global average pooling to extract sequence-level representation G. This global feature is replicated Li times along the temporal dimension, yielding context-expanded feature Grep. To enable temporal positioning in long-horizon forecasting, positional encoding function generates step-wise encodings across the prediction sequence. Feature fusion is then performed by concatenating Grep and , where [;] indicates vector concatenation. The function dynamically generates positional encodings based on prediction horizons, while and denote the hidden-layer and output-layer weights of the i-th prediction branch. These coefficients are optimized during training to learn the best mapping from the global context to the specific future sequence of length Li. By training a dedicated set of ‘adaptive weighting coefficients’ for each forecast horizon, the model can implicitly learn to prioritize different aspects of the input context. For instance, the weights for a short-term forecast might learn to refine the global information for near-future steps, whereas the weights for a long-term forecast might learn a smoother, trend-based generation pattern. This parameter-specialization approach endows the model with significant flexibility for multi-scale prediction.
The MS-Mamba model advances spectrum forecasting through three integrated innovations: First, dual selective SSM fused with dynamic gated convolutions adapts in real-time to non-stationary spectral dynamics while capturing both long-range and transient dependencies. Second, a multi-scale feature pyramid hierarchically abstracts spectral occupancy patterns, significantly reducing computational burden for long sequences. Third, adaptive prediction branches decouple computational complexity from forecasting horizon, enabling high-accuracy long-term predictions through scale-specific processing.
Algorithm 1 delineates the specific implementation process of MS-Mamba.
| Algorithm 1: The Detailed Procedures of the Proposed Multi-Scale Mamba Method |
| 1: Input: Sliding window spectral dataset 2: Output: Prediction results 3: Set feature embedding layer weights 4: Set time embedding layer weights 5: Initialize mamba blocks 6: Initialize feature pyramid 7: Initialize prediction heads weights 8: Set optimizer 9: for epoch e = 1 to T do 10: Forward propagation 11: 12: Calculate the loss 13: Backward propagation 14: 15: 16: Evaluate validation set: 17: Calculate MAE/RMSE per prediction length 18: Update learning rate 19: Save best model if validation loss improves 20: end 21: return |
5. Experiments and Discussion
This section presents quantitative performance evaluation of the MS-Mamba multi-scale forecasting framework, utilizing empirical spectrum measurements from the ElectroSense open monitoring platform.
5.1. Experimental Setup
All experiments were executed in PyCharm 2023 IDE on a personal laptop produced by Lenovo in Beijing, China, equipped with Intel Core i7-13700H CPU (2.4 GHz) and NVIDIA GeForce RTX 4060 GPU. Model generalization was validated using heterogeneous spectrum measurements from ElectroSense, comprising separately collected indoor and outdoor datasets. Critical evaluation targeted the spectrally dense 610–630 MHz TV white space band to assess forecasting capability in DSA scenarios. Following a 4:1 training-testing split, hyperparameter configurations are detailed in Table 1.

Table 1.
MS-Mamba parameter configuration.
5.2. Experimental Result Analysis on Predictive Performance
The spectral forecasting capability of MS-Mamba was quantified using established time-series evaluation metrics, Normalized Root Mean Square Error (RMSE) and Mean Absolute Error (MAE).
Let and denote ground-truth and predicted spectrum measurements, respectively. Benchmark evaluation against seven state-of-the-art spectrum forecasting models was conducted under identical data splits:
- (1)
- Convolutional feature extractors: ConvLSTM and ResNet.
- (2)
- Attention-based architectures: Transformer, Informer, Autoformer, and iTransformer.
- (3)
- Baseline: Vanilla Mamba without multi-scale pyramid or adaptive prediction heads.
All comparative models capture spatiotemporal features but incur substantial computational overhead from complex architectures. Performance was assessed on the 610–630 MHz band (20 MHz bandwidth) using 60 min look-back horizons, with forecasting steps ranging 60–300 min at 60 min intervals. Figure 4 visualizes quantitative metrics across indoor/outdoor datasets.
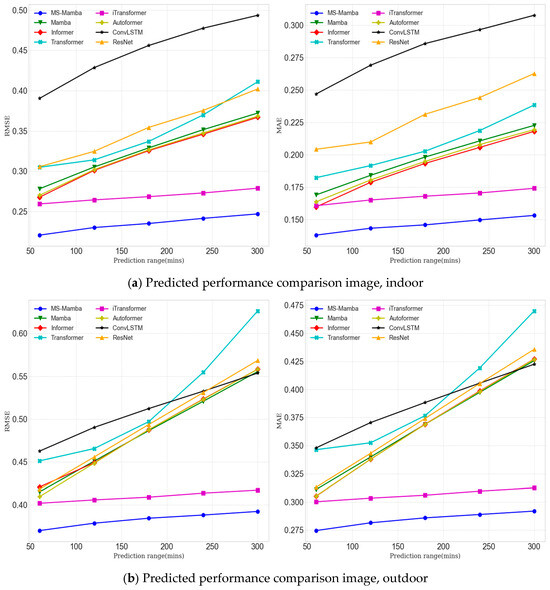
Figure 4.
Comparison chart of prediction performance for indoor and outdoor datasets in the frequency band of 620–630 MHz.
Figure 4 demonstrates that MS-Mamba achieves optimal overall performance compared to other prediction methods, significantly reducing prediction errors. While ConvLSTM and ResNet exhibit competence in data correlation capture, their long-term dependency limitations intensify with extended prediction horizons, leading to progressive performance degradation. Transformer variants excel in long-term dependency modeling but suffer from attention mechanisms’ insensitivity to local features. Quantitative improvements include: 7.9–14.9% overall gain versus iTransformer and 10.8–20.6% prediction performance increase over baseline Mamba.
All models show markedly enhanced performance on indoor datasets versus outdoor environments. As analyzed in Section 3.2, this stems from stronger temporal and spectral correlations in indoor data, coupled with lower variance, reduced mean values, and diminished fluctuations. These properties indicate superior data stationarity and correlation, facilitating more accurate predictions.
Comparative analysis of Figure 4a,b reveals that most models perform well indoors but exhibit abrupt error surges outdoors. MS-Mamba maintains robust performance due to its integration of state space models (SSMs) for long-term dependencies and dynamic convolution for local feature extraction. This dual mechanism enables comprehensive capture of multi-dimensional spectral correlations across short- and long-term contexts. Concurrently, the multi-scale feature pyramid and adaptive prediction head collaboratively allocate task-specific abstract features for each horizon, enhancing non-stationary feature handling.
MS-Mamba exhibits minimal performance fluctuation across increasing horizons, sustaining stable outputs in long-term forecasting a critical advantage. The multi-scale pyramid hierarchically extracts horizon-dependent features, while the adaptive prediction head tailors parameters to step-specific demands. This design eliminates full-sequence processing, focusing computational resources on immediate tasks to ensure stability in multi-step spectrum prediction.
5.3. Analysis of Model Efficiency
Computational efficiency was evaluated by comparing memory usage and power consumption of MS-Mamba against benchmark models during the training process of spectrum prediction on indoor/outdoor datasets. This assessment verifies whether optimal efficiency accompanies high prediction accuracy when processing complex data. To ensure fairness, each model underwent isolated GPU training to prevent cross-model interference, with all measurements meticulously recorded. Comparative computational efficiency is visualized via bubble plots in Figure 5, where axes represent memory footprint (GB) and energy consumption (Watt).
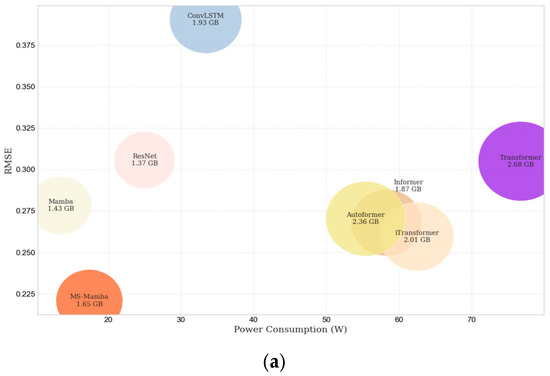
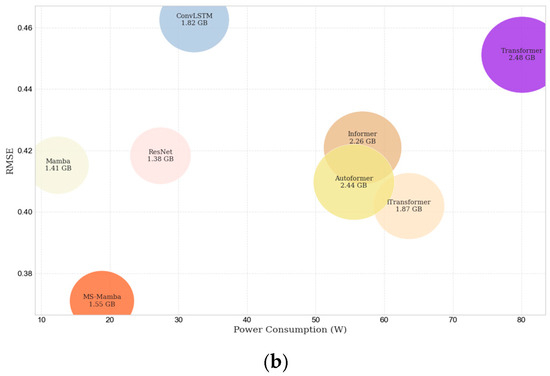
Figure 5.
Comparison chart of RMSE, GPU memory usage, and average power consumption for each model on the outdoor dataset. (a) Model RMSE, GPU memory usage and average power consumption, indoor; (b) Model RMSE, GPU memory usage and average power consumption, outdoor.
Figure 5 bubble chart depicts: vertical axis—RMSE at 60 min horizon, horizontal axis—average training power consumption (Watt-hours), bubble area proportional to GPU memory footprint (GB). Key observations:
- (1)
- MS-Mamba achieves optimal prediction accuracy with minimal resource consumption.
- (2)
- It reduces memory usage by 17% and power by 70% versus iTransformer.
- (3)
- Transformers exhibit quadratic complexity in sequence length, causing excessive resource demands.
- (4)
- ConvLSTM, ResNet show low resource usage but inferior accuracy.
- (5)
- Compared to basic Mamba, MS-Mamba’s enhanced architecture increases memory by 9% and power by 22%, representing an acceptable overhead for significant accuracy gains. The selective state space model (SSM) enables linear-time computation through recursive state updates, outperforming self-attention mechanisms. Integrated multi-scale pyramids further eliminate redundant full-sequence processing. This co-design yields a computationally efficient spectrum prediction framework with balanced accuracy-throughput trade-offs.
To further demonstrate the advantages of the proposed MS-Mamba model in reducing computational complexity, we compare its number of parameters, FLOPs, and inference time with those of other models, as summarized in Table 2. It can be observed that the MS-Mamba model maintains relatively low parameter count and FLOPs while achieving fast inference speed. This indicates that the proposed model can effectively conserve computational resources. Moreover, experimental results show that as the batch size gradually increases, the model’s memory consumption remains relatively stable, thereby confirming its capability to effectively adapt to varying computational resource conditions.

Table 2.
Model Complexity Comparison.
6. Conclusions
This study addressed the dual challenges of inadequate long-term spectrum prediction accuracy and high computational complexity in deep learning models, which hindered real-world deployment. We proposed a multi-band multi-step spectrum prediction framework based on MS-Mamba, jointly leveraging temporal and spectral correlations. The core architecture integrated the following: (1) A dual selective state space model (SSM) for capturing long-range dependencies. (2) Dynamic convolution for local feature extraction. (3) Gated fusion to reconcile both aspects—bridging SSM’s short-term feature neglect while enhancing cross-band correlations. Multi-scale pyramids synchronized features with prediction horizons, eliminating redundant full-sequence processing to boost computational efficiency. Real-world dataset validations confirmed superior prediction accuracy with reduced resource consumption, achieving an optimal efficiency-accuracy trade-off for edge deployment. Limitations included the following: increased prediction horizons might escalate pyramid complexity, necessitating adaptive head designs; and spatial correlations critical in communication scenarios remained unexplored. Future extensions would incorporate temporal–spectral–spatial features and task-adaptive pyramids.
Author Contributions
D.L. and D.X. put forward the idea of this paper. D.L. finished the design of the study and the algorithms. D.L. and G.H. contributed to the experimental work and the data analysis. D.L. and W.Z. made figures and tables. D.L. and D.X. drafted the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original data presented in the study are openly available in Electrosense at https://electrosense.org/ (22 January 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, F.; Shen, B.; Guo, J.; Lam, K.-Y.; Wei, G.; Wang, L. Dynamic Spectrum Access for Internet-of-Things Based on Federated Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2022, 71, 7952–7956. [Google Scholar] [CrossRef]
- Yucek, T.; Arslan, H. A Survey of Spectrum Sensing Algorithms for Cognitive Radio Applications. IEEE Commun. Surv. Tutor. 2009, 11, 116–130. [Google Scholar] [CrossRef]
- Ali, A.; Hamouda, W. Advances on Spectrum Sensing for Cognitive Radio Networks: Theory and Applications. IEEE Commun. Surv. Tutor. 2017, 19, 1277–1304. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive Radio: Brain-Empowered Wireless Communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Miuccio, L.; Panno, D.; Riolo, S. Dynamic Uplink Resource Dimensioning for Massive MTC in 5G Networks Based on SCMA. In Proceedings of the European Wireless 2019, 25th European Wireless Conference, Aarhus, Denmark, 2–4 May 2019; pp. 1–6. [Google Scholar]
- Sun, H.; Nallanathan, A.; Wang, C.-X.; Chen, Y. Wideband Spectrum Sensing for Cognitive Radio Networks: A Survey. IEEE Wirel. Commun. 2013, 20, 74–81. [Google Scholar] [CrossRef]
- Boulogeorgos, A.-A.A.; Chatzidiamantis, N.D.; Karagiannidis, G.K.; Georgiadis, L. Energy Detection under RF Impairments for Cognitive Radio. In Proceedings of the 2015 IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 955–960. [Google Scholar] [CrossRef]
- Xing, X.; Jing, T.; Cheng, W.; Huo, Y.; Cheng, X. Spectrum Prediction in Cognitive Radio Networks. IEEE Wirel. Commun. 2013, 20, 90–96. [Google Scholar] [CrossRef]
- Ding, G.; Jiao, Y.; Wang, J.; Zou, Y.; Wu, Q.; Yao, Y.-D.; Hanzo, L. Spectrum Inference in Cognitive Radio Networks: Algorithms and Applications. IEEE Commun. Surv. Tutor. 2018, 20, 150–182. [Google Scholar] [CrossRef]
- Suriya, M.; Sumithra, M.G. Study of Spectrum Prediction Techniques in Cognitive Radio Networks. In Proceedings of the 2022 8th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 25–26 March 2022; Volume 1, pp. 467–471. [Google Scholar]
- Pandian, P.; Selvaraj, C.; Bhalaji, N.; Arun Depak, K.G.; Saikrishnan, S. Machine Learning Based Spectrum Prediction in Cognitive Radio Networks. In Proceedings of the 2023 International Conference on Networking and Communications (ICNWC), Chennai, India, 5–6 April 2023; pp. 1–6. [Google Scholar]
- Wang, L.; Hu, J.; Zhang, C.; Jiang, R.; Chen, Z. Deep Learning Models for Spectrum Prediction: A Review. IEEE Sens. J. 2024, 24, 28553–28575. [Google Scholar] [CrossRef]
- Wen, Z.; Luo, T.; Xiang, W.; Majhi, S.; Ma, Y. Autoregressive Spectrum Hole Prediction Model for Cognitive Radio Systems. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Beijing, China, 21 May 2008; pp. 154–157. [Google Scholar]
- Gorcin, A.; Celebi, H.; Qaraqe, K.A.; Arslan, H. An Autoregressive Approach for Spectrum Occupancy Modeling and Prediction Based on Synchronous Measurements. In Proceedings of the 2011 IEEE 22nd International Symposium on Personal, Indoor and Mobile Radio Communications, Toronto, ON, Canada, 11–14 September 2011; pp. 705–709. [Google Scholar]
- Ghosh, C.; Cordeiro, C.; Agrawal, D.P.; Rao, M.B. Markov Chain Existence and Hidden Markov Models in Spectrum Sensing. In Proceedings of the 2009 IEEE International Conference on Pervasive Computing and Communications, Galveston, TX, USA, 9–13 March 2009; pp. 1–6. [Google Scholar]
- Li, Y.; Dong, Y.; Zhang, H.; Zhao, H.; Shi, H.; Zhao, X. Spectrum Usage Prediction Based on High-Order Markov Model for Cognitive Radio Networks. In Proceedings of the 2010 10th IEEE International Conference on Computer and Information Technology, Bradford, UK, 29 June–1 July 2010; pp. 2784–2788. [Google Scholar]
- Pan, G.; Wu, Q.; Zhou, B.; Li, J.; Wang, W.; Ding, G.; Yau, D.K.Y. Spectrum Prediction With Deep 3D Pyramid Vision Transformer Learning. IEEE Trans. Wirel. Commun. 2025, 24, 509–525. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Proceedings of the Advances in Neural Information Processing Systems, Online, 4–14 December 2021; Curran Associates, Inc.: Sydney, NSW, Australia, 2021; Volume 34, pp. 22419–22430. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series. Forecasting Preprint. 2024. Available online: https://arxiv.org/abs/2310.06625 (accessed on 8 July 2025).
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces 2024. Preprint. 2024. Available online: https://arxiv.org/abs/2312.00752 (accessed on 14 July 2025).
- Cai, X.; Zhu, Y.; Wang, X.; Yao, Y. MambaTS: Improved Selective State Space Models for Long-Term Time Series Forecasting. Preprint. 2024. Available online: https://arxiv.org/abs/2402.06274 (accessed on 14 July 2025).
- Luo, Y.; Wang, Y. A Statistical Time-Frequency Model for Non-Stationary Time Series Analysis. IEEE Trans. Signal Process. 2020, 68, 4757–4772. [Google Scholar] [CrossRef]
- Ozyegen, O.; Mohammadjafari, S.; Kavurmacioglu, E.; Maidens, J.; Bener, A.B. Experimental Results on the Impact of Memory in Neural Networks for Spectrum Prediction in Land Mobile Radio Bands. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 771–782. [Google Scholar] [CrossRef]
- Wang, Z.; Kong, F.; Feng, S.; Wang, M.; Yang, X.; Zhao, H.; Wang, D.; Zhang, Y. Is Mamba Effective for Time Series Forecasting? Neurocomputing 2025, 619, 129178. [Google Scholar] [CrossRef]
- Akbar, I.A.; Tranter, W.H. Dynamic Spectrum Allocation in Cognitive Radio Using Hidden Markov Models: Poisson Distributed Case. In Proceedings of the Proceedings 2007 IEEE Southeast Conference, Richmond, VA, USA, 22–25 March 2007; pp. 196–201. [Google Scholar]
- Park, C.-H.; Kim, S.-W.; Lim, S.-M.; Song, M.-S. HMM Based Channel Status Predictor for Cognitive Radio. In Proceedings of the 2007 Asia-Pacific Microwave Conference, Bangkok, Thailand, 11–14 December 2007; pp. 1–4. [Google Scholar]
- Tumuluru, V.K.; Wang, P.; Niyato, D. Channel Status Prediction for Cognitive Radio Networks. Wirel. Commun. Mob. Comput. 2010, 10, 829–842. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, R.C. Prediction of Channel State for Cognitive Radio Using Higher-Order Hidden Markov Model. In Proceedings of the IEEE Southeast Conference 2010 (SoutheastCon), Charlotte, NC, USA, 18–21 March 2010; pp. 276–282. [Google Scholar]
- Wang, X.; Peng, T.; Zuo, P.; Wang, X. Spectrum Prediction Method for ISM Bands Based on LSTM. In Proceedings of the 2020 5th International Conference on Computer and Communication Systems (ICCCS), Shanghai, China, 22–24 May 2020; pp. 580–584. [Google Scholar]
- Shawel, B.S.; Woldegebreal, D.H.; Pollin, S. Convolutional LSTM-Based Long-Term Spectrum Prediction for Dynamic Spectrum Access. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), Coruña, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar]
- Gao, Y.; Zhao, C.; Fu, N. Joint Multi-Channel Multi-Step Spectrum Prediction Algorithm. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–5. [Google Scholar]
- Pan, G.; Wu, Q.; Ding, G.; Wang, W.; Li, J.; Xu, F.; Zhou, B. Deep Stacked Autoencoder-Based Long-Term Spectrum Prediction Using Real-World Data. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 534–548. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, L.; Ben, C.; Peng, Y.; Wang, Y.; Shi, S.; Lin, Y.; Gui, G. A-GCRNN: Attention Graph Convolution Recurrent Neural Network for Multi-Band Spectrum Prediction. IEEE Trans. Veh. Technol. 2024, 73, 2978–2982. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).