Learning Human–Robot Proxemics Models from Experimental Data
Abstract
1. Introduction
2. Related Work
2.1. Empirical Studies
2.2. Modeling of Proxemics
3. Method
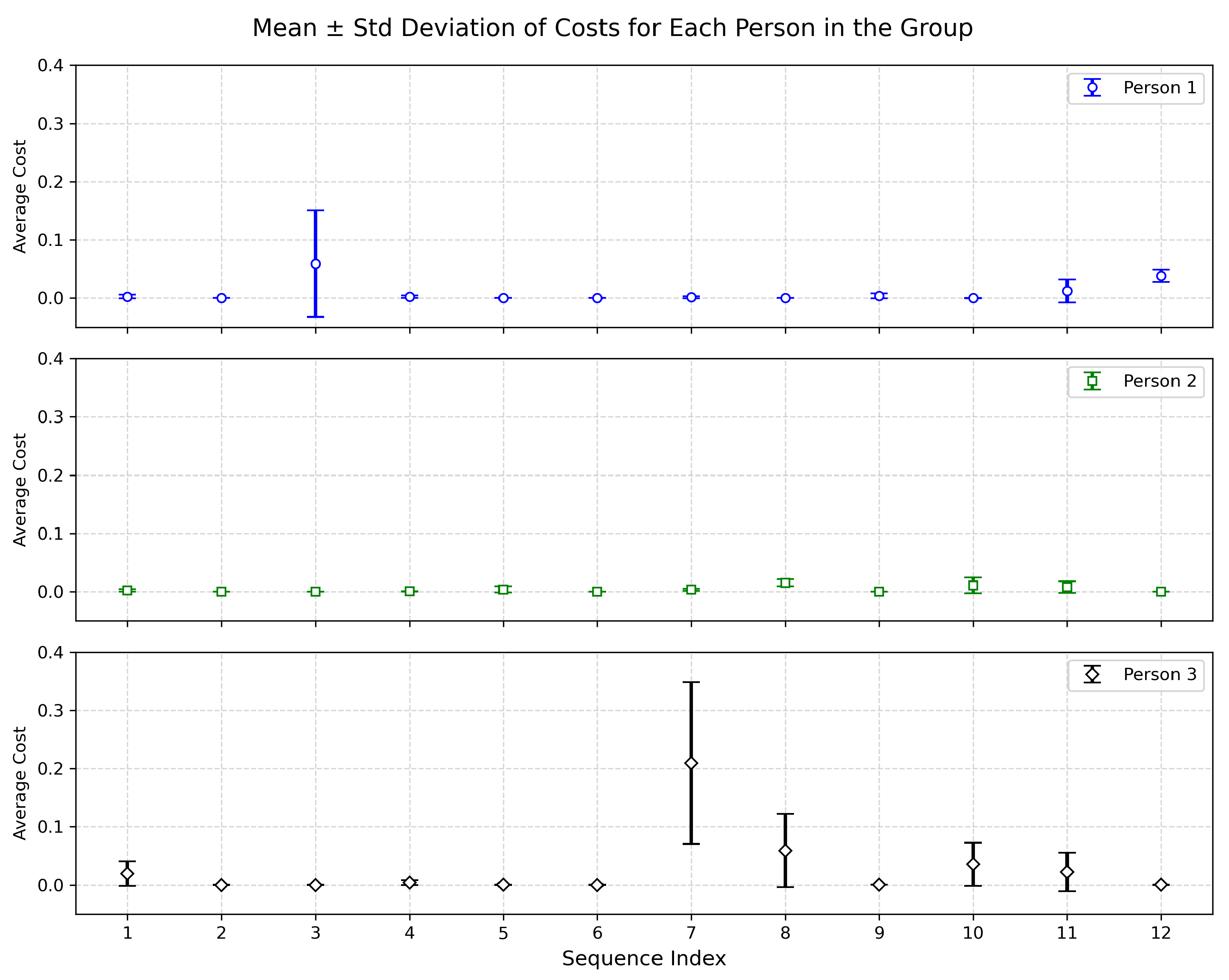
3.1. Data Preparation
3.2. Proxemic Model
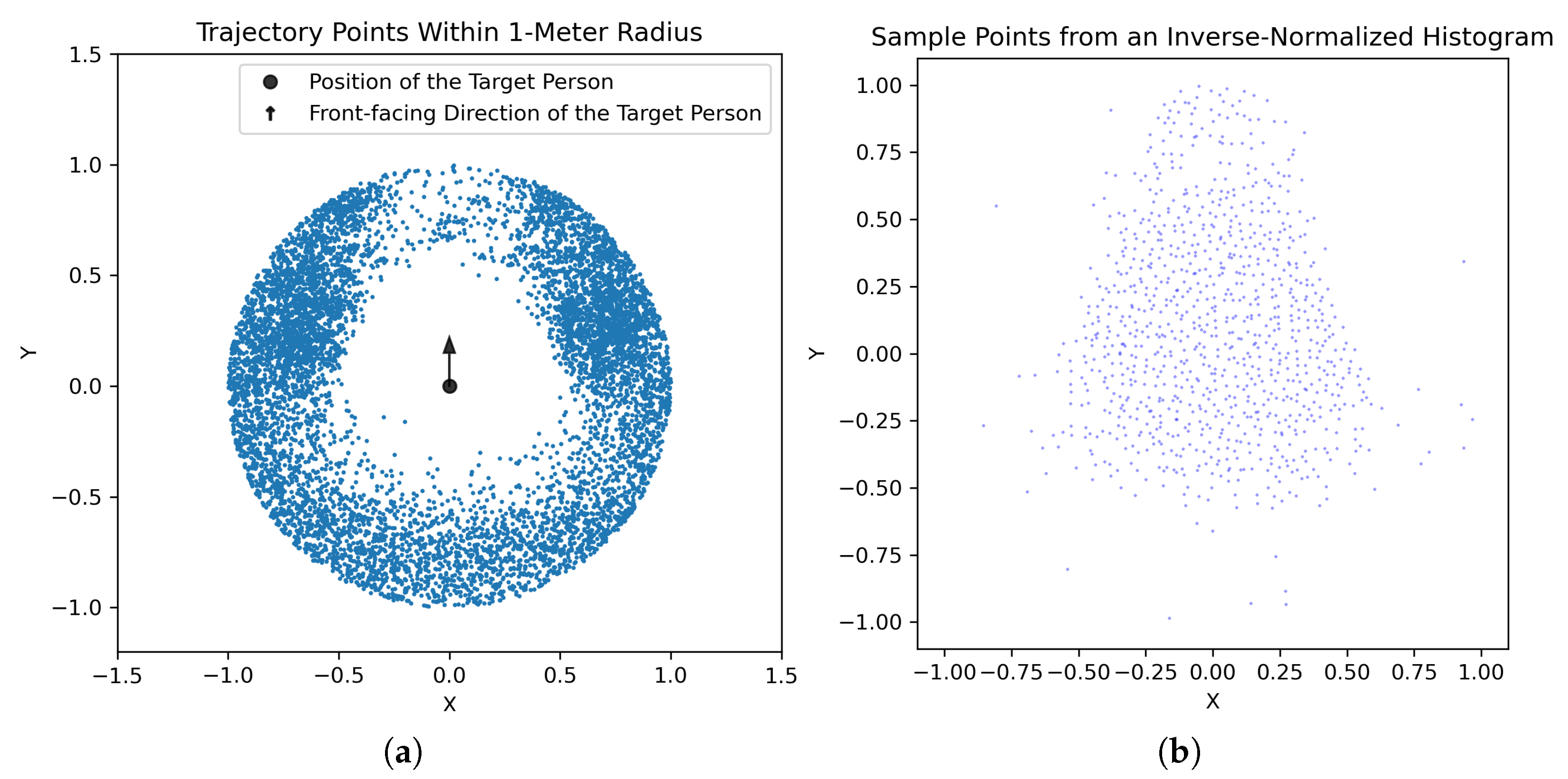
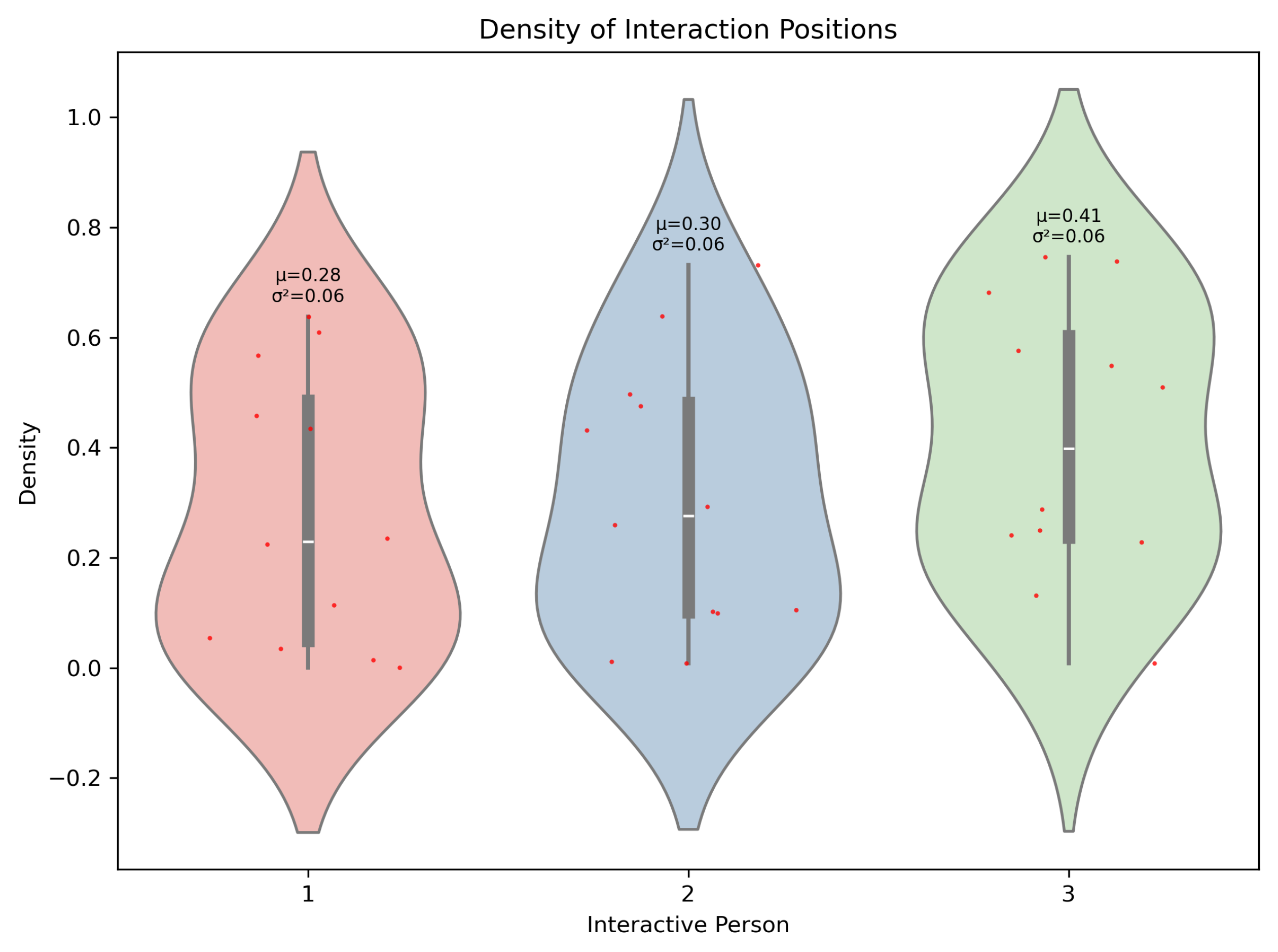
3.3. Model of Interaction Positions
4. Results
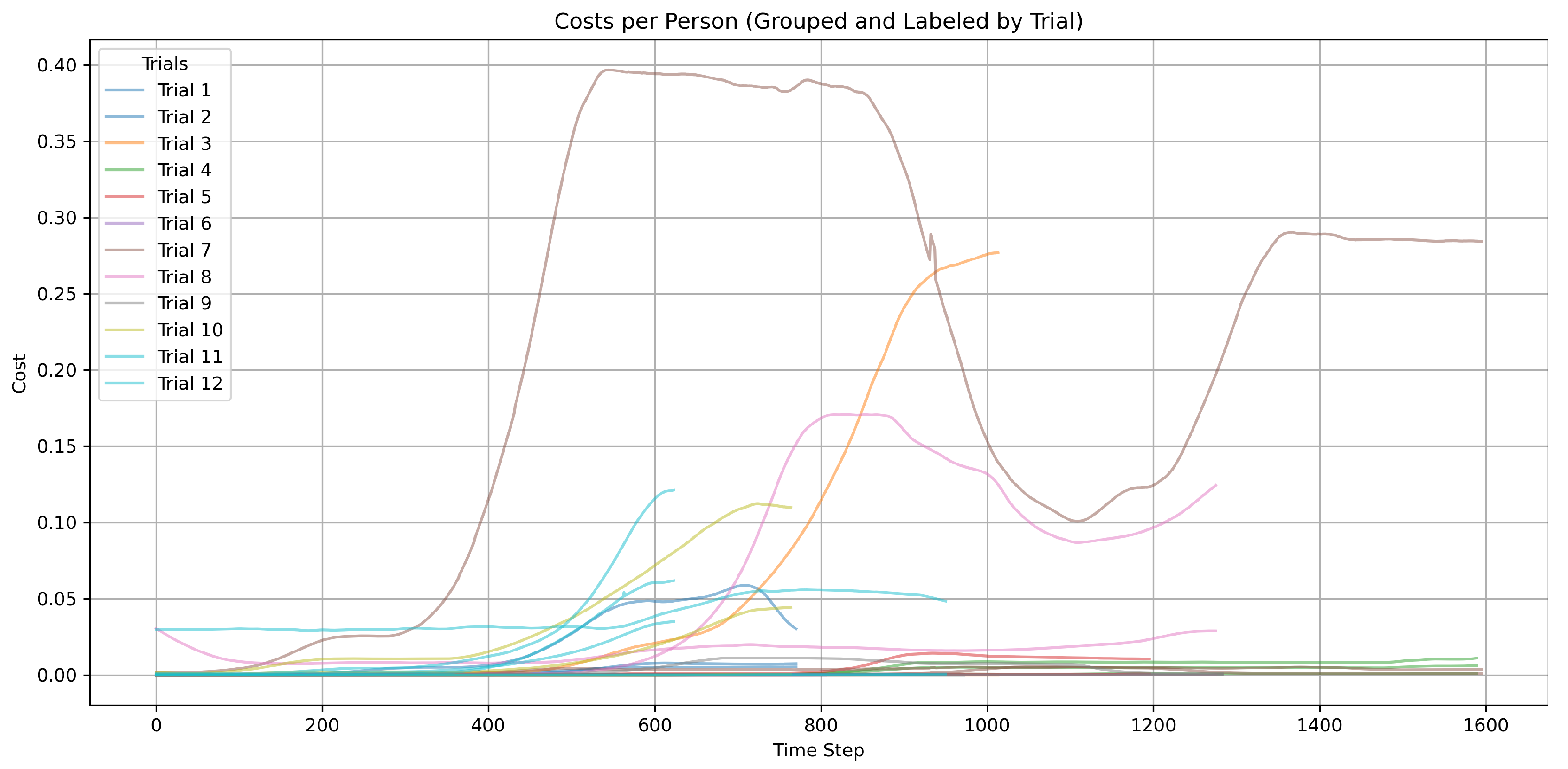
4.1. Proxemic Model
4.2. Model of Interaction Positions
5. Evaluation
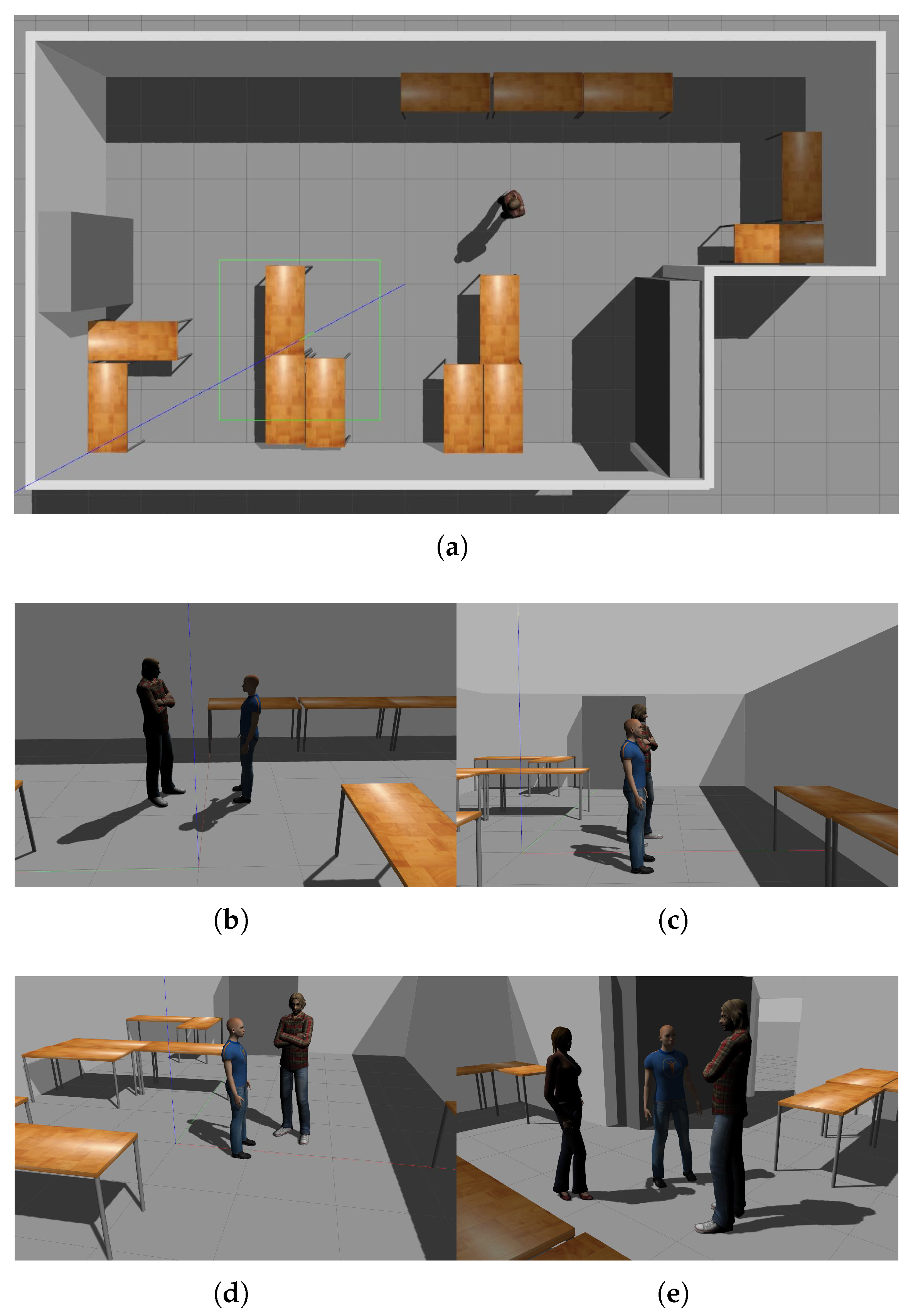
5.1. Experimental Setup
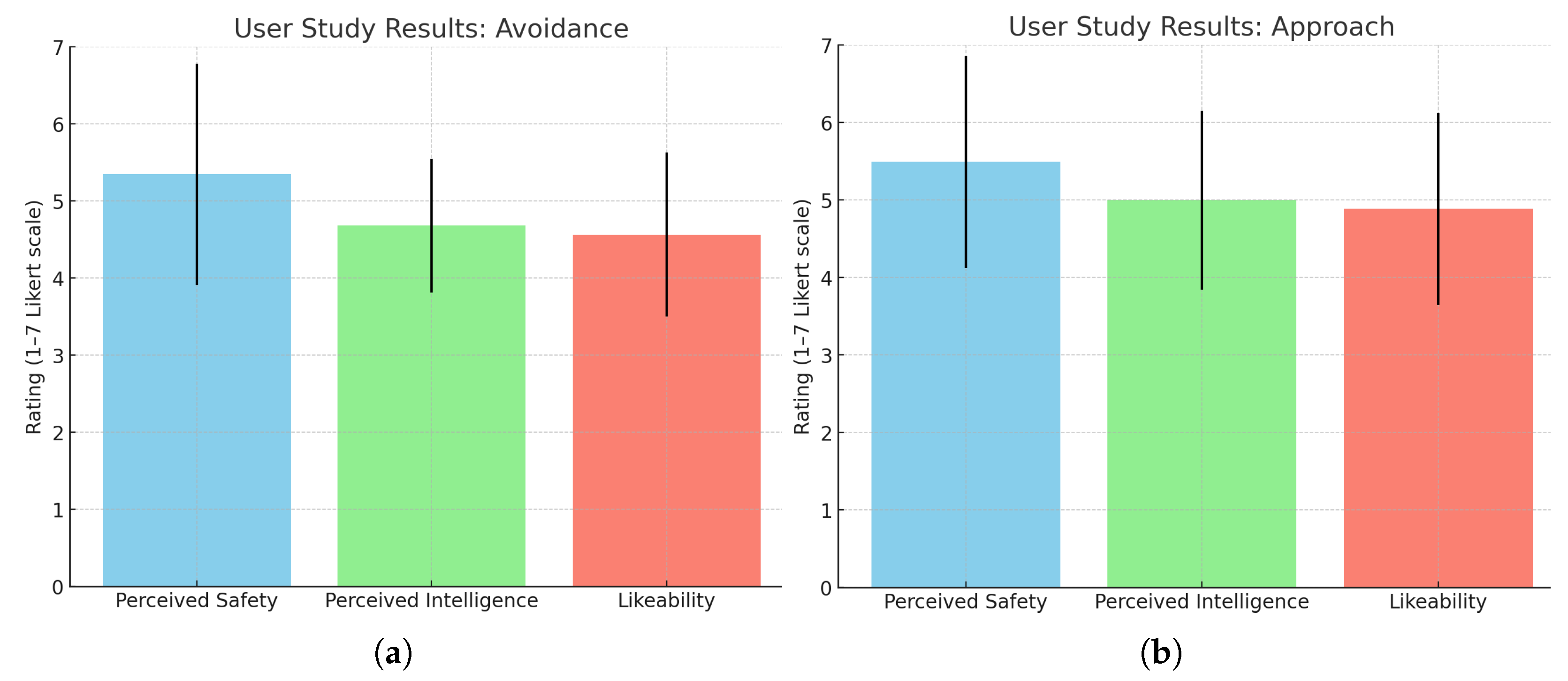
5.2. Proxemic Model
5.3. Model of Interaction Positions
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HRP | Human–Robot Proxemics |
| Skew Normal Distribution | |
| SFM | Social Force Model |
| RL | Reinforcement Learning |
| IRL | Inverse Reinforcement Learning |
| WoZ | Wizard of Oz |
| Probability Density Function | |
| EM | Expectation Maximization |
| KDE | Kernal Density Estimation |
References
- Hall, E.T.; Birdwhistell, R.L.; Bock, B.; Bohannan, P.; Diebold, A.R.; Durbin, M.; Edmonson, M.S.; Fischer, J.L.; Hymes, D.; Kimball, S.T.; et al. Proxemics [and Comments and Replies]. Curr. Anthropol. 1968, 9, 83–108. [Google Scholar] [CrossRef]
- Neggers, M.; Cuijpers, R.; Ruijten, P.; IJsselsteijn, W. Determining Shape and Size of Personal Space of a Human when Passed by a Robot. Int. J. Soc. Robot. 2022, 14, 561–572. [Google Scholar] [CrossRef]
- Wang, L.; Rau, P.L.P.; Evers, V.; Robinson, B.K.; Hinds, P. When in Rome: The role of culture & context in adherence to robot recommendations. In Proceedings of the 5th ACM/IEEE International Conference on Human-Robot Interaction, Osaka, Japan, 2–5 March 2010; pp. 359–366. [Google Scholar]
- Eresha, G.; Häring, M.; Endrass, B.; André, E.; Obaid, M. Investigating the Influence of Culture on Proxemic Behaviors for Humanoid Robots. In Proceedings of the International Symposium on Robot and Human Interactive Communication (RO-MAN 2013), Gyeongju, Republic of Korea, 26–29 August 2013; pp. 430–435. [Google Scholar]
- Kendon, A. Conducting Interaction: Patterns of Behavior in Focused Encounters; Studies in Interactional Sociolinguistics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Cristani, M.; Paggetti, G.; Vinciarelli, A.; Bazzani, L.; Menegaz, G.; Murino, V. Towards Computational Proxemics: Inferring Social Relations from Interpersonal Distances. In Proceedings of the Third International Conference on Privacy, Security, Risk and Trust and 2011 IEEE Third International Conference on Social Computing, Boston, MA, USA, 9–11 October 2011; pp. 290–297. [Google Scholar] [CrossRef]
- Samarakoon, S.M.B.P.; Muthugala, M.A.V.J.; Jayasekara, A.G.B.P. A Review on Human–Robot Proxemics. Electronics 2022, 11, 2490. [Google Scholar] [CrossRef]
- Fiore, S.M.; Wiltshire, T.J.; Lobato, E.J.; Jentsch, F.G.; Huang, W.H.; Axelrod, B. Toward understanding social cues and signals in human–robot interaction: Effects of robot gaze and proxemic behavior. Front. Psychol. 2013, 4, 859. [Google Scholar] [CrossRef] [PubMed]
- Petrak, B.; Weitz, K.; Aslan, I.; André, E. Let me show you your new home: Studying the effect of proxemic-awareness of robots on users’ first impressions. In Proceedings of the The 28th IEEE International Conference on Robot & Human Interactive Communication, New Delhi, India, 14–18 October 2019. [Google Scholar]
- Mead, R.; Matarić, M.J. Robots have needs too: How and why people adapt their proxemic behavior to improve robot social signal understanding. J. Hum.-Robot Interact. 2016, 5, 48–68. [Google Scholar] [CrossRef]
- Takayama, L.; Pantofaru, C. Influences on proxemic behaviors in human-robot interaction. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 5495–5502. [Google Scholar] [CrossRef]
- Kirby, R. Social Robot Navigation. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2010. [Google Scholar]
- Papadakis, P.; Rives, P.; Spalanzani, A. Adaptive spacing in human-robot interactions. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2627–2632. [Google Scholar] [CrossRef]
- Azzalini, A.; Valle, A.D. The Multivariate Skew-Normal Distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical Applications of the Multivariate Skew Normal Distribution. J. R. Stat. Soc. Ser. B Stat. Methodol. 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Helbing, D.; Molnár, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282–4286. [Google Scholar] [CrossRef] [PubMed]
- Kivrak, H.; Cakmak, F.; Kose, H.; Yavuz, S. Social navigation framework for assistive robots in human inhabited unknown environments. Eng. Sci. Technol. Int. J. 2021, 24, 284–298. [Google Scholar] [CrossRef]
- Patompak, P.; Jeong, S.; Nilkhamhang, I.; Chong, N. Learning Proxemics for Personalized Human–Robot Social Interaction. Int. J. Soc. Robot. 2020, 12, 267–280. [Google Scholar] [CrossRef]
- Millán-Arias, C.; Fernandes, B.; Cruz, F. Proxemic behavior in navigation tasks using reinforcement learning. Neural Comput. Appl. 2022, 35, 16723–16738. [Google Scholar] [CrossRef]
- Chen, Y.F.; Everett, M.; Liu, M.; How, J.P. Socially aware motion planning with deep reinforcement learning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1343–1350. [Google Scholar] [CrossRef]
- Abbeel, P.; Ng, A.Y. Apprenticeship learning via inverse reinforcement learning. In Proceedings of the Twenty-First International Conference on Machine Learning (ICML), Banff, AB, Canada, 4–8 July 2004; p. 1. [Google Scholar]
- Baghi, B.H.; Dudek, G. Sample Efficient Social Navigation Using Inverse Reinforcement Learning. arXiv 2021, arXiv:2106.10318. [Google Scholar] [CrossRef]
- Eirale, A.; Leonetti, M.; Chiaberge, M. Learning Social Cost Functions for Human-Aware Path Planning. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 5364–5371. [Google Scholar] [CrossRef]
- Yang, F.; Gao, A.Y.; Ma, R.; Zojaji, S.; Castellano, G.; Peters, C. A dataset of human and robot approach behaviors into small free-standing conversational groups. PLoS ONE 2021, 16, e0247364. [Google Scholar] [CrossRef]
- SoftBank Robotics Group. Pepper Robot. Available online: https://aldebaran.com/en/pepper/ (accessed on 4 September 2025).
- Dempster, A.; Laird, N.; Rubin, D. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Kulkarni, K. mvem: Maximum Likelihood Parameter Estimation in Multivariate Distributions Using EM Algorithms. Available online: https://github.com/krisskul/mvem (accessed on 15 September 2025).
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pages, J.; Marchionni, L.; Ferro, F. TIAGo: The modular robot that adapts to different research needs. In Proceedings of the International Workshop on Robot Modularity, IROS Workshop, Daejeon, Republic of Korea, 10 October 2016. [Google Scholar]
- Koenig, N.; Howard, A. Design and use paradigms for Gazebo, an open-source multi-robot simulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar] [CrossRef]
- Lu, D.V.; Hershberger, D.; Smart, W.D. Layered costmaps for context-sensitive navigation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 709–715. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Kachel, L.; Jung, M.; Al-Hamadi, A.; Wachsmuth, S. Learning Human–Robot Proxemics Models from Experimental Data. Electronics 2025, 14, 3704. https://doi.org/10.3390/electronics14183704
Yang Q, Kachel L, Jung M, Al-Hamadi A, Wachsmuth S. Learning Human–Robot Proxemics Models from Experimental Data. Electronics. 2025; 14(18):3704. https://doi.org/10.3390/electronics14183704
Chicago/Turabian StyleYang, Qiaoyue, Lukas Kachel, Magnus Jung, Ayoub Al-Hamadi, and Sven Wachsmuth. 2025. "Learning Human–Robot Proxemics Models from Experimental Data" Electronics 14, no. 18: 3704. https://doi.org/10.3390/electronics14183704
APA StyleYang, Q., Kachel, L., Jung, M., Al-Hamadi, A., & Wachsmuth, S. (2025). Learning Human–Robot Proxemics Models from Experimental Data. Electronics, 14(18), 3704. https://doi.org/10.3390/electronics14183704






