Monocular Camera Pose Estimation and Calibration System Based on Raspberry Pi
Abstract
1. Introduction
2. Related Research
3. Materials and Methods
3.1. Feature Point Extraction
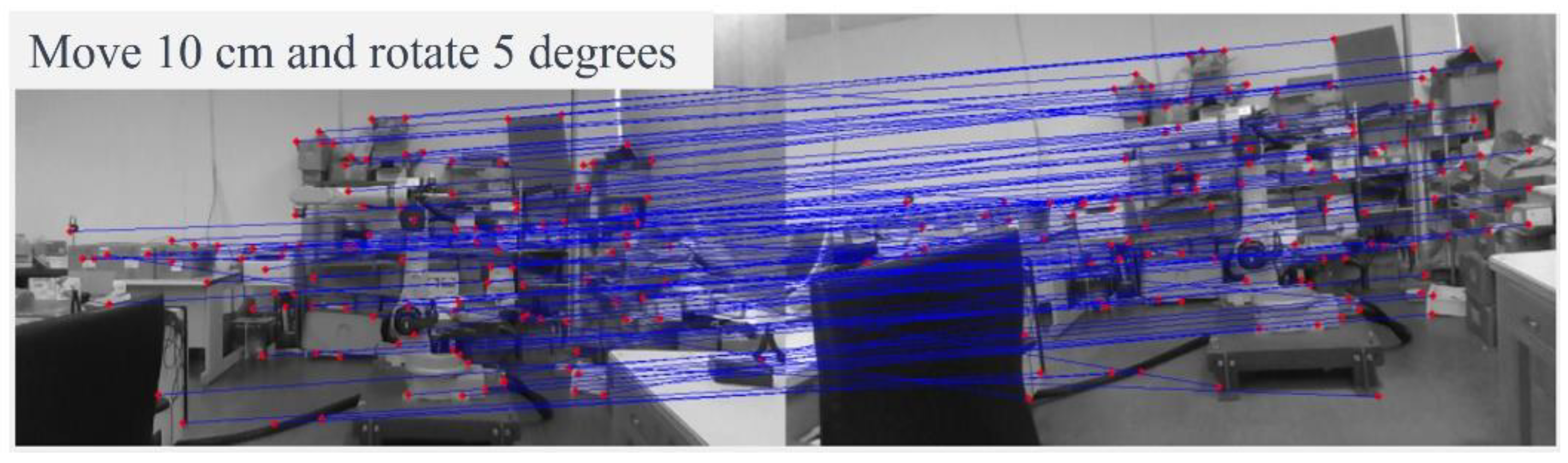
3.2. Keypoint Matching
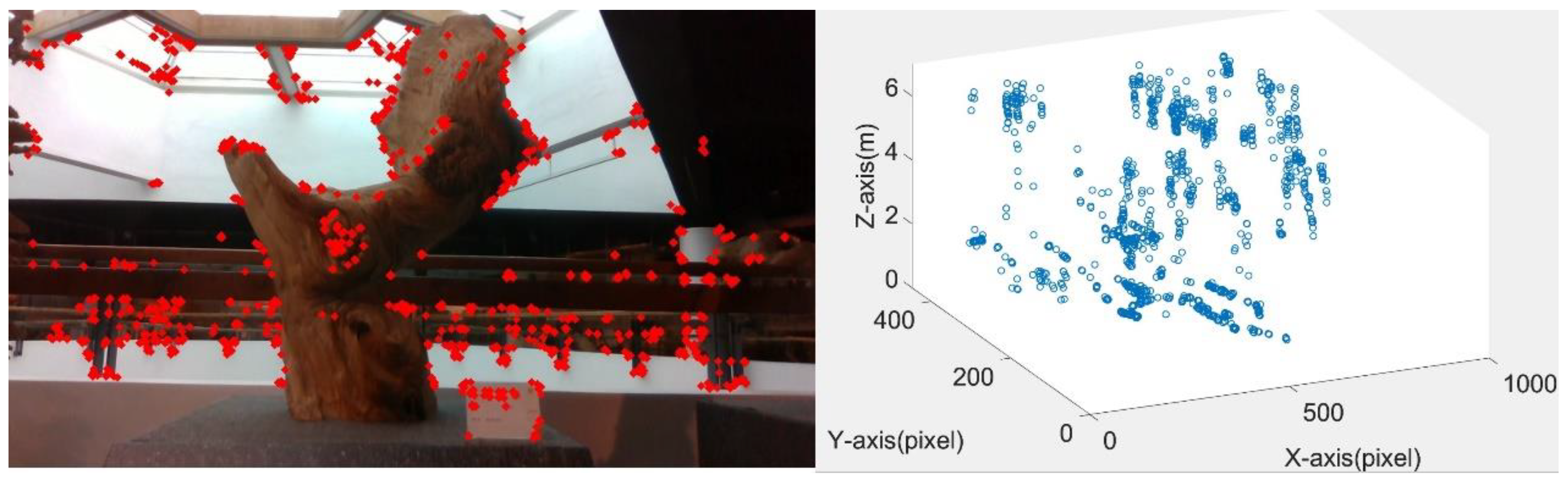
3.3. Creating Three-Dimensional Information
3.4. Camera Pose Estimation
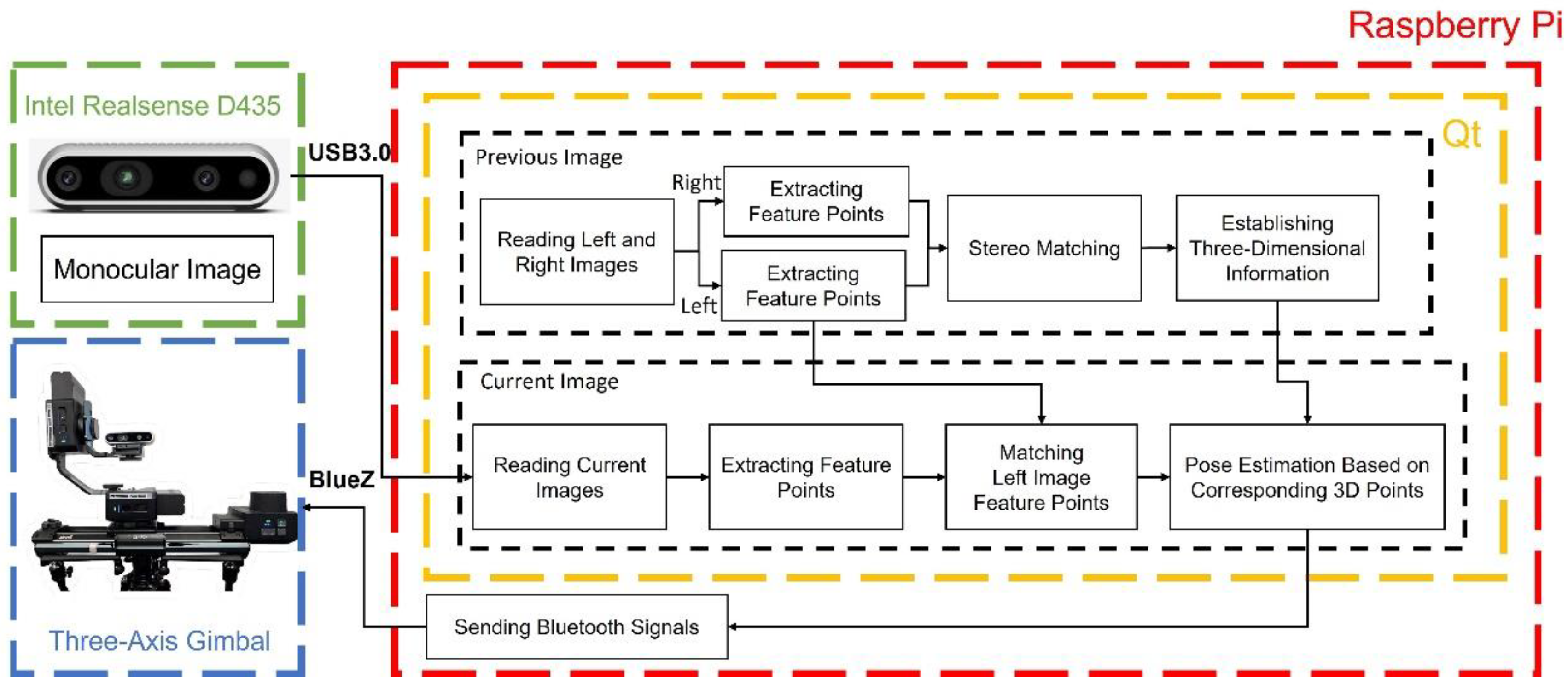
3.5. System Architecture and Algorithm Flowchart
4. Experiment and Results
4.1. Verifying the Accuracy of Calculated Camera Pose
4.2. Camera Pose Calibration Implementation
4.3. Comparing Pixel Discrepancies Between Original and Calibrated Images
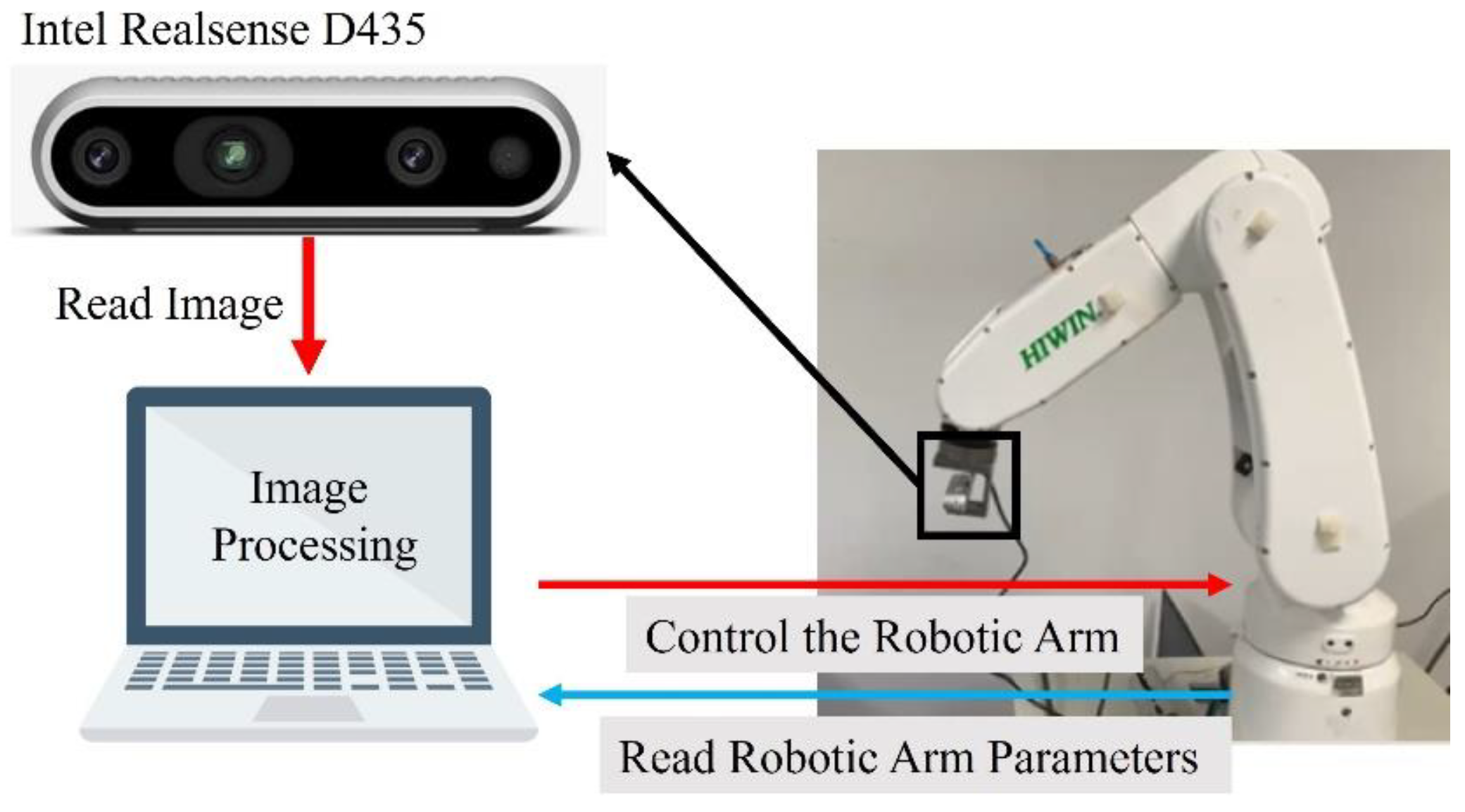
4.4. Raspberry Pi and Three-Axis Gimbal Camera Pose Calibration System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maksimović, M.; Ćosović, M. Preservation of Cultural Heritage Sites using IoT. In Proceedings of the 2019 18th International Symposium INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 20–22 March 2019; pp. 1–4. [Google Scholar]
- Lee, S.Y.; Cho, H.H. Damage Detection and Safety Diagnosis for Immovable Cultural Assets Using Deep Learning Framework. In Proceedings of the 2023 25th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 19–22 February 2023; pp. 310–313. [Google Scholar]
- Hung, C.-W.; Chou, Y.-C. Crack detection and Wooden Artifacts Preservation System Based on Random Forest Classifier and WGAN-GP Network. In Proceedings of the 30th International Display Workshops, Niigata, Japan, 6–8 December 2023; pp. 1041–1044. [Google Scholar]
- Cutajar, J.D.; Babini, A.; Deborah, H.; Hardeberg, J.Y.; Joseph, E.; Frøysaker, T. Hyperspectral Imaging Analyses of Cleaning Tests on Edvard Munch’s Monumental Aula Paintings. Stud. Conserv. 2022, 67 (Suppl. 1), 59–68. [Google Scholar] [CrossRef]
- Saunders, D.; Burmester, A.; Cupitt, J.; Raffelt, L. Recent applications of digital imaging in painting conservation: Transportation, colour change and infrared reflectographic studies. Stud. Conserv. 2000, 45 (Suppl. 1), 170–176. [Google Scholar] [CrossRef]
- Hung, C.-W.; Chen, X.-N. Pose Estimation and Calibration System for Monocular Camera. In Proceedings of the 14th International Conference on 3D Systems and Applications, Niigata, Japan, 6–8 December 2023; pp. 1408–1411. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Li, Z.X.; Cui, G.H.; Li, C.L.; Zhang, Z.S. Comparative Study of Slam Algorithms for Mobile Robots in Complex Environment. In Proceedings of the 2021 6th International Conference on Control, Robotics and Cybernetics (CRC), Shanghai, China, 9–11 October 2021; pp. 74–79. [Google Scholar]
- Sukvichai, K.; Thongton, N.; Yajai, K. Implementation of a Monocular ORB SLAM for an Indoor Agricultural Drone. In Proceedings of the 2023 Third International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP), Bangkok, Thailand, 18–20 January 2023; pp. 45–48. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE Features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2012; pp. 214–227. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Viswanathan, D.G. Features from accelerated segment test (fast). In Proceedings of the 10th Workshop on Image Analysis for Multimedia Interactive Services, London, UK, 6–8 May 2009. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 778–792. [Google Scholar]
- Lucas, B.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the IJCAI’81: 7th international joint conference on Artificial intelligence, Vancouver, BC, Canada, 24–28 August 1981. [Google Scholar]
- Horn, B.K.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar]





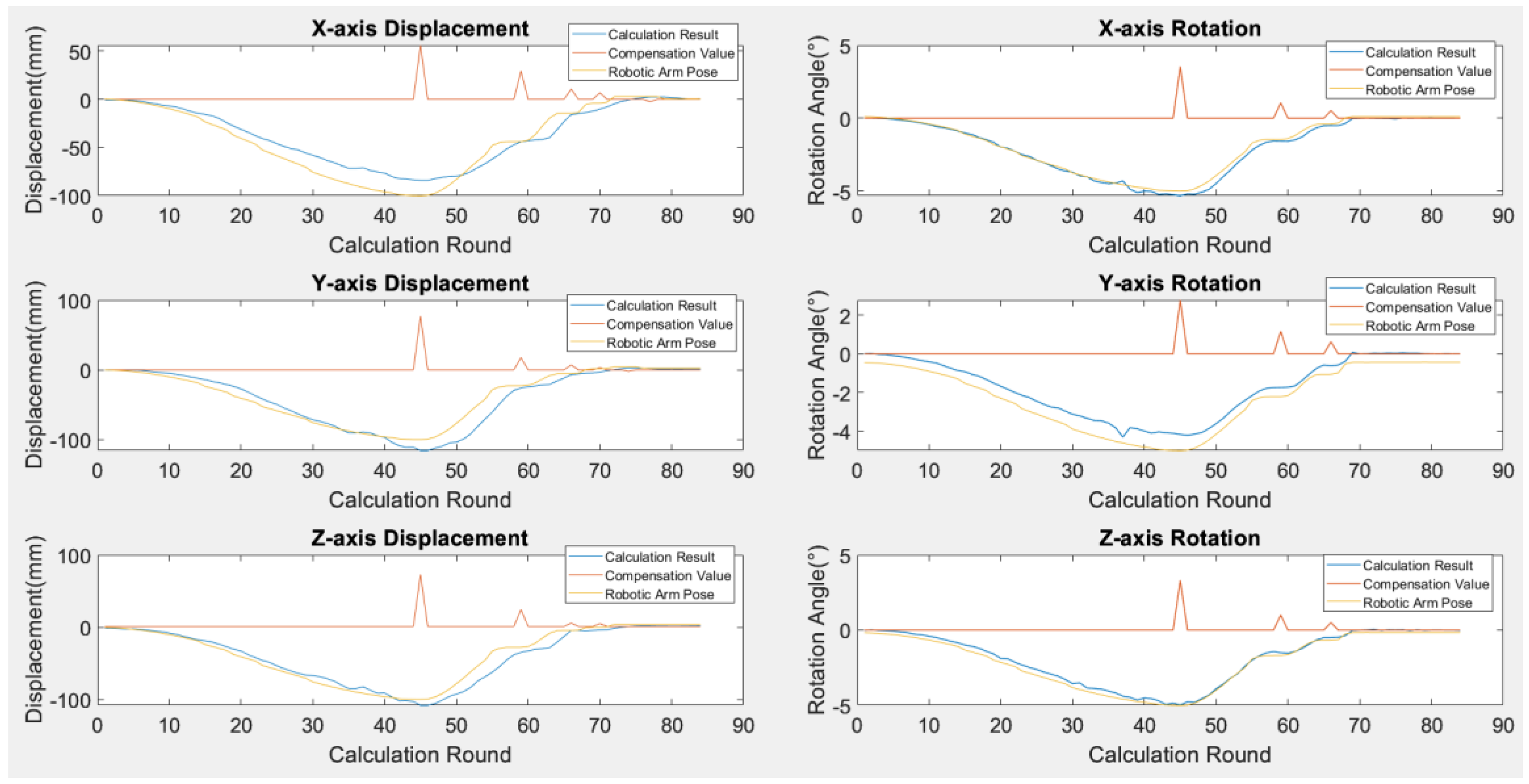








| Axis | Actual Pose | Calculated Pose | |
|---|---|---|---|
| X | Translation | 100 mm | 91.889 mm |
| Rotation | 0° | −0.108° | |
| Y | Translation | 0 mm | 3.428 mm |
| Rotation | 0° | −0.085° | |
| Z | Translation | 0 mm | 7.757 mm |
| Rotation | 0° | 0.066° | |
| Axis | Actual Pose | Calculated Pose | |
|---|---|---|---|
| X | Translation | 100 mm | 100.608 mm |
| Rotation | 0° | −0.099° | |
| Y | Translation | 0 mm | 2.065 mm |
| Rotation | 0° | −0.004° | |
| Z | Translation | 0 mm | 0.086 mm |
| Rotation | 0° | −0.034° | |
| Techniques | Initial Matches | Correct Pairs | Execution Time |
|---|---|---|---|
| FAST+BRIEF | 2322 | 2296 | 0.1437 s |
| SIFT | 2192 | 817 | 1.7063 s |
| ORB | 230 | 230 | 0.0699 s |
| Techniques | Initial Matches | Correct Pairs | Execution Time |
|---|---|---|---|
| Euclidean Distance | 199 | 199 | 0.0794 s |
| L1-Distance | 200 | 200 | 0.0714 s |
| Hamming Distance | 230 | 230 | 0.0699 s |
| Techniques | Initial Matches | Correct Pairs | Execution Time |
|---|---|---|---|
| Brightness Reduced by 25% | 220 | 220 | 0.0658 s |
| Brightness Reduced by 50% | 221 | 221 | 0.0555 s |
| Original Brightness | 230 | 230 | 0.0699 s |
| Brightness Increased by 25% | 216 | 216 | 0.0665 s |
| Brightness Increased by 50% | 221 | 221 | 0.1402 s |
| Axis | Actual Pose | Calculated Pose | |
|---|---|---|---|
| X | Translation | 0.372 mm | 3.66 mm |
| Rotation | 3.926° | 3.703° | |
| Y | Translation | 0 mm | −0.73 mm |
| Rotation | 4.448° | 4.648° | |
| Z | Translation | 0 mm | 6.910 mm |
| Rotation | 5.578° | 5.093° | |
| Axis | Actual Pose | Calculated Pose | |
|---|---|---|---|
| X | Translation | 100.492 mm | 82.4 mm |
| Rotation | 0.037° | 0.381° | |
| Y | Translation | −99.146 mm | −73.35 mm |
| Rotation | −0.371° | −0.221° | |
| Z | Translation | 99.667 mm | 99.07 mm |
| Rotation | −0.959° | 0.7739° | |
| Axis | Actual Pose | Calculated Pose | |
|---|---|---|---|
| X | Translation | 100.492 mm | 65.800 mm |
| Rotation | 4.581° | 4.498° | |
| Y | Translation | −99.146 mm | −83.710 mm |
| Rotation | 5.069° | 5.403° | |
| Z | Translation | 99.667 mm | 120.900 mm |
| Rotation | 5.878° | 5.327° | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, C.-W.; Chang, T.-A.; Chen, X.-N.; Wang, C.-C. Monocular Camera Pose Estimation and Calibration System Based on Raspberry Pi. Electronics 2025, 14, 3694. https://doi.org/10.3390/electronics14183694
Hung C-W, Chang T-A, Chen X-N, Wang C-C. Monocular Camera Pose Estimation and Calibration System Based on Raspberry Pi. Electronics. 2025; 14(18):3694. https://doi.org/10.3390/electronics14183694
Chicago/Turabian StyleHung, Chung-Wen, Ting-An Chang, Xuan-Ni Chen, and Chun-Chieh Wang. 2025. "Monocular Camera Pose Estimation and Calibration System Based on Raspberry Pi" Electronics 14, no. 18: 3694. https://doi.org/10.3390/electronics14183694
APA StyleHung, C.-W., Chang, T.-A., Chen, X.-N., & Wang, C.-C. (2025). Monocular Camera Pose Estimation and Calibration System Based on Raspberry Pi. Electronics, 14(18), 3694. https://doi.org/10.3390/electronics14183694






