Low-Voltage Stressed Inductive WPT System with Pull–Push Class EF2 Inverter

Abstract

A class E inverter has presented wide application prospects in inductive wireless power transfer (WPT) systems due to its significant advantages such as high operation frequency, high power density, and low cost. However, its semiconductor power device is subjected to voltage stress several times higher than the input DC voltage, which inevitably increases the risk of overvoltage failure and limits the system power level. In this manuscript, an inductive WPT system with the pull–push class EF2 inverter is proposed to significantly decrease the voltage stress and ensure soft switching characteristic. The working principle and time-domain waveforms of the pull–push class EF2 inverter are analyzed. Moreover, the differential equations and mathematical model of the resonant parameters are investigated. Compared with the conventional class E inverter, the output power of the proposed inductive WPT system is doubled under the same input voltage. A 100 W system prototype is designed at the operating frequency of 6.78 MHz (according to the A4WP standard) and its experimental results demonstrate the effectiveness and feasibility of the analysis.

1. Introduction

Wireless power transfer (WPT) technology [1,2,3] can be widely applied in some battery-powered systems, such as consumer electronics, implantable medical devices, and electric vehicles (EVs). Properties such as ultra-lightweight and thin are favored by most customers, which means it is mandatory to improve the inductive WPT system power density. The method of increasing system operating frequency to the Megahertz-wide band has been proven to be a viable solution [4,5,6].

The operating frequency is determined by an inverter, which is an important component of the inductive WPT system. Full-bridge inverters can be used for both low-power and high-power applications [7]. However, the class E inverter [8,9] is a resonant converter that can operate at MHz operating frequency and offers higher efficiency and low cost. It is usually useful for low power applications. In recent years, it has been widely promoted and applied in inductive WPT systems [10,11,12].

Reference [13] analyzes the load-independent output characteristic of the class E inverter. Also, its ZVS operation and constant output voltage are investigated at different load conditions. To eliminate the influence of conduction resistance and parasitic capacitance of the semiconductor power device, a cascaded class E inverter is proposed in [14]. The designed prototype operates at 13.56 MHz and its peak efficiency is up to 80.19%. Reference [15] applied the class E inverter and class E rectifier to an inductive WPT system. At the air gap of 5 mm, the inductive WPT system output power and efficiency, respectively, were 0.769 W and 74.1%.

For the class E inverter, however, the voltage stress of its semiconductor power devices is up to 3.5 times of the DC input voltage [16]. This can easily lead to overvoltage failure and limit the system power level. Adding high-order resonant networks has been proven to be an effective solution to reduce the voltage stress. A class EF2 inverter [17,18,19,20] is proposed and its added LC (inductive-capacitor) resonant network parallel with the power devices can reduce the voltage stress up to 2.5 times the input voltage. Additionally, Ref. [21] proposed a class EF2 inverter based on a T-type impedance matching network. Based on the proposed topology, a 1.7 kW/6.78 MHz inductive WPT prototype is designed, and its maximum efficiency is higher than 95%. However, the high voltage stress, complex design process (due to the tuning interactions) and harsh soft switching condition of the class EF2 inverter still constrain its widespread application in inductive WPT systems.

In this manuscript, a pull–push class EF2 inverter is proposed and applied in an inductive WPT system. For the proposed pull–push class EF2 inverter, the second harmonic is eliminated to decrease the voltage stress to 1.16 times the input voltage. The topology structure, working principle and mathematical model are analyzed. And the theoretical analysis is verified using a 100 W experimental prototype.

2. Modeling and Analysis of Pull–Push Class EF2 Inverter

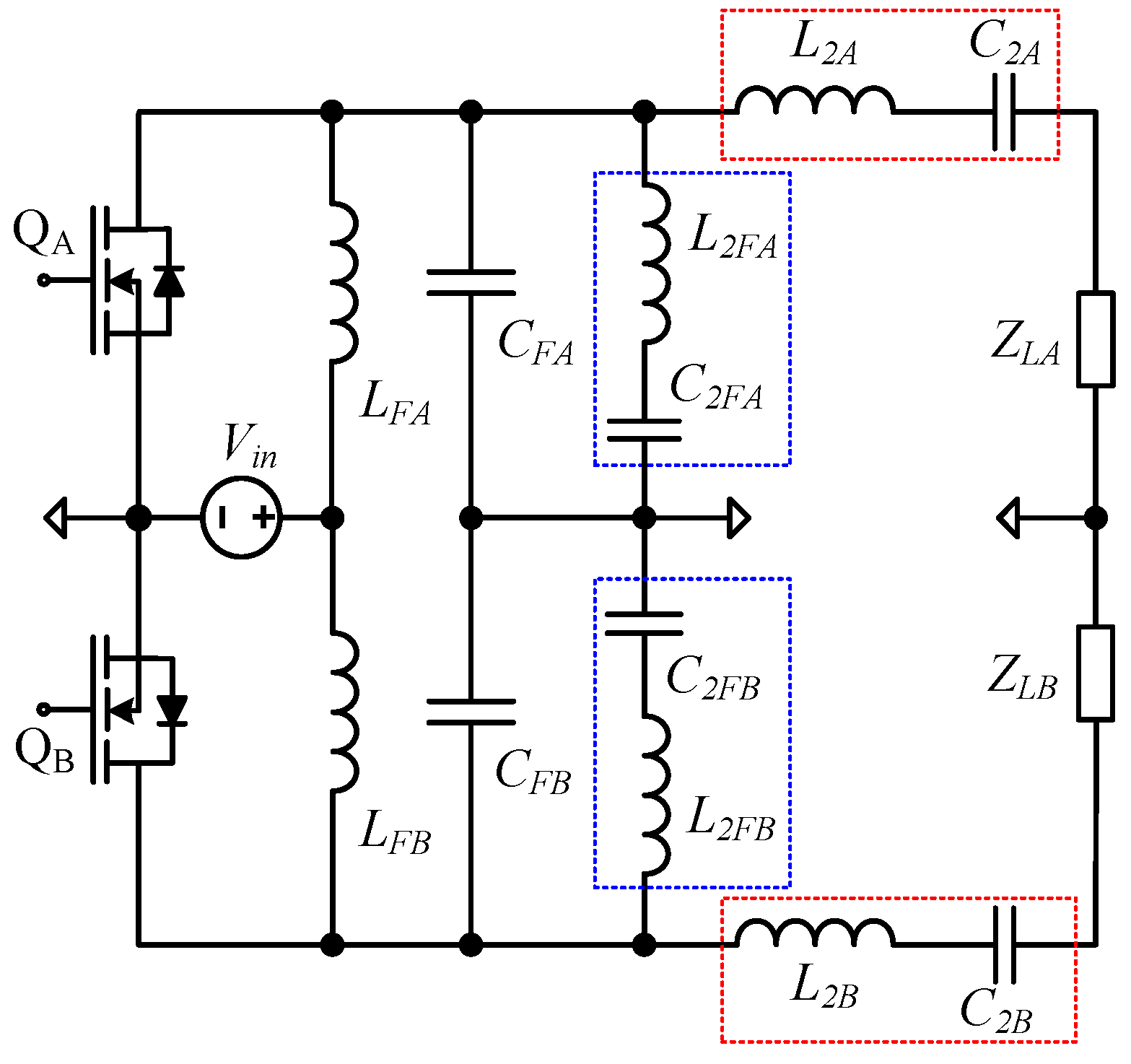
2.1. Topology Structure

Figure 1 shows the structure of the pull–push class EF2 inverter. It is composed of the DC input voltage, choke inductors (L_FA and L_FB), semiconductor power devices (Q_A and Q_B), parallel connected capacitors (C_FA and C_FB), and resonant networks. Figure 2 shows the time-domain waveforms of the pull–push class EF2 inverter. Here, Q_A and Q_B turn on alternatively.

2.2. Mathematical Model of the Resonant Parameters

In Figure 1, the power devices Q_A and Q_B alternatively turn on. So, the pull–push class EF2 inverter can be equivalent to two independent class EF2 inverter to simplify the analysis of the system and the design of parameters. Figure 3 shows a class EF2 inverter, and its voltage and current waveforms are shown in Figure 4.

The power device is turned on at the time interval of (1 − D)T ≤ t ≤ T. Here, D denotes the duty cycle and T is the period. In this case, the equivalent circuit is shown in Figure 3b. And the terminal voltage of the choke inductor is equal to the input DC voltage. The current of the inductor L_2F increases linearly. Moreover, one can obtain the following differential equation from Figure 3b:

$${\displaystyle \frac{d^2{v}_{C2F}}{d{t}^2}}+{\displaystyle \frac{1}{L_{2F}{C}_{2F}}}{v}_{C2F}=0$$

(1)

The solution of Equation (1) is expressed as follows:

$$v_{C2F}=H_1\cos {\displaystyle \frac{t}{\sqrt{L_{2F}{C}_{2F}}}}+H_2\sin {\displaystyle \frac{t}{\sqrt{L_{2F}{C}_{2F}}}}$$

(2)

To avoid series resonance between the inductor L_2F and the capacitor C_2F, they should satisfy

$$\left\{\begin{array}{l}{\left.v_{C2F}(t)\right|}_{t=(1-D)T}=0\hfill \\ {\left.C_{2F}{\displaystyle \frac{d{v}_{C2F}(t)}{dt}}\right|}_{t=(1-D)T}=0\hfill \end{array}\right.$$

(3)

By substituting Equation (2) into (1), one can obtain

$$H_1=H_2=0$$

(4)

From Equation (4), the voltage of capacitor C_2F is always equal to 0.

When the power device is turned off, the node current is expressed as follows:

$$i_{in}=i_{CF}+i_{C2F}+i_0$$

(5)

Equation (5) is equivalent to the following equation:

$${\displaystyle \frac{V_{in}-v_{CF}}{L_F}}=C_F{\displaystyle \frac{d^2{v}_{CF}}{d{t}^2}}+C_{2F}{\displaystyle \frac{d^2{v}_{C2F}}{d{t}^2}}+{\displaystyle \frac{1}{R_{\mathrm{L}}}}{\displaystyle \frac{d{v}_{CF}}{dt}}$$

(6)

Here, the terminal voltage of the capacitor C_F is given by

$$v_{CF}=v_{L2F}+v_{C2F}$$

(7)

By combining Equations (6) and (7), the following differential equations are obtained:

$$\left\{\begin{array}{l}{C}_F{\displaystyle \frac{d^2{v}_{CF}}{d{t}^2}}+C_{2F}{\displaystyle \frac{d^2{v}_{C2F}}{d{t}^2}}+{\displaystyle \frac{1}{R_{\mathrm{L}}}}{\displaystyle \frac{d{v}_{CF}}{dt}}+{\displaystyle \frac{v_{CF}}{L_F}}={\displaystyle \frac{V_{in}}{L_F}}\hfill \\ L_{2F}{C}_{2F}{\displaystyle \frac{d^2{v}_{CF}}{d{t}^2}}+v_{C2F}-v_{CF}=0\hfill \end{array}\right.$$

(8)

In addition, Equation (8) is equivalent to

$$\begin{array}{l}{L}_F{C}_F{L}_{2F}{C}_{2F}{\displaystyle \frac{d^4{v}_{C2F}}{d{t}^4}}+{\displaystyle \frac{L_F{C}_F{C}_{2F}}{R_{\mathrm{L}}}}{\displaystyle \frac{d^3{v}_{C2F}}{d{t}^3}}\\ +\left(L_F{C}_{2F}+L_F{C}_F+L_{2F}{C}_{2F}\right){\displaystyle \frac{d^2{v}_{C2F}}{d{t}^2}}+{\displaystyle \frac{L_F}{R_{\mathrm{L}}}}{\displaystyle \frac{d{v}_{C2F}}{dt}}+v_{C2F}=V_{in}\end{array}$$

(9)

Using Equation (9), variables $\alpha$₁, $\beta$₁, $\alpha$₂, $\beta$₂ and A₁, A₂, A₃, A₄, A₅ can be defined and applied to analyze the resonant parameters of the class EF2 inverter. The characteristic root of Equation (9) can be expressed as

$$\begin{array}{l}{r}_{1,2}={\displaystyle \frac{{\alpha }_1\pm {\beta }_1}{(1-D)T}}\\ r_{3,4}={\displaystyle \frac{{\alpha }_2\pm {\beta }_2}{(1-D)T}}\end{array}$$

(10)

Then, $v_{CF}(t)$ is given by

$$v_{CF}(t)={\displaystyle \frac{\left({\alpha }_1+{\alpha }_2\right){\left(1-D\right)}^2{T}^2}{{\alpha }_1\left({\alpha }_2^2+{\beta }_2^2\right)+{\alpha }_2\left({\alpha }_1^2+{\beta }_1^2\right)}}{\displaystyle \frac{d^2{v}_{C2F}}{d{t}^2}}+v_{C2F}$$

(11)

From (3) and (4), one can obtain v_C2F(0) = v_C2F(T) = 0 and i_C2F(0) = i_C2F(T) = 0. Therefore, the following expression can be obtained:

$$v_{C2F}(0)=0/{\left.{\displaystyle \frac{d{v}_{C2F}}{dt}}\right|}_{t=0}=0$$

(12)

To obtain ZVS and ZDVS characteristics, the following equation should be satisfied:

$$v_{CF}(0)=0/v_{CF}((1-D)T)=0/{\left.{\displaystyle \frac{d{v}_{CF}}{dt}}\right|}_{t=(1-D)T}=0$$

(13)

Also, the input current is given by

$$\left\{\begin{array}{l}{i}_{in}(0)=i_{in}(T)=i_{in}((1-D)T)+{\displaystyle \frac{1}{L_F}}{\displaystyle {\int }_{(1-D)T}^T{v}_{LF}dt}={\displaystyle \frac{DT{V}_{in}}{L_F}}\hfill \\ i_{in}((1-D)T)=i_{in}(0)+{\displaystyle \frac{1}{L_F}}{\displaystyle {\int }_0^{(1-D)T}{v}_{LF}dt=\frac{T{V}_{in}}{L_F}-\frac{1}{L_F}{\displaystyle {\int }_0^{(1-D)T}{v}_{CF}dt}}\hfill \end{array}\right.$$

(14)

Its solutions are as follows:

$$\left\{\begin{array}{l}{\left.{\displaystyle \frac{d{v}_{CF}}{dt}}\right|}_{t=0}={\displaystyle \frac{DT{V}_{in}}{C_F{L}_F}}\hfill \\ {\displaystyle {\int }_0^{(1-D)T}{v}_{CF}dt}=T{V}_{in}\hfill \end{array}\right.$$

(15)

By substituting the condition of v_C2F(0) = 0 into Equation (2), we can obtain

$$N{\left[\begin{array}{cccc}{A}_1& A_2& A_3& A_4\end{array}\right]}^T={\displaystyle \frac{\left({\alpha }_1^2+{\beta }_1^2\right)\left({\alpha }_2^2+{\beta }_2^2\right)V_{in}}{1-D}}{\left[\begin{array}{llllllll}0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & D\hfill & 1\hfill \end{array}\right]}^T$$

(16)

Here,

$$N=[\begin{array}{cccc}{N}_{11}& N_{12}& N_{21}& N_{22}\end{array}]$$

(17)

And

$$N_{11}=\left[\begin{array}{c}{e}^{{\alpha }_1}\cos {\beta }_1-1\\ {\alpha }_1\\ e^{{\alpha }_1}\left({\alpha }_1\cos {\beta }_1-{\beta }_1\sin {\beta }_1\right)\\ {\alpha }_1^2-{\beta }_1^2\\ e^{{\alpha }_1}\left[({\alpha }_1^2-{\beta }_1^2)\cos {\beta }_1-2{\alpha }_1{\beta }_1\sin {\beta }_1\right]\\ e^{{\alpha }_1}\left[{\alpha }_1({\alpha }_1^2-3{\beta }_1^2)\cos {\beta }_1-{\beta }_1(3{\alpha }_1^2-{\beta }_1^2)\sin {\beta }_1\right]\\ {\alpha }_1({\alpha }_1^2-3{\beta }_1^2)\\ \left({\alpha }_2^2+{\beta }_2^2\right)\left[e^{{\alpha }_1}({\alpha }_1\cos {\beta }_1+{\beta }_1\sin {\beta }_1)-{\alpha }_1-({\alpha }_1^2+{\beta }_1^2)\right]\end{array}\right]$$

(18)

$$N_{12}=\left[\begin{array}{c}{e}^{{\alpha }_1}\sin {\beta }_1\\ {\beta }_1\\ e^{{\alpha }_1}\left({\alpha }_1\sin {\beta }_1+{\alpha }_1\cos {\beta }_1\right)\\ 2{\alpha }_1{\beta }_1\\ e^{{\alpha }_1}\left[2{\alpha }_1{\beta }_1\cos {\beta }_1+({\alpha }_1^2-{\beta }_1^2)\sin {\beta }_1\right]\\ e^{{\alpha }_1}\left[{\beta }_1(3{\alpha }_1^2-{\beta }_1^2)\cos {\beta }_1+{\alpha }_1({\alpha }_1^2-3{\beta }_1^2)\sin {\beta }_1\right]\\ {\beta }_1(3{\alpha }_1^2-{\beta }_1^2)\\ \left({\alpha }_2^2+{\beta }_2^2\right)\left[e^{{\alpha }_1}({\alpha }_1\sin {\beta }_1-{\beta }_1\cos {\beta }_1)+{\beta }_1\right]\end{array}\right]$$

(19)

$$N_{21}=\left[\begin{array}{c}{e}^{{\alpha }_2}\cos {\beta }_2-1\\ {\alpha }_2\\ e^{{\alpha }_2}\left({\alpha }_2\cos {\beta }_2-{\beta }_2\sin {\beta }_2\right)\\ {\alpha }_2^2-{\beta }_2^2\\ e^{{\alpha }_2}\left[({\alpha }_2^2-{\beta }_2^2)\cos {\beta }_2-2{\alpha }_2{\beta }_2\sin {\beta }_2\right]\\ e^{{\alpha }_1}\left[{\alpha }_1({\alpha }_1^2-3{\beta }_1^2)\cos {\beta }_1-{\beta }_1(3{\alpha }_1^2-{\beta }_1^2)\sin {\beta }_1\right]\\ {\alpha }_2({\alpha }_2^2-3{\beta }_2^2)\\ \left({\alpha }_1^2+{\beta }_1^2\right)\left[e^{{\alpha }_2}({\alpha }_2\cos {\beta }_2+{\beta }_2\sin {\beta }_2)-{\alpha }_2-({\alpha }_2^2+{\beta }_2^2)\right]\end{array}\right]$$

(20)

$$N_{22}=\left[\begin{array}{c}{e}^{{\alpha }_2}\sin {\beta }_2\\ {\beta }_2\\ e^{{\alpha }_2}\left({\alpha }_2\sin {\beta }_2+{\alpha }_2\cos {\beta }_2\right)\\ 2{\alpha }_2{\beta }_2\\ e^{{\alpha }_2}\left[2{\alpha }_2{\beta }_2\cos {\beta }_2+({\alpha }_2^2-{\beta }_2^2)\sin {\beta }_2\right]\\ e^{{\alpha }_1}\left[{\beta }_1(3{\alpha }_1^2-{\beta }_1^2)\cos {\beta }_1+{\alpha }_1({\alpha }_1^2-3{\beta }_1^2)\sin {\beta }_1\right]\\ {\beta }_2(3{\alpha }_2^2-{\beta }_2^2)\\ \left({\alpha }_1^2+{\beta }_1^2\right)\left[e^{{\alpha }_2}({\alpha }_2\sin {\beta }_2-{\beta }_2\cos {\beta }_2)+{\beta }_2\right]\end{array}\right]$$

(21)

Then, the resonant parameters of the class EF2 inverter are given by

$$\left\{\begin{array}{l}{L}_F=-{\displaystyle \frac{2\alpha ({\alpha }_2^2+{\beta }_2^2)+2{\alpha }_2({\alpha }_1^2+{\beta }_1^2)}{({\alpha }_1^2+{\beta }_1^2)({\alpha }_2^2+{\beta }_2^2)}}(1-D)T{R}_{\mathrm{L}}\hfill \\ C_F=-{\displaystyle \frac{(1-D)T}{2({\alpha }_1+{\alpha }_2)R_{\mathrm{L}}}}\hfill \\ L_{2F}=-{\displaystyle \frac{2{({\alpha }_1+{\alpha }_2)}^2\left[{\alpha }_1({\alpha }_2^2+{\beta }_2^2)+{\alpha }_2({\alpha }_1^2+{\beta }_1^2)\right]}{{\alpha }_1{\alpha }_2\left\{\left({\alpha }_1^2+{\beta }_1^2-{\alpha }_2^2-{\beta }_2^2\right)+4({\alpha }_1+{\alpha }_2)\left[{\alpha }_1({\alpha }_2^2+{\beta }_2^2)+{\alpha }_2({\alpha }_1^2+{\beta }_1^2)\right]\right\}}}(1-D)T{R}_{\mathrm{L}}\hfill \\ C_{2F}=-{\displaystyle \frac{{\alpha }_1{\alpha }_2\left\{\left({\alpha }_1^2+{\beta }_1^2-{\alpha }_2^2-{\beta }_2^2\right)+4({\alpha }_1+{\alpha }_2)\left[{\alpha }_1({\alpha }_2^2+{\beta }_2^2)+{\alpha }_2({\alpha }_1^2+{\beta }_1^2)\right]\right\}}{2({\alpha }_1+{\alpha }_2)\left[{\alpha }_1({\alpha }_2^2+{\beta }_2^2)+{\alpha }_2({\alpha }_1^2+{\beta }_1^2)\right]R_{\mathrm{L}}}}(1-D)T\hfill \end{array}\right.$$

(22)

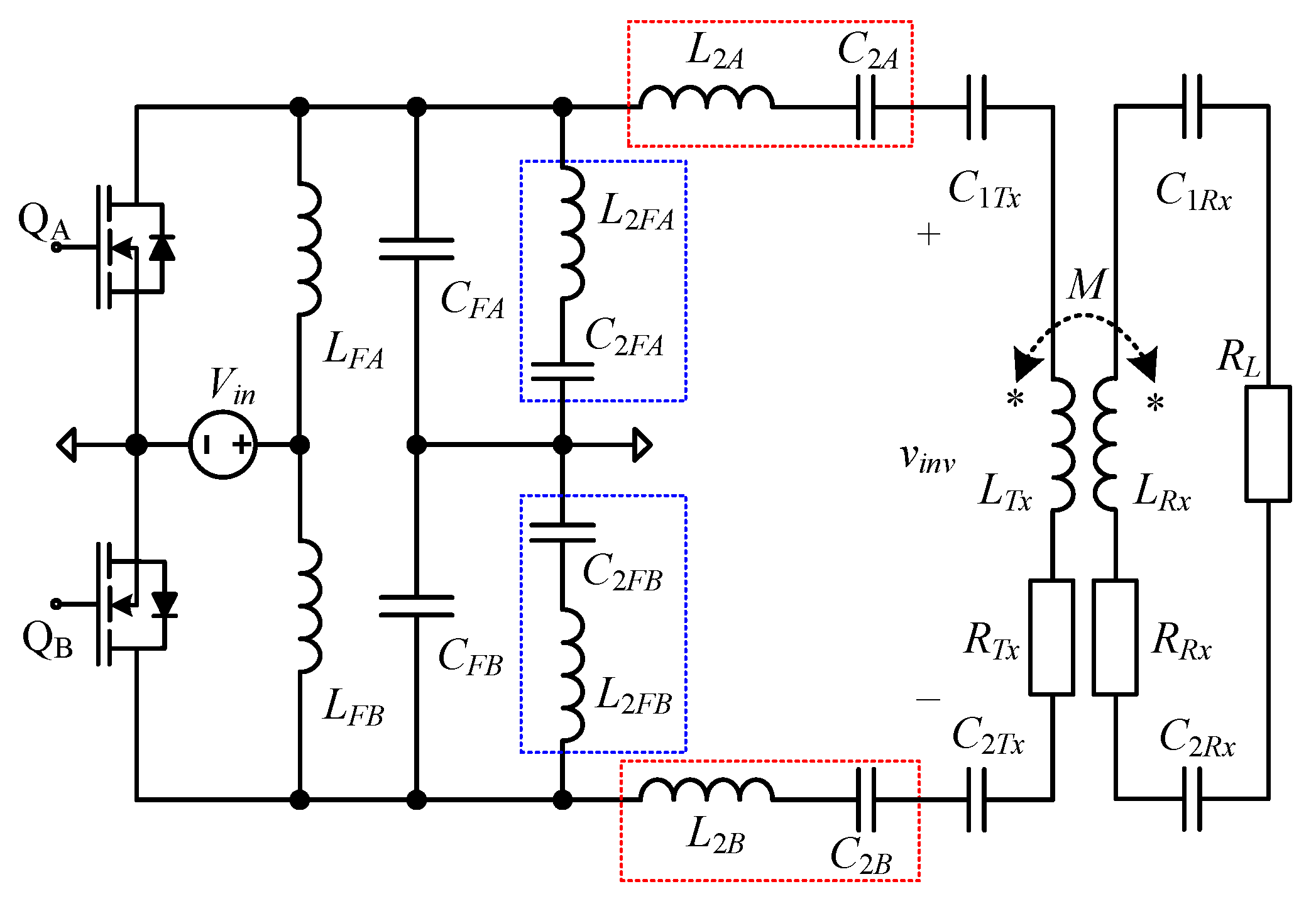
3. Wireless Power Transfer System with Pull–Push Class EF2 Inverter

Figure 5 shows the SS (series–series) compensated inductive WPT system with the proposed pull–push class EF2 inverter. L_Tx and L_Rx are the self-inductance of the Tx and Rx coils. C_Tx and C_Rx are the compensation capacitors at the Tx and Rx sides. M is the mutual inductance between the Tx and Rx coils. And there is no issue of electromagnetic compatibility. R_Tx and R_Rx are the ESR (equivalent series resistance) of the Tx and Rx coils. I_Tx and I_Rx represent the currents flowing through the Tx and Rx coils. The load is denoted as R_L.

According to the Kirchhoff’s Voltage Law (KVL), Figure 5 can be modeled as

$$\left\{\begin{array}{l}{V}_{inv}=(R_{Tx}+j\omega L_{Tx}+{\displaystyle \frac{1}{j\omega C_{Tx}}})I_{Tx}-(j\omega M)I_{Rx}\hfill \\ 0=(R_L+R_{Rx}+j\omega L_{Rx}+{\displaystyle \frac{1}{j\omega C_{Rx}}})I_{Rx}-(j\omega M)I_{Tx}\hfill \end{array}\right.$$

(23)

The currents flowing through the Tx and Rx coils can be solved as follows:

$$\left\{\begin{array}{c}{I}_{Tx}={\displaystyle \frac{Z_{Rx}{V}_{inv}}{Z_{Tx}{Z}_{Rx}+{(\omega M)}^2}}\\ I_{Rx}={\displaystyle \frac{-j\omega M{V}_{inv}}{Z_{Tx}{Z}_{Rx}+{(\omega M)}^2}}\end{array}\right.$$

(24)

Here, $Z_{Tx}=R_{Tx}+j\omega L_{Tx}+{\displaystyle \frac{1}{j\omega C_{Tx}}}$ and $Z_{Rx}=R_{Rx}+R_L+j\omega L_{Rx}+{\displaystyle \frac{1}{j\omega C_{Rx}}}$.

Then, the input and output power can be given by

$$P_{in}=V_{inv}{I}_{Tx}cos\theta ={\displaystyle \frac{Z_{Rx}{V}_{inv}^2}{Z_{Tx}{Z}_{Rx}+{(\omega M)}^2}}$$

(25)

$$P_{out}=I_{Rx}^2{R}_L={\displaystyle \frac{{\omega }^2{M}^2{V}_{inv}^2{R}_L}{{[Z_{Tx}{Z}_{Rx}+{(\omega M)}^2]}^2}}$$

(26)

The system efficiency is as follows:

$$\eta ={\displaystyle \frac{P_{out}}{P_{in}}}\times 100\%={\displaystyle \frac{{(\omega M)}^2{R}_L}{Z_{Rx}[Z_{Tx}{Z}_{Rx}+{(\omega M)}^2]}}\times 100\%$$

(27)

The following resonant conditions can be designed:

$$\begin{array}{l}j\omega L_{Tx}+{\displaystyle \frac{1}{j\omega C_{Tx}}}=0\\ j\omega L_{Rx}+{\displaystyle \frac{1}{j\omega C_{Rx}}}=0\end{array}$$

(28)

The efficiency is simplified as follows:

$$\eta ={\displaystyle \frac{{(\omega M)}^2{R}_L}{(R_L+R_{Rx})[R_{Tx}(R_L+R_{Rx})+{(\omega M)}^2]}}\times 100\%$$

(29)

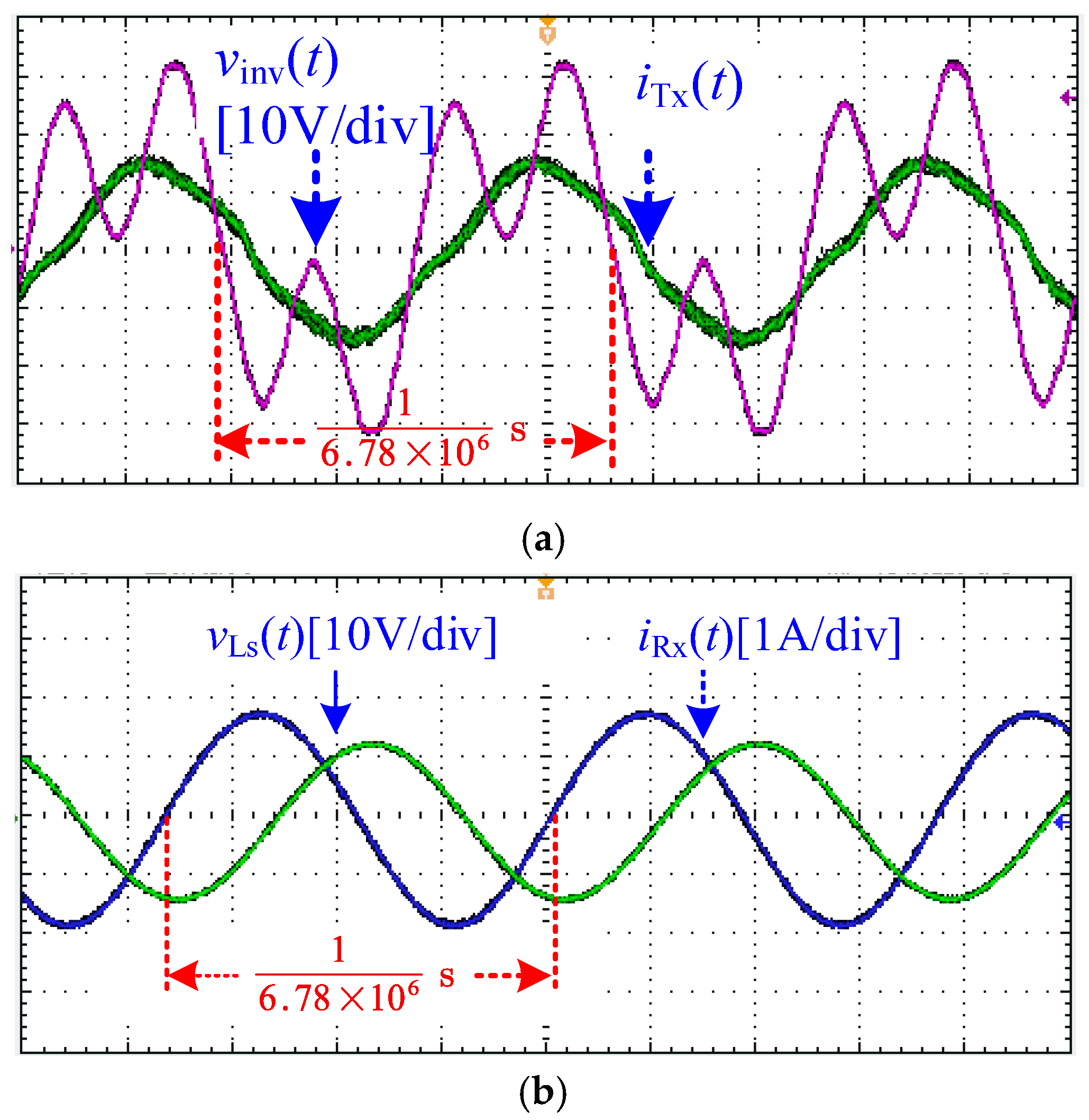
4. System Prototype and Experimental Results

A 6.78 MHz inductive WPT system based on the proposed pull–push class EF2 inverter is built and shown in Figure 6. And its parameters are given in

Table 1. System parameters.

Parameters	Symbol	Value (Unit)
Operating frequency	f	6.78 MHz
Self-inductances of the Tx and Rx coils	$L_{Tx}=L_{Rx}$	28.13 µH
Coupling factor	k	0.38
Rated load resistance	$R_L$	50 Ω
Choke inductances	$L_{FA}=L_{FB}$	180.00 nH
Parallel connected capacitances	$C_{FA}=C_{FB}$	1.45 nF
Parallel resonant network	$L_{2FA}=L_{2FB}$	185.00 nH
	$C_{2FA}=C_{2FB}$	0.75 nF
Series resonant network	$L_{2A}=L_{2B}$	6.30 μH
	$C_{2A}=C_{2B}$	87.46 nF

. Specifically, the PCB (Printed Circuit Board) coil is designed for the IPT coupler. Its turn number is 10 and the coil size is 10 cm × 10 cm. The air gap between the Tx coil and Rx coil is about 1 cm. GS66504B-TR (Infineon Technologies, Mansfield, Texas USA) is a GaN-on-Silicon transistor with fast switching bottom cooling and low thermal resistance, which is applied for the power switches (Q_A and Q_B). The KEMET MLCC capacitor is used for C_Tx and C_Rx.

Figure 7 shows the gate driver of the semiconductor power devices Q_A and Q_B. The measured waveforms align with the results of the analysis where the two switches are turned on alternatively.

Figure 8a shows the measured output voltage of the pull–push class EF2 inverter and the current flowing through the Tx coil. The waveforms are similar to those displayed in Figure 2. The voltage slightly reduces the current, which ensures soft switching characteristics. In addition, the induced voltage of the Rx coil and output current are presented in Figure 8b. They are both sinusoidal waves and their phase difference is about π/2. Figure 9a shows the measured waveforms when the load resistance is decreased from 50 Ω to 25 Ω and Figure 9b shows the measured v_inv(t) and i_Tx(t) when there is a 1 cm misalignment between the Tx and Rx coils. The measured efficiency of the inductive WPT system by a HIOKI power meter is shown in Figure 10. The peak efficiency is up to 90.1%. The comparison of the proposed WPT system with the pull-push class EF2 inverter with the conventional topologies in term of efficiency, rated output power, etc. is shown in

Table 2. Comparisons between this work with the conventional inductive WPT system.

	Topology	Frequency	Efficiency	Output Power	Power Switch Voltage Stress
This work	Pull–push class EF2 inverter	6.78 MHz	90.1%	100 W	1.16 × Vin
[10]	Class E inverter	1 MHz	85%	≈130 W	3.6 × Vin
[11]		100 kHz	75%	13 W	Not mentioned
[13]		1 MHz	89.2%	Not mentioned	Not mentioned
[14]	Cascaded class E inverter	13.56 MHz	80.19%	2 kW	3.564 × Vin
[15]	Class E inverter	6.78 MHz	97.2%	490 W	3.5 × Vin
[18]	Class EF2 inverter	1 MHz	Not mentioned	500 W	2.5 × Vin
[19]		85 kHz	Not mentioned	3.3 kW	Not mentioned
[21]		6.78 MHz	90.5%	30 W	2.54 × Vin

. It can be seen that the proposed system has significantly advantage, especially in terms of the voltage stress of the power device.

5. Conclusions

This manuscript proposed a pull–push class EF2 inverter. Compared with the conventional class E inverter, the voltage stress of the semiconductor power device decreases from 2.5 times the input DC voltage to 1.16 times, which will significantly reduce the risk of overvoltage failure and increase the system power level. Furthermore, an inductive WPT system based on the proposed pull–push class EF2 inverter is analyzed. The mathematical model of the currents flowing through the Tx and Rx coils, output power and efficiency are investigated. A 6.78 MHz inductive WPT prototype is built, and its experimental results verify the theoretical analysis.