AFSS Wide-Frequency Reconfigurable Design and Electromagnetic Characterization Research
Abstract
1. Introduction
2. Verification of Design Principles and Methods
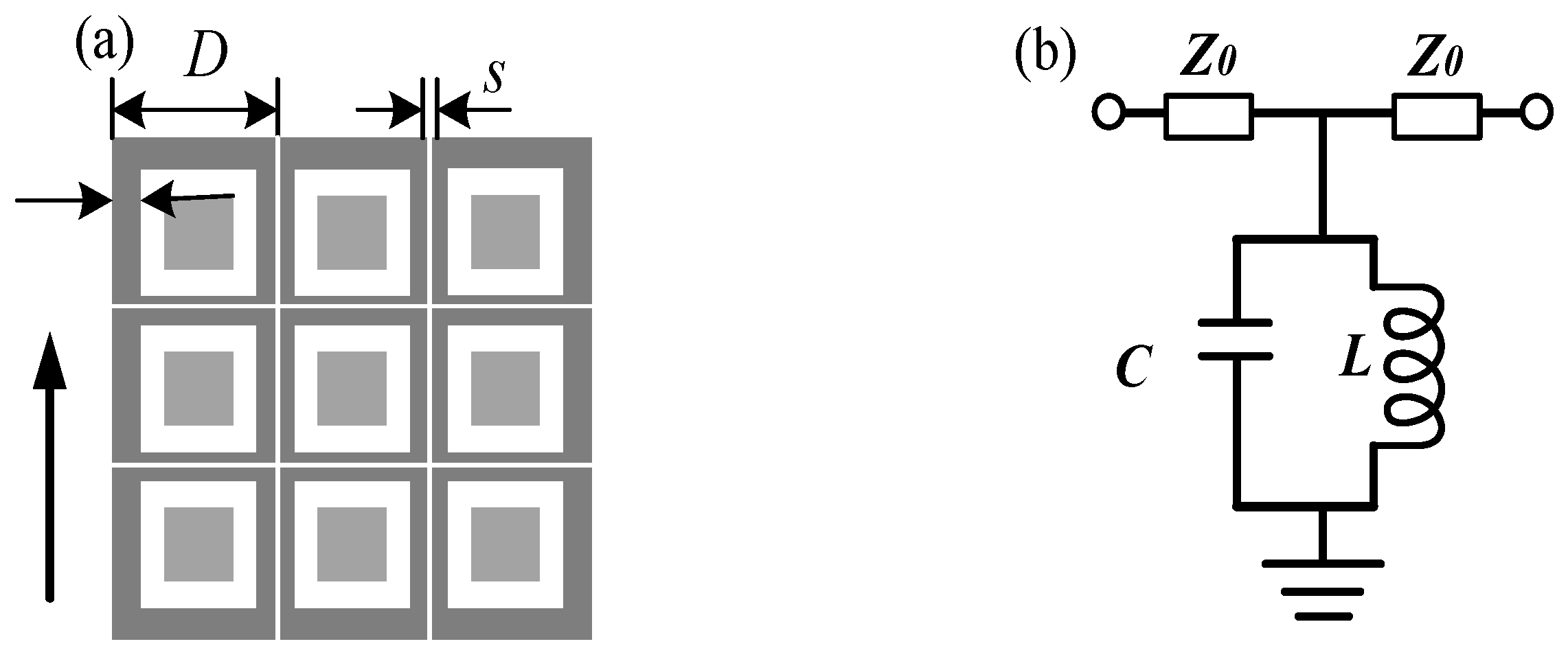
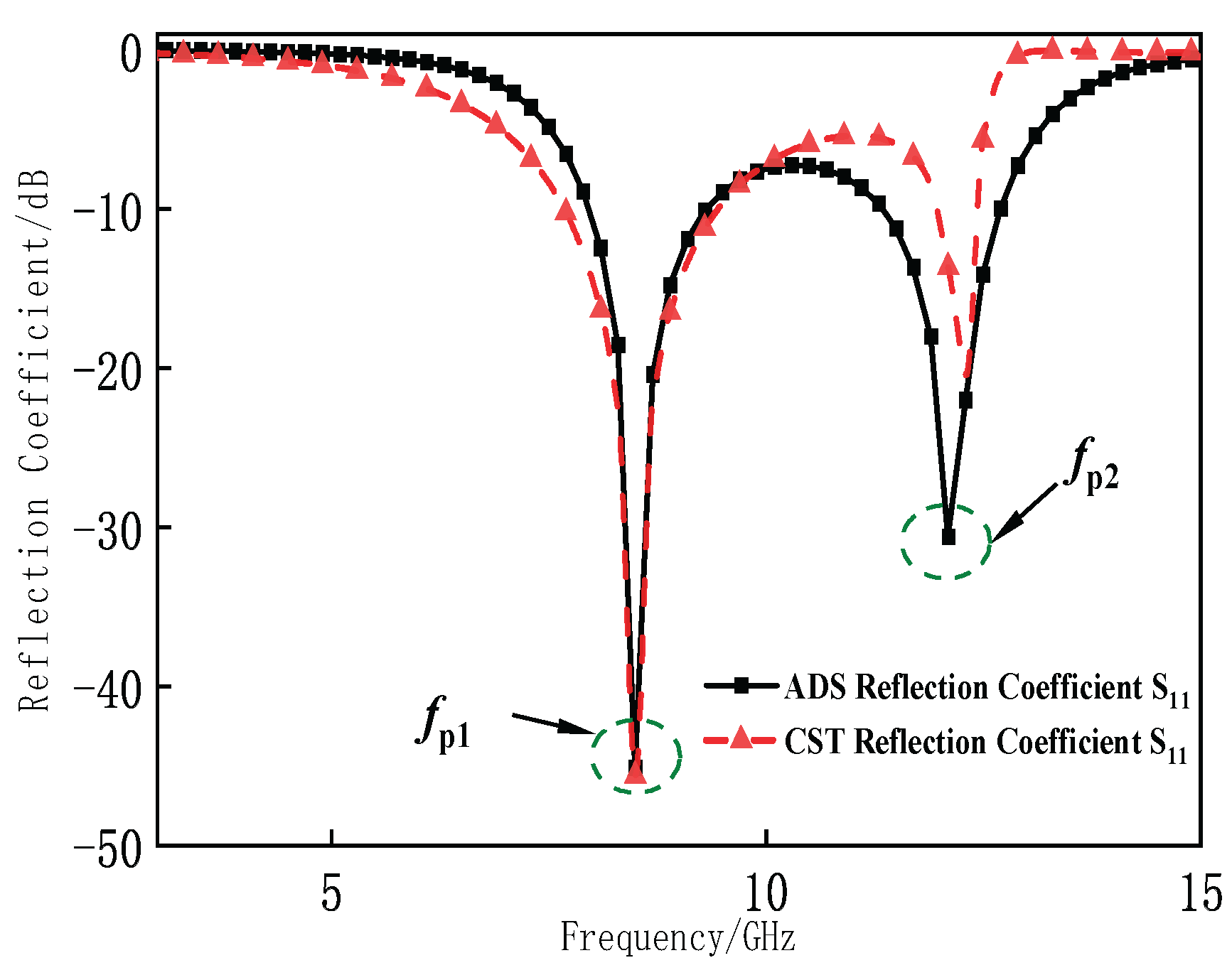
2.1. Equivalent Circuit Method
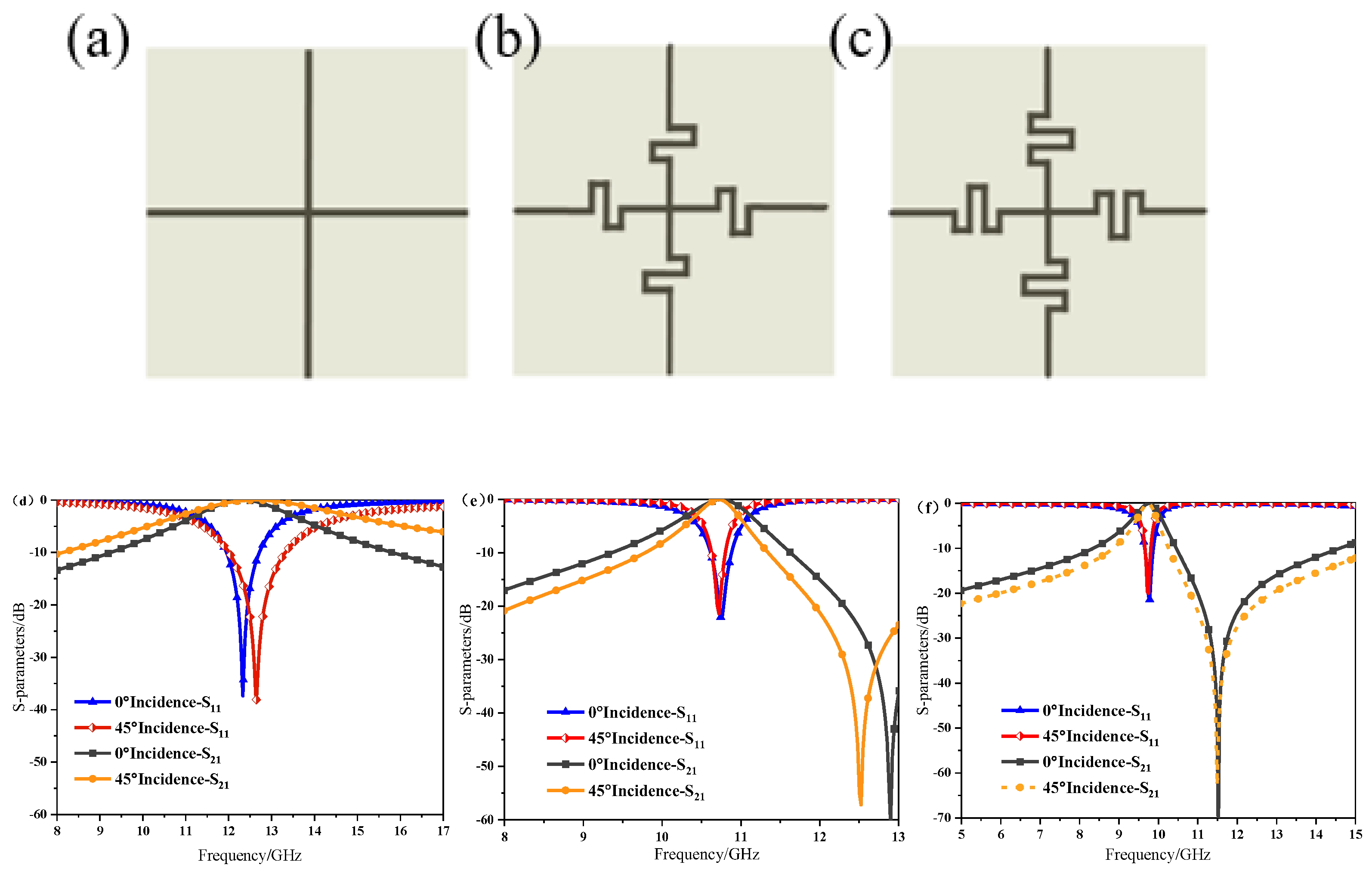
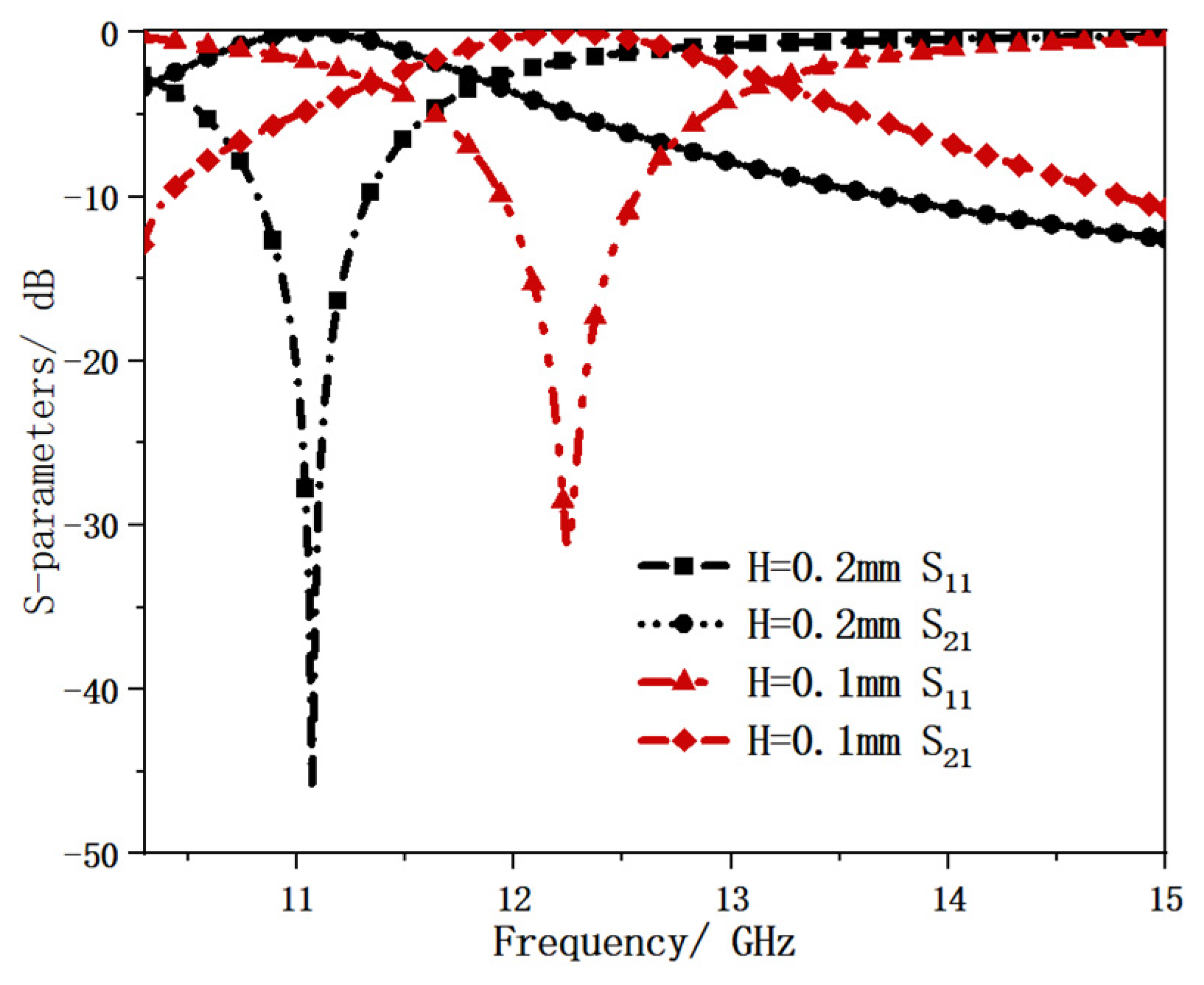
2.2. Structural Design and Numerical Simulation Research
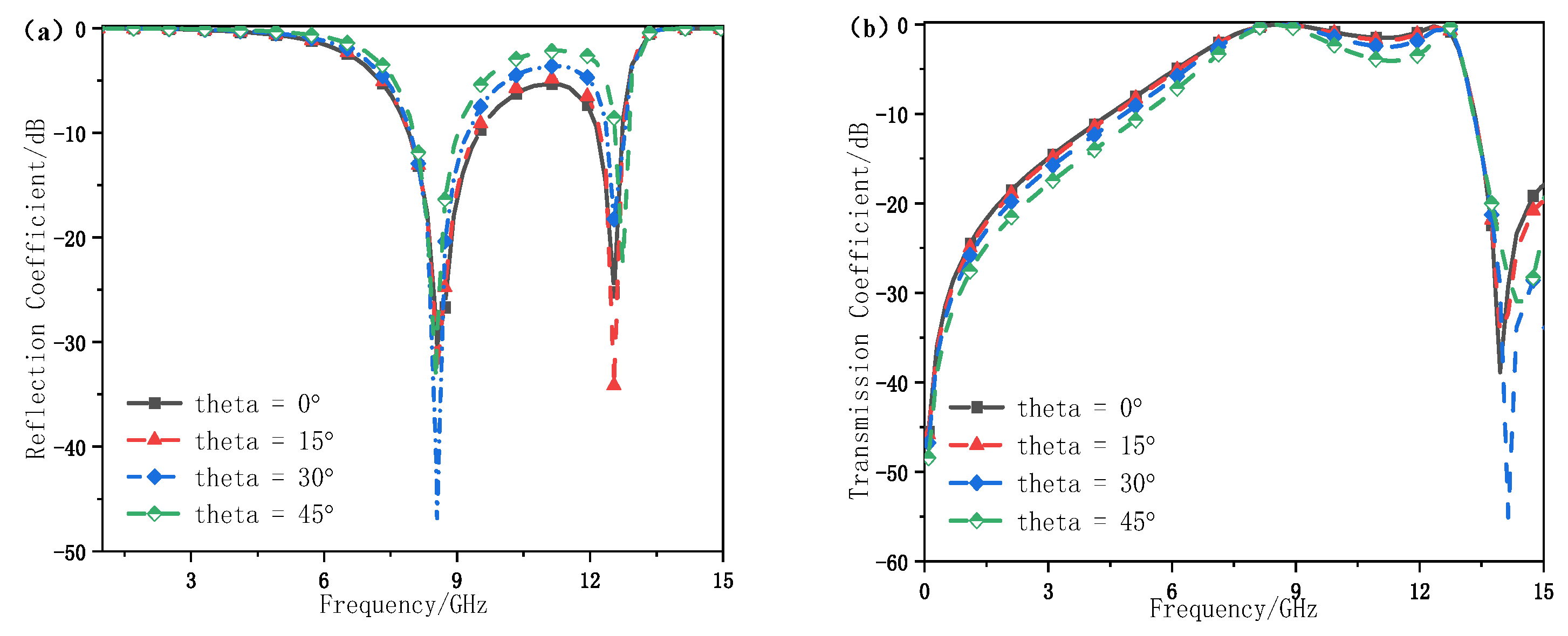
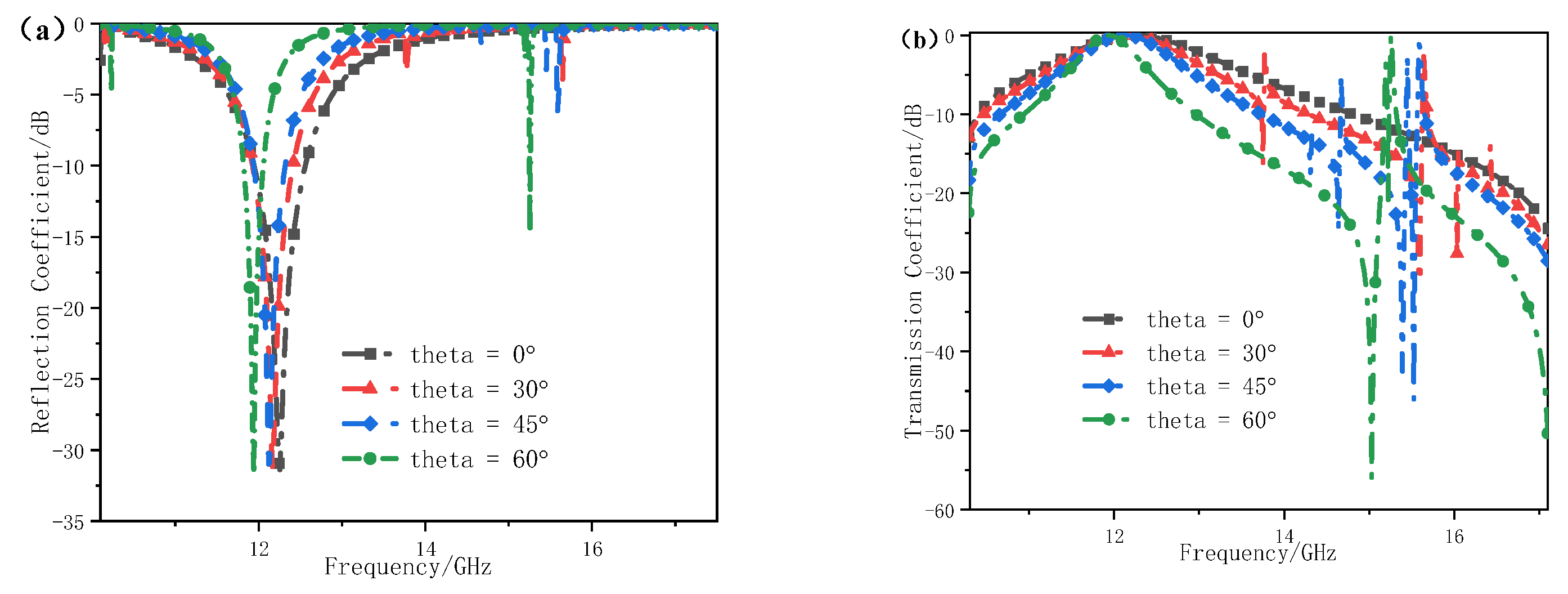
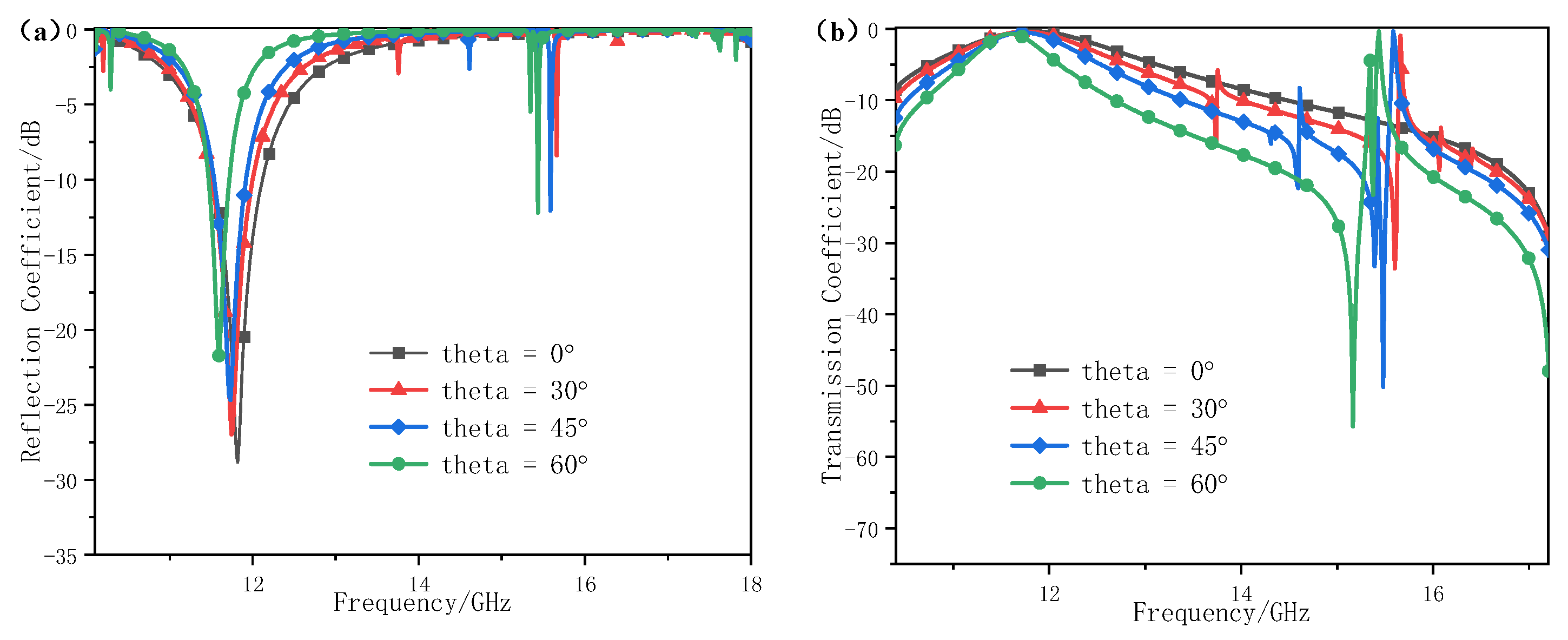
2.3. Angular Stability Validation
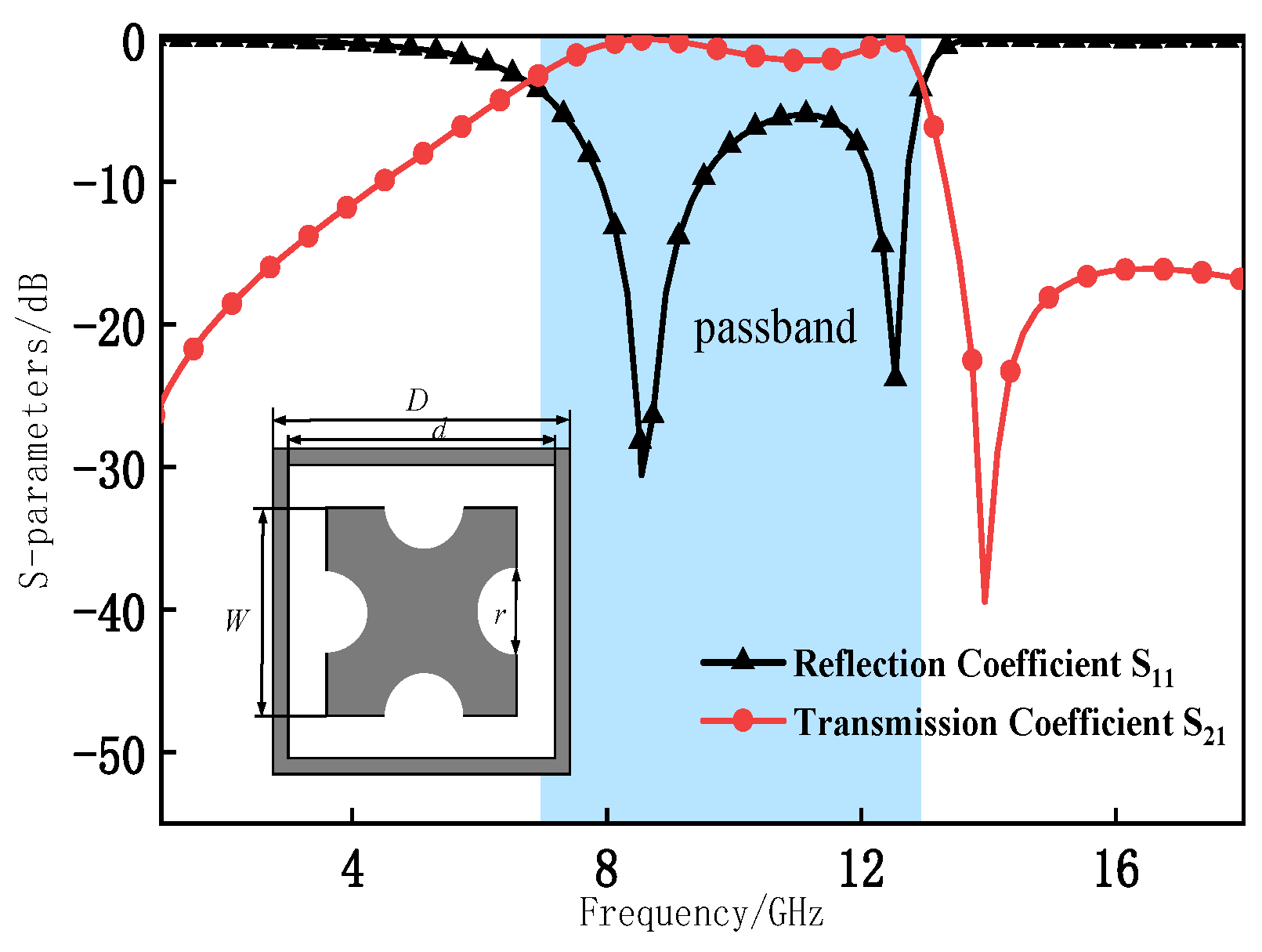
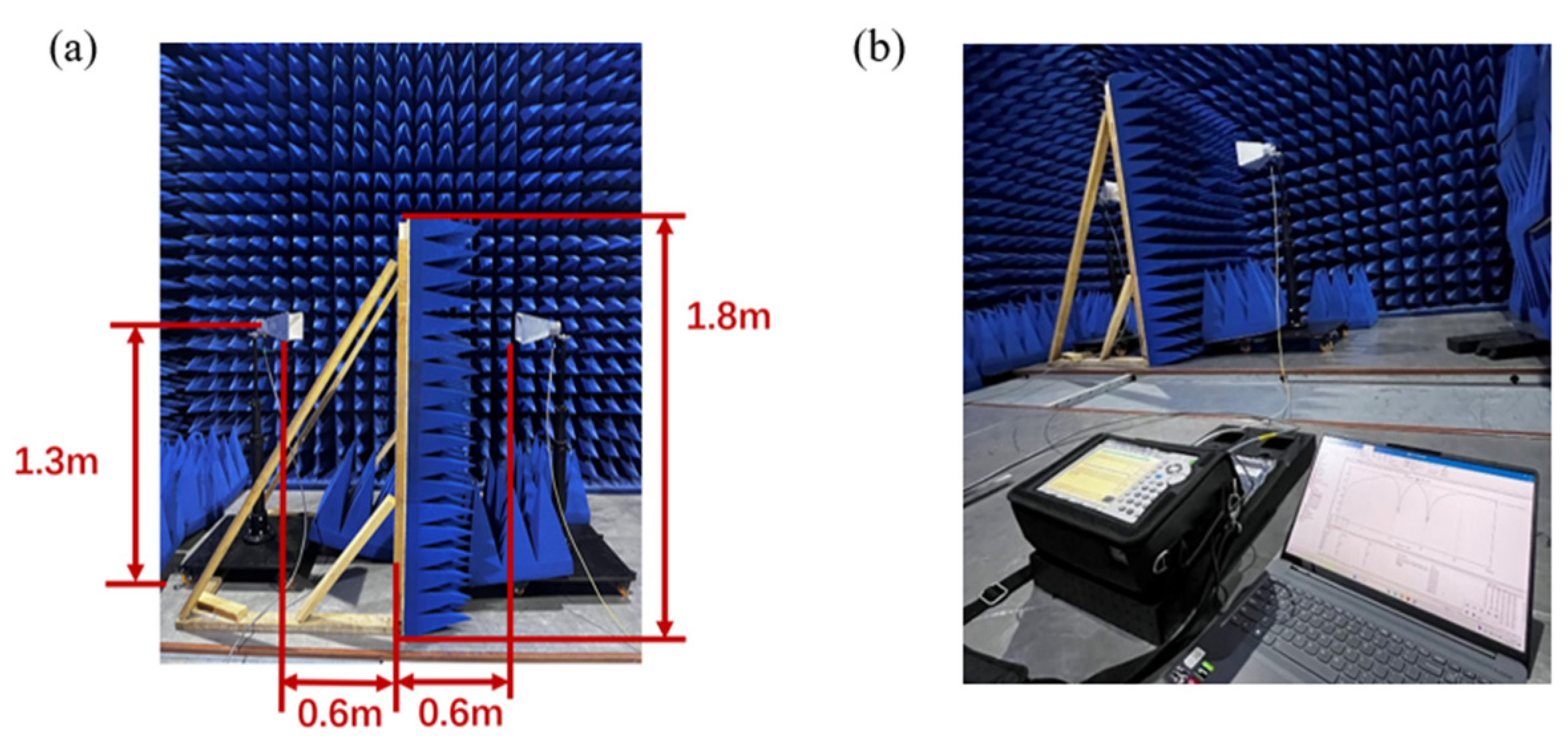
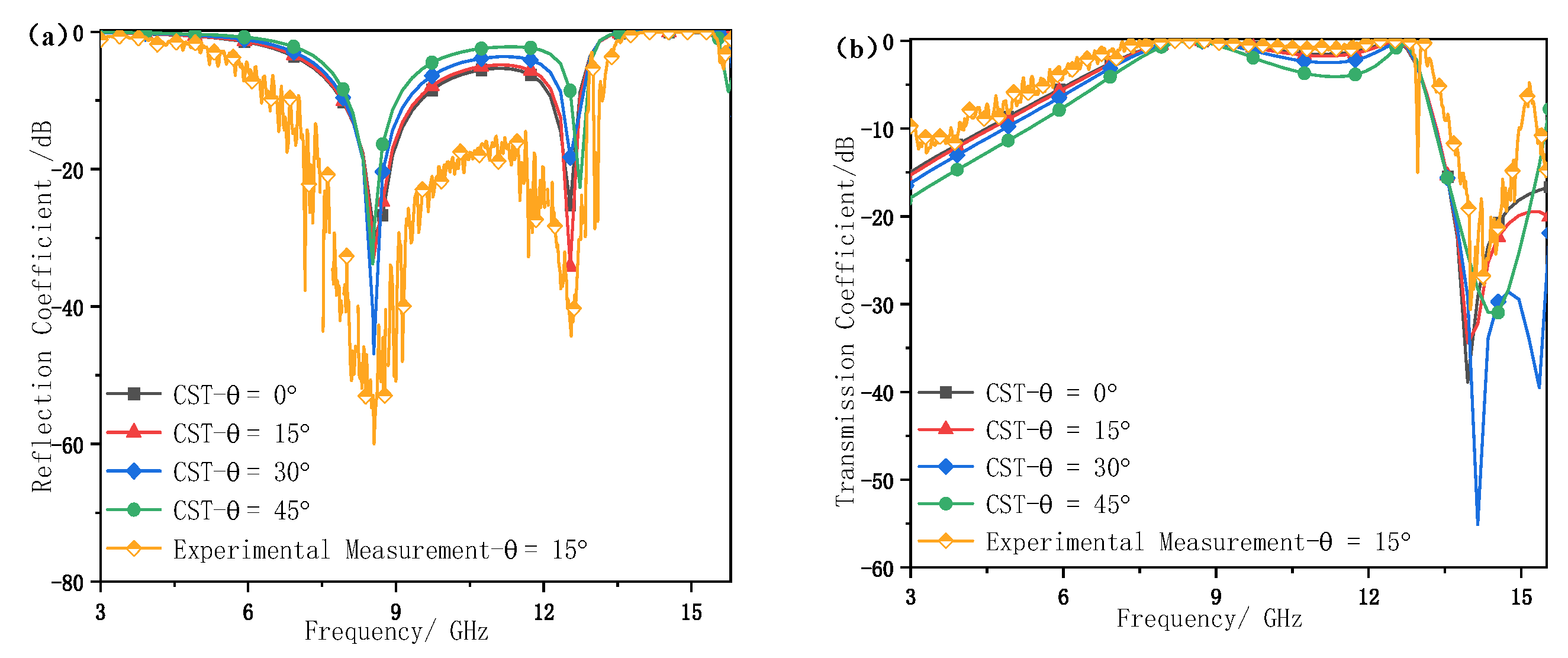
2.4. Experimental Testing and Data Analysis
3. Research on the Structural Model Design and Regulation Mechanism of AFSS
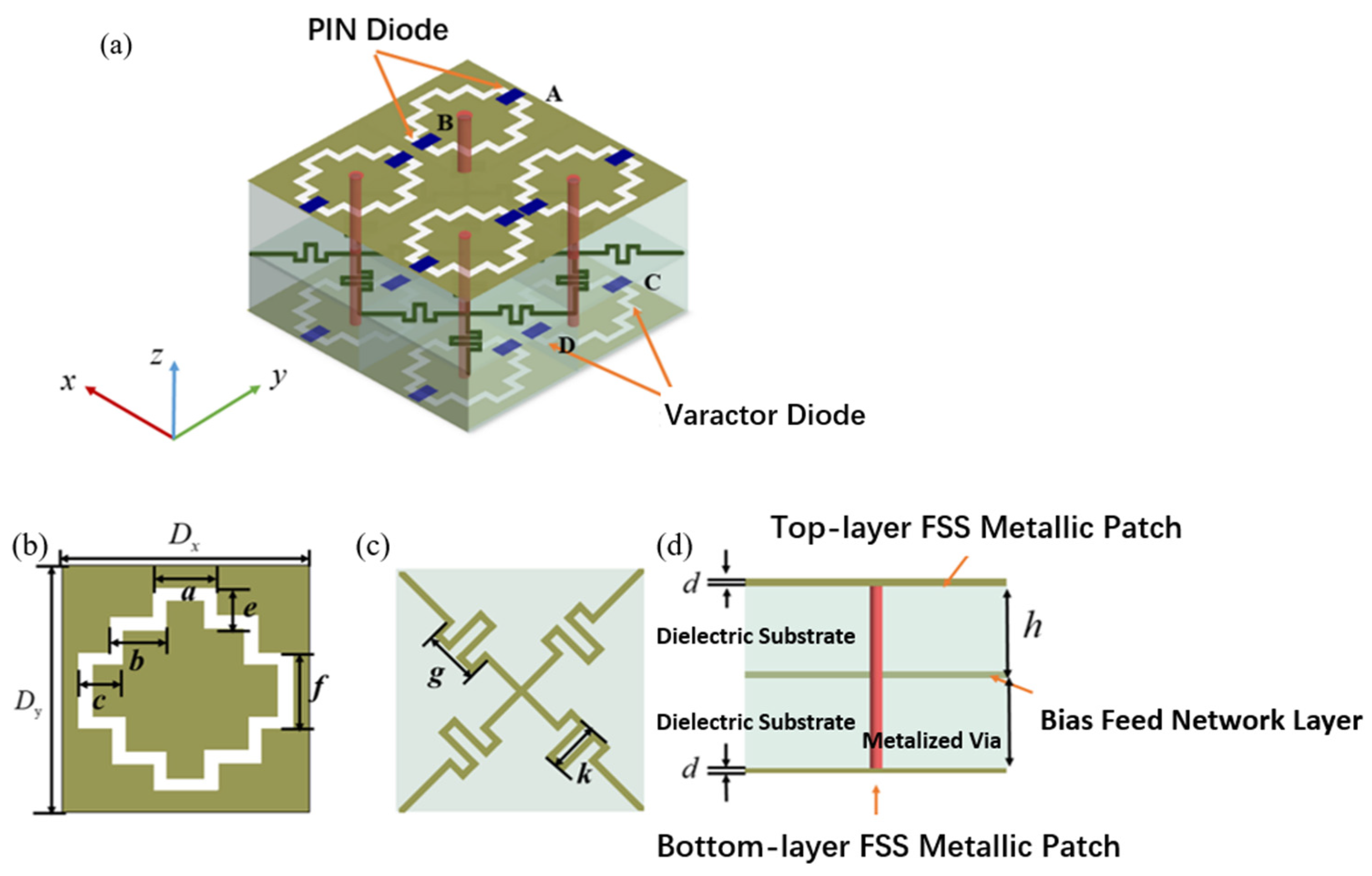
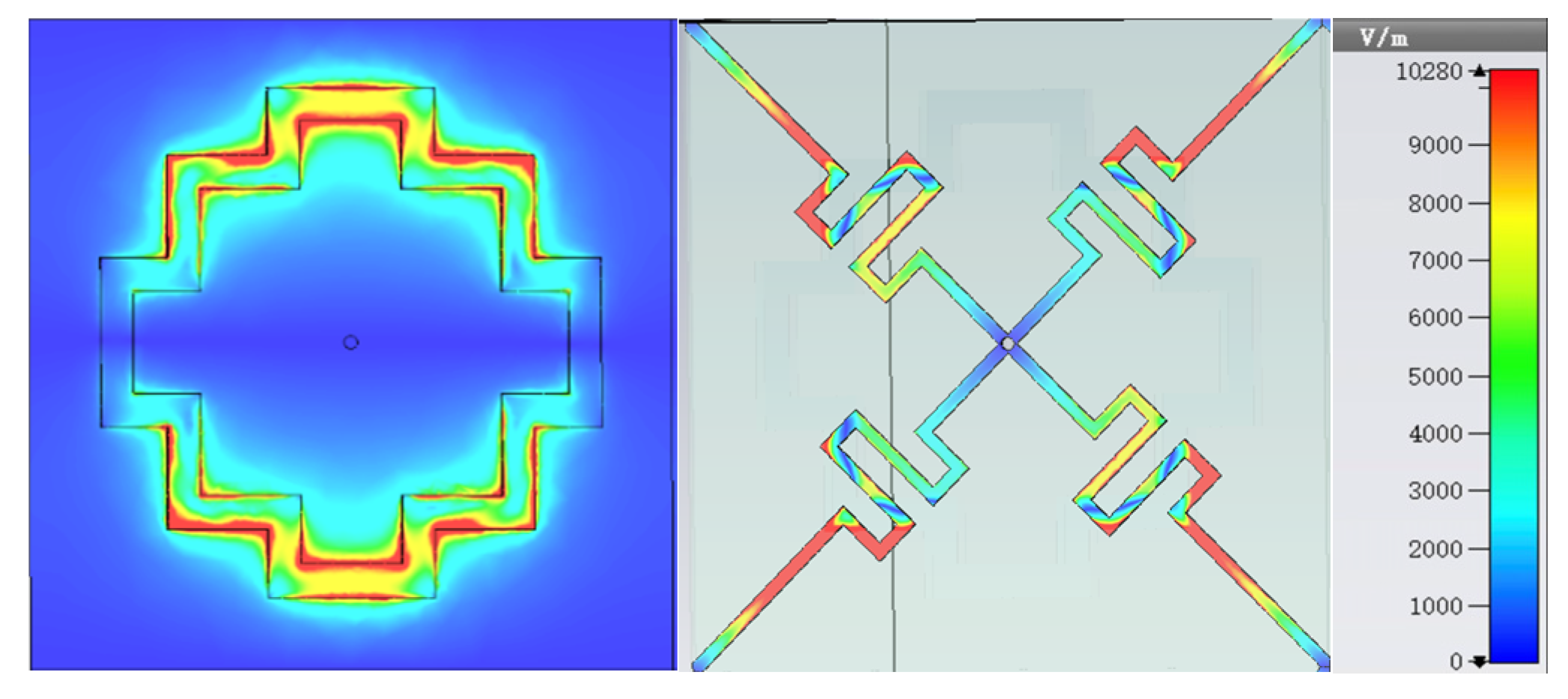
3.1. Resonant Structure Design
3.2. Analysis of Passive Structure Model and Transmission Characteristics
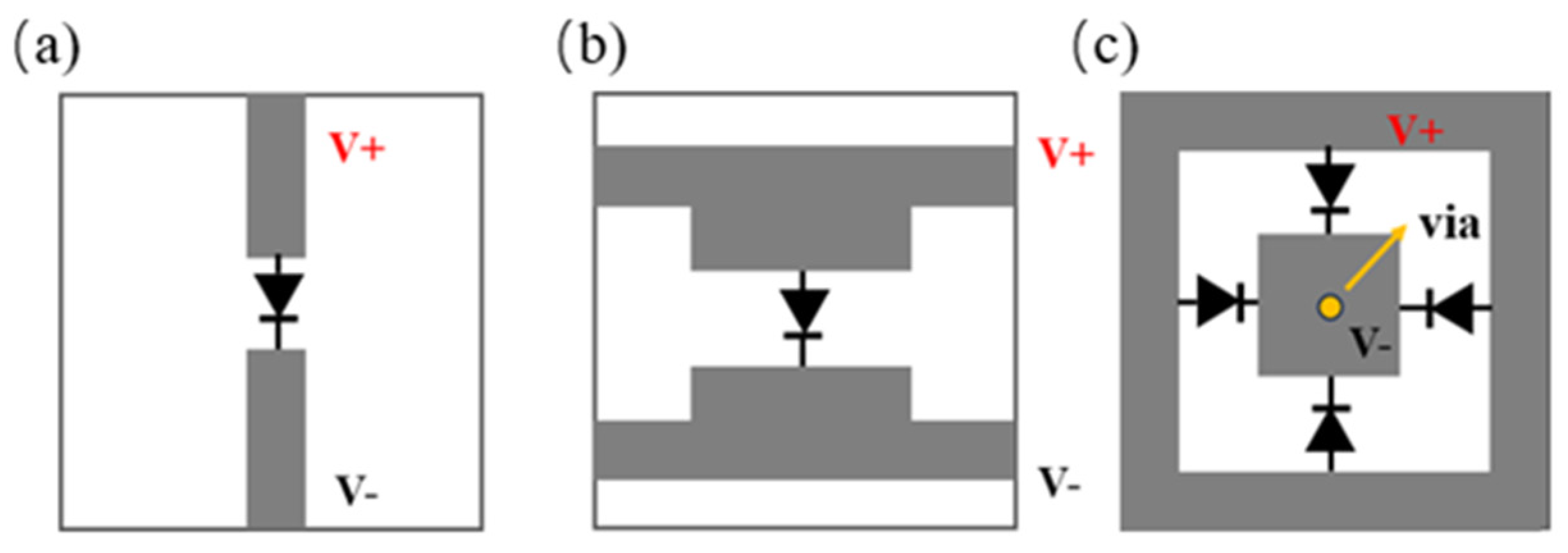
3.2.1. Design of Feeding and Bias Networks
3.2.2. Structural Model Design
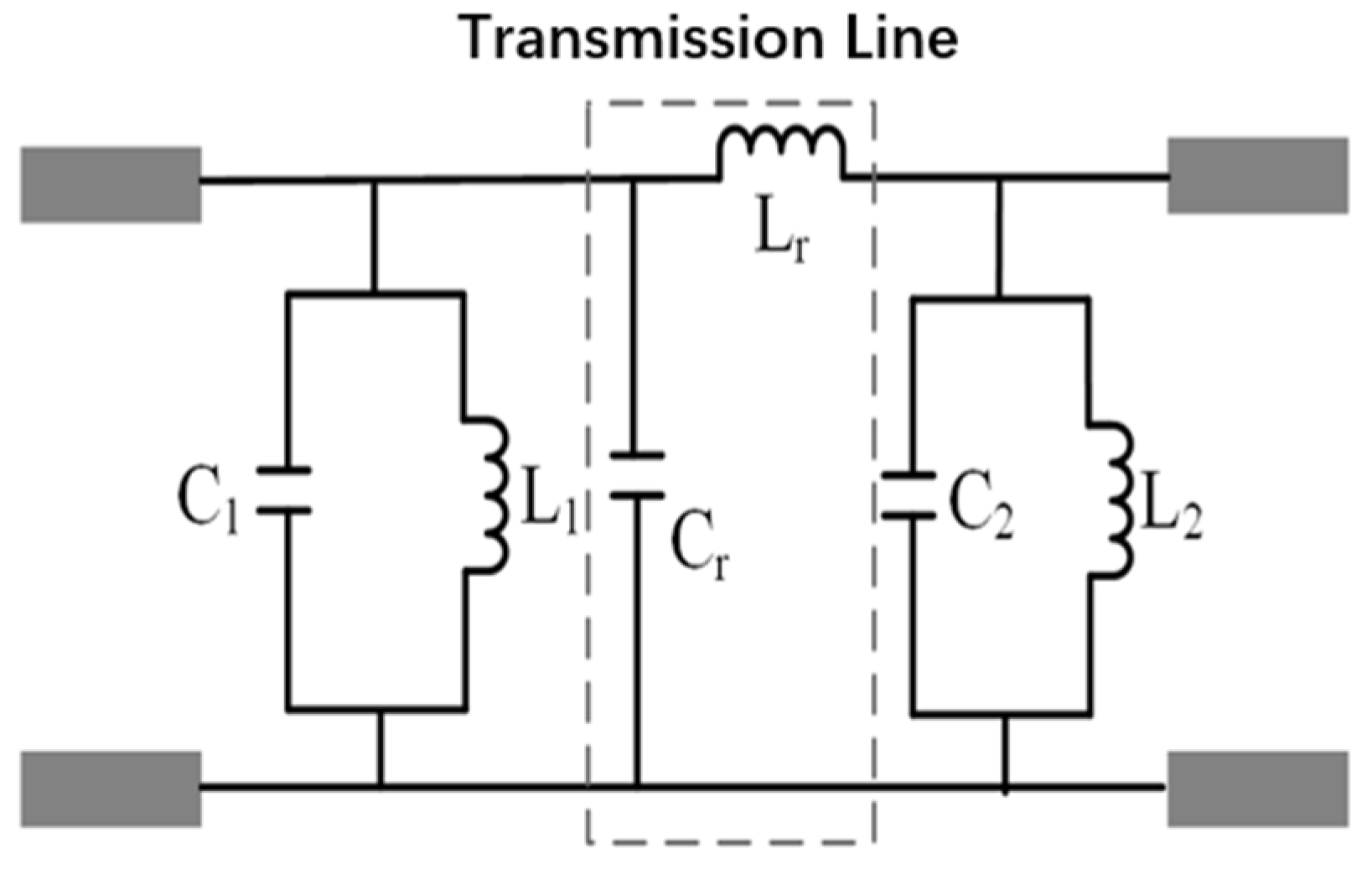
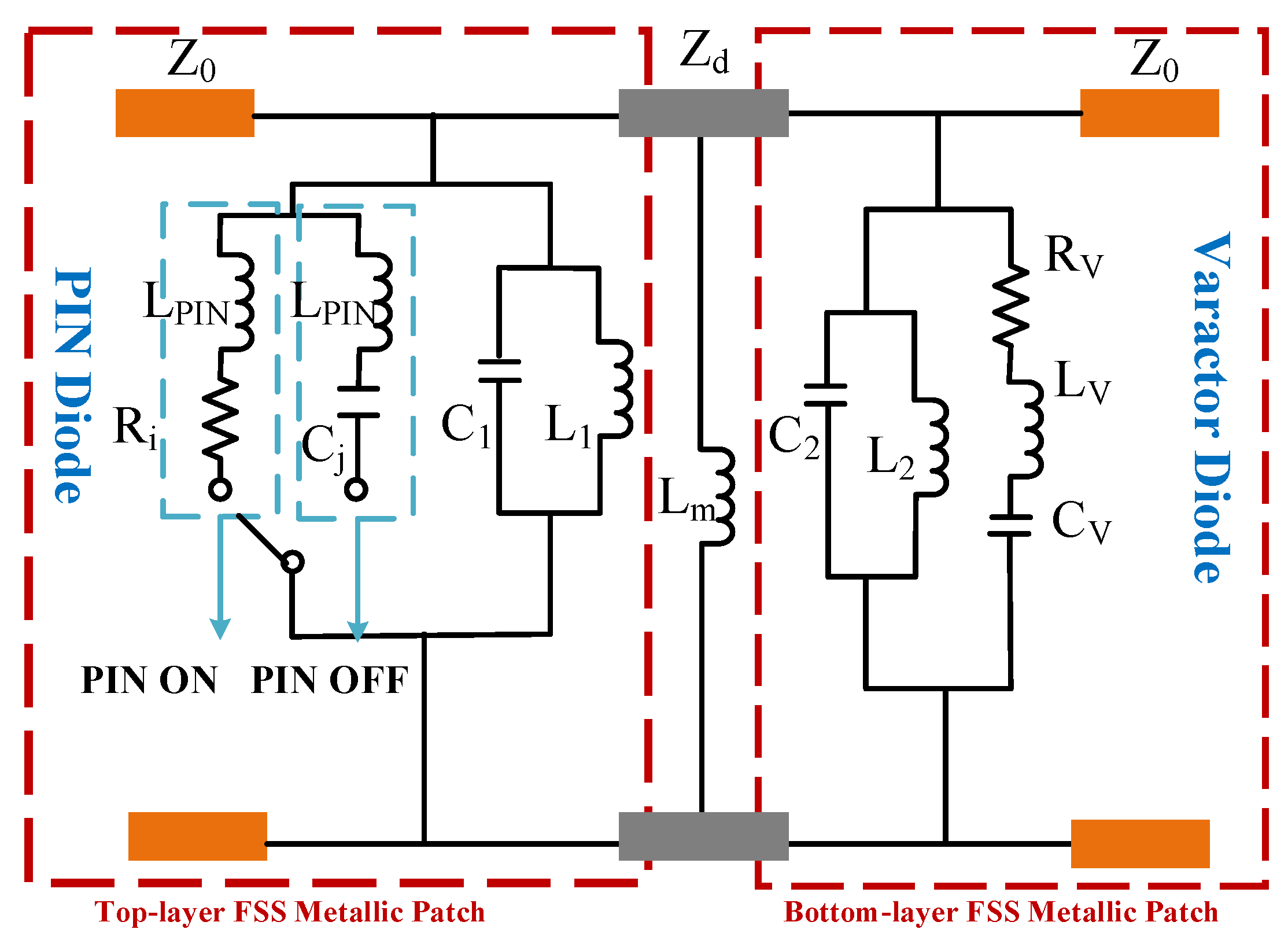
3.2.3. Equivalent Circuit Analysis of Passive Structures
3.3. Design of Active Structure Model for Loading PIN/Varactor Diode
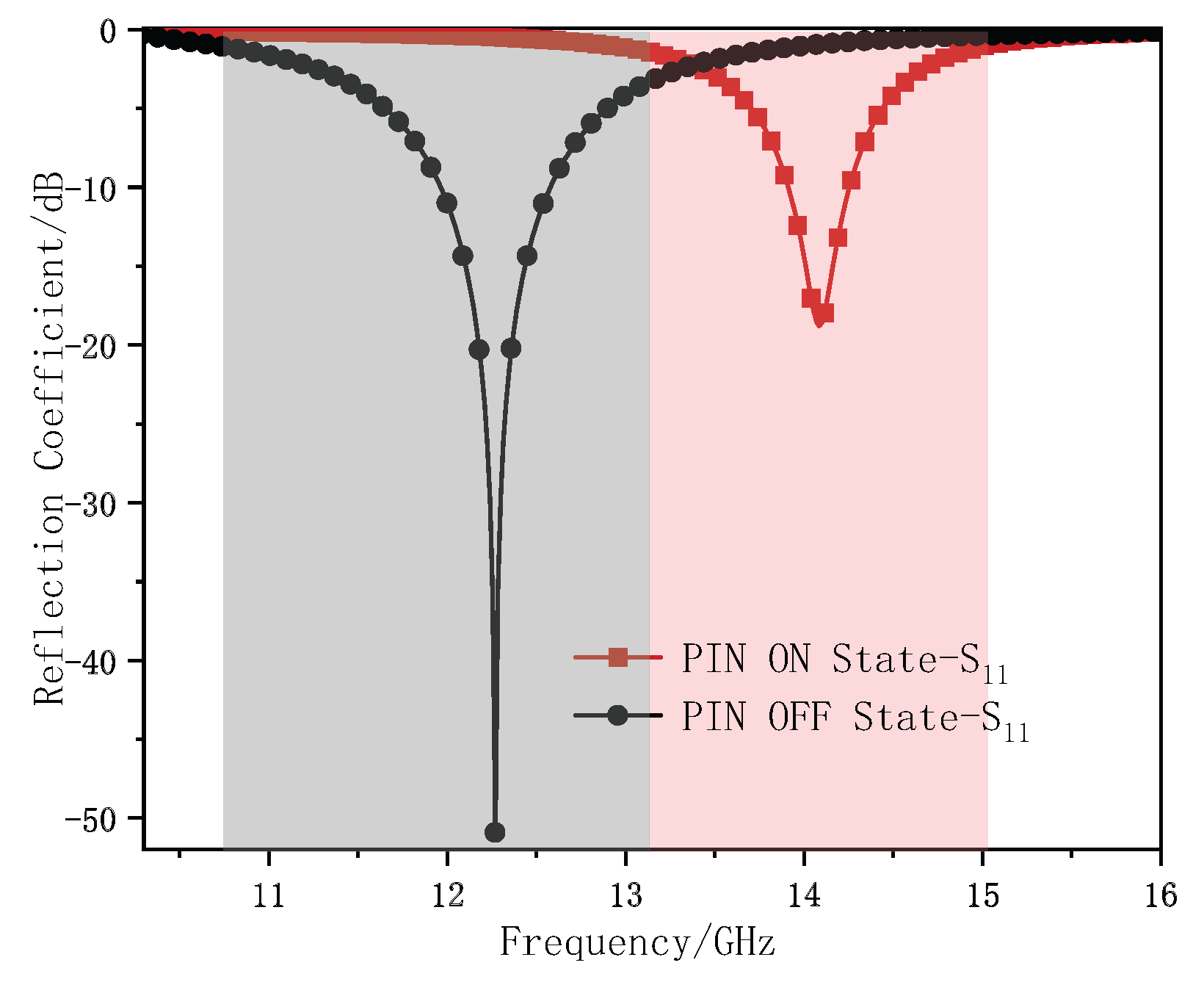
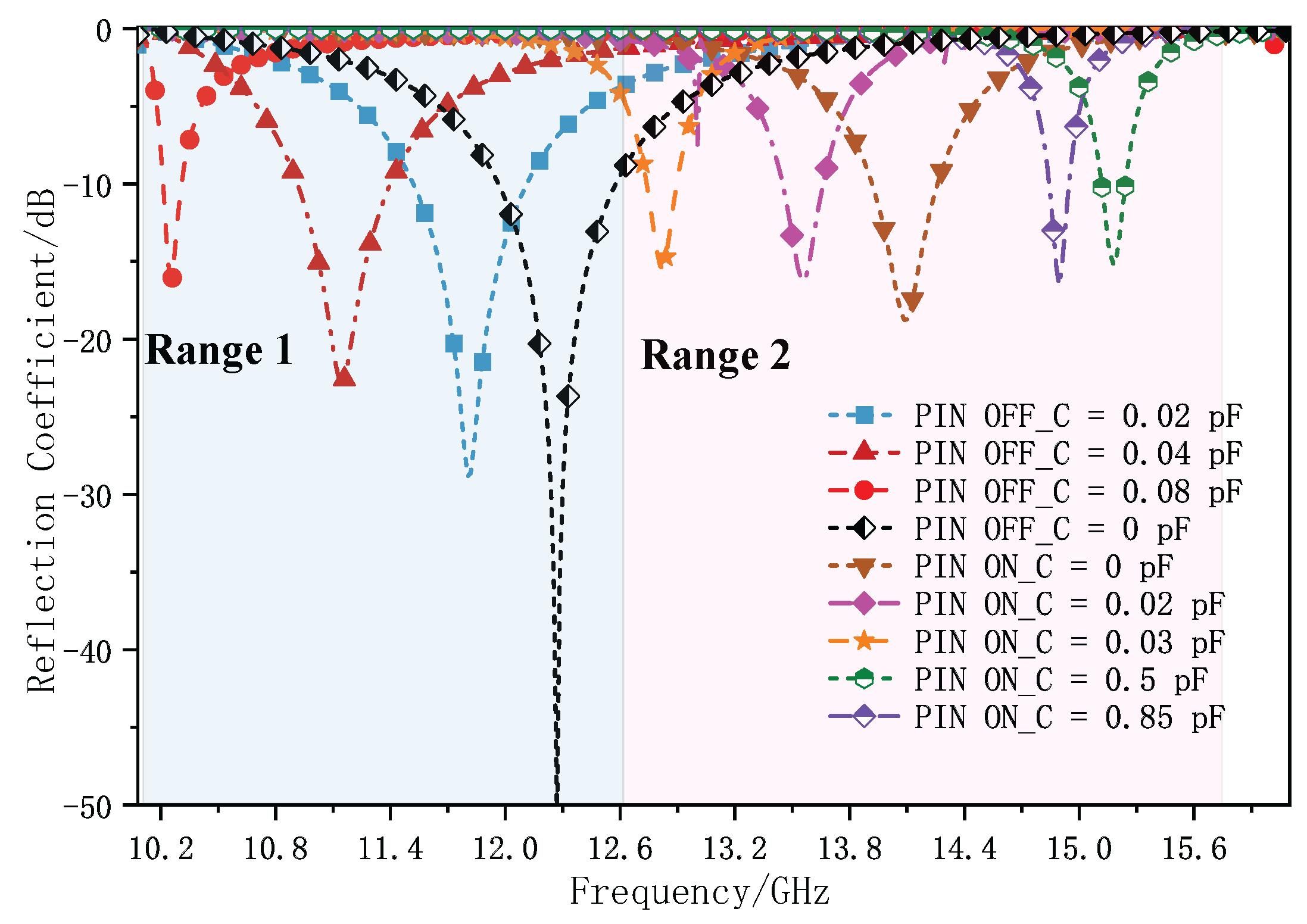
3.3.1. Analysis of the Transmission Characteristics of Loaded PIN Diodes
3.3.2. Analysis of the Transmission Characteristics of Loaded Varactor Diodes
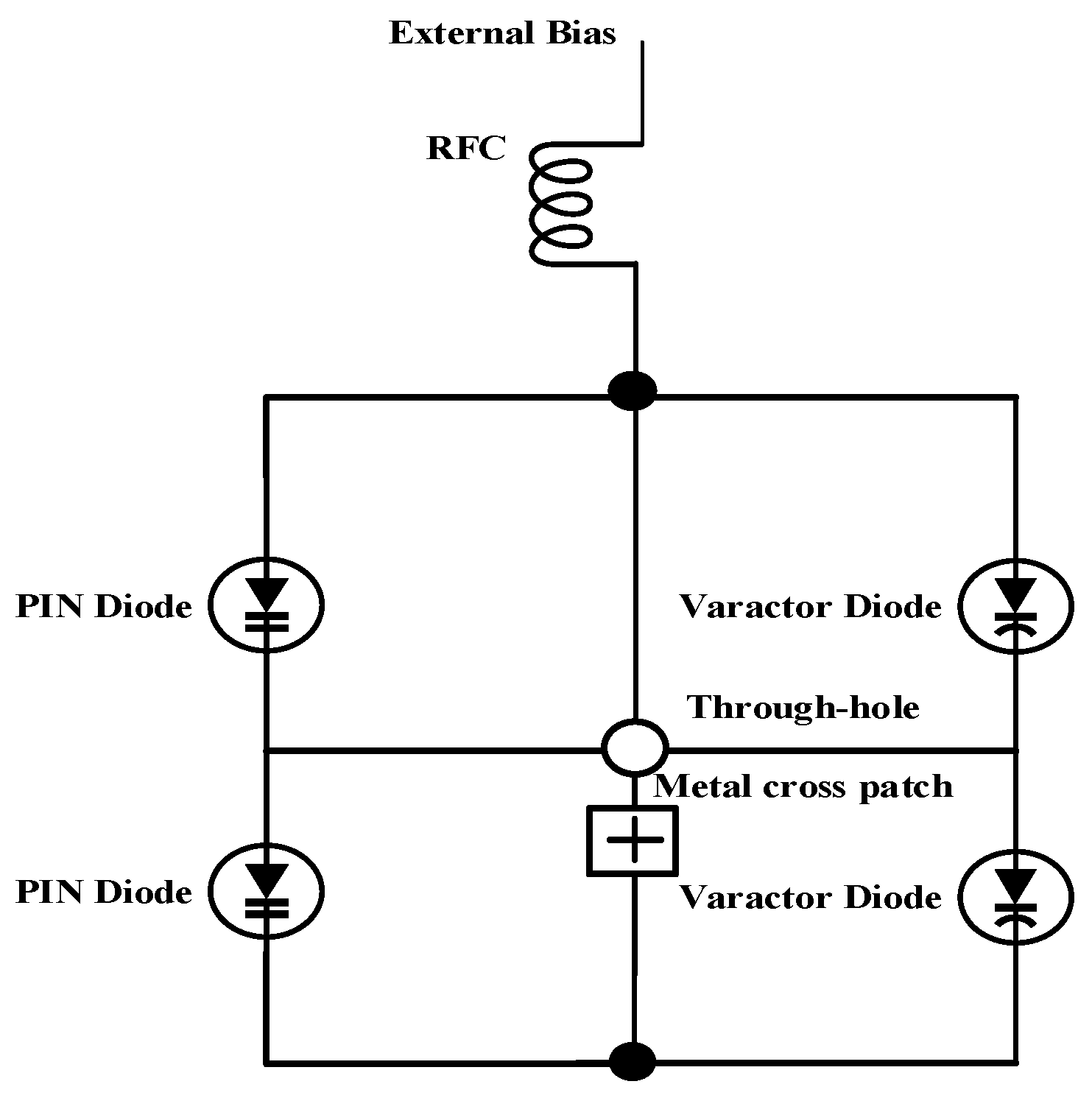
3.3.3. Equivalent Circuit Analysis of Integrated PIN/Varactor Diodes Loading
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, J. Research on Low-Profile High-Order Bandpass Frequency Selective Surfaces. Ph.D. Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2022. (In Chinese). [Google Scholar]
- Deng, B. Research on the Application of Metamaterials in Active Frequency Selective Surfaces. Master’s Thesis, Chengdu University of Information Technology, Chengdu, China, 2018. (In Chinese). [Google Scholar]
- Sainadh, P.M.; Ghosh, S. A Multifunctional Reconfigurable Frequency-Selective Surface with Simultaneous Switching and Tuning Capability. IEEE Trans. Antennas Propag. 2024, 72, 7700–7709. [Google Scholar] [CrossRef]
- Han, J.; Liao, X. A MEMS Microwave Phase Detector with Broadband Performance Operable at X-Band. Microw. Opt. Technol. Lett. 2016, 58, 806–809. [Google Scholar] [CrossRef]
- Schoenlinner, B.; Abbaspour-Tamijani, A.; Kempel, L.C.; Rebeiz, G. Switchable Low-Loss RF MEMS Ka-Band Frequency-Selective Surface. IEEE Trans. Microw. Theory Tech. 2004, 52, 2474–2481. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, L. Tunable Terahertz Dual-Band Band-Stop Filter Based on Surface Magnetoplasmons in Graphene Sheet Array. Opt. Laser Technol. 2020, 132, 106484. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, J.; Xu, N. Low-Frequency Bandpass and Bandstop Free-Switching Frequency Selective Surface. Opt. Precis. Eng. 2018, 26, 142–149. (In Chinese) [Google Scholar]
- Yang, C. Analysis and Design of Bandpass Reconfigurable Frequency Selective Surfaces. Master’s Thesis, Xidian University, Xi’an, China, 2023. (In Chinese). [Google Scholar]
- Zheng, H.; Zhang, S.; Xu, T. Research Progress on Tunable Electromagnetic Metasurfaces. Acta Opt. Sin. 2023, 43, 55–75. (In Chinese) [Google Scholar]
- Kiani, G.I.; Esselle, K.P.; Weily, A.R.; Ford, K.L. Active Frequency Selective Surface Using PIN Diodes. In Proceedings of the Antennas and Propagation Society International Symposium, Honolulu, HI, USA, 9–15 June 2007; pp. 1–4. [Google Scholar]
- Withayachumnankul, W.; Fumeaux, C.; Abbott, D. Planar Array of Electric-LC Resonators with Broadband Tunability. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 577–580. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Shen, Z.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Varactor-Tunable Second-Order Bandpass Frequency-Selective Surface with Embedded Bias Network. IEEE Trans. Antennas Propag. 2016, 64, 1672–1680. [Google Scholar] [CrossRef]
- Phon, R.; Ghosh, S.; Lim, S. Novel Multifunctional Reconfigurable Active Frequency Selective Surface. IEEE Trans. Antennas Propag. 2019, 67, 1709–1718. [Google Scholar] [CrossRef]
- Li, H.; Cao, Q.; Wang, Y. A Multifunctional Active Frequency Selective Surface and Its Control Method. Chinese Patent CN201610852810.9, 11 October 2019. (In Chinese). [Google Scholar]
- Bai, H.; Yan, M.; Li, W.; Wang, J.; Zheng, L.; Wang, H.; Qu, S. Tunable Frequency Selective Surface with Angular Stability. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1108–1112. [Google Scholar] [CrossRef]
- He, Z. Research on Miniaturized Multi-Frequency Reconfigurable Frequency Selective Surfaces. Master’s Thesis, Chongqing University of Posts and Telecommunications, Chongqing, China, 2022. (In Chinese). [Google Scholar]
- Li, H.; Ma, C.; Zhou, T.; Wang, J.; Ye, D.; Sun, Y.; Zhu, W.; Denidni, T.A.; Ran, L. Reconfigurable Fresnel Lens Based on an Active Second-Order Bandpass Frequency-Selective Surface. IEEE Trans. Antennas Propag. 2020, 68, 4054–4059. [Google Scholar] [CrossRef]
- Shao, W.; Ding, X.; Zhang, L.M. A Multifunctional Active Frequency Selective Surface with Scattering Diffusivity and Transmission Passband Tunability. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 229–233. [Google Scholar]
- Qu, M.; He, Z.; Su, J.; Nayyeri, V. A rasorber with energy-selective passband and ultrawideband absorptiveout-of-band. IEEE Trans. Microw. Theory Tech. 2024, 72, 5643–5652. [Google Scholar] [CrossRef]
- Wang, H.; Liu, N.; Sheng, X. A Dual-Band Reconfigurable Frequency Selective Surface with Independent Tuning Capability. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 3917–3921. [Google Scholar] [CrossRef]
- Fan, Y.D.; Li, D.; Ma, H.Z.; Li, E.-P. A Novel Reconfigurable Metasurface with Expanded Tuning Range for Electromagnetic Interference Shielding. In Proceedings of the 2024 IEEE Joint International Symposium on Electromagnetic Compatibility, Signal & Power Integrity: EMC Japan/Asia-Pacific International Symposium on Electromagnetic Compatibility, Okinawa, Japan, 20–24 May 2024; pp. 505–510. [Google Scholar]
- Chen, B. Design of Miniaturized Frequency Selective Surfaces Based on Equivalent Circuit Analysis. Fire Control Radar Technol. 2018, 47, 85–93. (In Chinese) [Google Scholar]
- Liang, J. Research and Design of Flexible, Wideband, and Tunable Multifunctional Active Frequency Selective Surfaces. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2021. (In Chinese). [Google Scholar]
- Langley, R.J.; Parker, E.A. Equivalent Circuit Model for Arrays of Square Loops. Electron. Lett. 1982, 18, 294–296. [Google Scholar] [CrossRef]
- Maity, S.; Tewary, T.; Mukherjee, S.; Roy, A.; Sarkar, P.P.; Bhunia, S. Wideband Hybrid Microstrip Patch Antenna and Gain Improvement Using Frequency Selective Surface. Int. J. Commun. Syst. 2022, 35, e5268. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Yang, H. Design of a Novel Miniaturized Stopband FSS for Ultra-Wideband Antennas. J. Magn. Mater. Devices 2019, 50, 50–56. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Y. Research on Novel Wideband and Multi-Band Three-Dimensional Frequency Selective Surfaces. Ph.D. Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, 2019. (In Chinese). [Google Scholar]
- Yao, Z. Design and Research of Miniaturized Frequency Selective Surfaces in the Microwave Band. Master’s Thesis, Jilin University, Changchun, China, 2024. (In Chinese). [Google Scholar]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Higher-Order Tunable Frequency Selective Surface with Miniaturized Elements. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Wang, S.; Hong, T. Design of an Active Frequency Selective Surface with Wide Tuning Range. In Proceedings of the 2023 National Conference on Antennas, Nanjing, China, 19–21 October 2023; pp. 865–867. (In Chinese). [Google Scholar]
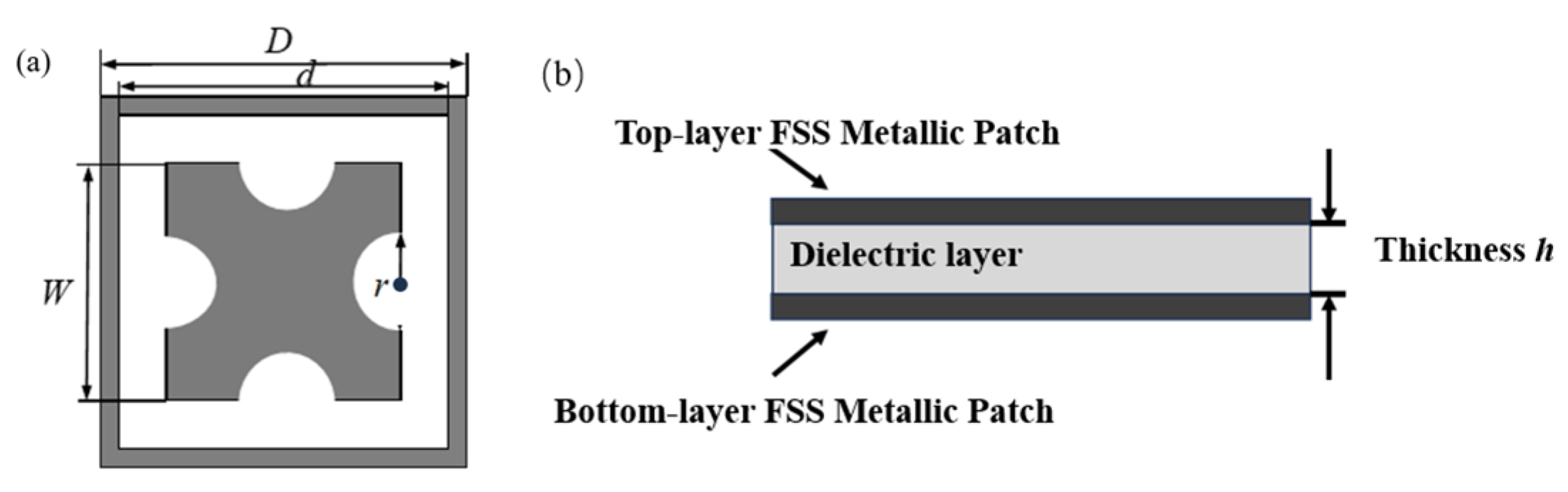





| Parameter | D | d | W | Rtop | Rbottom | h |
| Value/mm | 10.0 | 9.0 | 6.7 | 1.0 | 1.1 | 1.575 |
| Type | Dx | Dy | f | ||||||
| Value/mm | 10.00 | 10.00 | 2.60 | 1.56 | 1.04 | 1.04 | 2.60 | 2.00 | 1.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Tian, X.; Zhang, G.; Liu, X.; Song, S.; Song, J.; Liu, H.; Wang, L.; Yang, Z. AFSS Wide-Frequency Reconfigurable Design and Electromagnetic Characterization Research. Electronics 2025, 14, 3628. https://doi.org/10.3390/electronics14183628
Gong L, Tian X, Zhang G, Liu X, Song S, Song J, Liu H, Wang L, Yang Z. AFSS Wide-Frequency Reconfigurable Design and Electromagnetic Characterization Research. Electronics. 2025; 14(18):3628. https://doi.org/10.3390/electronics14183628
Chicago/Turabian StyleGong, Lei, Xinru Tian, Ge Zhang, Xuan Liu, Shigeng Song, Jian Song, Haoyang Liu, Liguo Wang, and Zhiqiang Yang. 2025. "AFSS Wide-Frequency Reconfigurable Design and Electromagnetic Characterization Research" Electronics 14, no. 18: 3628. https://doi.org/10.3390/electronics14183628
APA StyleGong, L., Tian, X., Zhang, G., Liu, X., Song, S., Song, J., Liu, H., Wang, L., & Yang, Z. (2025). AFSS Wide-Frequency Reconfigurable Design and Electromagnetic Characterization Research. Electronics, 14(18), 3628. https://doi.org/10.3390/electronics14183628






