VIFPE: Multimodal Fusion of Visible and Infrared Images for Pose Estimation in Large-Scale Urban Environments

Abstract

Most existing deep learning-based camera pose estimation methods rely solely on visible images, making them vulnerable to challenges such as drastic lighting variations and poor nighttime imaging quality. These limitations reduce the robustness and accuracy of traditional approaches. To address these issues, we propose VIFPE (Visible- and Infrared-Fusion-Based Pose Estimation), a novel framework that integrates features from both visible and infrared images to enhance pose estimation in urban environments. By leveraging the complementary advantages of visible images, which are rich in texture, and infrared images, which are resilient to illumination changes, VIFPE achieves robust and accurate localization across diverse lighting conditions. The framework consists of multiple key modules, including a feature extractor, a multimodal fusion module, a pose regressor, and a multi-task learning strategy. Specifically, VIFPE employs Multi-axis Vision Transformer (MaxViT) encoders to extract features from both modalities, which are then fused in a shared feature space through a cross-modal fusion module. A pose regression network is subsequently trained to estimate the camera’s position and orientation based on the fused representation. Our experimental results on diverse urban datasets demonstrate that VIFPE significantly outperforms conventional methods in terms of both accuracy and robustness, particularly under challenging lighting conditions. This work underscores the potential of multimodal fusion for camera localization in large-scale urban environments and lays a foundation for future advancements in the field.

1. Introduction

Localization, or absolute pose estimation, is a fundamental requirement for a wide range of intelligent systems, including mobile robots [1], virtual reality devices [2], and autonomous vehicles [3,4,5], as accurate location information is crucial for planning and decision-making in these systems. However, conventional Global Navigation Satellite System (GNSS)-based positioning often suffers from multi-path effects and signal occlusion in urban environments due to obstructions from buildings and trees, limiting its applicability in real-time, high-precision localization scenarios [6].

In GNSS-denied environments, vision-based localization has gained significant attention, leading to the development of numerous approaches that leverage visual information for robust pose estimation. Recently, end-to-end deep learning-based visual localization methods have demonstrated superior performance over traditional approaches, particularly in driving environments, due to their robustness to lighting variations and dynamic scene changes [7]. Traditional visual localization typically involves constructing high-precision maps followed by image-based matching for localization [8]. This process is computationally expensive, requires extensive labor, and scales poorly with scene complexity [9]. Moreover, such methods struggle under extreme lighting conditions or in textureless environments. In contrast, end-to-end neural network-based methods eliminate explicit mapping and matching steps, enabling low-latency localization suitable for real-time applications such as virtual reality.

Previous end-to-end pose estimation methods relied on deep neural network models trained on visible-light (RGB) images paired with ground-truth pose labels. These methods infer camera poses directly from a single image and have demonstrated strong performance in certain scenarios [7,10]. Early approaches such as PoseNet [7] and MapNet [11] validated the feasibility of deep learning-based localization but remained sensitive to dynamic object interference. AtLoc introduced attention mechanisms to improve localization robustness in dynamic scenes [12]. However, most end-to-end pose estimation models rely exclusively on RGB images, limiting their adaptability to extreme lighting conditions such as darkness or intense illumination changes.

To address these challenges, multimodal data fusion has emerged as a promising direction. Different sensing modalities provide complementary information that enhances scene understanding and robustness [13]. Infrared (IR) imaging, in particular, offers significant advantages over RGB-based methods: it is invariant to ambient lighting conditions and provides visibility through atmospheric obscurants like fog, smoke, and dust. Consequently, fusing RGB and infrared images enables robust, all-day localization, especially in environments where lighting conditions vary dramatically. However, research on multimodal fusion for visual localization remains limited.

In this work, we propose VIFPE, a novel end-to-end multimodal learning framework for Visual- and Infrared-Fusion-Based Pose Estimation, achieving accurate and reliable localization in large-scale urban environments. Our method leverages the complementary nature of these modalities to improve robustness under diverse lighting conditions. The proposed framework consists of four key components: feature extraction, feature fusion, pose regression, and a multi-task learning strategy. Specifically, we utilize two MaxViT-based backbone networks [14] for separate feature extraction from RGB and infrared images. MaxViT incorporates grid and block attention mechanisms to capture both local and global image features, enabling more effective scene representation. The extracted features are then fused using an interpretable attention-weighted fusion module, which dynamically assigns weights to each modality to achieve optimal feature integration. The fused features are passed to a pose regression module for final translation and rotation estimation. Additionally, a multi-task learning strategy is employed, wherein individual pose regressions are performed for each modality alongside a joint multimodal estimation. This approach ensures effective feature utilization by leveraging both shared and modality-specific information.

To validate the proposed method, we conducted extensive experiments using self-collected datasets in urban street environments, covering both long and short trajectories under daytime and nighttime conditions. We benchmarked our approach against state-of-the-art methods, including AtLoc, MapNet, PoseNet, and RobustLoc. The results demonstrate that VIFPE significantly improves localization accuracy, achieving mean translation and rotation error reductions of 26.25% and 18.05% in large-scale environments and 13.71% and 14.77% in smaller-scale settings compared to RobustLoc. Furthermore, our method exhibits superior pose estimation performance under normal, bright, and low-light conditions.

Our key contributions are as follows:

• We propose VIFPE, the first end-to-end multimodal learning framework for pose estimation that integrates infrared- and visible-light information.
• We introduce an interpretable, attention-weighted fusion module with only two convolutional layers for efficient feature-level fusion, effectively capturing the complementary characteristics of RGB and infrared modalities.
• We design a multi-task learning strategy that incorporates both modality-specific and joint loss functions, enhancing multimodal feature integration and improving pose estimation robustness.
• We develop an experimental platform and collect a dedicated dataset under diverse lighting conditions to validate our method. Extensive evaluations and saliency map analyses demonstrate the robustness and interpretability of our approach in extracting informative multimodal features

2. Related Work

2.1. Deep Learning-Based Camera Localization

End-to-end camera pose regression, or camera relocalization, trains a model on scene images and their corresponding poses to estimate camera poses directly from query images. This approach simplifies deployment by eliminating the need for a pre-built database and enhances robustness in dynamic and complex environments. PoseNet was a pioneering work in this field, leveraging GoogleNet for end-to-end camera pose regression [7]. MapNet integrates geometric constraints into end-to-end pose estimation, achieving promising results [11]. VidLoc employs a combination of visual and spatio-temporal information for camera localization [15]. AtLoc incorporates self-attention mechanisms into convolutional networks to emphasize stable structural features in dynamic scenes [12]. Fei et al. introduced a graph neural network-based framework for pose estimation using multi-view images [16]. CoordiNet enhances performance by integrating uncertainty estimation with end-to-end pose estimation networks [17]. Arthur’s ImPosing employs two separate neural networks to learn scene representations, achieving efficient visual localization [18]. Shavit’s MS-Transformer enables multi-scene training for pose estimation, particularly excelling in small-scale environments [19]. EffLoc proposes a lightweight transformer-based model to improve localization accuracy and efficiency [20]. RobustLoc improves robustness by integrating convolutional neural networks with neural differential equations, demonstrating improved localization reliability [21]. Guan’s EVI-SAM algorithm combines visual–inertial and event data from cameras for 3D mapping and pose tracking, balancing efficiency, accuracy, and robustness [9]. Crescitelli et al. introduced the first feature-level IR-RGB fusion for HPE (Human Pose Estimation), enabling reliable pose tracking in darkness. This breakthrough bridged a critical gap in multimodal HPE research [22]. Reloc3r, proposed by Siyan et al., achieves cross-scene real-time metric-scale visual localization through a symmetrical relative pose regression network coupled with a lightweight motion-averaging module, resolving the inherent trade-off between generalization capability and precision in traditional methods [23]. Ravuri et al. proposed the APR-Transformer absolute pose estimation framework based on images/LiDAR, which achieves state-of-the-art performance on benchmarks like the Radar Oxford Robot-Car Dataset and demonstrates robustness in GNSS-denied environments [24].

Most of these methods rely solely on visible-light images, making them highly susceptible to illumination changes. To address this limitation, we propose a multimodal localization framework that fuses features from both visible and infrared images, leveraging their complementary properties to achieve higher-precision pose estimation.

2.2. Deep Learning-Based Multimodal Fusion

Deep learning-based multimodal fusion capitalizes on complementary information from diverse data sources, often outperforming uni-modal approaches in various tasks. This research area has gained significant attention in recent years. Hong et al. proposed a Transformer-based fusion framework for RGB and point cloud data, enabling deep feature integration and improving 6D pose estimation accuracy across multiple datasets [25]. Wang et al. introduced a fusion network that combines progressive interaction with early fusion strategies for efficient object detection and classification in visible–thermal video data [26]. Zou developed a multimodal learning-based human–robot interaction framework, demonstrating improved robot perception and prediction of human intentions [27]. MultiMedRes is a multimodal medical reasoning system that enhances zero-shot prediction by mimicking physician communication patterns, addressing key limitations of large language models (LLMs) in healthcare [28]. Jiang et al. proposed an indoor object detection framework that embeds semantic information into hierarchical point cloud features, improving environmental perception and recognition [29]. Wang et al. introduced a language-assisted visual tracking framework that generates textual descriptions of visual images, validating its effectiveness across multiple datasets [30]. Yuan et al. proposed a Transformer-based fusion module that extracts complementary information from visible and infrared images, enhancing object detection performance [31]. Yi et al. introduced Diff-IF, a diffusion model-based multi-source image fusion method that integrates prior information to address the label scarcity in traditional approaches [32]. SmokeNav combines inertial sensor and millimeter-wave radar data to enhance situational awareness and positioning accuracy for first responders in smoky environments [33]. Cao developed a multimodal fusion method integrating EMG and BI signals, achieving a 96.2% motion recognition accuracy, with broad applications in Human–Machine Interaction (HMI) [34]. Zhuo et al. introduced 4DRVO-Net, which fuses 4D radar point clouds with camera images for pose refinement, incorporating multi-scale feature extraction and adaptive fusion modules [35]. Zhang et al. proposed LeGFusion, an infrared–visible image fusion method leveraging self-attention mechanisms for long-range dependency extraction and contextual integration [36]. Additionally, Zhang et al. implemented a mutual learning strategy and a modality-aware module, enabling inter-modal knowledge transfer, demonstrating robustness across medical datasets [37].

Our work builds upon these advancements by integrating multimodal fusion into visual localization. Unlike previous methods, we leverage both RGB and infrared images, dynamically fusing features to improve robustness under varying lighting conditions, thereby enhancing localization accuracy in challenging environments.

In summary, while SOTA methods demonstrate advances in end-to-end localization (e.g., AtLoc’s dynamic-scene robustness, and integration of geometric or uncertainty constraints of RobustLoc) and multimodal fusion (e.g., transformer-based feature integration), they exhibit critical limitations: RGB-dependent models suffer under illumination extremes, and fusion techniques neglect attention-weighted feature fusion and joint learning. These gaps—coupled with the need for all-day urban localization—motivate VIFPE’s design, which uniquely combines MaxViT-based feature extraction, attention-weighted fusion, and multi-task learning to address lighting vulnerabilities and the limitations of joint learning.

3. Multimodal Fusion of Visible and Infrared Images for Pose Estimation

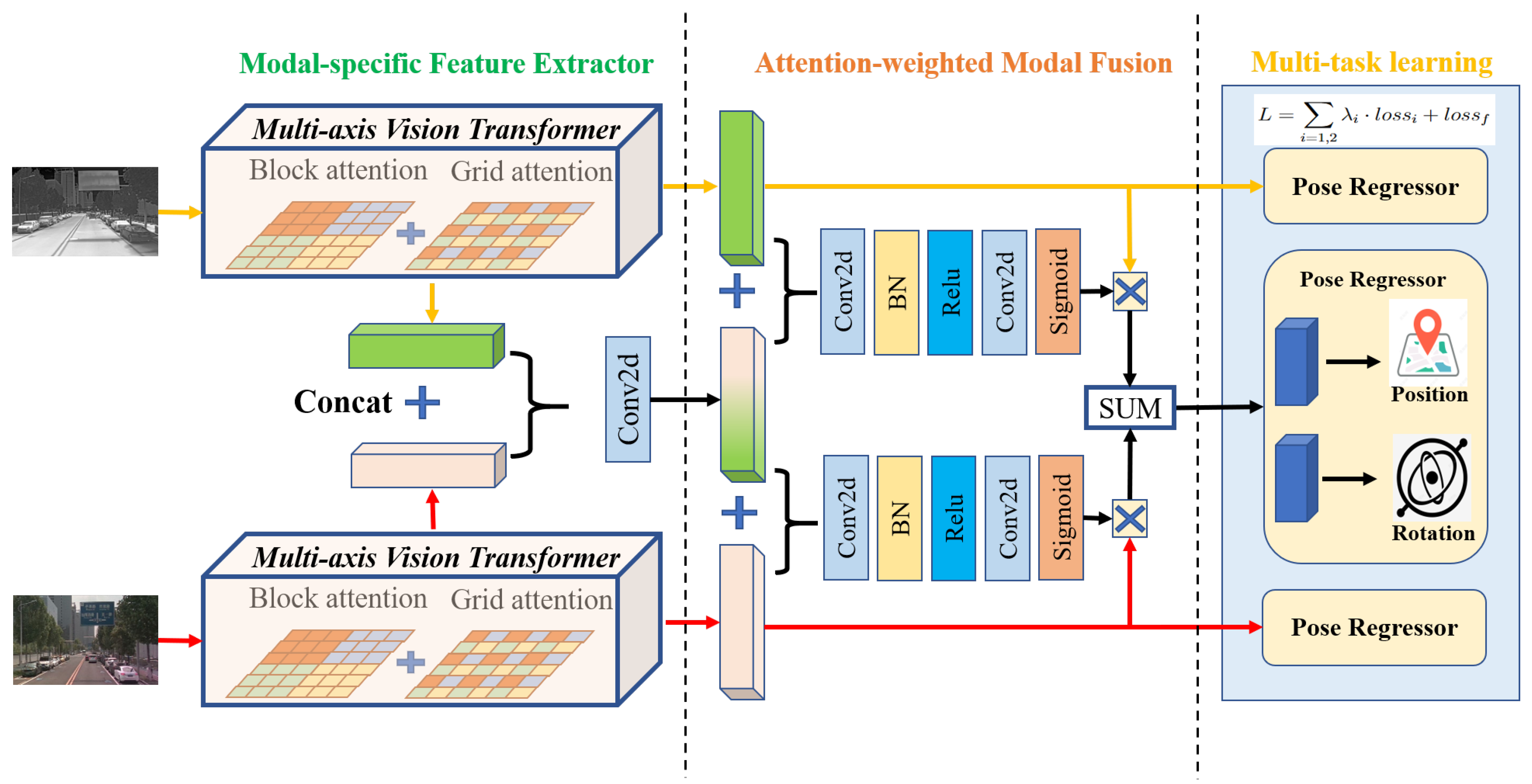
Our proposed VIFPE, a novel end-to-end multimodal learning framework that fuses visible and infrared images for pose estimation, is illustrated in Figure 1. It employs two modality-specific feature encoders to extract features from visible and infrared images, which are subsequently fused through a modality-aware fusion module. As shown in Figure 1, every pose regressor consists of two Multi-Layer Perceptrons (MLPs) that predict 6-Degree-of-Freedom (6DoF) pose information, including position and orientation. The pose regressor in the second row predicts the 6DoF pose from the fusion of two modal features, while another two separate MLPs directly estimate the pose from single-modal features without fusion. The final loss function jointly optimizes pose estimation across these three outputs. In general, we use the output of the MLPs in the second row as the final prediction of the 6DoF pose. Overall, the problem can be formally formulated as follows:

$$[{\mathbf{p}}_0,{\mathbf{q}}_0]=MLPs\left(Fusion(FeatureExtracto{r}_1\left({\mathbf{x}}_1\right),FeatureExtracto{r}_2\left({\mathbf{x}}_2\right))\right)$$

(1)

Here, $[{\mathbf{p}}_0,{\mathbf{q}}_0]$ denote the final outputs of the model, where ${\mathbf{p}}_{\mathbf{0}}\in R^3$ represents the 3D position coordinates and ${\mathbf{q}}_{\mathbf{0}}\in R^3$ represents the 3D orientation angles; ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$ are inputs, where ${\mathbf{x}}_1$ represents infrared-image input, with dimensions of 224 × 224 × 3; ${\mathbf{x}}_2$ represents an RGB image, with identical dimensions of 224 × 224 × 3; $FeatureExtracto{r}_1$ and $FeatureExtracto{r}_2$ represent MaxViT-based feature extraction networks for modality-specific feature encoding; $Fusion$ represents the feature fusion module integrating multi-modal features; and $MLPs$ represents the pose estimation module (specifically, the $MLPs$ block in the second row in Figure 1), directly predicting the 6DoF pose $[{\mathbf{p}}_0,{\mathbf{q}}_0]$.

3.1. Modality-Specific Feature Extractor

To extract visual features, we utilize Multi-axis Vision Transformer (MaxViT) for both visible and infrared images. MaxViT integrates convolutional layers and transformer-based attention mechanisms, balancing local and global feature extraction. Compared to traditional convolutional neural networks (CNNs) like those in AtLoc and PoseNet, MaxViT provides stronger global context modeling while maintaining computational efficiency. The core component of MaxViT, Multi-Axis Self-Attention (MaxSA), employs block attention (focusing on local regions) and grid attention (capturing global dependencies) to enhance feature representation. This structured attention mechanism mitigates the computational overhead of full self-attention. Each MaxViT block consists of an MBConv layer, block attention, and grid attention. The MBConv layer, comprising depth-wise convolution (DWConv) and a Squeeze-and-Excitation (SE) module, enhances channel representation while reducing parameters.

In this context, ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$ are inputs, where ${\mathbf{x}}_1$ represents the infrared-image input, ${\mathbf{x}}_2$ stands for the RGB input, and ${\mathbf{h}}_1$ and ${\mathbf{h}}_2$ denote the feature maps output by the MBConv layer, serving as inputs to the MaxSA module. Taking ${\mathbf{h}}_{\mathbf{1}}\in R^{H\times W\times C}$ as an illustrative example, the computation of block attention within the MaxSA module necessitates decomposing the input into $({\displaystyle \frac{H}{q}}\times {\displaystyle \frac{W}{q}},q\times q,C)$, allowing for the computation of attention within each q × q window, rather than applying full attention across the entire input. Conversely, grid attention requires partitioning the input to be computed into $(T\times T,{\displaystyle \frac{H}{T}}\times {\displaystyle \frac{W}{T}},C)$, enabling grid-based computation of global attention. This approach fosters comprehensive interaction between local and global attention, facilitating the generation of multi-level expressive features while circumventing the exponentially increasing computational complexity associated with traditional attention mechanisms. Hence, a complete MaxViT block encompasses MBConv and MaxSA, fully integrating the advantages of convolutional modules, multi-scale attention, and residual connection structures. The formula for this structure can be expressed as follows:

$${\mathbf{h}}_1=MBConv\left({\mathbf{x}}_1\right)$$

(2)

$${\mathbf{h}}_2=MBConv\left({\mathbf{x}}_2\right)$$

(3)

$${\mathbf{i}}_1=GridAtt\left(BlockAtt\left({\mathbf{h}}_1\right)\right)$$

(4)

$${\mathbf{i}}_2=GridAtt\left(BlockAtt\left({\mathbf{h}}_2\right)\right)$$

(5)

In this context, ${\mathbf{i}}_{\mathbf{1}}$ and ${\mathbf{i}}_{\mathbf{2}}$ denote the feature maps after passing through a single MaxViT block. Consequently, we denote ${\mathbf{I}}_{\mathbf{1}}$ and ${\mathbf{I}}_{\mathbf{2}}$ as the feature maps after they have undergone four consecutive MaxViT blocks. Therefore, during the feature extraction phase, the process of extracting image features from the two modalities can be expressed as follows:

$${\mathbf{z}}_1=MaxViT\left({\mathbf{x}}_1\right)=FC\left(Pool\left(Conv\left({\mathbf{I}}_1\right)\right)\right)$$

(6)

$${\mathbf{z}}_2=MaxViT\left({\mathbf{x}}_2\right)=FC\left(Pool\left(Conv\left({\mathbf{I}}_2\right)\right)\right)$$

(7)

3.2. Attention-Weighted Modal Fusion (AWMF)

As depicted in the figure, after modal-specific feature extraction, we obtain feature representations for two modalities. In this subsection, we explore the Attention-Weighted Modal Fusion Module (AWMF), which calculates the importance of the features obtained from each modality in the previous stage to derive individual modal weights. This, in turn, allows for the weighted summation of features from both modalities.

By directly concatenating the outputs obtained from the previous stage along the channel dimension and then reducing the channel dimension back to its original size using a convolutional neural network, we can obtain a mixed feature $\mathbf{F}$ that encapsulates information from both modalities. Simple convolutional operations are insufficient for effectively fusing these two features, and the resulting information often contains a significant amount of redundancy and interference. Therefore, instead of directly utilizing $\mathbf{F}$ for pose regression, we choose to employ an attention weight calculation module for post-processing. This module enables us to obtain the weight of each modality in the feature fusion process, facilitating adaptive feature fusion and leading to more accurate pose estimation results. Furthermore, we will also provide a visual explanation of the effectiveness of this module. In terms of input and output, the AWMF module takes the concatenation of $\mathbf{F}$ and ${\mathbf{z}}_i$ as the input and ultimately produces the weighted fused feature ${\mathbf{F}}_{\mathbf{w}}$. Specifically, the attention weight calculation module processes each input pair of ${\mathbf{z}}_i$ and $\mathbf{F}$ to obtain the corresponding weight map ${\mathbf{W}}_i$ for each ${\mathbf{z}}_i$:

$${\mathbf{W}}_i=\sigma \left(f_c\left([\mathbf{F};{\mathbf{z}}_{\mathbf{i}}]\right)\right),i\in 1,2$$

(8)

Here, $\sigma$ represents the sigmoid function, and $f_c$ denotes a 2D convolutional layer with a kernel size of 3 for both dimensions. Each convolutional layer is followed by batch normalization and a Leaky ReLU activation function. This module models the distribution relationship of uni-modal features within the multimodal fused features by outputting attention maps. Subsequently, we perform a weighted summation of the weights and features of the two modalities to obtain the fused feature map.

$${\mathbf{F}}_{\mathbf{w}}=\sum _{i=1,2}{\mathbf{W}}_i\ast {\mathbf{z}}_i$$

(9)

We leverage the AWMF module to compute the weights of features from different modalities during the fusion process, and then perform weighted summation on these features to obtain more discriminative fused features. In Equation (9), we perform an element-wise multiplication (denoted by *) between the weight map ${\mathbf{W}}_i$ and the feature map ${\mathbf{z}}_i$. This approach enables the complementary advantages of different modality data to be realized. Due to the method’s streamlined structure and excellent scalability, when the number of modalities increases, it suffices to incorporate the corresponding features and their weights for each additional modality into the weighted summation formula. This facilitates the integration of more features, holding great potential for future work involving the fusion of even more modalities, such as text, point clouds, and audio.

3.3. Multi-Task Learning Strategy for Multimodal Pose Estimation

Visible images often exhibit rich textures but are highly susceptible to variations in illumination. Conversely, infrared images are insensitive to changes in illumination but lack the rich textural information present in visible images. Therefore, we have devised a fusion learning strategy. This includes designing loss functions tailored for individual modalities and modal fusion, and also developing loss functions for collaborative learning between modal fusion and individual modalities. This approach enables the optimization of parameters for the fused modality while simultaneously refining the model parameters for individual modalities. Consequently, it facilitates collaborative learning among the parameters of the three models and achieves complementary integration of information from the two modalities. During the feature extraction stage, the parameters of the feature extraction networks for the two modalities can be mutually optimized during the optimization process. Therefore, we design pose regressors for each modality following the feature extraction stage, in order to design loss functions specifically tailored for individual modalities. The pose regressors are both two-layer MLPs (Multi-Layer Perceptrons), represented as

$$[{\mathbf{p}}_i,{\mathbf{q}}_i]=MLPs\left(z_i\right)i\in 1,2$$

(10)

where $[{\mathbf{p}}_i,{\mathbf{q}}_i]$ represents the 3D position and 3D orientation (quaternion) extracted and regressed from the single-modal feature. Accordingly, the pose predicted by MLPs from the fused feature ${\mathbf{F}}_{\mathbf{w}}$ can be described as

$$[{\mathbf{p}}_f,{\mathbf{q}}_f]=MLPs\left({\mathbf{F}}_{\mathbf{w}}\right)$$

(11)

where $[{\mathbf{p}}_f,{\mathbf{q}}_f]$ represents the 6DoF pose regressed from the fused feature ${\mathbf{F}}_{\mathbf{w}}$. To simplify the computational process, the pose is expressed in the relative coordinate, with the starting point of the trajectory serving as the origin of coordinates.

In Bayesian modeling, Homoscedastic uncertainty represents a task-related aleatoric uncertainty whose variation is independent of changes in input data but rather depends on variations in tasks. The output of our proposed model can be regarded as a multi-task learning model that combines and output pose information based on different modalities. In the context of multi-task learning, the uncertainty associated with tasks can reflect the degree of mutual trust among them. These relative confidences can, in turn, indicate the uncertainty inherent in the regression tasks themselves. Ref. [38] proposes utilizing Homoscedastic uncertainty as a reference to design the weights of different tasks in the loss function. By maximizing Gaussian likelihood through the utilization of task-dependent uncertainty, the outputs for translation and rotation can be designed as two tasks within a multi-task loss function. Furthermore, building upon this foundation, we extend the design to incorporate three regression outputs as three distinct tasks within a multi-task loss function. For single-modal outputs, we define ${\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right)$ as the model output with input $\mathbf{x}$ and weights $\mathbf{w}$. Based on this definition, we propose the following probabilistic model:

$$p\left(\mathbf{y}\right|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))=N({\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right),{\sigma }^2\mathbf{I})$$

(12)

We define the likelihood function as a Gaussian distribution, where the mean of this distribution corresponds to the pose output of the model with a uni-modal input. The symbol $\sigma$ represents the observation noise. For the position and orientation outputs of the model, we define the likelihood function for multiple outputs as their factorization, in which ${\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right)$ serves as the sufficient statistic:

$$p({\mathbf{y}}_{\mathbf{1}},{\mathbf{y}}_{\mathbf{2}}|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))=p\left({\mathbf{y}}_{\mathbf{1}}\right|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))p\left({\mathbf{y}}_{\mathbf{2}}\right|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))$$

(13)

In the process of estimation using Maximum Likelihood Estimation (MLE), we can take its logarithm and then maximize the log-likelihood value of the model. In the context of our method, we express the log-likelihood in the following form to represent the Gaussian likelihood function:

$$logp\left(\mathbf{y}\right|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))\propto {\displaystyle \frac{-1}{2{\sigma }^2}}\left|\right|\mathbf{y}-{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right){\left|\right|}^2-log\sigma$$

(14)

The symbol $\sigma$ denotes the magnitude of noise observed in the output; subsequently, we maximize the aforementioned logarithmic likelihood function with respect to the weights $\mathbf{w}$ and the noise parameter $\sigma$. Given that the uni-modal output consists of two results, position and orientation, which are considered to be two separate tasks, we obtain the following multi-task logarithmic likelihood function:

$$\begin{array}{cc}\hfill p({\mathbf{y}}_{\mathbf{1}},{\mathbf{y}}_{\mathbf{2}}|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))& =p\left({\mathbf{y}}_{\mathbf{1}}\right|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))·p\left({\mathbf{y}}_{\mathbf{2}}\right|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))\hfill \\ \hfill & =N({\mathbf{y}}_{\mathbf{1}};{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right),{\sigma }_1^2)·N({\mathbf{y}}_{\mathbf{2}};{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right),{\sigma }_2^2)\hfill \end{array}$$

(15)

Therefore, the loss function can be defined as

$$\begin{array}{cc}\hfill Loss(\mathbf{w},{\sigma }_1,{\sigma }_2)& =-logp({\mathbf{y}}_{\mathbf{1}},{\mathbf{y}}_{\mathbf{2}}|{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right))\hfill \\ \hfill & \propto {\displaystyle \frac{1}{2{\sigma }_1^2}}\left|\right|{\mathbf{y}}_{\mathbf{1}}-{\mathbf{f}}_{\mathbf{w}}{\left(\mathbf{x}\right)\left|\right|}^2+{\displaystyle \frac{1}{2{\sigma }_2^2}}\left|\right|{\mathbf{y}}_{\mathbf{2}}-{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right){\left|\right|}^2+log{\sigma }_1{\sigma }_2\hfill \\ \hfill & ={\displaystyle \frac{1}{2{\sigma }_1^2}}{L}_1\left(\mathbf{w}\right)+{\displaystyle \frac{1}{2{\sigma }_2^2}}{L}_2\left(\mathbf{w}\right)+log{\sigma }_1{\sigma }_2\hfill \end{array}$$

(16)

In this context, $L_i\left(\mathbf{w}\right)=\left|\right|{\mathbf{y}}_{\mathbf{i}}-{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right){\left|\right|}^2$, where it can be observed from the formula that during the process of minimizing this loss function, the weights of the position and orientation of the single-task output decrease as the noise parameter ${\sigma }_i$ increases, and vice versa. To simplify the expression, we define $\beta :=log\left({\sigma }_1^2\right)$ and $\gamma :=log\left({\sigma }_2^2\right)$, and use $L_i\left(\mathbf{w}\right)=\left|\right|{\mathbf{y}}_{\mathbf{i}}-{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right){\left|\right|}_1$ instead of $L_i\left(\mathbf{w}\right)=\left|\right|{\mathbf{y}}_{\mathbf{i}}-{\mathbf{f}}_{\mathbf{w}}\left(\mathbf{x}\right){\left|\right|}^2$. And we introduce $[\mathbf{p},\mathbf{q}]$ and $[\widehat{\mathbf{p}},\widehat{\mathbf{q}}]$ into the formula, the loss function for the single-modal multi-task output is expressed as

$$loss=\left|\right|\mathbf{p}-\widehat{\mathbf{p}}{\left|\right|}_1{e}^{-\beta }+\beta +\left|\right|log\mathbf{q}-log\widehat{\mathbf{q}}{\left|\right|}_1{e}^{-\gamma }+\gamma$$

(17)

During the training process, the loss function for the two uni-modal training tasks can be represented by the following equation:

$$los{s}_i=\left|\right|{\mathbf{p}}_i-\widehat{{\mathbf{p}}_i}{\left|\right|}_1{e}^{-{\beta }_i}+{\beta }_i+\left|\right|log{\mathbf{q}}_i-log\widehat{{\mathbf{q}}_i}{\left|\right|}_1{e}^{-{\gamma }_i}+{\gamma }_{i}i\in 1,2$$

(18)

where ${\beta }_i$ and ${\gamma }_i$ are learnable parameters used to determine the weightings of translation and rotation, respectively. In calculating the loss function, we use the logarithm of the quaternion ${\mathbf{q}}_i$, denoted as $log{\mathbf{q}}_i$, which comprises a real part u and an imaginary part $\mathbf{v}$, to more accurately describe the continuous changes in orientational motion. To ensure a unique solution for the quaternion during rotation, we constrain all quaternions to lie within the same hemisphere. Hence, we have

$$log{\mathbf{q}}_i=\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{\mathbf{v}}{\left|\right|\mathbf{v}\left|\right|}}co{s}^{-1}u,& & if \left|\right|\mathbf{v}\left|\right|\ne 0\hfill \\ \hfill 0,& & otherwise\hfill \end{array}\right.$$

(19)

Thus, the features obtained after fusing the two modal data are passed through a pose regressor to generate the fused pose output. The loss function optimized during this process is similar to that of the single-modal case, and is expressed as follows:

$$los{s}_f=\left|\right|{\mathbf{p}}_f-\widehat{{\mathbf{p}}_f}{\left|\right|}_1{e}^{-\beta }+\beta +\left|\right|log{\mathbf{q}}_f-log\widehat{{\mathbf{q}}_f}{\left|\right|}_1{e}^{-\gamma }+\gamma$$

(20)

Therefore, the loss function required for our collaborative learning strategy can be expressed as the weighted sum of three loss functions, as shown below:

$$\mathcal{L}=\sum _{i=1,2}{\lambda }_i·los{s}_i+los{s}_f$$

(21)

where ${\lambda }_i$ is a learnable hyper-parameter used to adjust the weights of the single-modal and fused-modal loss functions, which are both initially set to 0.5. From the design of the fusion loss function mentioned above, it can be observed that the role of the modal-specific $los{s}_i$ is to facilitate the optimization of the parameters of the respective modal-specific feature extractor, thereby promoting the optimization of the fused-modal $los{s}_f$, and vice versa. This forms a mutually reinforcing effect on optimization. The final output of the model can be described as

$$[{\mathbf{p}}_0,{\mathbf{q}}_0]=argmi{n}_{{\mathbf{p}}_f,{\mathbf{q}}_f}\mathcal{L}$$

(22)

where $[{\mathbf{p}}_0,{\mathbf{q}}_0]$ stands for the final result of the prediction of the pose. Therefore, on the whole, the multimodal collaborative learning strategy not only enhances the efficiency of feature extraction for each single modality but also optimizes the regression results of the fused modality. This allows each single modality to fully leverage its respective data characteristics and integrates complementary information in the fused modality, achieving the goal of collaborative optimization and thus obtaining more accurate pose estimation. Refer to Appendix A for detailed information of Multi-task learning strategy.

4. Experiments 

In this section, we evaluate the proposed method in terms of localization accuracy and robustness under varying illumination conditions. The multimodal fusion-based localization model is trained and tested using visible- and infrared-image data collected from diverse scenarios. First, we introduce the data collection methodology, followed by specific details of the experimental setup, including software/hardware configurations and training process parameters. Subsequently, a comparative evaluation of the method’s precision is conducted using the experimental results. The generalizability of the approach is validated across two distinct systems, while saliency analysis is employed to quantitatively assess the fusion efficacy of the proposed method across heterogeneous modalities.

4.1. Visible and Infrared Fusion Localization System

We developed two intelligent vehicle localization systems that leverage multimodal perception for robust pose estimation. Both systems implement our multimodal localization algorithms in Python3.7, with data acquisition handled via the Robot Operating System (ROS). To evaluate their effectiveness across various environments and route lengths, the systems were deployed on two platforms: a manned vehicle and a small autonomous unmanned ground vehicle (UGV). As illustrated in Figure 2, the first multimodal localization system integrates the following:

• A RealSense D455 monocular RGB camera for visible-light image acquisition.
• A MAGNITY infrared camera operating at 10 Hz.
• A SinoGNSS GNSS data collection system. Dual antennas mounted at the vehicle’s front and rear enable real-time kinematic (RTK) positioning, achieving ground-truth pose estimation with localization accuracy better than 1.0 m. Figure 3 demonstrates street-view images captured by the dual-modal RGB–infrared camera pair.

The second system, depicted in Figure 4, is implemented on a Scout Mini UGV platform designed for short-range, small-scale data collection. It includes the following:

• A RealSense D455 RGB camera.
• A Guide Sensmart PLUG617 infrared camera operating at 10 Hz.
• A dual-antenna GNSS configuration for high-precision positioning and orientation estimation. The antennas, installed at both ends of the UGV, enable centimeter-level ground-truth acquisition through differential GNSS measurements. This compact system is particularly optimized for mapping dense urban or confined environments.

From the collected data, we selected several representative routes for evaluation. These included a long-range route named Large-loop1, a medium-length route named Large-loop2, and a short-distance route captured during both daytime and nighttime, referred to as Small-loop and Small-loop-night, respectively. Additionally, after collecting data for Small-loop, we recorded a traversal of the same route in the opposite direction during daytime, termed Small-loop-oppo. Notably, Large-loop2 was collected at night. The Large-loop1 and Large-loop2 datasets were collected using the manned vehicle, while the Small-loop and Small-loop-oppo datasets were captured using the unmanned vehicle. Detailed information is provided in

Table 1. Details of the collected dataset.

Scenes	Training (Pairs)	Testing (Pairs)	Length	Time
Large-loop1	42,486	24,397	3500 m	Day
Large-loop2	24,298	11,780	1750 m	Night
Small-loop	5959	2684	210 m	Day
Small-loop-oppo	5588	2931	210 m	Day
Small-loop-night	6190	2878	210 m	Night

.

4.2. Experimental Setup

4.2.1. Training Details

The entire training and testing process was conducted based on the PyTorch1.13.0 framework, utilizing NVIDIA’s RTX 3090 GPU as the hardware foundation. Prior to inputting images into the model, their dimensions were resized to 224 × 224 pixels. For image augmentation, a random Colorjitter was applied, with saturation set to 0.7 and hue set to 0.5. The backbone network of the model, MaxViT, employed a pre-trained model obtained from training on ImageNet-1k. The optimizer used was ADAM, with the batch size configured to 32 and the dropout value set to 0.1. The initial values for the learnable parameters $\beta$ and $\gamma$ in the loss function were set to 0.0 and −3.0, respectively, while $\lambda$ was set to 0.5.

4.2.2. Baselines

We selected several superior end-to-end visual localization methods for comparison with our proposed method, including PoseNet, MapNet, AtLoc, and RobustLoc. These methods exhibit good performance in end-to-end localization under uni-modal conditions using visible images, hence their suitability for benchmarking against our proposed method to validate its effectiveness. However, since their models are only capable of processing uni-modal data, when handling multimodal data simultaneously, the two input images need to be concatenated along the channel dimension, resulting in a doubling of the channel number. Consequently, we doubled the number of input channels in the feature extraction components of these models to accommodate the adaptive training and testing of multimodal data.

4.3. Localization in Multi-Scale Urban Scenes

In the dataset we collected, there are scenes featuring roads with dynamic vehicles and pedestrians, as well as scenes with drastic illumination changes, posing significant challenges to visual localization tasks. Traditional visual localization methods often fail to adapt well to dynamic scenes and complex lighting conditions. Our multimodal fusion localization approach leverages the complementarity between visible and infrared information to achieve robust localization in dynamic scenes and under complex lighting conditions. Saliency map analysis also demonstrates the focus of our proposed method on different modalities, verifying the effectiveness of our approach.

Table 2. Mean and median errors of different methods in large scenes (m/°).

Scenes	Large-Loop1		Large-Loop2 (Night)		Average
	Median	Mean	Median	Mean	Median	Mean
PoseNet	$6.04/0.74$	$7.57/2.40$	$3.26/-$	$4.83/-$	$4.65/0.74$	$6.20/2.40$
MapNet	$15.85/3.29$	$19.14/5.59$	$12.45/-$	$14.97/-$	$14.15/3.29$	$17.06/5.59$
AtLoc	$3.20/0.67$	$5.17/2.40$	$3.36/-$	$4.27/-$	$3.28/0.67$	$4.72/2.40$
RobustLoc	$3.77/0.80$	$4.83/2.66$	$\mathbf{1}.\mathbf{24}/-$	$1.94/-$	$2.51/0.80$	$3.39/2.66$
(Ours)	$\mathbf{2}.\mathbf{84}/\mathbf{0}.\mathbf{44}$	$\mathbf{3}.\mathbf{53}/\mathbf{2}.\mathbf{18}$	$1.30/-$	$\mathbf{1}.\mathbf{47}/-$	$\mathbf{2}.\mathbf{07}/\mathbf{0}.\mathbf{44}$	$\mathbf{2}.\mathbf{50}/\mathbf{2}.\mathbf{18}$

The error marked in bold is the minimum error in that column, and the same applies to subsequent tables.

and

Table 3. Mean and median errors of different methods in small scenes (m/°).

Scenes	Small-Loop		Small-Loop-Oppo		Small-Loop-Night		Average
	Median	Mean	Median	Mean	Median	Mean	Median	Mean
PoseNet	$0.81/3.38$	$0.95/4.18$	$1.16/\mathbf{3}.\mathbf{36}$	$3.17/7.78$	$3.49/2.93$	$3.64/4.21$	$1.82/3.22$	$2.59/5.39$
MapNet	$2.30/6.61$	$2.57/8.20$	$2.61/6.64$	$3.99/10.82$	$4.69/3.12$	$4.88/4.06$	$3.20/5.46$	$3.81/7.69$
AtLoc	$0.88/\mathbf{2}.\mathbf{53}$	$0.99/\mathbf{4}.\mathbf{10}$	$1.39/3.83$	$2.93/6.67$	$3.49/3.72$	$3.68/4.40$	$1.92/3.36$	$2.53/5.06$
RobustLoc	$0.83/3.15$	$1.21/4.31$	$1.22/3.81$	$2.60/7.38$	$3.51/3.24$	$3.62/4.37$	$1.85/3.40$	$2.48/5.35$
(Ours)	$\mathbf{0}.\mathbf{69}/2.93$	$\mathbf{0}.\mathbf{83}/4.28$	$\mathbf{1}.\mathbf{00}/3.55$	$\mathbf{2}.\mathbf{09}/\mathbf{5}.\mathbf{89}$	$\mathbf{3}.\mathbf{27}/\mathbf{2}.\mathbf{66}$	$\mathbf{3}.\mathbf{50}/\mathbf{3}.\mathbf{52}$	$\mathbf{1}.\mathbf{65}/\mathbf{3}.\mathbf{05}$	$\mathbf{2}.\mathbf{14}/\mathbf{4}.\mathbf{56}$

presents a comparison of the pose regression accuracy between our proposed method and other state-of-the-art methods, including PoseNet, MapNet, AtLoc, and RobustLoc, across large and small scenarios. Figure 5 presents a comparison of localization trajectory maps obtained by different methods across various scenarios. It is evident from visual inspection that our proposed method demonstrates superior performance in terms of localization trajectories in each scenario. Specifically, it exhibits the lowest number of outliers, coupled with relatively smaller maximum values of localization errors.

4.3.1. Localization in Large-Scale Urban Scenes

Localizing in large-scale, long-route urban environments remains a significant challenge for conventional methods. Matching-based approaches typically require pre-constructed databases, which scale rapidly with the size of the environment, leading to substantial increases in storage and computational demands. As a result, these methods become costly and inefficient, limiting their practicality in real-world urban deployments. Similarly, ORB-SLAM-based methods struggle in large-scale settings, as they often fail to extract effective feature points at long distances, resulting in frequent tracking failures. To overcome these limitations, we propose a novel end-to-end pose estimation framework that fuses infrared- and visible-light information, enabling robust localization in large urban scenes without reliance on traditional feature matching or database-driven approaches. We evaluate our method on two large-scale datasets: Large-loop1, a daytime dataset consisting of 42,486 training images and 24,397 testing images over a route of approximately 3500 m, and Large-loop2, a nighttime dataset containing 24,298 training images and 11,780 testing images over a 1750 m route.

As shown in Table 2 and Table 3, our method consistently outperforms existing approaches in terms of mean localization error across all large-scale scenarios. For clarity, we compare our method with the best-performing baseline in each case. Specifically, in the Large-loop1 scenario, our method achieves a 26.9% reduction in mean localization error compared to RobustLoc. In the Large-loop2 scenario, the error is reduced by 24.2% over the same baseline.

Across both large-scale experiments, our method consistently delivers superior pose estimation accuracy. Comparative trajectory analyses further confirm our method’s robustness, exhibiting the fewest localization outliers and the smoothest trajectory reconstructions. These quantitative and qualitative results highlight the effectiveness of our approach under diverse lighting conditions and its potential for real-world deployment in complex urban environments.

4.3.2. Localization Across Different Lighting Conditions

To comprehensively evaluate the robustness of the proposed method under varying lighting conditions, we conducted data collection and experiments at different times of day. Three data collections were carried out:

• Small-loop, collected during the daytime, includes 5959 training images and 2684 testing images, covering a route of approximately 210 m.
• Small-loop-oppo, a reverse traversal of the same loop also collected during the daytime, contains 5588 training images and 2931 testing images.
• Small-loop-night, collected at night, comprises 6190 training images and 2878 testing images, with a route length of approximately 210 m.

In these experiments, our method consistently outperforms the state-of-the-art baselines. Specifically, in the Small-loop scenario, it achieves a 12.6% reduction in mean localization error compared to PoseNet. In the Small-loop-oppo and Small-loop-night scenarios, it reduces the mean localization error by 19.6% and 3.3%, respectively, compared to RobustLoc. On average, across both large-scale and small-scale scenes, our method achieves superior performance in both localization and attitude estimation. In large-scale scenarios, it reduces the mean localization error by 26.3% and the mean attitude error by 18.0% compared to RobustLoc. In small-scale scenarios, it reduces the mean localization error by 13.7% and the mean attitude error by 14.8%. Note: Due to the absence of ground-truth attitude data for the Large-loop2 scenario, only translational errors are reported for that case.

In this series of experiments, our method demonstrates consistent advantages in terms of both localization and orientation estimation compared to the existing baselines. The trajectory analysis shows comparable performance between our method and traditional approaches in the Small-loop (daytime) and Small-loop-night scenarios, where limited scene size and stable environmental conditions reduce the occurrence of major outliers. However, in the more challenging Small-loop-oppo scenario—featuring reverse traversal and increased environmental disturbances—our method exhibits significantly enhanced robustness. While existing methods are prone to large deviations in challenging segments (e.g., sharp turns or occluded areas), our approach maintains smoother and more consistent trajectory estimates with notably fewer outliers. These results highlight the effectiveness of our multimodal fusion strategy in handling directional changes and transient environmental variations in constrained operating environments.

4.4. Salience Map Analysis

As illustrated in Figure 6, we conducted a saliency map analysis on the proposed method. It was observed that in dark scenes (first row), the method effectively concentrates the attention of the visible-light image modality on the illuminated portions of streetlights, while the infrared image, leveraging its inherent imaging advantages, processes the contour structure of the overall scene. Consequently, our proposed method can still achieve robust scene modeling through multimodal learning in dark environments. Under normal lighting conditions, depicted in the second row, our multimodal fusion model pays greater attention to the edge feature information in the infrared images and focuses more on the overall texture features in the visible-light images. This complementary fusion of information from both modalities significantly enhances the robustness of pose estimation. Analyzing the saliency map in the third row, it is evident that even in environments where vehicle headlights interfere with ambient light, we can still rely on the light-insensitive nature of infrared images to capture the environmental edge features in overly illuminated areas, thereby enabling robust localization under dynamic lighting conditions.

4.5. Robustness in Fog and Rain

To further validate the robustness of our proposed method under extreme environmental conditions, we conducted comprehensive evaluations in fog and rain scenarios. The experimental results demonstrate that our approach maintains superior performance across varying intensities of both weather conditions. The original Small-loop dataset was artificially modified to simulate weather degradation, as visualized in Figure 7: the first row depicts clear weather, light mist, moderate fog, and thick fog; the second row shows clear weather, light rain, moderate rain, and heavy rain. For extreme weather cases, we benchmarked against two state-of-the-art robust methods: AtLoc and RobustLoc. As quantified in

Table 4. Mean errors of VIFPE, AtLoc, and RobustLoc under challenging weather conditions (m/°).

	Sunny	Fog			Rain			Average
Methods	-	Light	Moderate	Thick	Light	Moderate	Heavy	-
AtLoc	0.99/4.10	1.00/4.15	1.11/4.07	1.39/4.39	1.73/5.54	1.80/5.67	1.81/5.58	1.40/4.79
RobustLoc	1.21/4.31	1.22/4.25	1.23/4.29	1.38/4.67	1.22/4.29	1.24/4.38	1.26/4.46	1.25/4.38
VIFPE (Ours)	0.83/4.28	0.84/4.27	0.88/4.27	1.16/4.94	0.85/4.35	0.87/4.42	0.89/4.37	0.90/4.41

, our method consistently achieves higher pose regression accuracy across all fog/rain intensities, outperforming both comparative approaches. The results revealed that our proposed method excelled in localization accuracy, demonstrating an average improvement of 28% compared to RobustLoc, while achieving comparable performance in terms of orientation estimation. This substantiates that our framework effectively fuses infrared and visible features to ensure reliable localization under challenging weather conditions.

4.6. Ablation Study

4.6.1. Ablation Study into Fusion Strategies

To validate the superiority of our fusion method, we designed various multimodal localization approaches based on different fusion strategies for comparison during the experimental process. From the perspective of pose estimation results, our proposed method outperforms the localization methods designed based on other feature fusion strategies. These methods, designed based on distinct feature fusion strategies, include the following:

1.

Multimodal Fusion Localization Method Based on Mixture of Experts (MOE): This method employs MaxViT as the backbone network for feature extraction. Subsequently, the Mixture of Experts system models the correlation between two uni-modal localization tasks, thereby fully exploiting the task correlation to achieve task fusion across different modalities.

2.

Localization Method Based on DATFuse for Image Fusion (DATFuse): Combining this fusion method, we utilize the Dual Attention Residual Module (DARM) and Transformer Module (TRM) to initially extract features and model long-range dependency information for the two images during the fusion process. Subsequently, MaxViT is used as the backbone network for further feature extraction and regression, yielding the fused localization results.

3.

Localization Method Based on Cross-Attention Mechanism(CAM) for Image Fusion: The effectiveness of the feature fusion method based on the cross-attention mechanism in the field of image fusion has been thoroughly verified [39]. This method enhances complementary information and reduces redundant information during the image fusion process, facilitating efficient fusion of the two images. By integrating cross-attention with MaxViT, we designed a multimodal fusion localization framework and conducted training and testing based on double-loop data.

Table 5. Median and mean errors of frameworks based on different feature fusion methods (m/°).

	Large-Loop1		Small-Loop
Methods	Median	Mean	Median	Mean
MOE	4.49/0.85	5.89/2.72	1.22/3.88	1.70/4.95
DATFuse	3.0/0.41	4.49/2.11	0.78/3.46	1.01/5.10
CrossFuse	4.21/0.46	5.04/2.19	0.72/4.09	0.85/5.45
VIFPE (Ours)	2.84/0.44	3.53/2.18	0.69/2.93	0.83/4.28

presents a comparison of pose estimation errors between our proposed method and the aforementioned fusion approaches, demonstrating the superior performance of our method. Our ablation studies were all validated on the Large-loop1 dataset as it had the longest route length, complex road conditions, and diverse illumination scenarios, which collectively render it suitable for comparing various feature fusion techniques.

4.6.2. Ablation Study into Feature Extractors

To examine the influence of various feature extractors on pose estimation, we selected representative backbone networks currently employed for feature extraction for comparative analysis. Our validation confirms that the method proposed within this framework exhibits optimal performance. The comparative results are based on evaluations conducted using double-loop data.

Table 6. Median and mean errors of frameworks based on different feature extractors (m/°).

	Large-Loop1
Methods	Median	Mean
EfficientNet-B0	3.49/0.50	5.28/2.28
EfficientNet + Transformer	3.32/0.45	4.61/2.56
VIFPE (Ours)	2.84/0.44	3.53/2.18

presents the test results of the aforementioned methods and our proposed method on this dataset, demonstrating that our proposed method achieves the best performance in terms of pose estimation accuracy.

4.6.3. Ablation Study into Size of Attention (q and T)

To verify the impact of variations in our parameters q and T on pose estimation, we conducted ablation experiments with different pairs of q and T values. In our proposed method, q = T = 7, referencing the dimensions used in the Swin-Transformer. Therefore, during the process of varying q and T, we maintained q = T to ensure a balanced computational load between block and grid attention. In the experiments, we adopted parameter settings of q = T = 4 and q = T = 8, respectively. For the data from the Small-loop route, our final ablation experiment results are as shown in

Table 7. Median and mean errors of frameworks based on different pairs of q and T (m/°).

	Small-Loop
q/T	Median	Mean
4/4	0.72/3.36	0.92/4.84
8/8	0.71/3.06	0.84/4.31
7/7 (Ours)	0.69/2.93	0.83/4.28

. According to the results, when q and T are configured as q = T = 7, the pose estimation accuracy can achieve a relatively high level.

5. Conclusions

This work proposes an end-to-end robust localization method that fuses visible and infrared information. Initially, features are extracted from images of the two modalities using two MaxViT models, enabling the fusion and extraction of both global and local image features. Subsequently, attention-weighted feature fusion is performed at the feature level to obtain integrated scene features. These features are then passed through a regression module to estimate pose information. During training, a multi-task learning strategy is incorporated to optimize the pose estimation results, achieving robust and precise localization using multimodal data. To validate the method, practical measurements are conducted in various illumination and route scenarios collected independently. Saliency map analysis demonstrates that the proposed method effectively complements infrared and visible information under varying illumination conditions. Our experimental results yield smaller translation and rotation error estimates, proving the superiority of the proposed method compared to existing end-to-end visual localization approaches.