Abstract
This paper presents an integrated approach for optimizing the performance of a 36-pulses converter system by using artificial intelligence (AI) techniques to be included in a Supervisory Control and Data Acquisition (SCADA) environment. The focus of the proposal is on enhancing harmonic reduction through intelligent adjustment of switching angles and coordinated control of the reinjection transformer included in the power converter topology. A key component of the proposed methodology involves a simulation-based process to determine optimal firing angles (, , and ), based on Selective Harmonic Elimination (SHE) theory, that minimize Total Harmonic Distortion (THD). Using MATLAB with Simulink and PLECS models, a parametric sweep of the firing angles, generating a comprehensive dataset of THD outcomes. This dataset, consisting of THD evaluations across fine-grained angle variations, serves as the training foundation for supervised machine learning models—specifically, neural network regressors—that approximate the nonlinear mapping between firing angles and harmonic distortion. These predictive models are then employed as surrogates to estimate THD rapidly and guide the selection of optimal switching angles in real time without requiring iterative numerical solvers. Optimization heuristics and predictive models are then deployed to dynamically adapt system parameters in real time under varying load conditions. The proposed method demonstrates significant improvements in power quality and operational reliability, highlighting the potential of AI-assisted SCADA systems in advanced power electronics applications. Implementation results performed on a 36-pulses voltage source converter prototype are included to illustrate the appropriateness of the proposal.
1. Introduction
One of the persistent issues in current power electronic systems is the high level of Total Harmonic Distortion (THD) presented in points of load coupling. This high THD adversely affects efficiency, stability, and compliance with power quality standards. The growing integration of power converters in modern electrical systems demands advanced harmonic mitigation techniques to maintain power quality and ensure system reliability [1,2]. THD remains a key performance indicator, quantifying the extent of harmonic pollution introduced by power electronic devices into electrical systems [3]. Neutral Point Reinjection (NPR) has emerged as an effective strategy for reducing THD in power electronic inverters, particularly in high-pulses configurations such as the 36-pulses topology. The technique of injecting a common-mode voltage at six times the fundamental frequency into the system’s neutral point has been shown to facilitate harmonic cancelation without increasing the number of active switches, as reported in [4] and references therein. When applied to a 36-pulses converter, which inherently offers harmonic suppression through phase-shifted multi-winding transformers, NPR further enhances waveform quality and THD performance. This enables the design of high-performance, medium-voltage converters with improved efficiency and reduced component count, making it a cost-effective and scalable solution for advanced power systems. Traditional harmonic elimination techniques, such as Selective Harmonic Elimination (SHE), rely heavily on analytical solutions and exhaustive computational methods, which may become impractical for complex and rapidly varying systems. Recent advancements in artificial intelligence (AI) and machine learning (ML) provide promising avenues to optimize switching strategies dynamically and efficiently [5]. AI-driven approaches can learn nonlinear relationships between control parameters and harmonic outputs, enabling real-time adaptation to load variations and system perturbations. Specifically, neural-network-based regression models have demonstrated a remarkable capacity to predict and minimize THD, surpassing traditional heuristics in both accuracy and computational speed [6]. Incorporating AI into harmonic control not only enhances power quality, but also reduces computational burden, facilitating implementation within SCADA environments for intelligent monitoring and control [7]. The novelty of this work lies in the application of artificial intelligence (AI) techniques—specifically neural-network-based optimization of Neutral Point Reinjection (NPR)—to enhance harmonic performance in 36-pulses converters. The proposed approach integrates SHE and optimizes the transformer ratio of the NPR stage. This synergistic integration contributes to obtain a more intelligent, robust, and practical power electronic systems, representing a distinctive step beyond existing harmonic mitigation strategies.
2. Methodology
The traditional twelve pulses converter illustrated in the left part of Figure 1, with two three-phase six-pulses inverters enclosed in red and green boxes connected with a common neutral point, is the basis for this work.
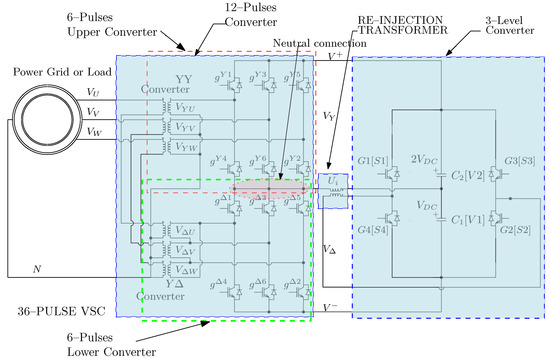
Figure 1.
The 36-pulses voltage source converter (modification of circuit presented in [8]).
It is possible to define the transfer function for the upper six pulses converter with YY connection in any of the three phases shifted by rad. We use the as an example of the transfer function value, which is defined in the left part of Figure 2, and illustrated in the right part of the same figure.
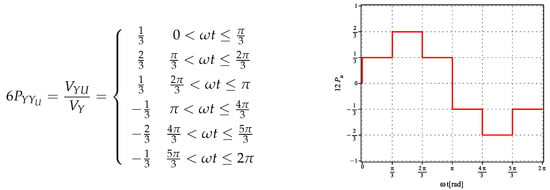
Figure 2.
Six-pulses transfer function definition and unit step response.
The Fourier series of this function is given by an infinite number of sinusoids [9], with frequencies in positions with .
The theory of SHE indicates that we can eliminate the most important harmonics by using pulse width modulation inverters initiating with two-level inverter [10]. For quarter wave symmetry Fourier coefficients, and are zero, while will exist only for odd harmonics. So, the first step in using Selected Harmonic Elimination, is to find the angle to eliminate the third harmonic and its multiples. To do so, and by using as the period of the signal, we can begin by using the following expression:
For canceling the third harmonic, we need to solve , which gives , and the shape can be gotten by using a six-pulses converter with connection, which is obtained with lower six-pulses converter.
The transfer function for the lower six-pulses converter with a three-phase transformer with a transformer ratio of 1: connected in is illustrated in Figure 3, and its Fourier series is the following [9]:
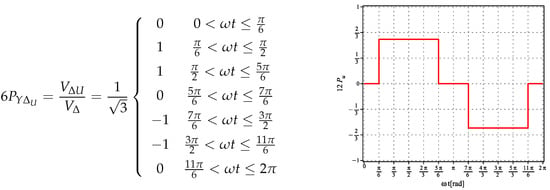
Figure 3.
Six-pulses transfer function definition and unit step response.
It is important to take into consideration that the obtained is shifted by , which must be compensated via the switching pattern used for controlling the gates of the switches used.
Adding Equation (3) to (1), harmonics on the positions with are eliminated. This is obtained by traditional twelve-pulses converter illustrated on the left part of Figure 1 where the summation is performed via the transformers at the output connected in series, and the transfer function and unit step response are depicted in Figure 4.
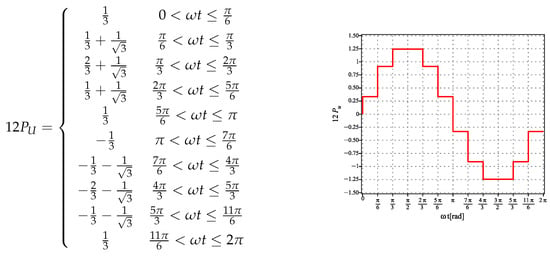
Figure 4.
Twelve-pulses transfer function definition and unit step response.
The Fourier expression for this transfer function is (4), that corresponds to a THD of around , with harmonics on the positions with eliminated [9].
The purpose of this proposal is to use NPR strategy along with the concepts of SHE to reduce the THD of the 36-pulses converter and leave it ready for SCADA systems.
Reinjection Through Neutral Point
The NPR at six times the fundamental frequency comes from the fact that a three-phase system can feed a three-phase full-wave rectifier in positive or negative configurations [11,12], giving an increase on the amplitude of the signal obtained, as presented in Figure 5a. This figure is labeled as Figure 5b, where the positive and negative rectified signals appear in thick black color. The positive thick red signal corresponds to the ideal , and the negative thick blue signal corresponds to the ideal that should be generated to eliminate all the harmonic content in a three-phase inverter.
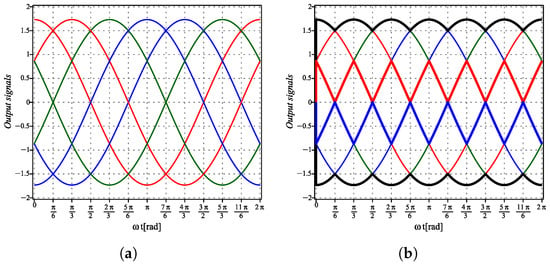
Figure 5.
Ideal reinjection. (a) Signal equivalent basis for three phase full wave rectifier. (b) Positive and negative rectified signals (thick black) with signals for ideal reinjection (thick red and blue).
The strategy of NPR at six times the fundamental frequency has been proven to be an excellent way to reduce THD in several applications, going from StatCom [13] to induction motor drive development [8,14,15]. As this quasi-triangular signal is not easy to be generated by power converters, the use single-phase staircased multi-level inverters is the common strategy to follow. As a multi-level inverter has positive and negative values, but considering that the input to the both six pulses converters of the left part of Figure 1 have to be positive because of the type of transistors, it is needed to generate the and from the summation of the multi-pulse signal obtained with a direct current (DC) level offset to prevent any negative part to enter to the six-pulses converters. This is illustrated in the right part of Figure 1 with the presence of capacitors and as DC sources.
The six-pulses signal of Figure 3, presented in Equation (3) removed a big amount of harmonic content on the signal output of Figure 2, when they are added in series. As generating the ideal quasi-triangular signals , and illustrated in Figure 5 at six times the frequency of the fundamental is not an easy task, on this strategy we combine a three level signal, similar to (3) but with higher frequency to produce a 36-pulses signal output. Then, we pursue a correction on the area that the quasi-triangular signal has and the one generated on the three-level converter as input to the twelve pulses to eliminate some extra pulses associated with SHE to reduce the harmonic distortion, as presented in Figure 6.
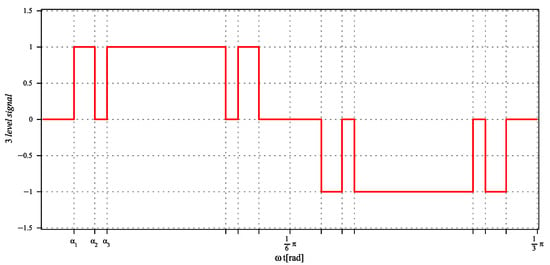
Figure 6.
Three-level reinjection signal proposed with angles , , and to be optimized.
3. AI Approach for Firing Angle Optimization
In this section, the procedure for obtaining the optimal firing angles , , and in the 36-pulses converter is described. This is performed by using AI-based methods, particularly using artificial neural networks multi-layer perceptron (MLP) combined with parameter optimization and supervised regression framework.
The complete flow AI-based optimization process is presented in the flow diagram of Figure 7, which is described in the following subsections. Furthermore, the implementation of this framework was carried out using Python 3.8.5.
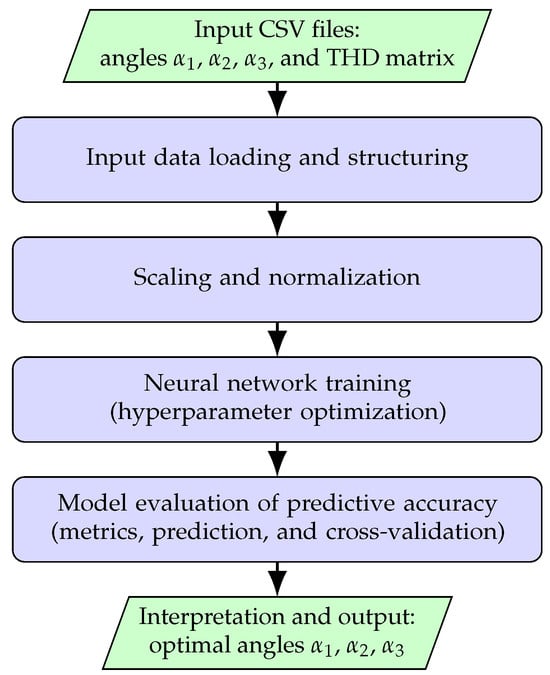
Figure 7.
Flow diagram of the optimization pipeline for determining the switching angles , , and that minimize THD.
3.1. Input CSV Files
The procedure begins by obtaining a data set of simulation using MATLAB R2024a, Simulink 24.1, and PLECS 4.9.6 of the 36-pulses converter. In this simulation, is incrementally adjusted within the interval radians using a fine step of radians. In each increment of the angle , the values of the remaining angles are , and . The values of the three angles, and the THD are captured on each simulation time. The main goal for this simulation stage is to obtain the data set that involves the nonlinear relationship between the combination of the firing angles and the THD given by the 36-pulses converter. The result of this simulation generates four output files in CSV format, corresponding to , , and , each comprising , and for the THD measurements obtaining a matrix of . The simulations runs with a fixed step of seconds and executes for a total duration of s, utilizing the ode45 (Dormand–Prince) solver. This dataset is considered sufficiently rich in dynamics, such that the proposed AI framework can determine the optimal firing angles.
3.2. Input Data Loading and Structuring
The CSV files data are loaded using the NumPy arrays to store in python the values of the three angles and THD. The files are read using Pandas library [16] and converted into flattened, one-dimensional arrays to facilitate subsequent processing. The dimension security is checked to guarantee data consistency and to ensure that the length of angle vectors match with the number of columns in the THD matrix. This is according to the number of values of each angle in the simulation process. After confirming the data consistency, the vectors are combined to form the matrix and a vector . This information is used to train the regression model that captures the nonlinear relation between the firing angles and the THD. Additionally, specific exceptions are raised for missing files, mismatched dimension, or passing error to prevent invalid data.
3.3. Scaling and Normalization of Input Data
To prepare the dataset for the training, it is necessary to transform the data already loaded into a specific numerical scale. This is needed to improve convergence speed, enabling reproducibility and reducing numerical instability of the involved variables [17,18]. Then, the MinMax normalization process is applied to each loaded variable, such that each value of angle and THD are in the range . With this, it is possible to facilitate the optimization and the improvement on the consistency of the training.
The resulting normalization process is displayed in Table 1. The normalized values are used in the next process for neural network training.

Table 1.
Minimum and maximum ranges for each variable in the normalization process.
3.4. Neural Network Model Training
The neural network proposed for obtaining the optimal angles is the MLP due to its versatility and efficiency when it is used in a regression framework with complex nonlinear relationships in inputs and outputs [19], as is the case of the firing angles and THD of the 36-pulses converter.
The neural network model proposed in this work proposal has the following characteristics:
- Input layer: three neurons are proposed representing the firing angles , , and .
- Hidden layers: two hidden layers are needed, with the following features:
- –
- First hidden layer with 128 neurons, with ReLU as the activation function. This is designed to capture the nonlinear interactions among the input angles.
- –
- Second hidden layer with 64 neurons, also using the activation function ReLU. This is to improve generalization and to form higher-level abstractions.
- Output layer: in this case, one neuron with linear activation function is used. This is suitable for continuous regression of the THD values.
- Training algorithm: the MLP was trained under a supervised regression framework using a dataset of 1500 switching angle–THD pairs. All inputs were normalized to , and the data were divided into training (70%), validation (15%), and testing (15%) subsets. The Adam optimizer [20] was employed to adapt learning rates per parameter, minimizing the mean squared error (MSE) loss between THDpredicted and THDreal. The model performance was assessed using the mean absolute error (MAE) and the coefficient of determination (), achieving and MAE on the test set. Once trained, the MLP surrogate model provided millisecond-scale inference for candidate switching angles, enabling efficient exploration of the search space without full harmonic computation and facilitating integration into SCADA systems for online THD minimization. To ensure efficient convergence and robust generalization while maintaining low computational requirements compared to traditional Fourier-based evaluations, the following hyperparameters were adopted: optimizer: Adam; learning rate ; batch size ; max. epochs ; loss function: MSE; dropout rate .
3.5. Model Evaluation
Once the neural network training is performed, the predictive performance is obtained by means of the neural network evaluation. This consists of quantifying regression accuracy and verifying the ability of the model to generalize the unseen configurations. For this, two metrics were used to compute the accuracy [21]: the mean absolute error (MAE), which measures the average magnitude of predictions deviations, and is robust to outliers, which is obtained as follows:
and the root mean squared error (RMSE) that reflects the variance in prediction quality, and is computed as follows:
where n is the total number of test samples; , is the index of each individual sample; the current value of THD obtained for the i-th sample; and the predicted value of THD by the model for the i-th sample.
Figure 8 depicts the vs. as scatter plots and reveals a high correlation degree and low prediction error across the full range of angle configurations.
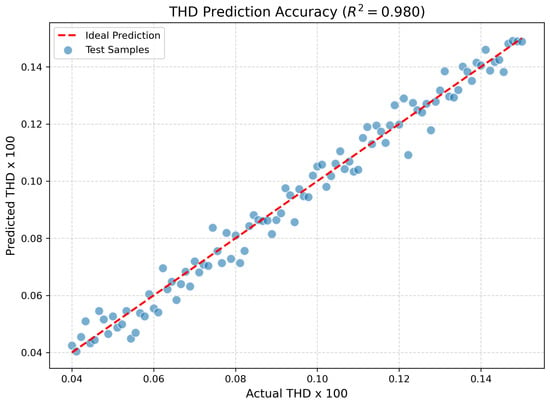
Figure 8.
Predicted vs. actual THD values on test data.
Additionally, the coefficient of determination ( Score) is computed. This coefficient quantifies the proportion of the variance in the target variable that is predictable from the input variables [22]. This is calculated as follows:
where denotes the mean of the true values. When , it means perfect prediction, while means that the model performs no better than simply predicting the mean of the observed data. Table 2 show the performance on the test set with different metrics.

Table 2.
Model performance on test set.
The results of Table 2 give confirmation that the proposed neural network model captures the nonlinear relations between the firing angles and THD of the 36-pulses converter. Furthermore, the values demonstrate that the predictions are reliable.
3.6. Optimal Switching Angles
Now, the optimal switching angles values are obtained and the resulting THD. These are shown in Table 3. Compared to the baseline minimum THD in the original dataset, the optimized THD value is . This confirms the improvement in the neural network for the firing angles.

Table 3.
Optimal switching angles and predicted THD.
These optimized angles can be directly applied to the 36-pulses converter in real-time to obtain the minimum THD value shown in Section 4.
3.7. Explanation of Execution Times
In this section, the analysis of the training process is presented, and Table 4 summarizes the execution times measured for each stage of the optimization and evaluation workflow. These times reflect the computational effort required by each Python script described previously. Below, each process is interpreted in the context of the corresponding .py program and the operations performed:
- Load Data (0.2159 s): this stage corresponds to the script that loads the CSV files containing the vectors of switching angles (, , ) and the matrix of THD results. The time remains very short because the operations mainly involve reading CSV files into memory and performing simple assertions to verify their dimensions. Since no heavy computations or iterations occur, the load time is well below one second.
- Normalization (0.2505 s): the normalization step applies a MinMaxScaler to rescale the feature matrix and the target vector to the interval [0,1]. This operation is computationally light because it only requires computing the minimum and maximum of each column and rescaling the values linearly. The execution time remains low as the dataset is relatively small (1001 samples and 3 features).
- Training (270.1720 s): this is by far the most time-consuming process and corresponds to the train_best_model() function, which uses Optuna hyperparameter optimization. The high execution time is mainly due to the following:
- –
- Performing 50 Optuna trials, each training a neural network with different configurations (number of layers, neurons, dropout rates, L2 regularization).
- –
- Training each network for up to 100 epochs.
- –
- Sequential evaluation of each configuration to identify the best combination of hyperparameters.
This combination of extensive hyperparameter search and repeated deep learning training loops explains why this step alone accounts for more than 95% of the total runtime. - Evaluation (0.9102 s): the evaluation step involves loading the trained model, making predictions on the dataset, denormalizing the outputs, and calculating regression metrics such as MAE and RMSE. This process is relatively fast because model inference is only a forward pass without weight updates. The time is slightly higher than loading or normalization because it also generates and saves prediction and error distribution plots.
- Cross-Validation (9.4400 s): this process performs fivefold cross-validation, training 5 separate models (one per fold). Each model uses the same architecture but is trained independently. The total time is higher than evaluation but much lower than Optuna training because of the following:
- –
- Each fold is trained for a maximum of 50 epochs.
- –
- No hyperparameter search is performed (the model configuration is fixed).
The process is still slower than loading and evaluation because each fold requires a complete training cycle. - Interpretation (0.9102 s): the interpretation script loads the model, generates predictions, identifies the optimal angle combination, and produces visualizations of the relationship between the switching angles and the predicted THD. Here, the time is comparable to the evaluation stage because it includes prediction and plotting steps.
Overall, the total execution time was approximately 282 s, with more than 95% of this duration attributable to the hyperparameter optimization conducted by Optuna during model training. This behavior is expected in machine learning workflows, where loading, normalization, and evaluation require minimal resources, while training and optimization consume significantly more computational effort.
These execution times depend upon factors such as dataset size, number of hyperparameter trials, and whether GPU acceleration is used. To reduce total time, the possible strategies include limiting the number of trials or epochs, parallelizing Optuna optimization, or leveraging dedicated hardware for acceleration.
The flowchart of Figure 7 visually represents the sequential stages of the optimization pipeline for determining the optimal switching angles , , and that minimize the THD. Each block in the diagram corresponds directly to one of the measured processes reported in Table 4.

Table 4.
Execution times of each optimization process.
Table 4.
Execution times of each optimization process.
| Process | Execution Time (s) |
|---|---|
| Load data | 0.215945 |
| Normalization | 0.250546 |
| Training | 270.1720 |
| Evaluation | 0.910192 |
| Cross-validation | 9.440011 |
| Interpretation | 0.910244 |
| Total | 281.8990 |
4. Results
This section presents the experimental results obtained from a laboratory prototype of the 36-pulses converter, whose configuration is shown in the diagram of Figure 1 and depicted in Figure 9. Since the main objective of this research is to optimize the switching angles (listed in Table 3) for the SHE strategy, we illustrate the stepwise evolution of the converter output under the proposed approach.

Figure 9.
The 36-pulses lab prototype for testing the strategy.
In the proposed experimental setup, the primary controlled variable was the output voltage of the 36-pulses inverter, which was regulated by minimizing the THD. The associated control variables were the firing angles, which were optimized specifically for THD minimization. This configuration ensured consistent operating conditions for evaluating the effectiveness of the proposed method.
Figure 10 shows the baseline performance of the 36-pulses converter, which combines a three-level inverter, a reinjection transformer, and a 12-pulses configuration with a neutral point connection. At this stage, no optimization has been applied to the transformer, no SHE strategy is implemented, and the switching angles remain unoptimized with , , and , which are the values to have standard three-level symmetric reinjection signal according to Figure 6. The waveform clearly reflects the dominant twelve-pulses structure, characterized by significant voltage steps. However, the inclusion of the three-level inverter introduces a relatively low ripple between these steps. The THD for this signal is around 12.8%.
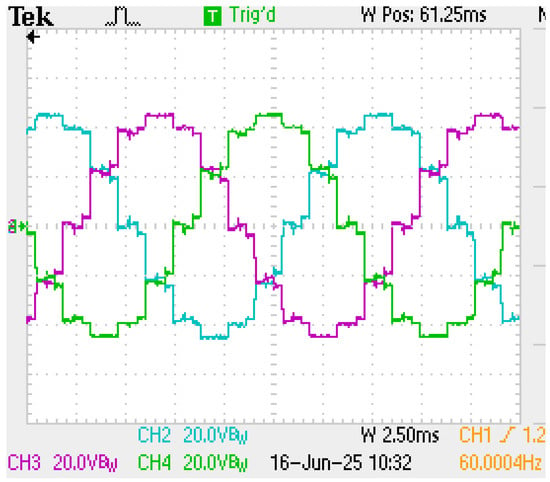
Figure 10.
Original 36-pulses waveform as the result of the connectivity presented in Figure 1.
The first step in the optimization process focused on the reinjection transformer. In this stage, the number of turns in the secondary winding was fixed at 10,000, while the primary winding was varied from 3200 to 3300 turns. By measuring the Total Harmonic Distortion (THD) across this range, the optimal configuration was found at 3275 turns, corresponding to a transformer ratio of approximately 144.1:440. From this training and simulation process, the optimal firing angles that minimized the THD were obtained, and these values were subsequently used in the experimental implementation. However, due to physical component availability, a transformer with a ratio of 127:440 was ultimately used for implementation. With this strategy, the previously observed voltage steps are significantly reduced, as shown in Figure 11. What previously appeared as noise now manifests as an increase in the number of visible pulses. Although the signal corresponds to a 36-pulses waveform, some pulses appear wider than others, producing a signal very similar to the one of 24-pulses with a THD of around 8.1%. This effect may result from the rise/fall times of the switching devices, combined with the dead time implemented in the switching scheme.
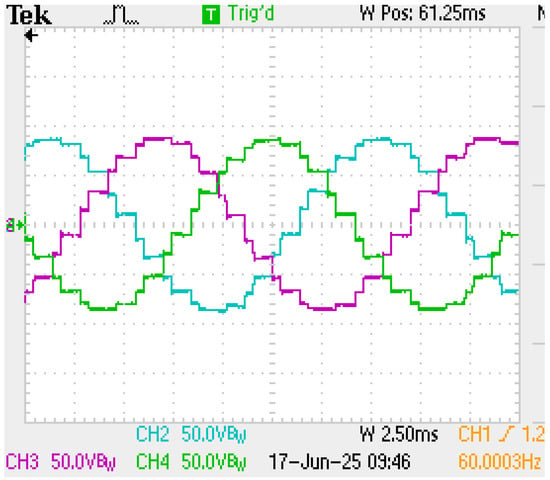
Figure 11.
The 36-pulses waveform with reinjection transformer optimized.
Next, the SHE strategy is applied to eliminate specific harmonics in the reinjection signal. This corresponds to the implementation shown in Figure 6, although the switching angles , , and are still not optimized. The output waveform exhibits improved definition; however, a certain amount of noise remains, likely caused by the presence of narrow pulses and their separation from the wider pulses in the reinjected signal as presented in Figure 12. The THD obtained is around 5.14%.
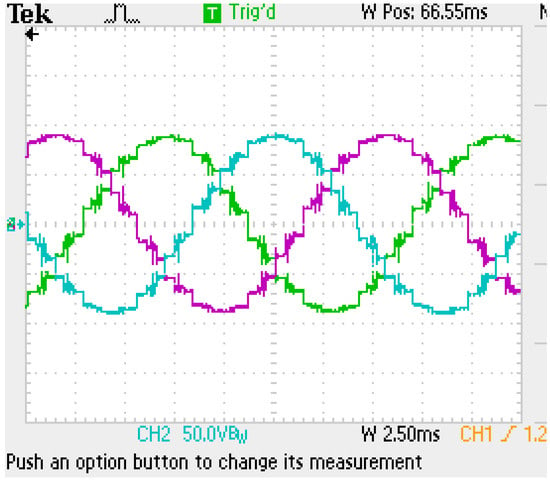
Figure 12.
The 36-pulses waveform with transformer optimized and three angles of the SHE strategy in the reinjection signal.
Finally, we combine the transformer optimization with the optimized SHE angles, obtaining the results shown in Figure 13. This figure demonstrates a significant improvement in pulses definition, although narrow pulses still appear at the edges of the wider ones. The THD obtained is around 5.09%. This outcome aligns with the harmonic reduction calculated in the previous section.
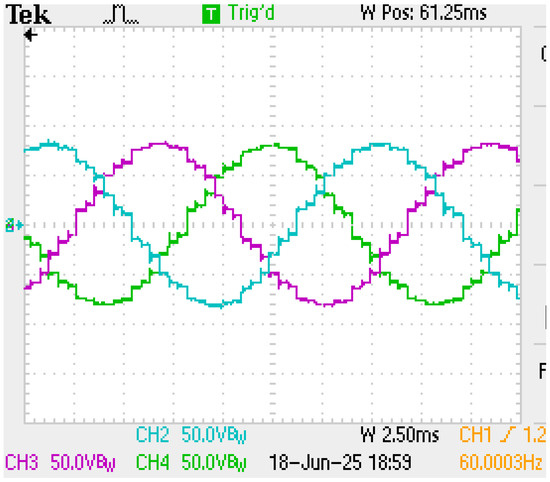
Figure 13.
The 36-pulses waveform with transformer and SHE angles optimized in the proposed strategy.
5. Discussion
In this work, an AI-based method correlation has been used, specifically MLP combined with parameter optimization and a supervised regression framework due to the fact that the switching angles and THD present a complicated and nonlinear relationship that can be difficult to treat with an analytically model. Furthermore, they have harmonic interactions due to the nature of the system design. The proposed neural network has demonstrated very good capabilities to absorb such nonlinear dependencies. The real-time results validate the benefits obtained in the present proposal. Furthermore, the use of Optuna hyperparameter optimization provides a very useful tool for the model architecture for obtaining the best predictive accuracy.
Alternative AI methods can be used for optimizing the switching angles to obtain the minimal THD, such as Genetic Algorithms, Bayesian Optimization, and so on. However, these techniques require many simulation runs and are even computationally expensive. A large space to obtain the necessary dataset for training the neural network is also required. Therefore, the AI-based approach used in this study provides very good prediction accuracy, computational efficiency, and model flexibility. Thus, this alternative of an AI-based optimization method results in a well-suited option where there are nonlinear complex dependencies between the variables that are related to the optimization process.
Although the numerical reduction in THD from to may appear marginal, its significance must be understood in the specific context of high-order multi-pulse converters. Systems of this type inherently operate with low distortion levels, where even slight improvements can determine compliance with international standards such as IEEE Std. 519 [23], which establishes strict limits of 5% for current and voltage distortion in low-voltage networks [24,25]. Therefore, a reduction of only in THD can be the difference between marginal non-compliance and full compliance in practical implementations. Beyond the numerical reduction, one of the main contributions of the proposed AI-based methodology lies in its predictive and adaptive capabilities. The trained neural surrogate enables the rapid inference of optimal switching angles without resorting to exhaustive numerical sweeps, with prediction times in the order of milliseconds. This feature makes the integration of the method into SCADA systems possible, allowing real-time adaptation of switching angles under varying load and grid conditions. Such adaptability enhances operational reliability and reduces the computational burden compared to traditional iterative approaches. Furthermore, recent works have shown that deep neural network surrogate models provide accurate and computationally efficient estimations of converter performance, enabling their use as fast optimization tools in power electronic design [26]. In this regard, the methodology presented here should not be evaluated solely by the incremental THD reduction, but by its ability to provide dynamic, real-time solutions that ensure compliance with harmonic standards, reduce computational costs, and extend scalability to converters of different pulse numbers and renewable energy applications.
To contextualize the proposed ANN-assisted optimization, Table 5 presents a qualitative comparison against classical and AI-based strategies reported in the literature. In particular, Newton–Raphson has been highlighted as a powerful tool for solving transcendental and nonlinear equations, though it may converge to local maxima and fail to identify the optimal switching angles [27]. Genetic Algorithms, on the other hand, are acknowledged as useful and powerful for minimizing THD, but they rely on a fixed population size throughout the evolutionary process [27]. Particle Swarm Optimization offers a good balance between accuracy and robustness, yet it remains computationally demanding for large systems [27]. Hybrid approaches such as ANFIS–PSO enhance robustness under voltage variations, though they require higher computational effort compared to classical PSO [28]. Surrogate-based models enable millisecond-scale inference, suitable for real-time SCADA integration, but depend on offline training and careful generalization [29]. Within this landscape, the proposed ANN-assisted method achieves competitive THD performance with real-time inference and enhanced robustness, making it especially promising for SCADA-based multi-pulse converter applications.

Table 5.
Qualitative comparison of classical and AI-based optimization methods for switching angle determination in multi-pulse converters.
Regarding real-time feasibility, it is important to clarify that the proposed ANN surrogate model was trained and executed offline to determine the optimal switching angles (, , and ) that minimize THD. The resulting angles are then applied to the 36-pulses converter, while the firing pulses continue to be generated by deterministic hardware at the microsecond level, ensuring that dynamic regulation is not affected. Nevertheless, the measured inference time of the trained model (approximately 1.7 ms for single prediction and sub-millisecond in batch mode) demonstrates that the approach is fully compatible with supervisory SCADA time windows. It should be emphasized that the ANN surrogate does not replace the microsecond-level hardware switching control; instead, it provides supervisory predictions at the millisecond scale. The measured inference times serve as test data, confirming that the method meets the timing requirements of SCADA-based supervisory control, without interfering with the converter’s fast dynamics.
Although neural networks are inherently black-box models, the proposed framework mitigates interpretability concerns by assigning the ANN only a supervisory role as a surrogate predictor of THD within the SCADA environment. The decision-making process of the converter remains under the SCADA supervisory logic, which cross-checks ANN predictions against direct harmonic measurements obtained from sensors. In cases of abnormal harmonics, discrepancies between predicted and measured THD values act as diagnostic indicators: large deviations suggest possible hardware or sensor faults, while systematic prediction errors point to model miscalibration. In addition, periodic retraining with updated datasets ensures that the ANN maintains reliable performance. This design allows abnormal situations to be effectively diagnosed while preserving the real-time benefits of ANN-based optimization.
It is important to note that while the ANN surrogate model is deployed for real-time inference, the most computationally demanding stages such as training and hyperparameter search are performed offline. To maintain accuracy and robustness under evolving operating conditions, the framework supports periodic retraining with updated datasets, allowing the seamless integration of refreshed models into the SCADA environment without affecting real-time performance.
The integration of AI-assisted modules into SCADA environments must address both compatibility and computational efficiency. In our framework, the most computationally intensive stages (training and hyperparameter search, cf. Table 4) are executed offline, whereas the online deployment relies exclusively on the inference step of the trained MLP. As shown in Table 4, the evaluation process required s for over 1000 samples, which corresponds to sub-millisecond inference per prediction in batch mode. When executed in single-prediction mode, the inference time is approximately 1.7 ms. Both scenarios confirm that the model meets the real-time requirements of SCADA operation. To ensure compatibility, the AI module is designed to be integrated through modular communication protocols such as OPC-UA or Modbus TCP/IP, which are standard in supervisory control architectures. Furthermore, validation in hardware-in-the-loop (HIL) environments will be performed prior to field deployment, ensuring that the AI-enhanced SCADA system can operate reliably under real-world conditions without introducing additional computational overhead.
6. Conclusions
This work presented an optimization strategy for a 36-pulses converter that combines SHE with reinjection through the neutral point by adjusting the transformer ratio. The baseline configuration exhibited noticeable harmonic distortion and uneven pulse structures, which were mitigated by optimizing the reinjection transformer, reducing voltage discontinuities and achieving a more uniform pulse distribution. Applying the SHE strategy, even with non-optimized switching angles, further improved waveform clarity. The proposed AI-based procedure, implemented with a multi-layer perceptron (MLP) in a supervised regression framework, captured the nonlinear relationship between switching angles and THD. This enabled the rapid identification of optimal firing angles and, when combined with reinjection optimization, produced a well-defined 36-pulses output waveform with THD reduced to 5.09198%, in line with IEEE 519 limits. Simulation and experimental results confirm the practical effectiveness of the approach, with residual narrow pulses remaining within acceptable limits. Beyond these results, this study opens the hypothesis that extending the AI-based methodology to a larger set of switching angles, higher converter levels, or different transformer ratios could yield even greater harmonic reduction. Future work may also include the analysis of load-unbalance conditions to further validate the robustness of the method. These findings highlight the potential of coordinated AI-assisted control strategies for high-pulse converters in smart grids and intelligent power systems. The proposed methodology is well suited for digital control platforms and SCADA integration, contributing to more adaptive and efficient energy conversion in the context of the evolving Internet of Energy.
Author Contributions
Conceptualization, A.V.-G. and C.E.C.; data curation, C.E.C.; formal analysis, A.V.-G. and C.E.C.; funding acquisition, A.V.-G.; investigation, A.V.-G. and C.E.C.; methodology, A.V.-G. and C.E.C.; project administration, A.V.-G. and C.E.C.; resources, A.V.-G.; software, C.E.C.; supervision, A.V.-G.; validation, A.V.-G.; visualization, A.V.-G.; writing—original draft, A.V.-G. and C.E.C.; writing—review and editing, A.V.-G. and C.E.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Universidad Panamericana through the Fondo Fomento a la Investigación UP 2024 under Project UP-CI-2024-GDL-10-ING.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors gratefully acknowledge the support of Universidad Panamericana Campus Guadalajara and Universidad de Guadalajara, Centro Universitario de los Lagos.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Parameter/Acronym | Description |
| VSC | Voltage source converter |
| THD | Total Harmonic Distortion |
| NPR | Neutral Point Reinjection |
| , , and | Optimal three-level switch-firing angles |
| Transfer function for the six-pulses converter with WYE connection | |
| Transfer function for the six-pulses converter with connection | |
| Transfer function for the twelve-pulses converter | |
| SHE | Selective Harmonic Elimination |
| AI | Artificial intelligence |
| MLP | Multi-layer perceptron |
| DC | Direct current |
| SCADA | Supervisory Control and Data Acquisition |
| MATLAB | MATLAB software (Matrix Laboratory) |
| Simulink | Simulation environment within MATLAB |
| PLECS | Power Electronics Circuit Simulation Software |
| THDactual | Actual value of Total Harmonic Distortion |
| THDpredicted | Predicted value of Total Harmonic Distortion by the AI model |
References
- Dehaghani, M.N.; Korõtko, T.; Rosin, A. AI Applications for Power Quality Issues in Distribution Systems: A Systematic Review. IEEE Access 2025, 13, 18346–18365. [Google Scholar] [CrossRef]
- Heidary, J.; Gheisarnejad, M.; Rastegar, H.; Khooban, M.H. Survey on microgrids frequency regulation: Modeling and control systems. Electr. Power Syst. Res. 2023, 210, 108719. [Google Scholar] [CrossRef]
- Alhafadhi, L.; Teh, J. Advances in Reduction of Total Harmonic Distortion in Solar Photovoltaic Systems: A Literature Review. Int. J. Energy Res. 2020, 44, 2455–2470. [Google Scholar] [CrossRef]
- Das, B.; Watson, N.; Liu, Y. DC ripple reinjection: A review. Int. J. Emerg. Electr. Power Syst. 2011, 12. [Google Scholar] [CrossRef]
- Shi, Y.; Lian, L.; Shi, Y.; Wang, Z.; Zhou, Y.; Fu, L.; Bai, L.; Zhang, J.; Zhang, W. Machine learning for large-scale optimization in 6G wireless networks. IEEE Commun. Surv. Tutor. 2023, 25, 2088–2132. [Google Scholar] [CrossRef]
- Panoiu, M.; Panoiu, C.; Mezinescu, S.; Militaru, G.; Baciu, I. Machine learning techniques applied to the harmonic analysis of railway power supply. Mathematics 2023, 11, 1381. [Google Scholar] [CrossRef]
- Sapkota, D.B.; Neupane, P.; Pokharel, K.; Khan, S. An artificial neural network based approach for harmonic component prediction in a distribution line. Energy Rep. 2024, 12, 3861–3873. [Google Scholar] [CrossRef]
- Castañeda, C.E.; Valderrabano-Gonzalez, A.; Gabbar, H.A.; Morfín, O.A. Sliding mode with equivalent control for induction motor drive based on multi-pulse VSC. Energies 2023, 16, 4866. [Google Scholar] [CrossRef]
- Naing, T. Analysis of 12-Pulse Controlled Rectifier Performance and Its Impacts on Power System. 2018. Available online: https://www.researchgate.net/profile/Tun-Naing-6/publication/326106738_Analysis_of_12-pulse_Controlled_Rectifier_Performance_and_its_Impacts_on_Power_System/data/5b3919d2aca272078500e8dc/12-pulse-rectifier.pdf (accessed on 5 September 2025).
- Ali, M.; Al-Ismail, F.S.; Gulzar, M.M.; Khalid, M. A review on harmonic elimination and mitigation techniques in power converter based systems. Electr. Power Syst. Res. 2024, 234, 110573. [Google Scholar] [CrossRef]
- Liu, Y.; Arrillaga, J.; Watson, N. Multi-level voltage sourced conversion by voltage reinjection at six times the fundamental frequency. IEE Proc.-Electr. Power Appl. 2002, 149, 201–207. [Google Scholar] [CrossRef]
- Liu, Y. Multi-Level Voltage and Current Reinjection Ac-Dc Conversion. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2003. [Google Scholar]
- Valderrabano, A.; Ramirez, J.M. A novel voltage source converter behind the StatCom. Electr. Power Components Syst. 2010, 38, 1161–1174. [Google Scholar] [CrossRef]
- Castañeda, C.E.; Valderrabano-Gonzalez, A.; Gabbar, H.A.; Sood, V.K. High-precision speed control of induction motors using a multi-pulse voltage source converter and advanced observer-based strategies. e-Prime-Adv. Electr. Eng. Electron. Energy 2025, 11, 100884. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Tapia-Olvera, R.; Valderrabano-Gonzalez, A.; Lopez-Garcia, I. Adaptive neuronal induction motor control with an 84-pulse voltage source converter. Asian J. Control 2021, 23, 1603–1616. [Google Scholar] [CrossRef]
- McKinney, W. Python for Data Analysis, 3rd ed.; O’Reilly: Sebastopol, CA, USA, 2022. [Google Scholar]
- LeCun, Y.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient BackProp. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–48. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Fox, J. Applied Regression Analysis and Generalized Linear Models; Sage Publications: Thousand Oaks, CA, USA, 2015. [Google Scholar]
- IEEE Std. 519-2022; Standard for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022; pp. 1–31.
- IEEE Std 519-2014; IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: Piscataway, NJ, USA, 2014; pp. 1–29, Revision of IEEE Std 519-1992.
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Duque-Perez, O. A review of total harmonic distortion factors for the measurement of harmonic and interharmonic pollution in modern power systems. Energies 2021, 14, 6467. [Google Scholar] [CrossRef]
- Avila Saccol, G.; Bui, V.H.; Su, W. A Deep-Neural-Network-Based Surrogate Model for DC/AC Converter Topology Selection Using Multi-Domain Simulations. Energies 2024, 17, 6467. [Google Scholar] [CrossRef]
- Reyes, M.M.; Alquicira, J.A.; Aldaco, S.D.L.; Campos, E.M.A.; Severiano, Y.R. Calculation of Optimal Switching Angles for a Multilevel Inverter using NR and GA-a comparison. In Proceedings of the 2018 14th International Conference on Power Electronics (CIEP), Cholula, Mexico, 24–26 October 2018; pp. 22–27. [Google Scholar]
- Sánchez Vargas, O.; Vela Valdés, L.G.; Borunda, M.; Lozoya-Ponce, R.E.; Aguayo Alquicira, J.; De León Aldaco, S.E. ANFIS-PSO-Based Optimization for THD Reduction in Cascaded Multilevel Inverter UPS Systems. Electronics 2024, 13, 4456. [Google Scholar] [CrossRef]
- Zolfaghari, H.; Momeni, H.; Karimi, H. Multilevel Inverter Real-Time Simulation and Optimization Through Hybrid GA/PSO Algorithm. arXiv 2021, arXiv:2110.13817. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).