Robust Sensorless Predictive Power Control of PWM Converters Using Adaptive Neural Network-Based Virtual Flux Estimation
Abstract
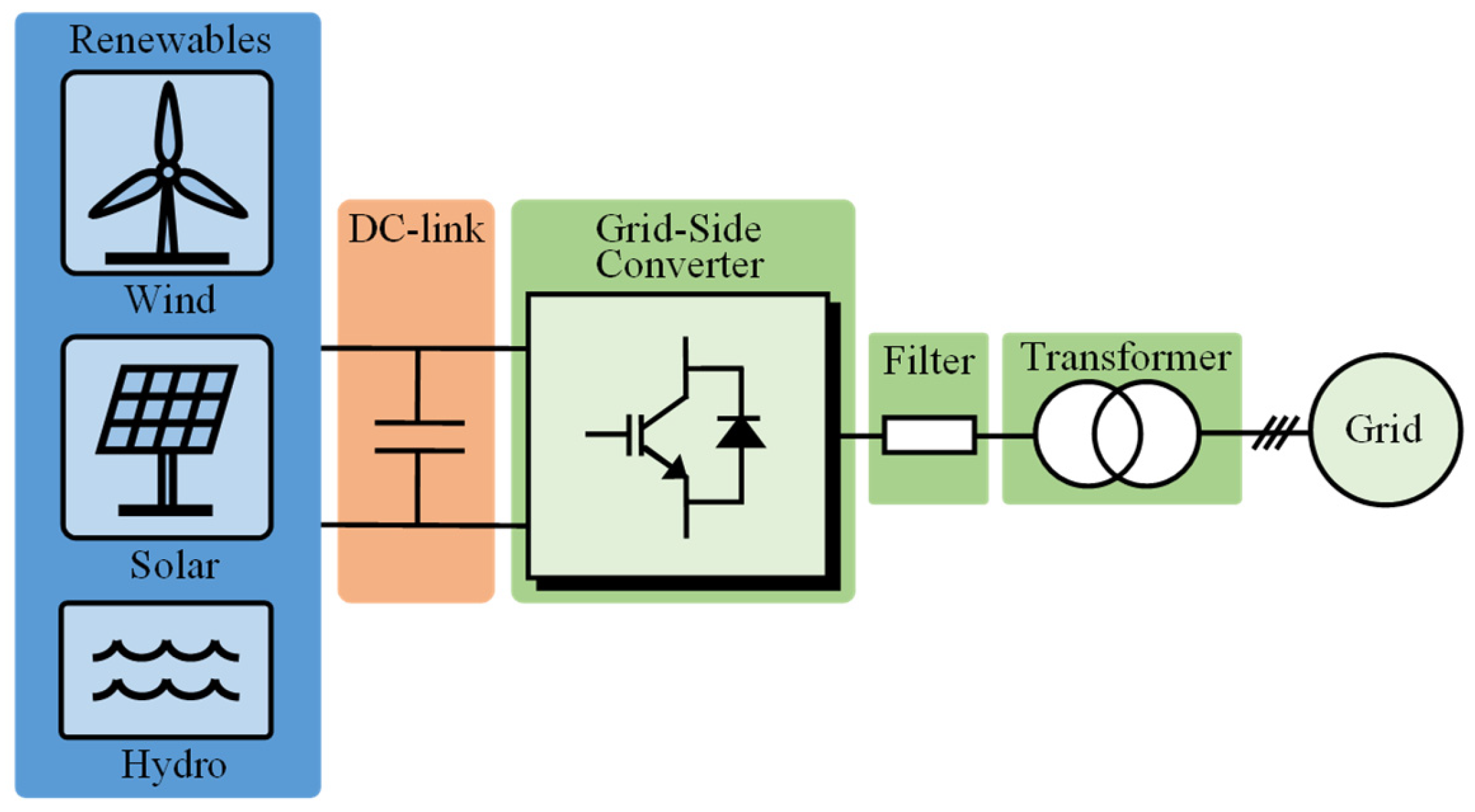
1. Introduction
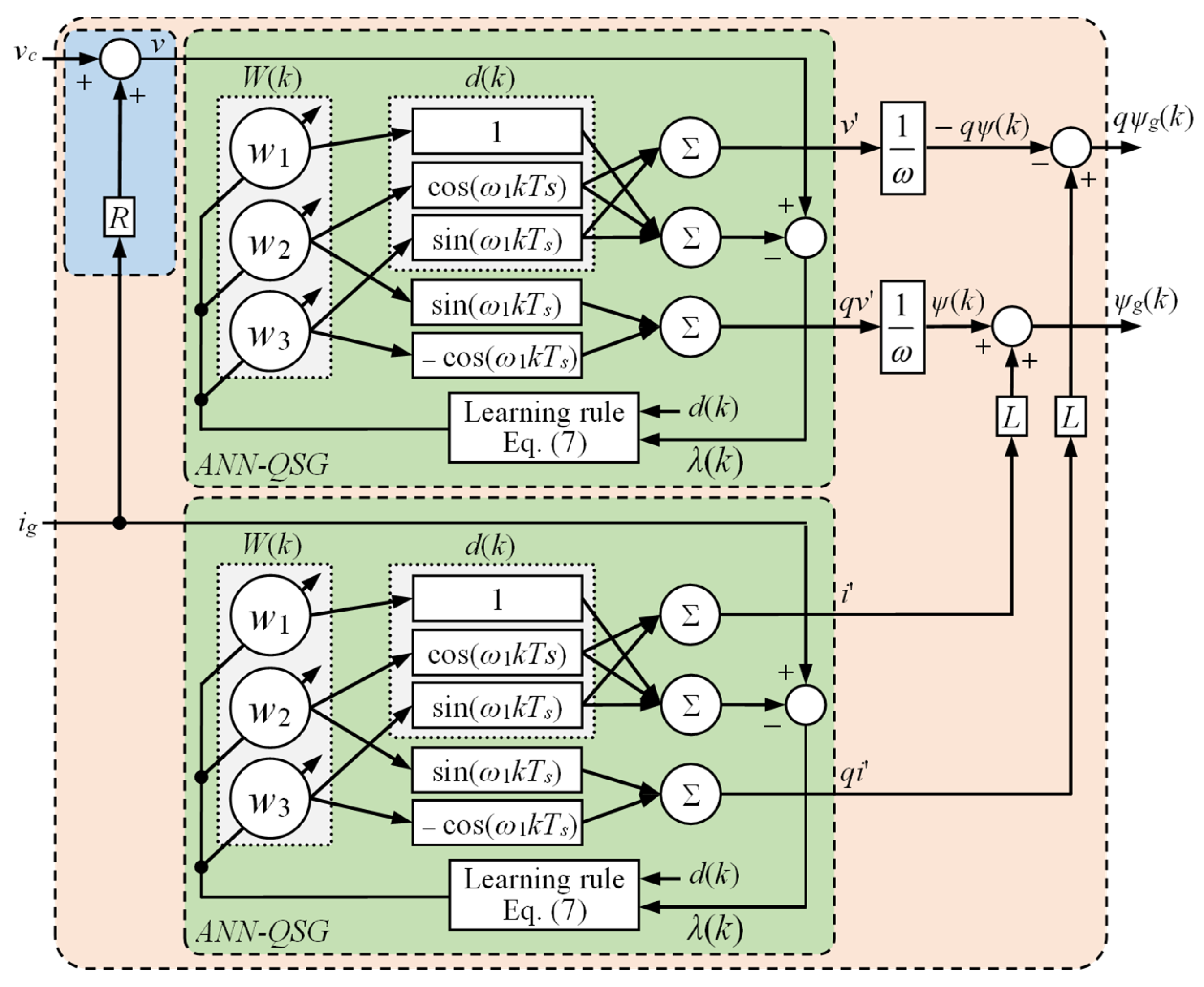
- An ANN-based VF estimator of the ADALINE type, configured as a quadrature signal generator, providing accurate VF estimation by compensating DC offset, voltage unbalance, and harmonics, while eliminating amplitude and phase errors.
- A simplified sensorless control scheme, achieved by directly exploiting the estimated VF components, thereby removing the need for voltage sensors and avoiding symmetrical component decomposition, which reduces both hardware and computational complexity.
- The proposed VF-PDPC strategy, integrating the ANN-QSG with the extended pq theory to enable stable active power regulation, sinusoidal current injection, and strong robustness under unbalanced and distorted grid conditions.
- Real-time validation on an OPAL-RT platform, confirming the robustness of the proposed approach.
2. Adaptive Neural Network-Based VF Estimation
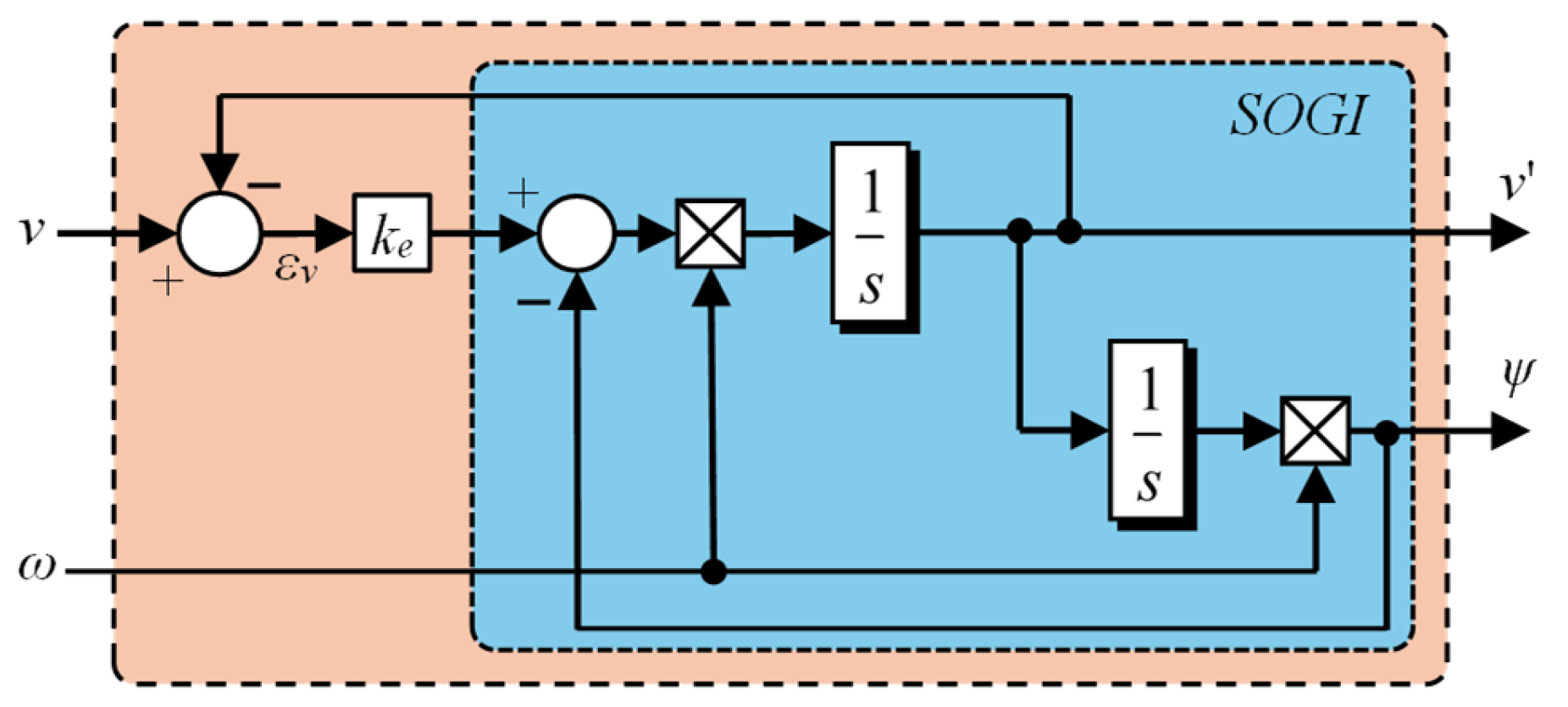
2.1. VF Concept
2.2. Proposed ANN-QSG Estimator
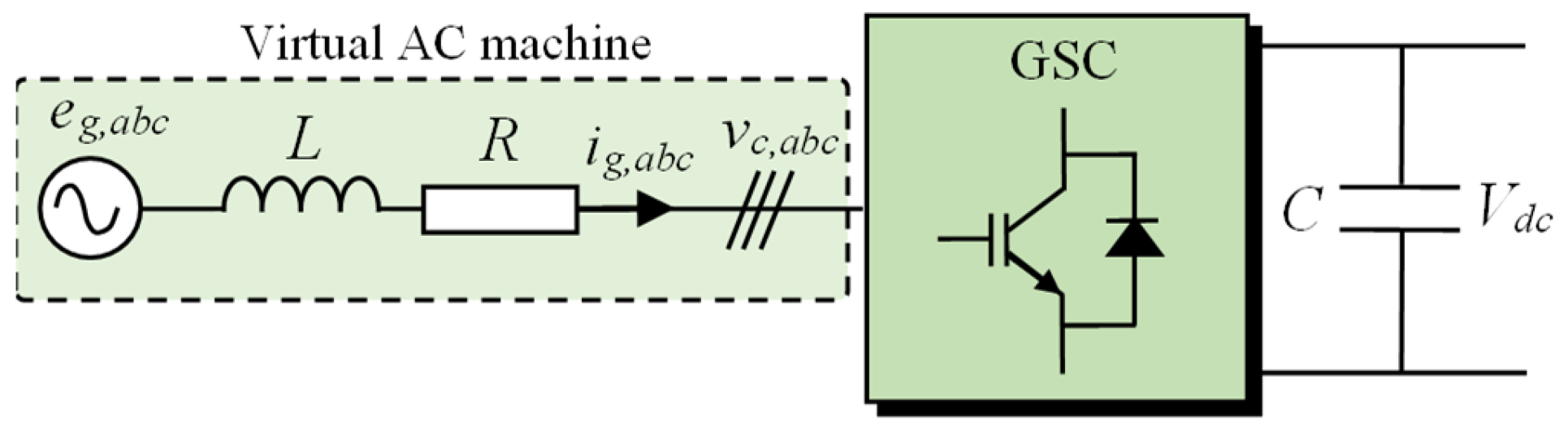
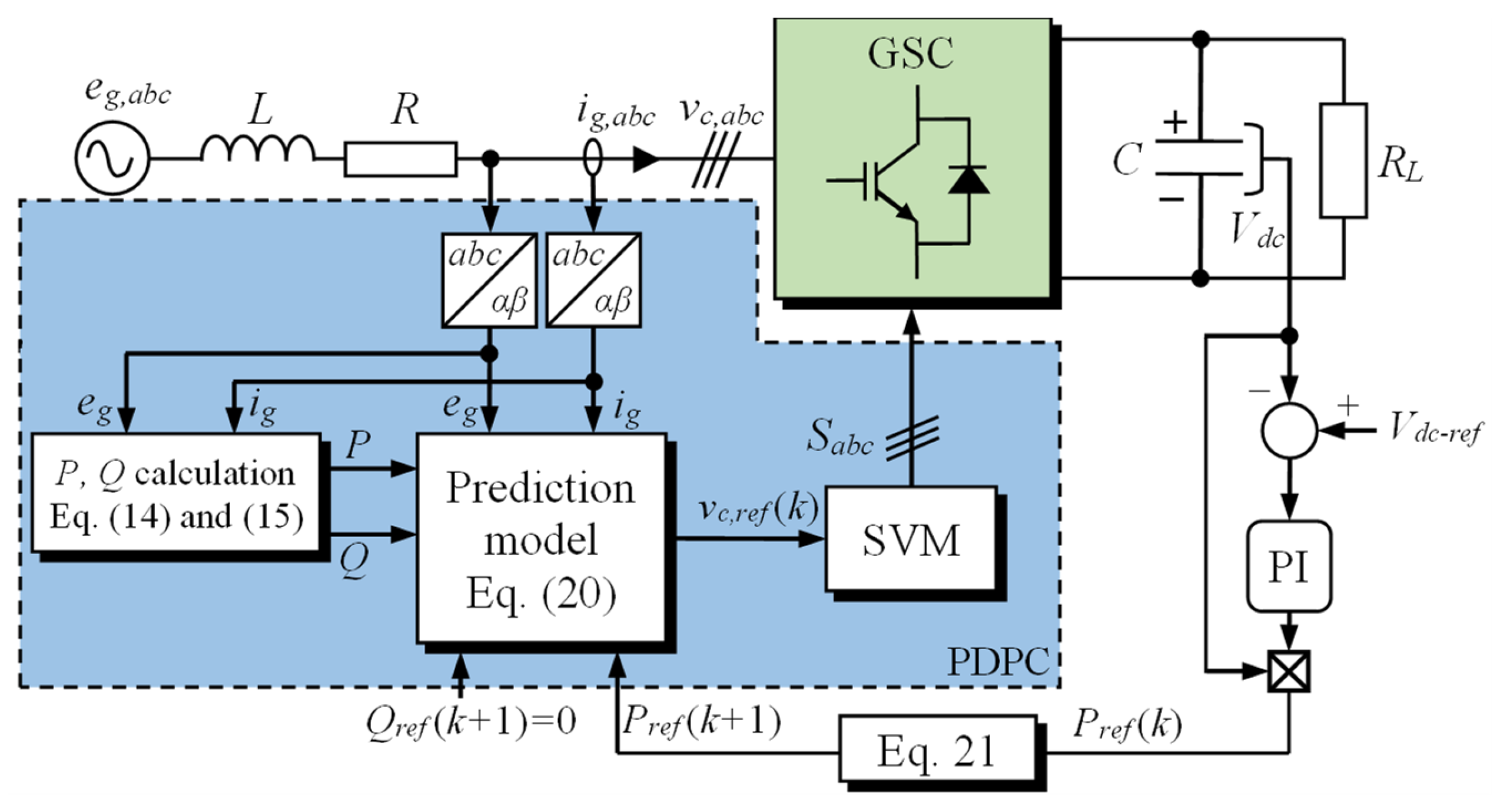
3. Predictive Control of the GSC
3.1. Conventional PDPC
3.2. Proposed VF-PDPC
4. Results
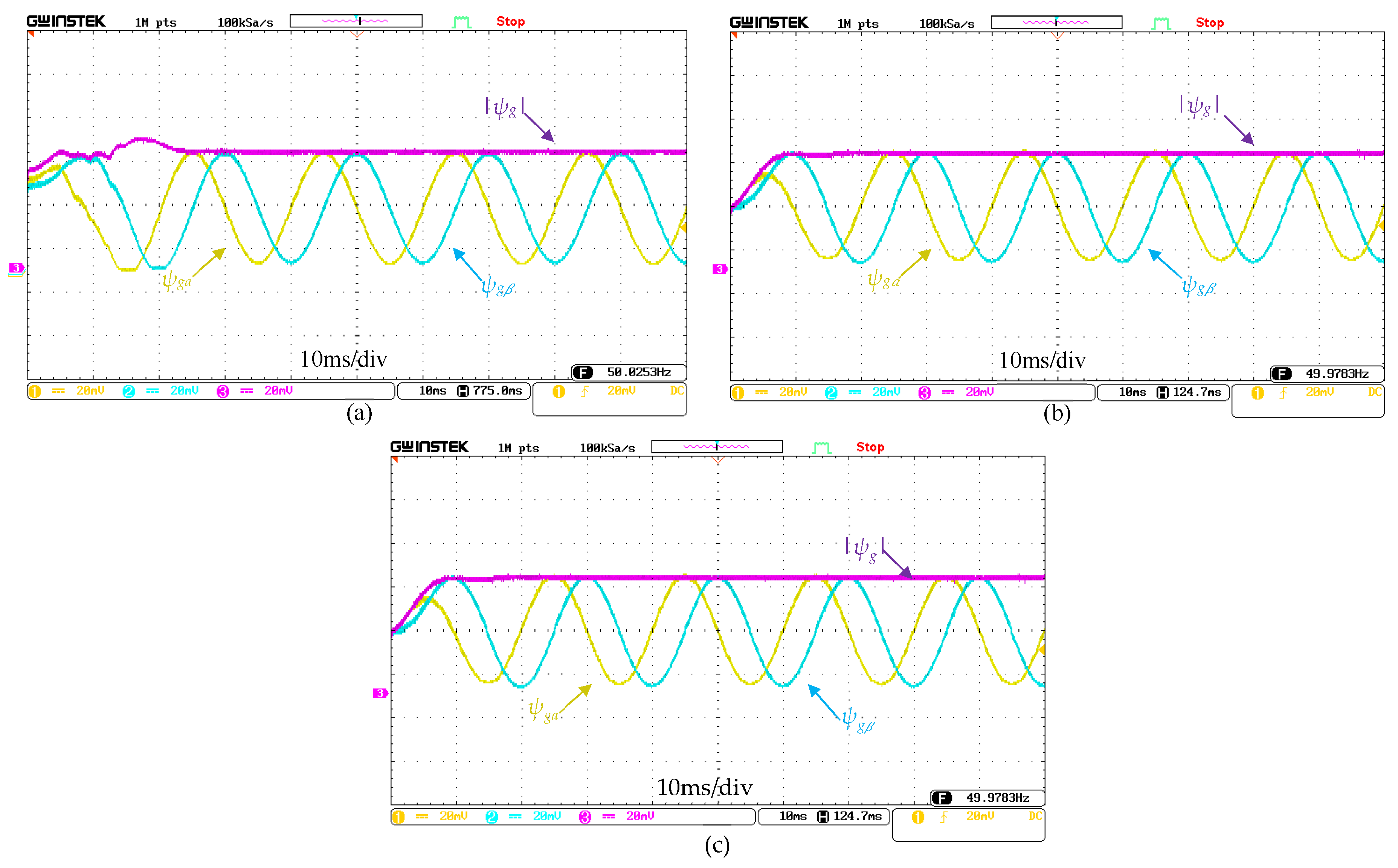
4.1. Comparison of VF Estimators
4.1.1. Startup Performance
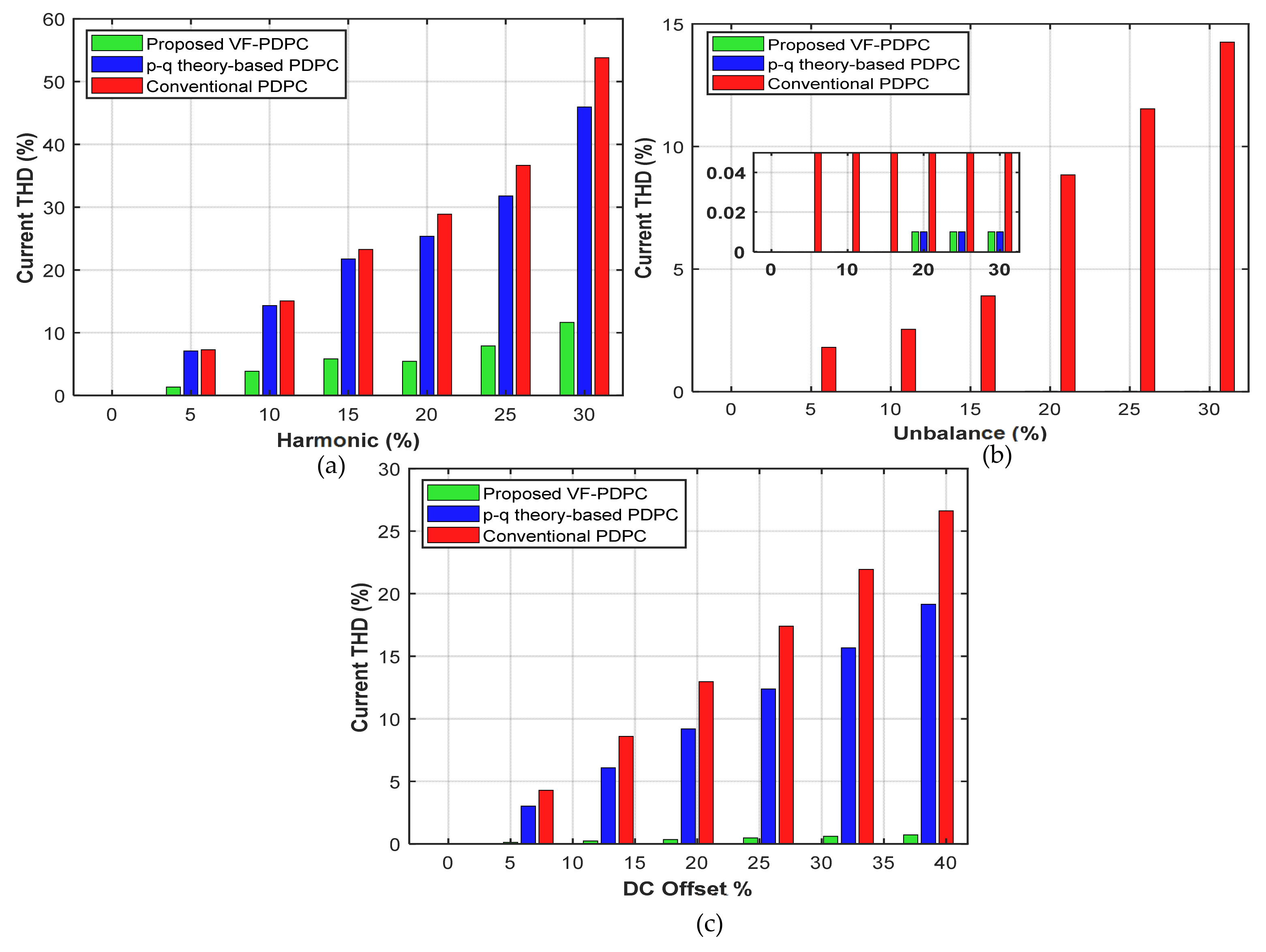
4.1.2. Harmonic Distortion
4.1.3. DC Offset
4.1.4. Unbalance, Harmonics and DC Offset
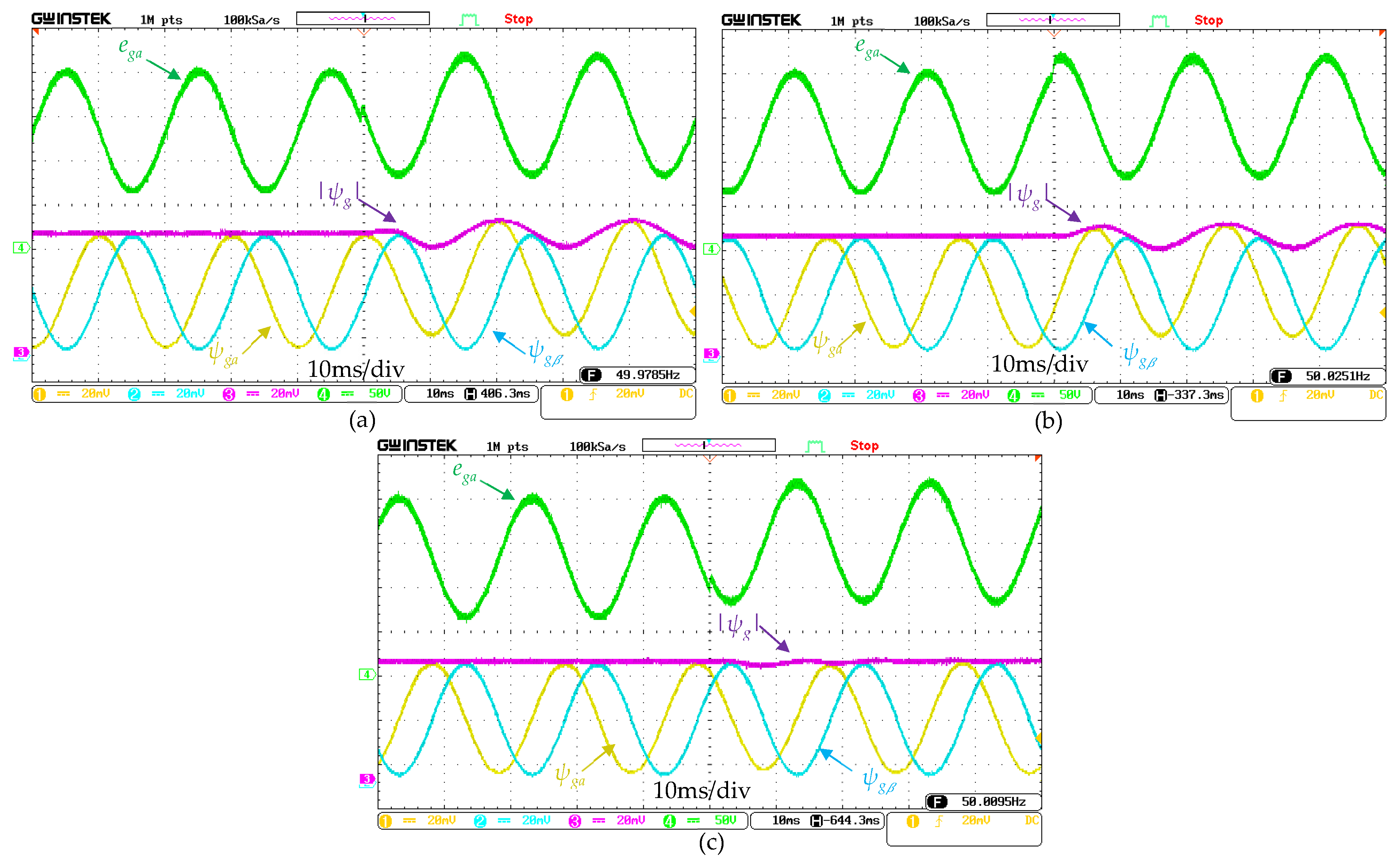
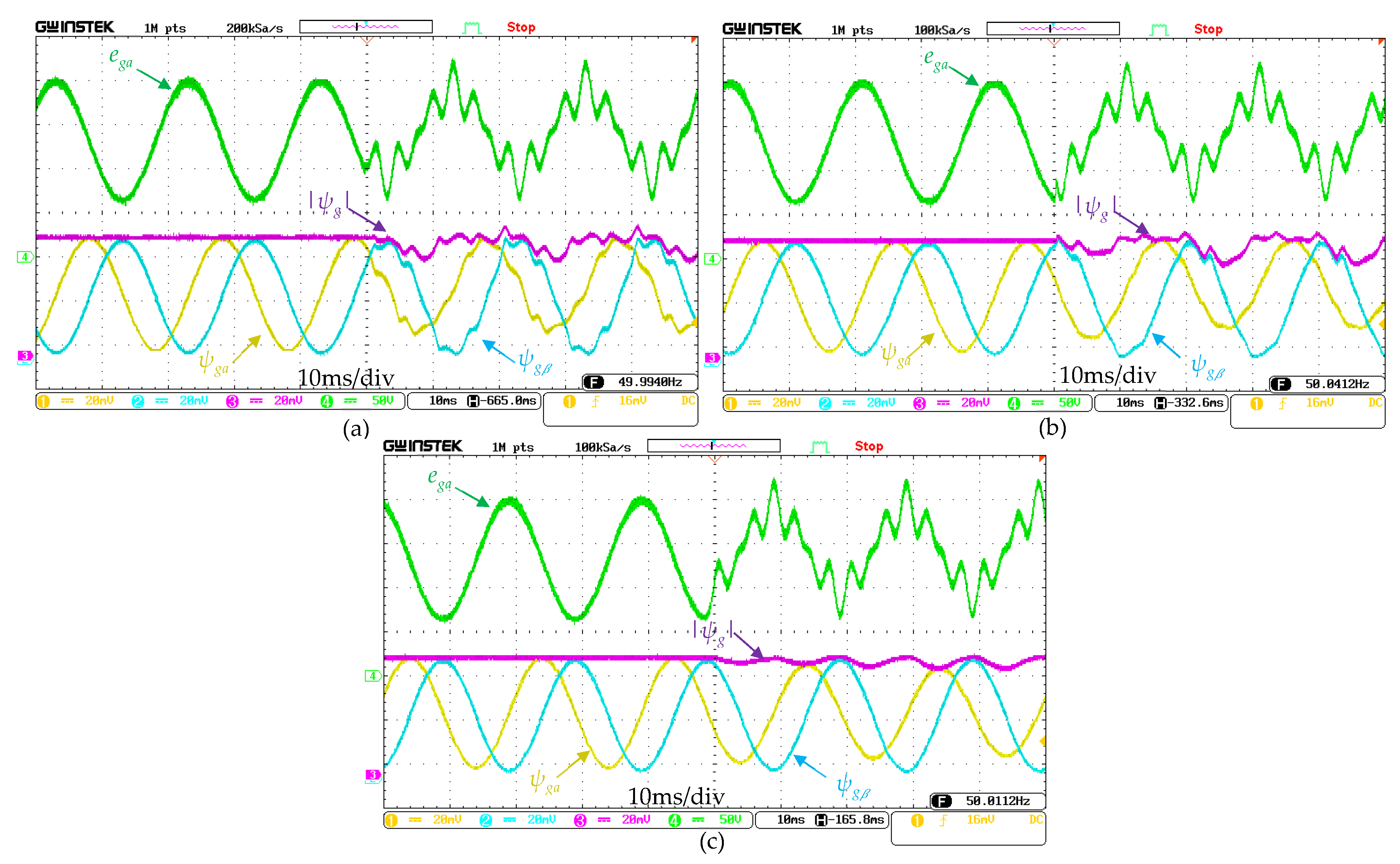
4.2. Comparison Results of Control Techniques
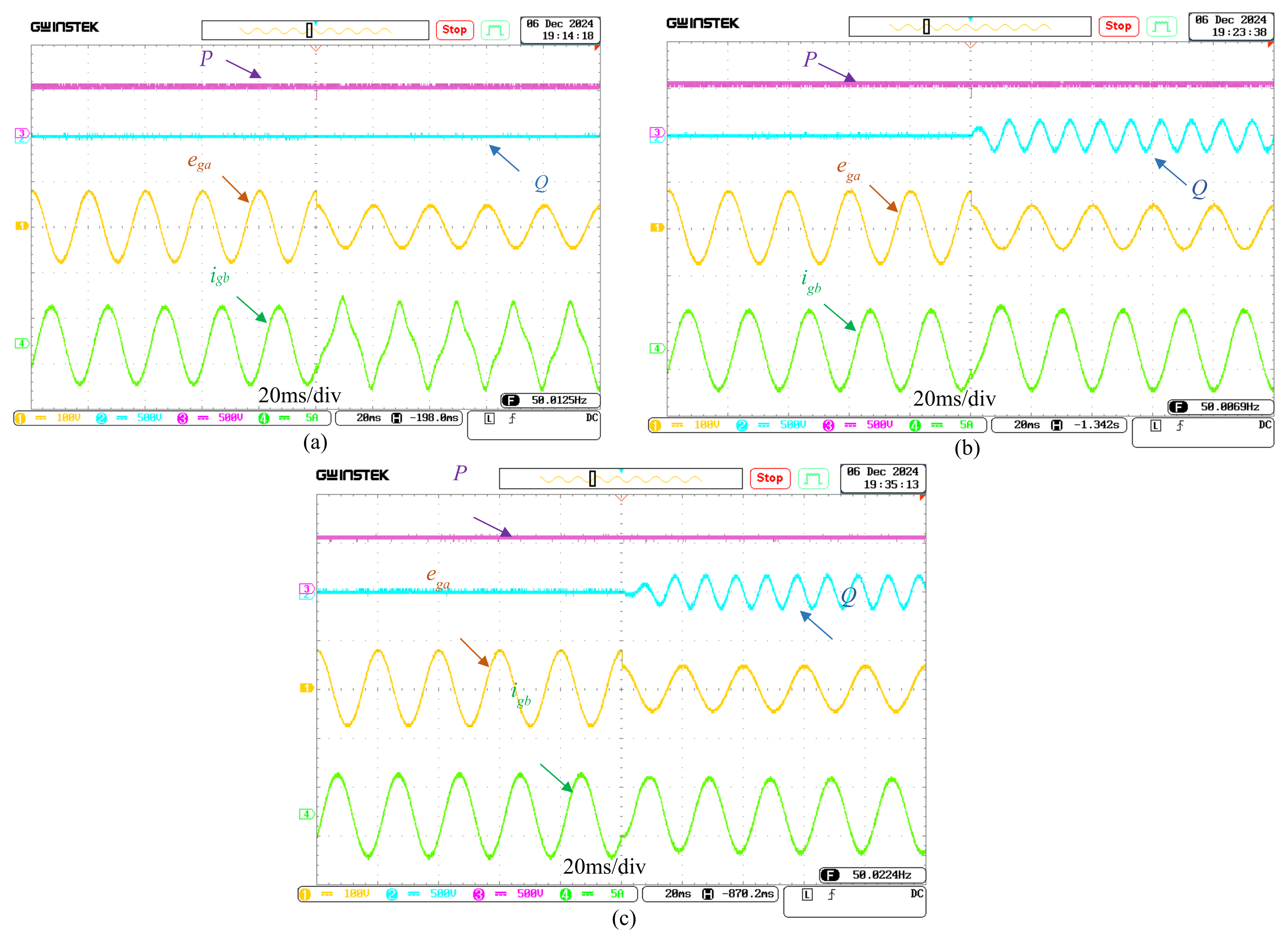
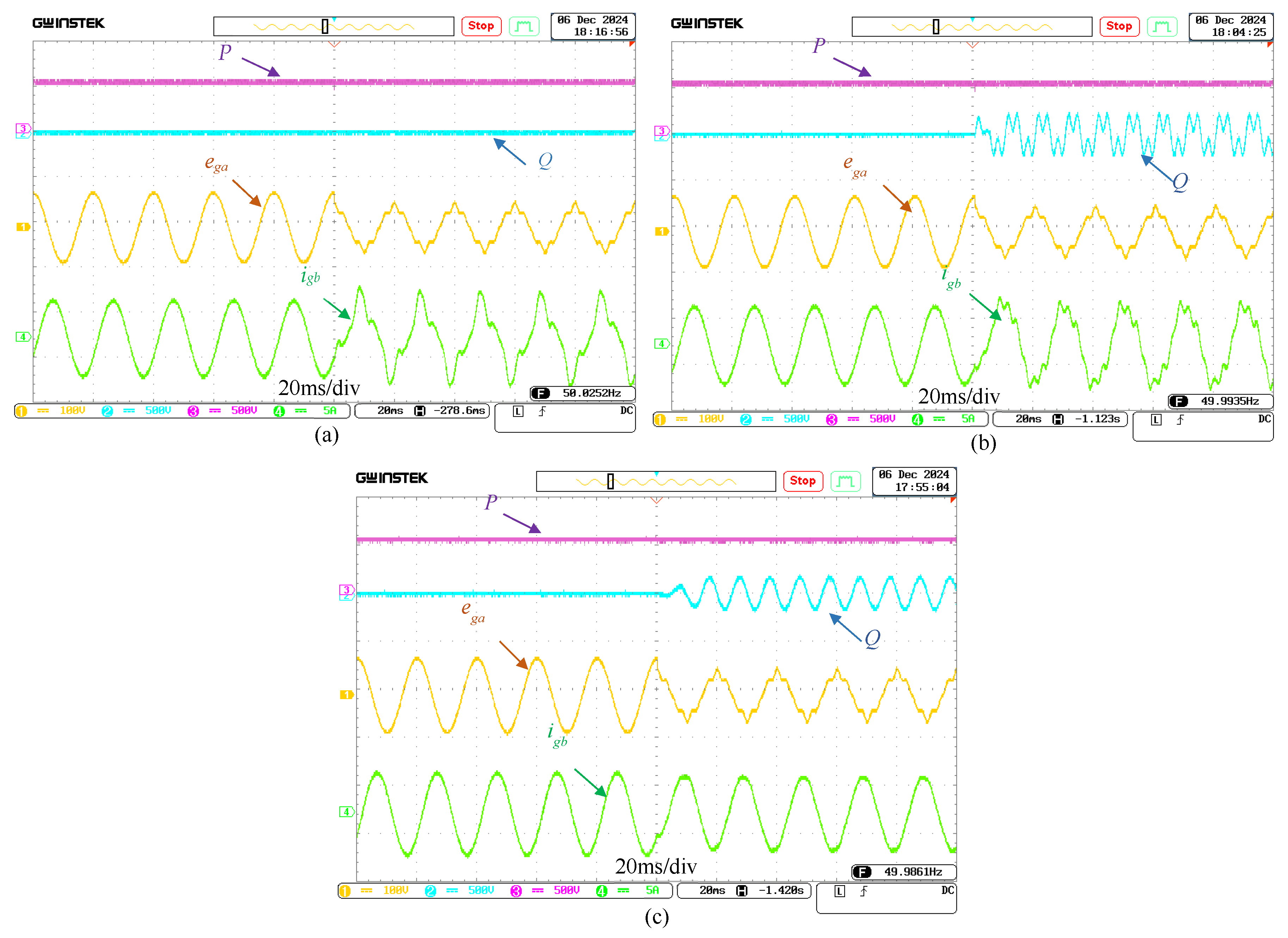
4.2.1. Comparison Under Unbalanced Grid Conditions
4.2.2. Comparison Under an Unbalanced and Distorted Grid Conditions
4.2.3. Robustness Evaluation of the VF-PDPC
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| vc | Converter voltage vector |
| eg | Grid voltage vector |
| ig | Grid current vector |
| ψg | Grid virtual flux vector |
| qψ | Quadrature component of the virtual flux |
| i′g, qi′g | Filtered and quadrature components of the grid current |
| R, L | Grid filter resistance and inductance |
| Ts | Sampling period |
| ω1 | Fundamental angular frequency of the grid |
| V1, ϕ1 | Amplitude and phase of the fundamental component |
| Vn, ωn, ϕn | Amplitude, angular frequency, and phase of the n-th harmonic |
| A,B | DC components (offsets) |
| d(k) | Input vector of the ANN-QSG |
| W | Adaptive weights of the ADALINE |
| η | Learning rate of the LMS algorithm |
| λ(k) | Voltage estimation error |
| S | Instantaneous complex power |
| P, Q | Instantaneous active and reactive powers |
| Pref, Qref | Active and reactive power references |
| Pc, Ps | Oscillatory components of the active power |
| Qc, Qs | Oscillatory components of the reactive power |
| Abbreviations | |
| ADALINE | Adaptive linear neuron |
| ANN | Adaptive neural network |
| ANN-QSG | Adaptive neural network-based quadrature signal generator |
| BPF | Band-pass filter |
| GSC | Grid-side converter |
| LPF | Low-pass filter |
| LMS | Least-mean-squares |
| MPDPC | Model predictive direct power control |
| PDPC | Predictive direct power control |
| PLL | Phased-locked loop |
| PWM | Pulse width modulation |
| SOGI | Second-order generalized integrator |
| SVM | Space vector modulation |
| THD | Total harmonic distortion |
| VF | Virtual flux |
References
- Boukais, B.; Mesbah, K.; Rahoui, A.; Saim, A.; Houari, A.; Benkhoris, M.F. Development of a 3 kW Wind Energy Conversion System Emulator Using a Grid-Connected Doubly-Fed Induction Generator. Actuators 2024, 13, 487. [Google Scholar] [CrossRef]
- Yang, S.; Wang, R.; Zhou, J.; Chen, B. Intermediate-Variable-Based Distributed Fusion Estimation for Wind Turbine Systems. Actuators 2022, 11, 15. [Google Scholar] [CrossRef]
- Rajendran, S.; Diaz, M.; Devi, V.S.K.; Jena, D.; Travieso, J.C.; Rodriguez, J. Wind Turbine Emulators—A Review. Processes 2023, 11, 747. [Google Scholar] [CrossRef]
- Tasnim, M.N.; Ahmed, T.; Dorothi, M.A.; Ahmad, S.; Shafiullah, G.M.; Ferdous, S.M.; Mekhilef, S. Voltage-Oriented Control-Based Three-Phase, Three-Leg Bidirectional AC–DC Converter with Improved Power Quality for Microgrids. Energies 2023, 16, 6188. [Google Scholar] [CrossRef]
- Lee, S.S.; Heng, Y.E. Optimal VF-PDPC of Grid Connected Inverter Under Unbalanced and Distorted Grid Voltages. Electric Power Syst. Res. 2016, 140, 1–8. [Google Scholar] [CrossRef]
- Ma, H.; Yao, X.; Wang, J.; Luo, X.; Huang, S. Improved Deadbeat Predictive Direct Power Control for Three-Phase PWM Rectifier Based on LADRC. J. Mar. Sci. Eng. 2025, 13, 402. [Google Scholar] [CrossRef]
- Tao, Y.; Wu, Q.; Wang, L.; Tang, W. Voltage Sensorless Predictive Direct Power Control of Three-Phase PWM Converters. IET Power Electron. 2016, 9, 1009–1018. [Google Scholar] [CrossRef]
- Jabbarnejad, A.; Vaez-Zadeh, S.; Jahanpour-Dehkordi, M. Combined Control of Grid Connected Converters Based on a Flexible Switching Table for Fast Dynamic and Reduced Harmonics. IEEE Trans. Energy Convers. 2020, 35, 77–84. [Google Scholar] [CrossRef]
- Bouafia, A.; Krim, F.; Gaubert, J.-P. Fuzzy-Logic-Based Switching State Selection for Direct Power Control of Three-Phase PWM Rectifier. IEEE Trans. Ind. Electron. 2009, 56, 1984–1992. [Google Scholar] [CrossRef]
- Ahmad, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M.; Pourdaryaei, A.; Ahmed, T.; Jhuma, U.K.; Afzal, S. Fuzzy Logic-Based Direct Power Control Method for PV Inverter of Grid-Tied AC Microgrid Without Phase-Locked Loop. Electronics 2021, 10, 3095. [Google Scholar] [CrossRef]
- Malinowski, M.; Jasinski, M.; Kazmierkowski, M.P. Simple Direct Power Control of Three-Phase PWM Rectifier Using Space-Vector Modulation (DPC-SVM). IEEE Trans. Ind. Electron. 2004, 51, 447–454. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Kwak, S.; Choi, S. Voltage Injection Based MPDPC Technique for Individual Phase Loss Reduction in Active Front-End Rectifier. IEEE Access 2024, 12, 51193–51207. [Google Scholar] [CrossRef]
- Rahoui, A.; Mesbah, K.; Boukais, B.; Amoura, N.; Saim, A.; Houari, A. Simplified Sensorless Predictive Control of Grid-Side Converter in Wind Energy Conversion Systems Under Distorted Grid Conditions. Energy Rep. 2025, 14, 1156–1168. [Google Scholar] [CrossRef]
- Rath, A.; Srungavarapu, G. Reduced Complexity Model Predictive Direct Power Control for Unbalanced Grid. Electr. Power Syst. Res. 2024, 234, 110563. [Google Scholar] [CrossRef]
- Amoura, N.; Rahoui, A.; Boukais, B.; Mesbah, K. Neural Networks-Based Adaptive Predictive Current Control of a Grid-Connected Three-Phase PWM Converter. In Proceedings of the 2024 2nd International Conference on Electrical Engineering and Automatic Control (ICEEAC), Setif, Algeria, 12–14 May 2024; pp. 1–6. [Google Scholar]
- Rahoui, A.; Mesbah, K.; Boukais, B.; Otmane-Cherif, T. Frequency-Adaptive Neural Network Based Virtual Flux Estimation for Sensorless Control of PWM Converters Under Unbalanced Conditions. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 25–27 September 2020; pp. 1–6. [Google Scholar]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Predictive Direct Power Control of Three-Phase Pulsewidth Modulation (PWM) Rectifier Using Space-Vector Modulation (SVM). IEEE Trans. Power Electron. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Mesbah, K.; Rahoui, A.; Boukais, B. Neural Network Quadrature Signal Generator-Based Virtual Flux Estimation for Predictive Control of PWM Converters. IEEE Trans. Ind. Electron. 2024, 71, 4785–4794. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, C. Direct Power Control of a Pulse Width Modulation Rectifier Using Space Vector Modulation Under Unbalanced Grid Voltages. IEEE Trans. Power Electron. 2015, 30, 5892–5901. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Liu, J.; Zhang, N.; Walker, P.D. Robust Deadbeat Predictive Power Control with a Discrete-Time Disturbance Observer for PWM Rectifiers Under Unbalanced Grid Conditions. IEEE Trans. Power Electron. 2019, 34, 287–300. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G.D. Virtual-Flux-Based Direct Power Control of Three-Phase PWM Rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Norniella, J.G.; Cano, J.M.; Orcajo, G.A.; Rojas, C.H.; Pedrayes, J.F.; Cabanas, M.F.; Melero, M.G. Melero Improving the Dynamics of Virtual-Flux-Based Control of Three-Phase Active Rectifiers. IEEE Trans. Ind. Electron. 2014, 61, 177–187. [Google Scholar] [CrossRef]
- Ketzer, M.B.; Jacobina, C.B. Jacobina Virtual Flux Sensorless Control for Shunt Active Power Filters with Quasi-Resonant Compensators. IEEE Trans. Power Electron. 2016, 31, 4818–4830. [Google Scholar] [CrossRef]
- Roslan, N.F.; Luna, A.; Rocabert, J.; Candela, J.I.; Rodriguez, P. Remote Power Control Injection of Grid-Connected Power Converters Based on Virtual Flux. Energies 2018, 11, 488. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Xue, M.; Chen, Z.; Sun, T.; Kennel, R.; Hackl, C.M. Hackl Predictive Control with Novel Virtual-Flux Estimation for Back-to-Back Power Converters. IEEE Trans. Ind. Electron. 2015, 62, 2823–2834. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Zhang, Y.; Li, Y.; Zhang, Z. A Time-Domain Virtual-Flux Based Predictive Control of Modular Multilevel Converters for Offshore Wind Energy Integration. IEEE Trans. Energy Convers. 2022, 37, 1803–1814. [Google Scholar] [CrossRef]
- Rahoui, A.; Boukais, B.; Mesbah, K.; Otmane-Cherif, T. Neural Networks Based Frequency-Locked Loop for Grid Synchronization Under Unbalanced and Distorted Conditions. In Proceedings of the 2020 International Conference on Electrical Engineering (ICEE), Istanbul, Turkey, 25–27 September 2020; pp. 1–6. [Google Scholar]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 978-1-118-36210-5. [Google Scholar]
- Buraimoh, E.; Davidson, I.E. Laboratory Procedure for Real-Time Simulation Experiment of Renewable Energy Systems on OPAL-RT Digital Simulator. In Proceedings of the 2022 10th International Conference on Smart Grid (icSmartGrid), Istanbul, Turkey, 27–29 June 2022; pp. 221–226. [Google Scholar]
- Golestan, S.; Golmohamadi, H.; Sinha, R.; Iov, F.; Bak-Jensen, B. Real-Time Simulation and Hardware-in-the-Loop Testing Based on OPAL-RT ePHASORSIM: A Review of Recent Advances and a Simple Validation in EV Charging Management Systems. Energies 2024, 17, 4893. [Google Scholar] [CrossRef]
- OPAL-RT Technologies, Inc. OP4512|Compact Entry-Level Real-Time Simulator for RCP and HIL Testing. OPAL-RT. Available online: https://www.opal-rt.com/hardware/simulators/real-time-simulators/op4512/ (accessed on 2 September 2025).
- Flack, C.; Ucer, E.; Smith, C.P.; Kisacikoglu, M. Controller Hardware-in-the-Loop (C-HIL) Testing of Decentralized EV-Grid Integration. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar]
- IEEE Std 519-2022 (Revision of IEEE Std 519-2014); IEEE Standard for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2022; pp. 1–31. [CrossRef]





| Parameters | Values |
|---|---|
| Grid voltage RMS value (V) | 55 |
| Grid voltage frequency f (Hz) | 50 |
| Input filter resistance R (Ω) | 1 |
| Input filter inductance L (mH) | 8 |
| DC bus capacitance C (mF) | 3.3 |
| Load resistance RL (Ω) | 60 |
| Sampling frequency ƒs (kHz) | 100 |
| Criterion and Test Conditions | SOGI | ANN-QSG [13] | Proposed ANN-QSG |
|---|---|---|---|
| Execution time (µs) | 0.6 | 0.57 | 0.7 |
| Startup response time (within 5% tolerance, ideal conditions) (ms) | 25 | 8 | 8 |
| Startup overshoot (ideal conditions) (%) | 18 | 0 | 0 |
| Output THD (under 30% 5th- and 7th-harmonic distortions) (%) | 10.2 | 0.20 | 0.18 |
| Output THD (under 25% DC offset of nominal voltage) (%) | 1.69 | 1.28 | 0.02 |
| Output THD (under all perturbation types) (%) | 10.70 | 4.29 | 0.74 |
| Criterion and Test Conditions | Conv.-PDPC | pq-Theory PDPC | Proposed VF-PDPC |
|---|---|---|---|
| Execution Time (Ideal conditions) (µs) | 3.8 µs | 4.3 µs | 5.5 µs |
| Current THD (30% Sag type A) (%) | 14.26% | 1.41% | 1.44% |
| Current THD (30% Sag type A + 5th and 7th harmonics (10%)) (%) | 27.87% | 18.27% | 2.29% |
| Current THD (All defaults included) (%) | 29.89% | 24.55% | 3.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amoura, N.; Rahoui, A.; Boukais, B.; Mesbah, K.; Saim, A.; Houari, A. Robust Sensorless Predictive Power Control of PWM Converters Using Adaptive Neural Network-Based Virtual Flux Estimation. Electronics 2025, 14, 3620. https://doi.org/10.3390/electronics14183620
Amoura N, Rahoui A, Boukais B, Mesbah K, Saim A, Houari A. Robust Sensorless Predictive Power Control of PWM Converters Using Adaptive Neural Network-Based Virtual Flux Estimation. Electronics. 2025; 14(18):3620. https://doi.org/10.3390/electronics14183620
Chicago/Turabian StyleAmoura, Noumidia, Adel Rahoui, Boussad Boukais, Koussaila Mesbah, Abdelhakim Saim, and Azeddine Houari. 2025. "Robust Sensorless Predictive Power Control of PWM Converters Using Adaptive Neural Network-Based Virtual Flux Estimation" Electronics 14, no. 18: 3620. https://doi.org/10.3390/electronics14183620
APA StyleAmoura, N., Rahoui, A., Boukais, B., Mesbah, K., Saim, A., & Houari, A. (2025). Robust Sensorless Predictive Power Control of PWM Converters Using Adaptive Neural Network-Based Virtual Flux Estimation. Electronics, 14(18), 3620. https://doi.org/10.3390/electronics14183620







