A Novel Self-Recovery Fragile Watermarking Scheme Based on Convolutional Autoencoder
Abstract
1. Introduction
1.1. Research Background
1.2. Research Motivation and Objectives
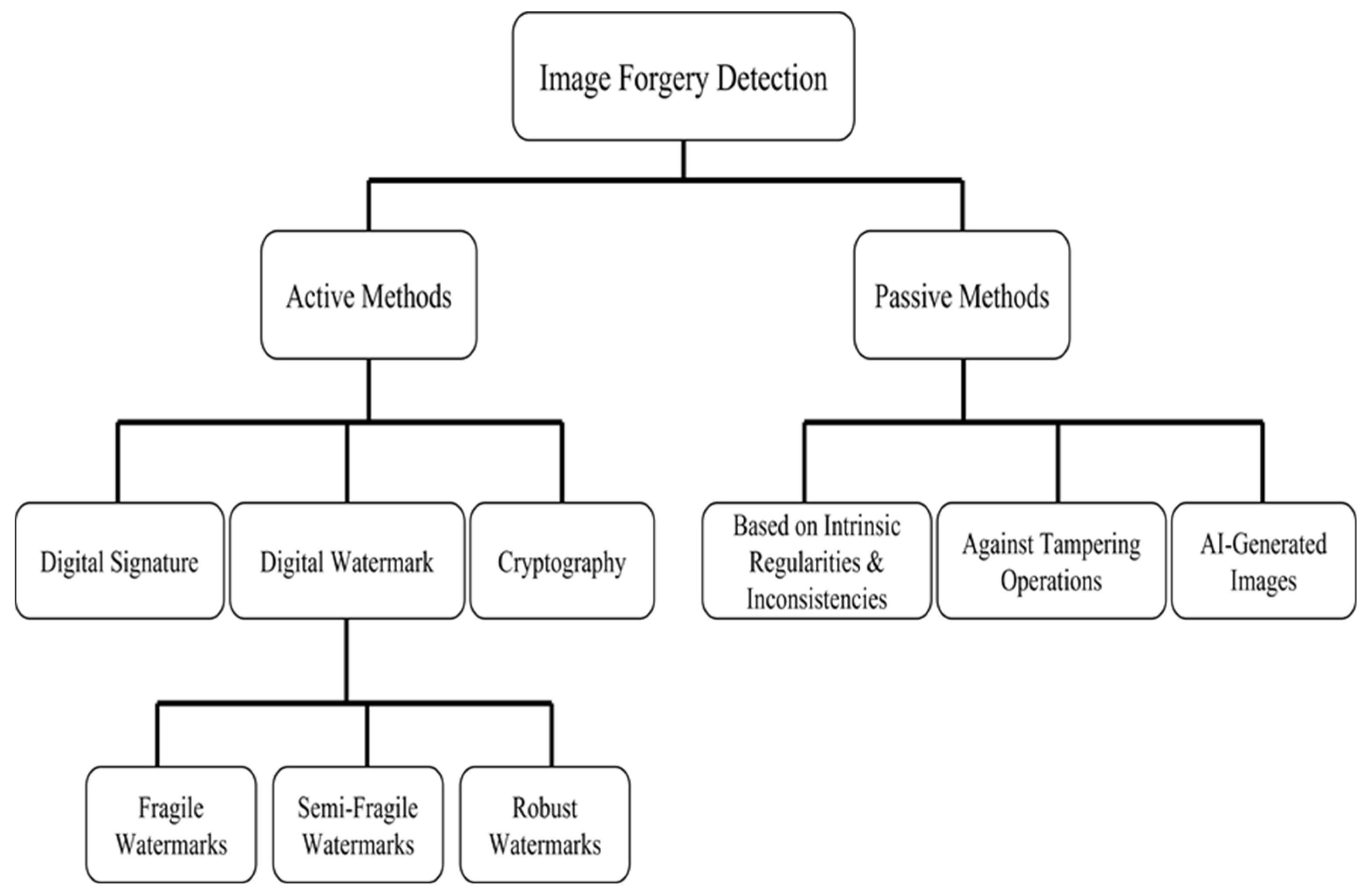
2. Related Work
2.1. Symbol Definitions
2.2. Fragile Watermarking
- (1)
- Pixel-wise schemes: Extract features from individual pixels. These offer high localization accuracy but may reduce image quality due to the large amount of embedded data.
- (2)
- Block-wise schemes: Divide the image into non-overlapping blocks. Although this method may falsely mark some untampered pixels, it improves image quality by reducing the amount of embedded data.
2.3. Block-Pixel Wised Image Authentication (BP Wised) and Singular Value Decomposition (SVD Based) Image Authentication
2.4. Rezaei’s Method [20]
3. Proposed Method
3.1. Watermark Generation and Embedding
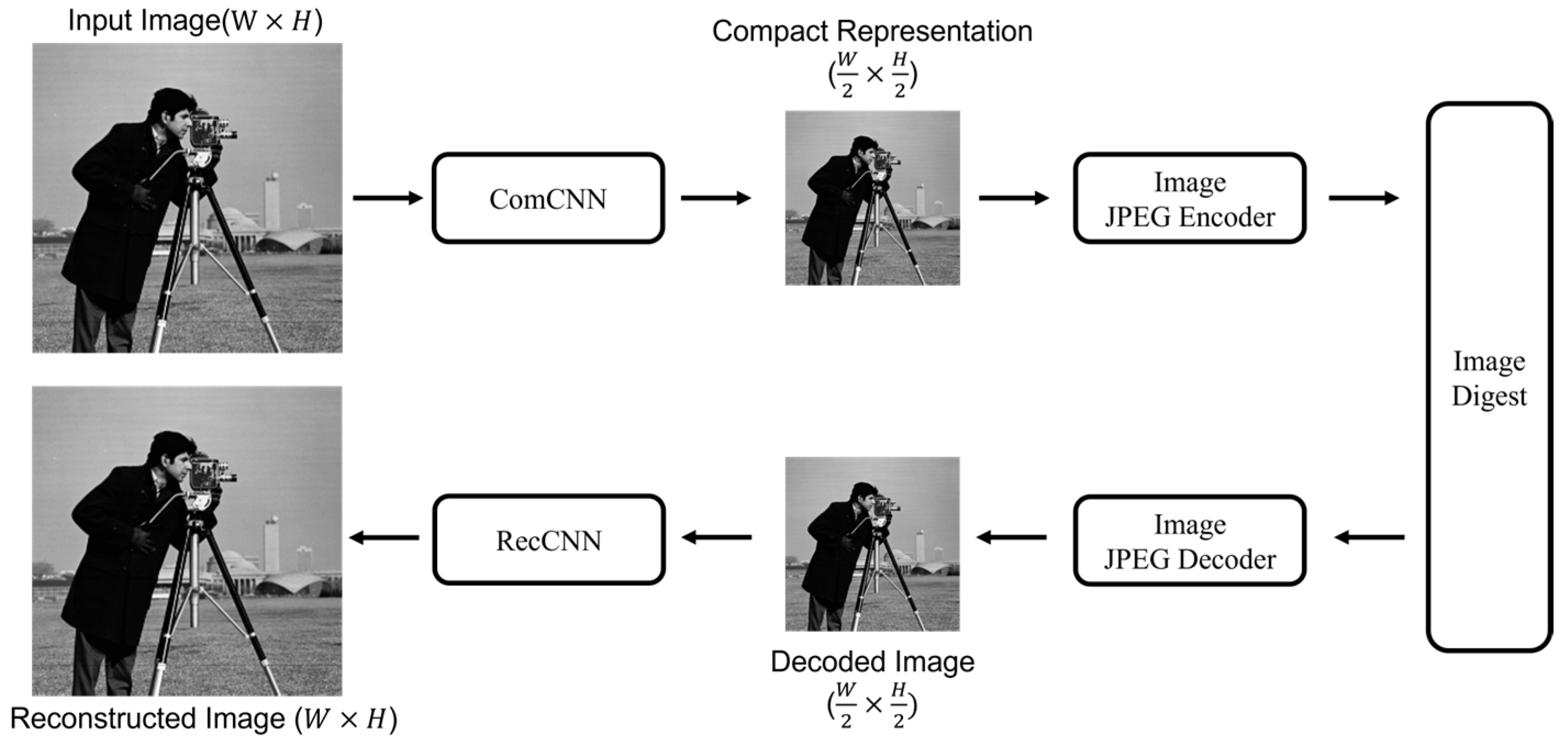
3.1.1. Encoder and Bottleneck
3.1.2. Multiple Copies
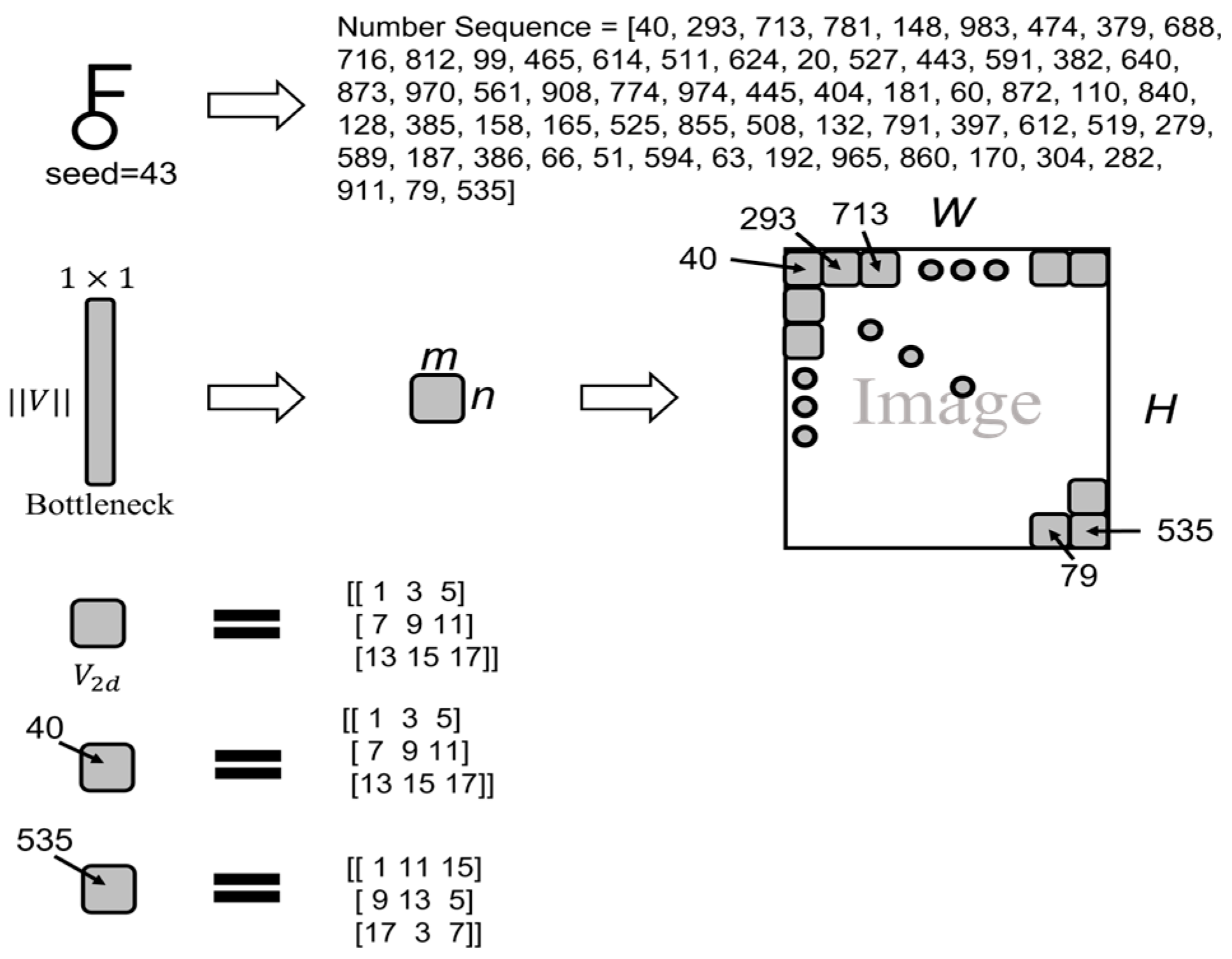
3.1.3. Number Sequence and Scrambling
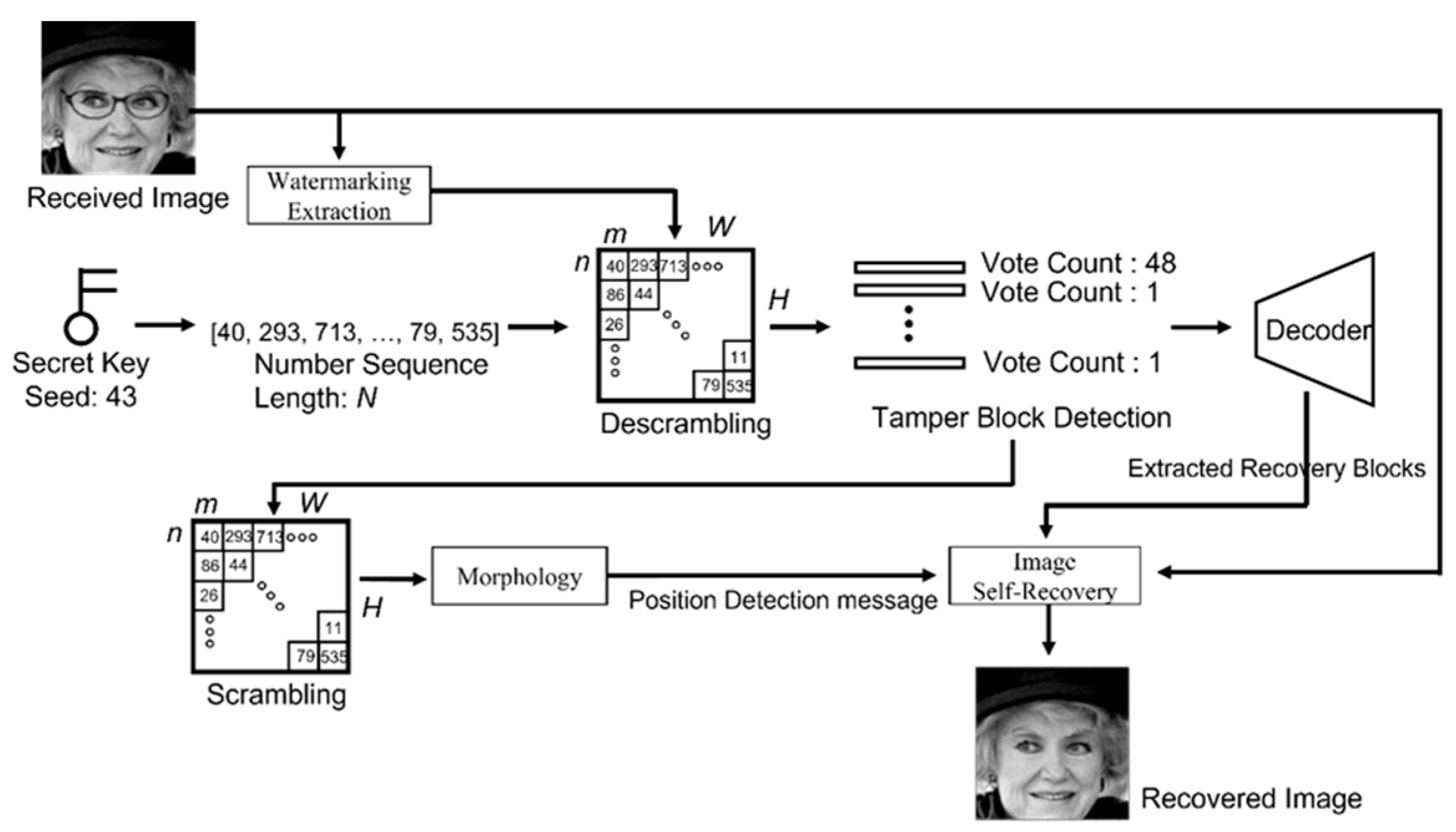
3.2. Tampering Localization and Self-Recovery
3.2.1. Watermarking Extraction, Number Sequence, and Descrambling
3.2.2. Tamper Block Detection (Vote), Scrambling, and Morphology
3.2.3. Decoder and Image Self-Recovery
4. Experimental Results
4.1. Experiment Environment and Dataset
4.2. Evaluation Metrics
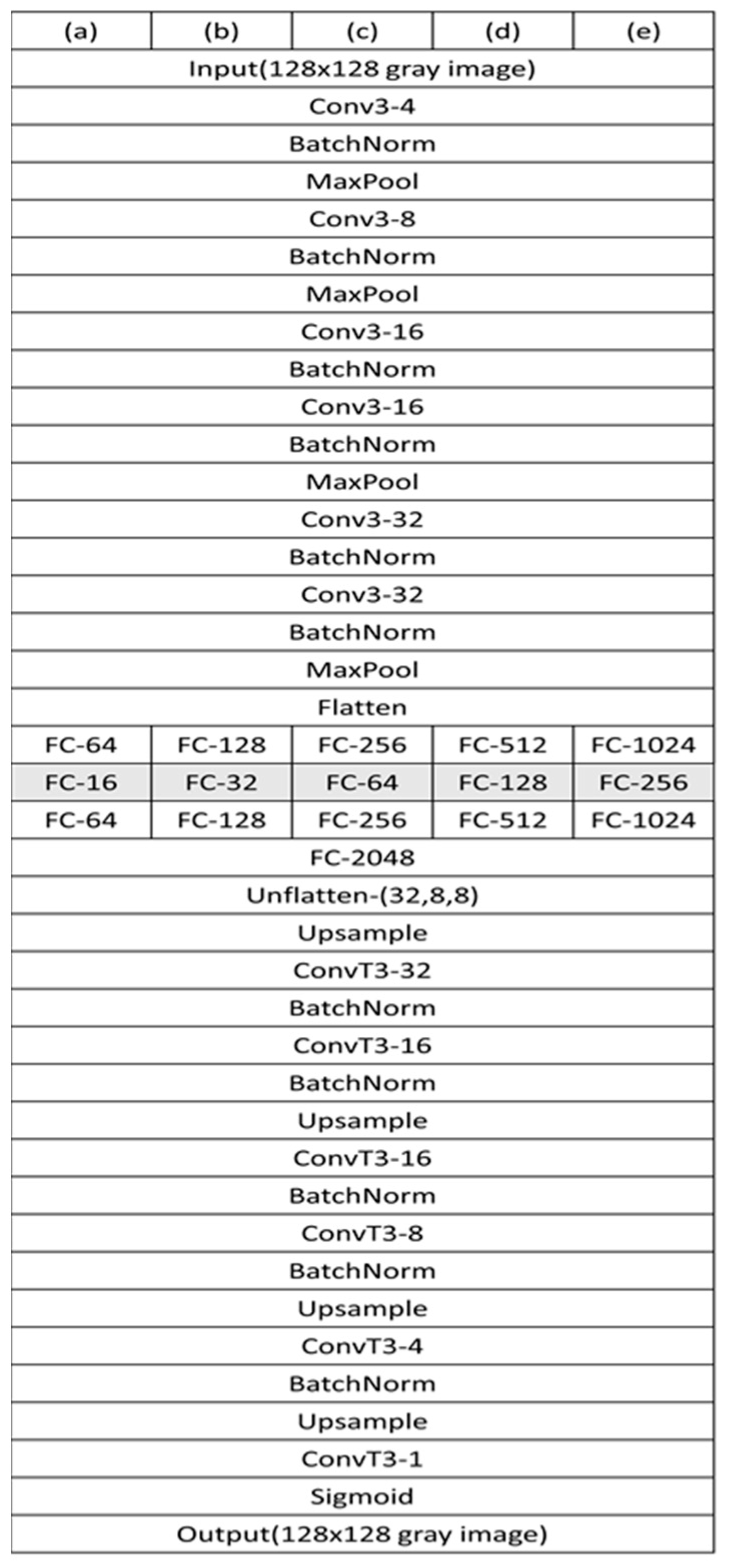
4.3. Comparison of Convolutional Autoencoders with Different Parameters
4.3.1. Need for Fully Connected Layer Design
4.3.2. Adjustment of Network Scale
4.3.3. Batch Normalization
4.3.4. Effect of Dropout
4.3.5. Loss Function Weight
4.3.6. Variation in the Number of Bottlenecks
4.4. Tampering Recovery Results Under Different Scenarios
4.4.1. Watermarked Image Quality
4.4.2. Tampering Methods in Different Scenarios
4.4.3. Analysis of Different Tampering Levels
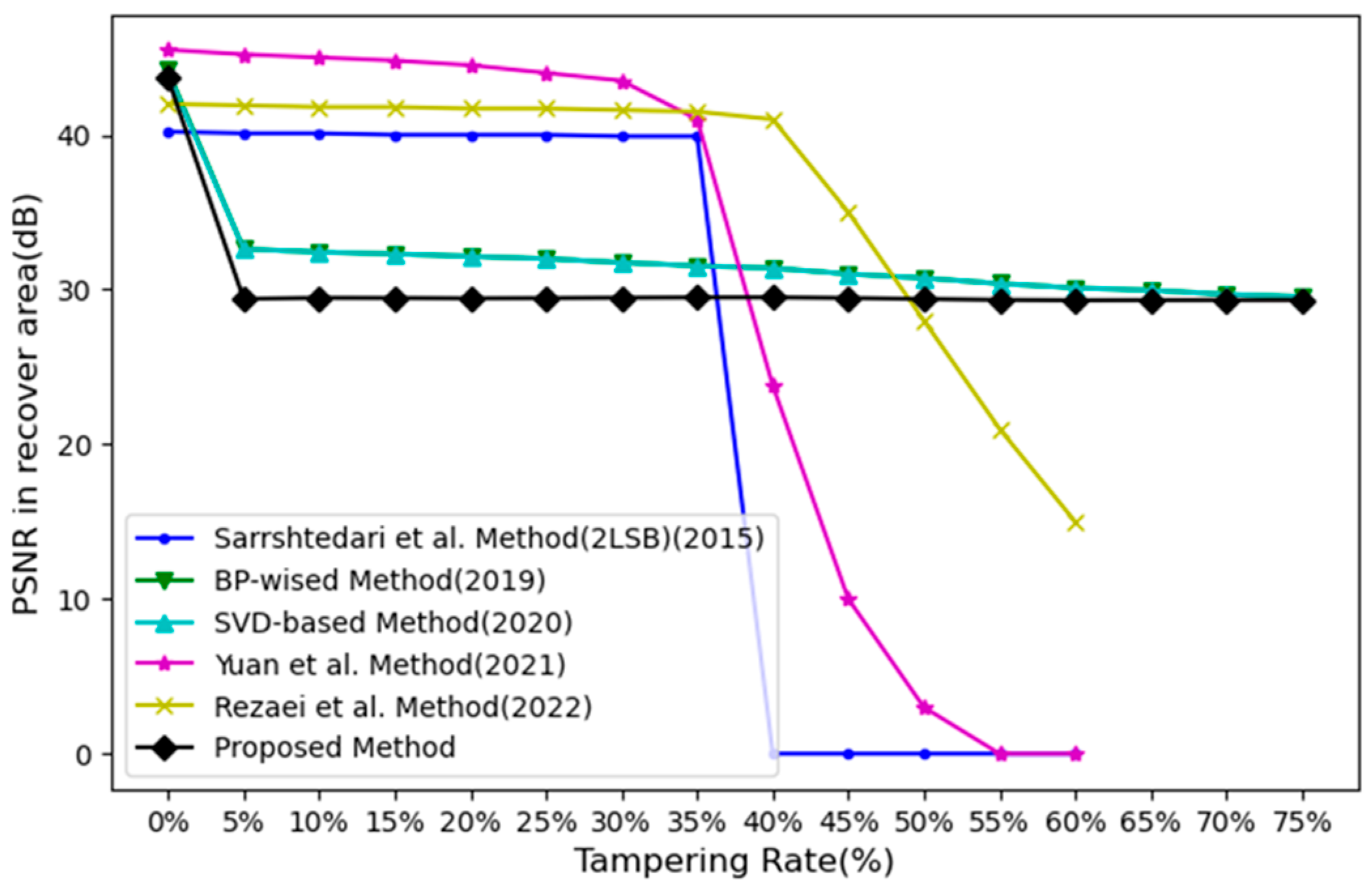
4.5. Comparison of Our Method with Other Researchers’ Methods
5. Conclusions and Future Work
5.1. Conclusions
5.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Capasso, P.; Cattaneo, G.; De Marsico, M. A Comprehensive Survey on Methods for Image Integrity. ACM Trans. Multimed. Comput. Commun. Appl. 2024, 20, 34. [Google Scholar] [CrossRef]
- Lee, W.-B.; Chen, T.-H. A Public Verifiable Copy Protection Technique for Still Images. J. Syst. Softw. 2002, 62, 195–204. [Google Scholar] [CrossRef]
- Li, X.; Guo, M.; Wang, Z.; Li, J.; Qin, C. Robust Image Hashing in Encrypted Domain. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 670–683. [Google Scholar] [CrossRef]
- Honsinger, C.W. Book Review: Digital Watermarking. J. Electron. Imaging 2002, 11, 414. [Google Scholar] [CrossRef]
- Ferrara, P.; Bianchi, T.; De Rosa, A.; Piva, A. Image Forgery Localization via Fine-Grained Analysis of CFA Artifacts. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1566–1577. [Google Scholar] [CrossRef]
- Jegou, H.; Douze, M.; Schmid, C. Hamming Embedding and Weak Geometric Consistency for Large Scale Image Search. In Computer Vision–ECCV 2008, Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008; Forsyth, D., Torr, P., Zisserman, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5302, pp. 304–317. [Google Scholar]
- Li, L.; Li, S.; Zhu, H.; Chu, S.-C.; Roddick, J.F.; Pan, J.-S. An Efficient Scheme for Detecting Copy-move Forged Images by Local Binary Patterns. J. Inf. Hiding Multim. Signal Process. 2013, 4, 46–56. [Google Scholar]
- Mushtaq, S.; Mir, A.H. Digital Image Forgeries and Passive Image Authentication Techniques: A Survey. Int. J. Adv. Sci. Technol. 2014, 73, 15–32. [Google Scholar] [CrossRef]
- Yang, C.-W.; Shen, J.-J. Recover the Tampered Image Based on VQ Indexing. Signal Process. 2010, 90, 331–343. [Google Scholar] [CrossRef]
- Di, Y.; Lee, C.; Wang, Z.; Chang, C.; Li, J. A Robust and Removable Watermarking Scheme Using Singular Value Decomposition. KSII Trans. Internet Inf. Syst. 2016, 10, 5268–5285. [Google Scholar] [CrossRef]
- Singh, D.; Singh, S. Effective self-embedding watermarking scheme for image tampered detection and localization with recovery capability. J. Vis. Commun. Image Represent. 2016, 38, 775–789. [Google Scholar] [CrossRef]
- Qin, C.; Ji, P.; Zhang, X.; Dong, J.; Wang, J. Fragile image watermarking with pixel-wise recovery based on overlapping embedding strategy. Signal Process. 2017, 138, 280–293. [Google Scholar] [CrossRef]
- Lee, C.; Shen, J.; Chen, Z.; Agrawal, S. Self-Embedding Authentication Watermarking with Effective Tampered Location Detection and High-Quality Image Recovery. Sensors 2019, 19, 2267. [Google Scholar] [CrossRef]
- Lee, C.-F.; Shen, J.-J.; Hsu, F.-W. A Survey of Semi-Fragile Watermarking Authentication. In Recent Advances in Intelligent Information Hiding and Multimedia Signal Processing; Pan, J.-S., Ito, A., Tsai, P.-W., Jain, L., Eds.; Smart Innovation, Systems and Technologies; Springer: Cham, Switzerland, 2019; Volume 109. [Google Scholar] [CrossRef]
- Rakhmawati, L.; Wirawan, W.; Suwadi, S. A recent survey of self-embedding fragile watermarking scheme for image authentication with recovery capability. EURASIP J. Image Video Process. 2019, 22, 61. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Theis, L.; Shi, W.; Cunningham, A.; Huszár, F. Lossy Image Compression with Compressive Autoencoders. arXiv 2017, arXiv:1703.00395. [Google Scholar] [CrossRef]
- Li, P.; Pei, Y.; Li, J. A comprehensive survey on design and application of autoencoder in deep learning. Appl. Soft. Comput. 2023, 138, 21. [Google Scholar] [CrossRef]
- Shen, J.-J.; Lee, C.-F.; Hsu, F.-W.; Agrawal, S. A Self-Embedding Fragile Image Authentication Based on Singular Value Decomposition. Multimed. Tools Appl. 2020, 79, 25969–25988. [Google Scholar] [CrossRef]
- Rezaei, M.; Taheri, H. Digital image self-recovery using CNN networks. Optik 2022, 264, 12. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, S. Fragile Watermarking with Error-Free Restoration Capability. IEEE Trans. Multimed. 2008, 10, 1490–1499. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Ma, B.; Zhang, Z. A novel self-recovery fragile watermarking scheme based on dual-redundant-ring structure. Comput. Electr. Eng. 2011, 37, 927–940. [Google Scholar] [CrossRef]
- Chow, Y.-W.; Susilo, W.; Tonien, J.; Zong, W. A QR Code Watermarking Approach Based on the DWT-DCT Technique. In Information Security and Privacy–ACISP 2017, Proceedings of the 22nd Australasian Conference on Information Security and Privacy, Auckland, New Zealand, 3–5 July 2017; Lai, J., Ed.; Springer: Cham, Switzerland, 2017; Volume 10343, pp. 314–331. [Google Scholar]
- Jiang, F.; Tao, W.; Liu, S.; Ren, J.; Guo, X.; Zhao, D. An End-to-End Compression Framework Based on Convolutional Neural Networks. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 3007–3018. [Google Scholar] [CrossRef]
- Padhi, S.K.; Tiwari, A.; Ali, S.S. Deep Learning-Based Dual Watermarking for Image Copyright Protection and Authentication. IEEE Trans. Artif. Intell. 2024, 5, 6134–6145. [Google Scholar] [CrossRef]
- Ben Jabra, S.; Ben Farah, M. Deep Learning-Based Watermarking Techniques Challenges: A Review of Current and Future Trends. Circ. Syst. Signal Process. 2024, 43, 4339–4368. [Google Scholar] [CrossRef]
- Bui, T.; Agarwal, S.; Yu, N.; Collomosse, J. Rosteals: Robust Steganography Using Autoencoder Latent Space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 933–942. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- jessicali9530. (n.d.). CelebA dataset. Kaggle. Available online: https://www.kaggle.com/datasets/jessicali9530/celeba-dataset (accessed on 8 April 2025).
- OpenCV Team. Color Conversions. Available online: https://docs.opencv.org/4.x/de/d25/imgproc_color_conversions.html (accessed on 17 May 2025).
- Sarreshtedari, S.; Akhaee, M. A Source-Channel Coding Approach to Digital Image Protection and Self-Recovery. IEEE Trans. Image Process. 2015, 24, 2266–2277. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.; Li, X.; Liu, T. Gauss-Jordan elimination-based image tampering detection and self-recovery. Signal Process.-Image Commun. 2021, 90, 14. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]

















| No. | Notation | Description |
|---|---|---|
| (1) | original image | |
| (2) | W | weight of the original image |
| (3) | H | height of the original image |
| (4) | every block in the original image | |
| (5) | size of a block | |
| (6) | total number of blocks in an image | |
| (7) | SK | secret key (Generate block-mapping sequence) |
| (8) | V | bottleneck |
| (9) | bottleneck length is represented in bytes | |
| (10) | reshape the bottleneck into a 2D format | |
| (11) | take the square root of the length of the bottleneck (to convert it into the side length of a 2D shape) i.e., | |
| (12) | mapping block | |
| (13) | recovery code of each block | |
| (14) | mapping block recovery data | |
| (15) | authentication code of each block | |
| (16) | watermarked image | |
| (17) | tampered image | |
| (18) | authentication message (receiver) | |
| (19) | recovered image | |
| (20) | t | hyperparameter for designing the number of neurons |
| (21) | T | number of Arnold Transform iterations |
| Model Architecture | PSNR | SSIM |
|---|---|---|
| (a) | 28.417 | 0.803 |
| (b) | 28.581 | 0.849 |
| (c) | 28.583 | 0.850 |
| (d) | 28.328 | 0.796 |
| Model Architecture | PSNR | SSIM |
|---|---|---|
| (a) | 28.583 | 0.850 |
| (b) | 29.160 | 0.906 |
| Model Architecture | PSNR | SSIM |
|---|---|---|
| (a) FC-16 | 28.664 | 0.857 |
| (b) FC-32 | 28.846 | 0.879 |
| (c) FC-64 | 29.297 | 0.921 |
| (d) FC-128 | 29.299 | 0.927 |
| (e) FC-256 | 29.351 | 0.939 |
| PSNR | SSIM | |
|---|---|---|
| (a) | 43.654 | 0.999 |
| Tampering Level | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 75% |
|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | 43.654 | 37.964 | 35.742 | 34.282 | 33.162 | 32.238 | 31.383 | 30.787 | 30.518 |
| SSIM | 0.999 | 0.991 | 0.984 | 0.977 | 0.971 | 0.963 | 0.953 | 0.946 | 0.943 |
| Tampering Level | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 75% |
|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | 43.654 | 29.462 | 29.432 | 29.468 | 29.492 | 29.390 | 29.311 | 29.324 | 29.322 |
| SSIM | 0.999 | 0.812 | 0.872 | 0.908 | 0.922 | 0.921 | 0.920 | 0.924 | 0.924 |
| Tampering Level | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 75% |
|---|---|---|---|---|---|---|---|---|---|
| Recall | - | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Precision | - | 0.941 | 0.984 | 0.989 | 0.984 | 1 | 0.989 | 0.995 | 1 |
| F1-Score | - | 0.969 | 0.992 | 0.994 | 0.992 | 0.999 | 0.994 | 0.997 | 0.999 |
| Tampering Level | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 75% |
|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | 43.654 | 37.964 | 35.742 | 34.282 | 33.140 | 32.218 | 31.364 | 30.771 | 30.502 |
| SSIM | 0.999 | 0.991 | 0.984 | 0.977 | 0.958 | 0.950 | 0.938 | 0.932 | 0.929 |
| Tampering Level | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 75% |
|---|---|---|---|---|---|---|---|---|---|
| PSNR (dB) | 43.654 | 29.397 | 29.402 | 29.425 | 29.466 | 29.368 | 29.29 | 29.307 | 29.306 |
| SSIM | 0.999 | 0.664 | 0.79 | 0.844 | 0.887 | 0.894 | 0.896 | 0.904 | 0.906 |
| Tampering Level | 0% | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 75% |
|---|---|---|---|---|---|---|---|---|---|
| Recall | - | 0.965 | 0.982 | 0.978 | 0.985 | 0.988 | 0.987 | 0.989 | 0.99 |
| Precision | - | 0.965 | 0.984 | 0.99 | 0.984 | 1 | 0.99 | 0.995 | 1 |
| F1-Score | - | 0.965 | 0.983 | 0.984 | 0.985 | 0.994 | 0.989 | 0.992 | 0.995 |
| Method | PSNR | SSIM |
|---|---|---|
| BP-wised (2019) [13] | 44.163 | 0.999 |
| SVD-based (2020) [19] | 44.013 | 0.999 |
| Rezaei et al. (2022) [20] | 44.2 | - |
| Proposed Method | 43.654 | 0.999 |
| Schemes | Tamper Rate | 10% | 20% | 40% |
|---|---|---|---|---|
| Sarreshtedari et al. [32] (2015) | Recall | 1 | 1 | 1 |
| Precision | 1 | 1 | 1 | |
| F1-Score | 1 | 1 | 1 | |
| BP-wised [13] (2019) | Recall | 0.999 | 0.999 | 1 |
| Precision | 0.839 | 0.914 | 0.984 | |
| F1-Score | 0.912 | 0.955 | 0.992 | |
| SVD-based [19] (2020) | Recall | 0.999 | 0.999 | 0.999 |
| Precision | 0.939 | 0.943 | 0.984 | |
| F1-Score | 0.968 | 0.971 | 0.992 | |
| Yuan et al. [33] (2021) | Recall | 0.988 | 0.964 | 0.899 |
| Precision | 0.956 | 0.935 | 0.817 | |
| F1-Score | 0.971 | 0.949 | 0.856 | |
| Rezaei et al. [20] (2022) | Recall | 0.995 | 0.991 | 0.978 |
| Precision | 1 | 1 | 1 | |
| F1-Score | 0.997 | 0.995 | 0.988 | |
| Proposed | Recall | 0.999 | 0.999 | 0.999 |
| Precision | 0.941 | 0.984 | 0.984 | |
| F1-Score | 0.969 | 0.992 | 0.992 |
| Schemes | Tamper Rate | 10% | 20% | 40% |
|---|---|---|---|---|
| Sarreshtedari et al. [32] (2015) | Recall | 0.403 | 0.237 | 0.112 |
| Precision | 1 | 1 | 1 | |
| F1-Score | 0.574 | 0.383 | 0.201 | |
| BP-wised [13] (2019) | Recall | 0.062 | 0.062 | 0.047 |
| Precision | 0.245 | 0.398 | 0.752 | |
| F1-Score | 0.099 | 0.107 | 0.089 | |
| SVD-based [19] (2020) | Recall | 0.062 | 0.015 | 0.015 |
| Precision | 0.490 | 0.231 | 0.504 | |
| F1-Score | 0.110 | 0.029 | 0.030 | |
| Yuan et al. [33] (2021) | Recall | 0.982 | 0.969 | 0.897 |
| Precision | 0.956 | 0.931 | 0.812 | |
| F1-Score | 0.968 | 0.949 | 0.852 | |
| Rezaei et al. [20] (2022) | Recall | 0.996 | 0.991 | 0.977 |
| Precision | 1 | 1 | 1 | |
| F1-Score | 0.997 | 0.995 | 0.988 | |
| Proposed | Recall | 0.965 | 0.982 | 0.985 |
| Precision | 0.965 | 0.984 | 0.984 | |
| F1-Score | 0.965 | 0.983 | 0.985 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-F.; Li, T.-M.; Lin, I.-C.; Rehman, A.U. A Novel Self-Recovery Fragile Watermarking Scheme Based on Convolutional Autoencoder. Electronics 2025, 14, 3595. https://doi.org/10.3390/electronics14183595
Lee C-F, Li T-M, Lin I-C, Rehman AU. A Novel Self-Recovery Fragile Watermarking Scheme Based on Convolutional Autoencoder. Electronics. 2025; 14(18):3595. https://doi.org/10.3390/electronics14183595
Chicago/Turabian StyleLee, Chin-Feng, Tong-Ming Li, Iuon-Chang Lin, and Anis Ur Rehman. 2025. "A Novel Self-Recovery Fragile Watermarking Scheme Based on Convolutional Autoencoder" Electronics 14, no. 18: 3595. https://doi.org/10.3390/electronics14183595
APA StyleLee, C.-F., Li, T.-M., Lin, I.-C., & Rehman, A. U. (2025). A Novel Self-Recovery Fragile Watermarking Scheme Based on Convolutional Autoencoder. Electronics, 14(18), 3595. https://doi.org/10.3390/electronics14183595







