Abstract
Current technical approaches find it challenging to reduce hydrogen production costs in combined cooling, heating, and power (CCHP) microgrids integrated with hydrogen refueling stations (HRS). Furthermore, the stability of such systems is significantly impacted by multiple uncertainties inherent on both the source and load sides. Therefore, this paper proposes a two-stage robust optimization for bi-level game-based scheduling of a CCHP microgrid integrated with an HRS. Initially, a bi-level game structure comprising a CCHP microgrid and an HRS is established. The upper layer microgrid can coordinate scheduling and the step carbon trading mechanism, thereby ensuring low-carbon economic operation. In addition, the lower layer hydrogenation station can adjust the hydrogen production plan according to dynamic electricity price information. Subsequently, a two-stage robust optimization model addresses the uncertainty issues associated with wind turbine (WT) power, photovoltaic (PV) power, and multi-load scenarios. Finally, the model’s duality problem and linearization problem are solved by the Karush–Kuhn–Tucker (KKT) condition, Big-M method, strong duality theory, and column and constraint generation (C&CG) algorithm. The simulation results demonstrate that the strategy reduces the cost of both CCHP microgrid and HRS, exhibits strong robustness, reduces carbon emissions, and can provide a useful reference for the coordinated operation of the microgrid.
1. Introduction
In the context of global warming and the depletion of fossil energy reserves, developing and utilizing renewable energy has attracted considerable attention worldwide [1]. The concept of a renewable energy microgrid, comprising WT and PV power generation, has garnered significant interest due to its dual benefits of cost-effectiveness and carbon emission reduction when integrated with a broader energy system [2]. The integration of high-penetration renewable energy sources into microgrids poses significant challenges to system stability and the reliability of smooth operation [3]. However, the inherent uncertainty of renewable energy generation and load demand in the microgrid has also prompted research by numerous scholars [4]. Hydrogen energy possesses high energy density and zero-pollution characteristics, and the production and utilization of hydrogen energy in the renewable energy microgrid can enhance the absorption rate of renewable energy. The literature [5,6] has been instrumental in enhancing the power utilization rate through the surplus electricity of microgrids or renewable energy hydrogen production. However, within the hydrogen energy industry, HRS that produce hydrogen energy must purchase energy from microgrids. Therefore, electricity price exerts a substantial influence on hydrogen production scheduling. Given the inherent difficulty of existing technical approaches in reducing hydrogen production costs within the hydrogen industry, this paper addresses this challenge by focusing on lowering the electricity consumption cost during the hydrogen production process. To this end, a rigorous analysis is conducted on the complex synergistic interactions between the microgrid and hydrogen refueling station. Simultaneously, significant attention is paid to the critical issue of uncertainty originating from both the source and load sides within the microgrid under low-carbon operations, as it poses a challenge to system stability.
To date, scholars worldwide have conducted research on the management of uncertainties in renewable energy microgrids. The predominant methodologies employed encompass stochastic optimization (SO) and robust optimization (RO) techniques [7]. Among the more novel stochastic optimization methods are the following: The distributed stochastic recursive gradient method and the distributed stochastic linear quadratic optimization method are two important algorithms in this field. The distributed stochastic recursive gradient method has been shown to reduce communication overhead and to converge rapidly. However, its theoretical analysis is complex and it exhibits sensitivity to communication constraints, rendering it suitable for simulating uncertainty scenarios in multi-area power systems. Distributed stochastic linear quadratic optimization is predicated on linear models, thus limiting its applicability to non-linear scenarios. Furthermore, the risk constraints that are introduced result in additional complexity [8,9]. Common RO methods include static RO and two-stage RO. The static RO method solves for the optimal solution in the worst case, but the result is too conservative. In contrast, the two-stage RO method enhances the optimization objective through two-stage optimization, taking into account the impact of uncertain parameters on decision-making processes. The uncertainty of PV and WT output has been considered in the literature [10], with interval linear programming adopted to address the relationship between decision and uncertain variables. However, this method is only applicable within a certain precision range, and the solution results of the linearization process are not accurate. In contrast, the literature [11] proposes a two-stage RO strategy, utilizing the C&CG algorithm to address the uncertainty in renewable energy output. This approach culminates in the identification of an optimal solution. In another study [12], the authors proposed a two-stage RO model to address the uncertainty in power and load in multi-energy microgrids. They employed the KKT conditions, the Big-M method, and the C&CG algorithm to solve the model, demonstrating the efficacy of this strategy in considering the economic and security aspects of microgrids. The C&CG algorithm exploits the inherent mathematical structure of the two-stage problem, thereby enabling it to deliver results efficiently and with precision. In the literature [13,14], the use of cascade carbon trading was demonstrated to constrain carbon emissions in microgrids. Furthermore, the literature [15,16] considers environmental factors in the renewable energy microgrid and integrates stepped carbon trading into the two-stage robust model, so that the microgrid can reduce carbon emissions while maintaining both economy and robustness.
The extant literature addresses the issue of uncertainty in microgrids, yet it does not consider the strategic interactions among the various stakeholders in microgrids. The literature [17,18,19,20,21,22] adopts a different approach by establishing microgrid operators as the upper echelon of the game and user aggregators as the lower level, to enhance economic efficiency. However, the literature [23,24] has addressed the impact of uncertain factors in the bi-level game process. Specifically, one piece of the literature [23] has focused on source-side uncertainty through scene reduction, while another [24] has concentrated on PV output uncertainty without addressing load-side uncertainty. Moreover, the extant literature fails to consider the joint supply of electricity, heat, and cooling load required by the staff of the two layers of game players, which makes it difficult to meet the actual needs of the project.
Therefore, reducing hydrogen production costs at refueling stations while ensuring microgrid economic operation necessitates research into win–win collaboration between microgrids and hydrogen stations under source–load uncertainties. Simultaneously, exploring the robustness economy and low-carbon trade-offs is critical for advancing both microgrid and hydrogen energy industries.
In summary, the principal distinctions between this paper and the extant literature are delineated in Table 1. The √ and × in Table 1 are used to denote consideration and non-consideration, respectively. The proposed two-stage robust bi-level game optimization scheduling strategy for a CCHP microgrid with an HRS is the primary focus of this paper, and its main contributions are as follows:

Table 1.
Summary of the literature review.
- (1)
- A bi-level game framework between the CCHP microgrid and HRS is established, where hydrogen production scheduling is dynamically optimized through electricity price interactions to achieve cost efficiency.
- (2)
- A two-stage RO method incorporating a game framework has been developed to mitigate the conservatism of traditional static RO strategies by simultaneously addressing uncertainties on both generation and load sides.
- (3)
- The integration of a stepped carbon trading mechanism into the two-stage robust game optimization model demonstrates synergistic improvements in operational economy, system robustness, and emission reduction.
2. Integrated System Architecture
The bi-level game architecture between the CCHP microgrid and the HRS constructed in this paper is illustrated in Figure 1. It involves two stakeholders: the CCHP microgrid and the HRS. The CCHP microgrid includes wind turbine (WT) and photovoltaic (PV) units, is connected to the external power grid and the natural gas network, and integrates combined heat and power (CHP), gas boilers (GBs), absorption chillers (ACs), electric chillers (ECs), electric energy storage (EES), and heat storage tanks (HSTs) to supply the electrical, thermal, and cooling loads required by consumers. HRS, utilizing electrolysis of water with Electrolyzers (ELs), are responsible for the production of hydrogen. This hydrogen is then stored in hydrogen energy storage (HES) to ensure a reliable supply to meet the energy demands. During operation, the upper layer of the CCHP microgrid provides electric energy to the lower HRS, supplies the HRS with electrolytic water to produce hydrogen, and prices the electric energy. The HRS reacts according to the electricity price to adjust its hydrogen production demand. As these two subjects are of differing interests, each seeks to maximize its interests. Therefore, the optimization of the process must take into account the interests of both.
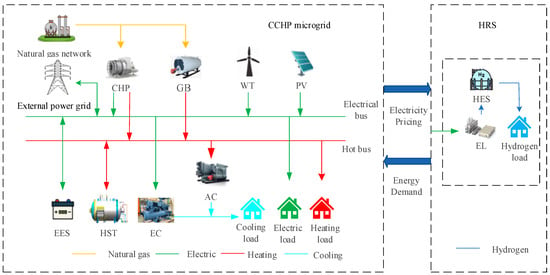
Figure 1.
Bi-level gaming architecture of CCHP microgrid and HRS.
The optimization of this process is primarily divided into two stages. The initial stage constitutes a bi-level game between the CCHP microgrid and the HRS, wherein the CCHP microgrid assumes a leadership role at the upper level. Utilizing scenarios on both sides of the source and load following uncertainty optimization in the second stage, the electricity price is set for the lower level to maximize its interests. It is the objective of HRS, operating as a subordinate entity, to minimize its own costs by adjusting its hydrogen production schedule in accordance with information regarding electricity prices. The system engages in demand response for hydrogen production in conjunction with HES, thereby providing feedback on electricity prices and participating in electricity price negotiations with the CCHP microgrid. The second stage addresses the uncertainty surrounding both sides of the source–load. The robust optimal scheduling scheme is obtained through two-stage RO, as per the conclusion of the bi-level game optimization in the first stage. It is imperative to reiterate the above two stages iteratively to ascertain the optimal solution.
3. Model Formulation
3.1. CCHP Microgrid
3.1.1. Objective Function of CCHP Microgrid
The objective of the CCHP microgrid is to minimize the cost of energy, including the income from selling electricity to the external grid and HRS, the cost of purchasing electricity from the grid, the cost of purchasing gas from natural gas, the cost of energy storage loss, and the cost of carbon trading.
where is the cost of purchasing electricity from the grid; is the cost of purchasing gas; is the cost of storage losses; is the cost of carbon trading; is the revenue from electricity sales to the grid; and is the revenue from electricity sales to HRS.
The details of each cost in Equation (1) are expressed below:
where T is a scheduling cycle, taken as 24 h in this paper; is the price of electricity purchased from the external grid at the time; is the amount of electricity purchased from the external grid at the time; is the price of gas purchased from the natural gas network at the time; is the amount of gas purchased from the natural gas network of the external grid at the time; , , and are the unit loss cost of electric, thermal, and hydrogen energy storage equipment, respectively; and are the charging and discharging quantities of electric energy storage equipment; and are the charging and discharging quantities of hydrogen energy storage equipment; and are the charging and discharging quantities of thermal energy storage equipment; is the price of electricity sold to the external grid at the time; is the amount of electricity purchased from the external grid at the time; is the price of electricity sold to the HRS at the time; and is the amount of electricity sold to the HRS at the time.
In this paper, a stepped carbon trading strategy is adopted to regulate carbon emissions in the CCHP microgrid. The following section details the system’s carbon trading cost calculation methodology.
The model under discussion is a stepped carbon trading model in a CCHP microgrid, which comprises three constituent parts: the carbon emission quota model, the actual carbon emission model, and the stepped carbon emission model.
In the microgrid under discussion in this paper, the carbon emission source is derived from the upper power grid, the CHP unit, and the GB unit. The calculation of carbon emission allowances is outlined as follows:
where , , and denote the carbon emission allowances for the external grid, CHP unit, and GB unit, respectively; and is the total carbon allowance; , , and are the carbon allowance coefficients of the external grid, CHP unit, and GB unit, respectively.
The actual carbon emissions are calculated as follows:
where is the total amount of actual carbon emissions; and , , and are the actual carbon emissions from the external grid, CHP unit, and GB unit, respectively. and are the actual carbon emission allowances per unit of thermal power and unit of electrical power, respectively; and is the electricity–heat conversion coefficient. and are the electric power and thermal power of the CHP unit, respectively; and is the thermal power of GB unit.
Stepped carbon emissions are modeled as follows:
where is the actual carbon trading amount of the CCHP microgrid; is the length of the step carbon emission interval; is the base price of the step carbon trading; and is the growth rate of the carbon trading price.
3.1.2. Constraints of CCHP Microgrid
To ensure proper operation of the CCHP microgrid, the following operational constraints must be satisfied:
The CHP unit operating constraints are
where and are the gas-to-electricity and gas-to-heat conversion efficiencies of the CHP unit, respectively; and are the gas-to-electricity and gas-to-heat conversion coefficients of the CHP unit, respectively; and and are the upper and lower bounds of the power generation of the CHP unit, respectively.
GB unit operational constraints:
where is the gas–heat conversion efficiency of GB unit; is the gas–heat conversion coefficient of GB unit; and and are the upper and lower limits of the thermal power of GB unit, respectively.
AC operational constraints:
where is the cooling power of AC equipment; is the refrigeration coefficient of AC equipment; is the heat dissipation power of AC equipment; and and are the upper and lower limits of the cooling power of AC equipment.
EC operational constraints:
where is the cooling power of EC equipment; is the refrigeration coefficient of EC equipment; is the power consumption of EC equipment; and and are the upper and lower limits of the cooling power of EC equipment.
Operational constraints on energy storage equipment:
The energy storage equipment of the CCHP microgrid includes the EES and the HST, and the energy storage equipment of the HRS is the HES, which is modeled uniformly in this paper because they have similar operation processes:
where is the storage capacity at the time of the energy storage device; and and are the charging and discharging efficiencies of the energy storage device, respectively.
where and are the “0–1” state variables of the energy storage device, respectively.
Purchase and sale of energy constraints:
where and are the ‘0–1’ state variables of electricity purchase and sale, respectively.
The constraint of gas purchase between the CCHP microgrids and the external natural gas network is reflected in the energy-using unit. The energy sale constraint between the CCHP microgrids and the HRS is reflected in the constraint conditions of the HRS.
Energy balance constraints of CCHP Microgrids:
The CCHP microgrid must satisfy the energy balance constraints for all three energy forms: electricity, heating, and cooling.
Energy price constraints:
3.2. HRS
3.2.1. Objective Function of HRS
The maintenance costs of HES are relatively fixed, with extended maintenance cycles that exert minimal influence on intraday optimization. Furthermore, they have negligible impact on revealing the core game-theoretic interaction mechanism discussed herein.
The objective function of the HRS is to minimize the cost of hydrogen production:
3.2.2. Constraints of HRS
The HRS operation is subject to four categories of constraints:
The EL operational constraints are as follows:
where is the hydrogen production coefficient of the EL device; and and are the upper and lower limits of the power consumption of the EL device, respectively.
HES operation constraints:
The HES operation process is similar to that of EES and HST and, therefore, will not be modeled separately.
Purchase of energy constraints:
Energy balance constraints of HRS:
HRS must be designed in a manner that facilitates the harmonious integration of electric and hydrogen power sources, thereby ensuring the optimal balance between these energy domains.
3.3. Two-Stage Robust Bi-Level Game Optimization Model
In this paper, the bi-level game process between the CCHP microgrid and the HRS is considered as well as the uncertainty on both sides of the source and load. To this end, a two-stage robust bi-level game optimization model is formulated as follows:
where x denotes the set of decision variables in the first stage, and y denotes the set of decision variables in the second stage.
In order to simplify the model’s complexity and computational burden, the present paper assumes that the uncertainties associated with each load are mutually independent. In this paper, polyhedral uncertainty sets are employed to delineate the uncertainties on both sides of the source and the load of the CCHP microgrid. The uncertainty of the PV output on the source side is taken as an example to describe its feasible domain:
The uncertainty patterns of WT output and load side are analogous to the aforementioned scenario, and thus, a detailed discussion on these subjects is deemed superfluous.
4. Model Solution
4.1. Transformation of the Bi-Level Game Between the CCHP Microgrid and the HRS
In the two-stage robust two-level game optimization model of Equation (22), the first stage involves a two-level game between the CCHP microgrid and the HRS. In order to solve this problem effectively, it is necessary to transform the two-level structure into an equivalent single-level mathematical programming problem with equilibrium constraints. The crux of this transformation is predicated on the substitution of the original lower-layer HRS problem with its optimality necessary conditions. In order to achieve this, it is necessary to equate the HRS expressions using KKT conditions and the Big-M method. This process should then be followed by the subsequent incorporation of these expressions as constraints into the CCHP microgrid model. The decisions made by the upper-layer leader are predicated on the assumption that the lower-layer follower will always respond in an optimal manner. This constitutes the fundamental mechanism for converting the two-layer game into a single-layer problem. The KKT conditions are the first-order necessary conditions for optimality in convex optimization problems. As the decision variables in the lower-level HRS problem form a linear programming formulation, its KKT conditions serve both as necessary and sufficient conditions for optimality. This suggests that the solution provided by the upper level constitutes the optimal solution for HRS precisely when it satisfies the KKT conditions and is incorporated as constraints into the CCHP microgrid model. The specific process is delineated as follows:
To facilitate the expression of the conversion process, the objective function (17) of the HRS and its constraints are written in compact form as follows:
where is the tariff set by the upper CCHP microgrid for the lower HRS; is the amount of electricity purchased by the lower HRS from the upper CCHP microgrid; is the coefficient matrix of the objective function (17); and , , and are the coefficient matrices and constant matrices of the upper and lower constraints, respectively.
The primary challenge in this transformation process stems from complementary slackness conditions, which are inherently non-linear and combinatorial in nature, rendering the resulting single-layer problem difficult to address directly. The Big-M method is employed to linearize these conditions. It is evident that each complementary slackness condition is replaced by a linear constraint that is described using a binary variable and a large constant, M.
The KKT conditions and the Big-M method were utilized to extract and linearize the linear and complementary constraints of the model as follows:
where is the Lagrange multiplier; M denotes a very large number; and is the state variable.
Through the described transformation, constraints (25) and (26) are integrated into the CCHP microgrid model, converting the original bi-level game into an equivalent single-level optimization problem.
It is evident that the objective function of the lower-level HRS is a composite variable, which is formed by the product of two independent variables. Consequently, it cannot be solved directly. Notwithstanding the KKT transformation, a non-linear term remains present in the upper-level objective function. The resolution of this issue is facilitated by the strong duality theorem. In the context of strong duality, it can be demonstrated that the optimal objective function values of the primal and dual problems are equal. Consequently, the lower-level objective function can be replaced by its dual counterpart. The dual objective is expressed as a linear expression involving dual variables and problem parameters. This substitution serves to eliminate the non-linear product term in the upper-level objective function, thereby generating a fully linearized model. Therefore, the objective function is linearized through the strong duality theory as follows:
The compact form of Equation (17) is
According to the strong duality theory, the aforementioned formula is converted to
where is the coefficient matrix of the variable ; and is the constant matrix of a variable . Substituting Equation (28) into Equation (2) completes the linearization process.
This transformation increases the scale of both variables and constraints. The introduction of dual variables, auxiliary binary variables from the Big-M method, and new constraints results in a large-scale MILP. However, integrating the KKT conditions, Big-M method, and strong dual theory provides a rigorous mathematical pathway to reformulate the intractable two-layer problem into a solvable single-layer MILP, facilitating convenient solution using solvers.
The existence and uniqueness of the two-layer game equilibrium in this paper are demonstrated by the following proof: In the context of a Stackelberg game, a distinctive equilibrium solution is attained when the leader’s objective function is characterized as a non-empty, continuous function over its policy set, and the follower’s objective function is defined as a continuous convex or concave function over its policy set. In this paper, the policy set for the CCHP microgrid as the leader is the electricity selling price, with its relevant constraints given by Equations (21) and (22), which are non-empty and continuous. The objective function is given by Equation (23), which is a non-empty, continuous function of its price policy set. The strategy set constraints for the HRS as follower are given by Equations (18) through (21), which are non-empty and continuous. In addition, the objective function in Equation (17) is a continuous function with respect to its strategy set. It is evident that all strategic options are constrained by their respective parameters. Consequently, a unique Stackelberg game equilibrium solution exists for both the CCHP microgrid and the HRS.
4.2. Solution Method for the Two-Stage Robust Bi-Level Game Optimization Model
In this paper, the C&CG method is employed to solve the two-stage RO model, which is decomposed into the primary problem and the secondary problem. For the sake of convenience in representation, the two are written in compact form as follows:
where is the number of iterations; the first line of constraints represents the equation constraints and inequality constraints associated with the first stage variable ; the second line of constraints represents the constraints associated with both stages of the decision variables; and the third line of constraints represents the constraints added by the sub-problem to the master problem after the -th iteration.
The max–min problem in Equation (30) remains a two-layer problem. As previously mentioned, the KKT conditions and Big-M method are employed for dualization and linearization, respectively, and the transformation process will not be repeated. The iterative process of C&CG solving the main problem and sub-problem is shown in Figure 2.
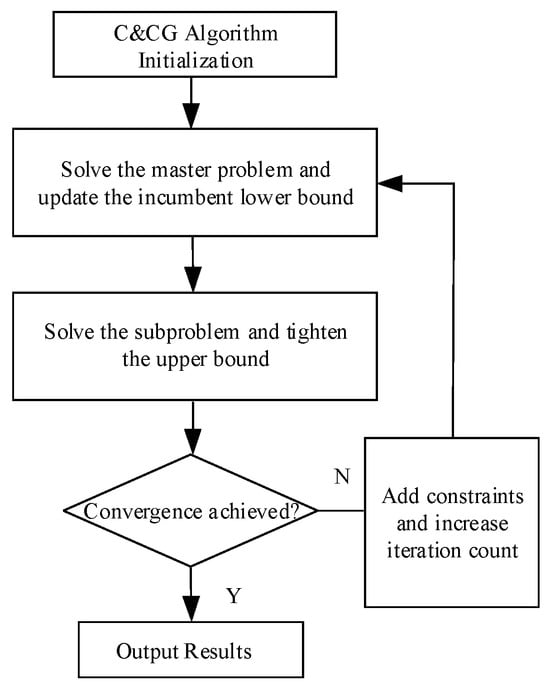
Figure 2.
The C&CG algorithm solution flow.
5. Case Study Analysis
5.1. Case Configuration
In this paper, the simulation analysis is conducted for a microgrid incorporating PV and WT, with a scheduling period of 24 h. The predicted values of electricity, heat, cold, hydrogen load, and WT and PV outputs in the microgrid are shown in Figure 3. The external grid electricity price is presented in Table 2. It is acknowledged that the works of references [7,13] have been cited in this paper. The optimized parameter selections for equipment within the CCHP microgrid are presented in Table 3. The maximum allowable fluctuation range for WT and PV outputs on the source side has been set at 15%, while the maximum permissible fluctuation range for the load side has been set at 10%. The base price of ladder carbon trading is set at 0.2 CNY/kg. The model described in this paper has been solved using the commercial solver Gurobi in MATLAB 2023b simulation platform. A comparison of the performance of Gurobi with that of CPLEX, as employed in references [4,5], demonstrates Gurobi’s superior performance in the domains of linear programming, mixed-integer programming, and quadratic programming. In this research, the authors conducted computer simulations, using a computer system with 11th Gen Intel (R) Core (TM) i5-1135G7 @ 2.40 GHz processor, 477 GB SSD drive (Dell, Xiamen, China), 16 GB RAM memory, with Microsoft Windows 11.
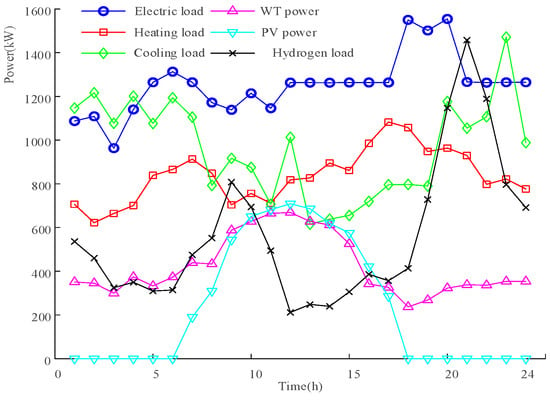
Figure 3.
Predicted values of source and load.

Table 2.
Electricity price of external grid.

Table 3.
Parameter table.
5.2. Convergence Analysis
Following the resolution of the model, the total runtime was determined to be 21.74 s, with a memory consumption of 413.77 MB being recorded. As demonstrated in Figure 4, C&CG iteratively solves the primary problem and sub-problem, updates the upper and lower bounds of the iteration, and achieves convergence conditions through two iterations. Consequently, C&CG solves the two-stage robust bi-level game optimization model in this paper with good convergence.
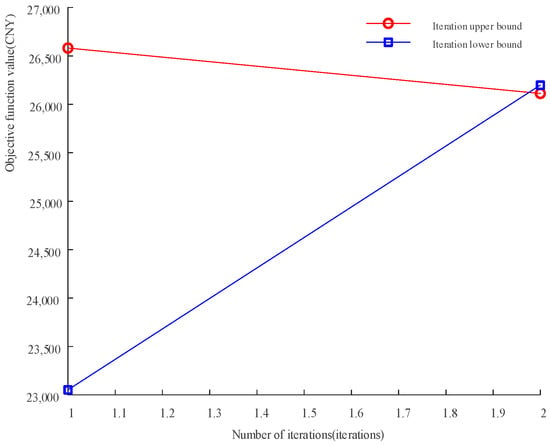
Figure 4.
C&CG iterative solution process.
5.3. Optimization Results Analysis
The optimization results for electric energy, thermal energy, and cold energy of the CCHP microgrid are presented in Figure 5. Figure 6 presents the results of the optimization of hydrogen energy and the purchase price of electricity at an HRS. Figure 7 presents the two-stage RO results of WT and PV output at the source side under a fluctuation range of 15% and at the load side under a fluctuation range of 10%.
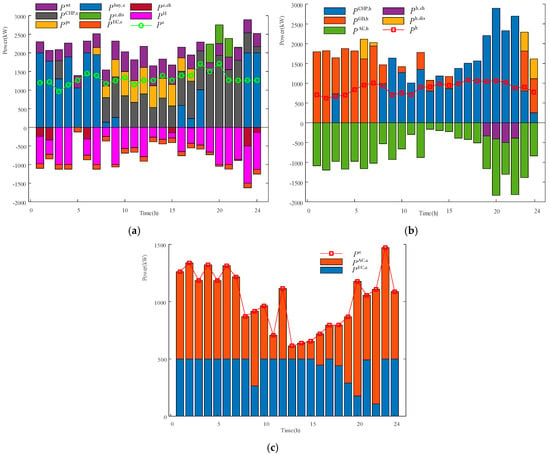
Figure 5.
CCHP microgrid dispatch results: (a) electric power balance diagram; (b) thermal power balance diagram; and (c) cooling power balance diagram.
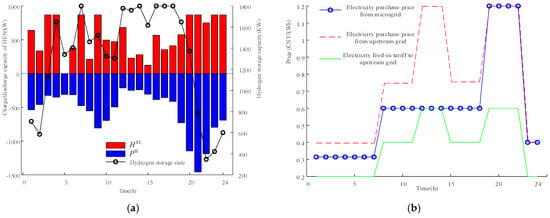
Figure 6.
HRS optimization results: (a) hydrogen power balance diagram; and (b) optimized electricity purchase pricing.
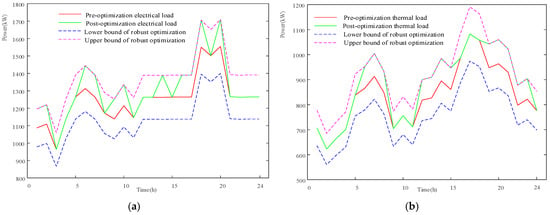
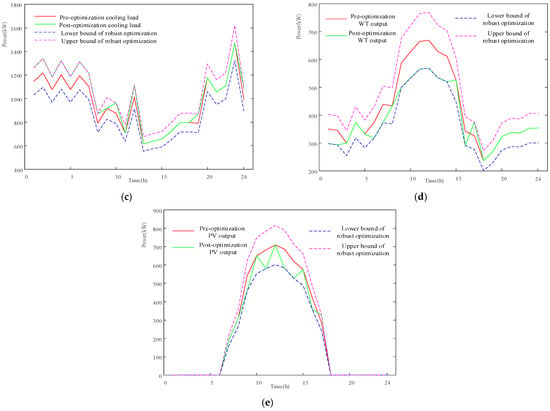
Figure 7.
Two-stage RO results: (a) two-stage RO results of electrical load; (b) two-stage RO results of thermal load; (c) two-stage RO results of cooling load; (d) two-stage RO results of WT output; and (e) two-stage RO results of PV output.
The scheduling strategy is primarily driven by time-of-use electricity pricing. The microgrid acquires substantial volumes of electricity during off-peak tariff periods with a view to minimize procurement costs. During daylight hours, priority is given to zero-marginal-cost wind and solar energy in order to avoid high electricity charges. The thermal storage tank plays a pivotal role in providing temporal flexibility to decouple the heat–power coupling constraints of the CHP unit. The coordination between EC and AC embodies energy grade optimization. In the context of air conditioning systems, residual heat is accorded a high priority, given that the marginal cost of this heat approaches zero. It is only when thermal energy is inadequate that electricity is employed for EC cooling, thereby ensuring that total cooling costs are minimized. As demonstrated in Figure 5a, during the 23:00 to 7:00 time period, the CCHP microgrid purchases a substantial volume of electricity from the external grid, as this period corresponds to the time of day when power purchase is at its lowest for the grid. Conversely, throughout the remainder of the day, the microgrid prioritizes the utilization of WT and PV power supplies, thereby ensuring the maximization of renewable energy consumption. During periods of high external grid electricity prices, the microgrid primarily supplies electricity via the internal CHP system. Concurrently, it utilizes electricity storage equipment to optimize the utilization of electricity from the external grid at low prices and electricity from renewable energy sources. The CCHP microgrid’s role is twofold: firstly, it supplies its electricity requirements; secondly, it supplies the electricity required for hydrogen production at the lower HRS.
As illustrated in Figure 5b, the CCHP microgrid employs a CHP power supply for heat supply concurrently, leveraging the characteristics of CHP equipment in heat supply. The presence of a heat storage tank serves to decouple the characteristics of the CHP power supply, thereby ensuring uninterrupted heat supply. In instances where the supply of heat is inadequate or in excess, the heat storage tank becomes operational to rectify the situation. GB is the predominant source of heating for the remainder of the time.
As illustrated in Figure 5c, the cooling load is met through a combination of electric and thermal cooling methods within the CCHP microgrid. During the periods of 9:00, 16:00, 18:00–20:00, and 22:00, EC usage is reduced because there is still surplus heat energy in the microgrid. It is notable that throughout the entire period under consideration, the AC and EC devices coordinate to supply the cooling load.
The electricity price between the CCHP microgrid and HRS represents the Nash equilibrium outcome of a two-player game. This price ensures high electricity sales revenue for the microgrid while guaranteeing that HRS electricity purchase cost remains lower than its direct grid procurement cost, thereby establishing a cooperative ‘win-win zone’. The HRS functions as a price-responsive flexible load, whereby electricity is procured during periods of low pricing to facilitate the production and storage of hydrogen. During periods of high prices, the company sells stored hydrogen in order to meet demand, thereby avoiding the purchase of expensive electricity. The HES plays a pivotal role in facilitating this energy shifting capability. In the combination of Figure 6a,b, it can be observed that through the interaction between the HRS and the CCHP microgrid, the price of electricity procured from the microgrid is situated between the price of electricity purchased from the external grid. This indicates that the CCHP microgrid sells electricity to the HRS at a price higher than that sold to the external grid, and the HRS sells electricity to the microgrid shopping at a price lower than that purchased from the external grid. Consequently, both parties achieve a mutually beneficial outcome. The strategic calibration of the electricity price within this range enables the HRS to modulate its hydrogen production rationally. To illustrate this, during the 23:00–7:00 time period, characterized by a reduction in electricity prices, the HRS can maximize its hydrogen production capacity. This is achieved by utilizing the hydrogen storage tank’s maximum capacity. Conversely, during the 19:00–22:00 period, when electricity prices are high, hydrogen production is reduced, with the hydrogen load primarily being met by the hydrogen stored in the hydrogen storage tank. However, when the storage capacity of the hydrogen storage tank is depleted, the hydrogen production process necessitates the consumption of electricity.
As illustrated in Figure 7, the renewable generation and load curves represent the worst-case scenario that is feasible in practice. The scheduling solution derived from the two-stage robust optimization model ensures the system can still meet all loads under these adverse conditions. In order to achieve this, the system incurs an additional ‘robustness cost’, yet gains absolute reliability in countering uncertainty. This situation is indicative of the fundamental trade-off between robustness and cost-effectiveness that is intrinsic to robust optimization. In this paper, the uncertainties on both sides of the source and load are considered, and the optimized load and renewable energy output results are obtained through the two-stage robust bi-level game optimization strategy. As illustrated in Figure 7a–e, the microgrid is engineered to cater to power, heat, and cooling demands in the worst-case scenario within a load fluctuation range of 10% and a renewable energy output fluctuation range of 15%. This strategy has the potential to enhance the resilience of microgrid operators in the face of uncertainties.
5.4. Analysis of the Relationship Between Operating Costs and Carbon Emissions
As demonstrated in Figure 8, the base price of stepped carbon trading exerts a substantial influence on the low-carbon operation of the CCHP microgrid. An escalation in the base price of carbon trading gives rise to an augmentation in the total cost, concomitant with a decline in carbon emissions of the microgrid. Furthermore, it is observed that when the base price of carbon trading exceeds 0.2 CNY/kg, the rate of cost escalation slows down. Additionally, it is noted that when the base price of carbon trading is within the range of 0.2 CNY/kg to 0.25 CNY/kg, there is a substantial decline in carbon emissions. This decline indicates that the increase in cost has a considerable impact on reducing carbon emissions at this time.
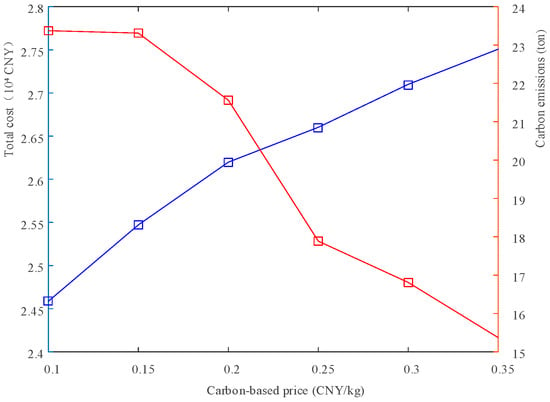
Figure 8.
Relationship between operating costs and carbon emissions.
5.5. Comparative Strategy Analysis
In order to systematically evaluate the individual contributions and synergistic effects of this paper’s two-layer game framework for HRS and CCHP microgrids, alongside its two-stage robust optimization method addressing multiple uncertainties on both the supply and demand sides, five comparative strategies have been devised.
Strategy 1: Do not deal with the uncertainty on both sides of the source and load, and do not consider the bi-level game between the CCHP microgrid and the HRS.
Strategy 2: Do not deal with the uncertainty on both sides of the source load, and consider the bi-level game between the CCHP microgrid and the HRS.
Strategy 3: The two-stage RO strategy is used to deal with the uncertainty on both sides of the source and load without considering the bi-level game between the CCHP microgrid and the HRS.
Strategy 4: The two-stage RO strategy is used to deal with the uncertainty on both sides of the source and load, and the bi-level game between the CCHP microgrid and the HRS is considered, which is the strategy of this paper.
Strategy 5: A static RO strategy is used to deal with the uncertainty on both sides of the source and load, and the bi-level game between the CCHP microgrid and the HRS is considered.
A comparative analysis of Strategies 1 and 2 (see Table 4) reveals that Strategy 2 incorporates a master–slave dynamic between the CCHP microgrid and the HRS. This results in a reduction in the CCHP microgrid’s operating cost by 795.87 CNY and a reduction in HRS operating cost by 1494.14 CNY, as compared to Strategy 1. This is attributable to the avoidance of the scenario of purchasing electricity from the grid at a high price and selling electricity at a low price, facilitated by the bi-level game strategy. Comparison and analysis of Strategies 1 and 3 are presented. Strategy 3 considers the uncertainty of source and load through a two-stage RO strategy. A cost comparison reveals that Strategy 3 incurs an additional expense of 2827.61 CNY compared to Strategy 1. This is because, following consideration of the uncertainty of source and load, the microgrid maintains operational stability within the fluctuation range, with part of the cost being sacrificed as a consequence. A cost comparison of Strategies 3 and 4 reveals that, in scenarios where the source load is uncertain, Strategy 4, which incorporates a bi-level game, results in a microgrid cost reduction of 775.94 CNY and an HRS cost reduction of 2080.03 CNY. Consequently, this strategy contributes to a reduction in the overall operating cost of the microgrid with the HRS. A comparison of Strategies 4 and 5 reveals that utilizing a static robust optimization strategy to address the uncertainty surrounding source and load can result in a substantial increase in cost. This is because static RO deals exclusively with the fluctuation range of uncertain factors through the optimization strategy of a single stage, resulting in a too conservative optimization strategy. Conversely, the two-stage RO strategy employed in this paper demonstrates clear advantages in terms of optimization conservatism, as evidenced by the results presented in Figure 7.

Table 4.
The strategy comparison table.
A comparative analysis of Strategies 1 and 2 in Table 4 reveals that Strategy 2 incorporates a master–slave game between the CCHP microgrid and the HRS. Consequently, the CCHP microgrid’s operating costs decreased by 795.87 CNY compared to Strategy 1, while HRS operating costs decreased by 1494.14 CNY. These reductions amount to 3.33% and 12.95%, respectively. This outcome is attributable to the game-theoretic strategies employed by both entities, which mitigate scenarios involving high-cost electricity procurement from the grid and low-value electricity sales. A comparison of Strategy 1 with Strategy 3 reveals that the latter employs a two-stage robust optimization approach to account for source–load uncertainty. Consequently, the costs associated with the CCHP microgrid are increased by 13.12% in comparison with Strategy 1. This cost increment arises from the necessity of maintaining microgrid operational stability within fluctuating parameters, necessitating a trade-off in cost efficiency. A comparison of Strategies 3 and 4 reveals that, under conditions of uncertain generation and load, Strategy 4 (which incorporates master–slave game theory) reduces CCHP microgrid costs by 2.88% and HRS costs by 17.64% relative to Strategy 3. Consequently, this strategy has the effect of lowering the overall operational costs of CCHP microgrids incorporating HRS. A comparison of Strategy 4 with Strategy 5 reveals that employing a static robust optimization strategy to address source–load uncertainty results in increased costs. This phenomenon can be attributed to the static robust optimization strategy, which employs boundary values within the uncertainty range, consequently yielding an optimization strategy that is excessively conservative. Concurrently, the robust optimization results for source–load uncertainty presented in Figure 7 of this paper demonstrate the advantage of the two-stage robust optimization strategy employed herein in mitigating this conservatism.
5.6. Analysis of the Relationship Between Uncertainty and Operating Costs
The uncertainty in the two-stage robust bi-level game model presented in this paper represents the maximum range of source and load fluctuations. When the uncertainty level equals zero, the microgrid operates under deterministic source–load conditions, indicating an idealized scenario devoid of stochastic fluctuations. As demonstrated in Figure 9, this scenario is characterized by the lowest operational cost. This is a gradient chart where the transition from blue to red represents rising costs—the redder the color, the higher the cost. When the uncertainty on the source side is 0.15 and the load side is 0.1, the micromesh can ensure stable operation in the worst scenario with fluctuation ranges of 15% on the source side and 10% on the load side, thereby enhancing the robustness of the microgrid. However, as depicted in Figure 9, an escalation in the uncertainty of the source and load concomitantly leads to an augmentation in the cost of the microgrid. A positive correlation between these variables is also evident, signifying that as the robustness of the microgrid increases, the economic efficiency diminishes. When the uncertainty on the supply side is maintained at zero, increasing the uncertainty on the demand side from 0 to 10% results in an 8.8% increase in costs. Conversely, when the uncertainty on the demand side is held constant at zero, increasing the uncertainty on the supply side from 0 to 10% leads to a 2.7% increase in costs. An analysis of cost trends under varying uncertainty levels reveals that the system’s total cost demonstrates a greater sensitivity to load-side uncertainty than to source-side uncertainty. This phenomenon can be attributed to the fact that the present study accounts for fluctuations in electricity, heating, and cooling loads, whereas renewable energy fluctuations are limited to wind and solar power. Consequently, microgrid operators should rationally establish uncertainty parameters based on their specific microgrid architecture and economic conditions, with the objective of enhancing robustness while maintaining economic viability.
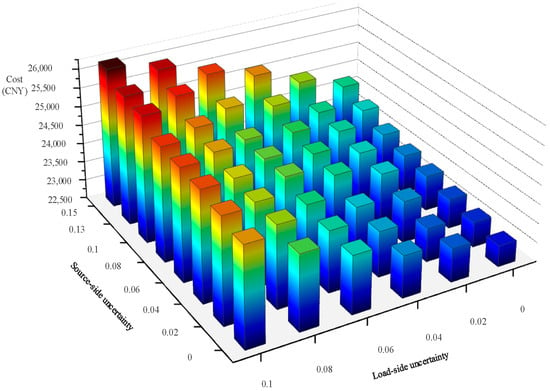
Figure 9.
Relationship between source–load uncertainty and operating costs.
5.7. Energy Price Sensitivity Analysis
As demonstrated in Table 5, the concentration of natural gas consumption within the CHP and GB equipment of the CCHP microgrid renders it susceptible to cost escalation in response to rising gas prices. However, it should be noted that the operation of the HRS consumes only electricity and does not directly utilize natural gas. The hydrogen production equipment is exclusively electrical in nature, thereby ensuring minimal impact on HRS costs from fluctuations in natural gas prices. As demonstrated in Table 6, an escalation in electricity prices to 10% has been shown to result in a concomitant rise in operational costs for both the CCHP microgrid and HRS, due to the electricity-dependent nature of their operation. However, as the price rises to 15%, the cost decreases due to the microgrid’s utilization of multiple energy sources in combined heat and power generation. In the context of elevated electricity costs, this approach can serve to mitigate the financial risks associated with high electricity expenses by decreasing electricity purchases and augmenting gas procurement.

Table 5.
Sensitivity analysis of natural gas price variations.

Table 6.
Sensitivity analysis of electricity price variations.
6. Conclusions
This paper proposes a two-stage robust bi-level game optimization scheduling strategy for a CCHP microgrid with an HRS, which addresses the uncertainties on both sides of the source and load and the bi-level game process between the CCHP microgrid and the HRS. Concurrently, a step carbon trading approach is adopted to impose constraints on the carbon emissions of the microgrid. The model is solved using the C&CG algorithm. Following simulation verification, the following main conclusions were drawn:
The CCHP microgrid and the HRS engage in a two-layer game, whereby the CCHP microgrid sells electricity at a premium, while the HRS purchases it at a discount. Concurrently, the HRS adjusts its hydrogen production behavior based on dynamic pricing information, thereby reducing the overall operational costs of the CCHP microgrid incorporating the HRS. It is noteworthy that the HRS costs are reduced by 17.64%.
The study ensures a 15% fluctuation range on the generation side and a 10% fluctuation range on the load side, thereby guaranteeing robustness. The findings of this study indicate a positive correlation between the increase in the operating cost of the CCHP microgrid and the uncertainty of source and load, as well as the increase in the carbon trading base price. Consequently, microgrid operators must balance economic requirements with robustness and low-carbon objectives.
The two-stage RO strategy outlined in this paper has the potential to enhance the resilience of the CCHP microgrid under uncertain conditions involving PV, WT, and multiple load fluctuations. Concurrently, the strategy enhances the conservatism of the static RO strategy, and the C&CG algorithm demonstrates effective convergence in addressing the model outlined in this study.
The robust optimization framework and game architecture, which are two-stage and two-layer in nature, respectively, have been proposed herein. It is important to note that these are not confined to the specific system scale and energy structure defined in this study. The method’s strength lies in its inherent generality and scalability.
The proposed scheduling mode is day-ahead scheduling; however, applications under extreme scenarios were not explored in this paper. Subsequent research endeavors will encompass the exploration of the implementation of this strategy within a range of scheduling horizons in large-scale systems confronted with extreme conditions.
Author Contributions
Methodology, J.L. and W.W.; formal analysis, J.L.; investigation, Z.Y.; data curation, J.L.; writing—original draft, Z.Y.; writing—review and editing, X.D.; supervision, Z.Y. and W.W.; project administration, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52367024).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Liu, X.; Shi, H.; Yang, D.; Chen, X.; Xia, X.A.; Xie, Y. Reducing the impact of climate change on renewable energy systems through wind–solar blending: A worldwide study with CMIP6. Sol. Energy 2025, 290, 113365. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, N.; Chen, Z.; Xu, J. Low-carbon and economic operation of energy hub considering cooperative operation strategy with wind farm and photovoltaic station. Sci. China Technol. Sci. 2024, 67, 3940–3955. [Google Scholar] [CrossRef]
- Hussan, U.; Hassan, M.; Ayub, M.A.; Peng, J.; Rasheed, H.; Jiang, H.; Asghar, F. Smooth and Uninterrupted Operation of Standalone DC Microgrid Under High and Low Penetration of RESs. IEEE Access 2024, 12, 48620–48629. [Google Scholar] [CrossRef]
- Li, B.; Zhou, Z.; Hu, J.; Yi, C. Research on Optimal Scheduling Strategy of Differentiated Resource Microgrid with Carbon Trading Mechanism Considering Uncertainty of Wind Power and Photovoltaic. Energies 2024, 17, 4633. [Google Scholar] [CrossRef]
- Li, X.; Du, Y.; Tan, Z.; He, H.; Fan, W. Optimal operation model of electrothermal integrated energy system including hydrogen production from offshore wind power participating in multi-level market. Int. J. Hydrogen Energy 2025, 114, 250–266. [Google Scholar] [CrossRef]
- Zheng, W.; Xiao, H.; Liu, Z.; Pei, W.; Beshir, M. Multi-scale coordinated optimal dispatch method of electricity-thermal-hydrogen integrated energy systems. IET Energy Syst. Integr. 2023, 5, 275–289. [Google Scholar] [CrossRef]
- Wang, L.; Dong, W.; Wang, S.; Shen, H.; Zhao, Z.; Wang, J. Optimizing flexibility and low-carbon emissions in integrated energy systems: A two-stage robust optimization model incorporating hydrogen and carbon trading. Energy Rep. 2025, 13, 1620–1631. [Google Scholar] [CrossRef]
- Hussan, U.; Wang, H.; Ayub, M.A.; Rasheed, H.; Majeed, M.A.; Peng, J.; Jiang, H. Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems. Mathematics 2024, 12, 3064. [Google Scholar] [CrossRef]
- Jia, H.; Ni, H.Y. Decentralized stochastic linear-quadratic optimal control with risk constraint and partial observation. Syst. Control Lett. 2024, 187, 105778. [Google Scholar] [CrossRef]
- Zeng, L.; Xu, J.; Wu, M.; Tang, J.; Wu, Q.; Wang, Q.; Fan, G. Day-ahead interval optimization for CCHP system considering uncertainty of wind power and PV. Int. J. Electr. Power Energy Syst. 2022, 138, 107895. [Google Scholar] [CrossRef]
- Yang, S.; Wu, H.; Song, J.; Li, H.; Chen, H. Two-stage robust optimization scheduling for integrated energy systems considering ammonia energy and waste heat utilization. Energy Convers. Manag. 2024, 319, 118922. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Li, Z.; Jiang, T.; Li, X. Two-stage robust operation of electricity-gas-heat integrated multi-energy microgrids considering heterogeneous uncertainties. Appl. Energy 2024, 37, 1123690. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhai, R.; Liu, S.; Liu, L. Low carbon economic scheduling of integrated energy system with concentrating solar power and multi-stage hydrogen utilization based on ladder-type carbon trading. Int. J. Green Energy 2025, 22, 722–739. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, J.; Tao, W.; Ai, Q. Optimization Scheduling of Combined Heat–Power–Hydrogen Supply Virtual Power Plant Based on Stepped Carbon Trading Mechanism. Electronics 2024, 13, 4798. [Google Scholar] [CrossRef]
- Zhu, Z.; Qu, Z.; Gong, J.; Li, J.; Xu, H. Robust optimal model for rural integrated energy system incorporating biomass waste utilization and power-to-gas coupling unit considering deep learning-based air conditioning load personalized demand response. Energy 2025, 321, 135484. [Google Scholar] [CrossRef]
- Zhang, L.; Hua, D.; Zheng, J.H.; Li, Z. Two-stage robust optimization for optimal operation of hybrid hydrogen–electricity storage system considering ladder-type carbon trading. J. Energy Storage 2024, 100 Pt A, 113473. [Google Scholar] [CrossRef]
- Wang, L.; Ma, Y.; Wang, S.; Dong, W.; Ni, L.; Liu, Z. Master-slave game-based optimal scheduling strategy for integrated energy systems with carbon capture considerations. Energy Rep. 2025, 13, 780–788. [Google Scholar] [CrossRef]
- Li, J.; Ji, S.; Wang, X.; Zhang, H.; Li, Y.; Qian, X.; Xiao, Y. A Stackelberg Game-Based Optimal Scheduling Model for Multi-Microgrid Systems Considering Photovoltaic Consumption and Integrated Demand Response. Energies 2024, 17, 6002. [Google Scholar] [CrossRef]
- Sun, H.; Zou, H.; Jia, J.; Shen, Q.; Duan, Z.; Tang, X. Master–Slave Game Optimization Scheduling of Multi-Microgrid Integrated Energy System Considering Comprehensive Demand Response and Wind and Storage Combination. Energies 2024, 17, 5762. [Google Scholar] [CrossRef]
- Pan, H.; Wu, Q.; Guo, H.; Bai, J. Low-Carbon Optimization Scheduling of Integrated Energy Systems Based on Bilateral Demand Response and Two-Level Stackelberg Game. Energies 2024, 17, 5491. [Google Scholar] [CrossRef]
- Shui, J.; Peng, D.; Zeng, H.; Song, Y.; Yu, Z.; Yuan, X.; Shen, C. Optimal scheduling of multiple entities in a virtual power plant based on the master-slave game. Appl. Energy 2024, 376 Pt B, 124286. [Google Scholar] [CrossRef]
- Shao, J.; Wang, J.; Qiao, R.; Wang, R.; Lei, Z.; Zhu, C.; Jin, Z. A Stackelberg game theory-based optimal scheduling of active distribution system considering multi-stakeholders. Electr. Power Syst. Res. 2024, 237, 111024. [Google Scholar] [CrossRef]
- Zhang, M.; Yan, Q.; Yu, P.; Lin, H. Game theoretic operation optimization of photovoltaic storage charging station considering uncertainty and carbon trading. J. Energy Storage 2024, 102 Pt A, 114111. [Google Scholar] [CrossRef]
- Kang, K.; Zhang, Y.; Miu, Y.; Gao, Q.; Chen, K.; Zeng, Z. Study on Master-Slave Game Optimization Operation of Integrated Energy Microgrid Considering PV Output Uncertainty and Shared Energy Storage: Regular Papers. J. Adv. Comput. Intell. Intell. Inform. 2024, 28, 528–540. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).