SwinT-SRGAN: Swin Transformer Enhanced Generative Adversarial Network for Image Super-Resolution

Abstract

To resolve the conflict between global structure modeling and local detail preservation in image super-resolution, we propose SwinT-SRGAN, a novel framework integrating Swin Transformer with GAN. Key innovations include: (1) A dual-path generator where Transformer captures long-range dependencies via window attention while CNN extracts high-frequency textures; (2) An end-to-end Detail Recovery Block (DRB) suppressing artifacts through dual-path attention; (3) A triple-branch discriminator enabling hierarchical adversarial supervision; (4) A dynamic loss scheduler adaptively balancing six loss components (pixel/perceptual/high-frequency constraints). Experiments on CelebA-HQ and Flickr2K demonstrate: (1) Very good performance (max gains: 0.71 dB PSNR, 0.83% SSIM, 4.67 LPIPS reduction vs. Swin-IR); (2) Ablation studies validate critical roles of DRB. This work offers a robust solution for high-frequency-sensitive applications.

1. Introduction

Image super-resolution (SR) technology seeks to overcome the inherent limitations of optical imaging systems. This is accomplished through the reconstruction of high-resolution (HR) images starting from their corresponding low-resolution (LR) versions [1]. As a prominent research topic in the field of computer vision (CV), SR has found significant applications in various domains. These include enhancing detail in CT scans for medical diagnostics [2], overcoming resolution limitations in satellite remote sensing [3], and improving the accuracy of facial recognition in security surveillance systems [4]. Although techniques for SR have made considerable progress, several significant challenges remain. These are primarily manifested in (1) the inherent conflict in jointly optimizing global image structure and local details, making it difficult to simultaneously achieve long-range spatial consistency and local texture fidelity; and (2) the trade-off dilemma between pixel fidelity and perceptual quality. Specifically, reconstruction methods driven primarily by Mean Squared Error (MSE) often produce overly smooth results, while complex textures are prone to introducing artifacts.

Traditional interpolation-based super-resolution methods (e.g., Bilinear interpolation [5], Bicubic interpolation [6], NEDI [7], and Contourlet-based interpolation [8]) were widely adopted due to their high computational efficiency and ease of implementation. However, they fundamentally rely on simple mathematical formulas for pixel filling and lack the ability to reconstruct realistic textures and details. This inherent limitation leads to significant drawbacks: the upscaled images often suffer from noticeable detail blurring and over-smoothing, alongside aliasing artifacts around edge regions. Consequently, their performance is limited, thus failing to meet the demand for high visual quality super-resolution outcomes.

Convolutional Neural Network (CNN) ushered in a new era of data-driven approaches, providing novel solutions for SR. SRCNN [9] pioneered an end-to-end mapping framework using a three-layer convolutional network, effectively overcoming the reliance on hand-crafted features inherent in traditional methods. However, it suffered from a limited receptive field and low computational efficiency. To expand the receptive field, VDSR [10] employed a 20-layer residual structure, enhancing reconstruction accuracy. However, its requirement for pre-interpolated input significantly increased memory consumption. Targeting high-frequency information recovery, RCAN [11] incorporated channel attention mechanisms and dense residual blocks (RRDBs). This design prioritized the enhancement of edge details and mitigated network degradation. However, its large parameter count impedes practical deployment. The SAN model [12] introduced the second-order attention mechanism, modeling long-range dependencies among channels through covariance normalization. This significantly enhanced feature representation capabilities and addressed the difficulty of capturing global correlations in traditional CNNs. Unfortunately, the computation of higher-order statistics led to a substantial increase in computational complexity. Its extension, HAN [13], constructed a multi-scale hierarchical attention structure. This progressively fused local details and global context across both spatial and channel dimensions, effectively improving cross-scale feature consistency and alleviating edge blurring. However, the redundancy introduced by its cascaded modules resulted in slow model convergence. Collectively, while these CNN-based methods have progressively addressed key challenges such as receptive field limitations, computational efficiency bottlenecks, and high-frequency detail modeling, they still commonly face persistent issues, including the accuracy-efficiency trade-off and limited multi-scale generalization capability.

The emergence of the generative adversarial network (GAN) [14] has brought image generation and image SR into a new world. The SRGAN model [15] pioneered the introduction of GAN into the SR domain. By leveraging perceptual loss and adversarial training, it could generate photo-realistic textures rich in detail, effectively addressing the overly smooth results typical of traditional methods. However, it was prone to producing artifacts and exhibited relatively low Peak Signal-to-Noise Ratio (PSNR) values. Its enhanced version, ESRGAN, incorporated Residual-in-Residual Dense Blocks (RRDBs) and a relativistic discriminator, greatly improving visual realism [16]. Nevertheless, it grappled with training instability and issues of high-frequency noise. Targeting practical application challenges, Real-ESRGAN [17] employed higher-order degradation modeling and a discriminator with spectral normalization. This effectively addressed complex blurring and noise in real-world images, albeit demanding extensive training with synthetic data. USRNet [18] embedded prior knowledge into the iterative GAN training process through unfolding optimization, achieving interpretable blind SR. However, this came with high computational costs due to iterative refinement. FeMaSR [19] introduced a feature matching mechanism to constrain the generation process, significantly enhancing identity consistency in face SR. Yet, it struggled to generalize effectively to natural scenes. Jia et al. proposed a generative adversarial network model specifically for super-resolution of retinal fundus images [20]. Its key feature is the introduction of a “vascular structure prior”. However, the performance of image super-resolution is highly dependent on the accuracy of the pre-trained vascular segmentation network. If the prior knowledge of vascular structure is inaccurate or noisy, it may mislead the super-resolution process and introduce artifacts. While current GAN-based methods have achieved breakthroughs in perceptual quality, they still commonly face challenges such as the risk of mode collapse and weak generalization to real-world scenarios.

In 2021, the Vision Transformer (ViT) model [21] was first proposed for image classification tasks. The IPT model [22] pioneered the adaptation of the ViT architecture for SR tasks. By leveraging multi-head self-attention to model global dependencies, it effectively addressed the long-range structural reconstruction problem inherent in CNNs caused by their limited receptive fields. However, it suffered from an enormous parameter count and demanded massive training data. Swin-IR [23] introduced a shifted window mechanism, extracting features within local windows to reduce computational complexity. This approach balanced global modeling with efficiency. Nevertheless, it exhibited sensitivity to rotational variations and demonstrated insufficient recovery of high-frequency details. Restormer [24] employed channel-wise self-attention combined with a gating mechanism. This design significantly reduced computational overhead and enhanced cross-channel interactions. However, it showed limited generalization capability for motion blur artifacts. The HiT-SR model [25] adopts a hierarchical architecture and processes image features at multiple scales (from coarse to fine), which is different from the standard Transformer that operates at a single scale. However, there are still challenges when dealing with extremely fine texture details. STGAN [26] is a remote sensing image reconstruction model based on reference super-resolution, integrating a generative adversarial network and self-attention mechanism (based on Swin Transformer). The core objective is to enhance the details of LR images using reference images to achieve high-quality super-resolution reconstruction. STGAN relies heavily on the quality and similarity of the reference images. If the quality of the reference image fluctuates (such as inconsistent resolution), the robustness of the model may decline.

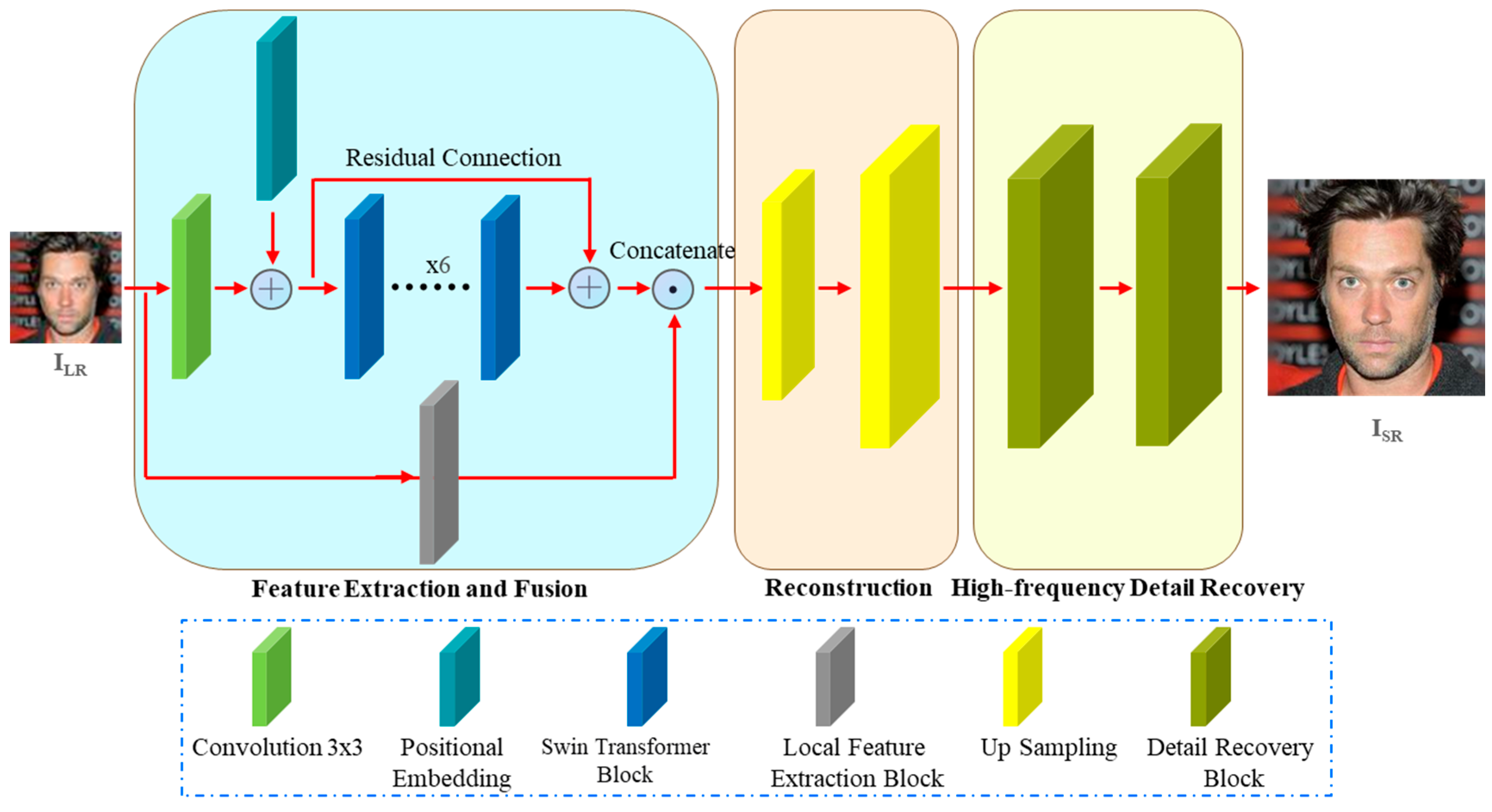
Given the complementary strengths of Transformers and GANs, we argue that their integration offers a promising solution to the aforementioned challenges. Transformers excel at capturing long-range dependencies through self-attention mechanisms, thereby enhancing global structural consistency. In contrast, GANs are particularly powerful in generating high-frequency details and photo-realistic textures through adversarial training. By combining these two paradigms, our approach aims to simultaneously achieve superior structural coherence and enhanced perceptual quality, effectively addressing the trade-offs between pixel-level accuracy and visual realism. Thus, we introduce SwinT-SRGAN, a novel GAN model that synergistically integrates Transformer and traditional CNN architectures. In this study, we contribute the following:

(1)

A dual-path feature fusion generator architecture is proposed. The window-based attention module of Transformer performs global modeling to address long-range dependencies in image features. These globally enhanced features are then explicitly fused with the output of Local Feature Extraction Block (LFEB), significantly enhancing structural consistency and detail fidelity.

(2)

An end-to-end high-frequency Detail Recovery Block (DRB) is innovatively introduced. This dedicated module specifically targets the restoration of crucial high-frequency details often lost during the SR process.

(3)

A triple-branch multi-scale discriminator is designed. This discriminator provides hierarchical adversarial supervision spanning from global structure to local texture, effectively guiding the generator to make high-quality images with coherent details at multiple scales.

(4)

A dynamic scheduling strategy for a six-component loss function is proposed. This strategy adaptively balances pixel fidelity, perceptual quality, and high-frequency constraints throughout the training process.

This paper is structured as follows: Section 2 covers foundational studies in related works, Section 3 elaborates on architectural enhancements of our proposed model, Section 4 evaluates performance through comprehensive experiments, and Section 5 summarizes conclusions.

2. Related Works

2.1. GAN

In 2014, Goodfellow et al. pioneered the GAN, significantly enhancing the realism of generative models through an adversarial training mechanism. The development of GAN stemmed from the need for implicit modeling of data distributions: traditional generative models, such as Variational Autoencoders (VAEs), rely on explicit likelihood functions. In contrast, GANs circumvent the complexity of probability density calculation by employing a minimax game between the discriminator and the generator. This framework would learn a direct mapping from a latent space to the target data space.

Fundamentally, a GAN constitutes a dynamic adversarial system comprising two subnetworks:

• Generator (G): The input is a random noise $z~P_z\left(z\right)$, and the output is a synthetic sample $G\left(z\right)$. Its objective is to generate realistic data capable of fooling the discriminator.
• Discriminator (D): The input is either real data $x~P_{data}\left(x\right)$ or synthetic data $G\left(z\right)$. Output is a scalar probability value $D\left(x\right)\in \left[\mathrm{0,1}\right]$, representing the likelihood that the input is a real sample. Its objective is to discriminate between real samples and generated samples with high accuracy.

The adversarial process between these two components is formalized as a minimax game, as displayed in Formula (1):

$$\underset{G}{\mathit{min}} \underset{D}{\mathit{max}} V\left(D,G\right)=E_{x~P_{data}\left(x\right)}\left|\mathit{log}D\left(x\right)\right|+E_{z~P_z\left(z\right)}\left|log(1-D(G\left(z\right)\left)\right)\right|$$

(1)

where $V(D,G)$ denotes the value function. D enhances its discriminative capability by maximizing V, while G minimizes $\mathrm{l}\mathrm{o}\mathrm{g}(1-D(G\left(z\right)\left)\right)$ to make the generated sample distribution $P_z$ approximate the real data distribution $P_{data}$. In practical training, an alternating optimization strategy is typically employed:

• Fix G, and then update D to maximize sample classification accuracy;
• Fix D, and then update G to minimize D’s ability to distinguish synthetic samples.

When applying GAN to SR, G’s input becomes an LR image rather than random noise, and its output corresponds to the HR counterpart.

2.2. Window-Based Multi-Head Self-Attention

In image processing tasks, strong correlations between pixels typically exist within local neighborhoods. Employing standard global attention mechanisms for full-image computation introduces significant redundancy. To address this limitation, Liu et al. pioneered Swin Transformer [27], introducing two kinds of attentions: Window Multi-Head Self-Attention (W-MSA) and Shifted Window Multi-Head Self-Attention (SW-MSA). This design achieves a good balance between linear computational complexity and hierarchical feature learning, establishing itself as a landmark architecture for vision tasks.

2.2.1. W-MSA

In Swin Transformer architecture, feature maps are partitioned into non-overlapping windows of equal size. Self-attention computation occurs independently within each window, with no information exchange between adjacent windows. This design dramatically reduces computational complexity. Consider an input feature map $x\in R^{H\times W\times C}$ and window size $(M,M)$. The feature map is divided into ${\displaystyle \frac{H}{M}}\times {\displaystyle \frac{W}{M}}$ non-overlapping windows. The W-MSA operation within a single window is expressed as:

$$W-MSA\left(x\right)=Softmax({\displaystyle \frac{Q{K}^T}{\sqrt{d}}}+B)V$$

(2)

where $B\in R^{M^2\times M^2}$ represents the learnable relative position bias, defined as follows:

$$B\left(i,j\right)=\theta \left({pos}_i-{pos}_j\right)$$

(3)

W-MSA focuses on modeling structural information within individual windows, with all windows sharing identical weight matrices. This design significantly reduces model parameters. However, the lack of cross-window interaction inherently limits its capacity for global structure modeling (e.g., continuity of object contours).

2.2.2. SW-MSA

SW-MSA enhances W-MSA by introducing a sliding window mechanism. This strategy progressively covers the entire image through multiple W-MSA computations.

Specifically, building upon standard window partitioning, SW-MSA shifts window boundaries diagonally by $({\displaystyle \frac{M}{2}},{\displaystyle \frac{M}{2}})$ pixels, creating new window configurations. This shift operation may result in irregular window boundaries, which are addressed through cyclic shifting and a mask. SW-MSA is formalized as follows:

$$SW-MSA\left(x\right)=Softmax({\displaystyle \frac{Q{K}^T}{\sqrt{d}}}+B+M)V$$

(4)

where $B\in R^{M^2\times M^2}$ denotes the relative position bias, identical to Equation (3). M represents the mask matrix, formally defined as follows:

$$M\left(i,j\right)=\left\{\begin{array}{c}\hspace{1em}0, if \omega \left({pos}_i\right)= \omega \left({pos}_i\right)\\ -\infty , otherwise\hfill \end{array}\right.$$

(5)

The shifted windows exhibit partial overlap with the original window partitions, enabling essential information flow between adjacent windows. By alternating W-MSA and SW-MSA layers in successive transformer blocks, this architecture achieves progressive expansion of the receptive field, thereby facilitating hierarchical feature fusion from local to global contexts.

3. The Proposed Method

We propose a SR model based on GAN and window-based multi-head self-attentions, termed SwinT-SRGAN. This section gives a detailed description to the architecture of our proposed generator and discriminator. Then, we introduce loss functions.

3.1. Generator Model

Our proposed SwinT-SRGAN comprises one generator and one multi-scale discriminator. As illustrated in Figure 1, the generator architecture incorporates three core modules: Feature Extraction and Fusion Block (FEFB), Super-Resolution Reconstruction Block (RB), and High-frequency Detail Recovery Block (HFDRB). This generator reconstructs a photo-realistic image with rich texture details from a given LR input. The modular design ensures effective capture of global semantic information, local texture features and critical high-frequency details.

3.1.1. Feature Extraction and Fusion Block (FEFB)

FEFB serves as the core initial processing stage of the generator. It extracts hierarchical characteristics from the LR input $I_{LR}\in R^{H\times W\times 3}$ and achieves deep fusion of global-local representations. Designed to overcome CNN’s limitations in modeling long-range dependencies, this module jointly captures global semantic structures and local textural details, thereby establishing a robust feature foundation for subsequent SR reconstruction.

(1)

Shadow Feature Extraction

The original image first passes through a convolutional layer (${Conv}_{3\times 3}$) for preliminary feature mapping. This operation transforms the image from pixel space into a higher-dimensional space, capturing low-level edge and color information. The mathematical formulation is expressed as:

$$X_0=LeakyReLU(W_{0 }\times I_{LR}+b_0)$$

(6)

where $W_0\in R^{3\times 3\times C}$ and $b_0$ are learnable parameters optimized during training.

(2)

Positional Embedding

Positional embedding explicitly injects spatial location information into feature maps, resolving the position insensitivity inherent in window-based attention mechanisms. This ensures accurate spatial structure reconstruction in the output image and is critical for reconstructing repetitive textures, preventing positional ambiguity caused by window partitioning. The positional encoding $P$ is implemented as a learnable parameter matrix that

➢

Is added to the generator’s trainable parameters;

➢

Is optimized during training;

➢

Maintains identical dimensionality to $X_0$.

So, we can obtain the following:

$$X_{\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{d}}=X_0+P$$

(7)

(3)

Swin Transformer Block (STB)

To address training instability and performance degradation during model scaling, Liu et al. proposed Swin Transformer V2 [28]. For window-based multi-head attention, Swin Transformer V2 introduces three enhancements:

➢

Cosine Attention: Replaces standard dot-product attention to stabilize training;

➢

Log-Spaced Continuous Position Bias (L-CPB): Improves position encoding generalization;

➢

Residual Post-Normalization: Modifies layer normalization placement to improve gradient flow.

We integrate these advanced window attention mechanisms to construct our Swin Transformer Block (STB), with the detailed architecture illustrated in Figure 2.

In STB, W-MSA precedes SW-MSA, with this sequential order being strictly invariant. The mathematical formulation of the STB is expressed as follows:

$$X_{stb}={\left({STB}_{SW-MSA}∎{STB}_{W-MSA}\right)}^6\left(X_{embed}\right)$$

(8)

where $\left(f∎g\right)\left(x\right)=f\left(g\right(x\left)\right)$ denotes function composition, and the superscript number 6 indicates six consecutive applications of the full STB operation.

W-MSA first computes self-attention within fixed non-overlapping windows, compelling the model to prioritize local features within each window—such as edges, textures, and fine-grained details. For SR tasks, restoring high-frequency details (e.g., sharp edges, intricate textures) is critical, as this information predominantly resides in local regions. W-MSA efficiently and directly captures these fundamental local pixel relationships, establishing a robust foundation for subsequent image reconstruction. Subsequently, the windows undergo a strategic shift, and self-attention is computed within the newly formed shifted windows. This elegantly introduces connections between adjacent original windows. Building upon the locally extracted features, the model now learns to integrate information from neighboring windows. After a single shift operation, a pixel can theoretically establish indirect connections to all other pixels from the previous layer through hierarchical propagation.

This “local → cross-local” processing sequence emulates a natural cognitive process: first perceiving details clearly, then comprehending their interrelationships and global structure. In SR, this translates to

➢

Prioritizing the recovery of localized details;

➢

Ensuring seamless integration of these details while preserving global semantic coherence.

(4)

Residual Connection

Residual connections mitigate vanishing/exploding gradient issues while enabling feature reuse. In SR tasks, the LR image and output share similar low-frequency components (e.g., color distributions). Residual connections preserve these low-frequency characteristics from the input, allowing the generator to focus its learning capacity on high-frequency detail recovery. This design significantly enhances training efficiency and improves reconstruction quality. The mathematical formulation is expressed as follows:

$$X_{st}=X_{\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{d}}+X_{stb}$$

(9)

(5)

Local Feature Extraction Block (LFEB)

LFEB serves as a critical component within the generator’s feature extraction and fusion pipeline. Operating in parallel with the Swin Transformer Block pathway, LFEB specifically addresses high-frequency detail loss and local structural ambiguity. The LFEB’s architecture is illustrated in Figure 3.

LFEB consists of one 3 × 3 convolutional layer and two residual blocks. The 3 × 3 convolution focuses on pixel neighborhood information to capture micro-textural patterns (e.g., skin pores, hair strands). The residual blocks employ scaled residual connections to balance newly synthesized features with preserved original information.

(6)

Concatenate

The outputs from the Swin Transformer branch ($X_{st}\in R^{H\times W\times C_T}$) and LFEB ($X_l\in R^{H\times W\times C_L}$) are concatenated along the channel dimension, generating fused features $X_{cat}\in R^{H\times W\times (C_{st}+C_l)}$:

$$X_{cat}=\left[X_{st; }{X}_l\right]$$

(10)

Swin Transformer features ($X_{st}$) provide global structural information, while the LFEB features ($X_l$) supply local detail representations. This explicit fusion strategy ensures subsequent modules can simultaneously leverage both high-level semantic context and low-level spatial information, significantly enhancing the representational capacity of the feature space.

3.1.2. Reconstruction Block (RB)

RB receives the deeply fused features from FEFB and performs spatial upsampling to the target scale, accomplishing image size enlargement. The detailed architecture is shown in Figure 4.

The block employs an efficient Pixel Shuffle layer for upsampling. This operation progressively increases the spatial resolution of fused features while learning optimal allocation of information from the LR feature space to the HR image domain. The upsampling process occurs in two distinct stages. Following each upsampling layer, additional 3 × 3 convolutional layers are inserted to refine the upscaled feature maps, mitigating potential blurring or unnatural artifacts introduced during upsampling and further integrating feature information.

3.1.3. High-Frequency Detail Recovery Block (HFDRB)

HFDRB constitutes a critical component of the generator architecture, designed to effectively restore and enhance fine textures, sharp edges, and high-frequency structural information (e.g., teeth, ocular features) that are susceptible to loss during SR reconstruction. While the upsampling block significantly increases spatial resolution, the generated results in complex scenes often exhibit persistent local blurring, unnatural textures, or insufficient high-frequency details. This block proactively extracts and reconstructs photo-realistic high-frequency components from rich intermediate features, substantially enhancing the visual realism and perceptual quality of super-resolved outputs. The detailed architecture is displayed in Figure 5.

The feature refinement path within this block comprises two consecutive 3 × 3 convolutional layers followed by a Bottleneck Attention Module (BAM) [29]. The BAM employs dual-path attention for feature recalibration:

➢

Channel Attention Path: Learns importance weights for feature channels, enhancing information-rich channels;

➢

Spatial Attention Path: Generates spatial attention heatmaps focusing on critical texture regions.

The outputs of both paths are fused through element-wise summation, producing a comprehensive attention weight map. The residual connection adds the original input image to the BAM-processed features, enabling the module to focus on learning the important details.

3.2. Discriminator Model

Through adversarial training, the discriminator and generator in a GAN improve each other’s skills. A more powerful discriminator can more accurately identify defects in super-resolved images (e.g., blurring, artifacts, etc.). This compels the generator to learn the authentic distribution of HR images through adversarial loss, rather than merely performing pixel-level matching. We construct a multi-scale discriminator comprising three parallel subnetworks. Each subnetwork processes input images at different scales, enabling hierarchical supervision of textural details. The network architecture is shown in Figure 6, with the formulation expressed as follows:

$$D\left(x\right)=[D_1\left(X_1\right), D_2\left(X_2\right), D_3(X_3\left)\right]$$

(11)

where $X_2$ and $X_3$ are obtained through progressive downsampling of the input image $X_1$.

The three sub-discriminators utilize identical processing modules while operating on input images of distinct resolutions. A downsampling discriminator block (stride = 2) is positioned at the front end of each branch, achieving downsampling via stride = 2 convolutions to enhance detail discrimination—focusing on both local textures and high-level global structures. The discriminator block (stride = 1) preserves spatial information integrity for high-frequency artifact detection, identifying distortions such as checkerboard artifacts and blur regions in generated images. Each processing module incorporates residual connections to mitigate vanishing gradients and enhance discriminative capability in deep networks, as illustrated in Figure 7.

3.3. Loss Functions

In GAN for SR, the design of loss functions is critical for generating high-quality images. The generator and discriminator have distinct optimization objectives, necessitating different loss functions. The generator’s composite loss function comprises multiple components designed to simultaneously optimize pixel-level accuracy, perceptual quality, and texture detail fidelity. Conversely, the discriminator’s loss function focuses exclusively on distinguishing real images from generated images.

The generator’s total loss function integrates six complementary components: Adversarial Loss ($L_{adv}$), Perceptual Loss ($L_{per}$), Content Loss ($L_{con}$), Gradient Loss ($L_{grad}$), Edge Loss ($L_{edge}$), and Frequency Loss ($L_{freq}$). Mathematically, the generator’s composite loss is formulated as follows:

$${Loss}_G={\gamma }_{adv}{L}_{adv}+{\gamma }_{per}{L}_{per}+{\gamma }_{con}{L}_{con}+{\gamma }_{grad}{L}_{grad}+{\gamma }_{edge}{L}_{edge}+{\gamma }_{freq}{L}_{freq}$$

(12)

where $\gamma =\left\{{\gamma }_{adv},{\gamma }_{per},{\gamma }_{con},{\gamma }_{grad},{\gamma }_{edge},{\gamma }_{freq}\right\}$ denotes the weighting coefficients for each loss function. These weights are dynamically adjusted throughout the training process.

The Adversarial Loss ($L_{adv}$) incentivizes the generator to produce super-resolved images indistinguishable from real HR images by the discriminator, addressing the inherent limitation of pixel-level losses in texture recovery. Implemented via a multi-scale discriminator architecture, it computes adversarial losses across multiple scales. Specifically, we employ Mean Squared Error (MSE) loss for each discriminator scale output, formulated as:

$$L_{adv}={\displaystyle \frac{1}{K}}{\sum }_{K=1}^K{E}_{I_{SR}}\left[{(D_k\left(I_{SR}\right)-1)}^2\right]$$

(13)

where $K$ denotes the number of sub-discriminators, $D_K$ represents discriminator’s output of the at the k-th scale, and $I_{SR}$ is the super-resolved image.

By calculating the distance between the generated image and the real HR image in feature space, Perceptual Loss ($L_{per}$) uses a pre-trained VGG-19 to extract high-level features. This directs the generator to produce visually realistic results that align with human perception, preventing over-optimization for pixel-level similarity at the expense of global structural and semantic coherence. Specifically, we utilize shallow features from VGG-19’s 26th layer (conv3_3) to compute feature discrepancies. The expression of the perceptual loss function is as follows:

$$L_{per}={‖{\varnothing }_{26}\left(I_{SR}\right)-{\varnothing }_{26}\left(I_{HR}\right)‖}_2^2$$

(14)

where ${\varnothing }_{26}$ denotes the feature extraction function at the conv3_3 layer of VGG-19, and $I_{HR}$ is the real HR image.

The Content Loss ($L_{con}$) serves as the foundational reconstruction loss, directly constraining pixel-space similarity between generated and real images. It ensures global structural and color consistency while mitigating blurring artifacts, formulated as follows:

$$L_{con}={‖I_{SR}-I_{HR}‖}_1$$

(15)

The Gradient Loss ($L_{grad}$) employs Sobel operators to compute horizontal and vertical gradients, constraining edge consistency between generated and real images. This enhances sharpness and clarity of edges in super-resolved outputs, formulated as follows:

$$L_{grad}={\displaystyle \frac{1}{2}}({‖G_x\left(I_{SR}\right)-G_x\left(I_{HR}\right)‖}_1+{‖G_y\left(I_{SR}\right)-G_y\left(I_{HR}\right)‖}_1)$$

(16)

where $G_x$ and $G_y$ represent gradient maps obtained using Sobel operators in the horizontal and vertical directions, respectively.

The Edge Loss ($L_{edge}$) extends this concept by computing gradient losses across multiple downsampled scales, capturing coarse-to-fine edge information. This enhances robustness in edge structure representation and ensures accurate edge preservation in generated images at all observational levels, formulated as follows:

$$L_{edge}={\sum }_{s=0}^2{\displaystyle \frac{1}{2^s}}{L}_{grad}^{\left(s\right)}(I_{SR},I_{HR})$$

(17)

where $L_{grad}^{\left(s\right)}$ denotes the gradient loss at downsampling level s.

The Frequency Loss ($L_{freq}$) extracts high-frequency components via Laplacian filtering and enforces consistency between generated and real images in the high-frequency domain. It specifically targets the restoration of critical details (e.g., ocular features, dental structures) that other losses may neglect, formulated as follows:

$$L_{freq}={‖{\tau \ast I}_{SR}-{\tau \ast I}_{HR}‖}_1$$

(18)

where $\tau$ denotes the Laplacian kernel and $\ast$ represents the convolution operation.

The discriminator employs a multi-scale architecture (three scales: original resolution, 1/2 downsampling, 1/4 downsampling), with each scale performing independent real/fake discrimination. This multi-scale design provides rich gradient information to guide the generator in producing realistic textures across varying receptive fields. Simultaneously, the discriminator enhances its discriminative capability by minimizing the following composite loss. The mathematical expression is as follows:

$${Loss}_D={\displaystyle \frac{1}{2K}}{\sum }_{K=1}^K(E_{I_{HR}}\left[{\left(D_K\left(I_{HR}\right)-1\right)}^2\right]+E_{I_{SR}}[{\left(D_K\right(I_{SR}\left)\right)}^2\left]\right)$$

(19)

where $D_K$ denotes the discriminator output at the k-th scale. For real images, the target output is 1; for generated images, the target output is 0.

4. Experiments

4.1. Datasets

Two publicly available datasets were utilized for model validation. CelebA-HQ is a dataset of excellent face images specifically designed for CV research, comprising 30,000 images at different resolutions. Flickr2K contains 2650 images covering diverse themes, including natural scenes, people, and architecture, and is primarily employed for research. We, respectively, selected 8000 images from CelebA-HQ and 2600 images from Flickr2K as the experimental datasets. Both datasets were partitioned into training sets and testing sets using a 9:1 ratio. Due to hardware constraints and training time considerations, images with resolutions of 64 × 64 and 256 × 256 were selected for the SR experiments.

4.2. Metrics

To comprehensively evaluate the quality of image SR reconstruction, this study employs three complementary evaluation metrics: PSNR, SSIM, and LPIPS [30]. These metrics provide quantitative assessment from three distinct dimensions: pixel-level fidelity, structural similarity, and perceptual quality, respectively.

PSNR measures the pixel-level error between the reconstructed image and the original HR image, reflecting the signal-to-noise ratio level. It is expressed in decibels (dB), where higher values show superior reconstruction quality. The mathematical expression is as follows:

$$PSNR=10{log}_{10}\left({\displaystyle \frac{{MAX}_I^2}{MSE}}\right)$$

(20)

where ${MAX}_I$ represents the maximum possible value, and MSE is defined as follows:

$$MSE={\displaystyle \frac{1}{HW}}{\sum }_{i=1}^H{\sum }_{j=1}^W{\left[I_{HR}\left(i,j\right)-I_{SR}(i,j)\right]}^2$$

(21)

where $H$ and $W$ represent the image’s height and width, respectively.

SSIM evaluates the similarity between images across three different dimensions: luminance, contrast, and structure. Its value falls between 0 and 1, inclusive, where better structural fidelity is indicated by values nearer 1. The mathematical expression is given by the following:

$$SSIM\left(x,y\right)={\left[l(x,y)\right]}^{\alpha }·{\left[c(x,y)\right]}^{\beta }·{\left[s(x,y)\right]}^{\gamma }$$

(22)

where $l,c$, and $s$ represent the luminance comparison, contrast comparison, and structure comparison functions, respectively, and $\alpha ,\beta ,\gamma$ are parameters typically set to 1 by default.

LPIPS is a similarity metric based on deep feature space distance, directly quantifying human visual perception of image differences. Its value falls between 0 and 1, inclusive; higher perceptual quality is indicated by lower values (0 indicates perfect perceptual similarity). The mathematical expression is defined as follows:

$$LPIPS={\sum }_l{\displaystyle \frac{1}{H_l{W}_l}}{\sum }_{h,w}{‖w_l\odot ({\varnothing }_l{\left(I_{HR}\right)}_{h,w}-{\varnothing }_l{\left(I_{SR}\right)}_{h,w})‖}_2^2$$

(23)

where ${\varnothing }_l$ denotes the feature map from the l-th layer of a pretrained CNN, $w_l$ is a learnable channel weight vector, and $\odot$ represents the channel-wise weighting operation.

It should be noted that all the quantitative data are obtained after three independent experiments.

4.3. Experiment Settings

A physical server with eight NVIDIA RTX 3090 GPUs was used for the experiments, running Ubuntu 20.04 with PyTorch 2.2.0. Training was conducted using data parallelism, with the generator’s learning rate adjusted via a cosine annealing strategy. During data preprocessing, channel-wise mean and standard deviation (std) values were calculated separately for the CelebA-HQ and Flickr2K datasets. Additional hyperparameters are listed in

Table 1. Hyperparameters of the model training.

Hyperparameters	Value	Hyperparameters	Value
Initial learning rate	Adam	Total epochs	1000
Optimizer	0.0002	Batch size	120
${\gamma }_{adv}$	0.1	$\mathrm{Initial} {\gamma }_{per}$	0.05
${\gamma }_{freq}$	0.2	$\mathrm{Initial} {\gamma }_{con}$	0.9
${\gamma }_{grad}$	0.3	$\mathrm{Initial} {\gamma }_{edge}$	0.2

, where ${\gamma }_{per},{\gamma }_{con}$, and ${\gamma }_{edge}$ follow linear scheduling rules. Specifically, ${\gamma }_{con}$ is defined as follows:

$${\gamma }_{con}=0.9-0.3\times {\displaystyle \frac{epoch}{E}}$$

(24)

where epoch denotes the current training epoch number, and E represents the total number of training epochs (1000 epochs). During the initial 300 epochs, ${\gamma }_{con}$ maintains a high value (>0.8) to ensure the generator rapidly converges to a reasonable pixel-level solution. The weight of Content Loss is progressively reduced over the training process. This prevents the L1 norm from dominating the optimization, thereby mitigating the loss of textural details while avoiding excessive pixel smoothing.

${\gamma }_{per}$ is defined as follows:

$${\gamma }_{per}=0.05+0.1\times {\displaystyle \frac{epoch}{E}}$$

(25)

During the initial training phase, the weight of the Perceptual Loss (${\gamma }_{per}$) is kept relatively low. This avoids premature optimization guided by deep semantic features, which could distort the generator’s learning direction. As training progresses, ${\gamma }_{per}$ is progressively increased. This allows it to work synergistically with the diminishing Content Loss, thereby preserving the overall reconstruction quality without degradation.

${\gamma }_{edge}$ is defined as follows:

$${\gamma }_{edge}=0.2+0.3\times {\displaystyle \frac{epoch}{E}}$$

(26)

Edge Loss is predominantly dedicated to edge formation during the early training stage. As optimization advances, its focus shifts to fine-grained refinement at the microscopic scale, such as recovering textures like wrinkles and hair strands.

Furthermore, it should be noted that the training time for the model on the CelebA-HQ dataset is approximately 35 h, while on the Flickr2K dataset, the training time is 9 h and 15 min.

4.4. Comparative Experiments

To scientifically assess the image SR performance of the SwinT-SRGAN model, qualitative and quantitative experiments were first conducted on the CelebA-HQ dataset. The models selected for comparison include SRGAN, ESRGAN, SAN, HAN, Real-ESRGAN, Swin-IR, and Omni-IR [31]. The models being compared are all classic models among different types of methods in recent years. Among these, SRGAN, ESRGAN, and Real-ESRGAN belong to the category of traditional GAN-based models. SAN and HAN represent typical SR models based on attention mechanisms, while Swin-IR serves as a Transformer-based approach for SR. Omni-IR, in contrast, is a lightweight SR model. As illustrated in Figure 8, the magnified views of the mouth region are displayed in the upper-right corner of all resulting images.

In Figure 8, we will focus on the overall structure of the teeth after super-resolution and whether interdental gaps are clear. As evidenced by Figure 8, SRGAN, ESRGAN, and Real-ESRGAN exhibit discernible artifacts and boundary blurring in critical facial regions (e.g., teeth, lips), accompanied by geometric distortions in the teeth. While SAN and HAN demonstrate superior structural preservation overall, their reconstructed teeth suffer from over-smoothing, resulting in the loss of interdental gaps that are inconsistent with anatomical reality. Swin-IR and Omni-IR perform well in maintaining the global image structure; however, they lack sufficient detail in high-frequency regions, indicating potential for further optimization. Critically, our proposed SwinT-SRGAN model demonstrably outperforms all seven comparative models in both global structural fidelity and high-frequency detail reproduction, achieving results closest to the original HR ground truth. Comparative analysis of features such as interdental gap clarity and lip contour geometry reveals SwinT-SRGAN’s superior capability in high-frequency detail reconstruction. The model achieves sub-pixel-level edge reconstruction while effectively suppressing geometric distortions.

To ensure a scientific comparison, SwinT-SRGAN was quantitatively compared to the seven baseline models.

Table 2. Quantitative comparison on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
SRGAN	21.46 ± 0.95	64.71 ± 1.78	27.42 ± 0.98
ESRGAN	22.50 ± 0.85	65.82 ± 1.20	26.19 ± 0.75
SAN	25.74 ± 0.45	75.96 ± 0.95	27.04 ± 0.42
HAN	25.54 ± 0.36	76.45 ± 1.11	26.84 ± 0.41
Real-ESRGAN	22.24 ± 0.78	66.83 ± 1.57	28.97 ± 0.56
Swin-IR	25.78 ± 0.21	76.87 ± 0.71	26.19 ± 0.14
Omni-IR	24.82 ± 0.32	72.48 ± 1.03	32.45 ± 0.41
Ours	26.49 ± 0.16	77.70 ± 0.67	21.52 ± 0.10

displays the relevant PSNR, SSIM, and LPIPS measurements. Among the baselines, SRGAN exhibits the poorest performance values. As the pioneering GAN-based SR model, it established a new paradigm for image SR; however, its relatively simplistic architecture results in suboptimal performance. Building upon SRGAN, ESRGAN incorporates Residual-in-Residual Dense Blocks to enhance feature reuse capability. Real-ESRGAN primarily focuses on degradation modeling and employs a U-Net structure. Consequently, it demonstrates limited improvement in image SR performance for the current experimental setup. Both SAN and HAN are designed to transcend the limitations of basic channel attention mechanisms. The SAN model delves into complex statistical relationships between channels, while the HAN model achieves multi-level feature fusion. These approaches significantly elevate the upper bound of image reconstruction quality, yielding quantitative metrics superior to the first three GAN models. The Swin-IR model leverages the long-range modeling capability of transformer architecture to further advance SR performance, achieving highly competitive results across PSNR, SSIM, and LPIPS metrics. Utilizing an innovative Omni-Scale Aggregation (OSA) mechanism, Omni-IR accomplishes image SR with exceptionally low computational overhead, albeit at the expense of less prominent quantitative scores.

Our proposed approach enhances the generator architecture by introducing a dual-path Transformer-CNN parallel feature extraction module, coupled with a multi-scale fusion discriminator network. Combined with a refined model training strategy, this comprehensive design achieves very good quantitative results across all evaluated metrics compared to the baseline models.

To further validate the generalization capability of the SwinT-SRGAN model for SR across diverse datasets, a cross-dataset experiment was conducted on the Flickr2K dataset. Experimental parameters retained identical configurations to those described in Section 4.3. Evaluation metrics remained consistent with those used for CelebA-HQ (PSNR, SSIM, and LPIPS). Qualitative comparative results and quantitative results are shown in Figure 9 and

Table 3. Quantitative comparison on Flickr2K.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
SRGAN	17.51 ± 0.88	44.82 ± 2.21	41.49 ± 1.82
ESRGAN	17.48 ± 0.71	45.86 ± 1.82	39.01 ± 1.84
SAN	20.21 ± 0.31	59.92 ± 1.34	42.69 ± 1.46
HAN	20.16 ± 0.48	59.76 ± 1.26	40.51 ± 1.51
Real-ESRGAN	19.16 ± 0.54	54.45 ± 1.82	35.45 ± 2.21
Swin-IR	20.26 ± 0.32	60.39 ± 1.13	39.99 ± 0.41
Omni-IR	19.96 ± 0.45	58.48 ± 1.42	43.76 ± 0.74
Ours	20.30 ± 0.23	60.49 ± 0.99	32.94 ± 0.24

, respectively.

Figure 9 presents a comparative visualization of SR results generated by different models on the Flickr2K dataset. To accentuate disparities in high-frequency detail recovery capabilities (e.g., textures, edges), a key region rich in intricate details is magnified in the upper-right corner of each image. We will focus on the magnified areas to reflect the advantages and disadvantages of each super-resolution algorithm. The super-resolved outputs from SRGAN, ESRGAN, and Real-ESRGAN exhibit pronounced artifacts and blurring in critical regions such as the eyes. While SAN and HAN leverage attention fusion mechanisms to recover more accurate textural structures in certain scenarios, the coherence of their restored details can be inconsistent. This limitation manifests as distortions and artifacts, particularly noticeable in high-frequency textures like facial features. The Swin-IR model demonstrates robustness in reconstructing regular structures; however, its restored details occasionally exhibit unnatural characteristics. Omni-IR, positioned as a practical lightweight model, delivers suboptimal performance for image SR tasks on smaller datasets like Flickr2K. Crucially, the superior high-frequency detail recovery capability demonstrated by the SwinT-SRGAN model on the Flickr2K dataset strongly corroborates the qualitative observations previously noted in the CelebA-HQ facial dataset analysis.

Comparison of the quantitative metrics (PSNR, SSIM, LPIPS) in Table 3 and Table 2 reveals a consistent trend: all evaluated models, including the proposed SwinT-SRGAN, exhibit lower performance on the Flickr2K compared to the CelebA-HQ dataset. In-depth analysis reveals that the disparity in training dataset scale is a critical factor underlying this cross-dataset performance gap. The powerful feature representation capabilities of deep learning models, particularly complex high-performance SR architectures (e.g., GAN-based, Transformer-based models), are highly dependent on large-scale and diverse training data. Notwithstanding this limitation, the data in Table 3 conclusively demonstrate that the SwinT-SRGAN model still achieves superior SR reconstruction quality compared to the other baseline models.

Collectively, the qualitative and quantitative experiments conducted on both CelebA-HQ and Flickr2K prove that our model excels in restoring intricate high-frequency features (e.g., teeth, eyes) and suppressing image artifacts relative to the comparative models. This superior and consistent performance across diverse datasets provides compelling evidence for the robust generalization capability inherent in the designed generator architecture of the proposed model. Its effectiveness in capturing and learning essential image priors enables high-quality SR reconstruction across varied and complex visual content.

4.5. Ablation Experiments of the Models

To confirm the efficacy of the core blocks within our proposed generator architecture, an ablation study on the generator was designed. Under fixed training settings (CelebA-HQ, loss functions, number of iterations) and a unified discriminator structure, the following four key modules were successively removed from the full model for comparative analysis: Positional Embedding (PE) module, Local Feature Extraction Block (LFEB), Residual Connection (RC) structure, and Detail Recovery Block (DRB). The construction methods for each variant model are as follows:

• w/o PE: PE is removed; feature maps are directly input into subsequent modules;
• w/o LFEB: LFEB is removed, and the corresponding concatenation operation is omitted;
• w/o RC: The residual connection path is eliminated, retaining only the forward propagation of the main branch;
• w/o DRB: DRB is removed; deep features are directly upsampled for output;
• Full Model: The complete model incorporating all four modules.

Figure 10 and

Table 4. Quantitative comparison of generator ablation experiments on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
w/o DRB	25.61	75.62	22.23
w/o LFEB	26.33	76.80	22.43
w/o PE	26.13	76.84	22.04
w/o RC	25.91	76.97	22.00
Ours	26.49	77.70	21.52

display the comparative visualization and quantitative findings of the generator ablation experiments, respectively.

Figure 10 presents a comparative visualization of SR results on facial images, with a magnified focus on the teeth and lip details in each output. Critical observations from the ablation study include the following:

• w/o DRB: Removal of DRB results in significantly blurred tooth edges and adhesion of adjacent interdental gaps, compromising the geometric separation of individual teeth. The absence of the DRB demonstrably weakens the model’s high-frequency detail synthesis capability.
• w/o LFEB: Elimination of LFEB introduces blocky artifacts on the tooth surfaces and produces deviations in natural gloss.
• w/o PE: Removal of the PE module causes blurring of the boundaries between the central incisors and lateral incisors.
• w/o RC: Ablation of the residual connection path leads to the near-complete disappearance of interdental gaps in the lateral teeth.

As presented in Table 4, the contributions of each core generator block to SR performance were systematically evaluated. On the CelebA-HQ test set, the full model (Ours) demonstrates comprehensive superiority over all variants where individual modules were ablated. The full model achieves the optimal overall performance: PSNR 26.49 dB, SSIM 77.70%, LPIPS 21.52. The removal of any single module consistently degrades all three metrics, confirming the indispensable synergistic role of each component in achieving high-quality SR. Crucially, the removal of DRB resulted in the most severe performance degradation: PSNR decreased significantly by 0.88 dB (25.61 vs. 26.49), SSIM dropped by 2.08 percentage points (75.62% vs. 77.70%), and LPIPS worsened by 0.71 (22.23 vs. 21.52). This quantitative evidence underscores the critical role of DRB in high-frequency detail reconstruction, aligning with the observed interdental gap adhesion in Figure 10. The absence of the other three components (RC, PE, LFEB) also negatively impacted SR performance to varying degrees. Considering the PSNR metric as an example, the magnitude of performance degradation is ranked as follows: DRB removal > RC removal > PE removal > LFEB removal.

Similarly, to validate the necessity of the discriminator’s multi-branch design, a single-branch variant model (1 branch) was constructed. Comparative experiments were conducted using a fixed generator structure (Full Model) and an identical training strategy. Figure 11 presents the comparative results, featuring magnified views of the mouth region in the upper-right corner. Close inspection reveals that images super-resolved by the single-branch variant exhibit the following:

• Relatively blurred tooth grooves;
• Diffused lip boundaries.

The three-branch discriminator design significantly enhances the generator’s reconstruction accuracy of image features through multi-scale adversarial supervision (global-local-edge). Conversely, the single-branch variant fails to provide hierarchical discriminative signals, leading to unacceptable image degradation, including structural distortion and edge blurring.

As presented in

Table 5. Quantitative comparison of discriminator ablation experiments on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
1 branch	25.91	76.97	22.00
Ours	26.49	77.70	21.52

, on the CelebA-HQ test set, the three-branch discriminator (Ours) achieves significant improvements across all evaluation metrics compared to the single-branch variant (1 branch). The three-branch design effectively constrains macro-structural integrity through global semantic supervision, substantially mitigating image distortion. This is quantitatively evidenced by an increase of 0.58 dB in PSNR and a 0.73 percentage point improvement in SSIM. Furthermore, a corresponding enhancement in LPIPS underscores its contribution to perceptual quality.

4.6. Ablation Experiments of Swin Transformer Block

Swin Transformer Block (STB) within the generator utilizes a hybrid configuration of SW-MSA and W-MSA. To investigate the contribution of this hybrid design, we conducted an ablation study comparing three variants:

• Exclusively SW-MSA: Two consecutive SW-MSA modules (no W-MSA);
• Exclusively W-MSA: Two consecutive W-MSA modules (no SW-MSA);
• Full Model: The original alternating arrangement of SW-MSA and W-MSA.

Comparative visual results are presented in Figure 12, while the corresponding quantitative analysis is provided in

Table 6. Quantitative comparison of STB ablation experiments on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
No SW-MSA	25.92	76.61	22.43
No W-MSA	26.11	76.61	22.43
Ours	26.49	77.70	21.52

.

The experimental results demonstrate that the hybrid utilization of both window attention mechanisms within the STB leads to significant improvements across PSNR, SSIM, and LPIPS. Crucially, the performance of the two variants where either module was removed individually (Exclusively SW-MSA and Exclusively W-MSA) closely approximates each other, indicating a strong complementary relationship between SW-MSA and W-MSA. Specifically:

• Exclusively W-MSA (no SW-MSA): Removal of SW-MSA results in blurring of the tooth-lip boundary. The fixed window partitioning inherent to W-MSA isolates information across windows, violating the biological continuity principle of dental tissue structures.
• Exclusively SW-MSA (no W-MSA): Utilizing solely SW-MSA within the STB introduces salt-and-pepper noise near tooth roots. The global shifting operation characteristic of SW-MSA induces misalignment artifacts, disrupting the stability of local features.

The cascaded/alternating integration of both attention mechanisms within the STB facilitates cross-scale fusion of image features, thereby maximizing the SR performance.

Furthermore, to investigate the impact of attention module order within the generator’s STB, we conducted an order reversal experiment: placing SW-MSA before W-MSA. Experiments were performed on the CelebA-HQ test set, with focused analysis on visual quality differences in critical regions such as the mouth, eyes, and ears (as illustrated in Figure 13). Key observations revealed are as follows:

• Blunting of the lip apex in super-resolved outputs;
• Subtle canthus details at the eye corners;
• Blurred internal contours of the ear structure.

This performance degradation stems from the reversed order: Performing shifted window attention first disrupts the inherent local structure. The resulting cross-window information leakage induces local distortion within the image. Quantitative data in

Table 7. Quantitative comparison with swapped window attention sequence on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
Swapped Sequence (SW-MSA → W-MSA)	26.06	77.22	21.95
Ours (W-MSA → SW-MSA)	26.49	77.70	21.52

confirms that reversing the attention order causes synchronous degradation across all metrics, with the most pronounced decrease observed in SSIM (0.48 percentage point reduction). Consequently, the sequential order W-MSA → SW-MSA within the STB is non-interchangeable. This design implements a progressive reconstruction strategy—prioritizing local detail refinement followed by cross-window correction—thereby achieving superior high-frequency fidelity.

4.7. Ablation Experiments of Generator Loss Functions

The generator employs six distinct loss functions to constrain model training: Adversarial Loss, Content Loss, Edge Loss, Frequency Loss, Gradient Loss, and Perceptual Loss. Among these, Adversarial Loss serves as the cornerstone of the adversarial training between the generator and discriminator and is indispensable. Under the fixed Adversarial Loss constraint, comparative experiments were conducted by sequentially removing a single loss function. Analysis focused on detailed discrepancies in high-frequency regions (e.g., the mouth), with magnified views displayed in the upper-right corner, as illustrated in Figure 14.

Key observations include the following:

• w/o Content Loss: Removal of the Content Loss results in excessive smoothness due to the lack of pixel-level constraints, manifesting as global blurring of the teeth region.
• w/o Edge Loss: The Edge Loss specifically targets the constraint of image edges and contours, aiming to ensure generated images exhibit sharp and well-defined outlines (e.g., lip contours, tooth boundaries). Its removal prompts the model to produce overly smoothed outputs, compromising critical edge information that defines object shape and structure. This leads to an overly “fleshy” appearance or ill-defined boundaries in the lip region.
• Similarly, the removal of each of the other three loss functions (Frequency Loss, Gradient Loss, Perceptual Loss) resulted in distinct forms of degradation in the super-resolved images.

Quantitative analysis in

Table 8. Quantitative comparison of loss functions’ ablation experiments on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
w/o Content Loss	25.53	75.86	22.52
w/o Edge Loss	26.22	75.50	22.40
w/o Frequency Loss	26.26	76.78	22.10
w/o Gradient Loss	25.94	76.44	25.02
w/o Perceptual Loss	26.38	77.63	21.78
Ours	26.49	77.70	21.52

further corroborates that the synergistic effect of multiple loss functions comprehensively enhances super-resolved image quality, particularly excelling at the level of human visual perception. The Content Loss exerts the most significant impact on PSNR, with its removal causing a substantial decrease of 0.96 dB. Without the constraint of the Edge Loss, blurred tooth and lip contours manifest, resulting in the most pronounced SSIM degradation (a 2.2 percentage point reduction). The Gradient Loss plays a crucial role for LPIPS, as its absence leads to a marked increase of 3.5 in the LPIPS value. Therefore, the loss function ablation experiments validate the unique contribution of each individual loss component. The removal of any single loss function induces specific, observable quality degradation in the generated SR images. Only the synergistic interplay of all loss functions enables the achievement of optimal performance across all objective metrics.

4.8. Experiments on the Validity of Dynamic Weights of Loss Functions

To validate the dynamic loss weighting strategy, comparative experiments were conducted:

• Fixed-weight group: All loss weights remained constant throughout training.
• Dynamic-weight group: Core loss weights were adaptively adjusted.

As demonstrated in Figure 15, the dynamic weighting strategy exhibits superior detail reconstruction:

• The lower lip maintains a textured and nuanced contour, avoiding a blurred or swollen appearance.
• The inner contours of the eye corners and ears remain relatively distinct.

Data presented in

Table 9. Quantitative comparison of dynamic weights experiments on CelebA-HQ.

Methods	$\mathbf{PSNR} \left(\mathbf{dB}\right)\uparrow$	$\mathbf{SSIM} (\%)\uparrow$	$\mathbf{LPIPS}\downarrow$
Fixed weights	26.31	76.82	23.14
Ours	26.49	77.70	21.52

demonstrate improvements across all three metrics. Both qualitative visual comparisons and quantitative experimental results confirm that the dynamic weighting strategy significantly outperforms the fixed-weight method in preserving both structural authenticity (as measured by PSNR/SSIM) and perceptual quality (as measured by LPIPS). This core advantage stems from the precise alignment of weight adjustment with the demands of visual feature reconstruction.

5. Conclusions and Future Work

This study proposes SwinT-SRGAN, a novel image SR framework that synergistically integrates Swin Transformer for global dependency modeling and CNN for local texture extraction. The dual-path generator resolves the conflict between long-range structural consistency and high-frequency detail preservation. Ablation studies validate the necessity of each module, particularly the sequential window attention (W-MSA→SW-MSA) and DRB design. Cross-dataset experiments on CelebA-HQ and Flickr2K demonstrate cutting-edge performance.

Despite its advantages, the current approach exhibits three limitations:

(1)

Higher computational complexity from Swin Transformer’s windowed attention, leading to slower inference than lightweight models (e.g., Omni-IR);

(2)

Heuristic-based loss scheduling relying on linear decay rules without data-driven adaptation;

(3)

Limited real-world generalization due to training on synthetic degradations, requiring enhanced robustness to extreme blur/noise.

To address these challenges, future work will focus on the following:

(1)

Model compression (e.g., knowledge distillation) to reduce computational overhead;

(2)

Differentiable loss schedulers using reinforcement learning for adaptive weight allocation;

(3)

Cross-modal SR integrating novel sensors (e.g., event cameras) for real-scene reconstruction;

(4)

Improving the generalization ability of the model in different image domains (such as medical or remote sensing images), and the robustness of the model against degradation types (such as motion blur or severe noise).