Anti-Windup Method Using Ancillary Flux-Weakening for Enhanced Induction Motor Performance Under Voltage Saturation
Abstract
1. Introduction
- (1)
- To address the FW delay caused by the three-stage PI cascade, a compensation path is designed, simplifying the FW structure to one PI controller during dynamic processes.
- (2)
- To mitigate FW failure due to orientation lag, the q-axis current error is utilized to measure and eliminate the magnetization component induced by the increase of q-axis current during dynamic processes.
| Methods | Structure Optimization of FW Loop | Number of PI Controller in FW Loop | Sensitivity to Parameter Changes | Voltage Fluctuations During Changes of and | Remarks | |
|---|---|---|---|---|---|---|
| 1 | Adaptive parameters of FW controller [6] | No | 3 | High | Medium | Failure to consider voltage fluctuations from changes |
| 2 | Unified design of controller Parameters [7] | Yes | 3 | High | Medium | |
| 3 | Limitation of [8] | No | 3 | Low | High | Utilizes the voltage overshoot rather than suppressing it |
| 4 | Smooth transition to FW condition [16] | No | 3 | Low | Medium | Designed for specific condition |
| 5 | Rapid convergence to steady state point [17] | No | 3 | High | High | |
| 6 | Single current control [7,14,15] | Yes | 2 | High | Low | Handoff is needed |
| 7 | Proposed method | Yes | 1 | Medium | Low | / |
2. Basic Theory of Flux-Weakening Control
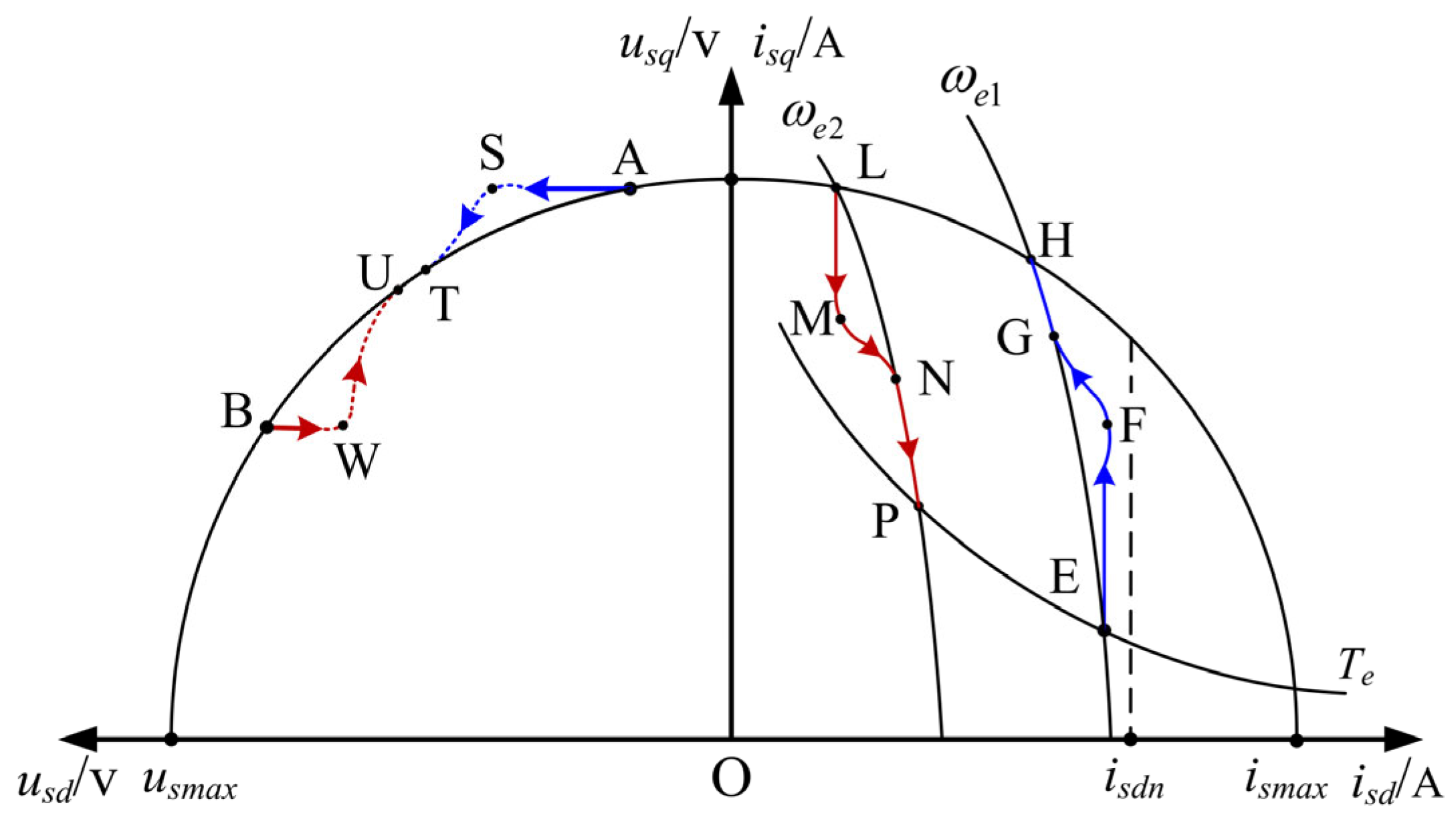
3. Analysis of Voltage Saturation Problem in Flux-Weakening Region
3.1. Voltage Saturation Caused by Cascaded PI Structure
3.2. Voltage Saturation Caused by Orientation Lag
- (1)
- Under the same , the voltage saturation increases noticeably as grows.
- (2)
- An increase in similarly results in voltage saturation, but when equals zero, the saturation caused by is minimal. However, when increases, the rate of increase in voltage saturation due to changes in rises significantly.
- (3)
- As analyzed in Section A, the failure to quickly synchronize the dq-axis current control is the direct cause of voltage saturation. Conclusion (2) suggests that orientation lag amplifies the voltage saturation issue induced by the current control.

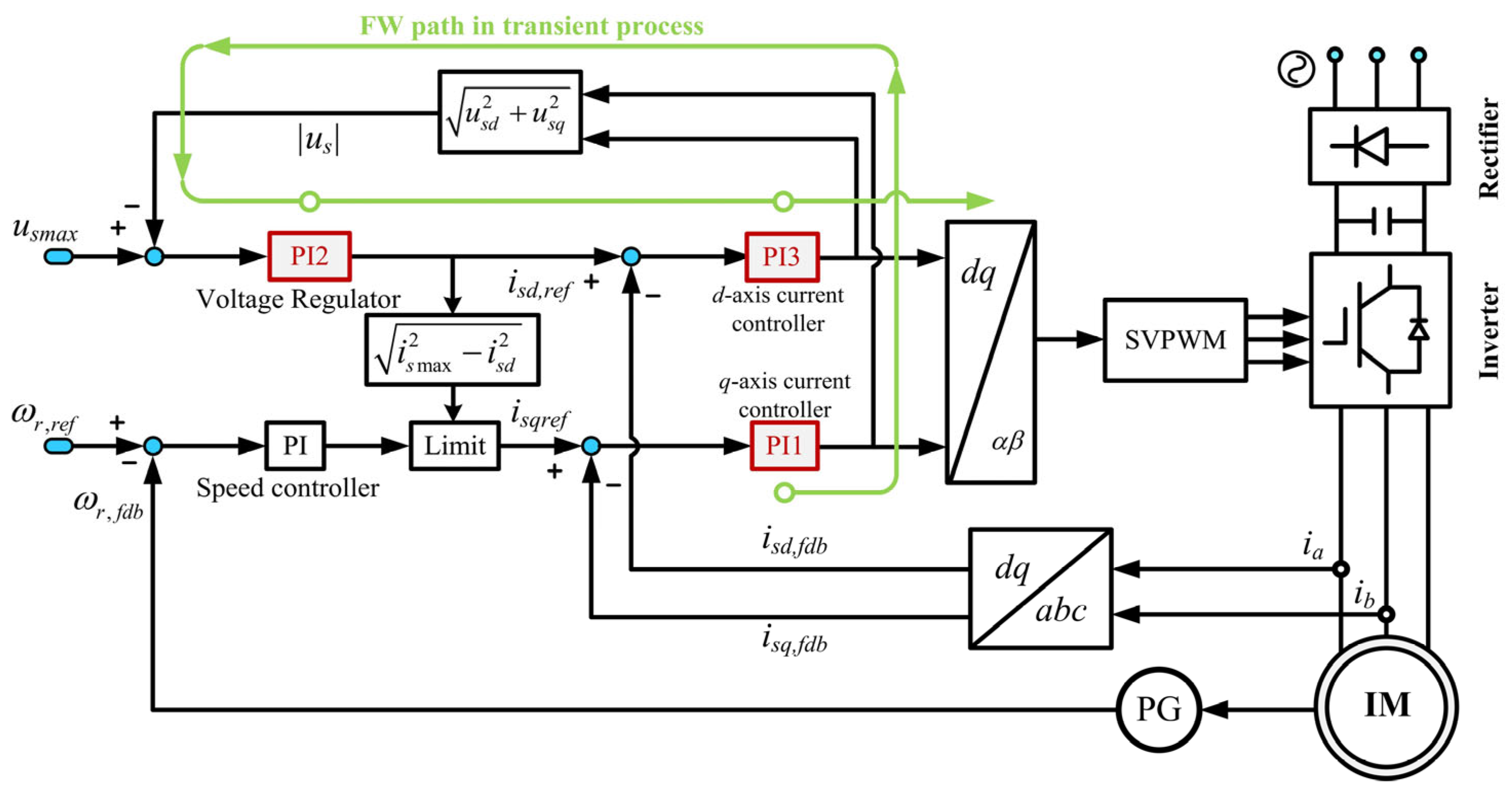
4. Proposal of the Ancillary Flux-Weakening Method for Voltage Anti-Saturation
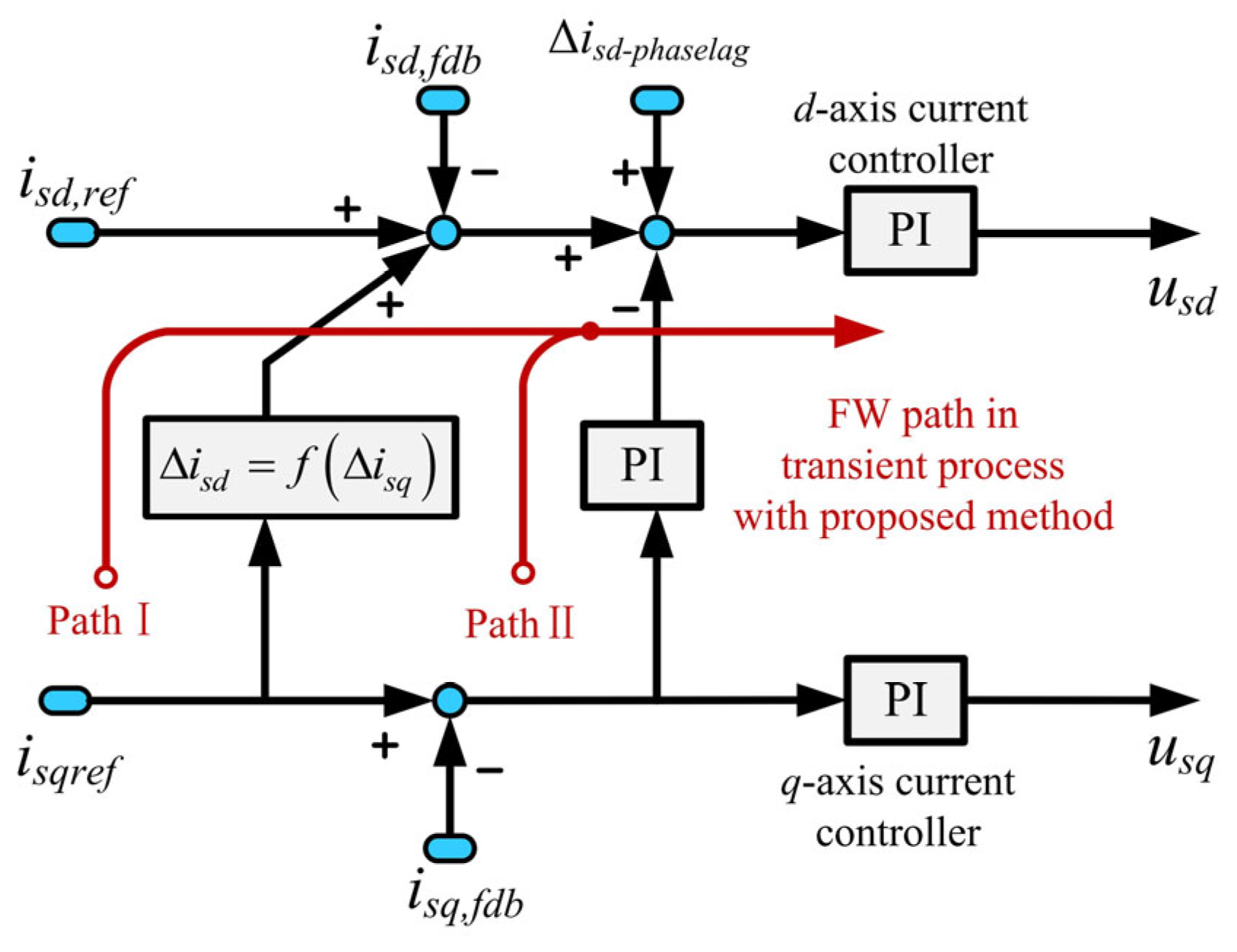
4.1. Auxiliary Flux-Weakening for Reducing Voltage Saturation Caused by the Cascade Structure Delay
4.2. Auxiliary Flux-Weakening for Reducing Voltage Saturation Causde by Orientation Lag
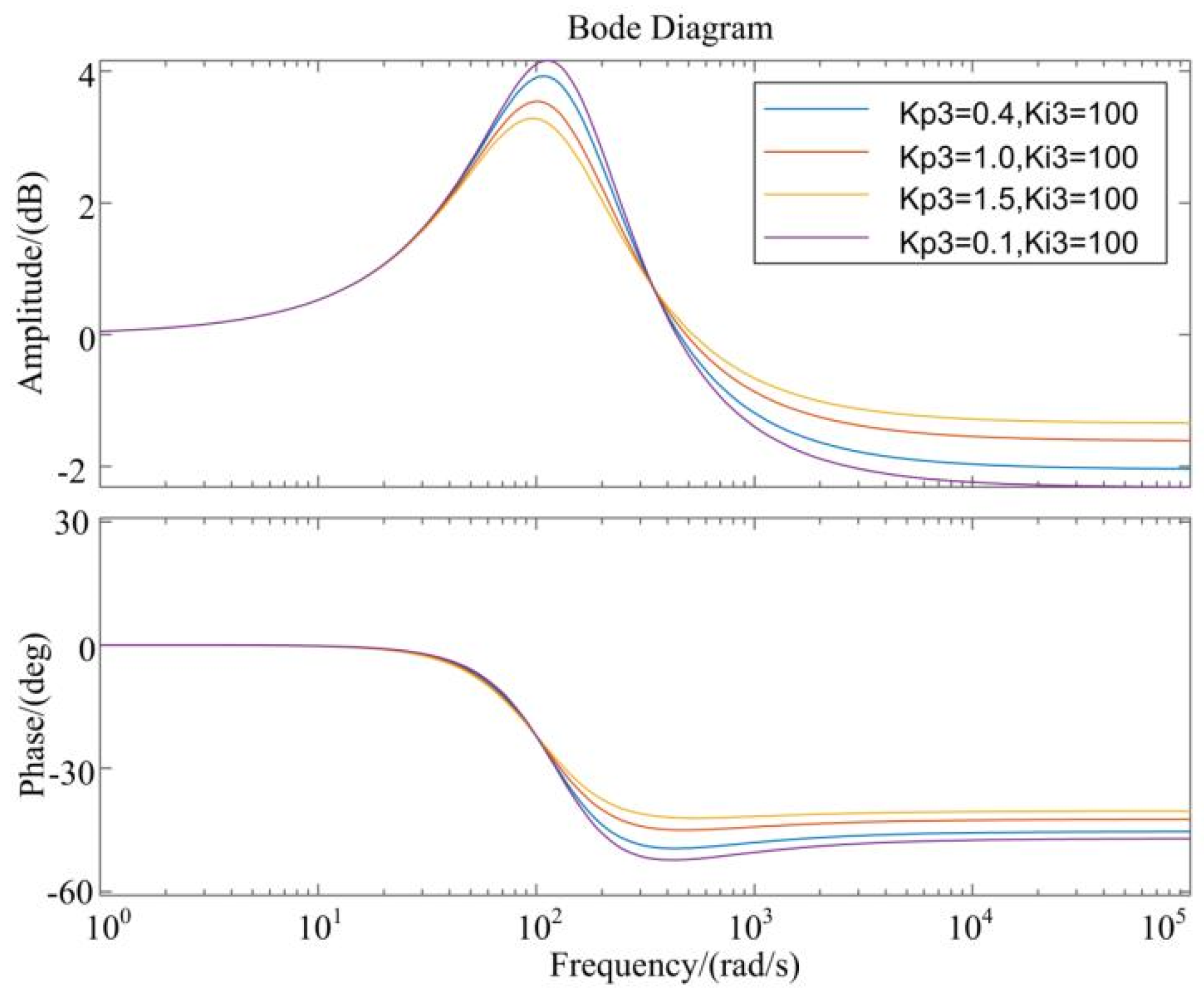
4.3. Method Stability Analysis
- (1)
- becomes larger: The system quickly approaches the steady-state value (response speed increases), but the stability time may be longer due to overshoot or oscillation.
- (2)
- becomes larger: the steady-state error is significantly reduced or even eliminated, but the excessively strong integral effect may cause the overshoot to increase and the adjustment time to be extended due to integral saturation.
5. Experimental Result
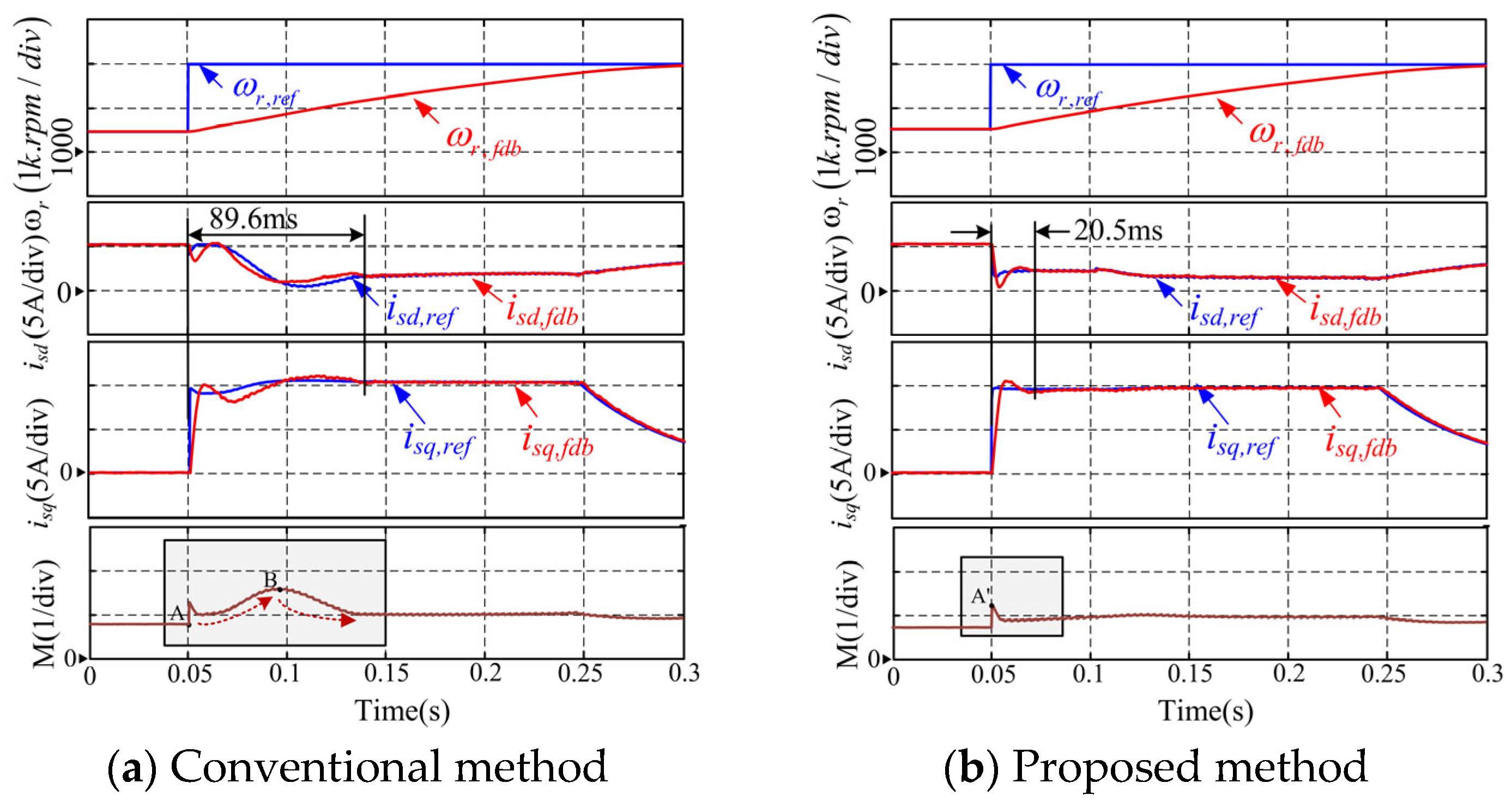
5.1. Acceleration Process Under Precise Orientation
5.2. Acceleration Process Under Inaccurate Orientation
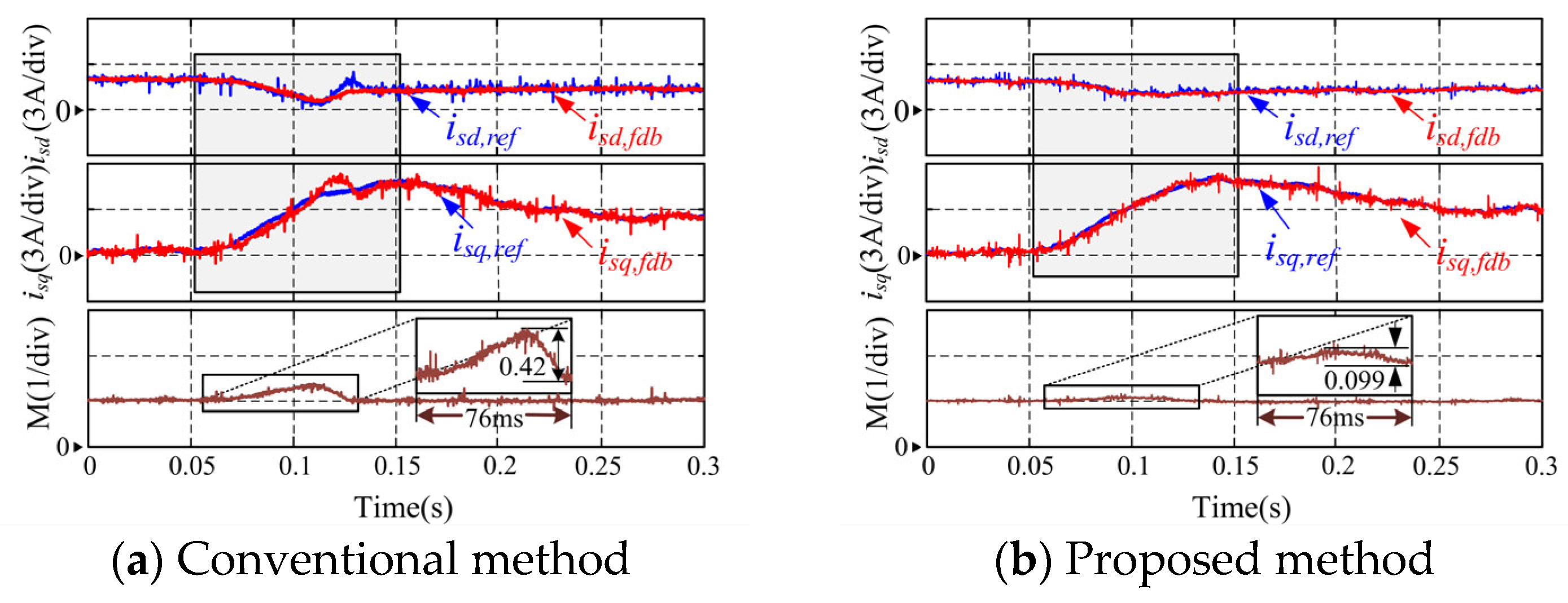
5.3. Torque Increase Process Under Inaccurate Orientation
5.4. Simulation Experiment to Increase Voltage
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Siddiki, A.B.M.I.; Sagor, I.H.; Amin, I.K.; Nasir Uddin, M. Adaptive Super-twisted Sliding Mode Control of Induction Motor for Enhanced Performance. In Proceedings of the 2025 IEEE Industry Applications Society Annual Meeting (IAS), Taipei, Taiwan, 15–20 June 2025; pp. 1–6. [Google Scholar]
- De Klerk, M.L.; Saha, A.K. A comprehensive review of advanced traction motor control techniques suitable for electric vehicle applications. IEEE Access 2021, 9, 125080–125108. [Google Scholar] [CrossRef]
- Kaewma, P.; Pothi, N.; Kraikitrat, K.; Rakpenthai, C.; Shuraiji, A.L.; Pahasa, J. Robust flux-weakening control approach for threephase induction motor drives. In Proceedings of the 2024 21st International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Khon Kaen, Thailand, 27–30 May 2024; pp. 1–6. [Google Scholar]
- Yang, Y.; Song, W.; Wen, R.; Ge, Y. Flux-Weakening Control in an IMC-PMaSynRM System Considering DC Voltage Disturbance. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 2306–2311. [Google Scholar]
- Zhou, Z.; Li, J.; Lu, Y.; Xu, H.; Zhang, Q.; Wu, L. Field Weakening Strategy Extended to Six-Step Operation for Dual Closed-Loop Current Control of Induction Motors. IEEE Trans. Transp. Electrif. 2025, 11, 2674–2683. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Z.Q.; Zhan, H. Adaptive voltage feedback controllers on nonsalient permanent magnet synchronous machine. IEEE Trans. Ind. Appl. 2020, 56, 1529–1542. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Yu, Y.; Zhang, X.; Xu, D. Unified complex vector field-weakening control for induction motor high-speed drives. IEEE Trans. Power Electron. 2021, 36, 7000–7011. [Google Scholar] [CrossRef]
- Gashtil, H.; Pickert, V.; Atkinson, D.J.; Dahidah, M.; Giaouris, D. Closed-Loop Voltage Control for Maximizing Inverter Output Voltage in the Field Weakening Region of Induction Machines. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7514–7526. [Google Scholar] [CrossRef]
- Dan, H.; Qian, M.; Wang, H.; Liu, Y.; Sun, Y.; Su, M. Implementation and Stability Analysis of an Improved V/f Induction Motor Control Scheme Based on Constant Rotor Flux. IEEE Trans. Energy Convers. 2024, 39, 1840–1850. [Google Scholar] [CrossRef]
- Gulbudak, O.; Gokdag, M.; Komurcugil, H. Model predictive control strategy for induction motor drive using lyapunov stability objective. IEEE Trans. Ind. Electron. 2022, 69, 12119–12128. [Google Scholar] [CrossRef]
- Ding, L.; Li, Y.W.; Zargari, N.R. Discrete-time smo sensorless control of current source converter-fed pmsm drives with low switching frequency. IEEE Trans. Ind. Electron. 2021, 68, 2120–2129. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, M.; Wang, C.; You, X. Analysis and applicability comparison of single current regulator methods of pmsm under squarewave mode. IEEE Trans. Ind. Electron. 2024, 71, 1410–1420. [Google Scholar] [CrossRef]
- Li, Z.; Xia, J.; Gao, X.; Garcia, C.; Rodriguez, J.; Guo, Y.; Zhang, X. Flux-Weakening Scheme for Four-Switch Inverter-Fed IM Drives with Optimized Overmodulation-Based Modulated Predictive Torque Control. IEEE Trans. Ind. Electron. 2024, 71, 13614–13624. [Google Scholar] [CrossRef]
- Gashtil, H.; Pickert, V.; Atkinson, D.J.; Dahidah, M.; Giaouris, D. Improved voltage boundary with model-based control algorithm for increased torque in the field weakening region of induction machines. IEEE Trans. Transp. Electrif. 2021, 7, 1600–1614. [Google Scholar] [CrossRef]
- Chen, S.-G.; Lin, F.-J.; Liang, C.-H.; Liao, C.-H. Development of fw and mtpv control for synrm via feedforward voltage angle control. IEEE/ASME Trans. Mechatron. 2021, 26, 3254–3264. [Google Scholar] [CrossRef]
- Dong, Z.; Ding, Z.; Wang, B.; Xu, D. Optimized anti-windup coordinating strategy for torque-maximized high-speed flux-weakening operation of constrained induction motor drives. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2030–2041. [Google Scholar] [CrossRef]
- Wang, H.; Gan, C.; Ni, K.; Yu, Z.; Qu, R. Virtual current constraint based segmented trajectory control strategy for flux-weakening operation of spmsm drives. IEEE Trans. Power Electron. 2023, 38, 2262–2274. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Yu, Y.; Wang, B.; Xu, D. Current redistribution method for induciton motor voltage closed-loop field-weakening control. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 4055–4059. [Google Scholar]
- Hu, Y.; Hua, W.; Hu, M.; Wang, Y. Inductance–Resistance Online Identification for Sensorless High-Speed PMSM Considering Resistive Characteristic of Invertor Nonlinearity. IEEE Trans. Ind. Electron. 2024, 71, 2343–2355. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Kang, J.; Wang, X. Motorast: A low-cost highperformance rapid control prototype platform for electric drives. In Proceedings of the 2023 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Wuhan, China, 16–19 June 2023; pp. 1–6. [Google Scholar]







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power | 2.2 kW | Stator resistance | 2.74987 Ω |
| Rated speed | 750 rpm | Rotor resistance | 1.30707 Ω |
| Maximum voltage | 155 V | Stator/Rotor inductance | 0.157 H |
| Maximum current | 9.5 A | Mutual inductance | 0.1458 H |
| Category | Component | Specification |
|---|---|---|
| Hardware Platform | Control Processor | TMS320F28335 (32-bit Floating-Point DSP) |
| development board | TMDSCNCD-28388D | |
| Motor | Induction motor (IM) | |
| Load Actuator | Magnetic Particle Brake | |
| Current Sensor | Closed-loop Hall-effect sensor (LA-50P) | |
| Position/Speed Sensor | Incremental Encoder (2500 P/R resolution) | |
| Data Acquisition | DL950 Scopecorder (for waveform recording) | |
| Host | LabVIEW | |
| Configuration Parameters | SVPWM Switching Frequency | 5 kHz |
| DC Bus Voltage | 155 V | |
| Clock frequency of the DSP control board | 200 MHz |
| Working Conditions | Key Indicators | Conventional Method | Proposed Method | Optimization Degree | |
|---|---|---|---|---|---|
| 155 V | Acceleration process under precise orientation | current response time | 90 ms | 58 ms | 35% |
| peak voltage fluctuation | 3.13 p.u. | 1.91 p.u. | 38.98% | ||
| Acceleration process under inaccurate orientation | current response time | 56 ms | 42 ms | 25% | |
| peak voltage fluctuation | 3.08 p.u. | 1.99 p.u. | 35.39% | ||
| Torque increase process under inaccurate orientation | maximum voltage ripple | 0.42 p.u. | 0.099 p.u. | 76.4% | |
| 310 V | Acceleration process under precise orientation | current response time | 89.6 ms | 20.5 ms | 77.12% |
| peak voltage fluctuation | 1.39 p.u. | 1.16 p.u. | 16.55% | ||
| Torque increase process under inaccurate orientation | maximum voltage ripple | 0.192 p.u. | 0.063 p.u. | 67.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xi, S.; Zhang, J. Anti-Windup Method Using Ancillary Flux-Weakening for Enhanced Induction Motor Performance Under Voltage Saturation. Electronics 2025, 14, 3496. https://doi.org/10.3390/electronics14173496
Zhang X, Xi S, Zhang J. Anti-Windup Method Using Ancillary Flux-Weakening for Enhanced Induction Motor Performance Under Voltage Saturation. Electronics. 2025; 14(17):3496. https://doi.org/10.3390/electronics14173496
Chicago/Turabian StyleZhang, Xu, Shuhan Xi, and Jing Zhang. 2025. "Anti-Windup Method Using Ancillary Flux-Weakening for Enhanced Induction Motor Performance Under Voltage Saturation" Electronics 14, no. 17: 3496. https://doi.org/10.3390/electronics14173496
APA StyleZhang, X., Xi, S., & Zhang, J. (2025). Anti-Windup Method Using Ancillary Flux-Weakening for Enhanced Induction Motor Performance Under Voltage Saturation. Electronics, 14(17), 3496. https://doi.org/10.3390/electronics14173496






