Redundancy-Interpolated Three-Segment DAC with On-Chip Digital Calibration for Improved Static Linearity
Abstract
1. Introduction
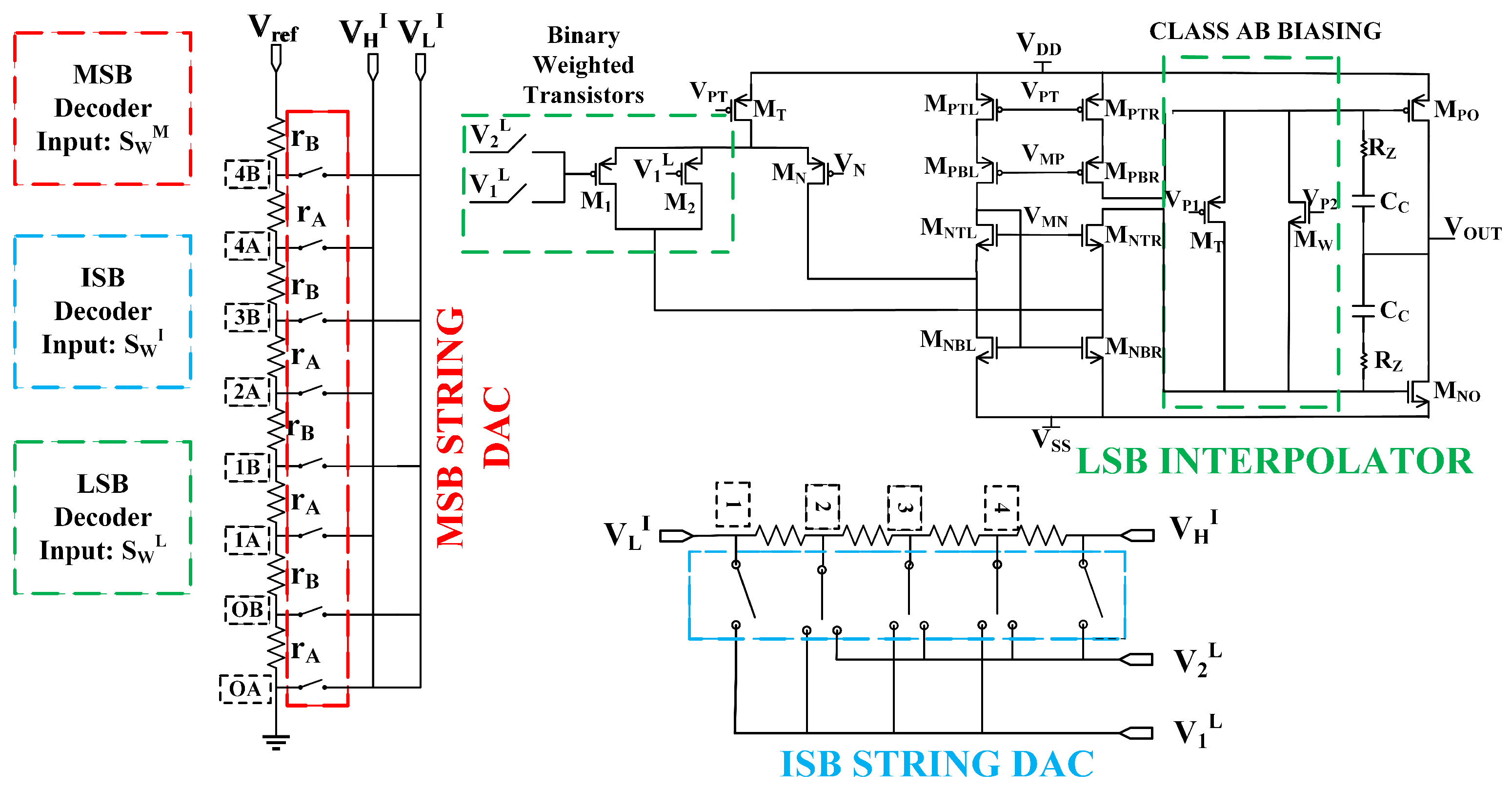
- MSB Stage: The MSB segment introduces a split-unit resistor structure (). This technique enhances the DAC’s sub-radix property to reduce post-calibration differential nonlinearity (DNL).
- ISB Stage: The ISB employs redundancy-based interpolation, achieved by adding an extra resistor to the string, which reduces voltage step errors and improves static linearity. The extra resistor directly counteracts the inter-stage loading effect. This loading effect is a source of nonlinearity, occurring when the ISB string draws current from the Most Significant Bit (MSB) stage and alters its tap voltages. By incorporating this extra resistor, we increase the total number of unit resistors () in the ISB string, which in turn raises its equivalent total resistance (). This increased resistance effectively compensates for the loading, a critical factor in achieving the precise sub-radix behavior required for calibration.
- LSB Interpolating Buffer: The LSB segment departs from the traditional design by replacing the resistor ladder with a custom-designed differential interpolating buffer. This buffer is built with a two-stage folded cascode amplifier and a Class AB output stage and interpolates between ISB outputs to eliminate the need for a fine resistor string DAC.
- Integrated Buffer Functionality: This integrated LSB interpolator serves a dual purpose: it performs high-resolution voltage interpolation while simultaneously acting as the load driving output buffer. This approach eliminates the need for a separate area-intensive buffer, reduces static loading on the ISB string, and lowers overall power consumption.
2. Proposed DAC Architectures
2.1. Existing Design
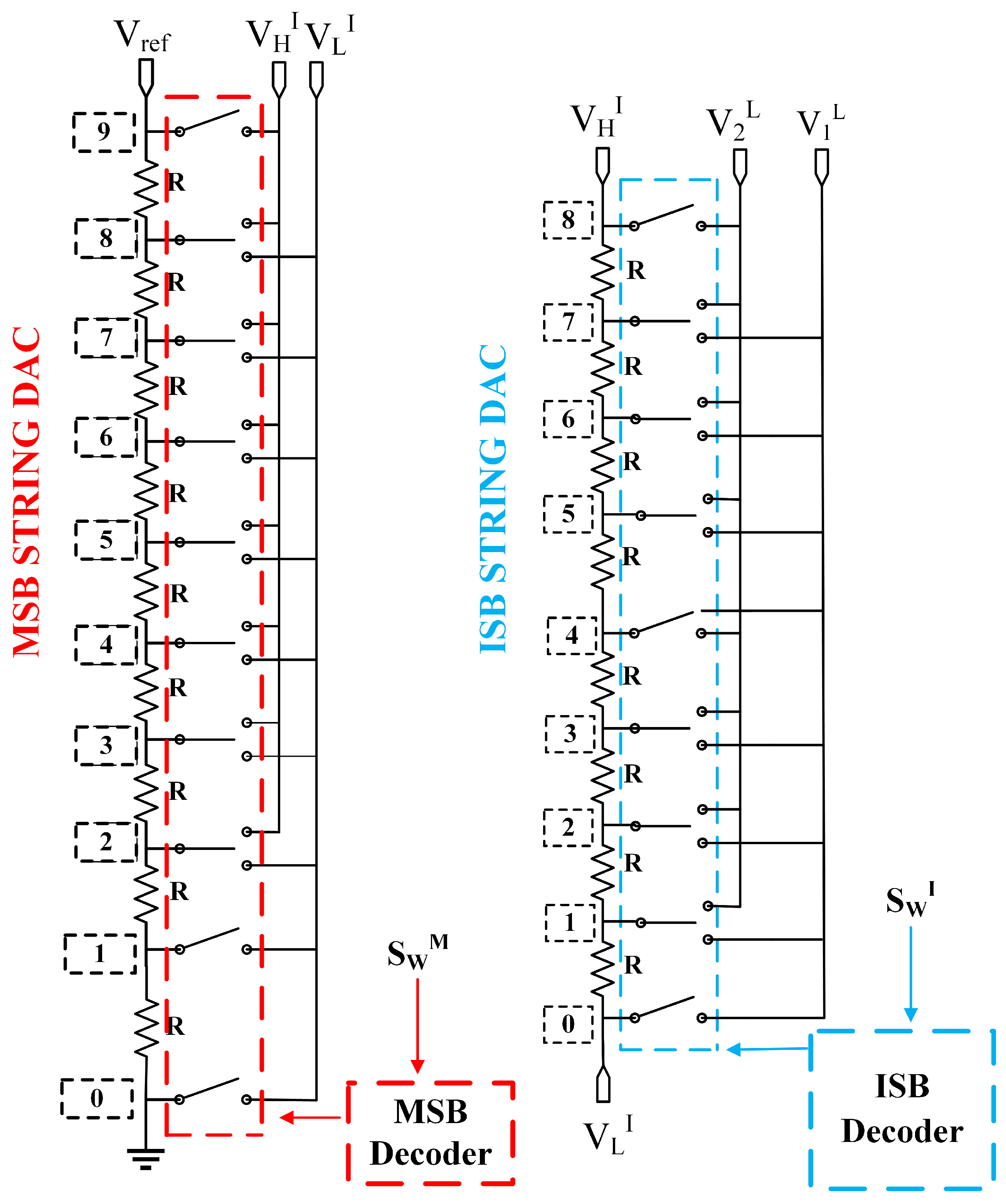
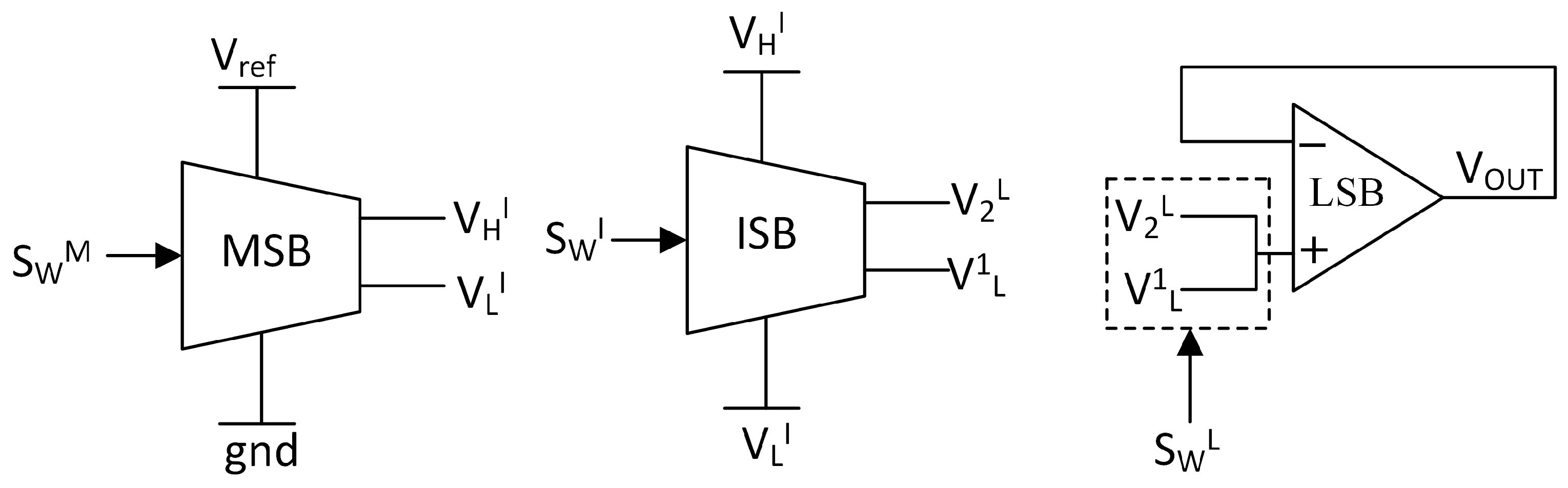
2.2. Review of Proposed DAC Structure 1
2.2.1. MSB String DAC
2.2.2. ISB String DAC
2.2.3. LSB Segment
2.3. Improved Redundancy-Interpolated Three-Segment DAC
3. Optimum Calibration (Binary Search Calibration)
4. Implementation
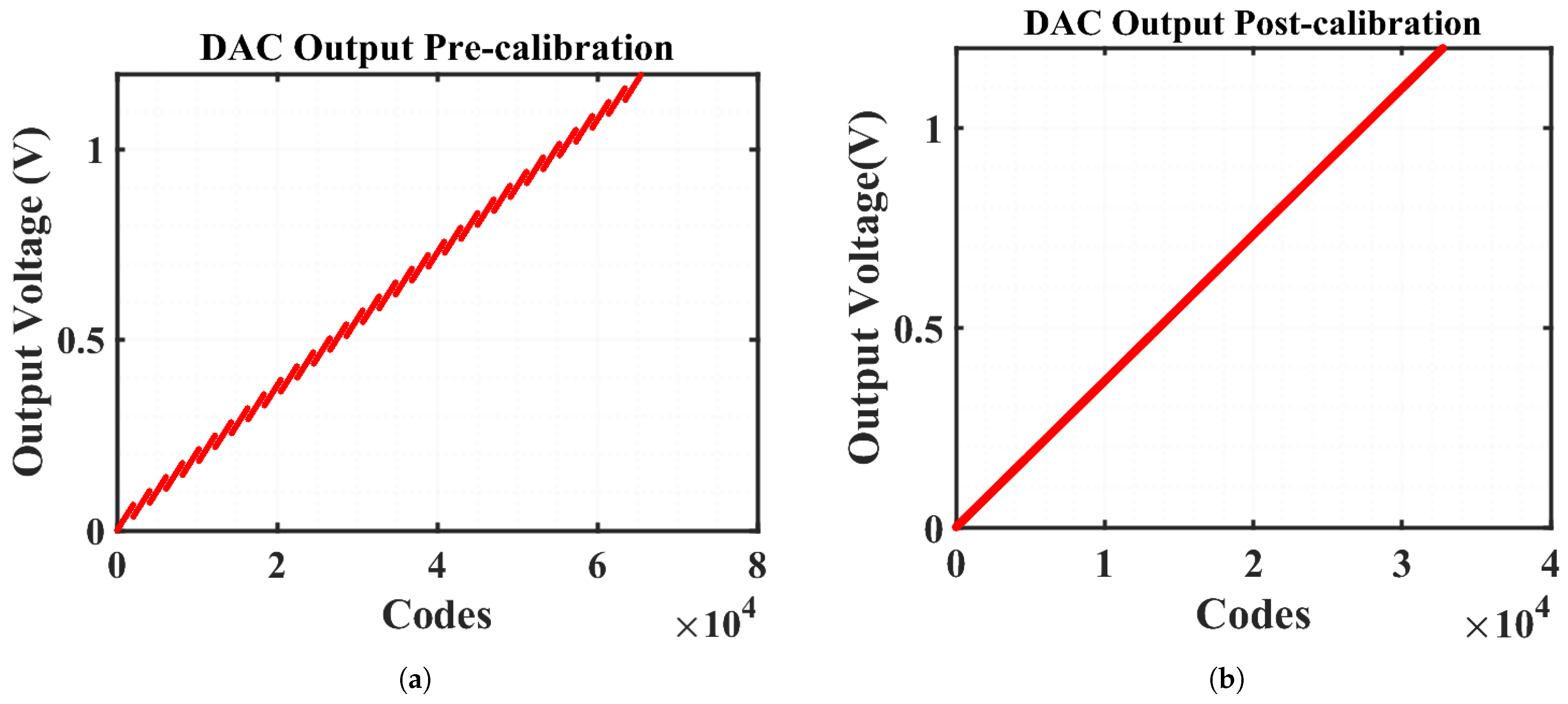
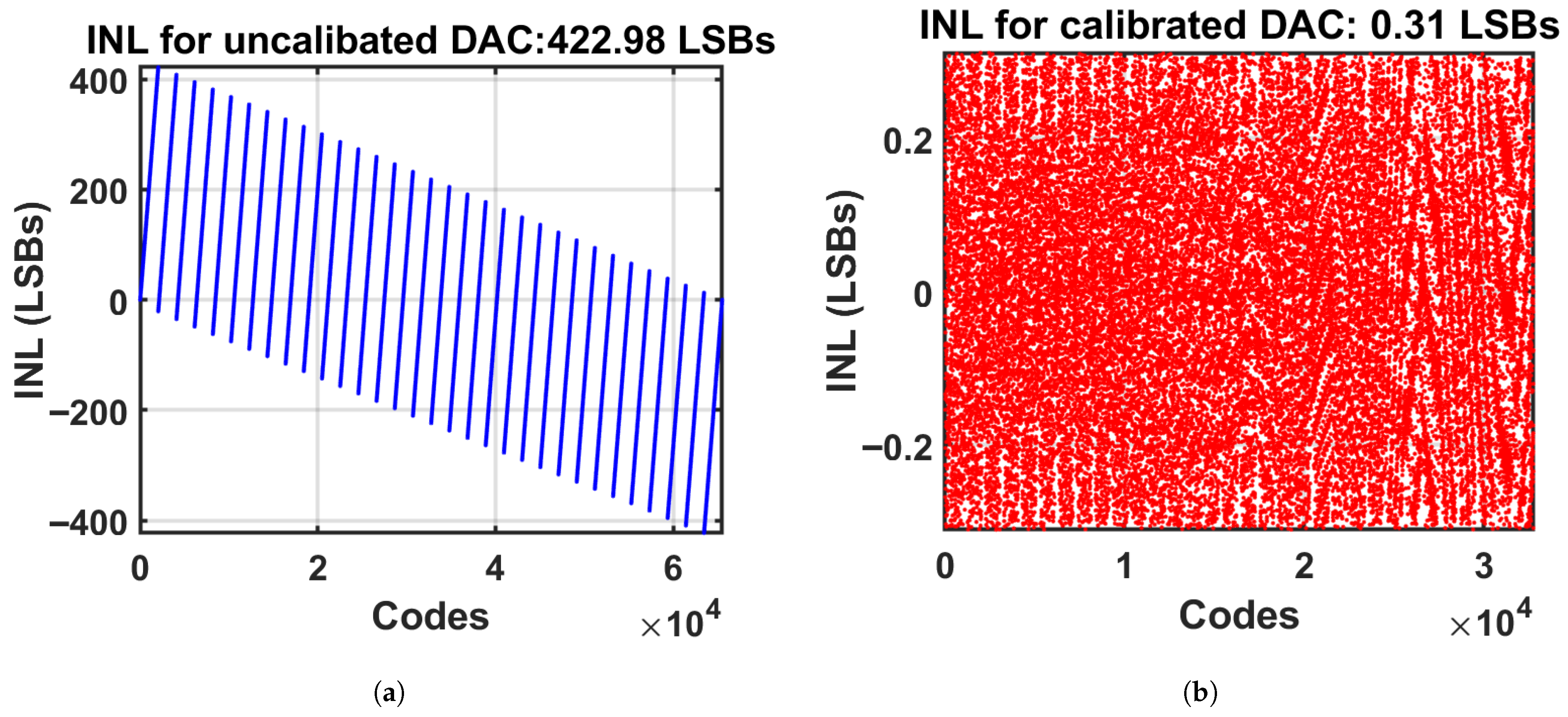
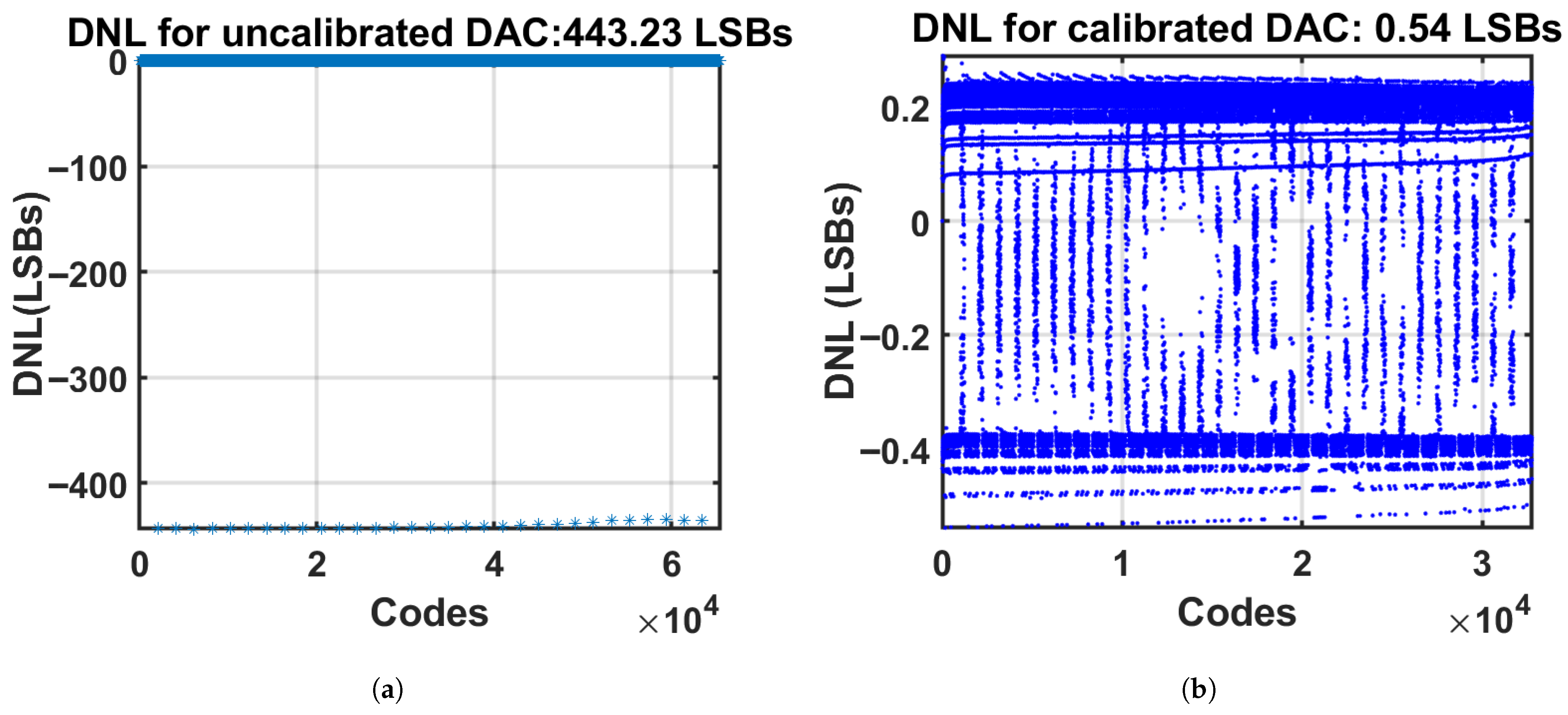
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Toledo, P.; Rubino, R.; Musolino, F.; Crovetti, P. Re-Thinking Analog Integrated Circuits in Digital Terms: A New Design Concept for the IoT Era. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 816–822. [Google Scholar] [CrossRef]
- Amankrah, E.; Geiger, R.; Tutuani, P. A Strategic Approach to Enhancing INL Performance in 10-Bit MOS-Based R-2R DACs through Area Allocation. In Proceedings of the IEEE National Aerospace and Electronics Conf. (NAECON), Dayton, OH, USA, 15–18 July 2024; pp. 163–167. [Google Scholar] [CrossRef]
- Mack, C.A. Fifty Years of Moore’s Law. IEEE Trans. Semicond. Manuf. 2011, 24, 202–207. [Google Scholar] [CrossRef]
- Beach, C.; Krachunov, S.; Pope, J.; Fafoutis, X.; Piechocki, R.J.; Craddock, I. An Ultra-Low-Power Personalizable Wrist-Worn ECG Monitor Integrated with IoT Infrastructure. IEEE Access 2018, 6, 44010–44021. [Google Scholar] [CrossRef]
- Yang, G.; Xie, L.; Mäntysalo, M.; Zhou, X.; Pang, Z.; Xu, L.D.; Kao-Walter, S.; Chen, Q. A Health-IoT Platform Based on the Integration of Intelligent Packaging, Unobtrusive Bio-Sensor, and Intelligent Medicine Box. IEEE Trans. Ind. Inform. 2014, 10, 2180–2191. [Google Scholar] [CrossRef]
- IEEE Innovation at Work. Make Batteries Last Longer: IEEE 802.11 Wake-Up Radio; IEEE: New York, NY, USA, 2017. [Google Scholar]
- Annema, A.-J.; Nauta, B.; van Langevelde, R.; Tuinhout, H. Analog Circuits in Ultra-Deep-Submicron CMOS. IEEE J. Solid-State Circuits 2005, 40, 132–143. [Google Scholar] [CrossRef]
- Murmann, B.; Nikaeen, P.; Connelly, D.J.; Dutton, R.W. Impact of Scaling on Analog Performance and Associated Modeling Needs. IEEE Trans. Electron. Devices 2006, 53, 2160–2167. [Google Scholar] [CrossRef]
- Maloberti, F. Data Converters; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Pelgrom, M. Analog-to-Digital Conversion; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Neidorff, R.A. Digital to Analog Converter Having Multiple Resistor Ladder Stages. U.S. Patent 5,554,986, 10 September 1996. Available online: https://patents.google.com/patent/US5554986A (accessed on 5 July 2025).
- Yenuchenko, M.S.; Pilipko, M.M.; Morozov, D.V. A 10-bit Segmented M-String DAC. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow, Russia, 29–31 January 2018; pp. 265–268. [Google Scholar] [CrossRef]
- Remper, W.C. Digital to Analog Converter. U.S. Patent 5,396,245, 7 May 1995. Available online: https://patents.google.com/patent/US5396245A (accessed on 5 July 2025).
- Basic DAC Architectures III: Segmented DACs by Walt Kester. Available online: https://www.analog.com/media/en/training-seminars/tutorials/MT-016.pdf (accessed on 27 August 2025).
- Sarkar, S.; Banerjee, S. A 10-Bit 500 MSPS Segmented DAC with Optimized Current Sources to Avoid Mismatch Effect. In Proceedings of the 2015 IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, 8–10 July 2015; pp. 172–177. [Google Scholar] [CrossRef]
- Alvarez-Fontecilla, E.; Wilkins, P.S.; Rose, S.C. Understanding High-Resolution Dynamic Element Matching DACs. IEEE Circuits Syst. Mag. 2024, 23, 34–43. [Google Scholar] [CrossRef]
- Chang, K.-H.; Hsieh, C.-C. A 12-bit 150-MS/s Sub-Radix-3 SAR ADC with Switching Miller Capacitance Reduction. J. Solid-State Circuits 2018, 53, 1755–1764. [Google Scholar] [CrossRef]
- Baker, R.J. CMOS Circuit Design, Layout, and Simulation, 3rd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2010; Available online: https://www.wiley.com/en-us/-p-9780470891179 (accessed on 12 July 2025).
- Gagliardi, F.; Dei, M. Accuracy Enhancement of Resistor-String Digital-to-Analog Converters through Averaging Dynamic Element Matching. In Proceedings of the 2025 IEEE 28th International Symposium on Design and Diagnostics of Electronic Circuits and Systems (DDECS), Lyon, France, 5–7 May 2025; pp. 74–79. [Google Scholar]
- IEEE Std 1658-2023; IEEE Standard for Terminology and Test Methods of Digital-to-Analog Converter Devices. IEEE: Piscataway, NJ, USA, 2023. [CrossRef]
- Cong, C.; Geiger, R.L. Formulation of INL and DNL yield estimation in current-steering D/A converters. In Proceedings of the 2002 IEEE International Symposium on Circuits and Systems (ISCAS), Phoenix-Scottsdale, AZ, USA, 26–29 May 2002; p. III. [Google Scholar]
- Ting, H.-W.; Wu, Z.-T.; Yan, J.-Z.; Wu, H.-Y. A Segmented Resistor-String DAC-Based Stimulus Generator for ADC Linearity Testing. In Proceedings of the 2018 International Symposium on Next-Generation Electronics (ISNE), Hsinchu, Taiwan, 7–9 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, N.; Todsen, J.; Chen, D. An 8-bit Low-Cost String DAC with Gradient-Error Suppression to Achieve 16-bit Linearity. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2157–2168. [Google Scholar] [CrossRef]
- Wen, M.K.K.; Ahmad, N.b.; Yusoff, Y.b.; Majid, H.A. Design of a 14-bit Hybrid DAC for High Resolution Applications in SAR ADCs. In Proceedings of the 6th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Kedah, Malaysia, 1–3 December 2021; pp. 1–6. [Google Scholar]
- Bruce, I.; Darko, E.N.; Odion, E.O.; Crabb, M.; Chen, D. Redundancy-Based Resistor-String DAC with an All-Digital Calibration Algorithm. In Proceedings of the 2024 IEEE 67th International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 4–7 August 2024; pp. 571–575. [Google Scholar] [CrossRef]
- Dempsey, D. Digital to Analog Converter. U.S. Patent 5,969,657, 22 July 1997. Available online: https://patents.google.com/patent/US5969657A/en (accessed on 5 July 2025).
- Binary Search Algorithm. Wikipedia. 1 June 2024. Available online: https://en.wikipedia.org/w/index.php?title=Binary_search_algorithm&oldid=1226792725 (accessed on 6 June 2025).
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 4th ed.; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Parthasarathy, T.; Kuyel, T.; Yu, Z.; Chen, D.; Geiger, R. A 16-bit resistor string DAC with full-calibration at final test. In Proceedings of the IEEE International Test Conference, Austin, TX, USA, 8 November 2005. [Google Scholar] [CrossRef]








| Voltage (V) | Node Number | Segmented DACs |
|---|---|---|
| MSB | ||
| MSB | ||
| ISB | ||
| ISB | ||
| is even: | LSB | |
| is odd: | LSB |
| Voltage (V) | Node Number | Segmented DACs |
|---|---|---|
| MSB | ||
| MSB | ||
| ISB | ||
| ISB | ||
| is even: | LSB | |
| is odd: | LSB |
| Parameter | ElConRus [12] | ITC [29] | TCAS-1 [23] | MWSCAS [25] | This Work |
|---|---|---|---|---|---|
| Technology (µm) | 0.18 | 0.5 | 0.13 | 0.18 | 0.18 |
| Resistor Material | ∼ | Poly | TaN | Poly | Poly |
| Architecture | Segmented string DAC | String DAC + calibration DAC | String DAC + interpolating amplifier | Segmented string DAC | String DAC + differential interpolator |
| Resolution (bits) | 10 | 16 | 8 | 13 | 15 |
| Output range (V) | 1.8 | 5 | 3.3 | 1.2 | 1.2 |
| INL (ppm/LSB) | 9k/9.4 | 122/7.99 | 21/5.37m | 95/0.78 | 16/0.48 |
| DNL (ppm/LSB) | 273/0.28 | 6.1/0.49 | 18/4.61m | 124/0.94 | 21/0.68 |
| Measurement | No | Yes | Yes | No | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonsu, G.; Tamakloe, K.; Bruce, I.; Nti Darko, E.; Chen, D. Redundancy-Interpolated Three-Segment DAC with On-Chip Digital Calibration for Improved Static Linearity. Electronics 2025, 14, 3477. https://doi.org/10.3390/electronics14173477
Bonsu G, Tamakloe K, Bruce I, Nti Darko E, Chen D. Redundancy-Interpolated Three-Segment DAC with On-Chip Digital Calibration for Improved Static Linearity. Electronics. 2025; 14(17):3477. https://doi.org/10.3390/electronics14173477
Chicago/Turabian StyleBonsu, Godfred, Kelvin Tamakloe, Isaac Bruce, Emmanuel Nti Darko, and Degang Chen. 2025. "Redundancy-Interpolated Three-Segment DAC with On-Chip Digital Calibration for Improved Static Linearity" Electronics 14, no. 17: 3477. https://doi.org/10.3390/electronics14173477
APA StyleBonsu, G., Tamakloe, K., Bruce, I., Nti Darko, E., & Chen, D. (2025). Redundancy-Interpolated Three-Segment DAC with On-Chip Digital Calibration for Improved Static Linearity. Electronics, 14(17), 3477. https://doi.org/10.3390/electronics14173477








