Design of Real-Time Gesture Recognition with Convolutional Neural Networks on a Low-End FPGA

Abstract

Hand gesture recognition is used in human–computer interaction, with multiple applications in assistive technologies, virtual reality, and smart systems. While vision-based methods are commonly employed, they are often computationally intensive, sensitive to environmental conditions, and raise privacy concerns. This work proposes a hardware/software co-optimized system for real-time hand gesture recognition using accelerometer data, designed for a portable, low-cost platform. A Convolutional Neural Network from TinyML is implemented on a Xilinx Zynq-7000 SoC-FPGA, utilizing fixed-point arithmetic to minimize computational complexity while maintaining classification accuracy. Additionally, combined architectural optimizations, including pipelining and loop unrolling, are applied to enhance processing efficiency. The final system achieves a 62× speedup over an unoptimized floating-point implementation while reducing power consumption, making it suitable for embedded and battery-powered applications.

1. Introduction

Hand gesture recognition has become an essential component of human–computer interaction, enabling touch-free control in applications such as assistive technologies, virtual reality, robotics, and smart home systems. Many existing gesture recognition systems rely on camera-based approaches, which, despite their effectiveness, present several challenges, including high computational complexity, sensitivity to environmental conditions, and privacy concerns. An alternative solution is the use of accelerometers, which offer a lightweight, low-power, and privacy-preserving method for capturing hand movements. However, the implementation of real-time gesture recognition on low-cost, portable hardware remains a significant challenge due to the limited computational resources and power constraints of embedded systems.

This work presents a hardware/software co-optimized system for real-time hand gesture recognition based on accelerometer data, implemented on a low-cost System-on-a-Chip Field-Programmable Gate Array (SoC-FPGA) from the Xilinx Zynq-7000 family. A SoC-FPGA integrates both processor and FPGA architectures into a single device, providing higher integration, lower power, smaller board size, and higher bandwidth communication between the processor and FPGA. FPGA technology is now widely applied in biomedical and industrial applications due to its energy efficiency, parallelism, and reconfigurablity. In this work, the CNN accelerator was implemented on the FPGA fabric, and the CPU coordinates its operation.

Three hardware optimizations were performed to reduce the execution time. The first optimization was the introduction of the pipeline, achieving an overall speedup of 26.7×. The second optimization was the Loop Unroll technique, resulting in an overall speedup of 41.5×. Finally, some of the layers were merged and implemented as one function, which decreased the resources needed while also achieving an overall speedup of 62× when compared to the unoptimized hardware architecture using floating-point representation.

2. Gesture Recognition with Convolutional Neural Networks

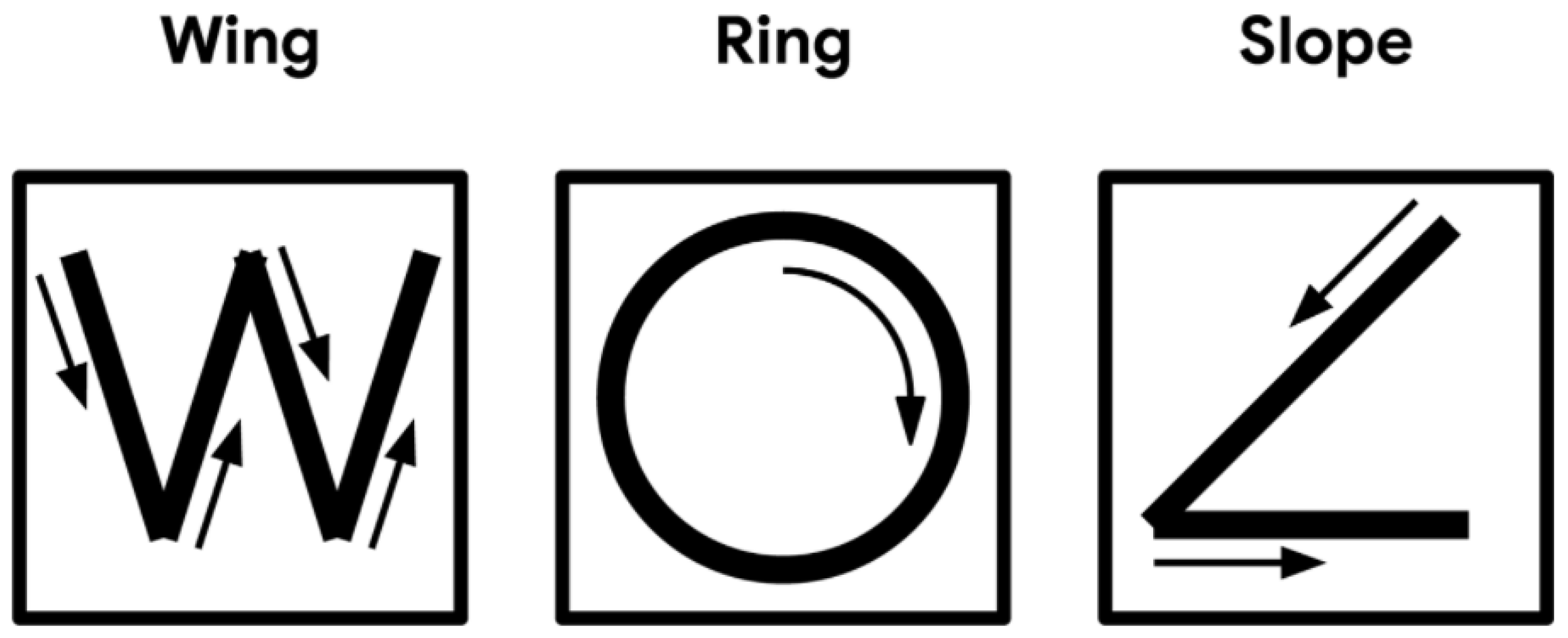
In this work, a gesture recognition system was used as an example of implementing a Neural Network (NN) for gesture recognition from an accelerometer placed on a subject’s hand to detect gestures, according to [1], see Figure 1. This model can detect three different gestures. The model was trained using the TensorFlow Lite framework [2].

Figure 2 shows the overview of the gesture recognition model. The input of the NN model is the data from the accelerometer. The model has seven layers, of which two of them are convolutional layers.

All the layers of the model are represented in

Table 1. Layers of gesture recognition NN model.

Layer	Input Shape	Output Shape	Number of Parameters
Convolution 2D	(128, 3, 1)	(128, 3, 8)	104
MaxPooling 2D	(128, 3, 8)	(42, 1, 8)	0
Convolution 2D	(42, 1, 8)	(42, 1, 16)	528
MaxPooling 2D	(42, 1, 16)	(14, 1, 16)	0
Flatten	(14, 1, 16)	(224)	0
Dense	(224)	(16)	3600
Dense	(16)	(4)	68

below. The table also has the input shape of the layer, in other words, the way the input data is organized. There are also the output shape of each layer and the number of parameters that each layer needs so they can compute the output values, for example, the kernels for the convolutional layers.

Training data and the corresponding output are needed for each gesture to train and test the model. Each gesture was collected from 10 people and stored in ten files, one file for each person. Each file has approximately 15 individual performances, and there are also 10 files for the unknown gestures. The data was split so that six files are used for the training, two are used for validation, and another two for testing. The model was tested with an accuracy of 93.23% and a loss of 0.2888. These values are considered very good as they predict the correct class with 93% certainty.

The first layer is a convolutional layer; it receives a set of input values directly from the accelerometer and then performs a convolution with those values. The input data has a shape of (128, 3, 1), which means that 128 sets of accelerometer measurements for all three axes (x, y and z) are necessary. It has eight kernels in the shape of 3 × 4, and the output is eight different matrices that capture different features of the input data. To perform a convolution, first, it is necessary to know all the values of the kernels and biases that are stored in the network model.

Each convolution operation produces only one result; then, the kernel iterates through all the input values. Once the first kernel finishes all the convolution operations, the second kernel iterates through all the input values until the last kernel finishes. This layer has output data in the shape of (128, 3, 8), and it needs 104 auxiliary parameters (96 ($3\times 4\times 8$) for the eight kernels plus eight additional values for the offset of each kernel).

After the convolutional layer, a MaxPooling is performed. This layer chooses the biggest values within a 3 × 3 matrix. The layer looks at nine values at the same time and then shifts through all the data. In the end, it shrinks the data into the shape of (42, 1, 8) by removing redundant information while retaining the most significant features.

The second convolution is a 3D convolution and has the shape of the input data as (42, 1, 8). There are 16 kernels which also have three dimensions (4, 1, 8). We have a 42 × 8 matrix as the input and a 4 × 8 kernel. Once again, the kernels shift through all the data, producing the output shape of (42, 1, 16). This layer needs 512 ($4\times 8\times 16$) parameters for all 16 kernels plus one bias for each kernel (16 in total), leading to 528 auxiliary parameters.

The second MaxPool is the same as the first one, with the differences being the input and output shapes. The input has the shape (42, 1, 16). The MaxPool chooses the highest values from a set of three values (3 × 1 matrix), and it shifts through all the values for all 16 channels. In the end, the data has the shape (14, 1, 16).

The flatten layer is used to reshape its input data into a single vector, and it “flattens” the values. In this case, it receives the output of the second MaxPool, in the shape of (14, 1, 16). It starts in the first dimension (first 14 values), then the second, and so on until it is all flattened out (14 values each time), producing an output with the shape (224). Notice that it only maintains one dimension.

The dense layer uses all the values of the input independently instead of as a set of values. It multiplies all the input values by a weight given by a kernel and sums all the products into a single value. In other words, instead of having a small kernel that shifts through the data, the dense layer has one big kernel that multiplies all the input data at once. It can also have multiple kernels. In the case of the first dense layer, it has 16 kernels, so it repeats the operations 16 times with different weights (kernels), computing 16 different values and giving an output shape of (16). It needs 3584 ($224\times 16$) auxiliary values for all the weights of each one of the outputs, and it also needs 16 extra values for the offset of each value, reaching a total of 3600 parameters.

The second dense layer is exactly like the previous layer, but now it has four kernels with different weights, which means that it outputs four values, and the output is in the shape of (4). Once again, this layer needs auxiliary parameters, 64 (16 × 4), for each one of the four kernels plus the four bias values for each output, giving a total of 68 parameters. With the output values, a Softmax computation can be performed. The outputs of the Softmax computation are the probabilities of our three gestures and one additional output for the unknown gestures, so the sum of all the values must be 1.

3. Software Model Implementation in C

The original TinyML source implementation code uses a compiled library for the target MCU. Thus, it was impossible to identify which operations were being executed. The solution was to study and implement the layers of the model and obtain information about the parameters and make a new implementation from scratch to use the NN model.

The first step was to create constants for all the parameters (kernels and bias), then create a variable for the input, and finally, start to process all the layers one by one and check at every step if the code is doing what it is supposed to. Finally, after all the layers are processed, it was necessary to create a function that reads a file, stores the input values in the corresponding variable, and starts going through all the layers to produce the output; repeat the process until the end of the file.

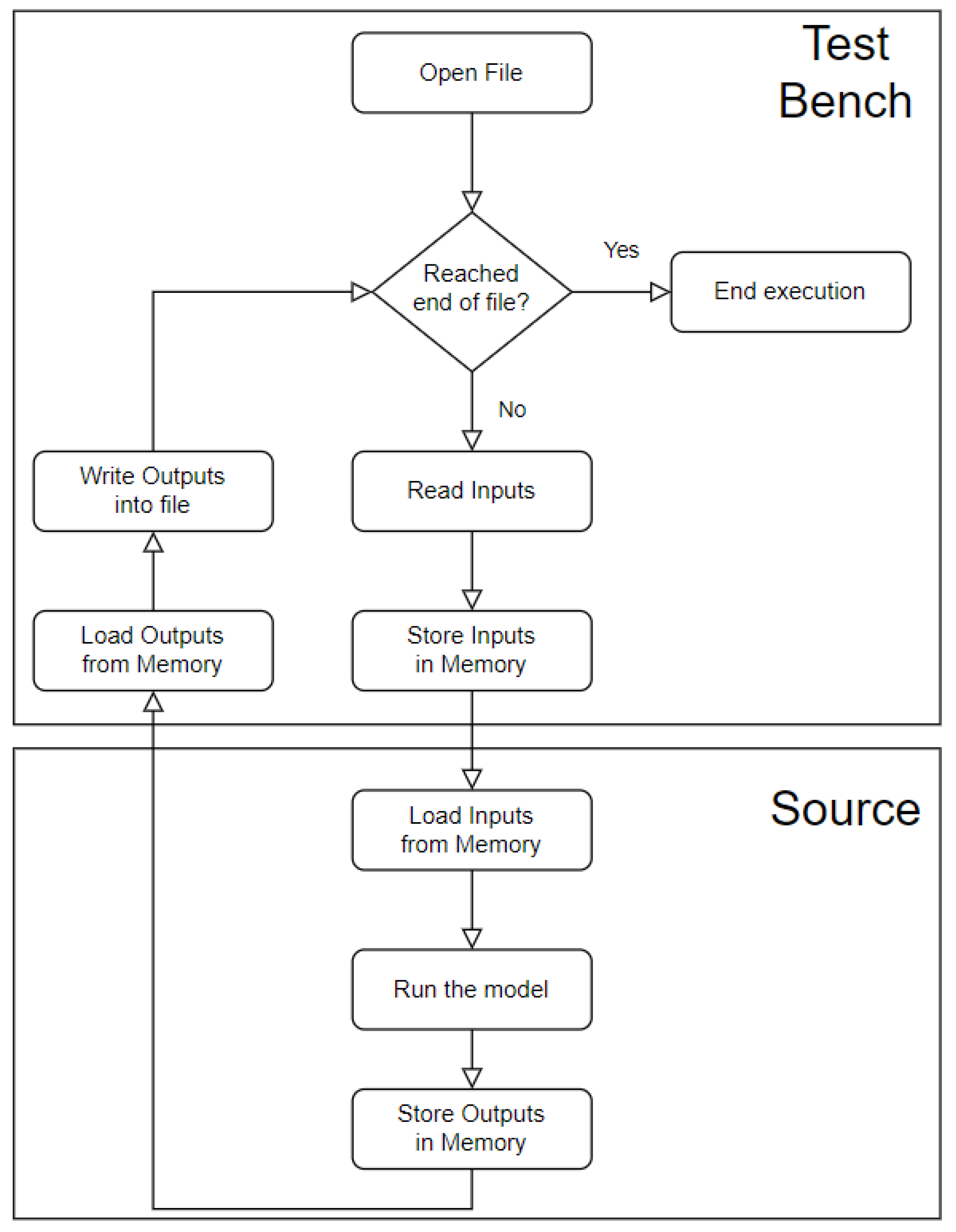
The source code flowchart is shown in Figure 3, where it is possible to see that the code has the following three actions: gather the input data, perform the model inference, and display the output.

Table 2. Classification errors between the original TinyML code and the custom C code.

Gesture	W	O	L	Negative	Total
Maximum Absolute Error	1.82 $\times {10}^{-6}$	1.88 $\times {10}^{-6}$	2.83 $\times {10}^{-6}$	2.50 $\times {10}^{-6}$	2.83 $\times {10}^{-6}$
Mean Absolute Error	1.95 $\times {10}^{-8}$	6.09 $\times {10}^{-8}$	1.50 $\times {10}^{-7}$	1.23 $\times {10}^{-7}$	8.17 $\times {10}^{-8}$
Quadratic Absolute Error	1.29 $\times {10}^{-14}$	2.65 $\times {10}^{-14}$	1.42 $\times {10}^{-13}$	1.26 $\times {10}^{-13}$	6.71 $\times {10}^{-14}$

shows the errors between the code that was performed in the C language and the original TinyML code. There are some errors, as expected, derived from several causes. For example, the operations are slightly different from the original TinyML code, and the variables are different in one code when compared to another. This is because the compilers are different. The original TinyML code was compiled in a Linux subsystem with a GCC 9.4.0 compiler, while the custom code was compiled in Windows with an MinGW-W64-builds-4.3.5 compiler. All of these factors can cause differences in the output of the model, but, as we can see in the table, the errors are too small and all the predictions stayed the same throughout all the test files.

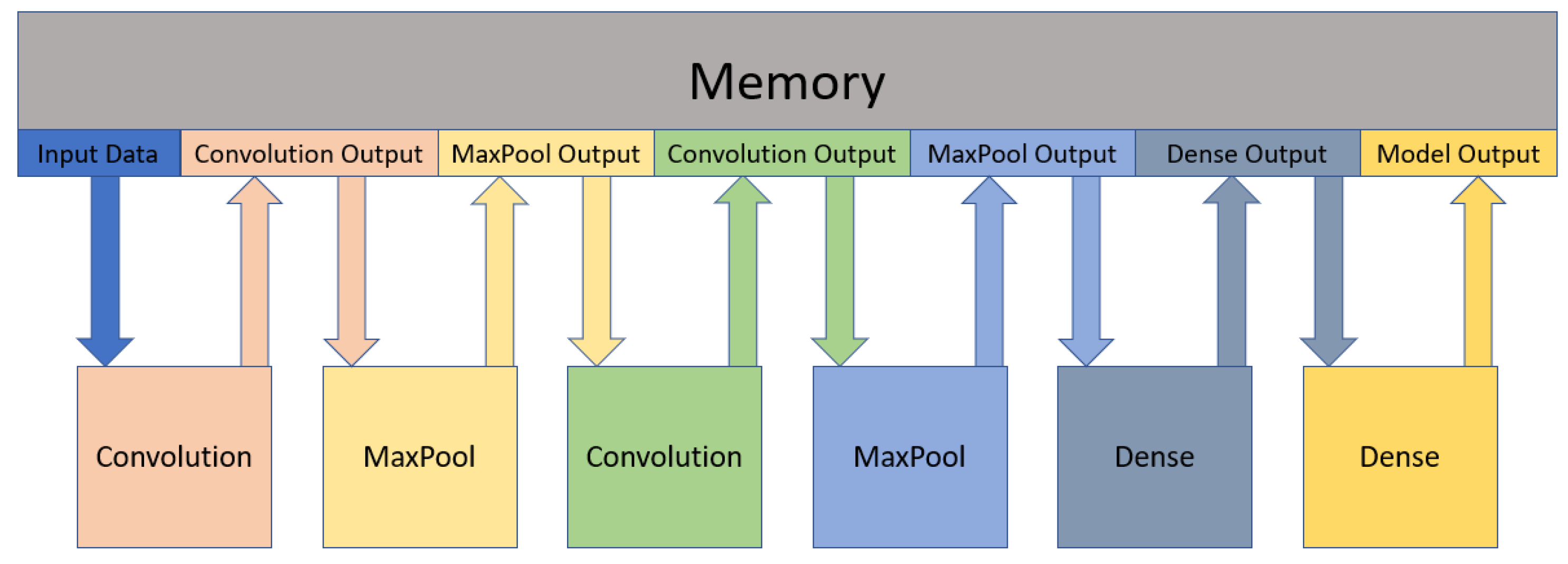
Figure 4 shows the dataflow of the model. So, at the end of each layer, the outputs are stored in the memory and the next layer loads these values to start executing.

4. Floating-Point vs. Fixed-Point Representation

The initial C description of the CNN model in Vitis HLS had the data variables in floating-point representation. However, to have better execution time and simpler hardware blocks (such as multipliers and adders), the floating-point representation was converted into a fixed-point representation. The downside of this representation is that it has a limited range and less precision than the floating-point representation, which may result in output errors. Therefore, a study was performed, where the number of bits required for the fixed-point representation was evaluated. This study helped to understand the tradeoff between the resources needed and the network model’s accuracy. If fewer bits are used, the resources needed are reduced, but the network model accuracy also decreases.

4.1. Floating-Point Representation

The first implementation in Vitis HLS used floating-point variables. In the IEEE standard for floating-point arithmetic representation [3] (32 bits), there is no set number of bits for the integer part or the decimal part. Instead, there is 1 bit for the sign, 8 bits for the exponent, and 23 bits for the mantissa.

When comparing to fixed-point representation, the operations with floating-point representation are much more complex and time-consuming. The adders take about three clock cycles, and the multipliers take about six clock cycles.

The code was implemented in Vitis HLS 2022.1, with the Zynq-7020 SoC-FPGA as the target device. After running the code through all the inputs of the provided files, all the predictions matched the predictions of the original TinyML code. However, some differences were presented in the output values.

Table 3. Errors between the original TinyML code and the VitisHLS code using floating-point representation.

Gesture	W	O	L	Negative	Total
Maximum Error	1.82 $\times {10}^{-6}$	1.94 $\times {10}^{-6}$	2.22 $\times {10}^{-6}$	1.55 $\times {10}^{-6}$	2.22 $\times {10}^{-6}$
Minimum Error	−1.79 $\times {10}^{-6}$	−1.97 $\times {10}^{-6}$	−2.21 $\times {10}^{-6}$	−1.46 $\times {10}^{-6}$	−2.21 $\times {10}^{-6}$
Average Error	2.70 $\times {10}^{-10}$	−1.37 $\times {10}^{-9}$	−8.34 $\times {10}^{-11}$	1.28 $\times {10}^{-9}$	−2.42 $\times {10}^{-10}$
Quadratic Error	7.08 $\times {10}^{-15}$	2.47 $\times {10}^{-14}$	6.35 $\times {10}^{-14}$	3.54 $\times {10}^{-14}$	3.21 $\times {10}^{-14}$
Standard Deviation	1.13 $\times {10}^{-7}$	2.13 $\times {10}^{-7}$	3.34 $\times {10}^{-7}$	2.83 $\times {10}^{-7}$	2.43 $\times {10}^{-7}$

presents the errors between the output of the original TinyML code and the Vitis HLS code using floating-point representation. These errors are not that significant because the minimum value for a gesture to be chosen is 0.25 (because there are four gestures, and the sum of all the values must be 1), which is 100,000× higher compared to the Maximum Absolute Error (MAE), which is about 2.22 $\times {10}^{-6}$.

Note that these errors are different from the C code from CLion despite the operations being the same and the overall code being very similar. The reason for the existence of these differences is that the compilers used are different from each other. In the CLion IDE, the compiler that was used is the MinGW-W64-builds-4.3.5. Vitis HLS has GCC as a compiler, and this implies that the operations are performed differently, which results in slightly different outputs. To prove that, the same code on CLion was compiled with GCC using an Ubuntu subsystem for Windows. On that test, the outputs were the same as the Vitis HLS outputs.

4.2. Fixed-Point Representation

Fixed-point adders only take one clock cycle, and multipliers take one to two clock cycles, which is less than floating-point operators. Moreover, the resources required to implement the operators in fixed-point representation are also reduced.

In fixed-point representation, there are bits set to the integer part and bits set to the decimal part, so, for instance, if a number has eight bits in the format Q4.4, this means that it has four bits to represent the integer part and four bits to represent the decimal part. This representation is better than the floating-point representation for this work. However, there are some downsides, like the loss of precision when compared with floating-point representation. The advantages are that with the fixed-point representation, all the operators are simpler to implement. Therefore, the complexity is smaller than the floating-point representation, while the computing time is faster. Also, by reducing the complexity, fixed-point representation needs fewer resources to implement when compared to floating-point representation. So, as long as the values are not too different during the computations of the algorithm or the error is acceptable, this option is much better than floating-point representation.

So, for instance, if we want to represent a number with eight bits, with three bits for the integer part and five bits for the decimal part, then the initialization needs to be “ap_fixed<8, 3> var;”. Therefore, when initializing a fixed-point variable, it is necessary to provide two arguments, (W and I), while the other arguments are optional and have default values.

The W and I arguments are 36 and 17, respectively, which means that the variables have 36 bits with 17 bits for the integer part and 19 bits for the decimal part. However, the number of bits can be decreased; more in information can be found in Section 6.1. To avoid overflows in this work, enough bits were provided for the integer part and hence the Q argument is the only optional argument that needs concern. By consulting the User Guide [4], seven options were withdrawn for this argument.

1.

RND: Round to plus infinity.

2.

RND_ZERO: Round to zero.

3.

RND_MIN_INF: Round to minus infinity.

4.

RND_INF: Round to infinity.

5.

RND_CONV: Convergent rounding.

6.

TRN: Truncation to minus infinity (default).

7.

TRN_ZERO: Truncation to zero.

Out of these seven options, four were chosen to be evaluated: TRN; TRN_ZERO; RND_ZERO; and RND_CONV. In this evaluation, the first kernel is initialized with the different quantization modes. These values are then compared with the floating-point values of the kernel.

The results of using different quantization modes are shown in

Table 4. Errors between fixed-point and the floating-point representation for different rounding modes.

	TRN	TRN_ZERO	RND_ZERO	RND_CONV
Maximum Error	1.89 $\times {10}^{-6}$	1.89 $\times {10}^{-6}$	9.31 $\times {10}^{-7}$	9.31 $\times {10}^{-7}$
Minimum Error	0.00 $\times {10}^0$	−1.82 $\times {10}^{-6}$	−9.37 $\times {10}^{-7}$	−9.37 $\times {10}^{-7}$
Mean Error	9.43 $\times {10}^{-7}$	−1.50 $\times {10}^{-7}$	2.90 $\times {10}^{-8}$	2.90 $\times {10}^{-8}$
Mean Absolute Error	9.43 $\times {10}^{-7}$	9.78 $\times {10}^{-7}$	4.47 $\times {10}^{-7}$	4.47 $\times {10}^{-7}$
Quadratic Error	1.23 $\times {10}^{-12}$	1.30 $\times {10}^{-12}$	2.85 $\times {10}^{-13}$	2.85 $\times {10}^{-13}$
Standard Deviation	5.84 $\times {10}^{-7}$	1.13 $\times {10}^{-6}$	5.33 $\times {10}^{-7}$	5.33 $\times {10}^{-7}$
Mode	1.70 $\times {10}^{-6}$	8.94 $\times {10}^{-7}$	7.00 $\times {10}^{-7}$	7.00 $\times {10}^{-7}$
Median	8.94 $\times {10}^{-7}$	−1.90 $\times {10}^{-7}$	9.69 $\times {10}^{-8}$	9.69 $\times {10}^{-8}$

. It can be concluded from the table that the best modes are RND_ZERO and RND_CONV, which have smaller errors in every metric. Both of them have the same errors because both modes try to round the value to the nearest integer. The problem comes when the number is in the middle of two integers; for example, 5.5 is in the middle of 5 and 6.

To choose the best mode for this work, another evaluation was performed. We evaluated how many resources were needed to perform a simple operation for each of the four modes.

Looking at

Table 5. FPGA resources used for the different quantization modes.

	DSP	FF	LUT
TRN	2	181	266
TRN_ZERO	2	182	320
RND_ZERO	2	182	321
RND_CONV	2	182	321

, it is possible to conclude that the default mode (TRN) is the one that consumes fewer resources. On the other hand, both RND_ZERO and RND_CONV are the ones that consume the most, with a small increase over TRN_ZERO. These two modes consume the same resources used and also generate the same errors. The conclusion is that both are suitable to use, and in this work, the one that was chosen was convergent rounding (RND_CONV).

Following the choice of quantization mode, a random input was chosen from the test files. This input goes through all the layers of the model, and all the variables that were in floating-point representation are now in fixed-point representation with the chosen quantization mode. The output of each layer is compared with the floating-point code in

Table 6. Errors between fixed-point and floating-point representation after each layer.

	First Convolution	First MaxPool	Second Convolution	Second MaxPool	First Dense	Second Dense	Softmax
Maximum Error	3.59 $\times {10}^{-3}$	3.59 $\times {10}^{-3}$	1.94 $\times {10}^{-3}$	1.94 $\times {10}^{-3}$	3.63 $\times {10}^{-3}$	4.12 $\times {10}^{-4}$	2.22 $\times {10}^{-4}$
Minimum Error	−2.76 $\times {10}^{-3}$	−2.31 $\times {10}^{-3}$	−2.78 $\times {10}^{-3}$	−2.77 $\times {10}^{-3}$	−3.44 $\times {10}^{-3}$	−4.81 $\times {10}^{-4}$	−2.22 $\times {10}^{-4}$
Mean Error	−1.00 $\times {10}^{-6}$	6.39 $\times {10}^{-5}$	−1.18 $\times {10}^{-5}$	−1.22 $\times {10}^{-5}$	−1.12 $\times {10}^{-4}$	5.25 $\times {10}^{-6}$	1.05 $\times {10}^{-8}$
Mean Absolute Error	1.51 $\times {10}^{-4}$	3.76 $\times {10}^{-4}$	1.22 $\times {10}^{-4}$	2.22 $\times {10}^{-4}$	8.87 $\times {10}^{-4}$	3.14 $\times {10}^{-4}$	1.11 $\times {10}^{-4}$
Quadratic Error	1.99 $\times {10}^{-7}$	5.58 $\times {10}^{-7}$	1.79 $\times {10}^{-7}$	3.27 $\times {10}^{-7}$	2.62 $\times {10}^{-6}$	1.18 $\times {10}^{-7}$	2.47 $\times {10}^{-8}$
Standard Deviation	4.46 $\times {10}^{-4}$	7.45 $\times {10}^{-4}$	4.23 $\times {10}^{-4}$	5.72 $\times {10}^{-4}$	1.62 $\times {10}^{-3}$	3.43 $\times {10}^{-4}$	1.57 $\times {10}^{-4}$
Mode	0.00	0.00	0.00	0.00	0.00	-	-
Median	0.00	0.00	0.00	0.00	0.00	0.00	0.00

.

Since the intermediate values (output values of each layer) are mostly big integer numbers (bigger than 100), the errors presented in the table compared to those numbers are very small. In all of these evaluations, the fixed-point variables had 36 bits, with 17 bits for the integer part and 19 for the decimal part. Further analysis of the number of bits required for the integer and decimal parts is performed in Section 6.1.

5. Digital System Design Optimizations

5.1. Pipelining

When scheduling without a pipeline, the next instruction only begins when the previous instruction is finished, but with a pipeline, that is not the case. Because the instructions are independent, it is possible to start the next instruction without the current one finishing, utilizing the available resources that are not being used.

Without a pipeline, all the operations of each layer are performed sequentially, producing one output only when the previous one finishes.

Initially, the first convolutional layer would load every value that was necessary for the convolution, that is, all the values of the kernel and all the input values needed. These loads were executed every iteration, which means that it would perform 18 to 24 loads for each output, storing this output in the end. The cause of this violation was the number of ports. There were not enough ports for all the necessary loads and stores. This means that there were not enough resources to pipeline this loop. The solution is to reformulate the code so the number of loads and stores decreases. First, the number of main loops was reduced, from one outer loop and two inner loops to one main outer loop.

In the convolutional layer, the kernel moves through the input data, as shown in Figure 5, and goes through the same values as before so the code can reuse those values. It only needs to have a 3 × 4 matrix with the values of the kernel at that moment and load a new value per iteration. This is a way to reduce the number of loads per iteration. Before, there were either 20 or 24 loads only in one iteration (12 for the kernel and 10 to 12 for the input data). Now the input data only needs one load per iteration and the kernel none because it is the same for all the input data. The only time this does not happen is in the beginning because it is necessary to load at least 11 values of the input data and all the 12 values of the kernel, and when the kernel changes, it is necessary to load all the 12 values again for the new kernel.

There are some precautions to be taken, as the user guide says “Arrays are typically implemented as a memory (RAM, ROM or FIFO) after synthesis” [4]. Therefore, the code cannot just load an input value, for instance, just to store it in another memory to solve this problem.

Without a pipeline, this new architecture is slower than the previous one when synthesized. Now, with a pipeline, the synthesis led to another error. This time it was a timing violation. The clock cycle was 10 ns, but the critical path was slower than the clock cycle. The fix was simple, just slow the clock a bit, from 10 ns to 10.4 ns. In the end, even with the fact that the clock cycle was slower, there were improvements in the speed, but the resource usage increased as well.

Advancing to the second convolution, the same steps were performed, and, although the number of loads per iteration after the optimization was eight, Vitis HLS was able to pipeline the loop, increasing the resources used as well as the speed. This optimization was performed on all layers of the model, enabling the use of a pipeline in every layer. The clock had to be changed yet again, from 10.40 ns to 10.41 ns, when optimizing the first dense layer due to a timing violation. In the end, the speedup achieved was 26.7× when compared with the code without a pipeline with a 10 ns clock cycle.

5.2. Loop Unroll

Loop unroll (LU) is a known optimization in which, instead of the loop performing one iteration at a time, it performs several iterations in parallel. This optimization tries to increase the execution speed while increasing the resources used in return. It is a space–time trade-off.

Starting with the first dense layer, in this function, there are three loops, the outer loop that shifts through the kernels and two inner loops to shift through all the data. By unrolling the innermost loop, it was possible to increase the speed as wished (11.1× function speedup). The problem was when the inner loop of the second dense layer was unrolled. This time, the speed got worse. There could be many, many causes for this problem. In this layer, there are many loads and stores, and when the loop is unrolled, it tries to process all the loads inside the loop, and all of these loads are followed by a store and a load that are outside the loop.

When a loop is unrolled, there is a possibility that there are not enough ports to load and store all the necessary values, and the circuit needs to stall and wait before it can load the values. This will limit the performance by suspending the execution of the computations in the pipeline, impacting the throughput and latency.

However, with the pipeline, the clock cycle had to be changed because of the critical path in the first convolutional layer, and after that in the first dense layer when the loop unroll was performed in the convolutional layer. Even though the execution time stayed the same, the critical path decreased. Now, the clock cycle can be faster, changing from 10.41 ns to 10.37 ns (1.004× overall speedup). In the end, after both the pipeline and the loop unroll optimizations, the speedup achieved was 41.5×.

5.3. Merging

After observing the Schedule Viewer tool in Vitis HLS, it was detected that a function/layer only starts its execution when the previous one finishes. Some layers do not need all the input values to begin their execution. Instead, they can start the execution with some of the inputs, and while it is performing the operations with those values, the remaining input values arrive from the previous layer. This way, it is possible to parallelize even more the overall execution of the architecture, increasing its speed.

The method to implement this in Vitis HLS is the following: instead of having independent functions, those functions can merge and code the new function in a way that the next layer starts before the previous one finishes. Starting with the first convolutional and the first MaxPool layers, this is a simple case. Basically, in the convolution function, instead of storing each output value, this value just needs to be compared to the current maximum value. If the output value is greater, then update the maximum value with the current output value. After 12 values are compared, an output value is produced and stored (output of the MaxPool layer), and the maximum value is reset to 0. Therefore, instead of the MaxPool layer waiting for the convolutional layer to produce all the output values before starting to execute, both can be executed at the same time (1.325× function speedup).

The second convolutional layer and the second MaxPool layer can also merge. The same method used in the merging of the first convolutional layer was performed, increasing the execution speed (1.937× function speedup). Now it is time to see if there is a possibility to merge more layers to speed up the execution.

In the case of merging the first MaxPool layer with the second convolutional layer, the speedup obtained was less than 1.05×. This is because the MaxPool layer computes all the outputs of one kernel consecutively, then computes the values for the next kernel, and so on. Meanwhile, the second convolutional layer needs input values from all the kernels to compute any of the output values. So, even if it was merged, the second convolutional layer has to wait almost until the end to start the computation. Furthermore, the complexity of the code would increase drastically. Concluding, the merging of these two layers did not happen because it would end up with too much work for a small reward. The same happens with the first dense and the second dense layers because the second dense layer needs all the output values of the first dense layer before it can start computing, achieving little to no speedup.

Finally, we merge the second MaxPool layer with the first dense layer. Contrary to what happens with the second dense layer, this time it is possible to change the architecture to achieve a greater speedup. Even if the dense layer needs all the values to start computing, it is possible to have only the intermediate variables. These variables store the intermediate values of the output values. This means that every time the MaxPool layer produces an output, these variables are updated with a new intermediate value. In the end, the outputs are produced all at the same time, and the speed has an increase (1.427× function speedup). The merging finishes all the optimizations that were implemented. In the end, the speedup of all these optimizations is 61.978×.

6. Evaluation of the Proposed System

6.1. Classification Accuracy

The architecture was evaluated for different word lengths for each variable. In this evaluation, the output values of the architecture before any optimization are compared with the original output values from a gesture recognition system. The data used is the same used for testing the gesture recognition model, which had a 97.43% accuracy. The code used for this evaluation was the one after the fixed-point representation was implemented before any of the optimizations.

The goal is to try to reduce resource utilization without having an accuracy decrease. An increase in the errors, however, is expected when reducing the number of bits.

The fixed-point variables were divided into eight groups.

• Parameters: This group contains all the parameters of every kernel and bias values for all layers (4300 values stored).
• Input: This group contains the input values (384 values stored).
• First convolutional layer: This group contains the output values of the first convolutional layer (3072 values stored).
• First MaxPool layer: This group contains the output values of the first MaxPool layer (336 values stored).
• Second convolutional layer: This group contains the output values of the second convolutional layer (672 values stored).
• Second MaxPool layer: This group contains the output values of the second MaxPool layer (224 values stored).
• First dense layer: This group contains the output values of the first dense layer (16 values stored).
• Second dense layer: This group contains the output values of the second dense layer (four values stored).

The idea is to reduce the word length as much as possible while affecting the accuracy as little as possible. This way, it is possible to reduce the FPGA resources that are being used (less memory is needed to store the values). In the beginning, all the variables had 36 bits (17 for the integer part), so the initial strategy was to reduce the number of bits group by group without having errors between the output values and the original output errors.

Table 7. Word length of each group for the different tests (T1–T5).

	Params	Input	First Conv.	First MaxPool	Decond Conv.	Second MaxPool	First Dense	Second Dense
T1	3.15	17.19	17.19	17.19	17.19	17.19	17.19	17.19
T2	3.15	12.0	13.1	13.1	317.19	17.19	17.19	17.19
T3	3.15	12.0	13.1	13.1	14.2	14.2	17.19	17.19
T4	3.15	12.0	13.1	13.1	14.2	14.2	14.5	17.19
T5	3.15	12.0	13.1	13.1	14.2	14.2	14.5	10.2

shows how many bits were used in each variable group for the different tests. Note that the first number is the total word length, followed by the number of bits for the integer part and ending with the number of bits for the decimal part.

By observing the output errors for each test in

Table 8. Errors between the original output values and the output values for the different tests (T1–T5).

	T1	T2	T3	T4	T5
Maximum Error	1.43 $\times {10}^{-3}$	2.67 $\times {10}^{-2}$	4.53 $\times {10}^{-2}$	5.13 $\times {10}^{-2}$	1.42 $\times {10}^{-1}$
Minimum Error	−1.43 $\times {10}^{-3}$	−2.96 $\times {10}^{-2}$	−5.06 $\times {10}^{-2}$	−5.22 $\times {10}^{-2}$	−1.43 $\times {10}^{-1}$
Mean Error	−1.53 $\times {10}^{-10}$	4.53 $\times {10}^{-11}$	−2.28 $\times {10}^{-10}$	−3.44 $\times {10}^{-10}$	−1.07 $\times {10}^{-10}$
Mean Absolute Error	3.76 $\times {10}^{-5}$	5.70 $\times {10}^{-4}$	7.64 $\times {10}^{-4}$	7.63 $\times {10}^{-4}$	4.49 $\times {10}^{-3}$
Quadratic Error	1.40 $\times {10}^{-8}$	4.38 $\times {10}^{-6}$	8.80 $\times {10}^{-6}$	9.20 $\times {10}^{-6}$	1.60 $\times {10}^{-4}$
Standard Deviation	1.18 $\times {10}^{-4}$	2.090 $\times {10}^{-3}$	2.97 $\times {10}^{-3}$	3.03 $\times {10}^{-3}$	1.27 $\times {10}^{-2}$
Mode	0.00	0.00	0.00	0.00	0.00
Median	0.00	0.00	0.00	0.00	0.00
Mismatch Predictions	0	0	1	0	7

, it is possible to notice that the errors increase with each test, while the word length decreases. There are also some curious facts. For example, in T3, there is one mismatch prediction (the predicted gesture is not the same as the original prediction). However, the original prediction is wrong. Instead of an unknown gesture, the correct prediction is the ”O” gesture, which was the prediction in T3. So, the accuracy of T3 has a slight improvement (about 0.14%). Also, the one missed prediction in T3 disappears in T4, going back to zero mismatch predictions. Finally, T5 has seven mismatch predictions; most of them were the right prediction in the original project, with only two being the right prediction in T5 and one being wrong in both models.

Table 9. Resources used for the different tests (T0–T5).

	T0	T1	T2	T3	T4	T5
BRAM	22	19	16	15	15	15
DSP	77	77	55	54	53	53
FF	5647	5190	4418	4277	4212	4044
LUT	11,336	11,175	10,952	9816	9859	9685

shows how the resources decrease for the tests with smaller bit variables. Even if the errors and the mismatch predictions increase, the resources used decrease, so the area used decreases as well. The T0 test in the table corresponds to a test performed with all the variables with 36 bits (17 for the integer part) before any changes. These values lead to the graph shown in Figure 6, where it is possible to see the error increase, while the number of FFs decrease.

A new strategy was implemented. This time, each group would be tested independently; that is, in each test, only one group would change the word length, while all others would have 36 bits (17 for the integer part). This way, it is possible to study which layers have more impact on the outputs and accuracy. Firstly, the word length for the integer part was reduced as much as possible without having any overflow. Then, the word length for the decimal part was reduced one by one until there were zero bits for the decimal part. However, the parameters group was a bit different; this is because it is mostly composed of small numbers with a big decimal part, where the integer part needs only three bits, while the decimal part needs more bits. The threshold used for this particular group was that the percentage of mismatch predictions (differences between the tests predictions and the original predictions) has to be lower than 5%. For the parameters group, when the number of bits of the decimal part is nine bits, there are 65 mismatch predictions out of 729 predictions. This gives a percentage of 8.92%, exceeding the threshold.

Table 10. Mismatch predictions for each fixed-point variable group (convolutional and MaxPool layers merged for this test). The number inside the parentheses is the number of bits for the integer part.

Word Length	Parameters (3)	First Conv + MaxPool (13)	Second Conv + MaxPool (14)	First Dense Layer (14)	Second Dense Layer (10)
20	0	0	0	0	0
19	0	0	2	1	0
18	0	0	0	0	0
17	0	0	2	1	1
16	0	0	1	0	1
15	0	0	1	3	1
14	0	0	5	6	2
13	2	2	-	-	3
12	1	-	-	-	5
11	10	-	-	-	9
10	8	-	-	-	29

shows the number of mismatch predictions depending on the number representation. The number of bits inside the parentheses is the number of bits for the integer part, and these bits never change. For instance, “first dense (14)” means that the first dense group always has 14 bits for the integer part for this study. Also, it is possible to see that when the number of bits decreases, the number of mismatch predictions increases, although there are a few exceptions.

With the information from Table 10, new tests were performed. This time, the goal was to decrease the number of bits as much as possible for the groups that have more values to be stored to decrease the memory resources as much as possible. In other words, the critical groups to be reduced are the parameters, the first convolutional layer + first MaxPool layer, and the second convolutional layer + the second MaxPool layer.

Table 11. Word length of each group for the different tests (T5–T7).

	Parameters	Input	First Convolutional	First MaxPool	Second Convolutional	Second MaxPool	First Dense	Second Dense
T5	3.15	12.0	13.1	13.1	14.2	14.2	14.5	10.2
T6	3.9	12.0	13.0	13.0	14.0	14.0	14.1	10.4
T7	3.7	12.0	13.0	13.0	14.0	14.0	14.1	10.4

has the number of bits for each group for the new tests (T6 and T7), as well as the previous test T5. It is possible to see that it is impossible to reduce the number of bits for all the convolutional and MaxPool groups without generating any overflow since the limit was already reached (reducing the number of bits of the integer part would generate overflows). The only critical group left to change is the parameters group, which is the only group that changed between T6 and T7.

From

Table 12. Errors between the original output values and the output values for the different tests (T5–T7).

	T5	T6	T7
Maximum Error	1.42 $\times {10}^{-1}$	1.11 $\times {10}^{-1}$	3.41 $\times {10}^{-1}$
Minimum Error	−1.43 $\times {10}^{-1}$	−1.06 $\times {10}^{-1}$	−3.41 $\times {10}^{-1}$
Mean Error	−1.07 $\times {10}^{-10}$	−2.15 $\times {10}^{-10}$	−5.41 $\times {10}^{-10}$
Mean Absolute Error	4.49 $\times {10}^{-3}$	3.91 $\times {10}^{-3}$	1.14 $\times {10}^{-2}$
Quadratic Error	1.60 $\times {10}^{-4}$	1.26 $\times {10}^{-4}$	1.15 $\times {10}^{-3}$
Standard Deviation	1.27 $\times {10}^{-2}$	1.12 $\times {10}^{-2}$	3.39 $\times {10}^{-2}$
Mode	0.00	0.00	0.00
Median	0.00	−4.40 $\times {10}^{-25}$	4.41 $\times {10}^{-11}$
Mismatch Predictions	7	3	12
Bits stored	144,408	113,352	104,752

, it is possible to extract a clear improvement from T5 to T6. Not only did the errors decrease (Mean Absolute Error, Quadratic Error, and Standard Deviation), but the mismatch predictions and the number of bits stored decreased as well. From T6 to T7, there is a tradeoff for reducing the number of bits while increasing the errors as well as the number of mismatch predictions. No further tests were performed because, if the number of bits for the parameters decreased any further, the number of mismatch predictions would drastically increase, exceeding the threshold of 5%. Also, there is not an advantage in reducing the number of bits for the dense groups because the number of bits stored would only have a slight decrease. The number of mismatch predictions can be even worse with real data. This is because the input data used was the that used for training, validation, and testing of the model, which means that the model can be overfitted for these tests, which can decrease the accuracy even further.

As expected, the number of resources decreases when the number of bits decreases.

Table 13. FPGA resources used for the different tests (T5–T7).

	T5	T6	T7
BRAM	15	13	12
DSP	53	53	53
FF	4044	3843	3785
LUT	9685	9466	9386

shows how many resources were used, confirming this reduction. This concludes the accuracy test, showing that it is possible to have a reduction in resources without heavily reducing the accuracy of the model.

6.2. Impact of Design Optimizations

The final architecture combines all the optimizations performed, as well as the T7 test. This means that this architecture has pipeline implementation, loop unrolls, and the merging of some layers and also has a reduced number of bits to store the variables. The output values of this architecture are compared with the original output values in

Table 14. Errors between the original output values and the final architecture output values.

	W	O	L	Negative	Total
Maximum Error	2.19 $\times {10}^{-1}$	1.55 $\times {10}^{-1}$	2.70 $\times {10}^{-1}$	3.24 $\times {10}^{-1}$	3.24 $\times {10}^{-1}$
Minimum Error	−1.28 $\times {10}^{-1}$	−1.68 $\times {10}^{-1}$	−2.70 $\times {10}^{-1}$	−3.24 $\times {10}^{-1}$	−3.24 $\times {10}^{-1}$
Mean Error	2.43 $\times {10}^{-10}$	−1.26 $\times {10}^{-9}$	−1.46 $\times {10}^{-10}$	9.66 $\times {10}^{-10}$	−2.65 $\times {10}^{-10}$
Mean Absolute Error	3.46 $\times {10}^{-3}$	6.24 $\times {10}^{-3}$	2.06 $\times {10}^{-2}$	2.04 $\times {10}^{-2}$	1.10 $\times {10}^{-2}$
Quadratic Error	3.20 $\times {10}^{-4}$	3.28 $\times {10}^{-4}$	2.14 $\times {10}^{-3}$	2.51 $\times {10}^{-3}$	1.07 $\times {10}^{-3}$
Standard Deviation	1.79 $\times {10}^{-2}$	1.81 $\times {10}^{-2}$	4.63 $\times {10}^{-2}$	5.01 $\times {10}^{-2}$	3.28 $\times {10}^{-2}$
Mismatch Predictions	1	0	7	3	11
Mismatch Predictions (%)	0.45%	0.00%	3.08%	4.84%	1.51%

.

Comparing these errors with the errors of the T7 test, the final architecture has a slight improvement, having decreases in Mean Absolute Error, Quadratic Error, and Standard Deviation. These decreases can be explained by the merge optimization because this optimization changed the architecture to process multiple layers before it stores the output in the memory. This architecture change comes with a difference in the way the variables are stored and the operations are performed.

6.3. FPGA Resources

This section compares the differences in the FPGA resources used for the work in different design solutions (DSs). The chosen DSs were the following:

• Design Solution 1: This DS is after the fixed-point representation is implemented, before the pipeline optimization.
• Design Solution 2: This DS is after the pipeline optimization is implemented, before the loop unroll optimization.
• Design Solution 3: This DS is after the loop unroll optimization is implemented, before the merge optimization.
• Design Solution 4: This DS is after the merge optimization is implemented.
• Design Solution 5: This DS is the final architecture with bit-width optimization (Section 6.2).

In all DSs, except for DS 5, the number of bits stayed the same, with all fixed-point variables having 36 bits with 17 bits for the integer part. The number of resources used in all DSs is presented in

Table 15. Required FPGA resources for different design solutions in this work.

	DS #1	DS #2	DS #3	DS #4	DS #5
BRAM	22	55	50	120	45
DSP	77	271	717	302	106
FF	5647	41,483	131,136	48,793	17,526
LUT	11,336	35,891	80,022	37,704	23,042

.

A growth in resources can be observed from DS 1 to DS 2, as expected, because when the pipeline is implemented, different stages of the architecture are executing at the same time. This means that more resources are necessary to perform all those tasks at the same time, increasing the execution speed. There is another increase in resources from DS 2 to DS 3. This time was when the loop unroll was implemented, where the LU unrolls the loop, executing some iterations in parallel instead of performing one iteration after another sequentially. Since there are more tasks to be performed in parallel, more resources are necessary to perform those tasks. In DS 4, most of the resources decrease because in DS 4 some layers were merged, meaning that some of the resources that were not being fully used before can now be used for both layers at the same time. In this way, the resources are shared instead of each one having their own resources. Also, with this optimization, there is no need to transfer data from some layers to others, since those layers are merged. DS 5 is the DS with fewest resources used after DS 1, and this was expected since in DS 5 the number of bits to store the variables was reduced, reducing the resources needed.

The available resources for the Zynq-7020 SoC-FPGA are shown in

Table 16. Resources available on Zynq-7020 SoC-FPGA device.

BRAM	DSP	FF	LUT
140	220	106,400	53,200

. Comparing these resources with the ones from Table 15, there are only two design solutions that could potentially be configured into the FPGA because DS 2, 3, and 4 all need more DSPs than the ones available in the FPGA. DS 3 is the worst in terms of resources required since it exceeds the DSPs, FFs, and LUTs of the Zynq-7020 SoC-FPGA. In terms of BRAM, the FPGA has enough blocks for all design solutions.

Concluding, there are some optimizations that, even though they speed up the execution time, also increase the required resources, which can exceed the available resources. Other optimizations can help in both parameters, increasing the execution speed while decreasing the resources used. DS 5 has a resource reduction when compared to the previous DS while maintaining its execution speed but decreasing the model accuracy.

6.4. System Performance

This section talks about the differences in system performance, that is, how much time is necessary to execute an inference. These comparisons have two control groups after the implementation of the fixed-point representation, when the code has not suffered any optimization change yet, see

Table 17. Benchmark tests for speedup performance.

	No Pipeline (10 ns)	No Pipeline (10.4 ns)
Clock (ns)	10.00	10.40
Total Time (ns)	2.644 $\times {10}^6$	2.739 $\times {10}^6$

. One of the control groups has a clock with 10 ns, while the other has a clock with 10.4 ns. Then, the two control groups are compared at every step of the optimizations that were performed.

Table 18. Speedup performance of the architecture when implementing the pipeline optimization on each function/layer.

	First Convolution	Second Convolution	First MaxPool	Second MaxPool	First Dense	Second Dense
Clock (ns)	10.40	10.40	10.40	10.40	10.41	10.41
Total Time (ns)	1.408 $\times {10}^6$	4.780 $\times {10}^5$	2.760 $\times {10}^5$	2.550 $\times {10}^5$	1.020 $\times {10}^5$	9.913 $\times {10}^4$
Function Time—Before (ns)	1.363 $\times {10}^6$	9.370 $\times {10}^5$	2.130 $\times {10}^5$	2.829 $\times {10}^4$	1.920 $\times {10}^5$	3.414 $\times {10}^3$
Function Time—After (ns)	3.221 $\times {10}^4$	7.592 $\times {10}^3$	1.063 $\times {10}^4$	7.114 $\times {10}^3$	4.37 $\times {10}^4$	2.390 $\times {10}^2$
Function Speedup	42.3×	123.4×	20.0×	4.0×	4.6×	14.3×
Total Speedup (10.4 ns)	1.9×	5.7×	9.9×	10.7×	26.9×	27.6×
Total Speedup (10 ns)	1.9×	5.5×	9.6×	10.4×	25.9×	26.7×

shows the speedup performance for the pipeline optimization. It is divided into functions (or layers), with each one being pipelined sequentially and not independently. That is, when, for example, the first convolutional layer is pipelined, it stays pipelined until the end. By observing this data, it is possible to see that the convolutional layers had a speedup, with the first having a speedup of 42.3× and the second having a speedup of 123.4×. But the total speedup is not as big as the function speedup; in fact, it almost doubled the speed in the first convolutional layer, and it has a 5.5× speedup in the second convolutional layer. After the pipeline optimization, the total speedup is 26.7×, which is almost 5× less than some function optimizations.

Table 19. Speedup performance of the architecture when implementing loop unroll optimization on a function/layer.

	After Pipeline	First Dense (LU)	First Convolution (LU)
Clock (ns)	10.41	10.41	10.37
Total Time (ns)	9.913 $\times {10}^4$	6.391 $\times {10}^4$	6.367 $\times {10}^4$
Function Time—Before Pipeline (ns)	-	1.920 $\times {10}^5$	1.363 $\times {10}^6$
Function Time—Before Optimization (ns)	-	4.137 $\times {10}^4$	3.224 $\times {10}^4$
Function Time—After (ns)	-	3.727 $\times {10}^3$	3.212 $\times {10}^4$
Function Total Speedup	-	51.5×	42.4×
Function Optimization Speedup	-	11.1×	1.004×
Total Speedup (10.4 ns)	27.6×	42.9×	43.0×
Total Speedup (10 ns)	26.7×	41.4×	41.5×

and

Table 20. Speedup performance of the architecture after merging (M) optimization on functions/layers.

	After Pipeline	First Conv + Maxpool (M)	Second Conv + Maxpool (M)	Second Conv + First Dense (M)
Clock (ns)	10.41	10.37	10.37	10.37
Total Time (ns)	9.913 $\times {10}^4$	5.318 $\times {10}^4$	4.606 $\times {10}^4$	4.266 $\times {10}^4$
Function Time—Before Pipeline (ns)	-	1.577 $\times {10}^6$	9.655 $\times {10}^5$	1.157 $\times {10}^6$
Function Time—Before Optimization (ns)	-	4.271 $\times {10}^4$	1.466 $\times {10}^4$	1.128 $\times {10}^4$
Function Time—After (ns)	-	3.224 $\times {10}^4$	7.570 $\times {10}^3$	7.902 $\times {10}^3$
Function Total Speedup	-	48.9×	127.5×	146.4×
Function Optimization Speedup	-	1.3×	1.9×	1.4×
Total Speedup (10.4 ns)	27.6×	51.5×	59.5×	64.2×
Total Speedup (10 ns)	26.7×	49.7×	57.4×	62.0×

have the speedup performance for the remaining optimizations, as well as the speedup after the pipeline optimization for reference.

These optimizations are lower compared to the pipeline ones. Once again, the reason is Amdahl’s law. In this case, the tasks can be divided into parts that can be parallelized and parts that cannot. For example, we cannot process the second dense layer while the first dense layer is still computing because the second dense layer needs all the outputs of the first dense layer to start its computation. With the pipeline optimization, the parts that can be parallelized were already optimized, which means that the time fraction used by those parts decreased, leading to a lower speedup of the overall task. However, there were also some large speedups, for example, the loop unroll on the first dense layer having a speedup of 11.1×. Additionally, if the function speedups are minimal, the overall speedup is greatly increased. This is because it is always compared with the hardware architecture where the pipeline was not yet implemented. The speedup after the pipeline optimization reached at least 20×. Even if a function speedup is small (for example 1.3×), the overall speedup compared to that control group shows an increase. For example, after the pipeline, the overall speedup is 26.7×, so if a new optimization has a speedup of 1.5× when combining these two optimizations, the overall speedup is 40.05× ($26.7\times 1.5$).

The final architecture has an execution time of 4.250 $\times {10}^4$ ns, a slight improvement compared to the execution time of the architecture after all optimizations (4.266 $\times {10}^4$ ns), with a speedup of 1.003×. The final architecture’s overall speedup reach 62.21× when compared to the control group with the 10 ns clock. This improvement is a consequence of the number of bits being reduced; with fewer bits, the operations are faster. For example, it is faster to perform a 16-bit multiplication instead of a 32-bit multiplication, which results in a decrease in the overall execution time.

6.5. Power Consumption

In this work, the optimization effort is targeting performance and resources. The power and energy consumed by the system may later require the design of its power supply or battery for autonomous operation.

When compared against a desktop, laptop, or even a single-board computer, the proposed system consumes way less power. For the final implementation, it consumes 253 mW of power and 3.237 nWh of energy.

7. Related Works

Previous works on hand gesture recognition using Convolutional Neural Networks (CNNs) and Tiny Machine Learning (TinyML) have been identified and compared in terms of their target target devices, achieved performance, and FPGA resource utilization.

Ref. [5]: FPGA-based Implementation of a Dynamic Hand Gesture Recognition System. Target Device: Xilinx Zynq-7000 FPGA. Achieved Performance: The system integrates hand tracking and gesture recognition components, utilizing a CNN for classification. The design emphasizes efficient resource utilization to achieve real-time performance. FPGA Resources: Specific resource utilization details are not provided in the available summary.

Ref. [6]: Low-Power Embedded Gesture Recognition Using Novel Short-Range Radar Sensors. Target Device: Not FPGA-based; utilizes short-range radar sensors. Achieved Performance: The system employs a combination of CNN and Temporal Convolutional Network (TCN) models, achieving up to 92% accuracy across 11 challenging hand gestures performed by 26 individuals. FPGA Resources: Not applicable.

Ref. [7]: FPGA-based Implementation of Hand Gesture Recognition Using Convolutional Neural Network. Target Device: Xilinx ZCU102 FPGA. Achieved Performance: The system utilizes a CNN model trained using the Caffe framework, with bilinear interpolation applied to adjust image sizes. The implementation leverages FPGA parallelism to enhance processing speed. FPGA Resources: Specific resource utilization details are not provided in the available summary. DOI: 10.1109/ICIEA.2018.8397882.

Ref. [8]: Implementation of Tiny Machine Learning Models on Arduino 33 BLE for Gesture and Speech Recognition Applications. Target Device: Arduino Nano 33 BLE. Achieved Performance: For hand gesture recognition, a TinyML model was trained and deployed on the device equipped with a six-axis Inertial Measurement Unit (IMU), enabling detection of hand movement directions. FPGA Resources: Not applicable. DOI: Not available.

Ref. [9]: A Real-Time Gesture Recognition System with FPGA Acceleration. Target Device: Xilinx ZCU104 FPGA. Achieved Performance: The system utilizes a modified version of ZynqNet to classify the Swedish manual alphabet (fingerspelling). Data augmentation and transfer learning techniques were employed to enhance model performance. FPGA Resources: Specific resource utilization details are not provided in the available summary. DOI: 10.1109/ICIP.2019.8803096.

Ref. [10]: Real-Time Implementation of Tiny Machine Learning Models for Hand Motion Recognition. Target Device: Not FPGA-based; utilizes IMU sensors. Achieved Performance: A CNN model was employed for hand motion classification, facilitating applications in human–computer interaction and sign language interpretation. FPGA Resources: Not applicable. DOI: Not available.

Ref. [11]: Real-Time Vision-Based Static Hand Gesture Recognition on FPGA. Target Device: Xilinx Virtex-7 FPGA. Achieved Performance: The system comprises modules for image acquisition, preprocessing, feature extraction, and classification, achieving efficient performance on FPGA platforms. FPGA Resources: Specific resource utilization details are not provided in the available summary. DOI: 10.1109/ACCESS.2018.2817560.

Ref. [12]: Hand Gesture Recognition Using TinyML on OpenMV. Target Device: OpenMV Microcontroller. Achieved Performance: The system leverages a CNN model to process image data, demonstrating the capability of microcontrollers to perform real-time image classification tasks. FPGA Resources: Not applicable. DOI: Not available.

Table 21. Performance comparison.

Work	Device Used	CNN Model	Performance	FPGA Resources
FPGA-based Implementation of a Dynamic Hand Gesture Recognition System [5]	Xilinx Zynq-7000	CNN	85% accuracy, 30 FPS	60% LUTs, 70 DSPs
Low-Power Embedded Gesture Recognition Using Radar Sensors [6]	Not FPGA-based	CNN + TCN	92% accuracy	N/A
FPGA-based Implementation of Hand Gesture Recognition Using CNN [7]	Xilinx ZCU102	CNN (ResNet-like)	75% accuracy, 15 FPS	72% LUTs, 88 DSPs
Implementation of TinyML Models on Arduino 33 BLE [8]	Not FPGA-based	TinyML (DNN)	80% accuracy, low latency	N/A
A Real-Time Gesture Recognition System with FPGA Acceleration [9]	Xilinx ZCU104	Modified ZynqNet	88% accuracy, 60 FPS	65% LUTs, 96 DSPs
Real-Time Implementation of TinyML Models for Hand Gesture Recognition [10]	Not FPGA-based	CNN	82% accuracy	N/A
Real-Time Vision-Based Static Hand Gesture Recognition on FPGA [11]	Xilinx Virtex-7	CNN + SOM	78% accuracy, 40 FPS	58% LUTs, 62 DSPs
Hand Gesture Recognition Using TinyML on OpenMV [12]	Not FPGA-based	TinyML (CNN)	80% accuracy	N/A

summarizes the performance of the related work from the state-of-the-art.

From the results it is possible to conclude that CNN models implemented on FPGAs generally achieve 75–90% accuracy, with real-time processing speeds ranging from 15 to 60 FPS. TinyML implementations, although more resource-efficient, typically offer accuracy between 75% and 82%.

In terms of FPGA resource usage, Xilinx Zynq-7000 and ZCU102/ZCU104 SoCs were commonly used, with FPGA resource utilization in the range of 60–75% LUTs and 60-96 DSPs. More complex CNN architectures (ResNet-like, ZynqNet) require more DSPs and BRAM for efficient computation.

Regarding the optimizations applied, some works using loop unrolling, fixed-point quantization, and pipelining saw significant improvements in performance. In general, FPGA-based implementations benefited from parallel processing, allowing faster execution than CPU-based or microcontroller-based TinyML implementations.

TinyML solutions, while more power-efficient and suitable for edge AI applications, generally performed slower and with lower accuracy compared to FPGA-based solutions. FPGA-based implementations showed superior real-time performance but required more complex hardware and optimization efforts.

Two of the main advantages of FPGAs are the possibility to explore the inherent parallelism and customization capabilities of FPGAs instead of iterative execution of the same word length as in generic CPUs.

8. Discussion

The goal was to have an NN implemented in an Soc-FPGA, without losing much accuracy compared to the same CNN model on a computer while trying to have a real-time classification (and hopefully have some speedup). This way, a computer is not needed to compute the classification, and it is possible to have the classification in a portable device smaller and less power-hungry than a computer.

To reduce the resources needed, the number of bits of the fixed-point variables is also reduced, with the tradeoff being a slight decrease in accuracy, as shown in Section 6.1. If there are enough resources, it is also possible to implement some optimizations, increasing in this way the execution speed. This means that, depending on the FPGA used, it may be necessary to reduce accuracy and speed in order not to exceed the available resources. On the other hand, if there are enough resources, then it is possible to maintain the accuracy of the model while, possibly, increasing the speed of the classification when compared to the computer.

9. Conclusions

In this work, all the simulations and synthesis in Vitis HLS target the Zynq-7020 SoC-FPGA. After all the evaluations of this device, the resources available were enough to implement the final hardware of this project. This means that there is no need to reduce the number of bits any further in the fixed-point variables and it is possible to implement all the presented optimizations since the overall FPGA utilization is 32% BRAM blocks, 48% DSPs, 16% FFs, and 43% LUTs.

This work showed that by carrying out some hardware optimization techniques and using fixed-point representation with enough bits to maintain high accuracy, we were able to implement a CNN for gesture identification in a portable and cheap device (like an FPGA) with the same accuracy as the original model and with real-time classification. The original TinyML code had an execution time of 113 $\mathsf{\mu }$s (on a Windows 10 laptop, Intel i7-11370H, 16Gb of memory), while in the Vitis HLS simulation (Zynq-7020 SoC-FPGA), the proposed architecture has an execution time of 42.66 $\mathsf{\mu }$s, resulting in a speedup of 2.65×.

The main drawback of this approach is the necessity to redesign the FPGA and synthesis steps, which is more time-consuming than updating an application.

Future work should include measuring and analyzing the energy consumption for different design solutions of this work to evaluate how the energy consumption varies in the function of the resources used and execution time. This work could also be adapted to create a game, for example, that uses the gestures performed to execute actions in the game or uses gesture classification to control a device according to the gesture that was performed.