Millimeter-Wave Interferometric Synthetic Aperture Radiometer Imaging via Non-Local Similarity Learning

Abstract

In this study, we propose a novel pixel-level non-local similarity (PNS)-based reconstruction method for millimeter-wave interferometric synthetic aperture radiometer (InSAR) imaging. Unlike traditional compressed sensing (CS) methods, which rely on predefined sparse transforms and often introduce artifacts, our approach leverages structural redundancies in InSAR images through an enhanced sparse representation model with dynamically filtered coefficients. This design simultaneously preserves fine details and suppresses noise interference. Furthermore, an iterative refinement mechanism incorporates raw sampled data fidelity constraints, enhancing reconstruction accuracy. Simulation and physical experiments demonstrate that the proposed InSAR-PNS method significantly outperforms conventional techniques: it achieves a 1.93 dB average peak signal-to-noise ratio (PSNR) improvement over CS-based reconstruction while operating at reduced sampling ratios compared to Nyquist-rate fast fourier transform (FFT) methods. The framework provides a practical and efficient solution for high-fidelity millimeter-wave InSAR imaging under sub-Nyquist sampling conditions.

1. Introduction

An interferometric synthetic aperture radiometer (InSAR) synthesizes an equivalent large aperture through an array of small-aperture antenna elements, overcoming the spatial resolution limitations inherent in traditional single large-aperture antenna designs and achieving high-resolution real-time imaging [1,2,3]. The ability of millimeter waves to penetrate natural obscurants, such as fog and clouds, enables millimeter-wave InSAR systems to operate in near-all-weather and day–night conditions [4,5]. Additionally, the system’s inherent low observability, stemming from its passive detection principle, coupled with high sensitivity to metallic objects [6], makes it a key component of modern detection systems. As a passive imaging technique, millimeter-wave InSAR is broadly applied in remote sensing, environmental monitoring, and public safety [7,8,9].

The core principle of InSAR imaging involves acquiring samples of the visibility function (i.e., complex cross-correlations between antenna pairs) within the spatial-frequency domain, which constitute sampled spatial spectra. To form the final image, the brightness temperature (BT) distribution must be reconstructed by inversely transforming these sampled spatial spectra. This reconstruction achieves a high angular resolution determined by the longest baseline, surpassing the diffraction limit of single-aperture systems, and is critical to the overall imaging capability [10,11]. Consequently, BT image reconstruction constitutes a crucial step in the InSAR imaging process. Under ideal conditions, the visibility function corresponds to the spatial Fourier transform of the BT distribution. Due to this relationship, the Fast Fourier Transform (FFT) is considered the fundamental reconstruction method for millimeter-wave InSAR imaging [12].

However, practical system implementations face two technical challenges: the limited number of antennas results in insufficient sampling in the spatial-frequency domain, failing to meet the Nyquist sampling criterion, and phase errors and system noise can significantly amplify reconstruction artifacts [13,14]. These effects are magnified in millimeter-wave bands due to sub-wavelength phase sensitivity and atmospheric absorption-induced thermal noise, severely constraining the performance of traditional reconstruction methods (e.g., FFT) under non-ideal conditions. Various strategies to bridge this performance gap have been proposed in the literature. For example, Anterrieu et al. [15] described an algorithm for performing discrete Fourier transform calculations on hexagonal grids and proposed an interpolation formula to resample data from such grids without introducing aliasing artifacts. In a separate approach, Zhou et al. [16] introduced an iterative method for BT image reconstruction from non-uniformly sampled visibility function data. This method combined the conjugate gradient algorithm with a min–max non-uniform FFT approach to enhance image quality.

Although these engineering solutions can mitigate the aforementioned shortcomings to some degree, traditional reconstruction methods (including enhanced FFT and its variants) remain vulnerable to millimeter-wave-specific distortions like non-uniform atmospheric phase errors, and still suffer from significant image degradation under high-noise scenarios or conditions of severe undersampling.

Compressed sensing (CS) was developed to address undersampling challenges by leveraging scene sparsity [17,18], enabling InSAR image reconstruction from limited-visibility samples while reducing hardware requirements. In [19], Chen et al. validated the feasibility of CS-based InSAR imaging. Their approach involved minimizing the ${\mathsf{\ell }}_1$-norm of the transformed image, achieving reconstruction with fewer receivers than FFT methods. While it reduced system complexity, it introduced noise sensitivity and artifacts due to dependence on random observation matrices requiring strict restricted isometry property (RIP) conditions. In [20], Wang et al. proposed the CS-based synthetic aperture interferometric technology (CS-SAIT), reconstructing BT images using visibility samples from selected receiver subsets to reduce hardware resources and data volume. However, validation was limited to homogeneous backgrounds and spatially sparse targets, constraining real-world robustness. Recently, Xu et al. incorporated spatial correlation priors during sparse reconstruction via a local region reweighting ${\mathsf{\ell }}_1$-norm (LRRL1) and a local region convolution-reweighted ${\mathsf{\ell }}_1$-norm (LRCRL1), enhancing contour preservation [21]. However, this method is constrained by a fixed-window mechanism and lacks adaptive adjustment capabilities, resulting in insufficient robustness to noise with varying intensities.

Consequently, although existing studies progressively optimize sparsity utilization to minimize hardware demands, these methods predominantly rely on fixed parameters without adaptive capabilities, resulting in suboptimal noise suppression. Furthermore, sparse recovery processes neglect the inherently high-dimensional characteristics of InSAR data, compromising imaging quality.

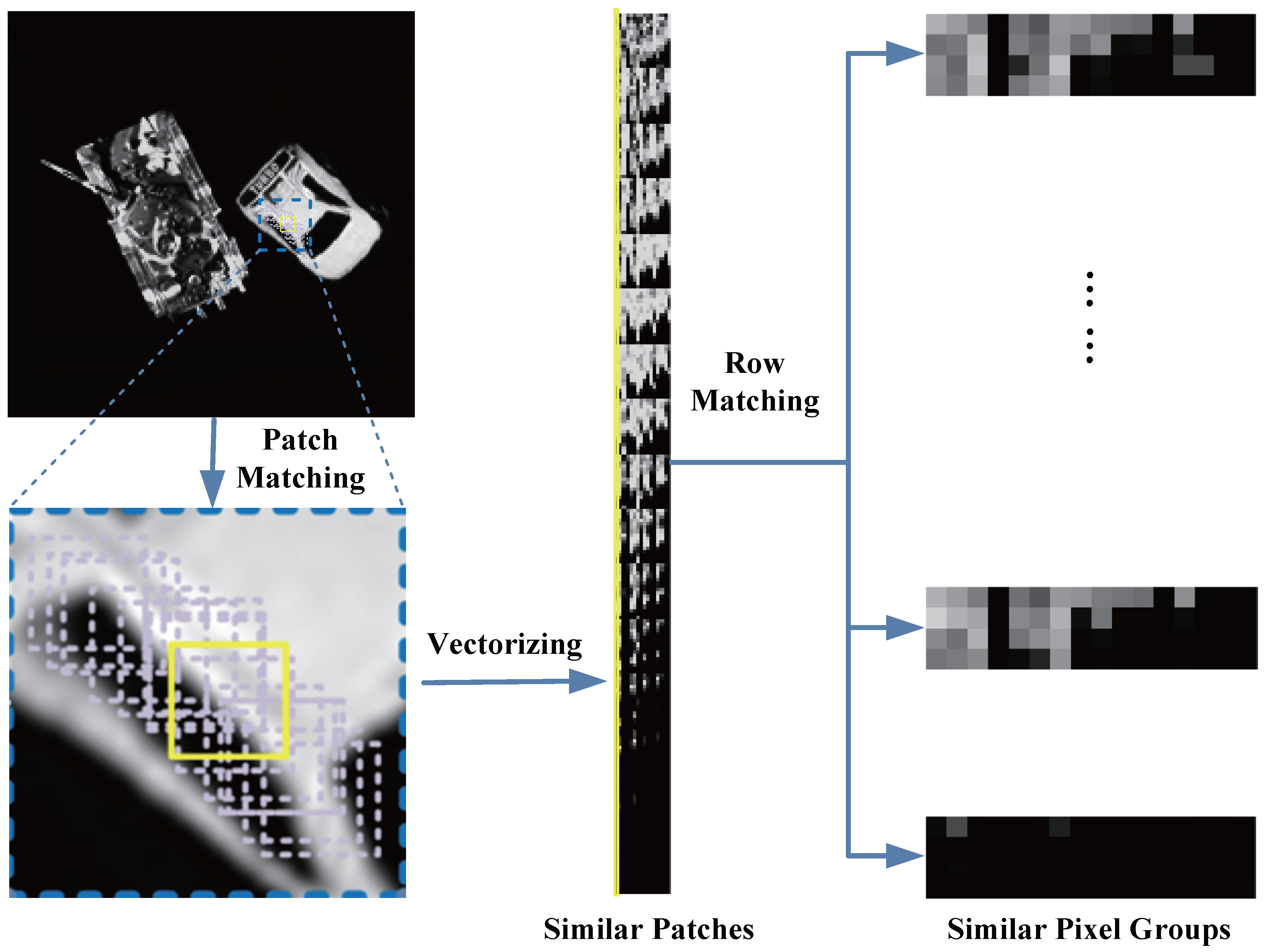
To better exploit these high-dimensional priors, non-local self-similarity (NSS) techniques were introduced. NSS improves upon CS by aggregating similar image patches, leveraging image correlations to achieve fewer reconstruction errors and superior visual quality under undersampling [22]. Nevertheless, NSS operates at the patch level, inherently limiting its ability to preserve fine details due to coarse granularity. Recognizing pixels as fundamental image constituents, Hou et al. developed a pixel-level NSS method for magnetic resonance imaging (MRI), employing row-matching similarity modeling to enhance reconstruction fidelity. This pixel-level paradigm has demonstrated robust, competitive performance against deep learning methods across diverse imaging domains, including MRI reconstruction [23], image denoising [24], and image smoothing [25].

Building on this foundation, we define Pixel-Level Non-Local Similarity (PNS) as the structural relationship between pixels that serve similar functions in different patches of an image. Unlike traditional patch-level methods (e.g., NSS), which ignore intra-patch variations, PNS identifies and matches corresponding pixels for precise processing. This enables finer detail preservation through pixel operations, better variance handling using within-patch correlations, and improved structural accuracy. Notably, while pixel-level NSS has demonstrated cross-domain applicability in InSAR mixed-noise suppression [26], a critical gap remains in its application to direct image reconstruction from undersampled data.

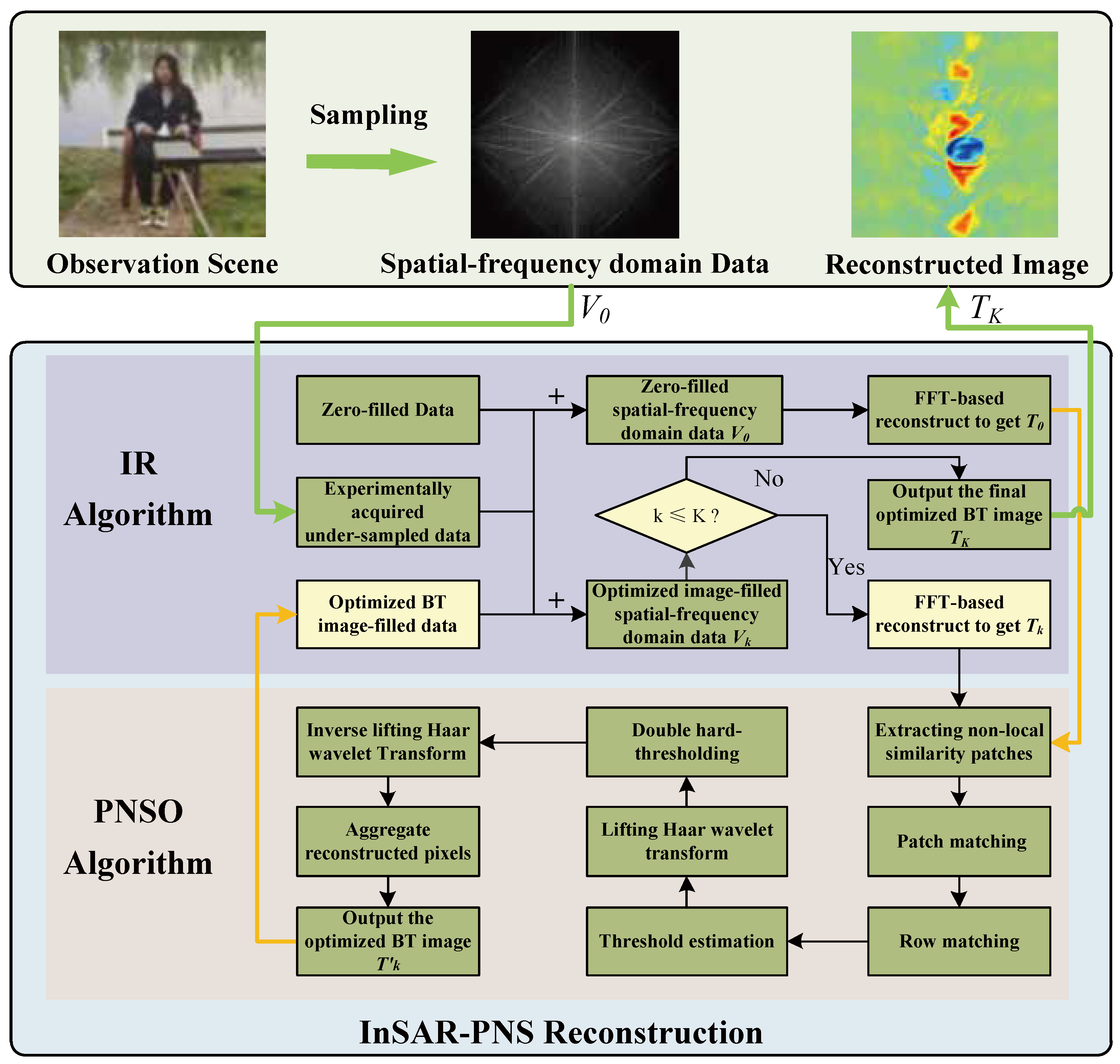
However, a straightforward transplantation of the MRI-oriented pixel-level strategy is ill-suited for millimeter-wave InSAR. This is due to fundamental differences in data characteristics: the coarser granularity, stronger long-range correlations, and particularly the complex system errors inherent in InSAR systems. To address this gap, we pioneer the integration of PNS into a dedicated millimeter-wave InSAR reconstruction framework, establishing the novel interferometric synthetic aperture radiometer pixel-Level non-Local similarity (InSAR-PNS) method. Our InSAR-PNS framework incorporates (1) a non-local search strategy adapted to low-resolution BT images, (2) a noise-adaptive mechanism to ensure robustness against system errors, and (3) an iteratively guided process constrained by raw data fidelity to prevent error accumulation. The main contributions of this work are summarized as follows:

(1)

We incorporated PNS into millimeter-wave InSAR reconstruction.We introduced the PNS framework to millimeter-wave InSAR, establishing a joint high-dimensional sparse representation model. This approach enhances structural feature extraction through pixel-level similarity mining, addressing detail-preservation limitations inherent in patch-based methods.

(2)

We developed an adaptive thresholding strategy for sparse coefficients, which dynamically adjusts parameters based on noise distribution during reconstruction stages. This design enhances robustness against complex noise interference while balancing detail preservation and noise suppression.

(3)

We implemented a raw data-guided iteratively guided reconstruction algorithm. This framework integrates high-dimensional feature learning from the initial image with strict fidelity constraints to the raw sampled data. It effectively prevents error accumulation throughout the iterations, ensuring reliable convergence especially under low-SNR conditions.

(4)

We achieve validation through simulations and physical experiments, confirming the method’s efficacy and applicability to complex environments in millimeter-wave InSAR imaging.

The rest of this article is organized as follows. Section 2 introduces the basic theoretical principles of millimeter-wave InSAR imaging. Section 3 presents the details of the proposed InSAR-PNS reconstruction method. The simulation and physical experiments are compared and discussed in Section 4. Finally, Section 5 provides the conclusions.

2. Theoretical Principles of Millimeter-Wave InSAR Imaging

Millimeter-wave InSAR imaging is based on the Van Cittert–Zernike theorem, and its core component is a two-element interferometer [27,28]. The InSAR imaging system utilizes a spatially separated antenna array to form a series of antenna pairs, measures millimeter-wave radiation within the target space, and performs complex correlation operations on the collected signals to obtain the visibility function.

A typical signal processing chain for a two-element interferometer is illustrated in Figure 1. The weak millimeter-wave radiation from a target at coordinates $(x_m, y_m)$ is collected by an antenna array. The received signals are then conditioned by their respective receiver chains, which have a frequency response characterized by $H_c\left(f\right)$ and $H_l\left(f\right)$, and perform critical operations such as amplification, frequency selection, and down-conversion. The signals are subsequently processed by the complex correlation module, which multiplies the two signals, introduces a $\pi /2$ phase shift, and integrates the results to extract both the in-phase ($V_I$) and quadrature ($V_Q$) components of the complex visibility function $V(u,v)$.

Subsequently, high-resolution millimeter-wave BT images are reconstructed from the measured visibility function, using reconstruction algorithms such as the FFT method or G-matrix method [29].

For a scene discretized into M surface elements, the visibility function sampled by the antenna pair $(A_c, A_l)$ is given by [30,31]

$$\begin{array}{c}\hfill V_{c,l}=〈E_c(R_m^c,t)·{E^{⁎}}_l(R_m^l,t)〉\end{array}$$

(1)

In spatial frequency coordinates $(u,v)$ and polar coordinates $\left(\xi ={\displaystyle \frac{x_m}{R}},\eta ={\displaystyle \frac{y_m}{R}}\right)$, the visibility function is defined as

$$V(u,v)=\int \int T(\xi ,\eta )e^{-j2\pi (u\xi +v\eta )}d\xi d\eta$$

(2)

When imaging accuracy requirement is not stringent, basic BT image reconstruction can be achieved directly taking an inverse Fourier transform on $V\left(u,v\right)$. Considering the observation errors and receiving noise, the basic signal model for InSAR imaging can be expressed as    

$$V\left(u,v\right)=\mathcal{F}\left[T(\xi ,\eta )\right]+\epsilon$$

(3)

Reconstruction that directly performs an inverse Fourier transform on $V\left(u,v\right)$ often requires rigorous calibration. Otherwise, its performance will degrade due to the presence of observation errors and receiving noise $\epsilon$. Interference of $\epsilon$ with InSAR imaging can be minimized by using an alternative reconstruction method, a generalized shock function operator, i.e., the G-matrix model instead of the Fourier transform relationship in Equation (3). Then, the approximate discrete linear system of the InSAR image reconstruction model can be rewritten as [32]

$$V_{M\times 1}=G_{M\times N}{T}_{N\times 1}+E_{M\times 1}$$

(4)

where T is the BT image, G is the generalized operator, V is the undersampled visibility data, and E represents the error and receiver noise.

3. InSAR-PNS Reconstruction Method

This section outlines the theoretical foundations of PNS, introduces the proposed InSAR-PNS reconstruction framework, and specifies the implementation methodology.

3.1. Principle of PNS

Building on the definition of PNS provided in Section 1, in this section, we formalize its mathematical implementation. The core premise stems from the inherent low-rank characteristics of millimeter-wave BT images [33]. From the perspective of prior knowledge, pixels within the image demonstrate strong spatial correlations. A single pixel existing independently lacks practical significance; instead, adjacent pixels collectively constitute textural or structural features. Such structures are extensively distributed across various regions of the image. For instance, regions exhibiting periodic repetition or texture characteristics contain substantial redundant structural information.

The NSS prior plays a pivotal role in fields such as texture synthesis [25,34], image denoising [35,36,37], super-resolution [38,39], and image reconstruction [23]. In denoising applications, the non-local means (NLM) algorithm pioneered NSS utilization, estimating true pixel values through weighted averaging of similar patches. This approach effectively preserves edges and textures while suppressing noise. Patch-level NSS was further advanced in the block-matching and 3D filtering (BM3D) algorithm [36] and subsequent studies [37]. While classical NLM and BM3D exploit patch-level self-similarity, they often disregard intra-patch pixel variations. Given that pixels constitute the fundamental units of images and exhibit intrinsic correlations within patches, the similarity prior information at the patch level can be used to locate and match similar pixels, thus achieving pixel-level image processing.

The workflow for identifying non-local similar pixels is as follows: First, extract non-local similar patches and vectorize each patch into column vectors. Then, combine all the column vectors to construct a similar-patch matrix. For each row in the matrix, use the patch-level NSS prior information to establish inherent correlations. Subsequently, compute the Euclidean distances between matrix rows to locate non-local similar pixels. Figure 2 provides a schematic overview of this process.

For an input image $T_{\mathrm{n}}\in {\mathbb{R}}^{a\times b}$, the procedure for identifying non-locally similar pixels comprises four stages:

(1)

Non-local patch extraction

Decompose $T_{\mathrm{n}}$ into L overlapping patches of size ($w\times w$)

$${\mathrm{t}}_l=P_l{T}_n$$

(5)

where $t_l\in {\mathbb{R}}^{w\times w},l\in \left\{1,\dots ,L\right\}$, and $P_l$ represents the patch extraction operator.

(2)

Patch matching

For a reference patch $t_{l,i}$ (framed in yellow in Figure 2), where l denotes the image patch index and i is the index of the reference patch, we identify similar patches (framed in purple) within a $C\times C$ search window (framed in blue) by minimizing the Euclidean distance:

$${\mathrm{D}}_{l,ij}={∥t_{l,i}-t_{l,j}∥}_2$$

(6)

Here, $t_{l,j}$ is a candidate patch within the search window, and j is its index. Both $t_{l,i}$ and $t_{l,j}$ are image patches of size $w\times w$ pixels.

Select the $d-1$ most similar patches (where d is the total number of similar patches, including the reference patch). Vectorize each patch ($w\times w\to w^2\times 1$) and concatenate them with the reference patch to form a patch-similarity matrix:

$$T_l=[t_{l,1},\dots ,t_{l,d}]=\left(\begin{array}{ccc}{t}_l^{1,1}& \dots & t_l^{1,d}\\ ⋮& \ddots & ⋮\\ t_l^{w^2,1}& \dots & t_l^{w^2,d}\end{array}\right)\in {\mathbb{R}}^{w^2\times d}$$

(7)

In this matrix $T_l$, each column is a vectorized patch, and each row contains the values of a specific pixel location across all d patches.

(3)

Row matching

For each row vector $t_l^i$ in the patch-similarity matrix $T_l$ (where the superscript $ii\in [1,w^2]$ denotes the row index, representing a specific spatial position within a patch), compute the Euclidean distances to all other rows $t_l^j$:

$${\mathrm{d}}_l^{ij}={∥t_l^i-t_l^j∥}_2$$

(8)

Here, $t_l^i$ and $t_l^j$ are row vectors of length d, and j is the index of another row.

Select g rows with minimal distances to form a pixel-similarity submatrix:

$$T_l^g=\left(\begin{array}{ccc}{t}_l^{i_1,1}& \dots & t_l^{i_1,d}\\ ⋮& \ddots & ⋮\\ t_l^{i_g,1}& \dots & t_l^{i_g,d}\end{array}\right)\in {\mathbb{R}}^{g\times d}$$

(9)

where $\left\{i_1,\dots ,i_g\right\}\subset \left\{1,\dots ,w^2\right\}$, $l\in \left\{1,\dots ,L\right\}$.

(4)

Iteration

Repeat Steps 2–3 for all reference patches.

3.2. InSAR-PNS Reconstruction Model

In InSAR imaging, although the FFT algorithm can achieve BT image reconstruction, it requires full visibility function sampling, necessitating a fully populated antenna array. This constraint severely limits the practical application of millimeter-wave InSAR imaging. A CS-based imaging algorithm can reconstruct images from undersampled visibility function, which can be measured with a smaller number of antennas. The CS reconstruction model is formulated as follows

$$min{∥\widehat{T}∥}_1\mathrm{s}.\mathrm{t}.V=G\Psi \widehat{T}+\epsilon$$

(10)

where $\widehat{T}={\Psi }^{-1}·T$ represents the sparse vector of the BT image T, which needs to be recovered from the sparse basis matrix $\Psi$. Additionally, G is the observation matrix, representing the sampling operation on the BT image T under various sampling modes. V denotes the actual undersampled data of the visibility function.

Traditional CS-based InSAR reconstruction techniques utilize the sparsity of millimeter-wave InSAR images. These methods employ predefined sparse transforms (e.g., wavelet, discrete cosine transform) to represent two-dimensional (2D) InSAR images as vectors and complete the reconstruction in a one-dimensional (1D) data space. The final outputs are reshaped to match the original image dimensions. This means that CS-based reconstruction methods cannot utilize high-dimensional signal features and prior knowledge and often fail to provide sufficient sparse representations for the images to be reconstructed. From a Bayesian perspective, sparsity regularization is critical in CS-InSAR imaging. To comprehensively capture high-dimensional priors in BT images, we design a PNS-based sparsifying operator $A(·)$ and formulate the InSAR-PNS reconstruction model:

$$\widehat{T}=\underset{T}{min}\underset{\mathrm{sparsity}}{\underbrace{{∥A\left(T\right)∥}_1}}+\lambda \underset{\mathrm{data}\mathrm{fidelity}}{\underbrace{{∥V-GT∥}_2^2}}$$

(11)

where $\lambda$ is the regularization parameter, which is used to balance sparsity (${\mathsf{\ell }}_1$-norm) and data fidelity (${\mathsf{\ell }}_2$-norm).

The PNS-derived operator $A(·)$ enforces structural sparsity constraints through pixel-level correlations. This model allows us to establish a general formula to balance the sparsity of these patches based on data consistency and enables the integration of prior information learned from undersampled data, thus optimizing the sparse representation of the images to be reconstructed.

3.3. InSAR-PNS Reconstruction Algorithm

As shown in Figure 3, the PNS-based InSAR image reconstruction framework comprises two parts: pixel-level non-local sparsification optimization (PNSO) and iterative refinement (IR). Given undersampled measurement data $V\in R^M$, we first apply zero-padding to generate full-sized spatial-frequency domain data $V_0$. Subsequently, by performing an inverse FFT on $V_0$, we obtain the preliminarily reconstructed BT image $T_0$.

However, this initial reconstruction typically suffers from aliasing artifacts and noise. Therefore, to improve reconstruction quality and exploit pixel-level self-similarity in the image, we introduce PNS before transformation. This allows for the construction of an adaptive sparsifying transform operator that facilitates pixel-level non-local coefficient updates, generating optimized images $T_k^{\prime }\left(k=1,\dots ,K\right)$. This procedure can not only recover undersampled signals and suppress artifacts but also maintains image sparsity. Next, FFT converts $T_k^{\prime }$ to spatial-frequency domain data $V_k$. Crucially, during each iteration, we update the k-th reconstruction’s frequency components $V_k$ in the originally zero-padded positions of $V_0$, ensuring data fidelity at the sampled locations. The visibility function update during iteration k is formulated as follows:

$$V_k=\left\{\begin{array}{cc}{v}_k\hfill & \mathrm{if}{v}_0=0,\hfill \\ v_0\hfill & \mathrm{if}{v}_0\ne 0.\hfill \end{array}\right.$$

(12)

PNS sparse optimization is primarily based on lifting Haar wavelet transform (LHWT) [40,41] due to its operational flexibility, computational efficiency, and lightweight memory. This approach then implements adaptive double hard-thresholding on the sparse coefficients of the pixel similarity matrix. For the initial InSAR BT image $T_0$ requiring optimization, this process follows the pixel similarity matrix search procedure detailed in Section 3.1. First, non-local patches $t_l$ are extracted. Subsequently, within a $C\times C$ local search window, the $d-1$ most similar patches are identified to construct a patch similarity matrix $T_l$. For each row in $T_l$, g similar rows are selected to form a pixel similarity matrix $T_l^g$, Then, the LHWT is applied to $T_l^g$ to generate sparse coefficients:

$$C_l^g=H\left(T_l^g\right)$$

(13)

where $H(·)$ represents the LHWT. Apply the first hard-thresholding on $C_l^g$:

$${\widehat{C}}_l^g(x,y)=\left\{\begin{array}{cc}{C}_l^g(x,y)& C_l^g\ge \beta {\sigma }_k\\ 0& C_l^g<\beta {\sigma }_k\end{array}\right.$$

(14)

where $x\in \{1,\dots ,g\}$ and $y\in \{1,\dots ,d\}$ denote the row and column indices of $C_l^g$; $\beta$ represents the filtering coefficient; and ${\sigma }_k$ is the threshold parameter with $k\in \{1,\dots ,K\}$ denoting the iteration index. During iterations, ${\sigma }_k$ decays logarithmically:

$$\left\{\begin{array}{c}{\sigma }_k={\sigma }_0/log(k+1)\hfill \\ {\sigma }_0={\displaystyle \frac{1}{L}}\sum _{l=1}^L{\sigma }_l\hfill \\ {\sigma }_l={\displaystyle \frac{1}{w^2(g-1)}}\sum _{j=2}^g\sum _{i=1}^{w^2}\sqrt{{\displaystyle \frac{1}{d}}{\left(d_l^{ij}\right)}^2}\hfill \end{array}\right.$$

(15)

where $log(·)$ denotes the natural logarithm. The global noise level ${\sigma }_0$ for the initial image $T_0$ is derived as ${\sigma }_0={\displaystyle \frac{1}{L}}{\sum }_{l=1}^L{\sigma }_l$, where ${\sigma }_l$ is the local noise level estimated via PNS prior information (Section 3.1). This estimation relies on the fact that pixels in the selected g rows of $T_l^g$ exhibit high similarity. Therefore, their standard deviation (std) can be interpreted as the local noise level ${\sigma }_l$. Assuming a Gaussian noise model with std ${\sigma }_l$ for simplicity, we compute the std over these similar pixel rows using Equation (15). During iterations, the threshold ${\sigma }_k$ decays as ${\sigma }_k={\sigma }_0/log(k+1)$, with k denoting the iteration index to progressively reduce hard-thresholding intensity. Early iterations suppress dominant artifacts, while later stages eliminate residual noise and preserve textural details.

According to wavelet theory [40], the coefficients in the last two rows (excluding Column 1) of the coefficient matrix correspond to high-frequency components dominated by artifacts and noise. Consequently, we apply a secondary hard-thresholding operation:

$${\tilde{C}}_l^g(x,y)=\left\{\begin{array}{cc}{\widehat{C}}_l^g(x,y)& \\ 0& \left(x=g-1,g\right)\&\left(y\ne 1\right)\end{array}\right.$$

(16)

Subsequently, we apply the inverse LHWT to ${\tilde{C}}_l^g$:

$${T^{\prime }}_l^g=H^{-1}\left({\tilde{C}}_l^g\right)$$

(17)

where $H^{-1}(·)$ denotes the inverse LHWT operator.

Finally, the filtering operations are applied to all pixel-similarity matrices. Aggregating the optimized pixels yields refined BT image $T_k^{\prime }$. The optimization workflow is formalized in Algorithm 1, with iterative reconstruction implemented through Algorithm 2. Detailed pseudocodes for both the PNSO (Algorithm 1) and IR (Algorithm 2) algorithms are provided accordingly.

Algorithm 1 PNSO: Pixel-Level Non-Local Sparsification Optimization

1: Input: The k-th input BT image $T_k$ 2: Output: The k-th Optimized BT image $T_k^{\prime }$ 3: function PNSO($T_k$, ${\sigma }_k$) 4:      $t_l\leftarrow \mathrm{Extract\_patches}(T_k,w)$ (Equation (5)) 5:      for ($l=1$ to L) do 6:           $T_l\leftarrow \mathrm{Find\_similar\_patches}(t_l,d)$ (Equations (6)∼(7)) 7:           for ($i=1$ to $w^2$) do 8:                 $T_l^g\leftarrow \mathrm{Form\_pixel\_group}(T_l,g)$ (Equations (8)∼(9)) 9:                 $C_l^g\leftarrow \mathrm{LHWT}\left(T_l^g\right)$ (Equations (13)) 10:               ${\tilde{C}}_l^g\leftarrow \mathrm{Bi}\_\mathrm{threshold}(C_l^g,{\sigma }_k)$ (Equations (14)∼(16)) 11:               ${T^{\prime }}_l^g\leftarrow \mathrm{ILHWT}\left({\tilde{C}}_l^g\right)$ (Equations (17)) 12:           end for 13:      end for 14:      $T_k^{\prime }\leftarrow \mathrm{Aggregate}\left({T^{\prime }}_l^g\right)$ 15:      return $T_k^{\prime }$ 16: end function

Algorithm 2 IR: Pixel-level Non-local Similarity Iterative Refinement

1: Input: Undersampled spatial-frequency domain data V 2: Output: The reconstructed InSAR brightness temperature image T 3: function IR($T_k$, ${\sigma }_k$) 4:      $V_0\leftarrow \mathrm{ZeroPad}\left(V\right)$ 5:      $T_0\leftarrow \mathrm{IFFT}\left(V_0\right)$ 6:      for ($k=1$ to K) do 7:            $T_k^{\prime }\leftarrow \mathrm{PNSO}(T_k,{\sigma }_k)$ 8:            $V_k\leftarrow FFT\left(T_k^{\prime }\right)$ 9:            $V_k^{\prime }\leftarrow \mathrm{Update}(V_0,V_k)$ (Equations (12)) 10:          $T_k\leftarrow \mathrm{IFFT}\left(V_k^{\prime }\right)$ 11:      end for 12:      return $T\leftarrow T_K$ 13: end function

3.4. Complexity Analysis

The proposed InSAR-PNS method comprises two parts: (1) For the PNSO algorithm, with a total iteration count K, the computational complexity of patch matching is $\mathcal{O}\left(L{C}^2{w}^2\right)$ per iteration, while pixel matching requires $\mathcal{O}\left(Ld{w}^4\right)$, and the complexity of noise estimation is $\mathcal{O}\left(Lg{w}^2\right)$. (2) For the IR algorithm, FFT and IFFT reconstruction operations exhibit $\mathcal{O}\left(ablog\left(ab\right)\right)$ complexity. Given that $C^2>g\ast d$ and $w^2>log\left(ab\right)$ are satisfied in practice, the overall complexity remains $\mathcal{O}\left(KL{w}^2*max\left(C^2,d{w}^2\right)\right)$.

4. Experimental Results and Discussion

This section describes the validation of the efficacy of the proposed InSAR-PNS reconstruction method through simulated and physical imaging systems under diverse interference scenarios and sampling rates. The comparative analysis includes the traditional modified fast Fourier transform (MFFT) and CS-based reconstruction methods.

4.1. Implementation Details

Experiments were conducted in MATLAB 2020a on a workstation with an Intel^® Core™ i7-10750H CPU (Intel Corporation, Santa Clara, CA, USA) and 16 GB RAM. The proposed method involves six key parameters: search window size ($C\times C$), patch size ($w\times w$), number of similar patches (d), number of similar pixel rows (g), filtering coefficient ($\beta$), and iteration count (K).

To quantitatively evaluate the reconstruction performance and guide the parameter optimization, we employed the structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) as objective evaluation metrics. Higher SSIM and PSNR values indicate less distortion and better quality in the reconstructed images.

The configuration of these parameters is critical to achieve high-quality reconstruction. To determine robust values, we conducted a systematic parameter sensitivity analysis. The core principle is to use weaker regularization for low-noise images to preserve detail and stronger regularization for high-noise images to ensure effective smoothing.

Specifically, the optimal values for the filtering coefficient $\beta$ and iteration count K were determined through a grid search aimed at maximizing the average PSNR on a validation set. This process revealed that, for weak noise (${\sigma }_0\le 30$), a coefficient of $\beta =0.5$ with $K=10$ iterations provides the best balance, effectively removing noise while minimizing the tendency of over-smoothing fine structures; for strong noise (${\sigma }_0>30$), however, a higher coefficient of $\beta =0.8$ and more iterations ($K=15$) were necessary to achieve sufficient noise suppression. The choice of these specific values is based on this optimization process: specifically, values lower than the optimum led to residual noise, while higher values resulted in perceptible blurring.

Since compatibility with Haar transforms requires d and g to be powers of 2, we constrained both parameters accordingly. Although larger window and patch sizes enhance image quality, optimal $21\times 21$ (window) and $13\times 13$ (patch) sizes were selected via validation to balance performance and computational efficiency. Complete parameter specifications are detailed in

Table 1. Parameters of the InSAR-PNS method.

Parameter		$\mathit{C}\times \mathit{C}$	$\mathit{w}\times \mathit{w}$	d	g	$\mathit{\beta }$	K
Value	${\sigma }_0\le 30$	$21\times 21$	$13\times 13$	32	8	0.5	10
	${\sigma }_0>30$					0.8	15

.

4.2. Simulation Platform Experiments

An InSAR imaging simulation model was implemented to emulate the millimeter-wave propagation and data acquisition chain. As depicted in Figure 1, this model comprehensively simulates the entire imaging process, including target radiation, antenna array visibility sampling, cross-correlation computation between antenna pairs, visibility function generation, and BT image reconstruction.

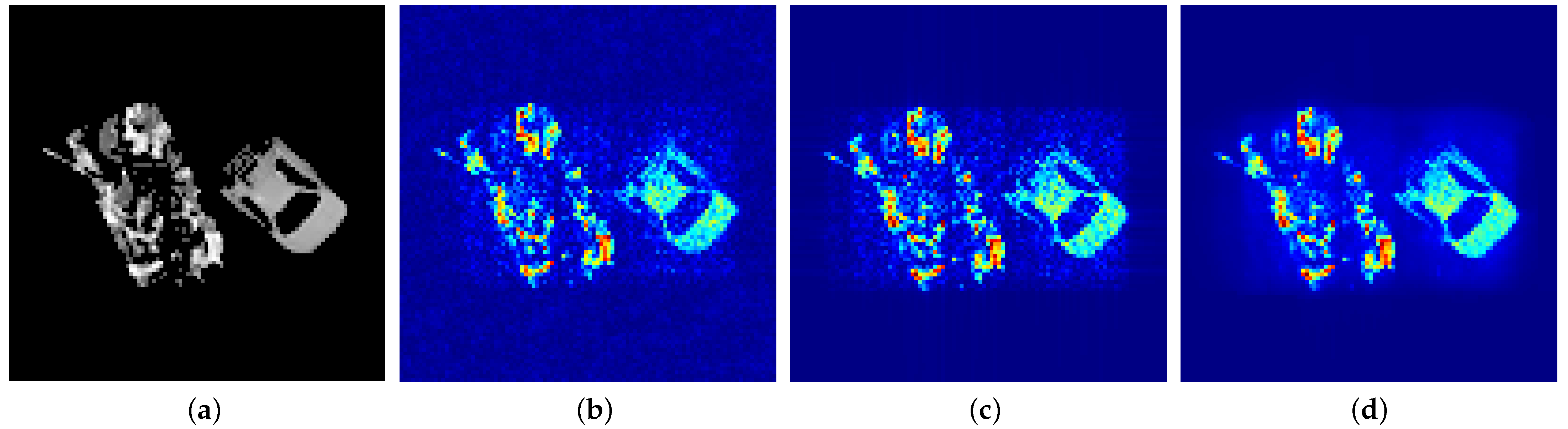
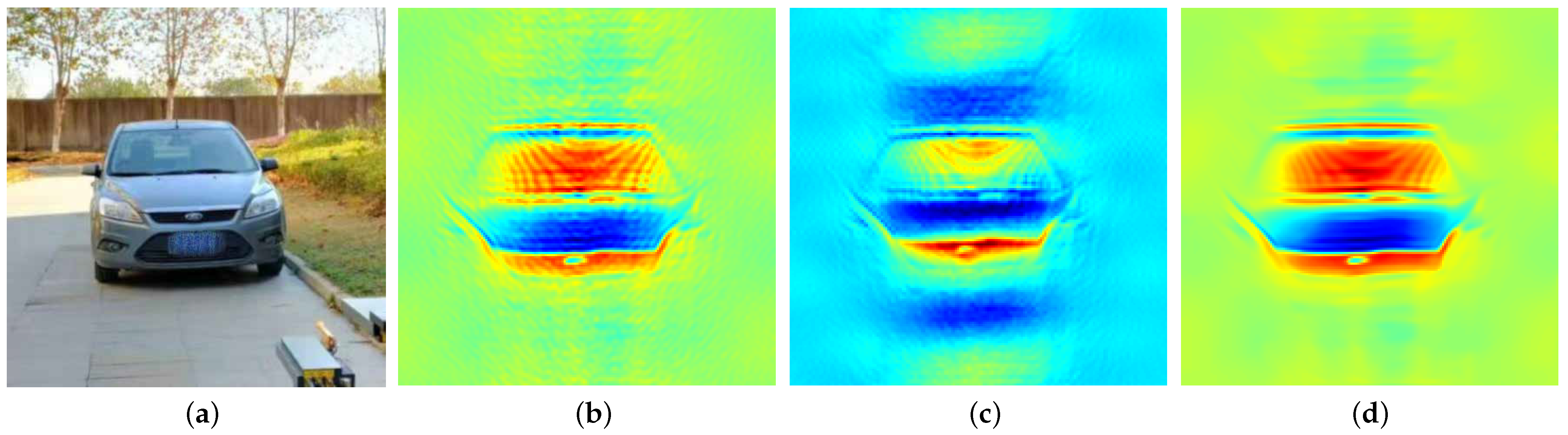
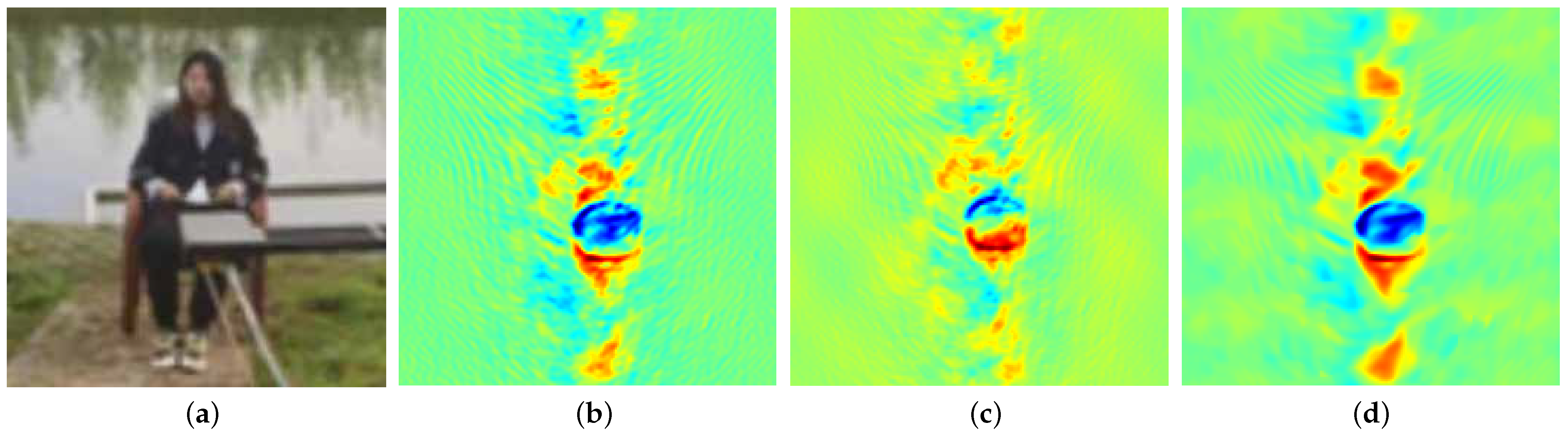
The simulation process started with millimeter-wave radiation source modeling, where each discrete point source was derived from two ideal scenes, as shown in Figure 4a and Figure 5a. The image dimension was 100 × 100 pixels, and the gray value of each pixel represented the intensity of the radiation emitted from a discrete point source. Subsequently, in-phase and quadrature (IQ) signals were acquired through coherent integration across the simulated scene. According to Equation (1), complex cross-correlation was applied to compute the visibility function V. Following phase compensation of the visibility data, the calibrated visibility function $V_m$ was generated. The BT image was ultimately reconstructed from $V_m$ using different inversion algorithms.

The system operates at 100 GHz ($\lambda =3$ mm) and employs a T-shaped antenna array configuration comprising 150 elements. The inter-element spacing was set to 12 mm ($4\lambda$), yielding a $1.2$ m equivalent synthetic aperture. The specific simulation parameters are provided in

Table 2. Parameter configuration of the InSAR imaging simulation system for modified fast Fourier transform (MFFT), compressed sensing (CS), and InSAR-PNS reconstruction methods.

Simulation Parameters	MFFT Reconstruction	CS and InSAR-PNS Reconstruction
Center frequency	100 GHz	100 GHz
Antenna array size	100 × 100	(90–40) × (90–40)
Receiver number	150	135–60
Inter-element spacing	12 mm	12 mm
Image distance	6 m	6 m
Image pixel size	100 × 100	100 × 100
image gray	0–255	0–255

. The MFFT method reconstructs BT images using the full set of visibility function samples, as demonstrated in Figure 4b and Figure 5b. In contrast, the CS and InSAR-PNS methods employ reduced sampling rates of 90% to 40%. Specifically, Figure 4c and Figure 5c present reconstruction results for both methods at an 80% sampling rate, while Figure 4d and Figure 5d correspond to results at a 50% sampling rate.

Comparative analysis of the reconstruction results in Figure 4 and Figure 5 demonstrates that the proposed InSAR-PNS method (Figure 4d and Figure 5d) outperforms both the MFFT (Figure 4b and Figure 5b) and CS (Figure 4c and Figure 5c) methods in terms of visual clarity, contour preservation, and target detail representation. The MFFT method exhibits performance degradation due to constraints from discrete and finite antenna array sampling, while the CS method, limited by its fixed sparse basis, fails to learn high-dimensional features of the BT image. Notably, at a 50% sampling rate, the CS method shows significant quality deterioration (Figure 5c), whereas the InSAR-PNS method produces a high-fidelity BT image with preserved fine details (Figure 5d) through its iterative adaptive learning mechanism.

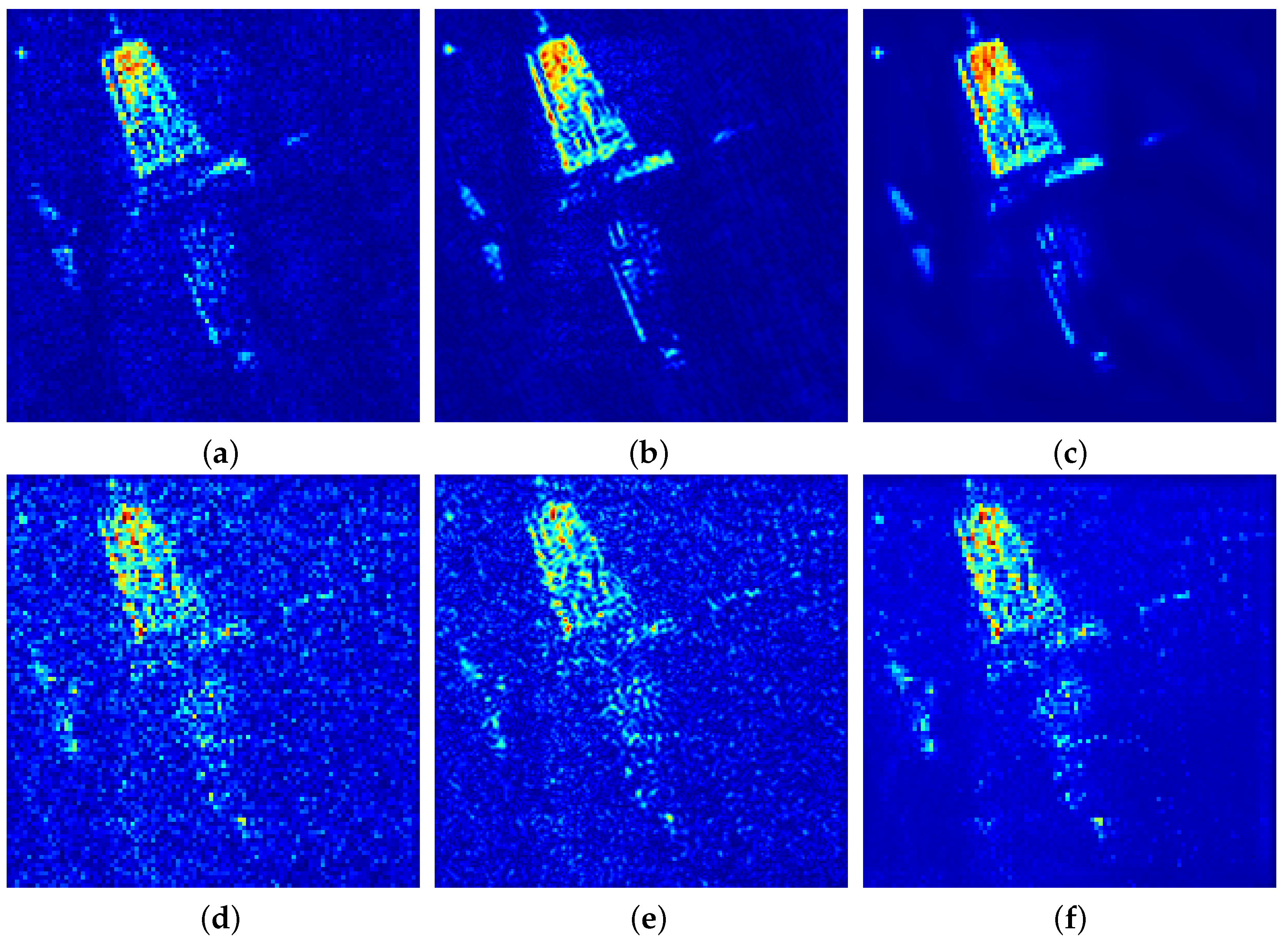
During practical imaging, noise interference and measurement errors are inevitable, they are primarily caused by hardware inconsistencies, antenna position deviations, and system noise. To simulate complex imaging environments, we employed zero-mean Gaussian white noise with varying variances ${\sigma }^2$ to characterize interference factors. To evaluate the robustness of the InSAR-PNS method, Gaussian white noise with varying intensities was added to the visibility function samples corresponding to the BT image shown in Figure 5a, simulating actual noise-corrupted imaging processes. Figure 6a–c display BT images reconstructed under low-intensity interference (${\sigma }^2=0.01$) using (a) MFFT with full visibility function samples, (b) CS with 80% visibility samples, and (c) InSAR-PNS with 80% visibility samples. Figure 6d–f show BT images reconstructed under high-intensity interference (${\sigma }^2=0.1$) using (d) MFFT with full visibility samples, (e) CS with 80% visibility samples, and (f) InSAR-PNS with 80% visibility samples.

An analysis of the reconstruction results in Figure 6 demonstrated that the MFFT output experiences severe noise degradation, nearly failing to preserve target contour information (Figure 6d) due to its lack of noise-suppression capability and susceptibility to the Gibbs phenomenon. Conversely, the CS and InSAR-PNS reconstructions both exhibit superior visual performance. The ability of the proposed InSAR-PNS method to preserve contours and fine details, as shown in Figure 6f, stems from its capability to distinguish signal from noise. This is achieved by exploiting the fundamental difference in their statistical properties: coherent signal structures within non-local similarity groups yield sparse, significant coefficients in the LHWT domain, while incoherent noise yields dispersed, small coefficients. Our adaptive double hard-thresholding strategy is designed to exploit this disparity—the first threshold removes the majority of the noise, while the second, targeted threshold cleans up the specific high-frequency sub-bands where noise dominates, thereby preserving structural information. In contrast, whereas CS relies on hand-crafted regularization parameters with fixed thresholds, the InSAR-PNS method dynamically adapts to the estimated noise distribution, which is the foundation of its robustness under strong interference.

Table 3. Quantitative results of structural similarity index measure (SSIM) and peak signal-to-noise ratio (PSNR) in the comparative study on the simulation system.

Sampling rate (%)		40	50	60	70	80	80	80	80	80	80
Interference Intensity (${\sigma }^2$)		0.00	0.00	0.00	0.00	0.00	0.02	0.04	0.06	0.08	0.1
SSIM	MFFT	–	–	–	–	0.965	0.947	0.908	0.895	0.804	0.752
	CS	0.901	0.913	0.935	0.951	0.979	0.973	0.953	0.938	0.904	0.885
	InSAR-PNS	0.925	0.948	0.959	0.972	0.988	0.981	0.970	0.966	0.952	0.911
PSNR	MFFT	–	–	–	–	29.28	26.67	24.53	21.87	19.96	17.28
	CS	23.36	25.18	26.12	27.52	30.95	29.82	27.72	26.32	23.86	21.48
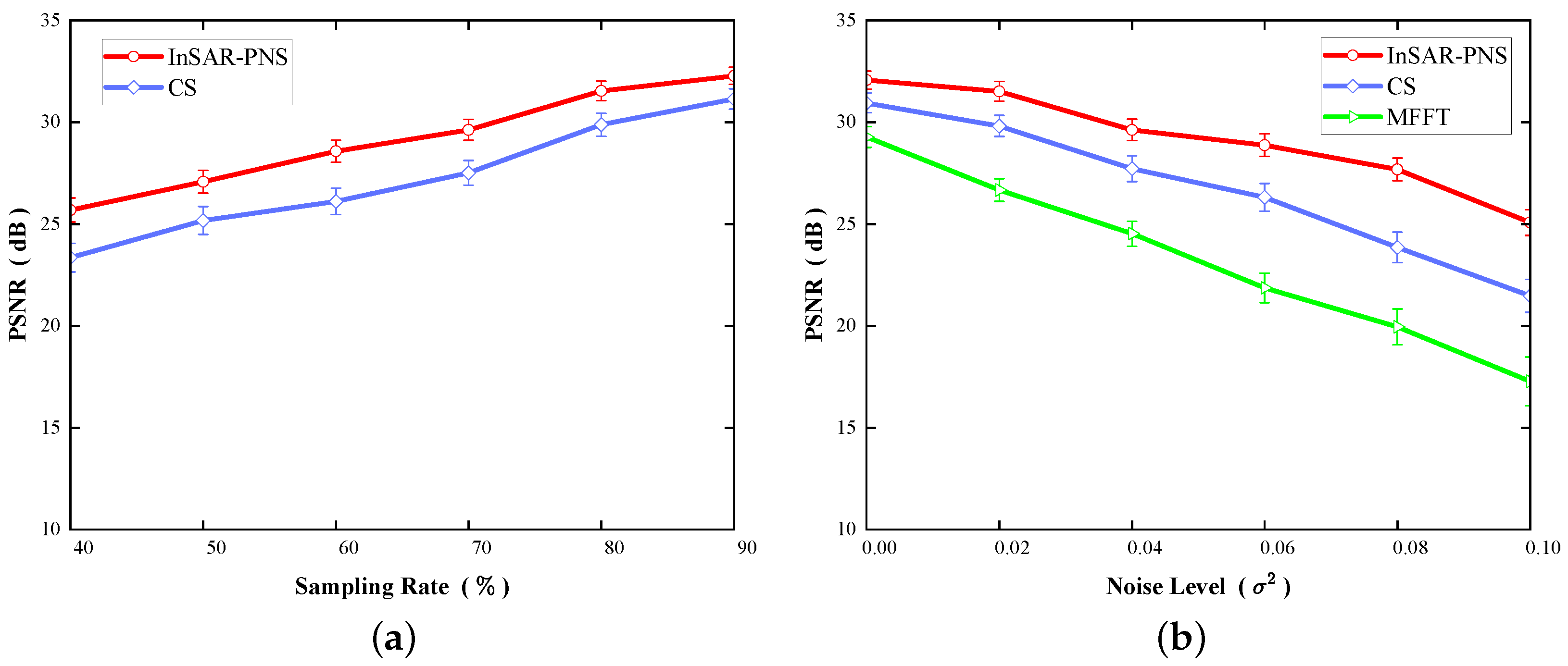
	InSAR-PNS	25.69	27.08	28.58	29.63	32.08	31.52	29.61	28.88	27.69	25.08

and Figure 7 summarize the quantitative performance metrics (SSIM and PSNR) of MFFT, CS, and InSAR-PNS under varying sampling rates and noise levels. The tabulated results demonstrate the consistently superior performance of InSAR-PNS across all tested conditions, with error bars in Figure 7 indicating measurement stability over five repeated trials. Specifically, the data indicate that, as the sampling rate decreases, InSAR-PNS demonstrates superior performance compared to CS. Concurrently, the PSNR values of all three algorithms decline with increasing noise intensity, reflecting a degradation in algorithmic performance. This deterioration is primarily attributed to the increasing dominance of noise components. Although heightened noise intensity poses greater challenges for reconstruction tasks, the proposed method (InSAR-PNS) consistently outperforms the other algorithms.

4.3. Physical Imaging System Experiments

In millimeter-wave InSAR imaging research, discrepancies between simulation environments and actual physical systems persist. Practical systems are frequently subject to non-ideal constraints such as hardware mismatches and environmental noise, leading to deviations in imaging outcomes from simulation predictions. Consequently, experimental validation using physical platforms is imperative.

Leveraging the principles of millimeter-wave InSAR imaging, a two-element interferometer enables 2D imaging through baseline scanning by trading time cost for hardware simplicity. This approach achieves spatially complete sampling equivalent to multi-antenna arrays, rigorously validating core algorithm performance when imaging latency is tolerable. Owing to its minimalist architecture and cost-effective design, this configuration is a standard testbed for algorithm verification in millimeter-wave InSAR studies. This work utilizes a T-shaped mechanically-scanned millimeter-wave InSAR system equipped with a two-element interferometer to assess the reconstruction performance of the proposed algorithm. Key system parameters are detailed in

Table 4. Main parameters of the two-element InSAR imaging system.

System Parameter	Value
Operating Frequency	100 GHz
Bandwidth	1 GHz
Number of Antenna Elements	2
Field of View (FOV)	20°
Angular Resolution	0.3°
Temperature Sensitivity	2K

.

The physical implementation of the system is presented in Figure 8. Full spatial baseline sampling within the observation airspace is achieved through the independent displacement of two array elements along orthogonal horizontal and vertical axes. The correlator receiver integrates two identical 3 mm wavelength radiometers, each consisting of a receiving antenna, front-end module, intermediate-frequency (IF) module, and local oscillator (LO) module.

The antenna unit employs two small-aperture conical horn antennas to capture radiation from the observed scene. The front-end module amplifies received signals and suppresses image band interference through bandpass filtering. The signals are then downconverted to the IF band by mixing with a 16.7 GHz LO reference. In the IF stage, the analog signals are subjected to quadrature demodulation to generate IQ components, which are forwarded to the digital processing unit. Following analog-to-digital conversion, the digitized in-phase and quadrature (I/Q) signals undergo cross-correlation to generate visibility function samples. These samples are transferred to a host computer for storing, processing, and rendering the reconstructed images using the BT reconstruction algorithm.

The effectiveness of the proposed InSAR reconstruction algorithm was validated using the scanning imaging system designed in this study. The test configurations are illustrated in Figure 8c,d: Figure 8c depicts the imaging scenario for a vehicle at 6 m under clear-weather and weak interference conditions, while Figure 8d shows the imaging scenario for a human subject carrying a metallic disc at 3.3 m under cloudy conditions with textile occlusion.

Figure 9 and Figure 10 comparably demonstrate the reconstruction characteristics of different methods: (a) displays the optical reference images of the targets, and images (b–d) show the reconstruction results of MFFT full sampling, CS, and InSAR-PNS 70% sparse sampling, respectively.

Experimental results indicate that in both strong and weak interference environments, InSAR-PNS can achieve superior reconstruction fidelity compared to the MFFT and CS methods. Our method generates smooth-textured images that preserve the essential features of the BT image, exhibiting well-defined boundaries with suppressed background noise. Further physical validation confirms dimensional accuracy: For the vehicle target (Figure 9), the Ford logo width was reconstructed as 140 mm against a ground truth of 150 mm, yielding a 6.7% dimensional error. Simultaneously, the 200 mm diameter disk tilted at 45° in Figure 10 produced a measured ellipticity ratio of 1.461 versus the theoretical value of 1.414, demonstrating a 3.3% shape deformation deviation. This demonstrates that the proposed InSAR-PNS method can adapt to complex environments, with sub-7% geometric errors validating its efficacy and practical utility in physical millimeter-wave InSAR applications.

In practical applications, reconstruction time is a crucial performance metric. The computation times of the compared methods under various sampling rates are presented in

Table 5. Computation time comparison of CS and InSAR-PNS.

Sampling Rate (%)	40	50	60	70	80	90
$t_{\mathrm{CS}}$ (s)	35.89	52.34	78.85	94.58	118.52	141.45
$t_{\mathrm{InSAR}-\mathrm{PNS}}$ (s)	12.05	12.46	12.77	12.82	12.94	13.04

.

As shown in Table 5, the computation time of the CS-based method increases significantly (35.89 to 141.45 s) as the sampling rate increases. In contrast, the proposed InSAR-PNS method maintains a stable computation time of approximately 12 to 13 s at all sampling rates. This stability arises because its core optimization process operates on a fixed-size matrix derived from the zero-padded image, making its computational cost largely independent of the sampling rate.

Although the non-local grouping step in InSAR-PNS introduces additional processing, the overall reconstruction process remains highly efficient. Notably, the InSAR-PNS method is not only 3.0 to 10.8 times faster than the CS method within the tested range but also produces superior visual and quantitative results. This efficiency-quality balance demonstrates that the InSAR-PNS approach shows promising potential for real-time reconstruction.

5. Conclusions

In this study, we propose a novel InSAR reconstruction method based on pixel-level non-local similarity, validating its reconstruction performance through simulations and practical millimeter-wave InSAR systems. Building upon millimeter-wave InSAR imaging principles, we introduce a pixel-level non-local similarity matching mechanism to construct an enhanced sparse representation model. This model leverages high-dimensional prior information from non-local similarity and dynamically optimizes threshold coefficients to effectively preserve image details while suppressing noise interference. Through iterative refinement, the algorithm simultaneously retains raw sampled data to enhance reconstruction accuracy.

Experimental results demonstrate that compared to traditional FFT methods requiring full sampling without calibration strategies, InSAR-PNS achieves an average PSNR gain of 5.88 dB across varying noise variances, with its advantages amplified under intensified interference. When benchmarked against CS reconstruction using fixed sparse dictionaries, InSAR-PNS exhibits an average PSNR improvement of 1.93 dB across different sampling rates. Both visual evaluation and quantitative analysis confirm that the proposed InSAR-PNS reconstruction method exhibits superior performance in improving reconstruction quality and noise suppression, providing a robust solution for millimeter-wave InSAR imaging in complex environments.

Although our method has clear advantages over conventional approaches, this study has limitations that point to future work. First, while the experimental validation utilized a two-element interferometer with mechanical scanning, the visibility function it produces is mathematically equivalent in scale and form to that of a full-scale array, thereby validating the core reconstruction algorithm and its intrinsic scalability. We recognize that practical large-scale arrays eliminate mechanical errors but introduce challenges, such as element-positioning deviations and channel response mismatches. The computational efficiency and noise-robust architecture demonstrated in this work provide a foundation for addressing these specific challenges in future multi-antenna systems. A second limitation lies in the comparative analysis. While deep learning has become highly relevant for image reconstruction, the absence of standardized public datasets for passive millimeter-wave InSAR BT image reconstruction precluded a direct and fair benchmarking against such data-driven approaches. To address these constraints, a multi-antenna prototype system is under development with the dual goals of (1) evaluating the algorithm’s robustness under realistic multi-antenna hardware conditions and (2) generating foundational data to enable meaningful benchmarking against deep learning approaches.