A Novel Autoencoder-Based Design for Channel Estimation in Maritime OFDM Systems

Abstract

This paper introduces a novel autoencoder-based channel estimation framework specifically designed for OFDM systems in the complex and rapidly time-varying maritime channel. We design a novel autoencoder architecture that integrates attention mechanisms with long short-term memory networks to adapt to the challenges posed by maritime communication. Additionally, to enhance the OFDM system’s ability to acquire precise channel response and improve operational efficiency, we introduce an improved fast super-resolution convolutional neural network. This enhancement is achieved through the incorporation of a residual denoising module specifically designed to mitigate the adverse effects of additive noise. By jointly training the autoencoder and the channel estimation network, we significantly enhance the reliability of maritime OFDM communication systems. Simulation results demonstrate that the proposed channel estimation network accurately estimates channel response across different pilot numbers, and the joint channel estimation method based on the autoencoder can be extended to accommodate different transmission rates and sea states.

1. Introduction

As a fundamental element of the space–air–ground–sea integrated framework, maritime communication is essential for extending the worldwide communication capabilities of the future sixth-generation (6G) wireless communication infrastructure [1,2]. Maritime wireless communication systems frequently employ orthogonal frequency division multiplexing (OFDM) technology, which is favored for its strong resilience against multipath fading, capability for rapid data transmission, and proficient bandwidth utilization. However, influenced by temperature, sea wave movements, and duct effects, maritime channels exhibit strong time-varying characteristics, making it difficult for receivers to accurately obtain channel state information and thereby affecting communication quality. Therefore, it is of great practical significance to develop more reliable maritime communication systems.

In recent years, the application of deep learning (DL) within the domain of wireless communications has been extensively explored, yielding promising system performance enhancements and offering valuable insights for various communication system designs. On the one hand, O’shea and Hoydis et al. in [3,4] pioneered a communication system based on the concept of autoencoders, which is optimized through end-to-end learning. This autoencoder architecture distinguishes itself from traditional communication systems by employing neural networks to jointly optimize both transmitters and receivers. Subsequently, authors in [5,6,7] employed fully connected (FC) neural network layers to implement an autoencoder-based OFDM system. However, such FC layers necessitate a large number of network parameters and may suffer from issues such as gradient vanishing during the training process. In contrast, ref. [8] proposed a novel convolutional neural network (CNN)-based autoencoder for channel estimation in dynamic maritime communication, demonstrating superior performance in Internet of vessel environments. Recent work presented in [9] introduces a polarization-aided scheme for polar-coded multi-user spatial modulation that enables joint decoding and improves BER at comparable complexity, a direction complementary to the DL-based autoencoder design.

On the other hand, high-precision channel estimation is indispensable for OFDM systems to compensate for channel distortions and guarantee reliable data recovery. Soltani et al. [10] pioneered the migration of image-processing techniques to OFDM channel estimation, cascading a super-resolution CNN (SRCNN) with a denoising CNN (DnCNN) to reconstruct the channel response. Subsequently, a deep residual channel estimation network (ReEsNet) was proposed in [11], which outperforms [10] in terms of accuracy while reducing the number of parameters significantly. Mei et al. [12] introduced a low-complexity online training channel estimation algorithm tailored for OFDM systems, addressing the issue of difficulty in obtaining datasets for offline training. Gao et al. [13] combined residual learning and attention mechanisms to propose a more accurate and robust channel estimation method. Ref. [14] innovatively proposed a fully progressive image super-resolution technique to address the channel estimation problem in OFDM systems, achieving excellent performance under different channel conditions with low computational complexity. Additionally, refs. [15,16,17] extend deep-learning–based channel estimation to OFDM systems in different scenarios such as mines and underwater acoustic, attaining high accuracy with low computing complexity. However, there is a lack of research specifically focused on the complex and variable maritime communication scenario.

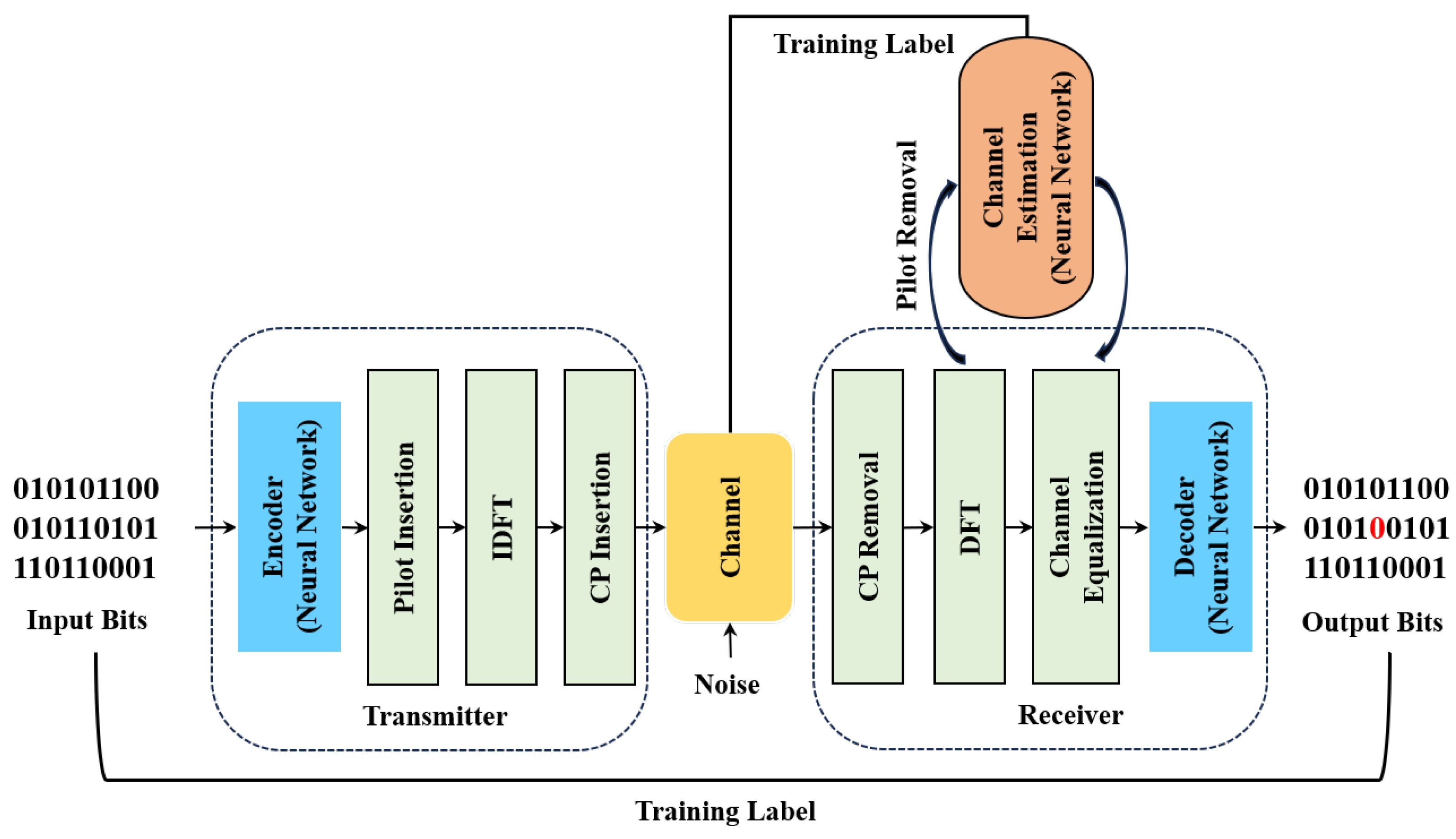
An autoencoder-based framework for channel estimation in maritime OFDM systems is proposed in this paper to overcome the aforementioned research limitations. The proposed autoencoder integrates attention mechanisms and long short-term memory (LSTM) on the basis of CNNs to better leverage dependencies on time series data, thereby adapting to the rapidly changing maritime environment. Compared to FC networks, the proposed framework converges faster with fewer network parameters. Additionally, we propose an improved fast super-resolution convolutional network (FSRCNN) that efficiently recovers high-resolution channel state information from sparse pilot patterns in maritime OFDM communication systems. More explicitly, the contributions of this article are as follows:

• An end-to-end autoencoder architecture is designed that combines attention mechanisms and LSTM layers to adaptively adjust and select the optimal signal representation in a variable maritime communication environment. This architecture supports both generalization capabilities and flexible transmission rates.
• We also design an improved fast super-resolution convolutional network for channel estimation in maritime communication scenarios. We design a residual denoising module to mitigate the impact of complex and diverse maritime noise, enabling rapid processing of complex and time-varying channel environments while avoiding performance degradation issues encountered by traditional methods in maritime environments.
• The proposed autoencoder and channel estimation network can be trained jointly, leveraging end-to-end training to achieve faster convergence. Simulation results demonstrate excellent performance at different transmission rates and sea states.

The remainder of this paper is structured as follows. In Section 2, traditional OFDM system modeling and channel estimation techniques are reviewed. Section 3 elaborates on the proposed autoencoder-driven channel estimation framework, detailing network architecture and training methodology. Experimental results and performance evaluations are examined in Section 4, with concluding remarks provided in Section 5.

2. Maritime OFDM Communication System

This section begins with an overview of foundational concepts in conventional OFDM systems, establishing the baseline for our autoencoder-based channel estimation approach. Subsequently, representative traditional channel estimation methods are introduced.

2.1. OFDM Communication System

This paper focuses on a single antenna maritime OFDM system with N subcarriers and T time slots (each containing one OFDM symbol). Figure 1 depicts a block diagram of a conventional OFDM communication system. At the transmitter, the input bits undergo channel coding, which introduces redundancy to facilitate error detection and correction at the receiver, thus enhancing system reliability. Through constellation mapping on the IQ plane, the encoded bits are modulated into complex-valued in-phase and quadrature (IQ) symbols. These symbols subsequently undergo serial-to-parallel (S/P) conversion, being allocated across N parallel data subcarriers where N denotes the number of subcarriers dedicated to data transmission. Pilot data are systematically inserted into each OFDM symbol in a specific manner [18], with common pilot insertion methods including comb, block, and scattered patterns. Subsequently, frequency-domain OFDM symbols undergo transformation to the time domain via inverse discrete Fourier transform (IDFT) operations. To mitigate intersymbol interference (ISI), a cyclic prefix (CP) is appended, with its length tailored to the channel’s multipath delay spread.

The baseband signal is subsequently up-converted to radio frequency (RF) for wireless transmission. The propagation channel is modeled as a multipath fading environment characterized by

$$\mathit{y}=\mathit{x}\otimes \mathit{h}+\mathit{n},$$

(1)

where vectors $\mathit{x}$ and $\mathit{y}$ correspond to time-domain transmitted and received signals respectively, n represents additive noise, h denotes the multipath channel impulse response (CIRs), and ⊗ signifies convolution. The channel is assumed quasi-static within individual OFDM symbols but time-varying across symbols. The CIRs [19] are expressed as

$$h(\tau ,t)=\sum _{k=1}^K{a}_k\left(t\right)\delta (\tau -{\tau }_k),$$

(2)

where $a_k\left(t\right)$ denotes the gain coefficient of the k-th path, ${\tau }_k$ represents its path delay, and K specifies the total number of multipath components.

At the receiver, CP removal precedes time-to-frequency domain conversion of OFDM symbols through discrete Fourier transform (DFT). Using known pilot data, the receiver estimates the full channel response to enable frequency-domain equalization. Finally, the equalized symbols are converted to binary output through demodulation and channel decoding operations corresponding to the transmitter.

2.2. Traditional Channel Estimation Methods

Traditional channel frequency response (CFR) estimation from pilot symbols follows a two-step process. First, CFR values at pilot positions are computed using known transmitter/receiver pilot signals. These estimates are then interpolated to data subcarrier positions. Figure 2 illustrates this pilot-based estimation framework, where $N_p$ and $T_p$ denote the pilot grid dimensions along frequency and time axes, respectively.

In this case, the least square (LS) estimation method at the pilot position can be obtained by the following minimization problem:

$${\widehat{\mathbf{H}}}_p^{LS}=arg\underset{{\widehat{\mathbf{H}}}_p}{min}{∥{\mathbf{Y}}_p-{\mathbf{X}}_p{\widehat{\mathbf{H}}}_p∥}_2^2.$$

(3)

The solution for LS channel estimation is thus derived as follows:

$${\widehat{\mathbf{H}}}_p^{LS}={\displaystyle \frac{{\mathbf{Y}}_p}{{\mathbf{X}}_p}}.$$

(4)

For the ${\mathbf{H}}_d$ at the data subcarrier location, it can be obtained by different interpolation methods [20]. The interpolation process can be expressed as follows:

$${\widehat{\mathbf{H}}}_d={\mathbf{W}}_d{\widehat{\mathbf{H}}}_p^{LS},$$

(5)

where ${\mathbf{W}}_d$ is the interpolation matrix. The LS channel estimation algorithm is widely used due to its simple structure and low computational complexity. However, since it does not consider the effect of additive noise, its estimation performance is sensitive to noise and performs poorly at low signal-to-noise ratios.

Compared with the LS channel estimation algorithm, the minimum mean square error (MMSE) algorithm fully considers the statistical properties of the channel and the noise variance, and better estimation performance can be obtained. Specifically, its estimation method is realized by multiplying the LS estimation by the interpolation matrix ${\mathbf{W}}_{d_{-}MMSE}$,

$${\widehat{\mathbf{H}}}_{MMSE}={\mathbf{W}}_{d_{-}MMSE}{\widehat{\mathbf{H}}}_p^{LS},$$

(6)

where ${\mathbf{W}}_{d_{-}MMSE}$ can be solved by the following minimization problem:

$${\mathbf{W}}_{d_{-}MMSE}=arg\underset{{\mathbf{W}}_d}{min}{∥{\mathbf{H}}_d-{\mathbf{W}}_{d_{-}MMSE}{\widehat{\mathbf{H}}}_p^{LS}∥}_2^2.$$

(7)

The final ${\mathbf{W}}_{d_{-}MMSE}$ can be provided by the following equation:

$${\mathbf{W}}_{d_{-}MMSE}={\mathbf{R}}_{{\mathbf{H}}_d{\mathbf{H}}_p}{\left({\mathbf{R}}_{{\mathbf{H}}_p{\mathbf{H}}_p}+{\sigma }_n^2\mathbf{I}\right)}^{-1},$$

(8)

where ${\mathbf{R}}_{{\mathbf{H}}_p{\mathbf{H}}_p}=E\left\{{\mathbf{H}}_p{\mathbf{H}}_p^H\right\}$ denotes the channel autocorrelation matrix at pilot subcarriers, and ${\mathbf{R}}_{{\mathbf{H}}_d{\mathbf{H}}_p}=E\left\{{\mathbf{H}}_d{\mathbf{H}}_p^H\right\}$ represents the channel-data cross-correlation matrix. Here, ${\sigma }_n^2$ denotes the noise variance and $\mathbf{I}$ is the identity matrix.

3. Proposed Autoencoder-Based Channel Estimation Method

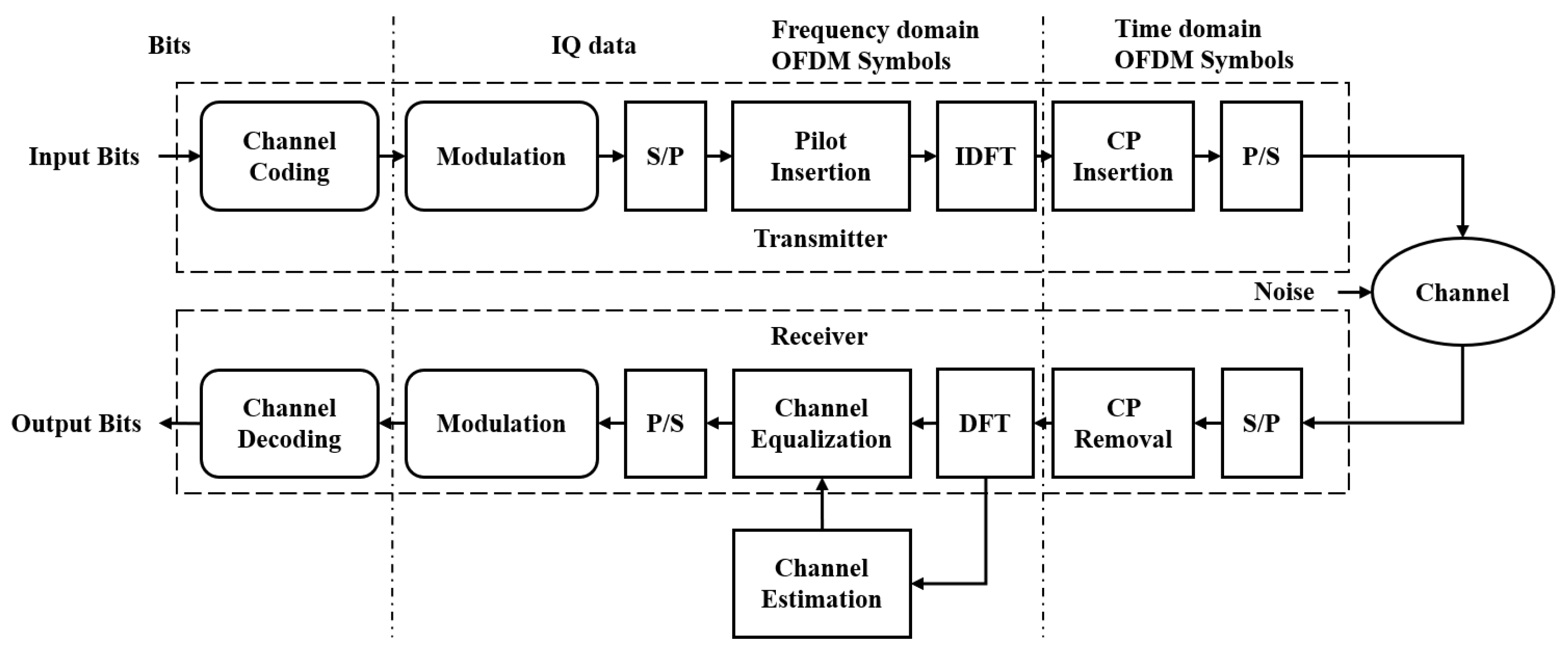
This section details the design and training of our proposed autoencoder-based channel estimation framework tailored to maritime OFDM systems, and the corresponding system block diagram is illustrated in Figure 3. The objective of the end-to-end architecture is to derive an optimal signal representation at the transmitter, thereby empowering the receiver to adapt to the time-varying characteristics of the maritime wireless channel and to reconstruct the transmitted information with the minimum attainable error probability. Specifically, we augment the CNNs with a dual-head attention module capable of joint reweighting along the real and imaginary parts, thereby achieving a flexible representation of a complex signal. Moreover, we leverage the temporal modeling capacity of LSTM layers to accurately capture long-range temporal dependencies across successive signaling instants, thereby enabling adaptive joint channel coding and modulation tailored to the intricate dynamics of maritime channels. Furthermore, we adapt the concept of image super-resolution to solve the maritime channel estimation problem by treating received pilot signals as low-resolution images and the full channel response as high-resolution counterparts. Since the maritime channel is line-of-sight dominant with sparse specular paths in the delay domain, an improved image super-resolution network is designed, which can restore these high-frequency details, outperforming standard interpolation methods at the same pilot density. Finally, through joint training and deployment of the proposed autoencoder and channel estimation modules, the reliability of maritime OFDM systems can be effectively enhanced. The specific autoencoder and channel estimation networks are presented below.

3.1. OFDM Autoencoder

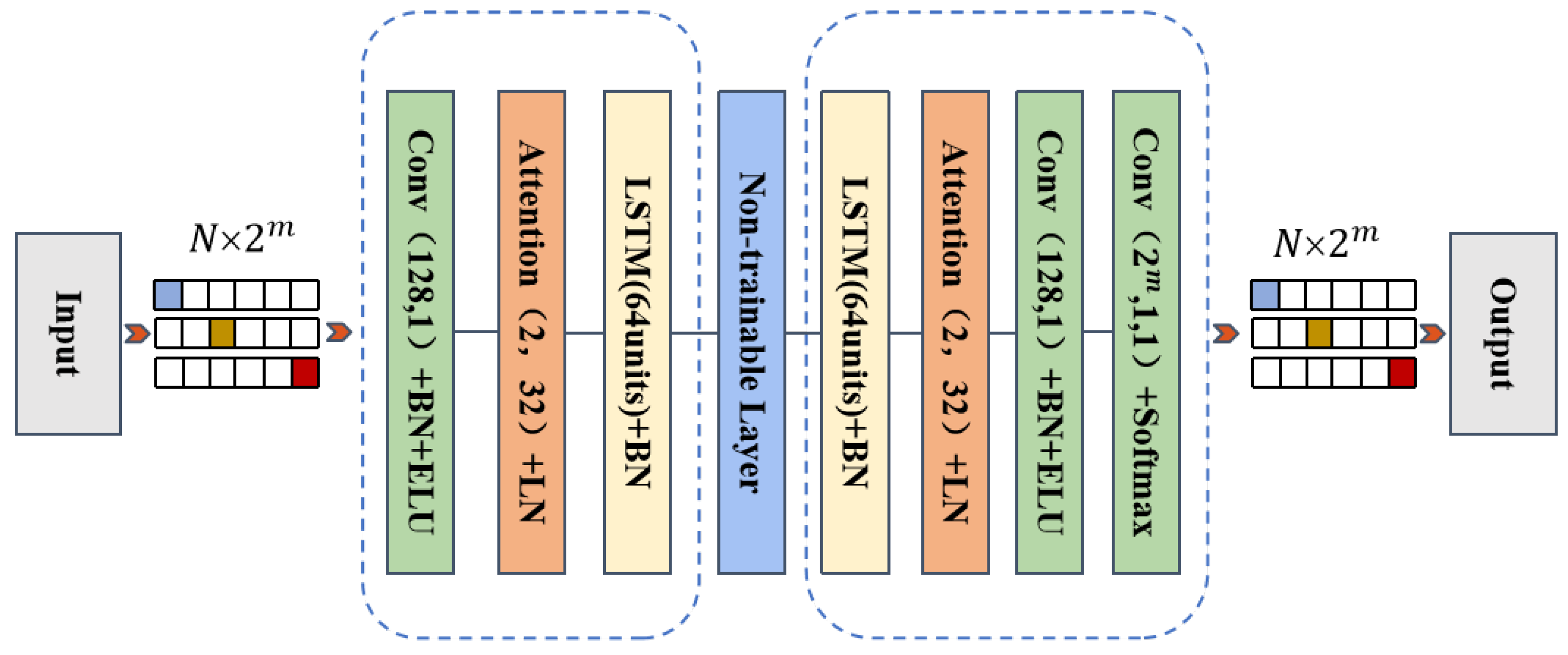
The architecture of the proposed autoencoder system is illustrated in Figure 4. It is worth noting that our autoencoder system is a symbol-wise autoencoder [21]. The input bit stream undergoes mapping, forming a one-hot vector with dimensions $N\times 2^m$, treating it as a block equivalent to N number of m-array QAM symbols in traditional OFDM. This one-hot representation, utilized as the network input, accelerates convergence toward the optimal solution.

At the transmitter, the one-hot matrix is initially processed by 128 $1\times 1$ convolutional kernels that extract salient features, thereby equipping the network with resilience to highly dynamic channels. Following this convolution layer, batch normalization (BN) is employed to expedite convergence and enhance stability. Additionally, the convolution layer introduces nonlinear characteristics by utilizing exponential linear units (ELUs) as activation functions, which further enhances the model’s expressiveness. To improve the model’s performance, we have designed a lightweight attention module with two multi-heads and a key dimension of 32. The two heads operate on the real and imaginary channels, explicitly preserving the quadrature structure and enabling phase-aware selection of salient information while keeping the model compact. By dynamically allocating weights across real and imaginary, the module highlights key features and improves signal-processing efficiency and accuracy. Subsequently, layer normalization (LN) is applied to the output of the attention module to preserve original feature information and enhance model training stability. Finally, we employ LSTM layers to process the output signals from the attention module, utilizing 64 LSTM units to capture signal dependencies in the time domain. The attention module’s output sequence feeds into LSTM cells, where input, output, and forget gates recurrently encode temporal dependencies by regulating information flow across time steps. We use 64 LSTM units to align with the OFDM grid, yielding one compact latent coefficient per subcarrier. A Batch Normalization (BN) layer is also added to the output to stabilize the training process. Thus, by integrating the attention mechanism and LSTM layers on top of the CNN, we complete the modulation and channel coding tasks of the autoencoder system.

At the receiver, the processing of the transmitted signal begins with an LSTM that has 64 units, which is employed to reconstruct the time sequence relationship that may have been damaged during transmission through the wireless channel. Following this, we utilize a lightweight attention module, analogous to the one used in the encoder, to enhance the model’s focus on critical features. This allows for dynamic weight allocation during the decoding process, thereby improving accuracy.

To further refine the output, two one-dimensional convolutional layers are employed to reconstruct the features derived from the decoder’s output. The first convolutional layer comprises 128 one-dimensional convolutional kernels, each with a kernel size of 1, which serve to restore the feature dimension in preparation for the final symbol decision. The subsequent convolutional layer, which employs Softmax activation, contains $2^m$ filters, each with a kernel size of 1, where m represents the modulation order. This layer effectively maps the features to the output space, reconstructing them into unigram vectors and thereby finalizing the data recovery process.

Unlike traditional OFDM systems that optimize channel coding and modulation/demodulation separately, our approach integrates attention mechanisms and LSTM layers into a CNN to perform joint coding and decoding of data. This integration allows for a more cohesive processing of the data. To facilitate convergence of the neural network, we utilize a one-dimensional convolution layer with a smaller kernel size, as larger kernels can hinder this process. Furthermore, by incorporating additional attention mechanisms and LSTM layers to establish correlations among time-series signals, an adaptive signal representation is achieved, which effectively mitigates the multipath effects and channel fading impacts that are prevalent in maritime communication environments.

3.2. Channel Estimation Method

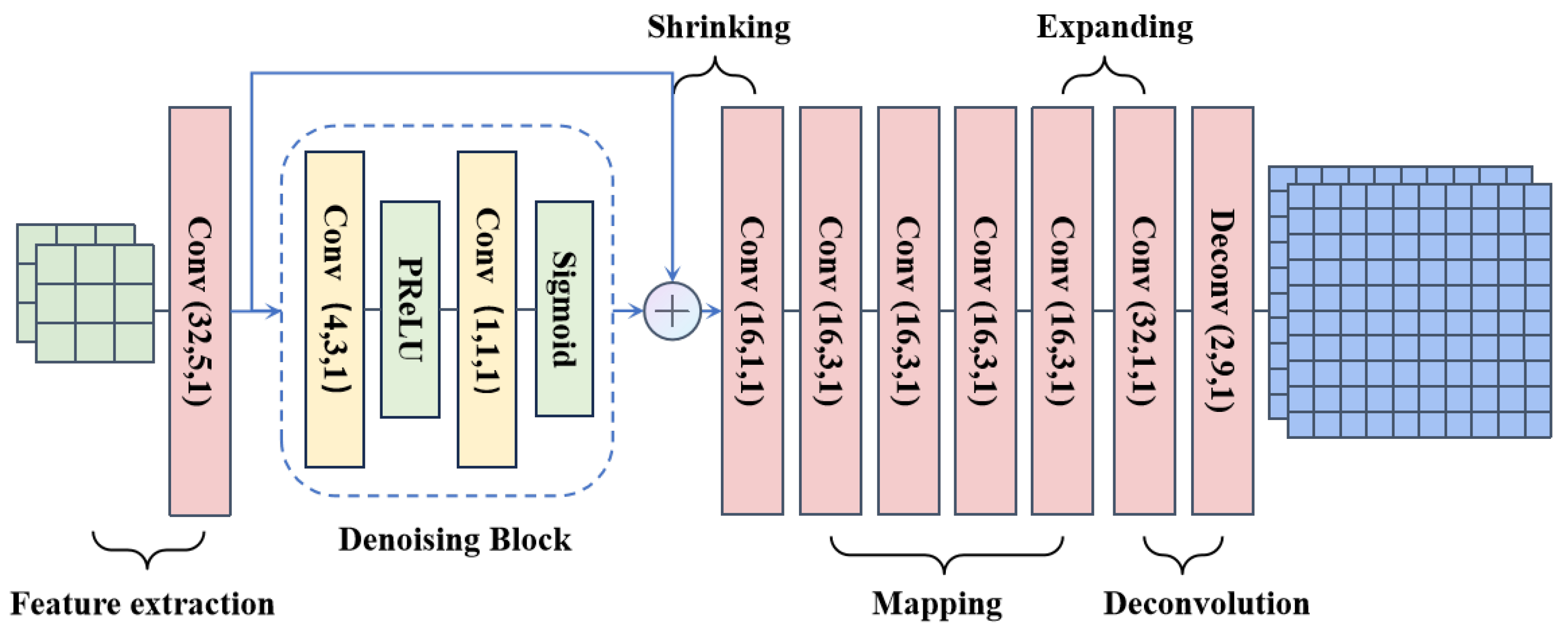
We combine the FSRCNN [22] from the field of image super-resolution to transform the channel estimation problem into an image super-resolution problem for processing. We also design a residual denoising module to reduce the impact of noise and propose a new channel estimation method; the specific structure is shown in Figure 5. The basic structure of the channel estimation network model primarily consists of six components: feature extraction, residual denoising block, contraction, mapping, expansion, and deconvolution.

At the receiver, we extract the received pilot signals as input to the network. First, the feature extraction module extracts features from the original low-resolution images. The feature extraction module consists of 32 convolutional kernels of size $5\times 1$, enabling the extraction of local features from the input tensor, which serves as the foundation for subsequent processing. To enhance the robustness of the channel estimation network, a residual denoising module is added to the original network. The lightweight denoising module learns and extracts the noise components from the input data. The output from the feature extraction layer is subtracted from the output from the noise extraction layer to obtain the denoised features. The extracted features are then input into 16 convolutional kernels of size $1\times 1$. This network layer reduces the number of parameters during transmission and lowers computational complexity, compressing the extracted output features while preserving important feature information. Next, the output is passed to the mapping layer to perform a nonlinear transformation on the image information, learning the complex mapping relationship between the input and output. The mapping layer consists of four convolutional layers with the same structure, each containing 16 convolutional kernels of size $3\times 1$. After the mapping layer, the output is passed to the expansion layer, which primarily consists of 32 $1\times 1$ convolution kernels to expand the output features from the nonlinear mapping layer, enabling upsampling in subsequent deconvolution layers. Finally, the deconvolution layer, composed of two $9\times 1$ deconvolution kernels, performs upsampling and aggregation using the previously generated feature images to generate the complete channel response.

To prevent the dead neuron problem associated with ReLU activations, we employ parametric rectified linear units (PReLU) after convolutional layers, which preserve negative values in their output. This property proves essential for our FSRCNN-based channel optimization network, as the channel matrix may contain negative components. By maintaining this sign information, PReLU enhances estimation accuracy through improved representation fidelity. The PReLU coefficient a is initialized to 0.25 for all channels and subsequently learned together with the network weights by gradient descent. During training, the optimizer automatically adjusts a to minimize the loss.

$$PReLU\left(x\right)=\left\{\begin{array}{c}x,x>0\hfill \\ ax,x\le 0,0<a<1\hfill \end{array}.\right.$$

(9)

3.3. Model Training

We employ cross-entropy loss for our OFDM autoencoder, treating the symbol recovery as a classification task. The cross-entropy loss function can more effectively measure the difference between the probability distribution of the model output and the true labels. The specific loss function expression is given by the following equation:

$$L_{\mathrm{Cross-Entropy}}=-\sum _{i=1}^U\sum _{j=1}^g{y}_{ij}log{x}_{ij},$$

(10)

where x and y represent the training data set and label data set, respectively, g is the number of categories, and U is the number of samples.

For our proposed improvement to the FSRCNN channel estimation method, we use the mean-square error (MSE) as the loss function, where the network input data is the extracted pilot signal and the label data is the perfect channel response. The network weights are continuously adjusted by calculating the MSE value between the network output and the label. The expression of the specific loss function is provided by the following equation:

$$L_{\mathrm{MSE}}={\displaystyle \frac{1}{U}}\sum _{i=1}^U{\left(y_i-x_i\right)}^2.$$

(11)

To reduce the risk of overfitting, we implement dropout and early stopping with a patience setting of 20, performing model selection based on a validation set that is kept separate. The dataset is randomly split into training, validation, and test partitions with an 8:1:1 ratio. We employ the ADAM optimization algorithm [23], which adjusts the gradient’s magnitude and direction adaptively. To speed up the training process and ensure better convergence of the neural network, we begin with an initial learning rate of 0.01. If the loss function defined in Equation (10) or Equation (11) stabilizes for five consecutive epochs, we reduce the learning rate by a factor of 10. Furthermore, mini-batch gradient descent is utilized for faster training, with the batch size set at 64.

Empirical results reveal that end-to-end direct joint training exhibits slow convergence and yields sub-optimal accuracy in related works. Consequently, training is decomposed into two sequential stages in this paper. The autoencoder is pretrained under perfect CIRs, while the channel estimation module is independently trained within a legacy OFDM framework. In addition, we find that the training signal-to-noise ratio (SNR) is also an important factor affecting the convergence of the network model. On one hand, training under low SNR conditions can cause excessive noise power to hinder the neural network’s ability to learn complex data structures. On the other hand, training under excessively high SNR conditions can cause the neural network to lose its generalization capability for handling noise-contaminated data, thereby affecting the network’s robustness. In this paper, we trained the proposed autoencoder system and channel estimation network under an SNR of 15 dB.

4. Simulation Results and Analysis

Table 1. Simulation parameters used.

Parameters	Values
Carrier Frequency	2.6 GHz
Sampling Rate	1080 kHz
Number of Subcarriers	64
Number of Pilots	8
Length of CP	32
FFT Size	64
Channel Model	Multipath Rayleigh fading channel
Doppler Frequency	5 Hz
Type of Pilot Insertion	Comb
Pilot value	$1+1i$

presents the detailed simulation parameters for the OFDM system. To accurately simulate the multipath effects caused by sea surface fluctuations in offshore wireless communication channels, we adopt a multipath Rayleigh fading model, setting the Doppler frequency to 5 Hz to represent the relative motion between ships [24,25]. In this section, we aim to demonstrate the accuracy of the proposed channel estimation method through extensive simulation comparison experiments. Specifically, we compare our method with several traditional channel estimation algorithms and deep learning-based algorithms within a standard OFDM system framework. Additionally, we evaluate the proposed joint design method against the CNN-based autoencoder system introduced in [8] and assess the block error rate (BLER) performance of an OFDM system with a perfect channel response. To further validate the model’s robustness in real-world maritime channel environments, we conduct testing on three different sea states using publicly available maritime channel datasets from [26,27,28,29].

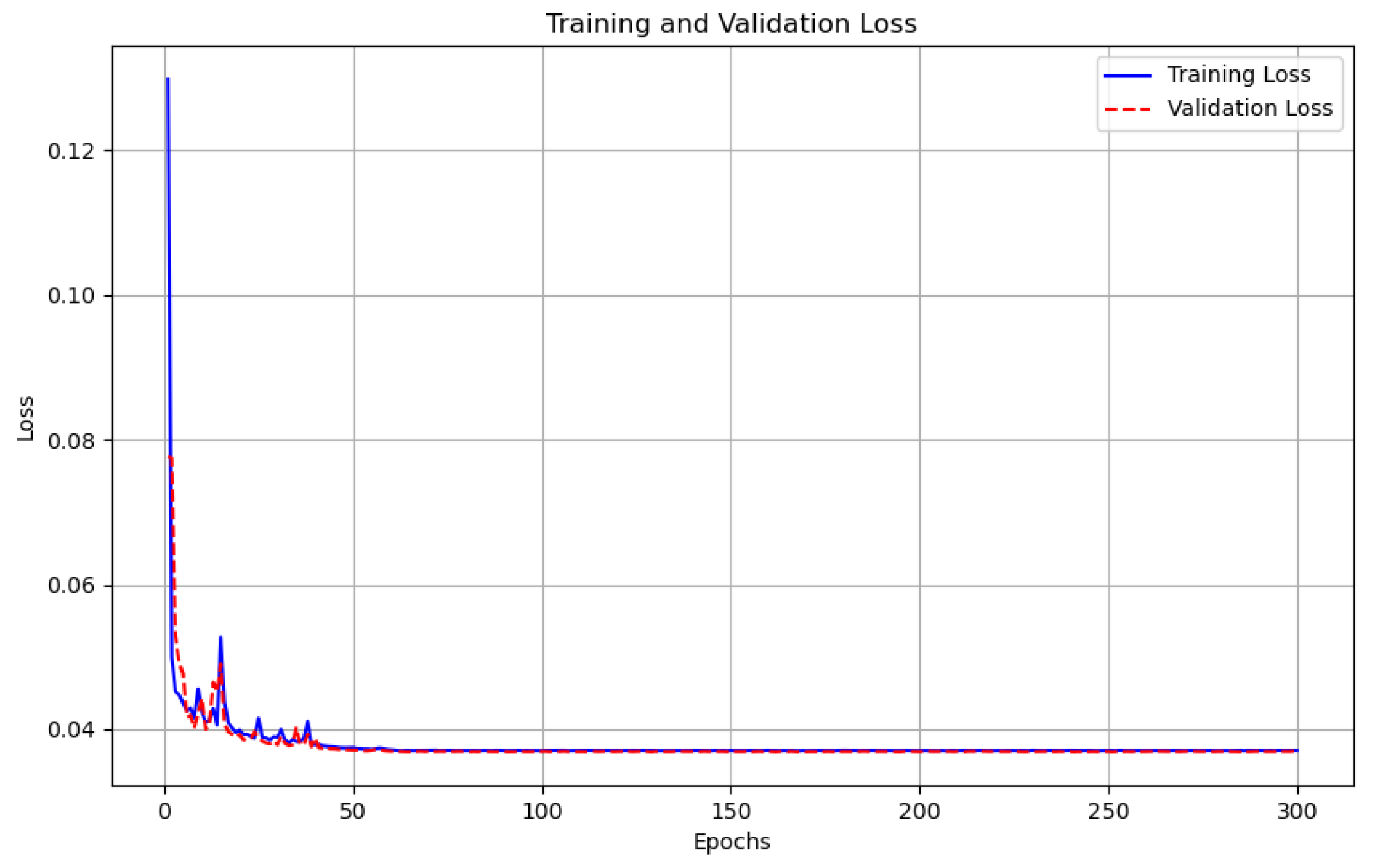
Figure 6 illustrates the training and validation losses of the proposed autoencoder-based channel estimation method operating under a multipath fading channel characterized by a Doppler frequency of 5 Hz. To enhance the complexity of the model’s learning process, we set $m=64$. In the context of this dynamic channel environment and high-rate transmission scenario, the figure reveals that, despite notable fluctuations during the initial training phase, the model achieves convergence around 40–50 epochs. This convergence is attributed to the inherent complexity of the channel environment, which necessitates that the network invest a significant amount of time in learning before it can arrive at the optimal solution. Moreover, the close alignment between the training loss and validation loss suggests that the proposed joint training method effectively addresses overfitting issues, thereby enhancing the model’s generalization capabilities.

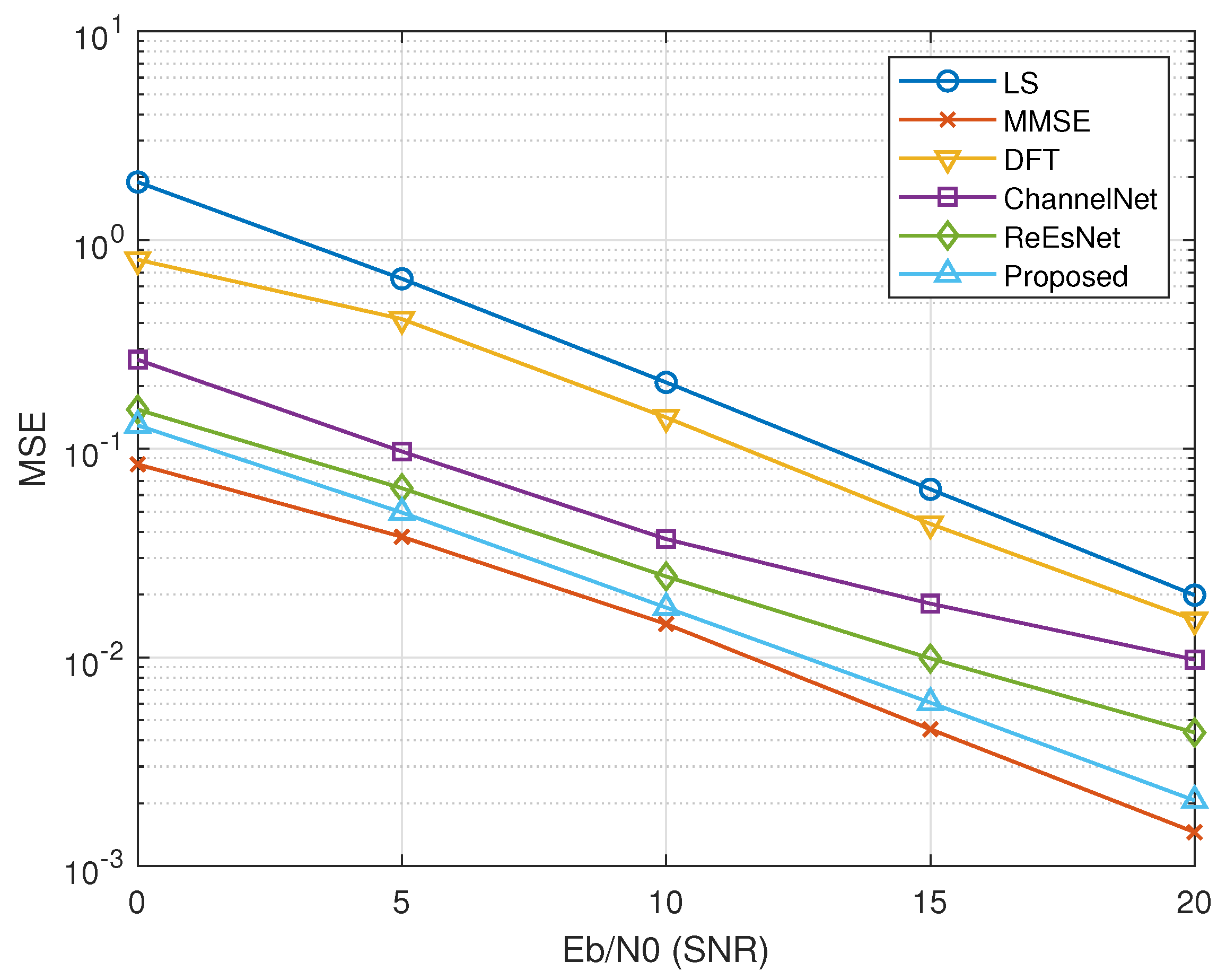
To explore the influence of pilot quantity on the proposed image-based super-resolution channel estimation algorithm, we configured the pilot numbers to 8 and 16, conducting simulations within the classic OFDM framework. The compared algorithms include the standard LS, DFT, and MMSE techniques, as well as ChannelNet from [10] and ReEsNet from [11]. Figure 7 presents the MSE performance of various channel estimation methods when the pilot number is set to 8. The results show that the LS algorithm performs the worst, as it overlooks noise and depends solely on linear interpolation for estimating non-pilot positions. Conversely, the proposed algorithm ranks just behind the MMSE method in performance. The MMSE algorithm requires second-order channel statistics and noise variance as prior inputs, which are often hard to acquire in practical communication systems. Notably, when compared to existing deep learning-based algorithms, the proposed channel estimation method consistently demonstrates superior performance. When the pilot number increases to 16, as depicted in Figure 8, the proposed channel estimation algorithm continues to outperform both traditional channel estimation methods and existing deep learning-based algorithms. Specifically, when the pilot number is 16, the proposed channel estimation algorithm shows a more pronounced advantage in MSE performance compared to when the pilot number is 8, with the MSE value decreasing further as the signal-to-noise ratio increases.

Figure 9 illustrates the BLER performance of the proposed autoencoder-based channel estimation algorithm under a fast multipath Rayleigh fading channel, in comparison to the CNN-based autoencoder system introduced in [8] and the traditional half-rate convolutional coded OFDM system with a perfect channel response. To assess the robustness of the proposed algorithm across different modulation orders, we conducted simulation experiments with m set to 2, 4, 16, and 64 for comparison. As depicted in Figure 9, under the fast Rayleigh multipath fading channel, the BLER performance of all algorithms is inferior to that of the OFDM system with a perfect channel response due to the high complexity and strong unpredictability of the channel. Furthermore, the figure shows that when $m=2$, the BLER performance closely resembles that of the OFDM system with a perfect channel response. However, as the modulation order increases, the error performance deteriorates, particularly in the high SNR region. Despite this, the proposed joint design method continues to demonstrate superior performance compared to the CNN-based autoencoder system introduced in [8].

To validate the robustness of the proposed joint design method in real maritime channel environments, we conducted tests under three sea conditions: smooth, moderate, and rough. The modulation order was set to 64, and the results were compared with those of the CNN-based method presented in [8], as illustrated in Figure 10. As shown in the figure, the BLER performance of both algorithms reaches saturation at an SNR of 16–18 dB, indicating that the network struggles to effectively capture environmental changes in real-world channel conditions. This is because the publicly available maritime dataset is different from the multipath Rayleigh fading channel used during training; the trained model cannot perfectly generalize to this real and complex propagation environment, thereby resulting in an unremovable error floor. Nevertheless, the proposed algorithm exhibits a significant improvement in BLER performance compared to the CNN-based autoencoder system under smooth sea conditions. As sea conditions deteriorate, the BLER performance of both algorithms declines; however, the proposed joint design method maintains higher accuracy. In other words, the proposed joint design scheme demonstrates its robustness when confronted with the complexities of actual maritime communication environments.

Furthermore, we compare the complexity of algorithms from two perspectives: the number of training parameters and computational complexity. Our proposed joint design method has a total of 135 k training parameters, which is a reduction compared to the 187 k training parameters of the method proposed in [8], while also enhancing model performance. In

Table 2. Complexity comparison of channel estimation methods.

Model	Complexity
LS	$\mathcal{O}\left(NT\right)$
DFT	$\mathcal{O}(N_p{T}_p+NT\log N)$
MMSE	$\mathcal{O}(NT{\left(N_p{T}_p\right)}^2+{\left(N_p{T}_p\right)}^3)$
ChannelNet	$\mathcal{O}\left(2NT(9^2·1·64+1^2·64·32+5^2·32·1+3^2·1·64+18·3^2·{64}^2+3^2·64·1)\right)$
ReEsNet	$\mathcal{O}\left(2N_p{T}_p(32·2·16+8·32·{16}^2+32·{16}^2)+2NT(112·{16}^2+2·32·16)\right)$
Improved FSRCNN	$\mathcal{O}\left(2N_p{T}_p(5·2·32+3·2·4+1·4·1+1·32·16+4·3·16·16+1·16·32)+2NT(2·32·9)\right)$

, we provide a rough comparison of the computational complexities of several channel estimation algorithms. Except for the MMSE algorithm, whose computational complexity increases cubically with the channel dimensions, other channel estimation algorithms, including those based on deep learning, exhibit a linear increase in complexity with respect to channel dimensions. Among the deep learning-based channel estimation methods, our improved FSRCNN algorithm demonstrates the lowest computational complexity while achieving comparable estimation performance.

5. Conclusions

In this paper, we propose a novel autoencoder-based channel estimation method tailored for maritime OFDM systems, addressing the challenges posed by complex and rapidly changing maritime environments. By integrating attention mechanisms and LSTM layers within the autoencoder architecture, our approach effectively captures the temporal dependencies of time-series signals, enhancing the system’s adaptability to dynamic channel conditions. We also introduce an improved FSRCNN that incorporates a residual denoising module, specifically designed to mitigate the adverse effects of additive noise. This dual approach not only facilitates accurate channel estimation but also significantly enhances the operational efficiency of the OFDM system. Simulation results demonstrate that the proposed method outperforms traditional and existing deep learning-based channel estimation methods. Furthermore, the proposed end-to-end joint design method demonstrates superior performance across various modulation orders and under three different sea states.