Optimization of Dynamic Frame Length for Random Access in Machine-Type Communication Systems

Abstract

With the rapid development of the Internet of Things and 5G communication technologies, the demand for the random access of a massive number of user equipment in burst scenarios has significantly increased. Traditional fixed-frame-length mechanisms, due to their inability to dynamically adapt to fluctuations in access traffic, are prone to exacerbating channel resource competition, increasing the probability of preamble collisions, and significantly elevating access delays, thereby constraining the system performance of large-scale machine-type communications. To address these issues, this paper proposes a dynamic frame length optimization algorithm based on Q-learning. By leveraging reinforcement learning algorithms to autonomously perceive access traffic characteristics, this algorithm can dynamically adjust frame length parameters without relying on estimates of the number of user equipment. It optimizes the frame length to improve random access performance, reduces collisions among user equipment competing for preambles, and enhances the utilization ratio of preamble resources.

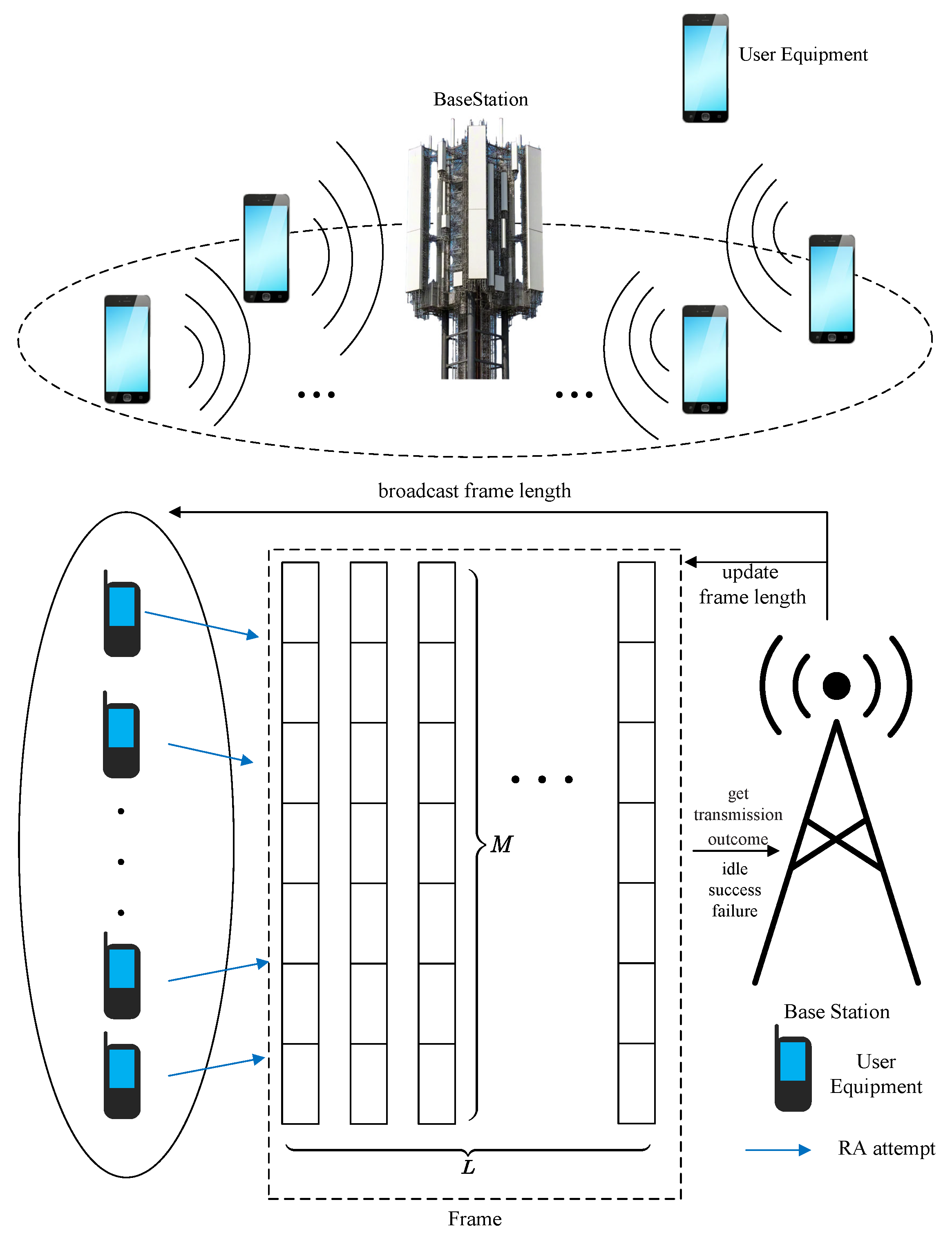
1. Introduction

In the current era of rapid advancements in wireless communication technology, the explosive growth in the number of user equipment (UE) and the continuous emergence of diverse service requirements have posed unprecedented challenges to the performance and efficiency of wireless access networks. The random access process, as the initial and critical step for UEs to establish communication connections with base stations, directly influences the system’s access success ratio, latency, and overall capacity. Traditional random access mechanisms typically employ a fixed frame length design [1]. However, this rigid model has gradually revealed numerous limitations when confronted with dynamically changing network environments and user behaviors.

In communication scenarios, the access behavior of UE exhibits a high degree of randomness and unpredictability. The number of access requests initiated by users can vary significantly across different time periods. Moreover, with the widespread deployment of Internet of Things (IoT) devices, a vast number of low-power, low-rate IoT devices are connecting to the network, further intensifying the dynamic nature and complexity of access requests. The random access mechanism with a fixed frame length fails to adapt resource allocation flexibly in response to these real-time changing access demands. As a result, it leads to issues such as increased access collision probabilities and prolonged access delays under high-load conditions, while also causing resource wastage and reducing the overall efficiency of the system during low-load periods.

To address these challenges, the concept of dynamically updating frame lengths has emerged. By monitoring information such as UE access patterns and service loads in the network, and flexibly adjusting the length of the random access frame based on this dynamic data, the system can better adapt to the ever-changing network environment. The mechanism of dynamically updating frame lengths allows for rational resource allocation according to actual access demands. During high-load periods, it can increase the frame length to provide more access opportunities and reduce collision probabilities; during low-load periods, it can shorten the frame length to minimize resource usage and enhance the overall efficiency of the system. This dynamic adjustment approach not only significantly improves the random access performance of user equipment but also optimizes the utilization of network resources, providing robust support for future wireless communication networks to meet the escalating user demands and service diversity. Therefore, in-depth research into user equipment random access technologies based on dynamically updated frame lengths holds significant theoretical importance and practical application value.

In communication systems, dynamically adjusting frame length to achieve optimal performance is crucial for maximizing throughput. Existing research has explored this problem from various perspectives:

The study in [2] investigates a dynamic frame length selection algorithm for slot access in LTE-Advanced systems. Although it does not employ Q-learning, simulations confirm that the algorithm effectively improves access success rates, reduces access delays, and minimizes preamble retransmissions. Meanwhile, ref. [3] presents a Q-learning-based distributed random access method to optimize the allocation of MTC devices in random access slots. Experimental results demonstrate that this approach converges reliably and maintains strong performance under varying device counts and network loads. This suggests that reinforcement learning can enhance slot allocation even with fixed frame lengths, though dynamically adjusting both frame length and slot numbers may further optimize performance in practical scenarios.

Recent advances integrate machine learning with frame length adaptation. For instance, the research in [4] explores random access control in satellite IoT by combining Q-learning with compressed random access techniques. Here, the frame length is dynamically adjusted based on a support set estimated via compressive sensing reconstruction, ensuring stable high throughput even under heavy traffic. Similarly, a dynamic frame length adjustment (DFLA) algorithm for Wi-Fi backscatter systems is introduced in [5], which outperforms existing Q-learning methods in collision avoidance and throughput efficiency.

Research on RFID systems also provides valuable insights. Dynamic frame length optimization and anti-collision algorithms are analyzed in [6], highlighting that improper frame lengths (either too large or too small) degrade throughput. The research in [7] enhances the dynamic frame-based slotted ALOHA (DFSA) algorithm with an improved tag estimation method, while ref. [8] presents a closed-form solution for optimal frame length in FSA systems, accounting for slot duration and capture probability—critical for dense RFID networks requiring rapid tag identification.

Additional noteworthy contributions in this field include the following: ref. [9] shows an innovative dynamic threshold selection mechanism for wake-up control systems, which shares fundamental principles with adaptive frame length adjustment methodologies. The study in [10] provides a comprehensive analysis of the energy efficiency trade-offs in wireless sensor networks, particularly focusing on the relationship between frame length configuration and frame error rate performance. In ref. [11], researchers developed a closed-form analytical solution for optimizing frame length in FSA systems, with special consideration given to systems with non-uniform slot durations. The study of [12] introduces a novel hybrid approach that combines EPC Global Frame Slotted ALOHA with neural network techniques to significantly enhance RFID tag identification efficiency. Ref. [13] shows a dynamic time-preamble table method based on the estimation of the number of UEs and compares it with the Access Class Barring (ACB) factor method, demonstrating that the proposed method better adapts to dynamic network scenarios. However, the method proposed in this paper does not employ reinforcement learning.

Q-learning has proven instrumental in mitigating communication collisions and enabling dynamic resource allocation in modern networks. Ref. [14] presents a cooperative distributed Q-learning mechanism designed for resource-constrained machine-type communication (MTC) devices. This approach enables devices to identify unique random access (RA) slots for transmission, substantially reducing collision probabilities. The proposed system adopts a frame-based slotted ALOHA scheme, where each frame is partitioned into multiple RA slots.

Further advancing this field, the authors of [15] introduce the FA-QL-RACH scheme, which implements distinct frame structures for Human-to-Human and Machine-to-Machine (M2M) communications. By employing Q-learning to regulate RACH access for M2M devices, the scheme achieves near collision-free performance. Meanwhile, the research in [16] leverages Q-learning combined with Non-Orthogonal Multiple Access technology to optimize random access in IoT-enabled Satellite–Terrestrial Relay Networks. The solution dynamically allocates resources by optimizing both relay selection and available channel utilization. Multi-agent Q-learning also plays a significant role in addressing random access challenges in mMTC networks [17]. By integrating Sparse Code Multiple Access technology with Q-learning, the system’s spectral efficiency and resource utilization can be notably enhanced [18,19]. While these studies do not explicitly address dynamic frame length adaptation, their underlying frameworks establish critical foundations for implementing frame length adjustment strategies. The Q-learning paradigms demonstrated in these works could be extended to incorporate dynamic frame length optimization, potentially yielding further performance enhancements in resource allocation and collision avoidance.

The performance impact of dynamic ACB parameters and dynamic frame length on random access is equivalent, with both approaches experimentally deriving an optimal preamble utilization ratio of $e^{-1}$ [20,21]. Traditional methods for updating random access parameters rely on estimating the number of users [22]. After the base station broadcasts to the UE, the UEs begin competing for preambles. The base station then tallies the number of unselected preambles and those successfully utilized. However, the number of UEs is unknown to the base station. Therefore, it is necessary to first estimate the number of UEs and then update the random access-related parameters, such as the Access Class Barring parameter or frame length, based on this estimated count.

In the method proposed in this paper, we utilize reinforcement learning to adaptively determine the adjustment of frame length, enabling the system to autonomously perceive the characteristics of access traffic. By dynamically adjusting the frame length, this method enhances the utilization efficiency of preamble resources. Under high-load conditions, increasing the frame length allows for full utilization of preamble resources, whereas under low-load conditions, shortening the frame length helps avoid resource wastage. Traditional methods typically require estimating the number of UE first and then updating random access parameters based on these estimates. In contrast, the method proposed in this paper eliminates the need for complex UE number estimation by directly employing a Q-learning algorithm to dynamically adjust the frame length, thereby simplifying system design and implementation.

The structure of this paper is as follows. In Section 1, we introduce the main methods for dynamically updating parameters in the current random access process and highlight the differences between our proposed approach and existing ones. In Section 2, we describe the frame structure utilized in this paper and elaborate on the Q-learning-based dynamic frame length optimization algorithm. In Section 3, we simulate the algorithm and present the performance of the Q-learning-based dynamic frame length optimization algorithm through graphical representations. Finally, in Section 4, we summarize the Q-learning-based dynamic frame length optimization algorithm.

2. System Model and Optimization Method

2.1. System Model

As depicted in Figure 1, a single-cell uplink MTC network system was considered, in which a base station located at the center of a circular coverage area and multiple IoT devices are randomly distributed in its coverage area. The number of user equipment may change dynamically to capture the mobility feature of the MTC network.

We integrated the frame structure into this system model, where N user equipments (UEs) are distributed within a certain area surrounding a base station. The system adopts a slotted Aloha access scheme, enabling each UE to randomly select one slot out of L slots within a frame for transmission. When the preamble resource selected by a UE is not chosen by any other UEs, the access is deemed successful; otherwise, it is considered a failure (collision). Preambles that are not selected by any user equipment remain idle. We assume that the UEs have attained global synchronization and commence listening to the Random Access Channel (RACH) upon receiving the synchronization signal broadcasted. Each UE always has a data packet to transmit in every frame, and no carrier sensing is conducted during the transmission process. At the conclusion of each frame, a feedback bit is transmitted to indicate the corresponding transmission outcomes, specifically the counts of idle, successful, and failed preamble resources [14].

We construct the following frame model: N user equipments (UEs) compete for preamble resources within an $L\times M$ frame (as illustrated in Figure 1). When a preamble resource $(m,l)$ selected by a UE is chosen exclusively by that UE, the access is deemed successful. Conversely, if the preamble resource selected by a UE is chosen by multiple UEs, a collision occurs, resulting in a failed access.

To evaluate the performance of random access, we define a metric: the average successful selected preamble ratio per slot within a frame, denoted as resource utilization ratio U.

$$U={\displaystyle \frac{s}{LM}}\times 100\%,$$

(1)

where s represents the number of preamble resources that are successfully selected, L denotes the number of time slots in a frame, and M signifies the quantity of preambles per slot.

As indicated in ref. [21], when N UEs compete for preambles within an $LM$-sized frame, the mean value of the number of successfully utilized preambles is

$$\hat{s}=LMN\left({\displaystyle \frac{1}{LM}}\right){\left(1-{\displaystyle \frac{1}{LM}}\right)}^{N-1}=N{\left(1-{\displaystyle \frac{1}{LM}}\right)}^{N-1}$$

(2)

Then, the preamble resource utilization ratio U can be approximated as $f={\displaystyle \frac{\widehat{s}}{LM}}={\displaystyle \frac{N}{LM}}{\left(1-{\displaystyle \frac{1}{LM}}\right)}^{N-1}$[21]. By calculating the reciprocal of f with respect to L, we can obtain

$${\displaystyle \frac{\partial U}{\partial L}}\approx {\displaystyle \frac{\partial f}{\partial L}}={\displaystyle \frac{N}{L^3{M}^2}}{\left(1-{\displaystyle \frac{1}{LM}}\right)}^{N-2}\left(N-LM\right)$$

(3)

The root obtained by Formula (3) to zero is $L={\displaystyle \frac{N}{M}}$. However, since frame length L must be an integer, when N UEs compete for preambles within an $LM$-sized frame, the theoretically optimal frame length $L_{opt}$ that maximizes the preamble resource utilization ratio U is determined as follows [21]:

$$L_{opt}=max\left\{1,\mathrm{round}\left({\displaystyle \frac{N}{M}}\right)\right\},$$

(4)

where round() denotes the operation of rounding to the nearest integer.

2.2. Q-Learning-Based Optimization Algorithm of Dynamic Frame Length

Q-learning is grounded in the relationship between an agent and its environment, as represented by the action–value (reward) function. During each time slot, an agent in state $S_i$ executes an action $A_i$ and endeavors to maximize its reward. The updates in the Q-table are defined by the following formula [16]:

$$Q\left(s_t,a_t\right)\leftarrow \left(1-\alpha \right)Q\left(s_t,a_t\right)+\alpha \left(\mathrm{reward}+\gamma \underset{a\in \mathcal{A}}{max}Q\left(s_{t+1},a\right)\right),$$

(5)

where $\alpha$ represents the learning rate, and $\gamma$ denotes the discount factor. The learning rate determines the extent to which an agent absorbs new information when updating its policy or value function, governing the balance between new and old estimates during each update. The discount factor reflects the degree to which an agent values future rewards; as a parameter ranging between 0 and 1, it serves to strike a balance between immediate and long-term rewards [16].

We define the base station as the agent, and its state is defined as

$$\mathcal{S}=\left(L, r, s\right),$$

(6)

where L represents the number of time slots in the current frame during preamble competition, r denotes the quantity of unselected preambles, and s signifies the number of preambles that have been successfully utilized.

An action of an agent is defined as

$$\mathcal{A}=\left(L\right),$$

(7)

where L represents the number of time slots in the frame that the base station needs to update before the next preamble competition begins.

According to ref. [20], the average probability of a preamble being successfully selected without collision is $e^{-1}$. Therefore, we define the base station’s reward as

$$\mathrm{reward}={\displaystyle \frac{s}{LM}}-e^{-1},$$

(8)

where s represents the number of successfully utilized preamble resources, and $LM$ denotes the total number of preamble resources available in the frame.

The Q-table of the base station is initialized with all 0s. In ref. [20], the average probabilities of a preamble being successfully selected without collision and remaining unselected are both $e^{-1}$. We use Algorithm 1 to update the number of time slots L in the frame every episode.

First, we obtain the current state $\mathcal{S}$ of the base station. Subsequently, in lines 3 to 9, we search the base station’s Q-table to find the maximum Q-value that is approximately equivalent to the current state and ensure that this maximum Q-value is greater than 0.

In lines 10 to 11, if such a value exists in the Q-table, we update the frame length for the next preamble contention based on the frame length specified in the action corresponding to that Q-value.

In lines 12 to 22, if such a value does not exist in the Q-table, we update the frame length for the next preamble contention according to the ratio of currently unselected and successfully selected preamble resources. If the ratio of unselected preambles is high, it indicates that the frame length is too large and needs to be reduced. Conversely, if the ratio of unselected and successfully selected preambles is low, it indicates that the frame length is too small and needs to be increased. For other scenarios, the frame length is randomly updated by choosing among increasing, decreasing, or keeping it unchanged, while ensuring that the updated frame length is a positive integer. After updating the frame length, we update the Q-table according to Formula (5).

Algorithm 1 A Dynamic Frame Length Optimization Algorithm Based on Q-Learning

1: Input: The current state of the base station ${\mathcal{S}}_t=\left(L_t, r_t, s_t\right)$ and Q-table 2: Output: Updated frame length L and Q-table 3: $\mathit{max\_Q\_value}\leftarrow -\infty$ 4: while Search the Q-table do 5:       Observe $Q(\mathcal{S},\mathcal{A})$, where $\mathcal{S}=\left(L, r, s\right)$, $\mathcal{A}=\left(L\right)$ 6:       if $r_t\in \left[0.9r,1.1r\right]$ and $s_t\in \left[0.9s,1.1s\right]$ and $Q(\mathcal{S},\mathcal{A})>0$ then 7:             if $Q(\mathcal{S},\mathcal{A})>\mathit{max\_Q\_value}$ then 8:                    $\mathit{max\_Q\_value}\leftarrow Q(\mathcal{S},\mathcal{A})$ 9:             end if 10:     end if 11: end while 12: if  $\mathit{max\_Q\_value}\ne -\infty$  then 13:       $L\leftarrow L_{max}$ where $L_{max}\in {\mathcal{A}}_{max}=\left(L_{max}\right)$ and $\mathit{max\_Q\_value}=Q({\mathcal{S}}_{max},{\mathcal{A}}_{max})$ 14: else 15:      if ${\displaystyle \frac{r}{LM}}>e^{-1}$ then 16:           $L\leftarrow max\left\{1,L-1\right\}$ 17:     else 18:           if ${\displaystyle \frac{r}{LM}}+{\displaystyle \frac{s}{LM}}<2e^{-1}$ then 19:                  $L\leftarrow max\left\{1,L+1\right\}$ 20:           else 21:                  L is randomly selected from $\left\{L-1, L, L+1\right\}$, ensuring that $L\ge 1$ 22:            end if 23:     end if 24: end if 25: Update the Q table according to Formula (5)

3. Results and Discussion

By leveraging Q-learning, we can effectively and dynamically adjust the number of time slots in a frame. According to ref. [21], we ascertain that the optimal number of time slots in a frame, denoted as $L_{opt}$, is given by $L_{opt}=max\left\{1,\mathrm{round}\left({\displaystyle \frac{N}{M}}\right)\right\}$, where the round() function represents rounding to the nearest integer, N signifies the number of UEs, and M denotes the number of preambles per time slot.

In this simulation, we set the initial number of time slots in a frame to 10. The relevant parameters are shown in

Table 1. Parameter table (the number of UEs remains unchanged).

Meaning	Symbol	Value
Number of UEs	N	100
Number of preambles	M	32
Initial number of time slots	$L_{init}$	10
Learning rate	$\alpha$	$0.1$
Discount factor	$\gamma$	$0.9$

. Based on Formula (4), we can readily calculate the theoretical optimal number of time slots $L_{opt}=3$ when the number of UEs $N=100$ and number of preambles $M=32$.

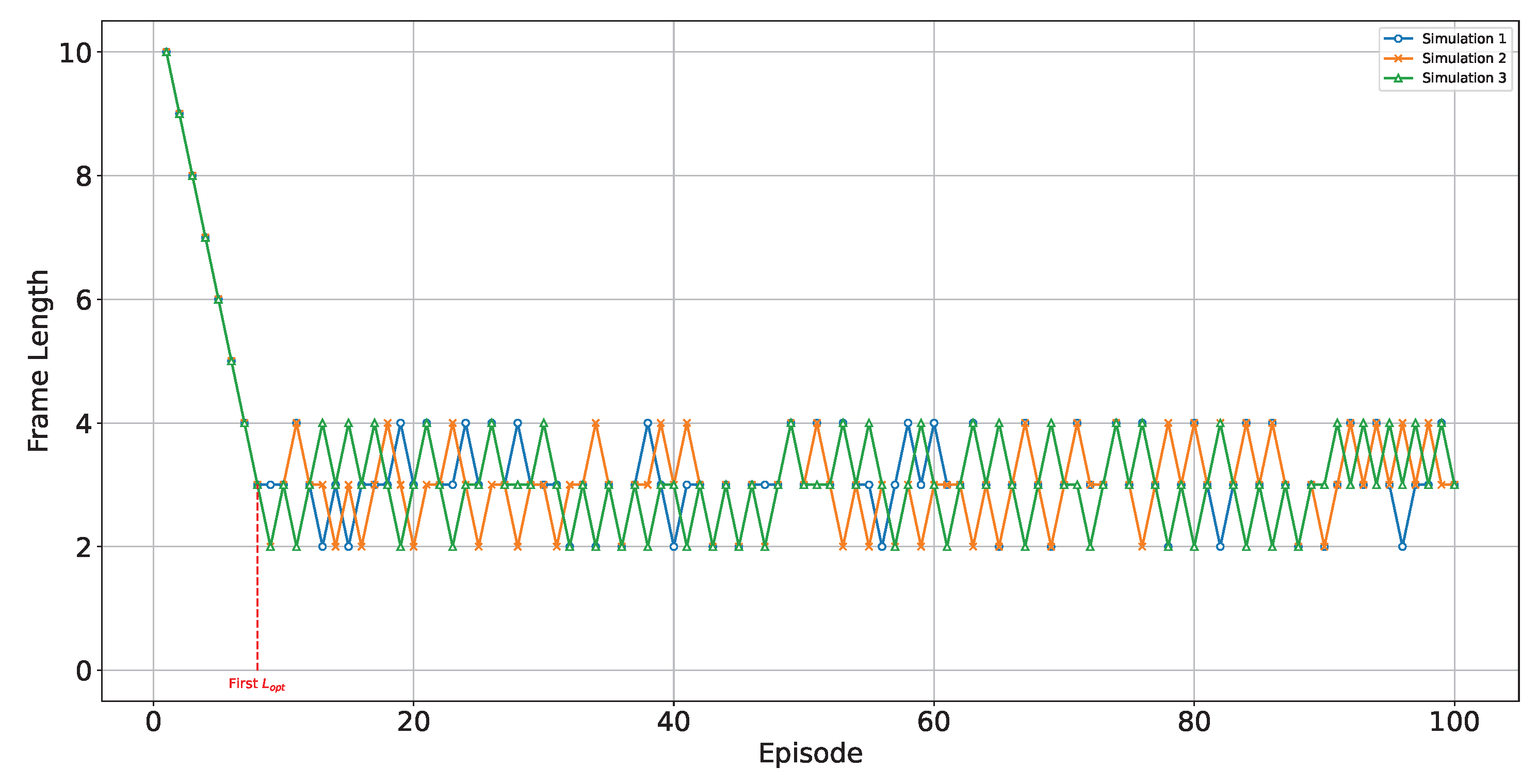
We employ Algorithm 1 to update the number of time slots in a frame, and the variation in the number of time slots, denoted as L, is illustrated in Figure 2.

As can be seen from Figure 2, we recorded the changes in frame length across three simulation runs. After several rounds of updates, the number of time slots in a frame rapidly converges to the optimal value, and subsequently fluctuates around this optimal value. This indicates that the time slot quantity updating method incorporating Q-learning can swiftly and dynamically adjust the number of time slots in a frame to the optimal level.

Next, we delve into examining how many rounds it takes for the Q-learning-based dynamic frame length update algorithm to reach the optimal frame length, given varying numbers of users. For this exploration, we set the initial number of time slots to 1. The relevant parameters are shown in

Table 2. Parameter table (the number of UEs increases).

Meaning	Symbol	Value
Number of UEs	M	32
Initial number of time slots	$L_{init}$	1
Learning rate	$\alpha$	$0.1$
Discount factor	$\gamma$	$0.9$

.

We set different numbers of users and conducted simulations over 100 rounds to verify whether this method can adjust the frame length to the optimal value under varying numbers of user devices. After the simulations, we recorded the corresponding theoretical optimal frame lengths $L_{opt}$ as well as the average frame lengths L achieved by Algorithm 1 over the final 10 rounds in

Table 3. Table of comparison of theoretical optimal frame lengths and average frame lengths under different numbers of UEs.

Number of UEs	${\mathit{L}}_{\mathit{opt}}$	L
100	3	$3.0$
300	9	$8.9$
500	16	$15.7$
1000	31	$31.2$

.

It is evident from the data presented in Table 3 that regardless of the disparity between the initial frame length and the theoretically optimal frame length, the Q-learning-based dynamic frame length optimization algorithm is capable of updating the frame length to a value close to the theoretically optimal one.

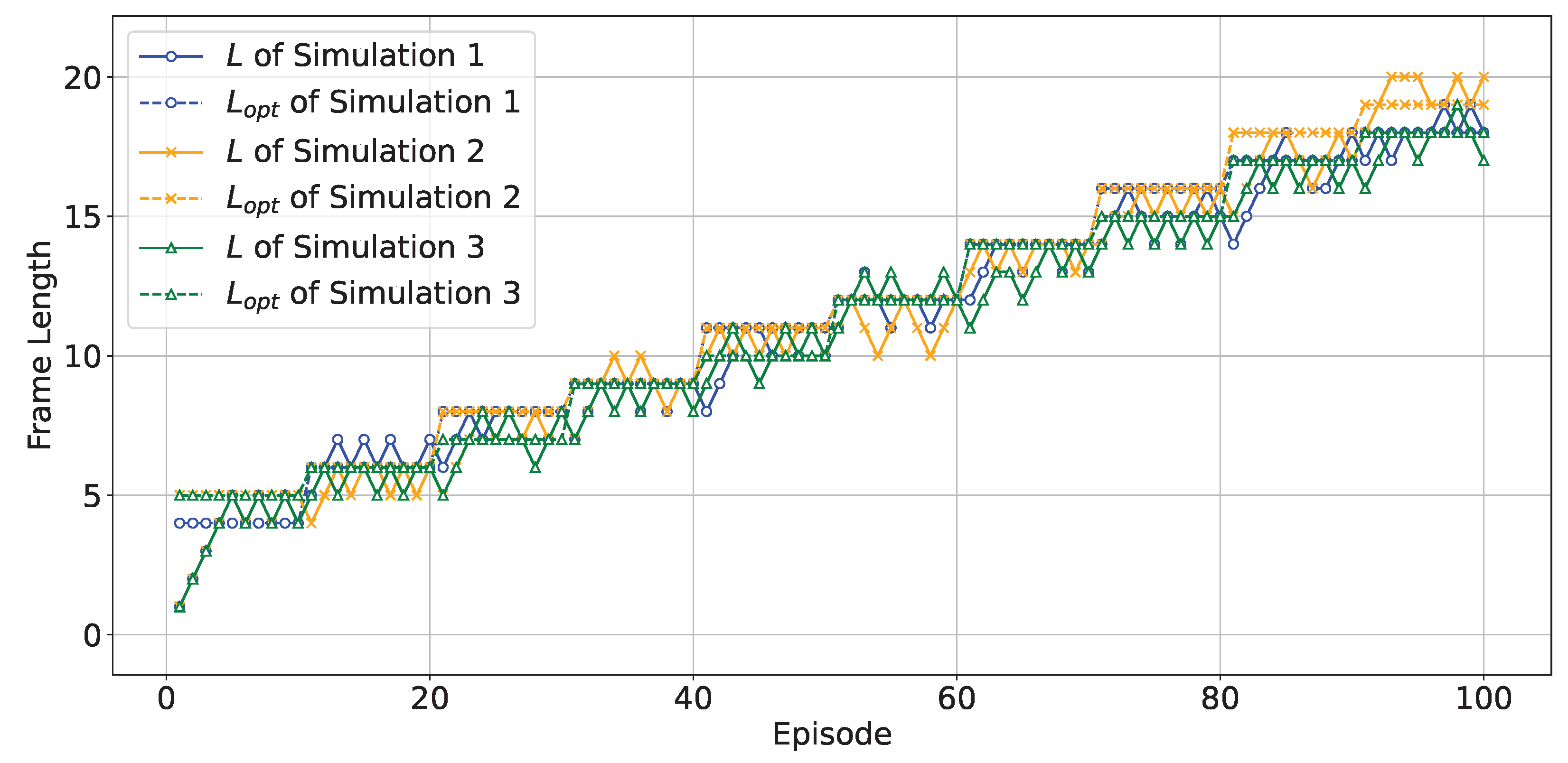
In practical scenarios of random access, the number of UEs is not constant but dynamically changing. To investigate whether the Q-learning-based dynamic frame length optimization algorithm can effectively adapt to such fluctuating numbers of UEs, we introduce the random addition of a certain number of UEs every 10 rounds. The number of newly added UEs follows a Poisson distribution.

$$P\left(X=k\right)=e^{-\lambda }{\displaystyle \frac{{\lambda }^k}{k!}}\left(k=0, 1, 2, \dots \right)$$

(9)

We set $\lambda =50$, meaning that a certain number of UEs are added randomly every 10 rounds, with the number of newly added UEs following a Poisson distribution with a parameter of 50. Under such circumstances, after utilizing the Q-learning-based dynamic frame length optimization algorithm, the variations in the actual frame length and the theoretically optimal frame length are depicted in Figure 3.

As shown in Figure 3, we recorded the changes in both the actual and theoretically optimal frame lengths across three simulation runs. As the number of user equipment (UE) increases, the theoretically optimal frame length also rises continuously. Meanwhile, under the influence of the Q-learning-based dynamic frame length optimization algorithm, the actual frame length keeps increasing and fluctuates around the theoretical optimal frame length. This indicates that even when the number of user equipment changes dynamically, the Q-learning-based dynamic frame length optimization algorithm can still ensure that the frame length is updated to the theoretical optimal value. We can observe little lag or overshoot in the figure. A relatively high learning rate may accelerate parameter updates, but if the step size is excessively large, it can cause the system to oscillate near the optimal solution, manifesting as delays in decision making or state adjustments. Additionally, it may result in overly aggressive single-update steps that surpass the optimal value, necessitating subsequent reverse adjustments to correct, thereby inducing fluctuations.

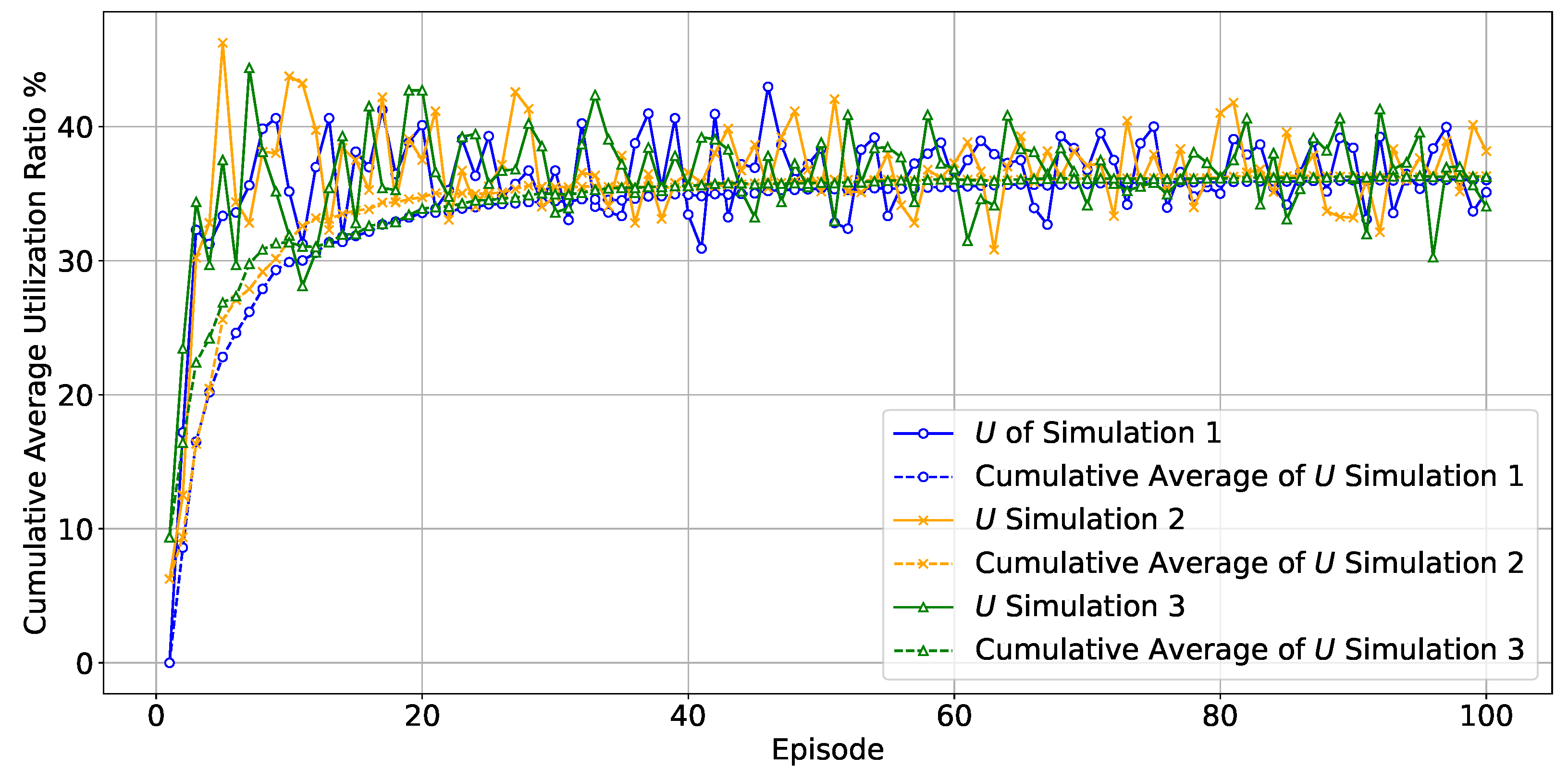
Meanwhile, the resource utilization ratio U of preamble resources, along with its cumulative average utilization ratio, is depicted in Figure 4.

As can be observed from Figure 4, we recorded the preamble resource utilization data from three simulation runs, along with their corresponding cumulative average resource utilization rates. Even with a continuous increase in the number of UEs, under the Q-learning-based dynamic frame length optimization algorithm, the preamble resource utilization ratio gradually stabilizes, and the cumulative average utilization ratio also converges to $e^{-1}$. From the figure, it can be observed that during the initial stage of the algorithm, due to the uncertainty of initial conditions, there are significant fluctuations in resource utilization and its cumulative average, reflecting the trade-off between exploration and exploitation. As iterations increase, the algorithm learns better strategies, leading to a reduction in fluctuations and the system approaching stability. The learning rate determines the step size for updating values in the Q-table; a larger learning rate accelerates convergence but may cause oscillations or miss the optimal solution, reducing stability, while a smaller learning rate results in slower convergence but greater precision, enhancing stability. A large learning rate speeds up convergence initially but may lead to getting stuck in local optima later on; a small learning rate ensures precision but has a prolonged convergence process. The discount factor reflects the algorithm’s emphasis on future rewards; a high discount factor enhances long-term stability but may be overly conservative, overlooking short-term opportunities, whereas a low discount factor focuses on immediate rewards, offering better short-term adaptability but potentially compromising long-term stability. A high discount factor slows down initial convergence as it requires more time to evaluate long-term rewards, but once the long-term optimal strategy is found, convergence can accelerate, with subsequent decisions becoming more stable and consistent. Conversely, a low discount factor may lead to faster short-term convergence, but the solution may be suboptimal, resulting in unstable long-term performance.

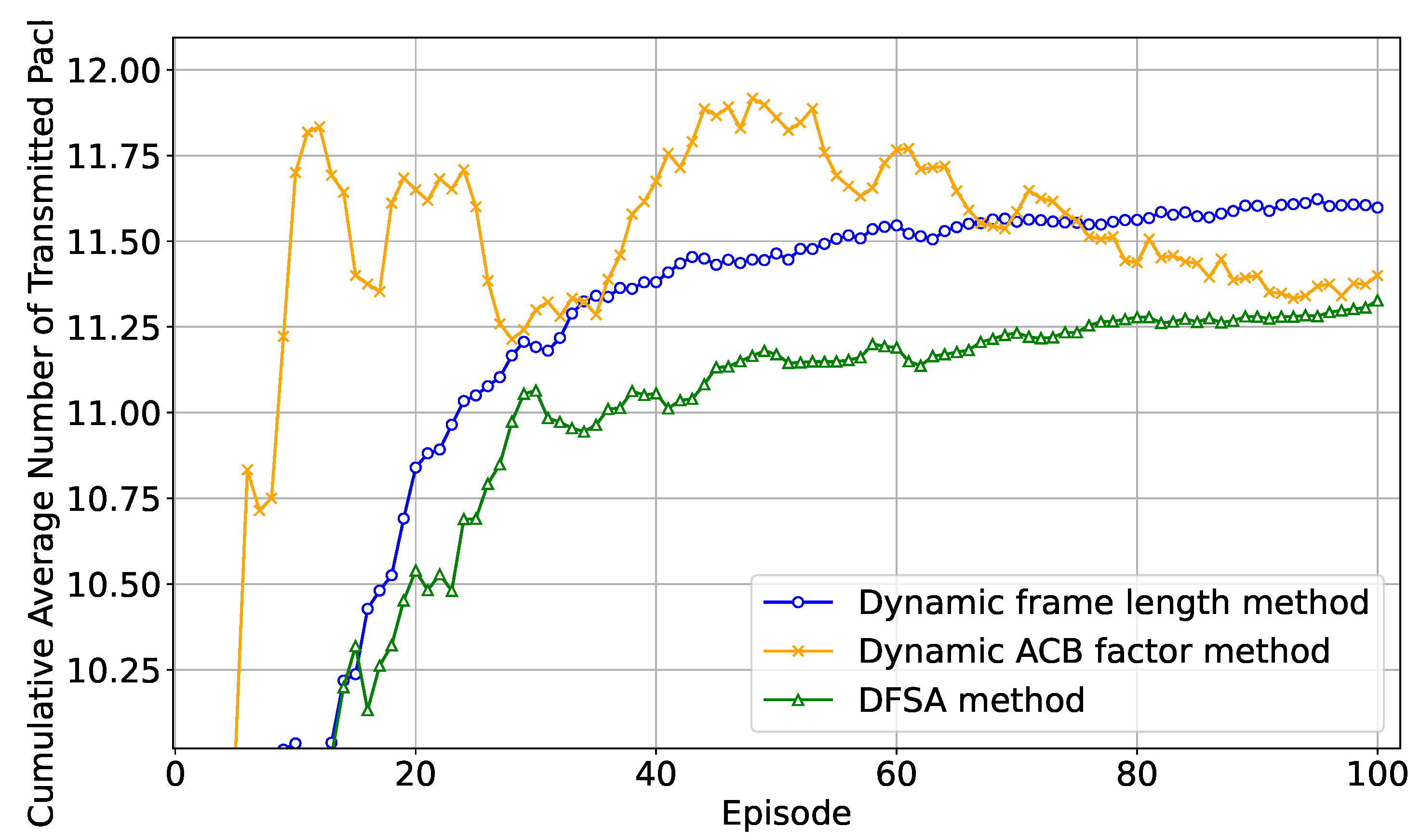
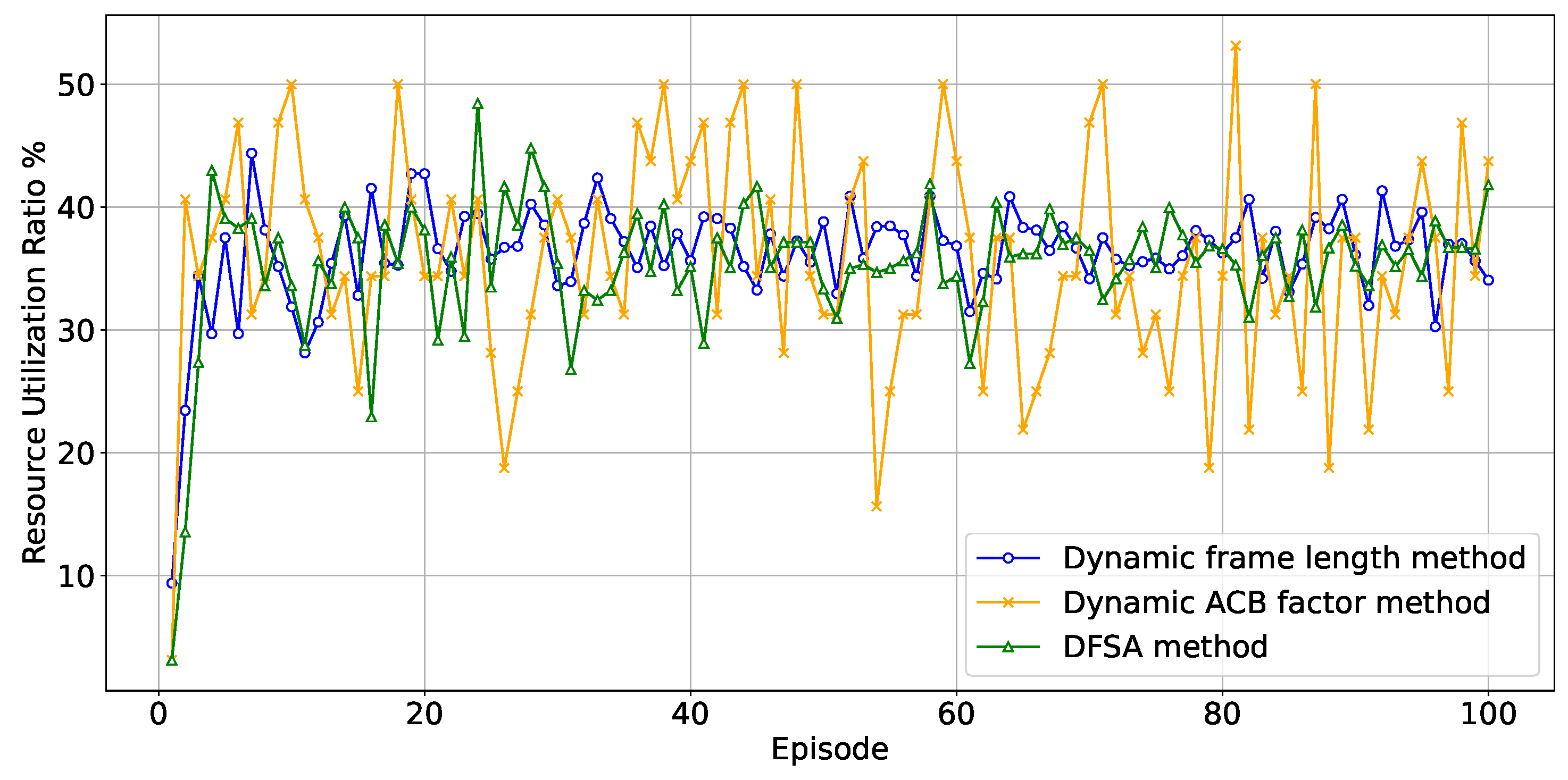
Under the same scenario of an increase in the number of UEs as described above, we compared the successful selected preamble ratio between the dynamic frame length optimization method based on Q-learning and the dynamic ACB factor method and DFSA (Dynamic Frame Slotted ALOHA) method based on probability model estimation. Comparisons of cumulative average throughput and the cumulative resource utilization ratio are presented in Figure 5 and Figure 6.

Analyzing the data presented in the figures above, we observe that the cumulative average throughput of the dynamic frame length optimization method based on Q-learning slightly surpasses that of the dynamic ACB factor method and DFSA method. After multiple rounds of simulation comparisons, we selected a set of representative figures. We calculated that the standard deviation of the dynamic frame length method is $0.0422$, while that of the dynamic ACB factor method is $0.0888$ and that of the DFSA method is $0.0549$. The standard deviation of the dynamic frame length method is only half of that of the dynamic ACB factor method and close to that of the DFSA method, indicating that the dynamic frame length method exhibits greater stability. When compared to the dynamic ACB factor method, which relies on a probability model for estimating the number of user equipment, the dynamic frame length method ensures a more consistent success ratio for the random access of user equipment. The core reason lies in Q-learning’s inherent adaptive decision-making capability. By continuously monitoring the occupancy status of preambles in the current frame, Q-learning dynamically adjusts the length of the subsequent frame. In contrast, the ACB method and DFSA method necessitate an initial estimation of the current number of users, followed by the calculation of the blocking probability based on this estimate. However, real-time estimation of the user count is susceptible to errors, resulting in a delay in ACB factor updates relative to actual load variations and consequently causing fluctuations in resource utilization.

4. Conclusions and Future Work

In this study, we proposed a dynamic frame length optimization method based on Q-learning, which aims to address the issues of channel resource competition and preamble collisions during the random access process in MTC systems. By leveraging reinforcement learning algorithms to autonomously perceive access traffic characteristics and dynamically adjust frame length parameters, this method has abandoned traditional approaches such as Access Class Barring, which employs maximum likelihood estimation algorithms to estimate the number of UEs. Instead, it utilizes Q-learning to directly update and adjust the frame length. We successfully achieved frame length optimization without relying on estimates of the number of UEs, significantly enhancing random access performance and preamble resource utilization. With the rapid development of IoT and 5G technologies, the random access problem in MTC systems has become increasingly prominent. The dynamic frame length optimization method proposed in this study effectively alleviated access congestion, improved system capacity, enhanced user experience, and has great potential for future applications in the field of communications.

As future work, we will focus on the performance of this dynamic frame length optimization method in complex scenarios such as asynchronous arrivals and delayed feedback. In doing so, through the systematic exploration and analysis of these complex scenarios, we aim to comprehensively uncover their underlying patterns and potential impacts. Subsequently, we will meticulously refine the existing research findings. In this way, we can effectively enhance the practicality and universality of the method, enabling it to exert a positive influence in a broader range of fields and real-world scenarios.