High-Density Neuromorphic Inference Platform (HDNIP) with 10 Million Neurons
Abstract
1. Introduction
2. HDNIP’s Architecture
2.1. Overall Organization and Design Philosophy
2.2. High-Density-Oriented Versatile Core Design
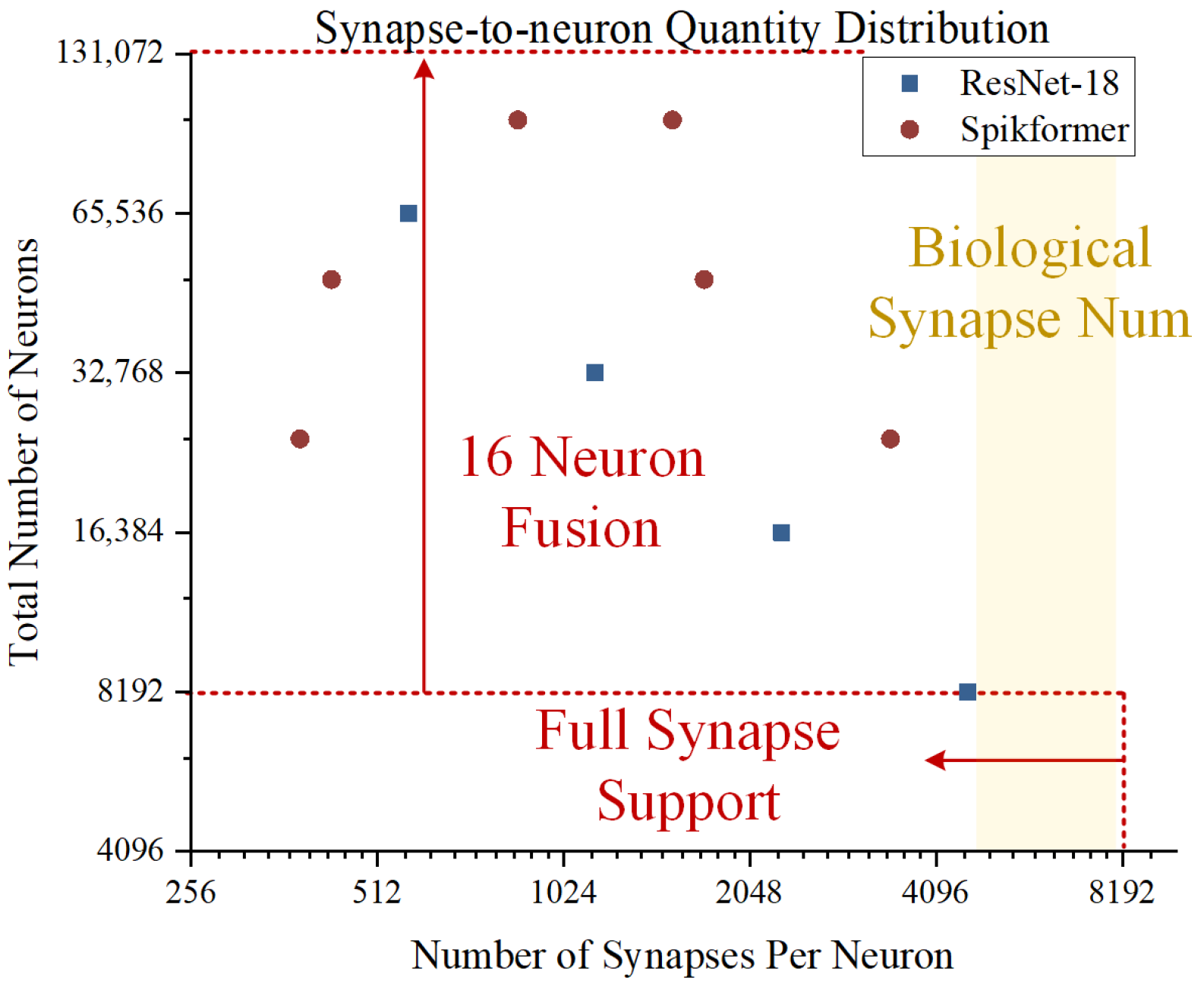
2.2.1. Compact Core Design
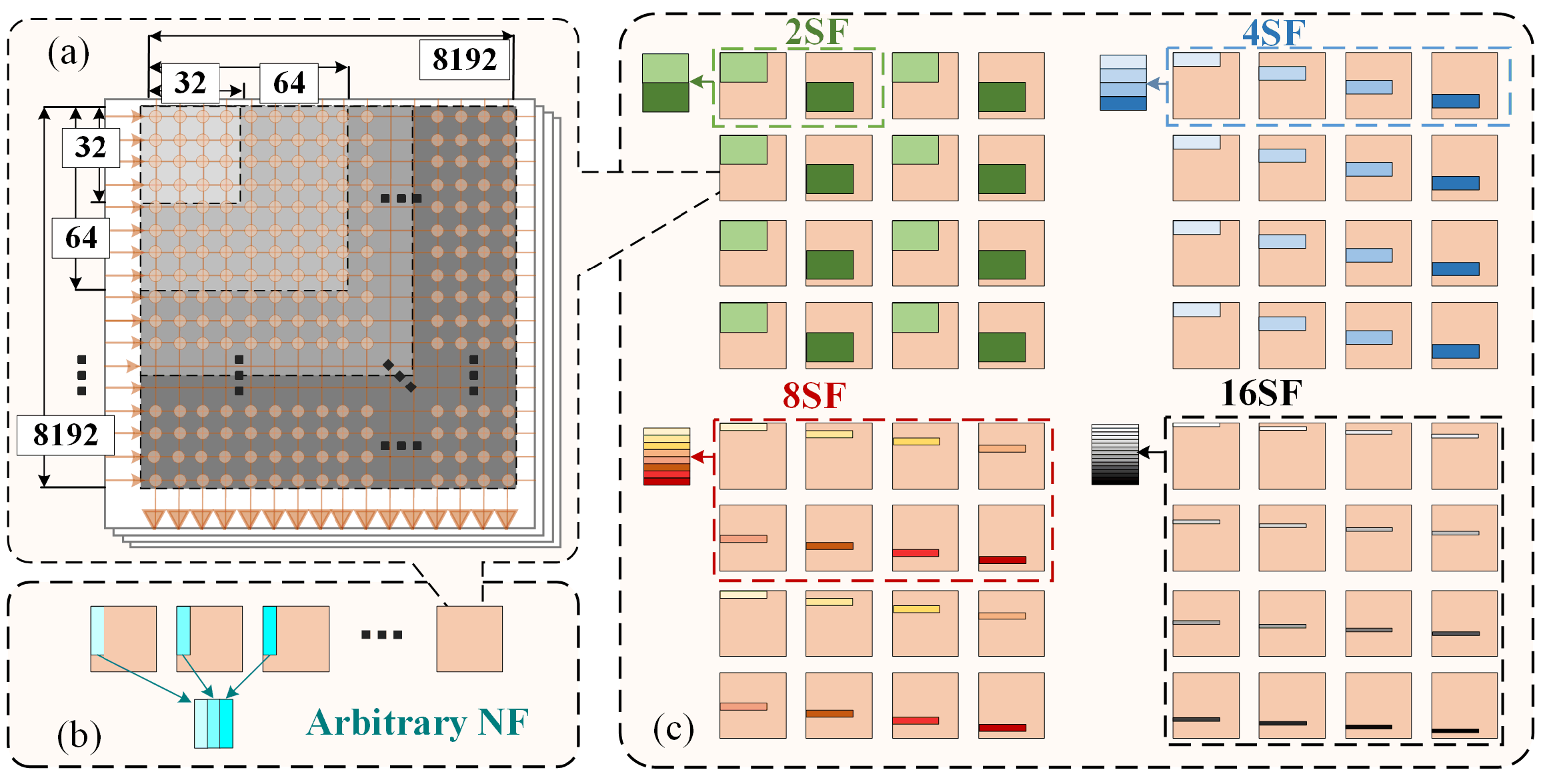
2.2.2. Adaptive Time-Division Multiplexing
2.2.3. Shared Core Fusion
2.3. Bandwidth Optimization Strategy
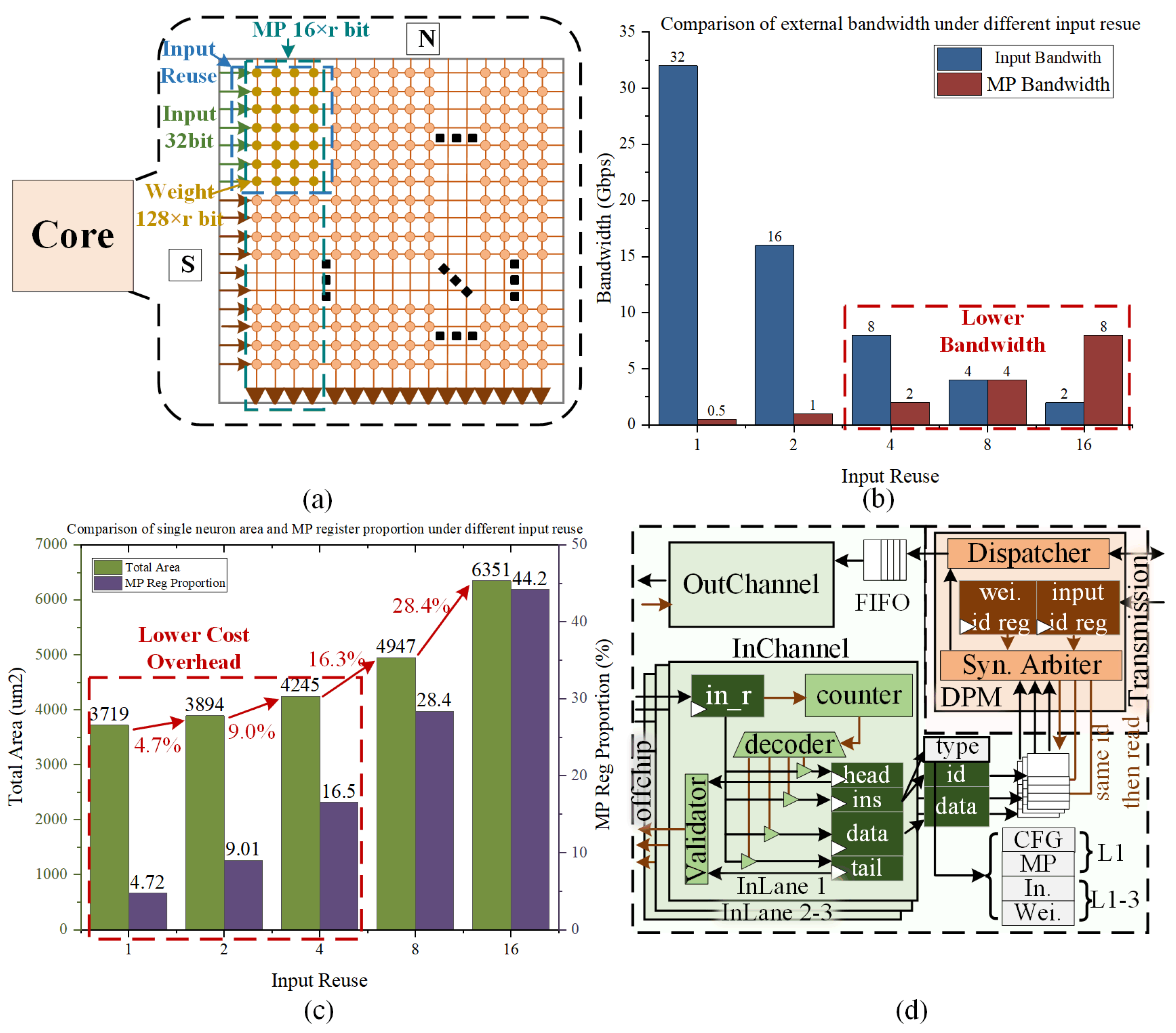
2.3.1. General Compact-Weight Near-Memory Computing
2.3.2. Input Reuse
2.3.3. Multi-Lane Interface
3. Experiments and Results
3.1. Deployment of the Emulation System
3.2. Emulation Deployment of Neural Network Architectures
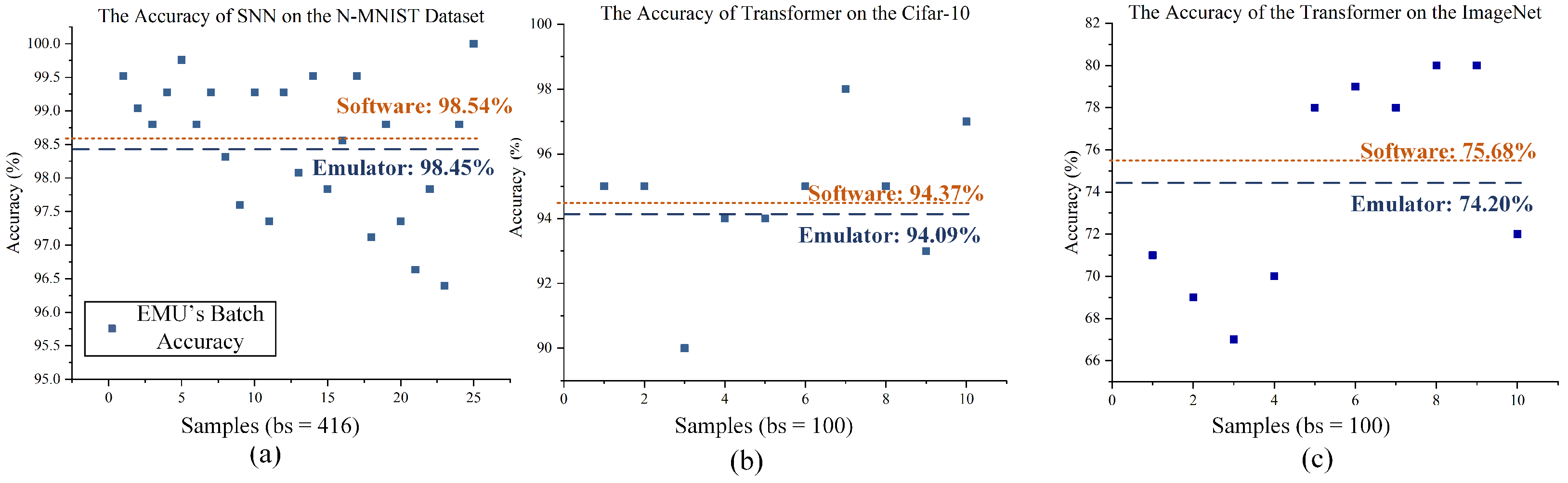
3.2.1. N-MNIST
3.2.2. CIFAR-10
3.2.3. ImageNet
3.3. Results and Measurements
3.3.1. Chip Synthesies
3.3.2. NMC and Off-Chip Computing Measurements
3.3.3. Core Fusion Measurements
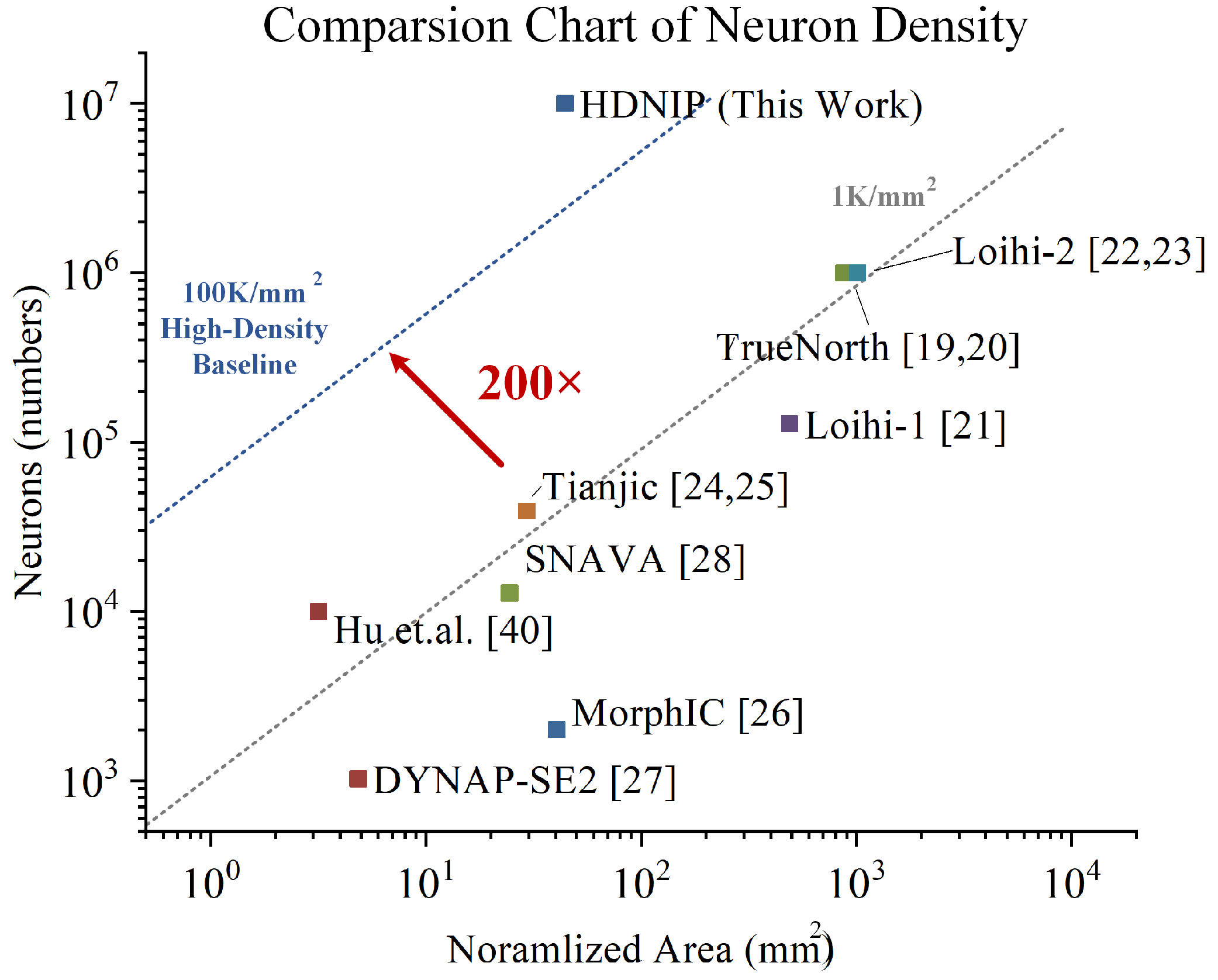
3.4. Comparison
3.4.1. Comparison with Conventional GPU
3.4.2. Comparison with Other Neuromorphic Works
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehonic, A.; Kenyon, A.J. Brain-inspired computing needs a master plan. Nature 2022, 604, 255–260. [Google Scholar] [CrossRef]
- Li, G.; Deng, L.; Tang, H.; Pan, G.; Tian, Y.; Roy, K.; Maass, W. Brain-Inspired Computing: A Systematic Survey and Future Trends. Proc. IEEE 2024, 112, 544–584. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, S.; Ji, X.; Liu, X.; Cong, Y.; Shi, L. The development of general-purpose brain-inspired computing. Nat. Electron. 2024, 7, 954–965. [Google Scholar] [CrossRef]
- Shrestha, A.; Fang, H.; Mei, Z.; Rider, D.P.; Wu, Q.; Qiu, Q. A survey on neuromorphic computing: Models and hardware. IEEE Circuits Syst. Mag. 2022, 22, 6–35. [Google Scholar] [CrossRef]
- Furber, S. Large-scale neuromorphic computing systems. J. Neural Eng. 2016, 13, 051001. [Google Scholar] [CrossRef]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 2017 ACM/IEEE 44th Annual International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Tirumala, A.; Wong, R. Nvidia blackwell platform: Advancing generative ai and accelerated computing. In Proceedings of the 2024 IEEE Hot Chips 36 Symposium (HCS), Stanford, CA, USA, 25–27 August 2024; pp. 1–33. [Google Scholar]
- Rathi, N.; Chakraborty, I.; Kosta, A.; Sengupta, A.; Ankit, A.; Panda, P.; Roy, K. Exploring neuromorphic computing based on spiking neural networks: Algorithms to hardware. ACM Comput. Surv. 2023, 55, 1–49. [Google Scholar] [CrossRef]
- Basu, A.; Deng, L.; Frenkel, C.; Zhang, X. Spiking Neural Network Integrated Circuits: A Review of Trends and Future Directions. In Proceedings of the 2022 IEEE Custom Integrated Circuits Conference (CICC), Newport Beach, CA, USA, 24–27 April 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Kuang, Y.; Cui, X.; Wang, Z.; Zou, C.; Zhong, Y.; Liu, K.; Dai, Z.; Yu, D.; Wang, Y.; Huang, R. ESSA: Design of a Programmable Efficient Sparse Spiking Neural Network Accelerator. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1631–1641. [Google Scholar] [CrossRef]
- Tan, P.Y.; Wu, C.W. A 40-nm 1.89-pJ/SOP Scalable Convolutional Spiking Neural Network Learning Core With On-Chip Spatiotemporal Back-Propagation. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2023, 31, 1994–2007. [Google Scholar] [CrossRef]
- Xie, C.; Shao, Z.; Chen, Z.; Du, Y.; Du, L. An Energy-Efficient Spiking Neural Network Accelerator Based on Spatio-Temporal Redundancy Reduction. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2024, 32, 782–786. [Google Scholar] [CrossRef]
- Cadwell, C.R.; Bhaduri, A.; Mostajo-Radji, M.A.; Keefe, M.G.; Nowakowski, T.J. Development and arealization of the cerebral cortex. Neuron 2019, 103, 980–1004. [Google Scholar] [CrossRef]
- Ballard, D.H. Cortical connections and parallel processing: Structure and function. Behav. Brain Sci. 1986, 9, 67–90. [Google Scholar] [CrossRef]
- Mosier, K.; Bereznaya, I. Parallel cortical networks for volitional control of swallowing in humans. Exp. Brain Res. 2001, 140, 280–289. [Google Scholar] [CrossRef] [PubMed]
- Herculano-Houzel, S. The human brain in numbers: A linearly scaled-up primate brain. Front. Hum. Neurosci. 2009, 3, 31. [Google Scholar] [CrossRef] [PubMed]
- Azevedo, F.A.; Carvalho, L.R.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.; Leite, R.E.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef]
- Pakkenberg, B.; Gundersen, H.J.G. Neocortical neuron number in humans: Effect of sex and age. J. Comp. Neurol. 1997, 384, 312–320. [Google Scholar] [CrossRef]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J. Truenorth: Design and tool flow of a 65 mw 1 million neuron programmable neurosynaptic chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S. Loihi: A neuromorphic manycore processor with on-chip learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Orchard, G.; Frady, E.P.; Rubin, D.B.D.; Sanborn, S.; Shrestha, S.B.; Sommer, F.T.; Davies, M. Efficient neuromorphic signal processing with loihi 2. In Proceedings of the 2021 IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, 20–22 October 2021; pp. 254–259. [Google Scholar]
- Davies, M. Taking neuromorphic computing to the next level with Loihi2. Intel Labs’ Loihi 2021, 2, 1–7. [Google Scholar]
- Pei, J.; Deng, L.; Song, S.; Zhao, M.; Zhang, Y.; Wu, S.; Wang, G.; Zou, Z.; Wu, Z.; He, W. Towards artificial general intelligence with hybrid Tianjic chip architecture. Nature 2019, 572, 106–111. [Google Scholar] [CrossRef]
- Deng, L.; Wang, G.; Li, G.; Li, S.; Liang, L.; Zhu, M.; Wu, Y.; Yang, Z.; Zou, Z.; Pei, J. Tianjic: A unified and scalable chip bridging spike-based and continuous neural computation. IEEE J. -Solid-State Circuits 2020, 55, 2228–2246. [Google Scholar] [CrossRef]
- Frenkel, C.; Legat, J.D.; Bol, D. MorphIC: A 65-nm 738k-Synapse/mm2 Quad-Core Binary-Weight Digital Neuromorphic Processor With Stochastic Spike-Driven Online Learning. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 999–1010. [Google Scholar] [CrossRef]
- Richter, O.; Wu, C.; Whatley, A.M.; Köstinger, G.; Nielsen, C.; Qiao, N.; Indiveri, G. DYNAP-SE2: A scalable multi-core dynamic neuromorphic asynchronous spiking neural network processor. Neuromorphic Comput. Eng. 2024, 4, 014003. [Google Scholar] [CrossRef]
- Sripad, A.; Sanchez, G.; Zapata, M.; Pirrone, V.; Dorta, T.; Cambria, S.; Marti, A.; Krishnamourthy, K.; Madrenas, J. SNAVA—A real-time multi-FPGA multi-model spiking neural network simulation architecture. Neural Netw. 2018, 97, 28–45. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Yu, L.; Zhou, Z.; Ma, Z.; Zhang, H.; Zhou, H.; Tian, Y. Spikingformer: Spike-driven residual learning for transformer-based spiking neural network. arXiv 2023, arXiv:2304.11954. [Google Scholar]
- Zhu, R.J.; Zhao, Q.; Li, G.; Eshraghian, J.K. Spikegpt: Generative pre-trained language model with spiking neural networks. arXiv 2023, arXiv:2302.13939. [Google Scholar]
- Harbour, S.; Sears, B.; Schlager, S.; Kinnison, M.; Sublette, J.; Henderson, A. Real-time vision-based control of swap-constrained flight system with intel loihi 2. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–6. [Google Scholar]
- Perryman, N.; Wilson, C.; George, A. Evaluation of xilinx versal architecture for next-gen edge computing in space. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–11. [Google Scholar]
- Shamwell, E.J.; Nothwang, W.D.; Perlis, D. A deep neural network approach to fusing vision and heteroscedastic motion estimates for low-SWaP robotic applications. In Proceedings of the 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Daegu, Republic of Korea, 16–18 November 2017; pp. 56–63. [Google Scholar]
- Neuman, S.M.; Plancher, B.; Duisterhof, B.P.; Krishnan, S.; Banbury, C.; Mazumder, M.; Prakash, S.; Jabbour, J.; Faust, A.; de Croon, G.C.; et al. Tiny robot learning: Challenges and directions for machine learning in resource-constrained robots. In Proceedings of the 2022 IEEE 4th International Conference on Artificial Intelligence Circuits and Systems (AICAS), Incheon, Republic of Korea, 13–15 June 2022; pp. 296–299. [Google Scholar]
- Kudithipudi, D.; Schuman, C.; Vineyard, C.M.; Pandit, T.; Merkel, C.; Kubendran, R.; Aimone, J.B.; Orchard, G.; Mayr, C.; Benosman, R. Neuromorphic computing at scale. Nature 2025, 637, 801–812. [Google Scholar] [CrossRef]
- Chicca, E.; Stefanini, F.; Bartolozzi, C.; Indiveri, G. Neuromorphic Electronic Circuits for Building Autonomous Cognitive Systems. Proc. IEEE 2014, 102, 1367–1388. [Google Scholar] [CrossRef]
- Wu, S.Y.; Lin, C.; Chiang, M.; Liaw, J.; Cheng, J.; Yang, S.; Tsai, C.; Chen, P.; Miyashita, T.; Chang, C.; et al. A 7nm CMOS platform technology featuring 4 th generation FinFET transistors with a 0.027 μm 2 high density 6-T SRAM cell for mobile SoC applications. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 2–6. [Google Scholar]
- Yeap, G.; Lin, S.; Chen, Y.; Shang, H.; Wang, P.; Lin, H.; Peng, Y.; Sheu, J.; Wang, M.; Chen, X.; et al. 5nm cmos production technology platform featuring full-fledged euv, and high mobility channel finfets with densest 0.021 μm 2 sram cells for mobile soc and high performance computing applications. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 36–37. [Google Scholar]
- Wu, S.Y.; Chang, C.H.; Chiang, M.; Lin, C.; Liaw, J.; Cheng, J.; Yeh, J.; Chen, H.; Chang, S.; Lai, K.; et al. A 3nm CMOS FinFlex™ platform technology with enhanced power efficiency and performance for mobile SoC and high performance computing applications. In Proceedings of the 2022 International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2022; pp. 27.5.1–27.5.4. [Google Scholar]
- Hu, S.; Qiao, G.; Liu, X.; Liu, Y.; Zhang, C.; Zuo, Y.; Zhou, P.; Liu, Y.; Ning, N.; Yu, Q. A Co-Designed Neuromorphic Chip With Compact (17.9 KF 2) and Weak Neuron Number-Dependent Neuron/Synapse Modules. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 1250–1260. [Google Scholar] [CrossRef]
- Zuo, Y.; Ning, N.; Cao, K.; Zhang, R.; Wang, S.; Meng, L.; Qiao, G.; Liu, Y.; Hu, S. Design of a Highly Flexible Hybrid Neural Network Inference Platform with 10 Million Neurons. In Proceedings of the 2024 IEEE Biomedical Circuits and Systems Conference (BioCAS), Xi’an, China, 24–26 October 2024; pp. 1–5. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Tang, Y.; Nyengaard, J.R.; De Groot, D.M.G.; Gundersen, H.J.G. Total regional and global number of synapses in the human brain neocortex. Synapse 2001, 41, 258–273. [Google Scholar] [CrossRef]
- Wang, Z.; Song, Y.; Zhang, G.; Luo, Q.; Xu, K.; Gao, D.; Yu, B.; Loke, D.; Zhong, S.; Zhang, Y. Advances of embedded resistive random access memory in industrial manufacturing and its potential applications. Int. J. Extrem. Manuf. 2024, 6, 032006. [Google Scholar] [CrossRef]
- Chen, A. A review of emerging non-volatile memory (NVM) technologies and applications. Solid-State Electron. 2016, 125, 25–38. [Google Scholar] [CrossRef]
- Kargar, S.; Nawab, F. Challenges and future directions for energy, latency, and lifetime improvements in NVMs. Distrib. Parallel Databases 2023, 41, 163–189. [Google Scholar] [CrossRef]
- Strenz, R. Review and outlook on embedded NVM technologies–from evolution to revolution. In Proceedings of the 2020 IEEE International Memory Workshop (IMW), Dresden, Germany, 17–20 May 2020; pp. 1–4. [Google Scholar]
- Kim, S.; Yoo, H.J. An Overview of Computing-in-Memory Circuits with DRAM and NVM. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 1626–1631. [Google Scholar] [CrossRef]
- Liu, S.; Yi, Y. Unleashing Energy-Efficiency: Neural Architecture Search without Training for Spiking Neural Networks on Loihi Chip. In Proceedings of the 2024 25th International Symposium on Quality Electronic Design (ISQED), San Francisco, CA, USA, 3–5 April 2024; pp. 1–7. [Google Scholar]
- Zhao, L.; Chen, Z.; Manea, D.; Li, S.; Li, J.; Zhu, Y.; Sui, Z.; Lu, Z. Highly reliable 40nm embedded dual-interface-switching RRAM technology for display driver IC applications. In Proceedings of the 2022 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Honolulu, HI, USA, 12–17 June 2022; pp. 316–317. [Google Scholar]
- Prabhu, K.; Gural, A.; Khan, Z.F.; Radway, R.M.; Giordano, M.; Koul, K.; Doshi, R.; Kustin, J.W.; Liu, T.; Lopes, G.B. CHIMERA: A 0.92-TOPS, 2.2-TOPS/W edge AI accelerator with 2-MByte on-chip foundry resistive RAM for efficient training and inference. IEEE J. Solid-State Circuits 2022, 57, 1013–1026. [Google Scholar] [CrossRef]
- Cassidy, A.S.; Alvarez-Icaza, R.; Akopyan, F.; Sawada, J.; Arthur, J.V.; Merolla, P.A.; Datta, P.; Tallada, M.G.; Taba, B.; Andreopoulos, A.; et al. Real-time scalable cortical computing at 46 giga-synaptic OPS/watt with ~100× speedup in time-to-solution and ~100,000× reduction in energy-to-solution. In Proceedings of the SC’14: International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; pp. 27–38. [Google Scholar]
- Wei, Y.; Huang, Y.C.; Tang, H.; Sankaran, N.; Chadha, I.; Dai, D.; Oluwole, O.; Balan, V.; Lee, E. 9.3 NVLink-C2C: A coherent off package chip-to-chip interconnect with 40Gbps/pin single-ended signaling. In Proceedings of the 2023 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 19–23 February 2023; pp. 160–162. [Google Scholar]
- Segal, Y.; Laufer, A.; Khairi, A.; Krupnik, Y.; Cusmai, M.; Levin, I.; Gordon, A.; Sabag, Y.; Rahinski, V.; Ori, G.; et al. A 1.41 pJ/b 224Gb/s PAM-4 SerDes receiver with 31 dB loss compensation. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), Francisco, CA, USA, 20–26 February 2022; Volume 65, pp. 114–116. [Google Scholar]





| Config. Name | Config. Param. | Emu. Resources | Utilization |
|---|---|---|---|
| Computation Clock | 50 MHz | ALM | 1,317,449 |
| Interface Clock | 200 MHz | LUT | 2,634,898 |
| NVM Clock | 25 MHz | FF | 785,843 |
| NVM Bit Width | 3072 bit | BRAM | 1,607,168 |
| NVM Depth | 2048 | LUTRAM | 434 |
| NVM Block | 16 | DDR | 100,663,296 |
| Datasets | Architecture | Deployed Layers | Batch Size | FCC Utilized | NMC Throughput |
|---|---|---|---|---|---|
| N-MNIST | 3FC | 3FC | 416 | 78 | 13.29 GSOP/s |
| Cifar-10 | 3Tokenizer +2Transformer | 1Transformer | 8 | 80 | 13.30 GSOP/s |
| ImageNet | 5Tokenizer +8Transformer | 8Transformer | 1 | 80 | 13.59 GSOP/s |
| Memory Type | Mem. Area () | HDNIP Area () | Mem. Power (mW) | HDNIP Power (mW) |
|---|---|---|---|---|
| SRAM | 4.13 | 75.95 | 61.16 | 180.38 |
| ReRAM | 2.17 | 44.39 | 27.15 | 146.37 |
| Platform | This Work (HDNIP) | RTX4090 (GPU) |
|---|---|---|
| Technology (nm) | 40 | 4 |
| Power (mW) | 146.37 | 450,000 |
| Throughput (GSOP/s) | 13.64 | 28,121 |
| Energy Efficiency (pJ/SOP) | 10.73 | 16.00 |
| Platform | This Work | Hu et al. [40] | True-North [19,20] | Loihi-1 [21] | Loihi-2 [22,23] | Tianjic [24,25] | Morph-IC [26] | DYN-AP-SE2 [27] | SNA-VA [28] |
|---|---|---|---|---|---|---|---|---|---|
| Technology (nm) | 40 | 55 | 28 | 14 | 7 | 28 | 65 | 180 | 28 |
| Clock (MHz) | 25–200 a | 100 | Async | Async | Async | 300 | 55/210 | Async | 125 |
| Neuron Number | 10 M | 10 k | 1 M | 128 k | 1 M | 39 k | 2 k | 1 k | 12.8 k |
| Synapse Number | 80 G | 10 M | 256 M | 128 M | 114.4 M | 9.75 M | 2.06 M | 65 k | 20 k |
| Area () | 44.39 | 6 | 430 | 60 | 31 | 14.44 | 3.5 | 98 | 12 |
| Normalized neuron density (K/) b | 225.28 | 3.15 | 1.14 | 0.26 | 0.99 | 1.32 | 1.5 | 0.21 | 0.52 |
| Virtual Neurons Per Core | 8192 | 1024 | 256 | 1024 | 8192 | 256 | 512 | 1 | 1024 |
| Core Number | 1280 | 9 | 4096 | 128 | 128 | 156 | 4 | 4 | 100 |
| Power (mW) | 146.37 | 14.9 | 42–323 | - | - | 950 | 19.9 | - | 625 |
| Avg. Throughput (GSOP/s) | 13.64 | 0.22 | 2.99 | - | - | - | 0.11 | - | - |
| Energy Efficiency (pJ/SOP) | 10.73 | 33.26 | 21.73 | 23.6 | - | 1.54 | 51 | 150 | - |
| Normalized Compute Density (MSOPS /) c | 307 | 69 | 34 | - | - | - | 83 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Y.; Ning, N.; Cao, K.; Zhang, R.; Fu, C.; Wang, S.; Meng, L.; Ma, R.; Qiao, G.; Liu, Y.; et al. High-Density Neuromorphic Inference Platform (HDNIP) with 10 Million Neurons. Electronics 2025, 14, 3412. https://doi.org/10.3390/electronics14173412
Zuo Y, Ning N, Cao K, Zhang R, Fu C, Wang S, Meng L, Ma R, Qiao G, Liu Y, et al. High-Density Neuromorphic Inference Platform (HDNIP) with 10 Million Neurons. Electronics. 2025; 14(17):3412. https://doi.org/10.3390/electronics14173412
Chicago/Turabian StyleZuo, Yue, Ning Ning, Ke Cao, Rui Zhang, Cheng Fu, Shengxin Wang, Liwei Meng, Ruichen Ma, Guanchao Qiao, Yang Liu, and et al. 2025. "High-Density Neuromorphic Inference Platform (HDNIP) with 10 Million Neurons" Electronics 14, no. 17: 3412. https://doi.org/10.3390/electronics14173412
APA StyleZuo, Y., Ning, N., Cao, K., Zhang, R., Fu, C., Wang, S., Meng, L., Ma, R., Qiao, G., Liu, Y., & Hu, S. (2025). High-Density Neuromorphic Inference Platform (HDNIP) with 10 Million Neurons. Electronics, 14(17), 3412. https://doi.org/10.3390/electronics14173412





