Research on Combinations of Stator Poles and Rotor Teeth for Conventional Flux-Switching Brushless Machines with Composite Phase Numbers

Abstract

In this paper, a method for determining the optimal stator-rotor combinations of conventional flux-switching permanent magnet (FSPM) machines with composite phase numbers covering symmetrical and asymmetrical topologies is proposed by changing the equivalent number of coils per pole per phase (ENCPP) or the number of coil-pairs having complementarity (K) of the optimal stator-rotor combinations of the corresponding machines with prime phases. Taking composite phase machines such as four-phase, six-phase, nine-phase, and twelve-phase machines as examples, a detailed analysis is conducted on how the optimal stator-rotor combinations of four-phase machines are derived from the optimal stator-rotor combinations of the corresponding prime phase machines (i.e., two-phase machines) and how the optimal stator-rotor combinations of six-phase, nine-phase, and twelve-phase machines are derived from the optimal stator-rotor combinations of the corresponding prime phase machines (i.e., three-phase machines). Then, the winding factor of the conventional FSPM machines with composite phase numbers is calculated. Finally, taking a 24-slot/22-tooth (24/22) conventional FSPM topology as an example, the topology is connected into a standard six-phase machine (symmetrical topology) and a dual three-phase machine (asymmetrical topology), and a comparative study between them is conducted in terms of the phase back electromotive force (EMF) waveform, electromagnetic torque, torque ripple, and inductances. The results indicate that both machines have sufficiently large and symmetrical back-EMFs, as well as sufficiently large electromagnetic torque, which validates the correctness of the proposed method for determining the optimal stator-rotor combinations.

1. Introduction

Flux-switching (FS) permanent magnet (FSPM) machines have garnered considerable attention in recent years due to their large torque capability, high torque density, essentially sinusoidal back-EMF waveforms, and robust structure [1,2,3]. Related research covers electromagnetic performance analysis [4,5,6,7], optimization design and optimization methodology [8,9,10], advanced control strategies [11,12], and fault-tolerant control methods [13,14,15]. According to the phase number of the machines, they can be divided into prime phase FSPM machines and composite phase FSPM machines. The composite phase machines usually have a large number of winding phases and are attractive candidates in the ship propulsion system, electric traction system, etc., due to their advantages such as high-power supply at low voltage, small torque ripple, and high reliability, which decreased inverter power ratings per phase for a given total power [16,17]. For FSPM machines, if suitable stator-rotor combinations are selected, excellent electromagnetic performance can be achieved through subsequent optimization design; if the wrong stator-rotor combinations are chosen, even with a lot of optimization design work, it is possible that excellent electromagnetic performance may not be achieved. Therefore, choosing the appropriate stator-rotor combinations is the first and very important step in the motor design process. Since the PMs of FSPM machines are located on the stator and the coils are complementary, the stator-rotor combinations of rotor PM machines [18,19] cannot be fully applied to FSPM machines. Therefore, specialized research is needed on the stator-rotor combinations of the FSPM machines.

For prime phase FSPM machines, a general model for determining the optimal stator-rotor combinations has been established [20], and the concluded stator-rotor combination is shown in Equation (1), where p_r, p_s, and p_sc are, respectively, the numbers of rotor teeth, stator poles, and stator coils, and K is the number of coil-pairs having complementarity.

$$p_r=p_s\pm K=p_{sc}\pm K$$

(1)

However, for composite phase FSPM machines, existing research is restricted to specific stator-rotor combinations, and no general method has been proposed to determine the stator-rotor combinations. For example, four-phase 16-stator-poles/12-rotor-teeth (16/12), 16/14, and 16/18 machines were proposed in [21], and a four-phase 8/15 E-core FSPM machine was investigated [22]; the conventional and alternate six-phase 24/20, 24/22 FSPM machines were presented in [23]; nine-phase 18/17, 18/19, 36/34 structures [24], and a twelve-phase 24/22 structure were raised in [25]. The works in [26] showed that the stator-rotor combinations of four-phase and six-phase machines are p_r = p_s ± 2 or p_r = p_s ± 1. Though the research findings are extremely useful for composite phase FSPM machines, the stator-rotor combinations are incomplete, such as the cases of p_r = p_s ± 3 and p_r = p_s ± 4 are not considered, and the results of other composite phase machines have not been obtained.

Though the stator-rotor combinations of the composite phase FSPM machines do not satisfy the conclusion of prime phase machines, namely Equation (1), they can be derived from the results of the prime phase machines. The purpose of this paper is to propose a method to determine the optimal stator-rotor combinations of the composite phase FSPM machines with symmetrical and asymmetrical topologies by changing the equivalent number of coils per pole per phase (ENCPP) or K of the optimal stator-rotor combinations of the corresponding prime phase machines. Then, a detailed analysis is conducted on how the optimal stator-rotor combinations of four-phase, six-phase, nine-phase, and twelve-phase machines are derived from the optimal stator-rotor combinations of the corresponding prime phase machines (i.e., two-phase or three-phase machines). Thereafter, Section 3 presents the winding factor (k_w) of the machines with composite phases, including the distribution factor (k_d) and pitch factor (k_p). Afterwards, taking the 24/22 structure as an example, the electromagnetic performance in terms of back-EMFs, torques, cogging torques, and inductance waveforms is compared between the standard six-phase 24/22 machine (symmetrical topology) and the dual three-phase 24/22 machine (asymmetrical topology) to confirm the correctness of the proposed method for determining the optimal stator-rotor combinations.

2. Conventional FSPM Machines with Composite Phase Numbers

The common conventional FSPM machines with composite phases are four-, six-, nine-, and twelve-phase machines, which can be considered as a combination of multiple machines with prime phases. For example, four-phase conventional FSPM machines can be deduced from two-phase machines, and six-, nine-, and twelve-phase conventional FSPM machines can be deduced from three-phase machines.

2.1. Six-Phase Conventional FSPM Machines

According to different connection styles, the machines with prime phase numbers could be connected into symmetrical and asymmetrical topologies with composite phases. For six-phase conventional FSPM machines, the standard six-phase machine has a symmetrical structure, and the dual three-phase machine has an asymmetrical structure, as shown in Figure 1.

Both the symmetrical and asymmetrical six-phase structures can be obtained by combining three-phase machines. The parameter q′ is the equivalent number of coils per pole per phase, i.e., the number of the consecutively adjacent coils belonging to the same phase, and K is the number of coil pairs having complementarity for the three-phase machines. Similarly, q₆′ and K₆ are the corresponding parameters of six-phase machines, i.e., the numbers of the consecutively adjacent stator coils belonging to the same phase and coil-pairs having complementarity for six-phase machines. 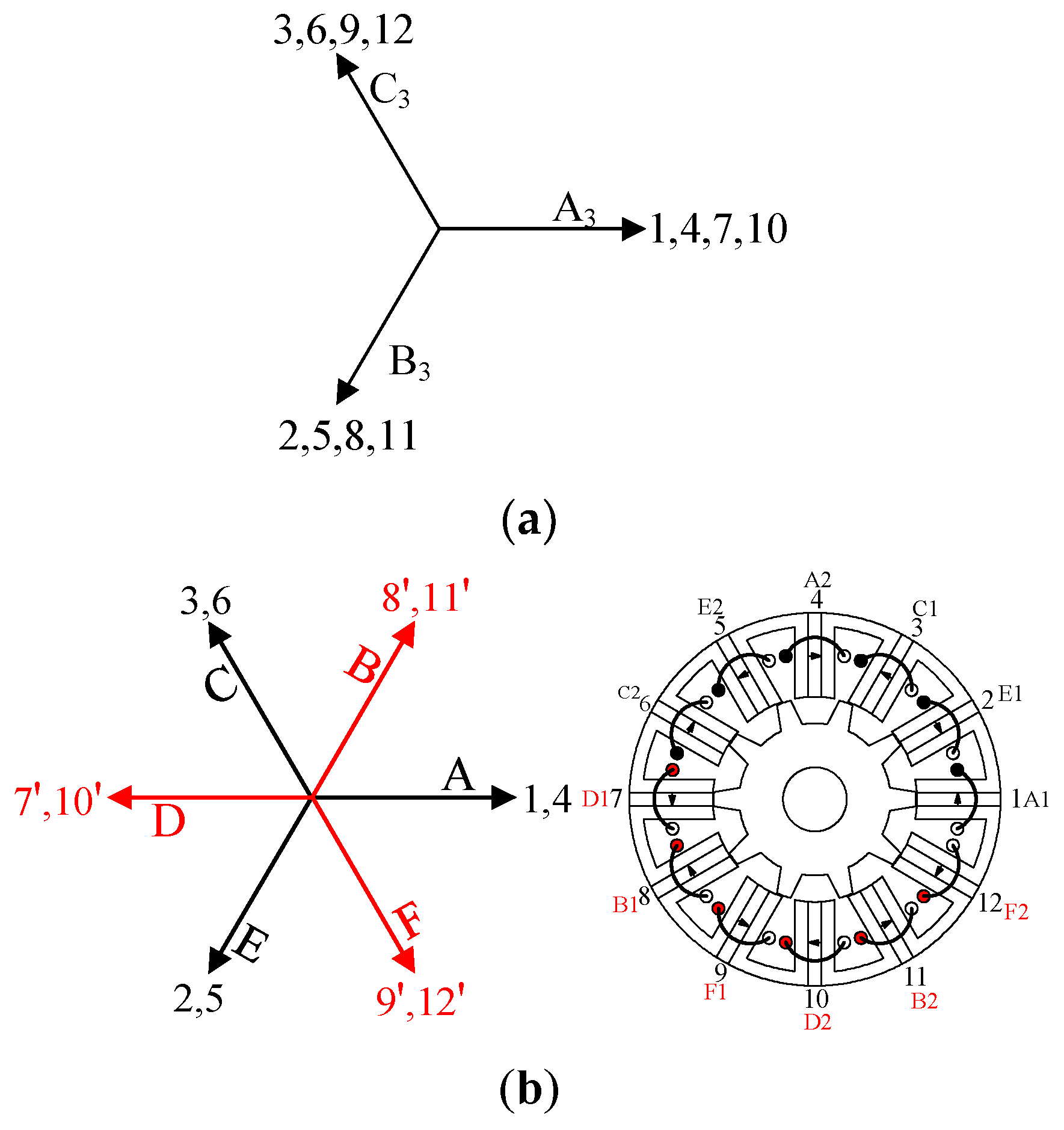For the three-phase machines with q′ being an odd number and K being an even number, including 12/10, 12/14, 24/20, 24/28, 36/34, and 36/38 topologies, if half of the stator coils connect in opposite polarity, the machines could be connected into a standard six-phase machine. Taking a 12/10 topology shown in Figure 2 as an example, the 12/10 topology shown in Figure 2a is a three-phase structure with q′ = 1 and K = 2, where coils 1, 4, 7, and 10, coils 2, 5, 8, and 11, and coils 3, 6, 9, and 12 belong to phases A₃, B₃, and C₃, respectively (A₃, B₃, and C₃ represent the three phases of three-phase machines). However, the structure can be connected into a standard six-phase 12/10 machine shown in Figure 2b by half coils connected in opposite polarity to A₃, B_3, and C₃. Coils 1 and 4, coils 2 and 5, and coils 3 and 6 remain the same polarity with A₃, B₃, and C₃, composing phases A, E, and C. Coils 7 and 10 are connected in opposite polarity, composing phase D. Similarly, the phases B and F are composed of coils 8 and 11 and coils 9 and 12 in opposite polarity, respectively. It should be noted that the coils connected in reverse are marked with prime indices, such as 7′ in Figure 2b. For the reconnected standard six-phase machine, the number of the consecutively adjacent stator coils belonging to the same phase and coil-pairs having complementarity are both 1, namely, q₆′ = 1 and K₆ = 1.

The three-phase machines, with q′ being an even number, such as 12/11, 12/13, 24/22, 24/26, 24/23, 24/25, etc., could be reconnected into dual three-phase machines. Taking the three-phase 12/11 topology (q′ = 2 and K = 1) as an example, phases A₃, B₃, and C₃ are, respectively, composed of coils 1, 2, 7, and 8, coils 3, 4, 9, and 10, and coils 5, 6, 11, and 12, as is illustrated in Figure 3a, where winding-EMF vectors of phases A₃, B₃, and C₃ are, respectively, synthesized from two coil-EMF vectors. Hence, if the coils of the same coil-EMF vector connect into a phase winding, i.e., coils 1 and 7, coils 3 and 9, coils 5 and 11, coils 2 and 8, coils 6 and 12, and coils 4 and 10, respectively, connect into phases A, B, C, D, E, and F; the three-phase 12/11 machine then turns into a dual three-phase 12/11 machine, as is shown in Figure 3, where q₆′ = 1 and K₆ = 1.

It should be noted that when q′ is an even number, on the one hand, the machines can all be connected into dual three-phase machines, whatever the parameter K is. On the other hand, if K is also an even number, the machines could also be connected to standard six-phase machines. Taking a three-phase 24/22 structure shown in Figure 4a as an example, where q′ = 2 and K = 2, phase A₃ consists of coils 1, 2, 7, 8, 13, 14, 19, and 20, and phases B₃ and C₃ are, respectively, composed of coils 3, 4, 9, 10, 15, 16, 21, and 22 and coils 5, 6, 11, 12, 17, 18, 23, and 24. Winding vectors of phases A₃, B₃, and C₃ are, respectively, synthesized from two coil vectors. If half of the coils in phases A₃, B₃, and C₃ are connected in opposite polarity, it turns out to be a standard six-phase 24/22 machine with q₆′ = 2 and K₆ = 1 shown in Figure 4b, where the coil connections of phases A and B are exhibited. 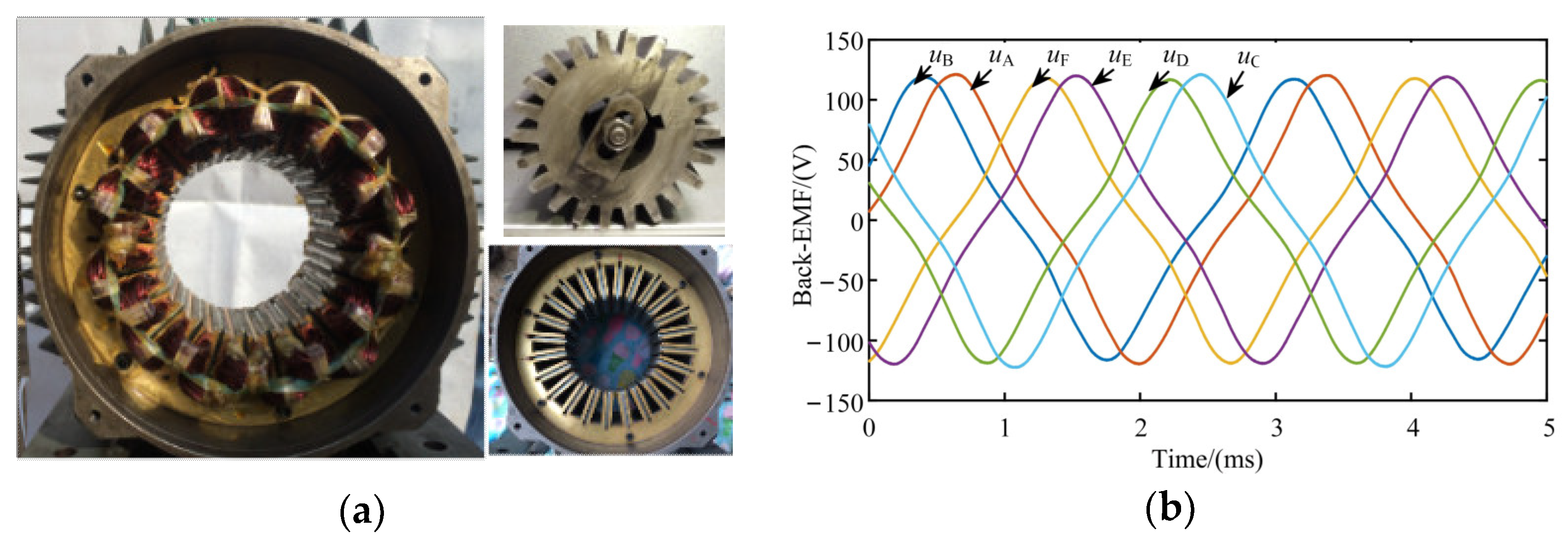If the coils of the same coil-EMF vector connect into a phase winding, the three-phase machine changes into a dual three-phase 24/22 machine with q₆′ = 1 and K₆ = 2, as is presented in Figure 4c, where the coil connection of phases A and B is shown. 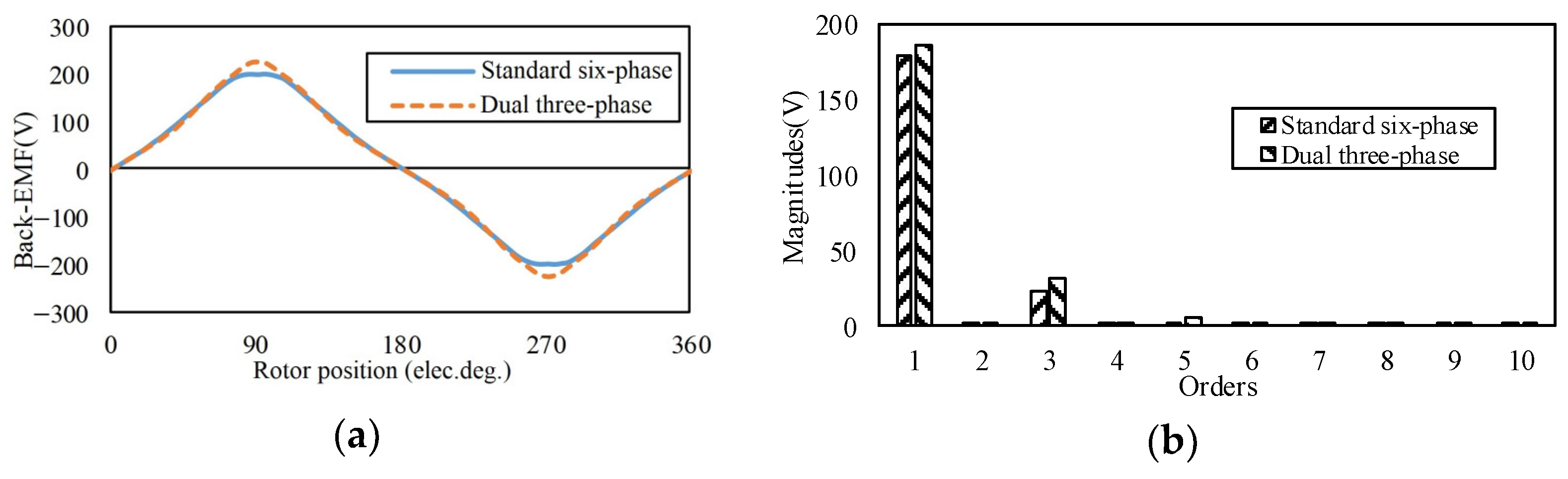A dual three-phase 24/22 conventional FSPM prototype has been manufactured and measured, as presented in Figure 5a, and the specific parameters are listed in

Table 1. Key parameters of the dual three-phase 24/22 FSPM prototype.

Items	Dimensions and Parameters
Stator-rotor combination	24/22
Measured speed	1000 r/min
Rated speed	1500 r/min
Magnet type	NdFeB N35
Iron core	50 WW470
Stator outer diameter	226 mm
Split ratio	0.58
Active stack length	75 mm
Air-gap length	0.9 mm
Rotor inner diameter	22 mm
Number of coil turns, Nc	28
Rated phase current (rms), IN	9.5 A

. The measured back-EMF waveforms at 1000 r/min are presented in Figure 5b. It can be seen that the back-EMF waveforms are exactly symmetrical.

Based on the above analysis, some conclusions can be drawn. At first, when q′ is an odd number and K is an even number, or q′ is an even number, the corresponding three-phase machines can be reconnected into six-phase machines. Secondly, among the three-phase machines that can be connected into six-phase machines, some machines, where K is an even number, can be reconnected into standard six-phase machines (symmetrical structure); meanwhile, the machines with q′ being an even number can be connected into dual three-phase machines (asymmetrical structure). That is to say, the three-phase combinations with q′ being an even number and K being an even number not only could be connected into standard six-phase structures but also could be connected into dual three-phase structures. Thirdly, if the three-phase structures are connected into six-phase structures, the parameters q′, K, q₆′, and K₆ must satisfy Equation (2). In addition, for standard six-phase machines, K₆ is half of K and q₆′ is the same as q′, namely Equation (3), while for dual three-phase machines, K₆ is equal to K and q₆′ is half of q′, namely Equation (4), i.e., when three-phase machines are connected into six-phase machines, one of the parameters, q′ or K will be reduced to half. The types of six-phase structures and the relationship of parameters q′, K, q₆′, and K₆ are concluded and listed in

Table 2. Six-phase machines derived from three-phase structures.

q′	K	Types of the Six-Phase	q6′	K6
odd	even	standard six-phase	q′	K/2
even	even	standard six-phase	q′	K/2
		dual three-phase	q′/2	K
	odd	dual three-phase	q′/2	K

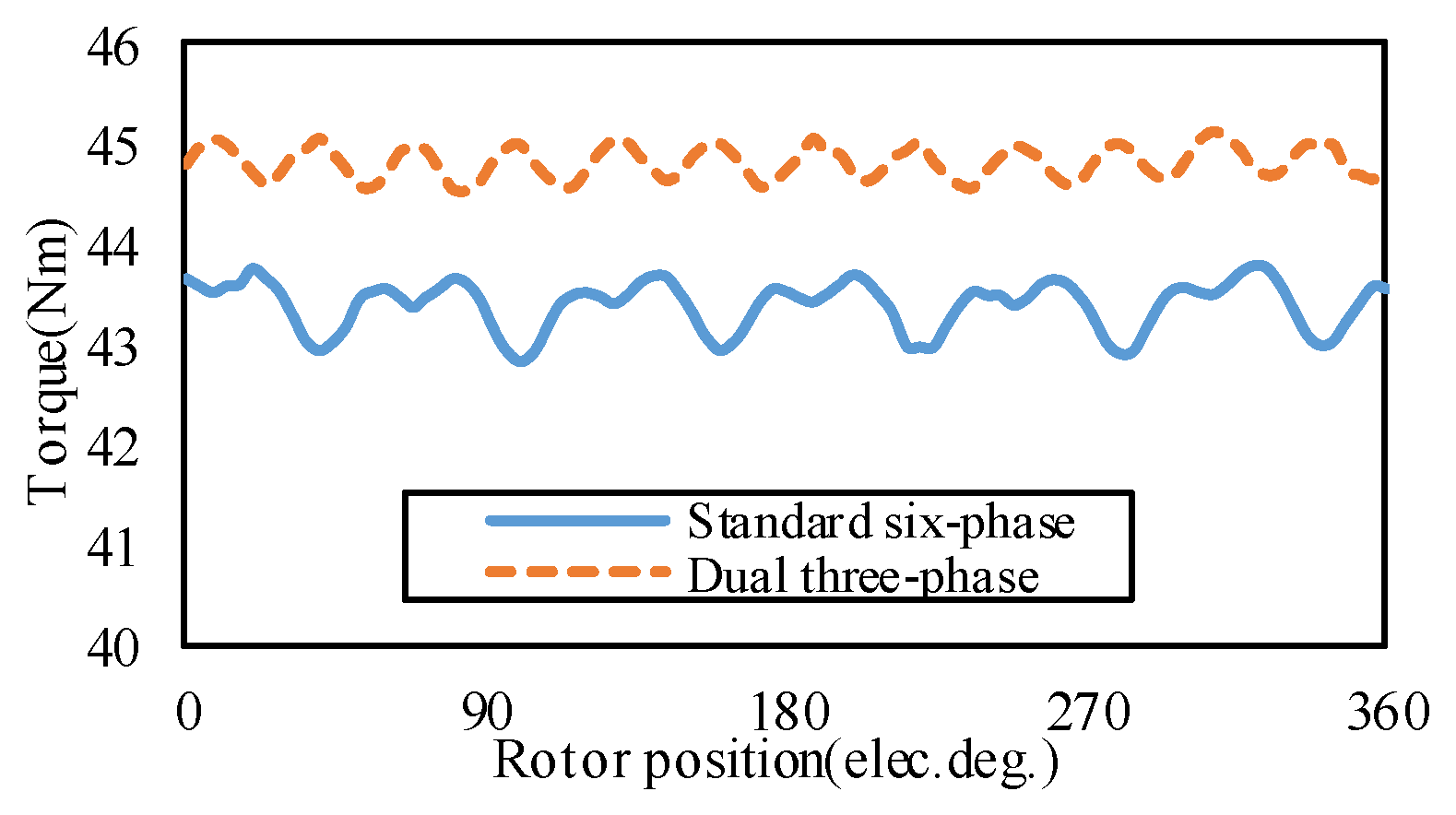
. Taking the combination of three-phase 24/22 where K = 2 and q′ = 2 as an example, this machine could be connected into a standard six-phase machine (K₆ = K/2 and q₆′ = q′) and can also be connected into a dual three-phase machine (K₆ = K and q₆′ = q′/2). The specific performance comparisons between the 24/22 standard six-phase machine and the 24/22 dual three-phase machine will be conducted in Section 4. The combinations of stator poles and rotor teeth for six-phase conventional FSPM machines, including symmetrical and asymmetrical structures, are listed in

Table A1. Stator and rotor pole combinations of conventional FSPM machines with composite phase numbers and winding factors: (a-1) four-phase (standard four-phase), (a-2) four-phase (dual two-phase), (b-1) six-phase (standard six-phase), (b-2) six-phase (dual three-phase), (c) nine-phase, (d-1) twelve-phase (standard twelve-phase), (d-2) twelve-phase (four three-phase).

(a-1)
q′	K	psc = ps = 2Kmq′	pr = ps ± K	q4′	K4	kd	kp	kw
1	2	8	6	1	1	1	0.707	0.707
			10
	4	16	12		2
			20
2	2	16	14	2	1	0.924	0.924	0.854
			18
	4	32	28		2
			36
3	2	24	22	3	1	0.911	0.966	0.880
			26
4	2	32	30	4	1	0.906	0.981	0.889
			34
(a-2)
q′	K	psc = ps = 2Kmq′	pr = ps ± K	q4′	K4	kd	kp	kw
2	1	8	7	1	1	1	0.924	0.924
			9
	2	16	14		2
			18
	3	24	21		3
			27
	4	32	28		4
			36
4	1	16	15	2	1	0.981	0.981	0.962
			17
	2	32	30		2
			34
(b-1)
q′	K	psc = ps = 2Kmq′	pr = ps ± K	q6′	K6	kd	kp	kw
1	2	12	10	1	1	1	0.866	0.866
			14
	4	24	20		2
			28
2	2	24	22	2	1	0.966	0.966	0.933
			26
	4	48	44		2
			52
3	2	36	34	3	1	0.960	0.985	0.945
			38
	4	72	68		2
			76
4	2	48	46	4	1	0.958	0.991	0.950
			50
	4	96	92		2
			100
(b-2)
2	1	12	11	1	1	1	0.966	0.966
			13
	2	24	22		2
			26
	3	36	33		3
			39
	4	48	44		4
			52
4	1	24	23	2	1	0.991	0.991	0.983
			25
	2	48	46		2
			50
	3	72	69		3
			75
	4	96	92		4
			100
(c)
q′	K	psc = ps = 2Kmq′	pr= ps± K	q9′	K9	kd	kp	kw
3	1	18	17	1	1	1	0.985	0.985
			19
	2	36	34		2
			38
	3	54	51		3
			57
(d-1)
q′	K	psc = ps = 2Kmq′	pr = ps± K	q12′	K12	kd	kp	kw
2	2	24	22	1	1	1	0.966	0.966
			26
	4	48	44		2
			52
4	2	48	46	2	1	0.991	0.991	0.983
			50
	4	96	92		2
			100
(d-2)
4	1	24	23	1	1	1	0.991	0.991
			25
	2	48	46		2
			50
	3	72	69		3
			75
	4	96	92		4
			100

in Appendix A.

$$q{\prime }_6{K}_6=q\prime K/2$$

(2)

$$\left\{\begin{array}{l}{K}_6=K/2\\ q{\prime }_6=q\prime \end{array}\right.$$

(3)

$$\left\{\begin{array}{l}{K}_6=K\\ q{\prime }_6=q\prime /2\end{array}\right.$$

(4)

2.2. Nine-Phase Conventional FSPM Machines

Like six-phase machines, q₉′ and K₉ are, respectively, the number of the consecutively adjacent stator coils belonging to the same phase and the number of coil-pairs having complementarity for nine-phase machines coils per pole per phase and the number of coil-pairs having complementarity for nine-phase machines. Nine-phase conventional FSPM machines can also be deduced from three-phase machines where q′ is a multiple of three. For example, 18/17, 18/19, 36/34, 36/38 (q′ = 3), and 36/35, 36/37 (q′ = 6) three-phase machines can be reconnected to nine-phase machines. Taking an 18/17 structure (q′ = 3, K = 1) as an example, each phase winding of the three-phase 18/17 machine shown in Figure 6a is composed of six coils, covering three coil-EMF vectors, and if the coils with the same coil-EMF vector connect into a phase winding and the coils connect in positive polarity, the three-phase 18/17 machine turns into a standard nine-phase 18/17 machine (symmetrical structure), as is shown in Figure 6b, where q₉′ = 1 and K₉ = 1. The three-phase machines, being able to be connected to standard nine-phase machines, can also be reconnected into triple three-phase machines. Like the standard nine-phase machine in Figure 6b, if coils 2 and 11, coils 5 and 14, and coils 8 and 17 connect in opposite polarity, the standard nine-phase machine turns into a triple three-phase 18/17 machine with q₉′ = 1 and K₉ = 1, shown in Figure 6c.

Overall, at first, when q′ is a multiple of three, the corresponding three-phase conventional FSPM machines can be reconnected into nine-phase machines, and in addition, the three-phase topologies cannot only be connected into symmetrical structures (standard nine-phase machines) but also can be connected into asymmetrical structures (triple three-phase machines). Then, if the three-phase structures are connected into nine-phase structures, regardless of symmetrical structures or asymmetrical structures, the parameters q′, K, q₉′, and K₉ all satisfy Equation (5). The types of nine-phase structures and the relationship of parameters q′, K, q₉′, and K₉ are listed in

Table 3. Nine-phase machines and the corresponding three-phase structures.

q′	K	Types of the Nine-Phase	q9′	K9
multiple of 3	all	standard nine-phase	q′/3	K
		triple three-phase

. The specific stator pole and rotor teeth combinations for nine-phase machines are all listed in Table A1 in Appendix A.

$$\left\{\begin{array}{l}{K}_9=K\\ q{\prime }_9=q\prime /3\end{array}\right.$$

(5)

In addition, a standard nine-phase 36/34 conventional FSPM prototype was manufactured and presented in Figure 7, which was detailedly described in the reference [24]. From the measured no-load EMF waveforms at 500 r/min shown in reference [24], it can be seen that the EMF waveforms are exactly symmetrical.

2.3. Twelve-Phase Conventional FSPM Machines

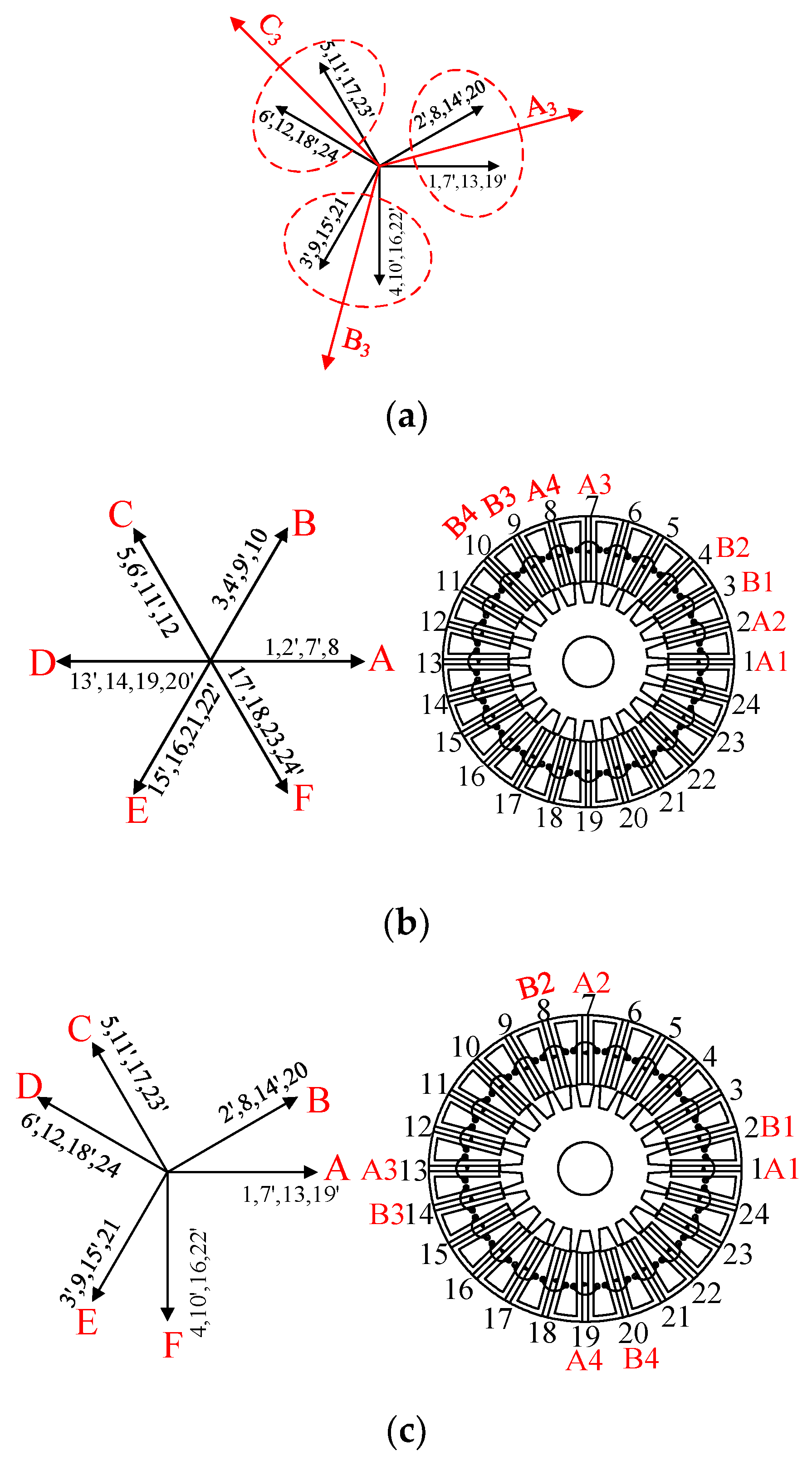
Twelve-phase conventional FSPM machines, including symmetrical structure (standard twelve-phase machine) and asymmetrical structure (four three-phase machines), as shown in Figure 8, can be derived from three-phase structures.

When q′ is an even number and K is also an even number, such as 24/22, 24/26, 48/46, 48/50, etc., the corresponding three-phase structure can be connected into a standard twelve-phase machine. For example, if q′ = 2 and K = 2, the corresponding three-phase 24/22 structure shown in Figure 4a will turn into a standard twelve-phase machine exhibited in Figure 9a if half of the coils change their polarity, and for the obtained machine, the parameters satisfy q₁₂′ = 1 and K₁₂ = 1, where q₁₂′ and K₁₂ represent, respectively, the number of the consecutively adjacent stator coils belonging to the same phase and the number of coil-pairs having complementarity for twelve-phase machines.

All the three-phase structures, where q′ is a multiple of 4 and K is not restricted, could be reconnected into four three-phase machines, shown in Figure 8b, such as 24/23, 24/25, 48/46, 48/50 (q′ = 4), etc. For example, a three-phase 24/23 structure (q′ = 4, K = 1) can be connected into a four three-phase machine shown in Figure 9b, where q₁₂′ = 1 and K₁₂ = 1.

In addition, the machines where q′ is a multiple of 4 and K is an even number, such as 48/46 and 48/50 (q′ = 4, K = 2), can not only be connected into standard twelve-phase machines but also can be connected into four three-phase machines.

Overall, the parameters q′, K, q₁₂′, and K₁₂ must satisfy Equation (6). For standard twelve-phase machines, q₁₂′ and K₁₂ are half of q′ and K, namely Equation (7); meanwhile, for four three-phase machines, q₁₂′ is a quarter of q′ and K₁₂ is equal to K, namely Equation (8). The types of twelve-phase structures and the relationship of parameters q′, K, q₁₂′, and K₁₂ are concluded and listed in

Table 4. Twelve-phase machines and the corresponding three-phase structures.

q′	K	Types of Twelve-Phase	q12′	K12
even (not a multiple of 4)	even	standard twelve-phase	q′/2	K/2
multiple of 4	even	standard twelve-phase	q′/2	K/2
		four three-phase	q′/4	K
	odd	four three-phase	q′/4	K

. The combinations of stator poles and rotor teeth for twelve-phase conventional FSPM machines, including symmetrical and asymmetrical structures, are listed in Table A1 in Appendix A.

$$q{\prime }_{12}{K}_{12}=q\prime K/4$$

(6)

$$\left\{\begin{array}{l}{K}_{12}=K/2\\ q{\prime }_{12}=q\prime /2\end{array}\right.$$

(7)

$$\left\{\begin{array}{l}{K}_{12}=K\\ q{\prime }_{12}=q\prime /4\end{array}\right.$$

(8)

A standard twelve-phase 24/22 FSPM prototype was manufactured and presented in Figure 10, which was described in the reference [25]. From the measured no-load EMF waveforms at 500 r/min shown in reference [25], it can be seen that the EMF waveforms are exactly symmetrical.

2.4. Four-Phase Conventional FSPM Machines

Similar to six-phase machines deduced from three-phase machines, four-phase machines could be deduced from two-phase structures.

When K is an even number, the corresponding machines, such as 8/6, 8/10, 16/12, 16/20, 24/18, 24/30, 24/22, 24/26, etc., can be connected into standard four-phase machines (symmetrical structure) as is shown in Figure 11a by half of the coils connecting in opposite polarity, such as the standard six-phase topologies.

All the two-phase machines, where q′ is an even number and K is not restricted, such as 8/7, 8/9, 16/14, 16/18, 24/21, 24/27, 32/28, and 32/36, etc., could be reconnected into dual two-phase machines (asymmetrical structure) shown in Figure 11b, such as the dual three-phase topologies. In addition, the machines where q′ and K are all even numbers, such as 16/14, 16/18 (q′ = 2, K = 2), 32/28, and 32/36 (q′ = 2, K = 4), can be connected into standard four-phase machines and also can be connected into dual two-phase machines.

q₄′ and K₄, respectively, represent the number of the consecutively adjacent stator coils belonging to the same phase and the number of coil-pairs having complementarity for four-phase machines. Parameters q′, K, q₄′, and K₄ must satisfy Equation (9). For standard four-phase machines, they satisfy Equation (10); meanwhile, for dual two-phase machines, they satisfy Equation (11). The types of four-phase structures and the relationship of parameters q′, K, q₄′, and K₄ are concluded and listed in

Table 5. Four-phase machines and the corresponding two-phase structures.

q′	K	Types of Four-Phase	q4′	K4
odd	even	standard four-phase	q′	K/2
even	even	standard four-phase	q′	K/2
		dual two-phase	q′/2	K
	odd	dual two-phase	q′/2	K

. The specific combinations of stator and rotor poles for four-phase conventional FSPM machines, including symmetrical and asymmetrical structures, are listed in Table A1 in Appendix A.

$$q{\prime }_4{K}_4=q\prime K/2$$

(9)

$$\left\{\begin{array}{l}{K}_4=K/2\\ q{\prime }_4=q\prime \end{array}\right.$$

(10)

$$\left\{\begin{array}{l}{K}_4=K\\ q{\prime }_4=q\prime /2\end{array}\right.$$

(11)

3. Winding Factors

Winding factors include the distribution factor and pitch factor. The distribution factor k_d can be given [26,27]:

$$k_d={\displaystyle \frac{\sin (Qv\alpha /2)}{Q\sin (v\alpha /2)}}$$

(12)

where Q is the number of least EMF vectors per phase, α is the angle between two adjacent coil-EMF vectors, and v is the order of the harmonic. The parameter α is given in Equation (13), where for prime phase machines, m′ is the phase number, and for composite phase machines, m′ is the phase number of the corresponding prime phase machines, which is given in Equation (14).

$$\alpha ={\displaystyle \frac{2\pi }{2m\prime q\prime }}={\displaystyle \frac{\pi }{m\prime q\prime }}$$

(13)

$$m\prime =\left\{\begin{array}{l}m\hspace{1em}Primephase\\ 2\hspace{1em}Four\text{-}phase\\ 3\hspace{1em}Six\text{-},nine\text{-},twelve\text{-}phase\end{array}\right.$$

(14)

The parameter Q is equal to q_m′, where q_m′ is the number of the consecutively adjacent stator coils belonging to the same phase for m-phase machines with composite phase numbers, which is shown in Equation (15). Finally, the distribution factor k_d is expressed as Equation (16).

$$Q=q_m\prime =\left\{\begin{array}{l}q\prime \hspace{1em}primephase\\ q_4\prime \hspace{1em}four\text{-}phase\\ q_6\prime \hspace{1em}six\text{-}phase\\ q_9\prime \hspace{1em}nine\text{-}phase\\ q_{12}\prime \hspace{1em}twelve\text{-}phase\end{array}\right.=\left\{\begin{array}{l}q\prime \hspace{1em}primephase\\ q\prime \hspace{1em}standardfourphase\\ q\prime /2\hspace{1em}dualtwo\text{-}phase\\ q\prime \hspace{1em}standardsixphase\\ q\prime /2\hspace{1em}dualthree\text{-}phase\\ q\prime /3\hspace{1em}ninephase\\ q\prime /2\hspace{1em}standardtwelve\text{-}phase\\ q\prime /4\hspace{1em}fourthree\text{-}phase\end{array}\right.$$

(15)

$$k_d={\displaystyle \frac{\sin (Qv\pi /2m\prime q\prime )}{Q\sin (v\pi /2m\prime q\prime )}}={\displaystyle \frac{\sin (q_m\prime v\pi /2m\prime q\prime )}{q_m\prime \sin (v\pi /2m\prime q\prime )}}$$

(16)

The pitch factor, k_p can be calculated by Equation (17):

$$k_p=\cos {\displaystyle \frac{{\theta }_c}{2}}=\cos ({\displaystyle \frac{\pi vK}{P_s}})=\cos ({\displaystyle \frac{\pi v}{2mq\prime }})$$

(17)

where parameter K is the number of complementary coil-pairs of corresponding prime phase machines, which can be easily obtained. Taking a standard six-phase 12/10 (q₆′= 1, K₆ = 2) as an example, the corresponding prime phase machine is the three-phase 12/10 machine (q′ = 1, K = 2); hence, the parameter K in Equation (17) is 2.

Therefore, the winding factor k_w can be expressed by Equation (18).

$$k_w=k_d{k}_p={\displaystyle \frac{\sin (q_m\prime v\pi /2m\prime q\prime )}{q_m\prime \sin (v\pi /2m\prime q\prime )}}\cdot \cos ({\displaystyle \frac{\pi v}{2mq\prime }})$$

(18)

The fundamental winding factors of the four, six, nine, and twelve-phase FSPM machines with different stator-rotor combinations, including symmetrical and asymmetrical structures, are calculated and listed in Appendix A.

4. Comparisons Between Two Six-Phase Machines

Based on the foregoing analysis, it is known that some machines with prime phase numbers can be connected into symmetrical structures and can also be connected into asymmetrical structures. Taking a 24/22 structure as an example, a standard six-phase 24/22 machine and a dual three-phase 24/22 machine are derived from a three-phase 24/22 machine, shown in Figure 4. Two six-phase machines have identical configurations, but for winding connections, the specific parameters are listed in Table 1. In this section, the electromagnetic performances in terms of back-EMFs, torques, cogging torques, and inductance waveforms are compared between the two types of six-phase machines using FEA, and the solution method used was the ICCG method.

The fundamental and the third harmonic winding factors of two 24/22 six-phase machines are listed in

Table 6. The fundamental winding factors of two 24/22 six-phase machines.

q′	K	psc/pr	Type	q6′	K6	kd	kp	kw
2	2	24/22	Standard six-phase	2	1	0.966	0.966	0.933
		24/22	Dual six-phase	1	2	1	0.966	0.966

and

Table 7. The third harmonic winding factors of two 24/22 six-phase machines.

q′	K	psc/pr	Type	q6′	K6	kd(3)	kp(3)	kw(3)
2	2	24/22	Standard six-phase	2	1	0.707	0.707	0.5
		24/22	Dual six-phase	1	2	1	0.707	0.707

, where it can be seen that the fundamental and the third harmonic winding factors of the dual three-phase one are both greater than those of the standard six-phase one. The FEA-simulated phase EMF waveforms of the standard six-phase and dual three-phase 24/22 FSPM machines are shown in Figure 12. The EMFs are both symmetrical, confirming the 24/22 combination is suitable for a six-phase machine. Then the FFT results of both machines are shown in Figure 12b, where it can be seen that the even-order harmonics are very small, and the main harmonics include the 3rd and 5th order harmonics. The magnitudes of fundamental and 3rd harmonic EMFs of the dual three-phase machine are higher than those of the standard six-phase machine, since the fundamental and 3rd harmonic winding factors of the dual three-phase 24/22 machine (0.966, 0.707) are higher than those of the standard six-phase 24/22 machine (0.933, 0.5).

Due to the doubly salient structure and PMs in FSPM machines, there must be cogging torques. It can be seen from Figure 13 that the cogging torques of standard six-phase and dual three-phase 24/22 machines are identical but for a phase shift, due to the identical stators and rotors of the two six-phase machines.

Figure 14 shows the FEA-simulated electromagnetic torque waveforms of two six-phase 24/22 FSPM machines with the rated phase current, namely I_p = I_N = 9.5 A, under i_d = 0 control. Both machines can achieve smooth electromagnetic torques; nevertheless, for the dual three-phase machine, the average torque is 3.4% greater, and the torque ripple is smaller.

The FEA-simulated self-inductances of phase A and the mutual inductances of phases B, C, D, E, and F to phase A in two six-phase 24/22 machines, which are calculated under the condition of phase current of 0.1 A, are shown in Figure 15. For the standard six-phase machine presented in Figure 15a, the self-inductance L_AA changes between 2.7 and 3.6 mH, and all the mutual inductances are far lower. The mutual inductances L_BA, L_CA, and L_FA are, respectively, 11%, 5.4%, and 5.6% of the self-inductance L_AA, while the mutual inductances L_DA and L_EA only occupy 0.05% and 0.1%, respectively. Therefore, the mutual inductances are negligible. Figure 15b presents that for the dual three-phase structure, the self-inductance L_AA is changing between 2 and 2.7 mH, which is lower than that of the standard six-phase machine. The mutual inductances L_BA and L_DA cannot be ignored, for both account for 37% of L_AA, which is considerable. The other mutual inductances, L_CA, L_EA, and L_FA, can be ignored since they only occupy 3.6%, 3.6%, and 0.0006%, respectively. It should be noted that when the magnetic field of the iron core is not saturated, the inductances are not affected by the phase current, that is, the inductances do not change with the change of current; when the iron core is magnetically saturated, the degree of magnetic saturation is affected by the current, so the inductance will change with the change of current. This paper only compares the inductances of two machines when the magnetic field is not saturated.

Through the above performance combinations between the two six-phase 24/22 FSPM machines, namely the standard six-phase and dual three-phase structures, we draw the following conclusions. Firstly, back-EMF waveforms of both machines are exactly symmetrical, and the magnitude of the fundamental EMF of dual three-phase machines is higher than that of standard six-phase machines, since the winding factor of the dual three-phase 24/22 machine is higher. Secondly, the electromagnetic torque of both machines is sufficiently large, with the dual three-phase machine being 3.4% greater than the standard six-phase machine. Finally, the sufficiently large and symmetrical back-EMFs and the sufficiently large electromagnetic torque confirm the correctness of the stator poles and rotor teeth combinations of six-phase machines.

5. Conclusions

In this paper, the optimal stator-rotor combinations of conventional FSPM machines with composite phases are derived from the corresponding machines with prime phases by changing the parameters of q′ or K. Taking composite phase machines, such as four-phase, six-phase, nine-phase, and twelve-phase machines as examples, a detailed analysis is conducted on how the optimal stator-rotor combinations of composite phase machines are derived from the optimal stator-rotor combinations of the corresponding prime phase machines.

Secondly, for the machines with composite phase numbers, both the symmetrical and asymmetrical structures have been researched. By changing the parameters of q′ or K, the machines with prime phases can be connected into symmetrical or asymmetrical structures based on different connection styles. Then, the winding factor of the conventional FSPM machines with composite phases is calculated.

Finally, taking a three-phase 24/22 conventional FSPM machine as an example, the machine is connected to a standard six-phase 24/22 machine and a dual three-phase 24/22 machine. The sufficiently large and symmetrical back-EMFs and sufficiently large electromagnetic torque confirm the correctness of the proposed method for determining the optimal stator-rotor combinations of the composite phase machines.