Cycle-Iterative Image Dehazing Based on Noise Evolution

Abstract

Benefiting from the prevalence of machine learning theory, deep learning-based image dehazing algorithms have made remarkable progress. However, limited by (1) the incompleteness of symmetric datasets, (2) insufficient extraction of deep priors, and (3) the excessive scale of the network, such algorithms have poor generalization ability on real-world datasets and lack real-time performance. To address these issues, this paper proposes a noise evolution-based cycle-iterative dehazing algorithm. In our method, the noise evolution in each iteration includes an atmospheric scattering model (ASM)-based dehazing module, a random haze addition module, and a Retinex-based inverse enhancement module. More specifically, the ASM-based image dehazing module initially clarifies hazy images by extracting haze-related features according to the ASM. The random haze addition module combines the depth-related parameters extracted by the previous module with a random adjustment or an assignment mechanism to expand the samples, thereby addressing the problem of data shortage. The Retinex-based inverse enhancement module is introduced to mine “depth” features related to illumination, aiming to ensure the extraction of richer priors from the Retinex model. It is worth noting that both the dehazing module and the inverse enhancement module use the low-complexity U-Net as the main backbone, and the random haze addition module only involves simple operation. Therefore, it effectively suppresses the deployment scale and computational complexity of our algorithm. Experiments reveal that the proposed algorithm not only robustly restores hazy images but also exhibits promising advantages in terms of running time and the scale of network parameters.

1. Introduction

Haze, dust, and suspended particles in the atmosphere, under adverse weather conditions, typically scatter and absorb reflected light during imaging, resulting in reduced image contrast and the loss of crucial details. This degradation severely impacts both the visual quality of images and the performance of downstream high-level vision tasks that rely on high-quality inputs, such as object detection [1] and image recognition [2]. As a result, developing an efficient haze removal technique has become a critical research challenge, drawing significant attention from both academia and industry.

According to the existing literature, dehazing algorithms can be broadly classified into three categories: image enhancement-based methods, atmospheric scattering model-based methods, and learning-based methods. Image enhancement-based methods, unlike the other two categories, do not rely on prior knowledge or physical models. Instead, they directly perform global or local contrast stretching, color correction, and detail enhancement to restore hazy images. Common techniques in this group include histogram equalization (HE) [3], color correction methods [4], and Retinex-based methods [5]. These algorithms are relatively simple and computationally efficient. However, they often neglect the underlying optical degradation mechanisms involved in the imaging process, making them susceptible to over-enhancement, artifacts, and other undesired side effects during the dehazing process.

In contrast, atmospheric scattering model-based methods treat the hazy image as a result of the superposition of the scene’s true radiance and the airlight component after atmospheric attenuation. Notable examples include the dark channel prior (DCP) [6], the color attenuation prior (CAP) [7], and the gamma correction prior (GCP) [8]. These methods are more effective in preserving real color and structural details, thanks to the incorporation of physical constraints. Nevertheless, they often rely on prior assumptions that may not hold in more complex scenarios, such as those involving dense or uneven haze. This can lead to inaccuracies in the estimation of atmospheric light and transmission maps, ultimately impairing the effectiveness of the dehazing results.

With the rapid development of artificial intelligence, deep learning models have gradually become the main research strategy in the field of image dehazing, offering superior performance over traditional methods in both restoration quality and computational efficiency. However, persistent challenges, especially for incomplete symmetric datasets and inadequate depth prior extraction, as well as oversize network architectures, continue to restrain the generalization capability and real-time applicability of existing learning-based dehazing algorithms.

Recently, diffusion models [9] have gained widespread use in computer vision, leading to several impactful advancements. A diffusion model typically consists of two stages, noise addition and denoising, which allows for the deep model to explore a wider range of possibilities. Motivated by this, we propose a cycle-iterative image dehazing algorithm from the perspective of noise evolution, which effectively integrates denoising, noise addition, and re-denoising into a unified framework. Specifically, the noise evolution in each iteration comprises three modules: a dehazing module, a random haze addition module, and an inverse enhancement module. These components simulate haze degradation and restoration, optimizing feature extraction and enhancing the algorithm’s applicability in real-world scenarios. It is important to note a key distinction between our noise evolution and traditional diffusion models. Unlike the two-stage process of diffusion (which involves only noise addition and denoising), our method adopts a cyclic iterative strategy of denoising, adding noise, and re-denoising, which helps to learn more possibilities. Moreover, the atmospheric scattering model (ASM) is embedded within the dehazing module, while the Retinex model is incorporated in the inverse enhancement module. This integration leverages physical models to guide network training. Specifically, the Retinex model is applied to enhance the inverse of the hazy images synthesized by the previous result produced by the ASM-based dehazing module. As such, the two models work independently without interfering with one another, each contributing its own functionality for denoising. Experiments demonstrate that the proposed algorithm achieves impressive dehazing results, significantly improving generalization in real-world environments. Furthermore, it outperforms existing state-of-the-art methods in terms of computational efficiency. Our contributions are summarized as follows:

• To the best of our knowledge, we are the first to propose a novel dehazing framework grounded in the concept of noise evolution. This innovative approach not only enables the virtualization of haze data during the process but also facilitates the extraction of richer, more informative priors from both the atmospheric scattering model (ASM) and Retinex model. By integrating these models within a dynamic iterative cycle, our framework introduces a new paradigm for image dehazing that enhances both the interpretability and effectiveness of haze removal.
• In response to the limitations of existing symmetric datasets, particularly in terms of sample diversity and completeness, we introduce a novel random haze addition module. This module innovatively simulates haze and applies it to the existing dataset, effectively expanding the sample space. By generating virtual haze variations, our method not only enriches the dataset but also significantly enhances its robustness. This expansion improves the performance of our approach across both real-world images and their virtual counterparts, marking a substantial advancement in dehazing techniques by addressing the gap in diverse, high-quality training data.
• To address the limitation of existing algorithms, which primarily focus on haze-related depth features or overlook the Retinex model, we propose an innovative inverse enhancement module that leverages a reverse strategy. This module is designed to extract and refine depth features related to illumination, thereby solving the critical issues of over-dehazing and under-dehazing. By incorporating illumination-driven enhancements, our approach enables a more balanced and accurate dehazing process, offering a significant advancement over traditional methods that fail to account for these complex scenarios.

The paper is organized as follows. Section 2 provides a comprehensive review of the related works in image dehazing, highlighting key advancements and identifying the limitations of existing approaches. Section 3 introduces the proposed method, detailing its core components and the technical innovations. In Section 4, we present the experimental results along with a comparative analysis against state-of-the-art methods. Finally, Section 5 concludes the paper.

2. Related Works

In this section, a brief overview of the research related to single-image dehazing techniques is provided, which can be generally divided into Retinex-based image dehazing algorithms, atmospheric scattering model (ASM)-based dehazing algorithms, and learning-based image dehazing algorithms [10].

2.1. Retinex-Based Image Dehazing

Early image dehazing algorithms primarily relied on image enhancement techniques to remove haze. These methods typically improve visual perception by enhancing the local or global contrast of images. Essentially, such approaches lack a physically grounded degradation model. Meanwhile, they do not consider the underlying causes of image degradation but rather focus on visual appearance, aiming to improve image quality through techniques. Among them, the most representative algorithm is the well-known Retinex algorithm, which is based on Retinex theory [11] to achieve enhancement by decomposing an image into reflection and illumination components. Mathematically, it can be expressed as

$$\begin{array}{c}\hfill \mathit{I}(x,y)=\mathit{R}(x,y)·L(x,y)\end{array}$$

(1)

where $(x,y)$ denotes a pixel coordinate in an image, and $\mathit{I}$ is the observed image that can be expressed as the product of the reflection component $\mathit{R}$ and the illumination component L.

Traditional Retinex methods, e.g., Single-Scale Retinex (SSR) [5] and Multi-Scale Retinex (MSR) [12], can significantly brighten low-light images and improve the corresponding contrast. However, they suffer from high computational cost and require careful tuning of enhancement parameters to prevent over-enhancement and color artifacts. Recent work has therefore focused on integrating Retinex principles into deep neural networks for more efficient and robust low-light enhancement. For instance, Zhang et al. [13] introduced the Kind++ network, which explicitly decomposes input images into reflectance and illumination components. Moreover, it also employs a multi-scale illumination attention module to boost restoration accuracy. In Ref. [14], Yi et al. fused Retinex concepts with diffusion-based generative models, embedding a supervised attention mechanism guided by Retinex theory to learn and extract illumination-invariant features. More recently, to predict the initial illumination map directly, Fan et al. [15] eliminated the traditional Retinex illumination refinement stage and instead trained a convolutional neural network, streamlining the enhancement pipeline.

Image enhancement-based dehazing algorithms offer some advantages, especially for simplicity in operation and flexibility in implementation, and they have been widely applied in various image processing scenarios. However, due to the drawbacks of the Retinex model, these methods always lack the modeling of the atmospheric scattering process and often ignore the physical interactions between illumination and the medium. As a result, the restored images using this model may suffer from poor physical plausibility, which leads to deficiencies in color fidelity and detail restoration. Furthermore, most Retinex-based methods are based on global processing strategies despite using the learning method, which are inadequate in handling the spatial non-uniformity of haze distribution. Therefore, there are over-enhancement or under-enhancement issues in certain regions, thereby restricting their applicability in high-quality image restoration tasks.

2.2. Atmospheric Scattering Model-Based Image Dehazing

Atmospheric scattering model (ASM)-based [16] image dehazing algorithms are typically grounded in the prior knowledge to estimate the imaging parameter in this model, which aims to simulate the image degradation process under hazy weather conditions by modeling the underlying physical imaging mechanisms. Mathematically, the ASM can be formally expressed as follows:

$$\begin{array}{c}\hfill \mathit{I}(\mathit{x},\mathit{y})=\mathit{J}(\mathit{x},\mathit{y})·\mathit{t}(\mathit{x},\mathit{y})+\mathit{A}·(1-\mathit{t}(\mathit{x},\mathit{y}))\end{array}$$

(2)

where $\mathit{I}$ is the observed hazy image, $\mathit{J}$ is the clear image, $\mathit{A}$ is atmospheric light, and t is the transmission map. It is clear that recovering $\mathit{J}$ requires accurate estimates of both $\mathit{A}$ and t from $\mathit{I}$; thus, their estimation accuracy directly governs the quality of the recovery result.

The nature of ASM-based dehazing methods is to utilize handcrafted priors to solve for the unknown parameters of the ASM and then recover the clear scene using these parameters. A typical example is the well-known dark channel prior (DCP) by He et al. [6], which states that, in clear outdoor images, most local patches contain at least one color channel with near-zero intensity; this insight is then employed to infer the transmission map. In Ref. [7], Zhu et al. proposed the color attenuation prior (CAP), formulating a relationship between scene depth and the difference between image brightness and saturation. Subsequently, Ju et al. introduced the region line prior (RLP) [17] and the gamma correction prior (GCP) [8] to leverage inherent spatial structures for constraining the haze degradation. To enable joint dehazing and exposure compensation in a unified framework, Ju et al. [18] augmented the scattering model with a transmission-dependent absorption coefficient.

Although the above ASM-based dehazing methods have achieved remarkable progress in visual quality, their effectiveness is often constrained by the applicability of the underlying prior assumptions. For example, the DCP algorithm tends to fail when processing images with large bright regions or low-contrast scenes, as its assumption no longer holds in such cases. Moreover, these methods typically rely on a globally selected atmospheric light value, which further limits their adaptability under complex lighting conditions, thereby hindering their robustness and generalization ability in real-world applications.

2.3. Learning-Based Image Dehazing

The surge of deep learning has propelled learning-based dehazing into the forefront of research. These methods fall into two broad classes. The first class embeds the ASM within a neural network to mitigate the reliance on handcrafted priors for parameter estimation. For instance, Ren et al. [19] employed a dual-branch architecture—coarse and fine scales—to estimate the transmission map and thereby refine image details. In Ref. [20], Li et al. introduced a framework combining fuzzy region segmentation with haze-density decomposition to adapt the standard scattering model and apply multi-scale fusion to bolster enhancement quality. To further improve the performance, Liu et al. [21] proposed an illumination-adaptive scattering model to synthesize training data and incorporate an illumination-adaptive module. The other class learns haze characteristics directly from data via end-to-end networks. For example, Zhang et al. [22] unified depth estimation and dehazing objectives in a single network, fostering mutual reinforcement between the two tasks, while Su et al. [23] improved generalization by combining multiple priors with physics-driven domain transfer. Cheng et al. [24] leveraged contrastive learning to update negative samples dynamically, ensuring reconstructed images converge toward clear references while remaining distinct from adversarial examples. Fang et al. [25] designed a structure-guided dehazing network that exploits YCbCr-domain texture and channel cues to inform RGB-domain feature learning, which is able to boost color fidelity.

Benefiting from leveraging powerful nonlinear mapping capabilities and feature extraction mechanisms, deep learning-based dehazing methods have demonstrated superior performance over prior-based and enhancement-based algorithms in terms of detail restoration, edge preservation, and color fidelity. However, most deep learning-based dehazing models are trained on synthetic datasets, which are usually generated using simplified physical models and fail to fully capture the diversity and complexity of haze distributions in real-world scenarios. As a result, these models often exhibit limited generalization ability when applied to real hazy images. Moreover, due to the imbalanced distributions of haze density, illumination conditions, and scene content in synthetic datasets, the trained models may struggle to learn comprehensive degradation patterns during training, thereby affecting robustness and practical applicability. In summary, while deep learning-based dehazing approaches have achieved groundbreaking advances in both theoretical research and experimental validation, further improvements are still needed in terms of data realism, model generalization, and computational efficiency.

2.4. Iterative Image Dehazing and Enhancement

Iterative frameworks have become a promising approach in image dehazing and enhancement, which address the ill-posed nature of these tasks through progressive refinement. For instance, Fu et al. [26] introduced IPC-Dehaze, an iterative predictor–critic architecture that leverages progressively refined codebook priors through cyclic prediction–evaluation iterations, enabling stable dehazed outputs while mitigating error accumulation in real-world scenarios. Zheng et al. [27] proposed T-Net and constructed a recursively unfolded Stack T-Net, using it as a submodule. By iteratively inputting “stage output + original image,” the system achieves coarse-to-fine haze removal. In Ref. [28], Sun et al. proposed a novel framework that leverages large vision-language models (VLMs) to generate textual instructions describing normal illumination conditions. These instructions are iteratively refined to guide a diffusion model, enabling controllable and high-quality low-light image enhancement. Liang et al. [29] proposed an iterative prompt learning framework that progressively refines positive and negative textual prompts to optimize Contrastive Language-Image Pretraining (CLIP) priors, effectively minimizing the distribution gap among backlit images, enhanced results, and well-lit images in the latent space, which achieves high-quality and generalizable image enhancement without paired training data. Liu et al. [30] developed a cyclic “brightness stretching coefficient estimation-fusion” framework to progressively correct non-uniform low illumination. This method iteratively optimizes local luminance mapping through two-stage refinement while preserving structural details and color fidelity.

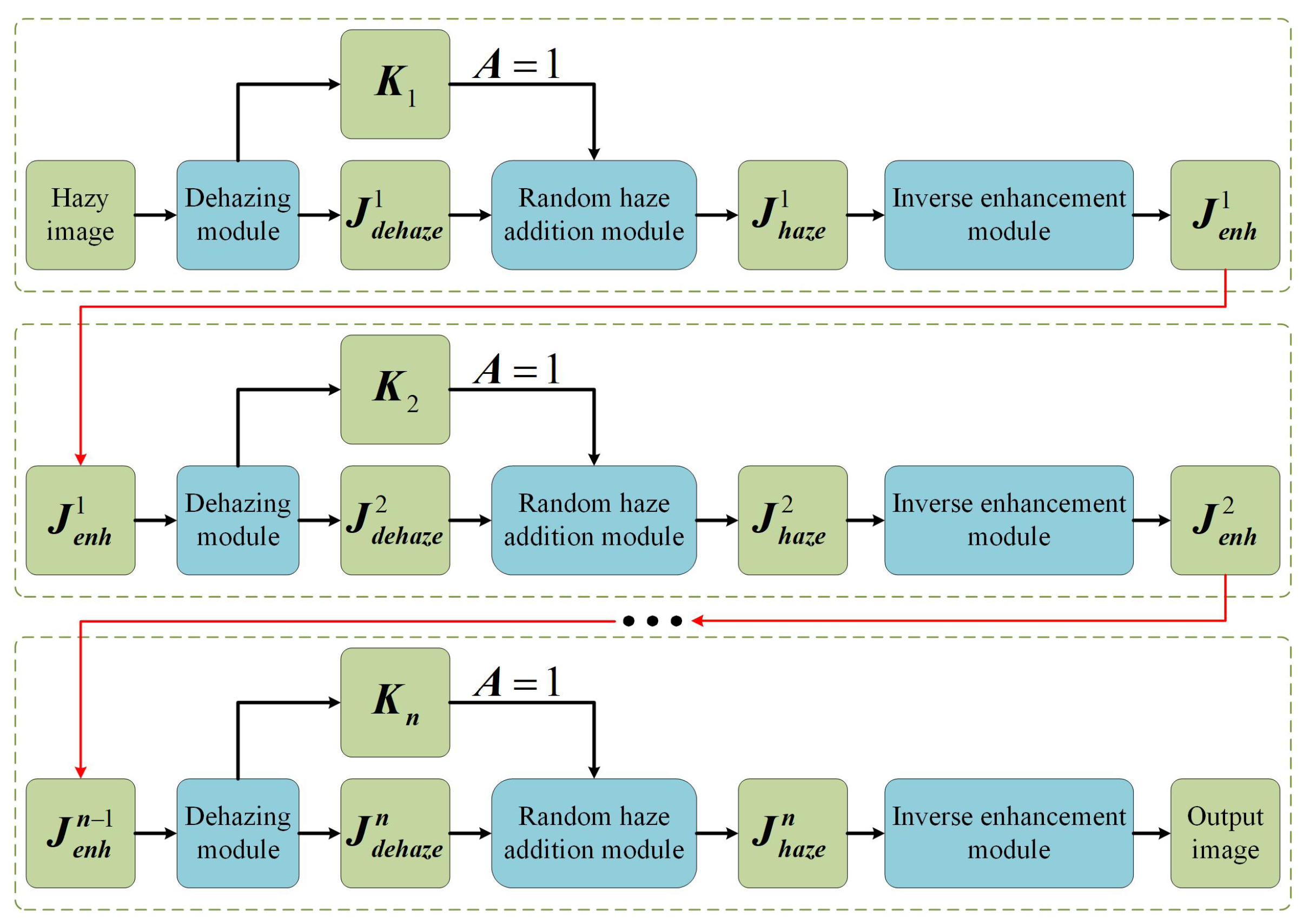
3. Cycle-Iterative Image Dehazing Based on Noise Evolution

3.1. Overall Network Architecture

To address these challenges mentioned above, we introduce a cycle-iterative image dehazing framework, which is inspired from the perspective of noise evolution. Its core idea is to alternately denoise and add noise for an input image in order to enhance our method’s generalization capability. More specifically, each iteration consists of three sequential modules: The atmospheric scattering model (ASM)-based dehazing module (evolution 1) extracts haze-related features from an input image and performs initial denoising to attenuate the haze effect using the ASM. The responsibility of the random haze addition module (evolution 2) is to re-inject the controlled synthetic haze by randomly sampling from atmospheric light distribution combined with the estimated transmission map. This evolution is able to generate varied haze intensities, effectively augmenting the training data. The Retinex-based inverse enhancement module (evolution 3) inverts the synthetically hazed image, processes it through a Retinex-based image enhancement network, and then re-inverts the output to reconstruct the dehazed image. This invert–enhance cycle preserves structural details and delivers improved contrast and color fidelity in the final result. Figure 1 provides an overview of the proposed framework, illustrating the hierarchical relationships and interactions among its core components. A more detailed depiction of the overall architecture is shown in Figure 2. As demonstrated, the proposed method iteratively refines the input through cycles of denoising and noise evolution, leading to enhanced detail preservation and visual clarity. This iterative strategy significantly improves the robustness and generalization ability of the model when applied to complex real-world hazy scenes.

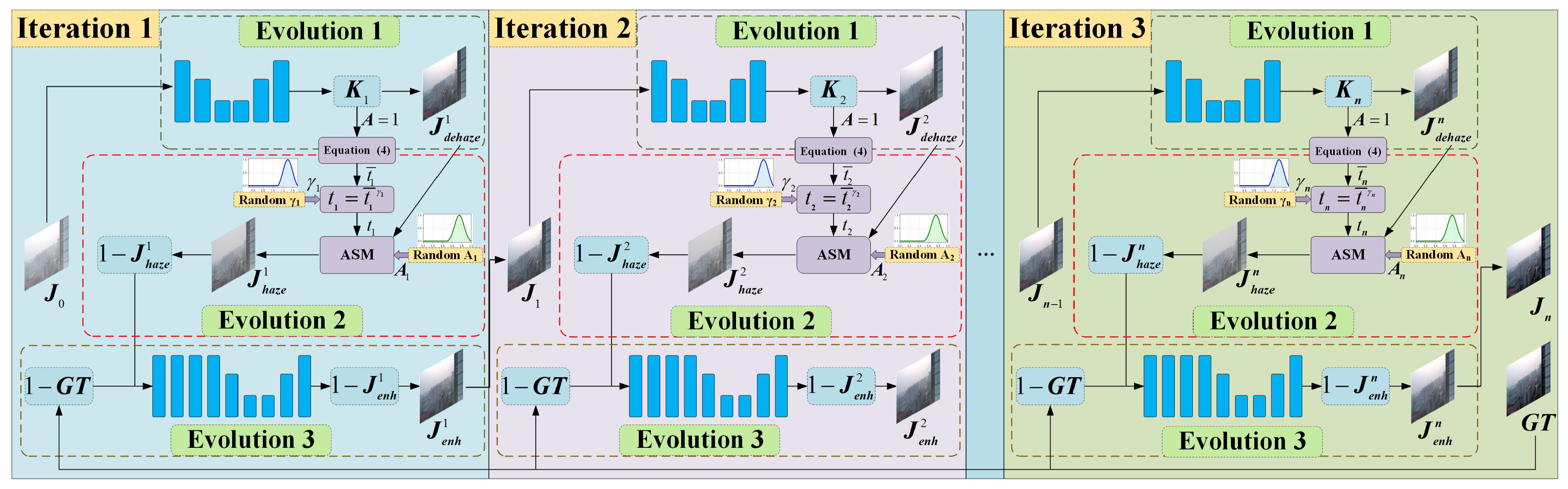
3.2. ASM-Based Dehazing Module (Evolution 1)

Motivated by the unified parameter estimation strategy proposed in AOD-Net [31], this paper combines the atmospheric light $\mathit{A}$ and transmission $t\left(x\right)$ into a single parameter matrix $\mathit{K}\left(\mathit{x}\right)$. Formally, according to this strategy, the ASM, i.e., Equation (2), can be reformulated to be

$$\begin{array}{c}\hfill \mathit{J}(\mathit{x},\mathit{y})=\mathit{K}(\mathit{x},\mathit{y})·\mathit{I}(\mathit{x},\mathit{y})-\mathit{K}(\mathit{x},\mathit{y})+\mathrm{b}\end{array}$$

(3)

where

$$\begin{array}{c}\hfill \mathit{K}(\mathit{x},\mathit{y})={\displaystyle \frac{\frac{1}{\mathit{t}(\mathit{x},\mathit{y})}(\mathit{I}(\mathit{x},\mathit{y})-\mathit{A})+(\mathit{A}-\mathrm{b})}{\mathit{I}(\mathit{x},\mathit{y})-1}}\end{array}$$

(4)

where $\mathit{K}$ encapsulates the atmospheric light $\mathit{A}$ and transmission map t, and b denotes a constant offset.

To reduce the complexity and computational burden associated with the AOD-Net, this paper replaces conventional CNN architectures with a U-Net encoder–decoder structure [32], augmented by residual blocks [33] to facilitate effective feature representation and propagation. In the encoder stage, multi-scale features are progressively extracted through max-pooling operations combined with residual connections. In the decoder stage, features are up-sampled via transposed convolutions, while skip connections concatenate corresponding encoder feature maps to recover detailed information. A final $1\times 1$ convolutional layer outputs the joint estimation parameter. The network then produces the dehazed image by applying Equation (3) using $\mathit{K}$ and the original hazy input $\mathit{I}$. The architecture of this dehazing module is illustrated on the left side in Figure 3. As the initial step in the proposed method using noise evolution, this module reduces haze and suppresses noise in the input image.

3.3. Random Haze Addition Module (Evolution 2)

As aforementioned, the random haze addition module is created to simulate hazy images that can expand the training datasets to some extent. Meanwhile, it is obvious that the joint parameter $\mathit{K}$ obtained from the previous dehazing module is related to depth and thus can be further served as a key input for the haze addition module. To align the $\mathit{K}$ and t as much as possible, here we utilize Equation (4) and assume $\mathit{A}=1$ to compute the coarse transmission map ${\overline{\mathrm{t}}}_i$ in the i-th iteration. Here, we remark that, although the coarse transmission map is produced by $\mathit{A}=1$ and $\mathit{K}$, the computed transmission map still can provide a relatively accurate result since the atmospheric light value in real-world images is typically less than 1. Now, we only need to randomly reassign the value of atmospheric light and the distribution of the transmission map to simulate hazy images. Here, two strategies are proposed:

• The first strategy applies a statistically guided linear normalization to the initial transmission map. Specifically, it is formulated as

  $$\begin{array}{c}\hfill t_i={\alpha }_i·{\overline{t}}_i+{\beta }_i\end{array}$$

  (5)

  where ${\alpha }_i$ and ${\beta }_i$ denote the scaling coefficient and offset term in the linear transformation, respectively. These parameters are derived from the statistical distribution of ${\overline{t}}_i$. By applying the linear transformation in Equation (5), the distribution of ${\overline{t}}_i$ is normalized to $[0,1]$ as follows:

  $$\begin{array}{c}\hfill \begin{array}{c}{\alpha }_i·{\overline{t}}_{min}^i+{\beta }_i=0\hfill \\ {\alpha }_i·{\overline{t}}_{max}^i+{\beta }_i=1\hfill \end{array}\end{array}$$

  (6)

  where symbols ${\overline{t}}_{max}^i$ and ${\overline{t}}_{min}^i$ denote the maximum and minimum values of the coarse transmission map ${\overline{t}}_i$, respectively. To reduce the influence of outliers, the 5th and 95th percentiles are used in place of global extrema during experiments to improve robustness. This linear transformation maps the original values into the standard interval $[0,1]$, ensuring physical plausibility of the transmission map generated.
• The other strategy is based on gamma correction [8] to perform nonlinear adjustment. To effectively refine the transmission map t, the gamma value $\gamma$ is randomly sampled within the range [1.1, 1.5]. Setting this range aims to balance low- and high-transmission regions and avoid excessive correction. By introducing randomness into gamma sampling, this method simulates the non-uniformity of haze in natural environments, thereby enhancing the realism and diversity of the synthesized hazy images. Mathematically, the expression of such a transformation is given by

  $$\begin{array}{c}\hfill t_i={{\overline{t}}_i}^{{\gamma }_i}\end{array}$$

  (7)

  where ${\gamma }_i$ denotes the randomly selected gamma value in the i-th iteration. Subsequently, the adjusted transmission map t and randomly generated atmospheric light $\mathit{A}$ are substituted into Equation (2) to synthesize a hazy image. The second stage of each iteration not only facilitates effective collaboration with the subsequent enhancement module but also significantly diversifies the training data through controlled noise introduction. For clarity, the architecture of the haze addition module is illustrated on the right side in Figure 3. Thanks to the second stage within the proposed noise evolution framework, the random haze addition module systematically introduces synthetic haze and is able to control noise into the output from the previous dehazing stage. The benefit of doing so is that it can expand the dataset from the original samples that may contain non-uniform haze cover, which is very useful to improve the robustness or generalization of our method.

3.4. Retinex-Based Inverse Enhancement Module (Evolution 3)

Low-light images typically exhibit characteristics such as reduced brightness and blurred details. Following the assumption in [8] that the inversion of a hazy image closely resembles a low-light scenario, we invert hazy images to generate visually low-light equivalents (see Figure 4). By applying Retinex-based image enhancement techniques to these inverted images and subsequently re-inverting the enhanced outputs, an effective dehazing outcome can be achieved. This is due to the fact that employing Retinex to enhance an image is not only a visual enhancement by learning a deep prior on illumination, but it also distills latent knowledge of the Retinex model into our proposed network.

Motivated by this fact, a Retinex-based inverse enhancement module is proposed, whose nature is to deeply exploit the “illumination”-related depth features in hazy images based on a reverse strategy, and then use it to effectively enhance the dehazed image quality. According to Ref. [8], the mathematical formulation corresponding to the complete dehazing process can be written as

$$\begin{array}{c}\hfill \mathit{H}=1-f\left(1-\mathit{L}\right)\end{array}$$

(8)

where $\mathit{L}$ represents the output from the haze addition module, $f\left(·\right)$ denotes the image enhancement network, and $\mathit{H}$ is the final enhanced image obtained after applying the inversion operation. It can be analyzed from the above equation that this module firstly employs an image inversion operation on both the hazy image produced by the haze addition module, and then using a Retinex deep network to deal with this inverted scenario, the final output can be further obtained by using inversion operation again. Therefore, once these inverted images are produced, they are fed into a decomposition network composed of multiple convolutional layers with ReLU activations for feature extraction. The network ultimately outputs the reflectance component ${\mathit{R}}_{\mathrm{low}}^i$ and illumination component ${\mathit{L}}_{low}^i$ of the inverted hazy image, alongside the reflectance component ${\mathit{R}}_{\mathrm{normal}}^i$ and illumination component ${\mathit{L}}_{\mathrm{normal}}^i$ of the inverted clear image.

The enhancement network takes the illumination component ${\mathit{L}}_{\mathrm{low}}^i$ from the decomposition network and processes it using a U-Net architecture to generate an illumination variation map ${\widehat{\mathit{L}}}_{\mathrm{low}}^i$ with the same dimensions as the input. This map captures the necessary illumination corrections for enhancing low-light representations. It is then combined with the denoised reflectance variation ${\widehat{\mathit{R}}}_{\mathrm{low}}^i$ to reconstruct the enhanced image. Finally, an inverse transformation is applied to bring the enhanced result back into the natural image domain, thereby effectively improving the visual quality. The architecture of this module is depicted in Figure 5.

Relative to Retinex-Net [34], the proposed module incorporates an inversion operation, reduces the convolutional depth of the decomposition network, and leverages a U-Net architecture to extract the illumination variation map ${\widehat{\mathit{L}}}_{\mathrm{low}}^i$. This design effectively reduces computational complexity while preserving the core capabilities of image decomposition. As the third stage in the proposed noise evolution framework, the Retinex-based inverse enhancement module brightens and enhances the hazy image again from the perspective of the Retinex model, ultimately producing a clean output.

3.5. Loss Function

To ensure the effectiveness and robustness of the proposed dehazing framework, a set of multi-type constraints is introduced and optimized to enhance overall network performance. The dehazing module employs a mean squared error (MSE) loss to measure the pixel-wise discrepancy between the initial dehazed output and the clear image. By accumulating this loss across multiple iterations, the method reinforces the reliability and accuracy of the dehazing process. The corresponding mathematical formulation is given as

$$\begin{array}{c}\hfill {\mathcal{L}}_1={\displaystyle \frac{1}{n}}\sum _{i=1}^N{∥\mathit{J}-{\mathit{J}}_{\mathrm{dehaze}}^i∥}_2^2\end{array}$$

(9)

where ${\mathit{J}}_{dehaze}^i$ denotes the output of the dehazing module at the i-th iteration, $\mathit{J}$ denotes the corresponding clear image, ${\parallel \parallel }_2$ represents the ${\mathrm{L}}_2$ norm, n is the total number of image pixels, and i is the total number of iterations.

In the inverse enhancement module, following the design principles of Retinex-Net, three loss terms are jointly employed to supervise learning: reconstruction loss, reflectance consistency loss, and relighting loss. The reconstruction loss ensures the accuracy of the illumination and reflectance components predicted by the decomposition network. The reflectance consistency loss enforces alignment between the reflectance components of the inverted (low-light) and clear images. The relighting loss encourages the illumination condition of the inverted image to better approximate that of the clear image. The overall loss function for this module is defined as

$$\begin{array}{c}\hfill {\mathcal{L}}_2=\sum _{i=1}^{\mathrm{N}}\left({\mathcal{L}}_{\mathrm{rec}}^i+{\mathcal{L}}_{\mathrm{rcl}}^i+{\mathcal{L}}_{\mathrm{rl}}^i\right)\end{array}$$

(10)

where ${\mathcal{L}}_{\mathrm{rec}}^i$, ${\mathcal{L}}_{\mathrm{rcl}}^i$, and ${\mathcal{L}}_{\mathrm{rl}}^i$ represent the reconstruction loss, reflectance consistency loss, and relighting loss at the i-th iteration, respectively:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{L}}_{\mathrm{rec}}^i=\sum _{m=\mathrm{low},\mathrm{normal}}\sum _{n=\mathrm{low},\mathrm{normal}}{\lambda }_{mn}{∥{\mathit{R}}_m^i\times {\mathit{L}}_n^i-{\mathit{S}}_n^i∥}_1\hfill \\ {\mathcal{L}}_{\mathrm{rcl}}^i={∥{\mathit{R}}_{\mathrm{low}}^i-{\mathit{R}}_{\mathrm{normal}}^i∥}_1\hfill \\ {\mathcal{L}}_{\mathrm{rl}}^i={∥{\mathit{R}}_{\mathrm{low}}^i·{\widehat{\mathit{L}}}_{\mathrm{low}}^i-{\mathit{S}}_{\mathrm{normal}}^i∥}_1\hfill \end{array}\right.\end{array}$$

(11)

where ${\mathit{S}}_{\mathrm{normal}}^i$ denotes the inverted version of the clear image at the i-th iteration, and ${\parallel \parallel }_1$ represents the ${\mathrm{L}}_1$ norm.

The MSE loss and total variation (TV) loss are introduced as global constraints at each iteration. The MSE loss encourages the enhanced output to remain aligned with the clear image, while the TV loss penalizes abrupt gradient changes to suppress noise and artifacts during dehazing and enhancement, thereby preserving the natural appearance of the image. The corresponding mathematical expressions are defined as

$$\begin{array}{c}\hfill {\mathcal{L}}_3=\sum _{i=1}^N\left({\mathcal{L}}_{\mathrm{mse}}^i+{\mathcal{L}}_{\mathrm{TV}}^i\right)\end{array}$$

(12)

where

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{mse}}^i={\displaystyle \frac{1}{n}}{∥\mathit{J}-{\mathit{J}}_{\mathrm{enh}}^i∥}_2^2\end{array}$$

(13)

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{TV}}^i=\sum _{\left(x,y\right)}\sqrt{{\nabla }_h{M}_i{\left(x,y\right)}^2+\nabla v{M}_i{\left(x,y\right)}^2}\end{array}$$

(14)

where ${\mathit{J}}_{\mathrm{enh}}^i$ denotes the output of the inverse enhancement module at iteration i, while ${\nabla }_h{M}_i{\left(x,y\right)}^2$ and ${\nabla }_v{M}_i{\left(x,y\right)}^2$ represent the horizontal and vertical gradients at pixel location $(x,y)$, respectively.

A weighted combination of the aforementioned loss terms is employed to construct a unified total loss function, enabling joint optimization across all modules and ensuring the robustness of the network in hazy environments. The total loss function is formulated as follows:

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{total}}={\beta }_1{\mathcal{L}}_1+{\beta }_2{\mathcal{L}}_2+{\beta }_3{\mathcal{L}}_3\end{array}$$

(15)

where ${\beta }_i$ represents the weighting coefficient used to balance the contribution of each loss term.

4. Experiment Results Analysis

4.1. Experiment Settings

The proposed method is implemented using the PyTorch framework and trained on a system equipped with an NVIDIA GeForce RTX 3080 GPU, an Intel Core i5-10900X CPU, and 32 GB of RAM. During training, images are randomly cropped to a fixed size of 640 × 480, followed by random augmentations, such as rotation at arbitrary angles, horizontal and vertical flipping, or remaining unchanged, to enhance data diversity. The batch size is set to 8, with the Adam optimizer employed and an initial learning rate of 0.001.

4.2. Dataset and Benchmark

The RESIDE [35] dataset is a large-scale synthetic hazy image benchmark that provides both indoor and outdoor training subsets. In this study, the ITS (Indoor Training Set) and OTS (Outdoor Training Set) are employed to train the proposed network. For evaluation, the O-HAZE [36], I-HAZE [37], Real-world Task-Driven Testing Set (RTTS) [35], and hybrid Subjective Testing Set (HSTS) [35] datasets are used. The proposed approach is compared against several typical or state-of-the-art dehazing algorithms, including DCP [6], T-Net [27], IPC-Dehaze [26], C2PNet [38], RIDCP [39], KANet [40], DCMPNet [20], and DNMGDT [23]. It is worth noting that both T-Net and IPC-Dehaze adopt iterative strategies similar to our noise evolution framework. Therefore, including them in the comparison helps to highlight the advantages and effectiveness of our proposed algorithm.

4.3. Experiment on Synthetic Datasets

To quantitatively assess the dehazing performance on synthetic hazy datasets, the Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) are employed as objective evaluation metrics. The PSNR quantifies the intensity-level differences between the dehazed and reference clear images, while the SSIM evaluates their structural similarity in terms of luminance, contrast, and structural consistency. Higher values of the PSNR and SSIM indicate superior dehazing quality. In addition, the runtime of each algorithm is recorded as an indicator of computational efficiency to provide a comprehensive performance comparison.

As shown in

Table 1. Objective metrics comparison of different methods on the SOTS dataset.

Method	Indoor		Outdoor
	PSNR (dB)	SSIM	PSNR (dB)	SSIM
DCP	17.13	0.446	16.62	0.392
T-Net	21.79	0.813	19.03	0.674
IPC-Dehaze	22.87	0.793	20.06	0.694
C2PNet	21.32	0.605	17.35	0.525
RIDCP	22.54	0.542	17.26	0.461
KANet	23.22	0.725	19.18	0.618
DCMPNet	24.53	0.756	21.25	0.750
DNMGDT	24.55	0.873	21.12	0.757
Proposed Method	23.83	0.834	20.23	0.702

and

Table 2. Objective metrics comparison of different methods on the I-HAZE and O-HAZE datasets.

Method	I-HAZE		O-HAZE
	PSNR (dB)	SSIM	PSNR (dB)	SSIM
DCP	16.33	0.477	16.03	0.407
T-Net	20.13	0.803	19.23	0.594
IPC-Dehaze	22.09	0.699	19.97	0.673
C2PNet	19.79	0.577	19.05	0.563
RIDCP	20.71	0.537	19.52	0.515
KANet	22.17	0.725	18.89	0.598
DCMPNet	23.29	0.773	21.25	0.714
DNMGDT	23.55	0.786	21.17	0.710
Proposed Method	23.83	0.834	21.23	0.702

, the proposed method outperforms most of the selected benchmark approaches on synthetic datasets, demonstrating the superiority of our approach. It is worth noting that although the PSNR and SSIM scores are slightly lower than those of DNMGDT and DCMPNet, our method offers significantly faster computational speed (see

Table 3. Runtime comparison of different methods on the SOTS dataset.

Method	Publication	Platform	Time (s)
DCP	CVPR’09	Matlab	0.3276
T-Net	TMM’22	Pytorch	0.297
IPC-Dehaze	CVPR’25	Pytorch	0.0393
C2PNet	CVPR’23	Pytorch	0.0284
RIDCP	CVPR’23	Pytorch	0.0541
KANet	TPAMI’24	Pytorch	0.0326
DCMPNet	CVPR’24	Pytorch	0.0380
DNMGDT	TMM’25	Pytorch	0.0367
Proposed Method	–	Pytorch	0.0276

). These results highlight the effective balance between high-quality dehazing and computational efficiency, making our approach particularly suitable for practical applications, such as on mobile devices and in real-time video processing, where low latency is essential. Moreover, both DNMGDT and DCMPNet struggle to process outdoor images collected from real-world scenarios, as will be further demonstrated and discussed later.

As illustrated in Figure 6 and Figure 7, there are clear disparities in image restoration quality among different dehazing algorithms. The DCP algorithm, which relies on the dark channel prior, effectively eliminates haze but results in overall low image brightness and introduces artifacts in high-intensity regions. Among the deep learning-based approaches, T-Net and IPC-Dehaze exhibit limitations in local chromatic adaptation, resulting in noticeable hue inconsistencies on objects such as chairs. C2PNet and RIDCP exhibit limited capability in restoring details, often leaving residual haze and causing localized color distortions. KANet tends to produce overexposed outputs, leading to the loss of detail in bright areas. Moreover, DCMPNet and DNMGDT demonstrate unsatisfied performance in complex scenes, such as sidewalks and distant regions, where haze remnants or structural blurring remain apparent. In contrast, the algorithm proposed exhibits notable superiority. Specifically, the proposed approach significantly enhances the overall brightness of the dehazed images and achieves superior performance in haze removal, color fidelity, and detail preservation, producing clearer and more visually realistic restoration results.

4.4. Experiment on Real-World Datasets

To further evaluate the performance of the proposed algorithm on real-world hazy images, we conducted comparative experiments using widely adopted real hazy images from the RTTS and HSTS datasets. As shown in Figure 8, the traditional dark channel prior (DCP) algorithm exhibits notable limitations when applied to real hazy images, often resulting in underexposed dehazed outputs. Although deep learning-based approaches, such as DCMPNet and DNMGDT, show promising results on synthetic datasets, they still struggle with real-world applications. This is because the haze in the synthetic dataset is simulated based on simplified physical rules, which leads to these methods being unable to fully learn the potential haze feature in the real world. For example, as seen in the sixth row of Figure 8, DNMGDT fails to adequately remove haze in background regions, leading to incomplete detail recovery. Furthermore, color restoration is unstable in some cases, with DCMPNet and IPC-Dehaze introducing noticeable color distortions in reconstructed structures, such as roads and buildings. In contrast, our algorithm effectively bridges the domain gap between synthetic and real-world images by not only removing haze more thoroughly but also preserving natural color fidelity and structural details. This advantage can be attributed to our noise addition module, which can simulate richer haze features for alignment with the real world.

4.5. Ablation Experiments

To systematically validate the effectiveness and contribution of the key components in the proposed algorithm, a set of ablation experiments was designed based on hazy images from various scenarios. The ablation study includes the following four comparative variants:

• Variant I: Both the inverse enhancement module and the random haze addition module are removed.
• Variant II: The random haze addition module is removed, while the dehazing and inverse enhancement modules are retained.
• Variant III: The complete network structure is preserved, but the haze addition module adopts a linear transformation strategy to calibrate the initial transmission map, replacing the gamma correction method.
• Variant IV: The random haze addition module uses the gamma correction strategy, but the transmission-related parameter ${\gamma }_i$ is fixed to 1, and the atmospheric light value is set to 0.85. This variant examines the model’s robustness and generalization ability under fixed parameter settings.

As the baseline for comparison, the complete proposed network that uses gamma correction as the calibration method is employed. All the experiments are conducted under the same training environment, using identical training parameters and data processing strategies to ensure result comparability and consistency. The experiment results are quantitatively evaluated using the PSNR and SSIM metrics, as shown in

Table 4. Ablation results of different variants in terms of PSNR and SSIM.

Method	Indoor		Outdoor
	PSNR (dB)	SSIM	PSNR (dB)	SSIM
Variant I	18.13	0.546	16.62	0.592
Variant II	21.32	0.605	18.35	0.525
Variant III	21.45	0.674	18.26	0.653
Variant IV	22.56	0.765	19.36	0.674
Proposed Method	23.74	0.834	21.05	0.702

, with qualitative dehazing comparisons presented in Figure 9.

According to the results shown in Table 4, comparing Variant I (only the basic dehazing module) with Variant II (with the added inverse enhancement module), the PSNR improves by 3.19 dB and 1.73 dB, respectively. This validates the inverse enhancement module’s role in enhancing illumination and detail visibility, aiding the model in recovering the real structure and color of the scene. The SSIM also increases, indicating improved structural consistency and visual perception. Introducing the random haze addition module further boosts the PSNR by 2.42 dB and 2.7 dB, and the SSIM by 0.229 and 0.177, compared to Variant II. This highlights the module’s ability to simulate varying haze intensities and distributions.

Between the gamma correction and linear transformation strategies in the haze addition module, the gamma correction approach yielded a higher PSNR and SSIM, indicating its superior capability in simulating the non-uniform lighting and perceptual consistency in real hazy images. The nonlinear nature of gamma correction better approximates the complex attenuation effects caused by scattering and absorption in natural scenes, thereby narrowing the domain gap between synthetic and real data. In addition, the algorithm proposed incorporates a strategy based on a random parameter generation mechanism. Compared with Variant IV, which utilizes fixed parameter settings, both the PSNR and SSIM metrics demonstrate improvement. This suggests that by introducing a stochastic process for generating atmospheric light values and transmittance, the training bias caused by fixed parameters can be effectively mitigated. Consequently, the model exhibits enhanced adaptability and stability when confronted with complex and dynamic real-world environments.

In summary, through the stepwise integration and quantitative evaluation of key modules, the experiment results fully validate the effectiveness of the inverse enhancement module, the random haze addition module, and the random parameter sampling mechanism in enhancing the dehazing performance. These modules work in synergy to provide solid theoretical support for building a high-performance dehazing network architecture.

By deeply analyzing the ablation experiment results, the following findings can be drawn: In terms of the dehazing effect, Variant I (only basic dehazing module) and Variant II (dehazing module + reverse enhancement module) still have obvious haze residue in this area. In terms of color restoration quality, in the gradual improvement process from Variant I to the complete algorithm, the experiment results gradually presented a natural color distribution that was closest to the real scene, as shown in the framed area of Figure 9. This series of changes strongly proves the synergy between the reverse enhancement module and the parameter randomization mechanism in improving color fidelity. In addition, as illustrated in the second-row image of Figure 9, by comparing the edge detail preservation of Variant III and the complete algorithm, it can be found that the complete algorithm has obvious advantages in preserving vegetation details. So, we can conclude that gamma correction strategies can better adapt to the characteristic differences in different scenes than the linear correction strategy, thereby achieving finer detail preservation in the dehazing process.

4.6. Performance Test on Different Gamma Value Ranges

To further evaluate the influence of different gamma ranges, we implemented randomized value selection across four gamma intervals. Given that gamma values approaching zero exert minimal impact on transmission map correction, our experimental setup begins at $\gamma =0.1$. The quantitative evaluation results for these intervals are presented in

Table 5. Experiment results on different ranges of gamma value on SOTS.

Gamma Ranges	PSNR (dB)	SSIM
$[0.1,0.5)$	18.61	0.513
$[0.5,1.0)$	21.32	0.627
$[1.0,1.5)$	22.97	0.723
$[1.5,2.0)$	21.51	0.677
$[2.0,2.5]$	20.98	0.691

, and their corresponding visual effects are illustrated in Figure 10. As shown in Table 5 and Figure 10, a smaller gamma value ($\gamma \in [0.1,1.0]$) results in a small amount of haze remaining on the restored result. On the contrary, a larger gamma value ($\gamma \in [1,2.5]$) is capable of removing the haze cover in an image thoroughly, but the over-enhancement becomes more obvious as $\gamma$ increases. As a trade-off, $\gamma \in [1,1.5]$ is selected as the optimal range in this work.

4.7. Impact of Algorithm on Object Detection Performance

To further evaluate the impact of the proposed algorithm on high-level visual tasks, we conducted an experiment focusing on object detection. Given that hazy weather conditions can significantly degrade image quality in practical applications, adversely affecting the performance of subsequent visual tasks, it is essential to assess the impact of dehazing on these downstream tasks. For this purpose, we utilized the representative real hazy dataset RTTS (Realistic Traffic-signs in Hazy Scenes) and deployed YOLOv10 [41] as the object detection model. Both hazy images and clear images processed through various dehazing algorithms were used as input. To ensure consistency in our experiment results, all the parameters of the detection model, including input resolution and confidence thresholds, were held constant.

Figure 11 illustrates the hazy images and their corresponding detection outcomes from different dehazing algorithms. The visual results suggest that detecting directly on hazy images leads to a significant number of missed detections, particularly in the case of distant targets or those in low-contrast regions, which are frequently overlooked. In contrast, after applying the proposed method, the overall image clarity is markedly improved, with effective minimization of background interference, allowing the detector to more accurately locate and recognize targets. In comparison to other dehazing algorithms, the method proposed exhibits notable advantages in visual quality; it not only effectively restores color fidelity but also enhances detail in critical areas, thereby improving the robustness of the detection model. The experiment results indicate that our algorithm can effectively meet the requirements of object detection tasks without introducing additional semantic errors, highlighting its potential for real-world applications.

5. Conclusions

In this paper, we proposed a cycle-iterative dehazing algorithm based on noise evolution theory. The algorithm organically integrates an ASM-based dehazing module, a random haze addition module, and a Retinex-based inverse enhancement module within a multi-stage alternating iterative framework. The main advantage of this design concept is that it can simulate more virtual data with different haze levels to enhance the performance of the network. Another advantage is that our method can have an ability to better learn the mapping between hazy images and their clear versions under the joint supervision of the Retinex mode and ASM. The experiment results demonstrate that the proposed algorithm outperforms existing state-of-the-art methods across multiple objective evaluation metrics and subjective visual assessments, particularly excelling in color fidelity and texture detail preservation. Moreover, the algorithm features a concise architecture and high computational efficiency, making it well-suited for deployment in resource-constrained real-world environments.