Hippopotamus Optimization-Sliding Mode Control-Based Frequency Tracking Method for Ultrasonic Power Supplies with a T-Type Matching Network
Abstract
1. Introduction
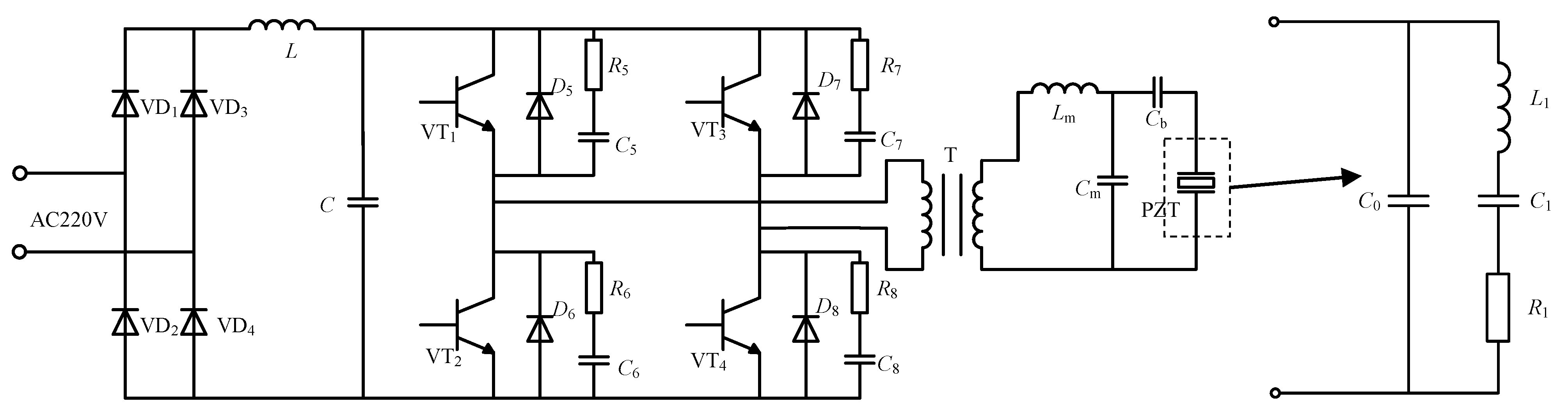
2. Analysis of the PT and Matching Network
2.1. Equations for the Piezoelectric Transducers Equivalent Model
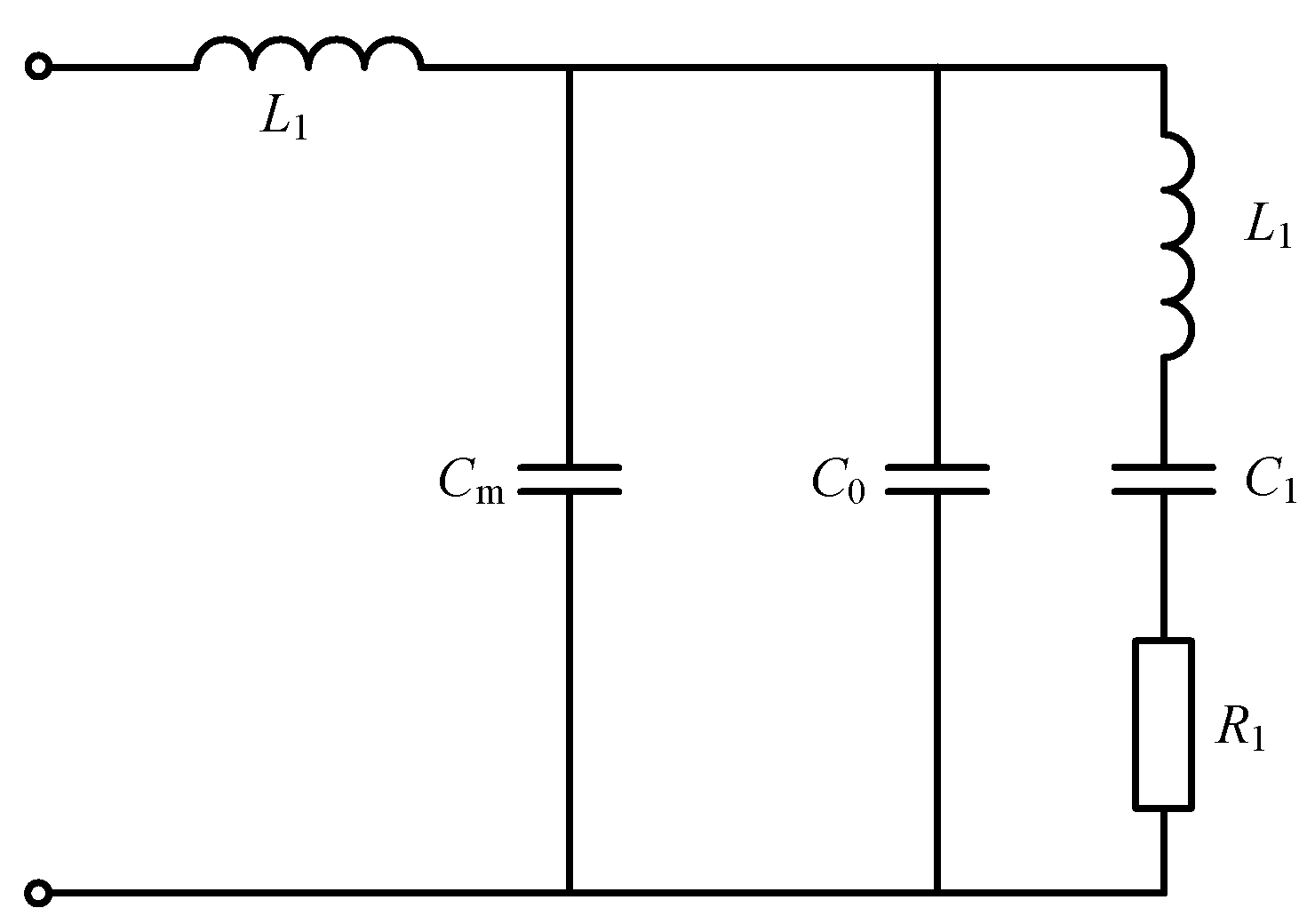
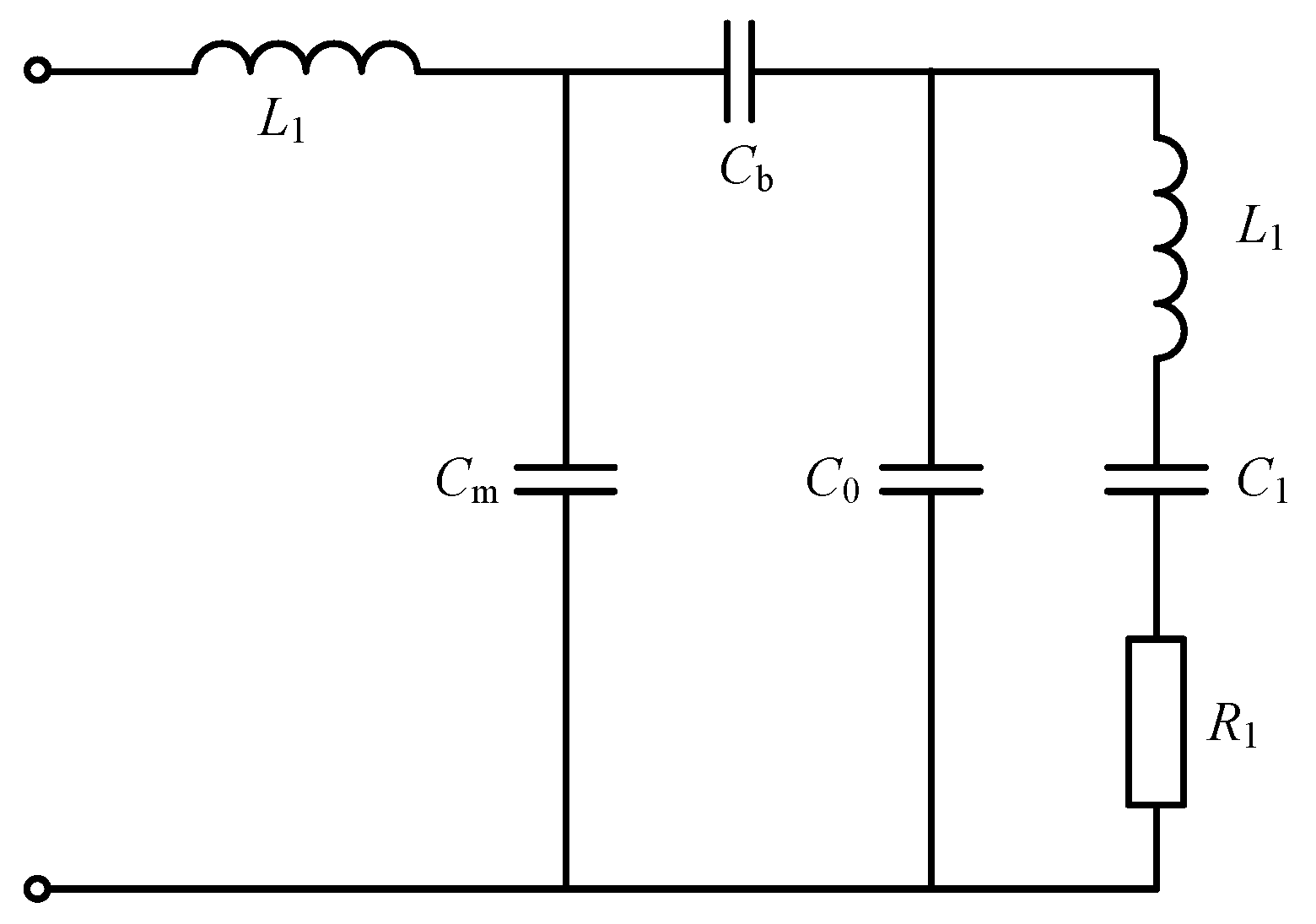
2.2. Matching Network
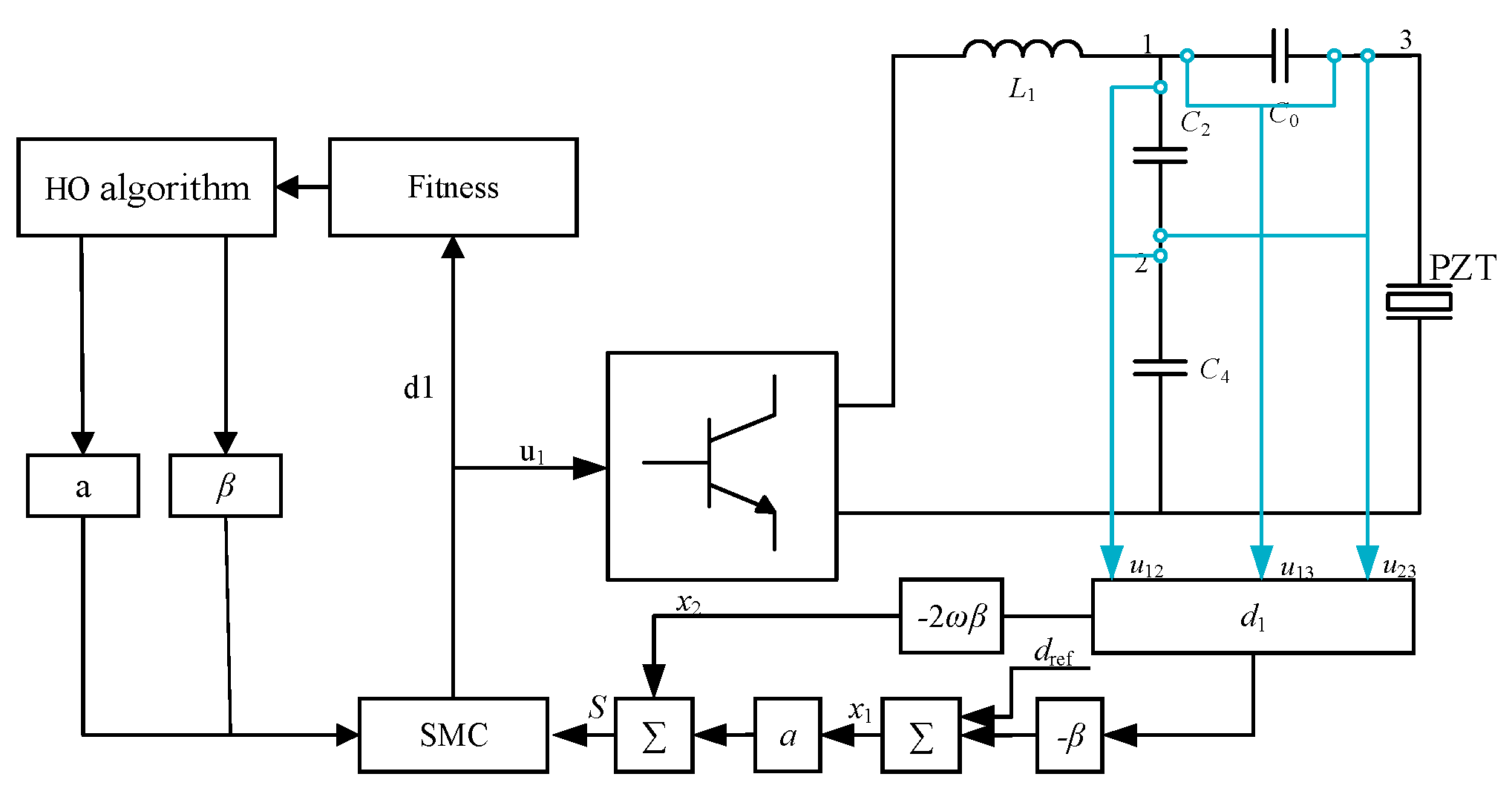
3. Tracking Method
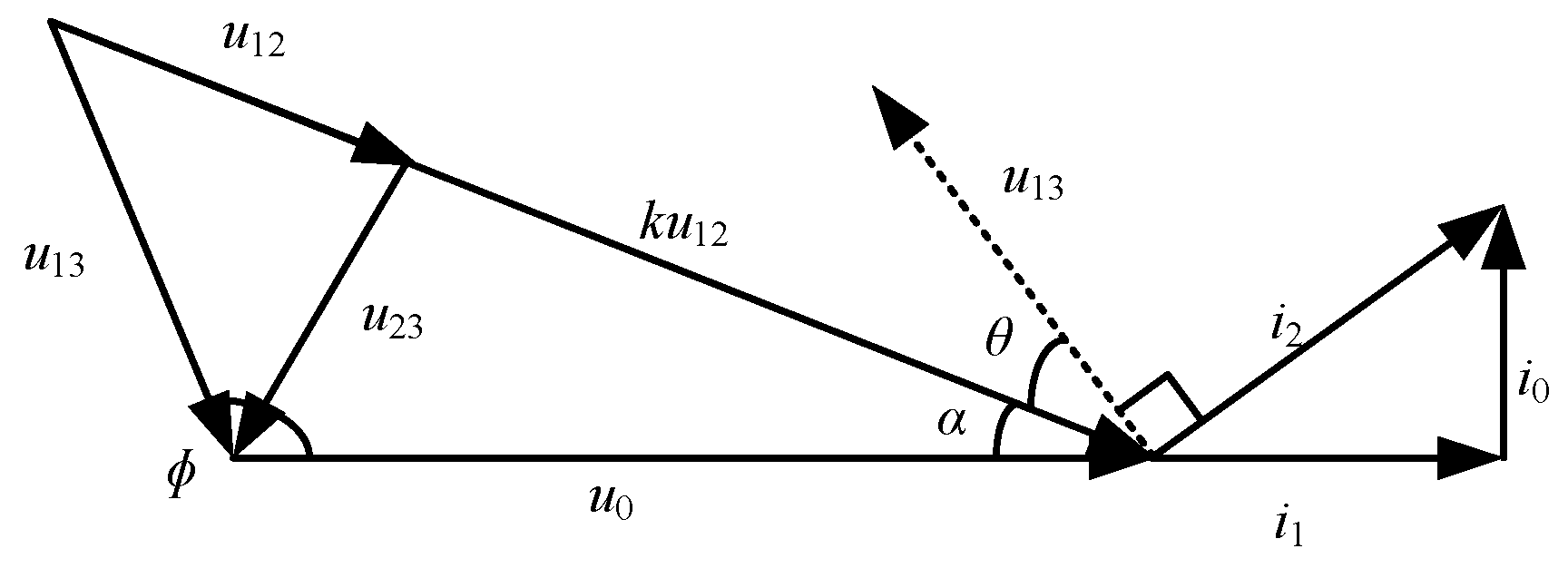
3.1. Principle of the Voltage Difference Method
3.2. Application of SMC in Ultrasonic Power Supply
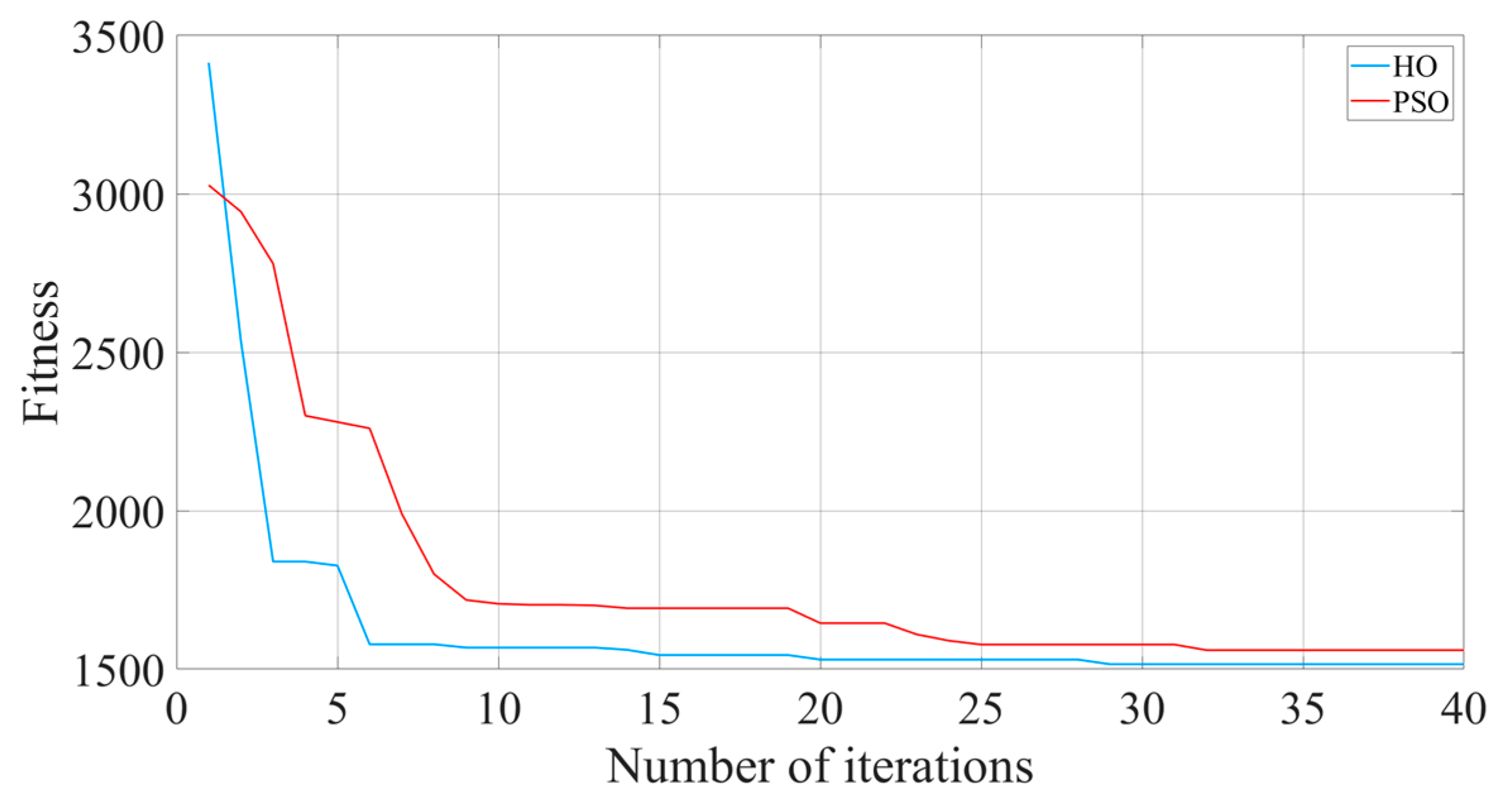
3.3. HO Algorithm Optimization for SMC
- The initial population positions are generated. In this step, the initial solution vectors are generated using the following equation:
- 2.
- Within the spatial domain, the population positions are updated.
- 3.
- Local optimization is performed during the position update process to avoid entrapment in local minima.
- 4.
- A random exploration mechanism is applied for population position updates.
- Definition of the fitness function.
- 2.
- Initialization of the HO algorithm parameters.
- 3.
- Iterative optimization of the HO algorithm.
- 4.
- Determination of the optimal parameters.
- 5.
- Application of the optimized parameters.
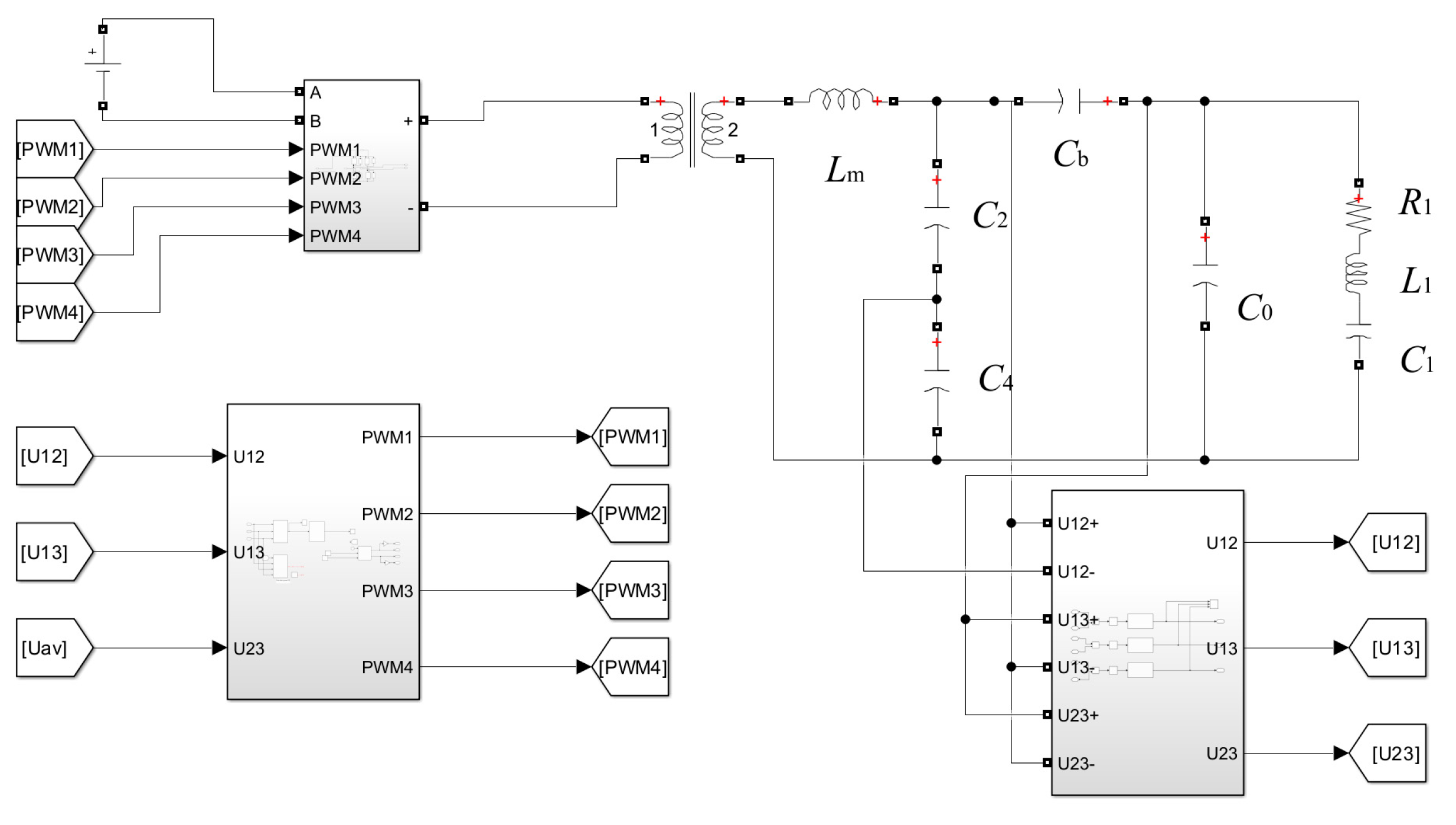
4. Simulation and Analysis
4.1. Simulation Parameters
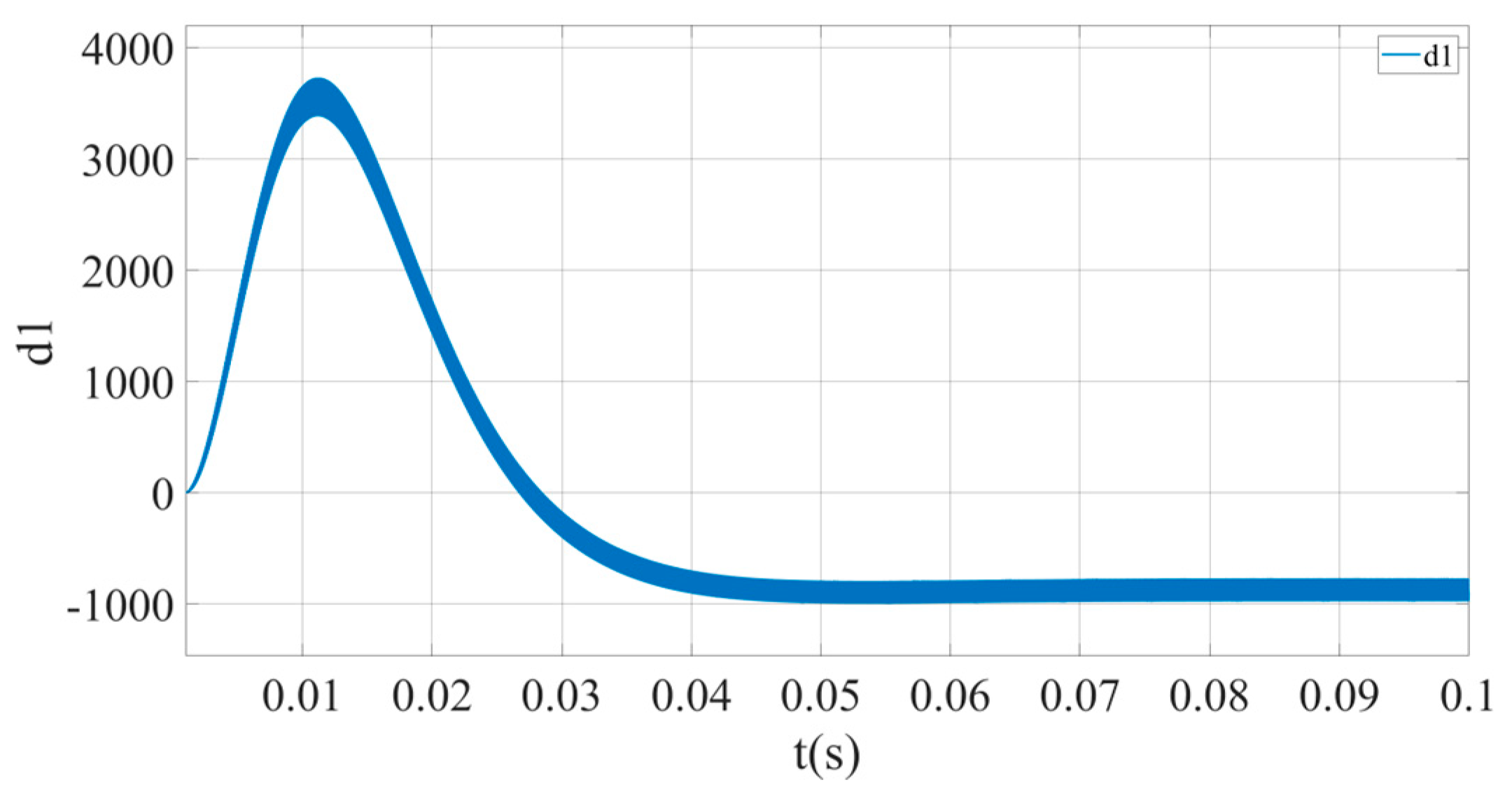
4.2. Simulation Comparison
- Simulation analysis under static conditions.
- 2.
- Simulation analysis under dynamic conditions.
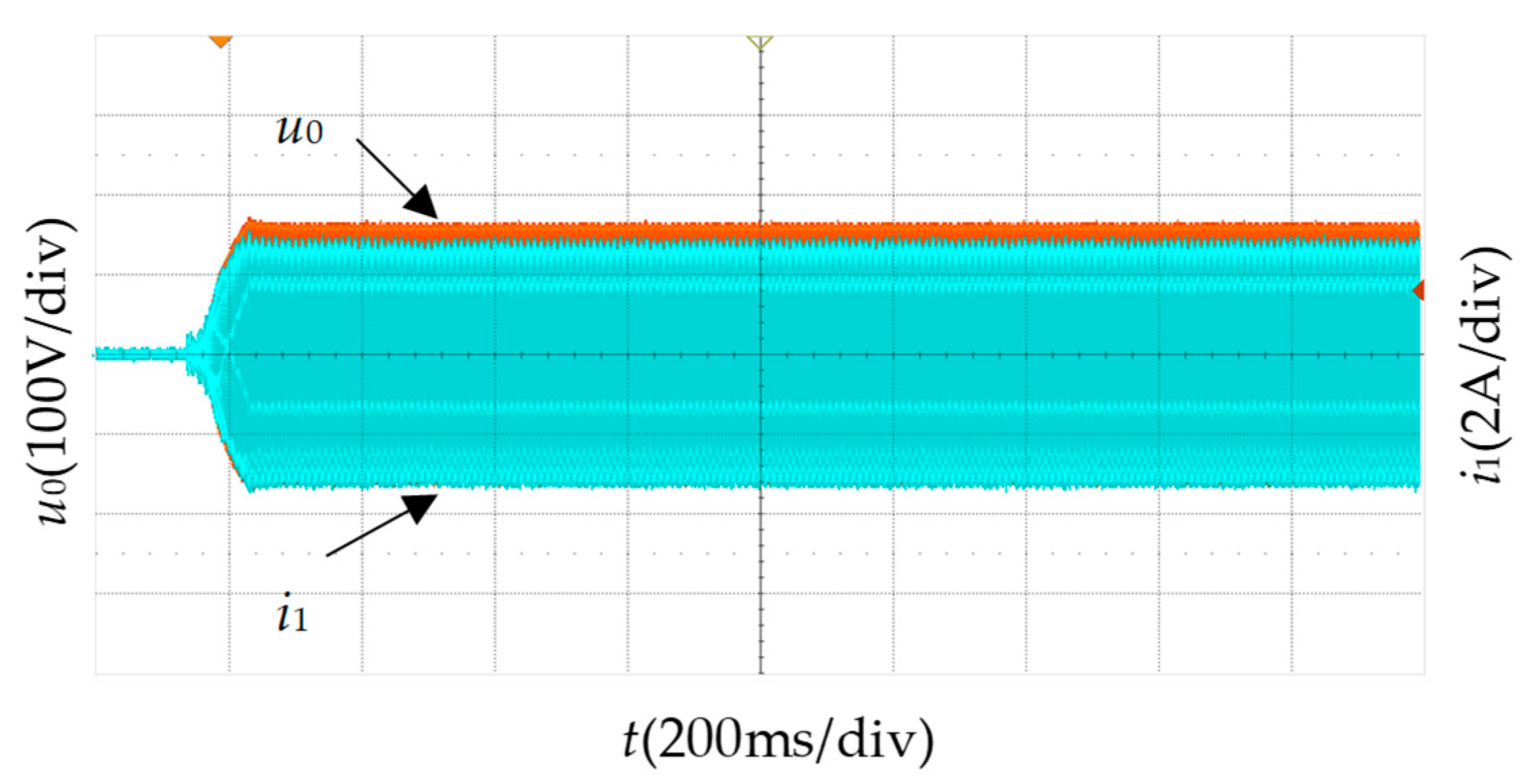
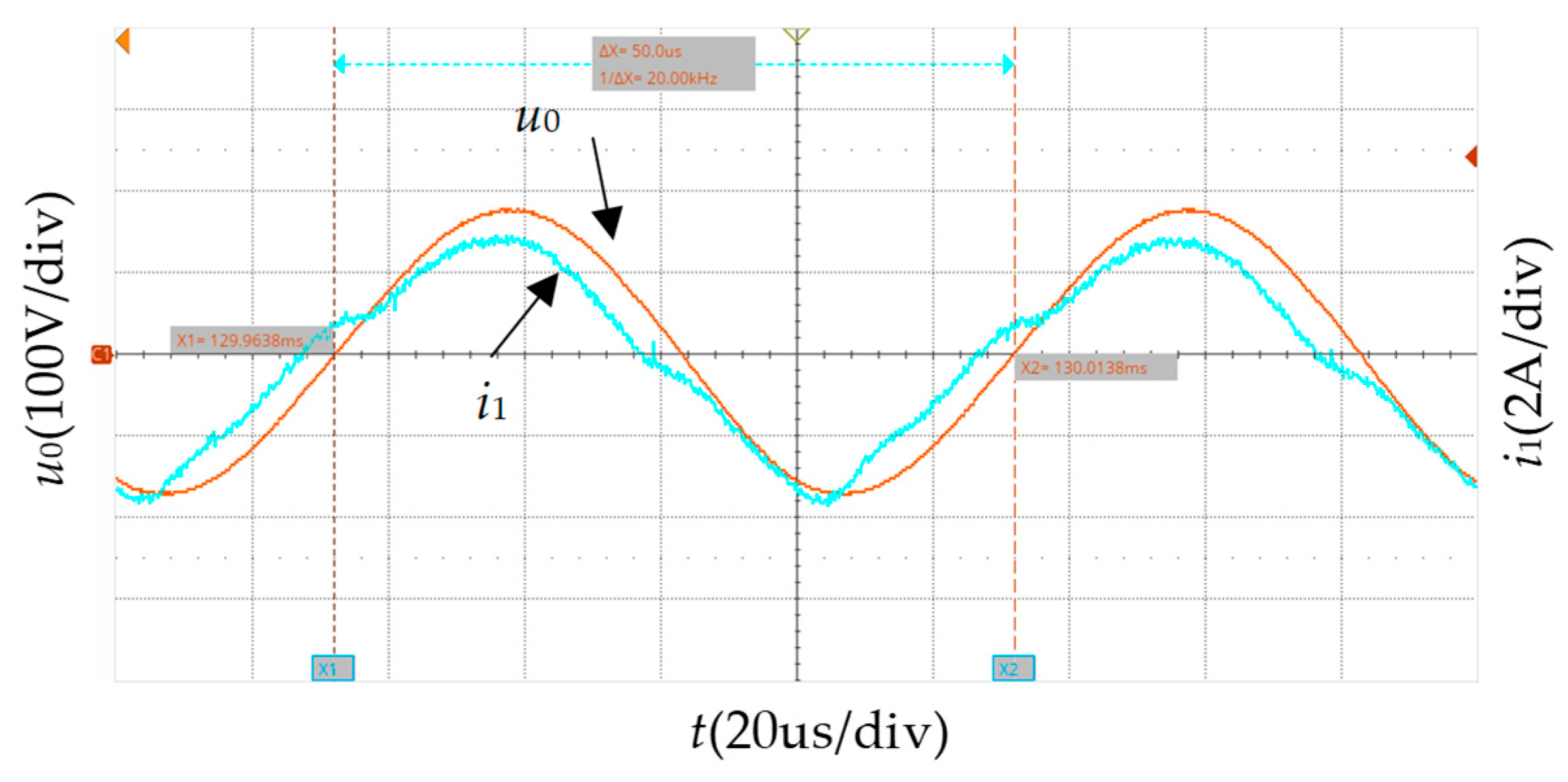
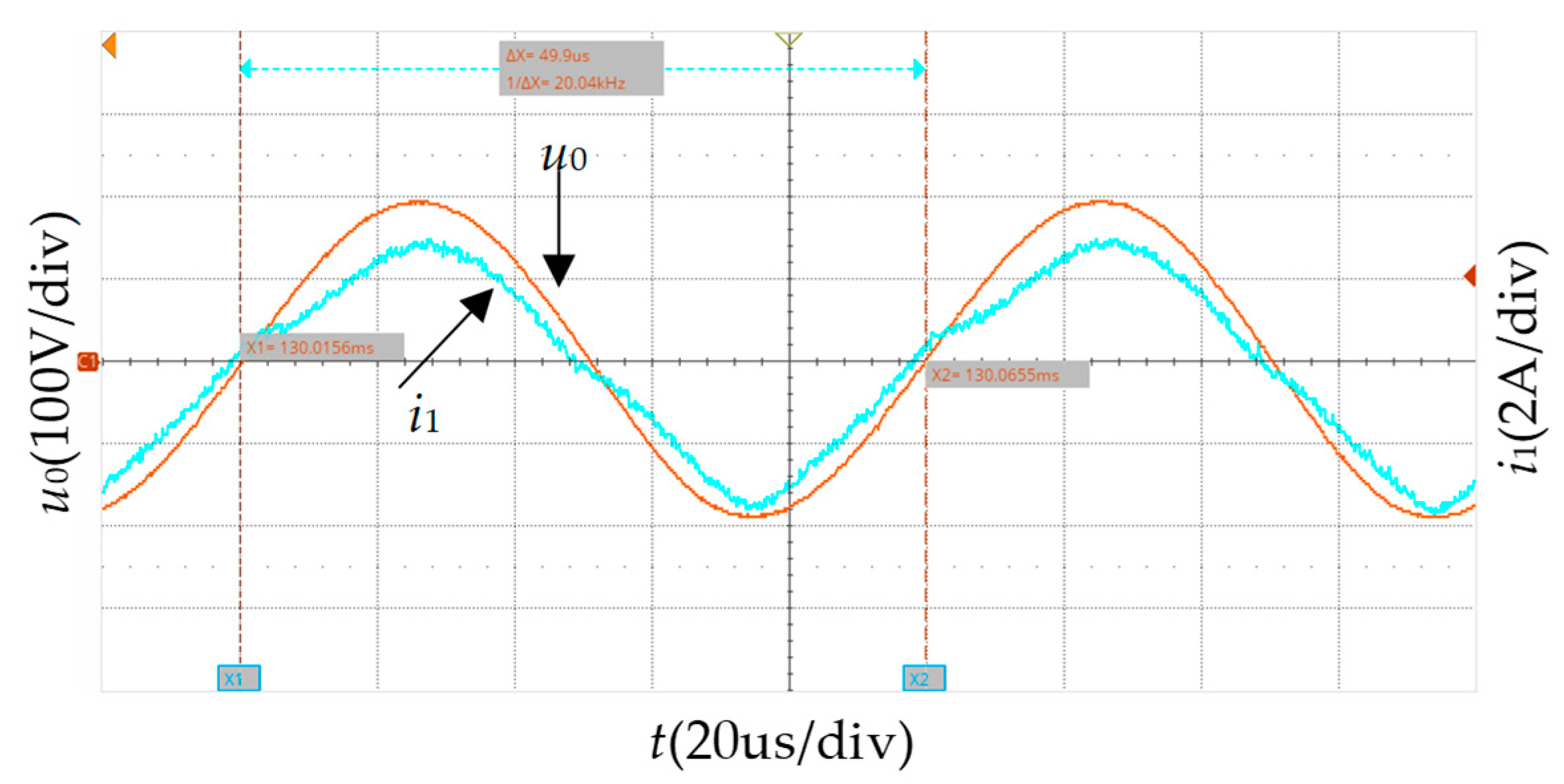
5. Experimental Verification
5.1. Experimental Setups
5.2. Frequency Tracking Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhudolia, S.K.; Gohel, G.; Leong, K.F.; Islam, A. Advances in Ultrasonic Welding of Thermoplastic Composites: A Review. Materials 2020, 13, 1284. [Google Scholar] [CrossRef]
- Chen, T.-R.; Chen, C.-M.; Chen, P.-H.; Juan, Y.-L.; Lee, Y.-L.; Chang, H.-M. Coreless inductive power supply for ultrasonic transducer on machine tool. IEICE Electron. Express 2018, 15, 20180833. [Google Scholar] [CrossRef]
- Zhang, H.-F.; Wang, B.-J.; Zhao, A.-L. Research on power supply for adaptive ultrasonic vibration cutting based on piezoelectric technology. Agro Food Ind. Hi-Tech. 2017, 28, 2661–2665. [Google Scholar]
- Milewski, A.; Kluk, P.; Kardyś, W.; Kogut, P. Modeling and designing of ultrasonic welding systems. Arch. Acoust. 2015, 40, 93–99. [Google Scholar] [CrossRef]
- Taşlıyol, M.; Öncü, S.; Turan, M.E. An implementation of class D inverter for ultrasonic transducer mixed powder mixture. Ultrason. Sonochemistry 2024, 104, 106838. [Google Scholar] [CrossRef]
- Cheng, L.-C.; Kang, Y.-C.; Chen, C.-L. A Resonance-Frequency-Tracing Method for a Current-Fed Piezoelectric Transducer. IEEE Trans. Ind. Electron. 2014, 61, 6031–6040. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, A. Dynamic compensation optimization and frequency characteristic analysis for contactless energy transfer under load variations in rotary ultrasonic machining. IEEE Trans. Ind. Electron. 2022, 70, 2948–2958. [Google Scholar] [CrossRef]
- Gemmen, R.S. Analysis for the Effect of Inverter Ripple Current on Fuel Cell Operating Condition. J. Fluids Eng. 2003, 125, 576–585. [Google Scholar] [CrossRef]
- Kuang, Y.; Jin, Y.; Cochran, S.; Huang, Z. Resonance tracking and vibration stablilization for high power ultrasonic transducers. Ultrasonics 2014, 54, 187–194. [Google Scholar] [CrossRef]
- Sonmezoglu, S.; Darvishian, A.; Shen, K.; Bustamante, M.J.; Kandala, A.; Maharbiz, M.M. A Method and Analysis to Enable Efficient Piezoelectric Transducer-Based Ultrasonic Power and Data Links for Miniaturized Implantable Medical Devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3362–3370. [Google Scholar] [CrossRef]
- Mortimer, B.; du Bruyn, T.; Davies, J.; Tapson, J. High power resonant tracking amplifier using admittance locking. Ultrasonics 2001, 39, 257–261. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, J.-M. Frequency searching and tracking for multimodal ultrasonic vibration system. Tech. Acoust. 2008, 3, 361–364. [Google Scholar]
- Dong, H.; Zhang, G.; Dong, W.; Cai, H.; Zhang, Q. Current feedback frequency tracking control with matching of piezoelectric. J. Harbin Inst. Technol. 2000, 32, 115–122. [Google Scholar]
- Suzuki, T.; Ikeda, H.; Yoshida, H.; Shinohara, S. Megasonic transducer drive utilizing MOSFET DC-to-RF inverter with output power of 600 W at 1 MHz. IEEE Trans. Ind. Electron. 2000, 46, 1159–1173. [Google Scholar] [CrossRef]
- Jia, H.; Feng, P.X.L. Design of an automatic impedance matching circuit based on frequency tracking of ultrasonic transducer. In Proceedings of the 2020 IEEE 5th ITME Conference (ITOEC), Chongqing, China, 12–14 June 2020. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, T.H.; Chen, X.D.; He, B.; Xu, X.S. The Design and Dynamic Analysis of High Frequency Ultrasonic Transducer for Wire Bonding Application. Appl. Mech. Mater. 2012, 226–228, 199–202. [Google Scholar] [CrossRef]
- Jia, H.; Feng, P.X.L. Fast and Precise Control for the Vibration Amplitude of an Ultrasonic Transducer Based on Fuzzy PID Control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 2766–2774. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Li, R. Ultrasonic Power Load Forecasting Based on BP Neural Network. J. Inst. Eng. India Ser. C 2019, 101, 383–390. [Google Scholar] [CrossRef]
- Ding, Y.; Zheng, H.; Xiao, F.; Ma, H. Design of Ultrasonic Power Frequency Tracking System Based on PSO-PID. Chin. J. Electron Devices 2021, 44, 575–578. [Google Scholar]
- Jiang, X.; Zhang, X.; Zhu, X.; Sui, H.; Zhang, D. Study of Phase Shift Control in High-Speed Ultrasonic Vibration Cutting. IEEE Trans. Ind. Electron. 2018, 65, 2467–2474. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, M.; Zhu, Y.; Wang, S. Push–Pull Inverter Using Amplitude Control and Frequency Tracking for Piezoelectric Transducers. Micromachines 2023, 14, 2147. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.; Park, S.; Lim, S. A Novel High-Speed Resonant Frequency Tracking Method Using Transient Characteristics in a Piezoelectric Transducer. Sensors 2022, 22, 6378. [Google Scholar] [CrossRef]
- Jiang, K.; Zhang, J.; Chen, Z. A new approach for the sliding mode control based on fuzzy reaching law. In Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, China, 10–14 June 2002. [Google Scholar] [CrossRef]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Utkin, V. Discussion Aspects of High-Order Sliding Mode Control. IEEE Trans. Autom. Control 2016, 61, 829–833. [Google Scholar] [CrossRef]
- Cao, Y.; Kao, Y.; Wang, Z.; Yang, X.; Park, J.H.; Xie, W. Sliding mode control for uncertain fractional-order reaction–diffusion memristor neural networks with time delays. Neural Netw. 2024, 178, 106402. [Google Scholar] [CrossRef]
- Li, W.; Wu, C.; Lin, S.; Li, G.; Zhang, P. Active heave compensation of marine winch based on hybrid neural network prediction and sliding mode controller with a high-gain observer. Ocean. Eng. 2025, 322, 120448. [Google Scholar] [CrossRef]
- Liang, C.; Ding, Y.; Weng, F.; Chen, W.; Li, J. Dual observers based sliding mode control for QUAVs with unknown disturbances and time varying delays. Sci. Rep. 2025, 15, 5488. [Google Scholar] [CrossRef]
- Wang, J. Design of Ultrasonic Power Supply Based on Frequency Automatic Tracking and Power Regulation Technology. Ph.D. Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2021. [Google Scholar] [CrossRef]
- Amiri, M.H.; Hashjin, N.M.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef]
- Zheng, Y.; Gao, Y.; Gao, J. Energy Saving in Building Air-Conditioning Systems Based on Hippopotamus Optimization Algorithm for Optimizing Cooling Water Temperature. Energies 2025, 18, 2476. [Google Scholar] [CrossRef]
- He, X.; Liu, X.; Lin, C.; Fu, M.; Wang, J.; Zhang, J. Early Bearing Fault Diagnosis in PMSMs Based on HO-VMD and Weighted Evidence Fusion of Current–Vibration Signals. Sensors 2025, 25, 4591. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Lin, S. Analysis of a Cascaded Piezoelectric Ultrasonic Transducer with Three Sets of Piezoelectric Ceramic Stacks. Sensors 2019, 19, 580. [Google Scholar] [CrossRef]
- Gan, Y.; Meng, B.; Chen, Y.; Sun, F. An intelligent measurement method of the resonant frequency of ultrasonic scalpel transducers based on PSO-BP neural network. Measurement 2022, 190, 110680. [Google Scholar] [CrossRef]
- Wang, J.; Qin, L.; Wei, P.; Tang, L. Modeling and analysis of multilayer piezoelectric-elastic spherical transducers. J. Intell. Mater. Syst. Struct. 2018, 29, 2437–2455. [Google Scholar] [CrossRef]
- Wang, J.-D.; Jiang, J.-J.; Duan, F.-J.; Zhang, F.-M.; Liu, W.; Qu, X.-H. A Novel Fast Resonance Frequency Tracking Method Based on the Admittance Circle for Ultrasonic Transducers. IEEE Trans. Ind. Electron. 2019, 67, 6864–6873. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J. Theoretical and Empirical Verification of Electrical Impedance Matching Method for High-Power Transducers. Electronics 2022, 11, 194. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, Y.; Yan, H.; Cai, H. A Driving Power Supply for Piezoelectric Transducers Based on an Improved LC Matching Network. Sensors 2023, 23, 5745. [Google Scholar] [CrossRef] [PubMed]



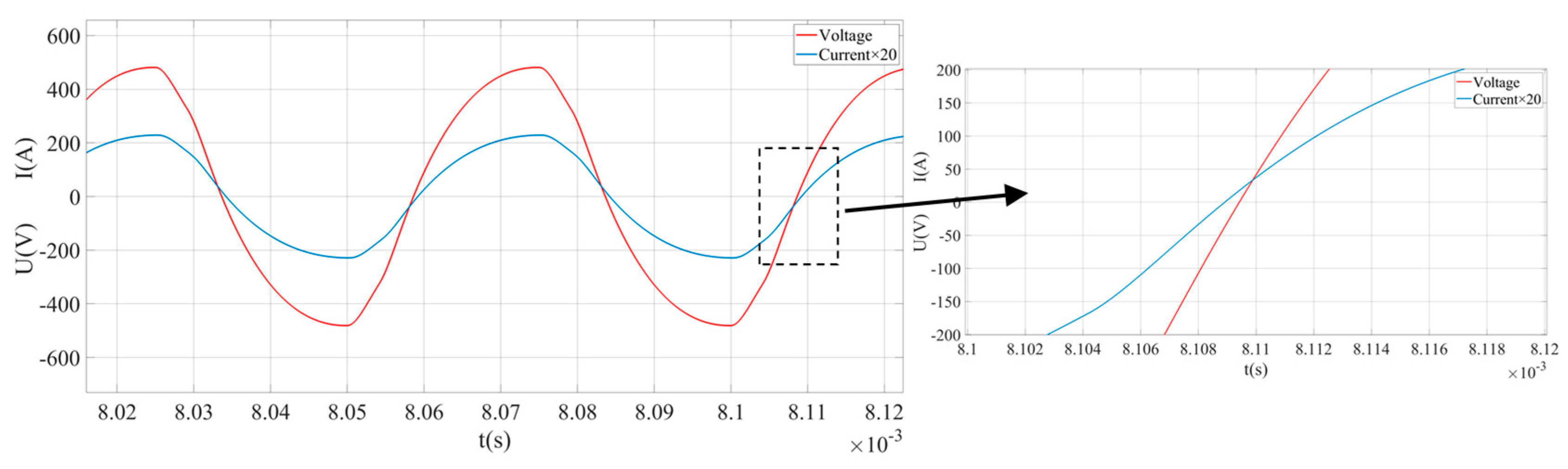


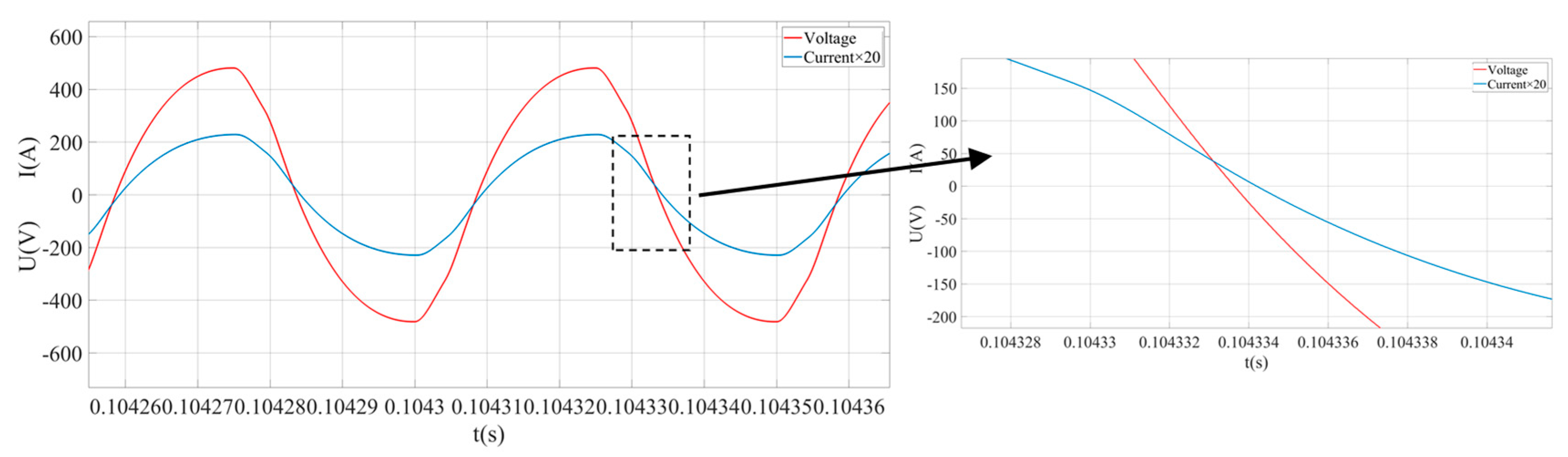
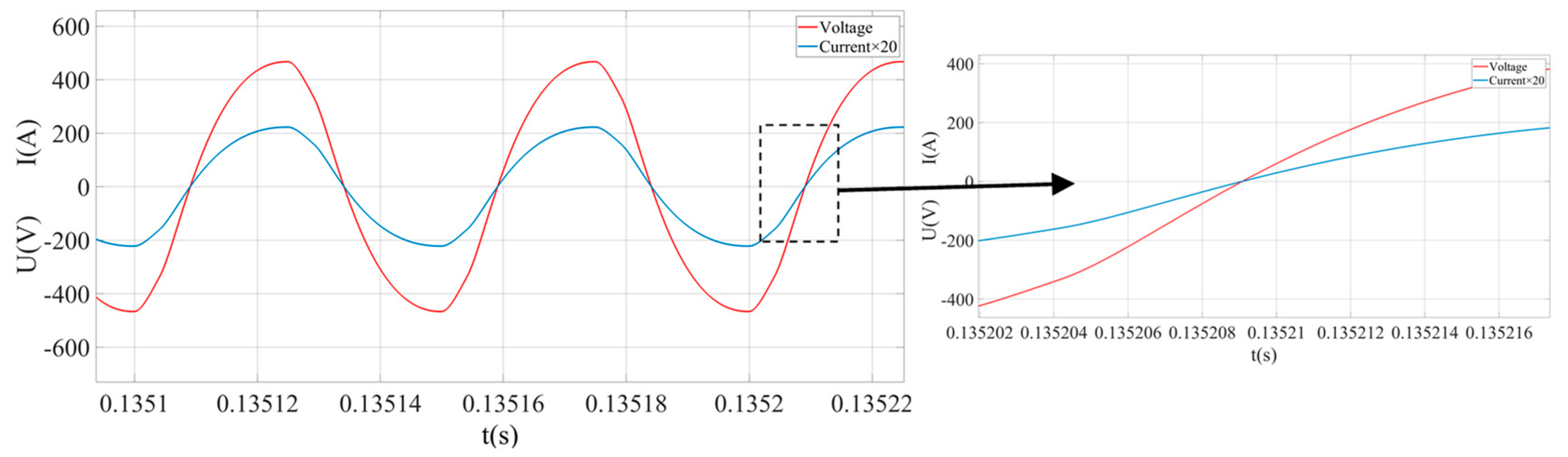




| Parameters | C0 (nF) | C1 (nF) | L1 (mH) | R1 (Ω) | fs (Hz) |
|---|---|---|---|---|---|
| Value | 4.5 | 0.273 | 231.8 | 42 | 20,007 |
| Parameters | Unit | Value |
|---|---|---|
| Input Voltage | V | 220 |
| Rated Power | kW | 2 |
| Input Frequency | Hz | 50 |
| Resonant Frequency | Hz | 20,007 |
| Transformer Ratio | 0.96 | |
| Matching Inductance Lm | mH | 0.19 |
| Matching Capacitance C4 | nF | 44 |
| Static Capacitance C0 | nF | 4.5 |
| Dynamic Inductance L1 | mH | 231.8 |
| Matching Capacitance C2 | nF | 440 |
| Matching Capacitance Cb | nF | 440 |
| Dynamic Resistance R1 | Ω | 42 |
| Dynamic Capacitance C1 | nF | 0.273 |
| Parameter | Value |
|---|---|
| Hippopotamus Population | 50 |
| Adult Hippo Ratio | 0.3 |
| Territory Radius | 0.5 |
| Maximum Iterations | 40 |
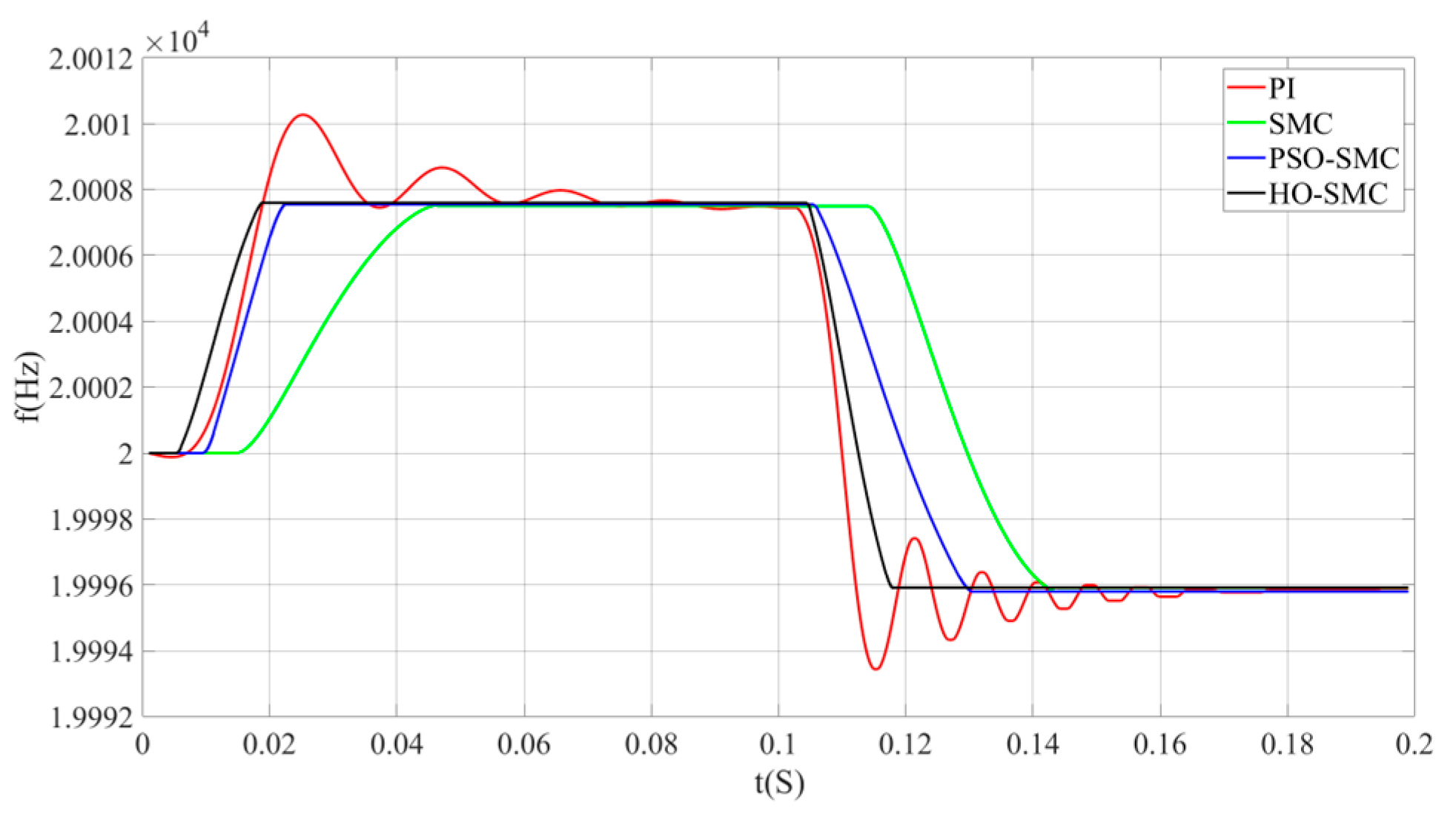
| Control Method | Settling Time (s) | Overshoot (Hz) |
|---|---|---|
| PI | 0.08 | 2.85 |
| SMC | 0.046 | 0.03 |
| PSO-SMC | 0.023 | 0.03 |
| HO-SMC | 0.019 | 0.02 |
| Control Method | Settling Time (s) | Overshoot (Hz) |
|---|---|---|
| PI | 0.064 | 2.55 |
| SMC | 0.043 | 0.03 |
| PSO-SMC | 0.03 | 0.03 |
| HO-SMC | 0.018 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, L.; Cai, H. Hippopotamus Optimization-Sliding Mode Control-Based Frequency Tracking Method for Ultrasonic Power Supplies with a T-Type Matching Network. Electronics 2025, 14, 3358. https://doi.org/10.3390/electronics14173358
Ye L, Cai H. Hippopotamus Optimization-Sliding Mode Control-Based Frequency Tracking Method for Ultrasonic Power Supplies with a T-Type Matching Network. Electronics. 2025; 14(17):3358. https://doi.org/10.3390/electronics14173358
Chicago/Turabian StyleYe, Linzuan, and Huafeng Cai. 2025. "Hippopotamus Optimization-Sliding Mode Control-Based Frequency Tracking Method for Ultrasonic Power Supplies with a T-Type Matching Network" Electronics 14, no. 17: 3358. https://doi.org/10.3390/electronics14173358
APA StyleYe, L., & Cai, H. (2025). Hippopotamus Optimization-Sliding Mode Control-Based Frequency Tracking Method for Ultrasonic Power Supplies with a T-Type Matching Network. Electronics, 14(17), 3358. https://doi.org/10.3390/electronics14173358






