A New Dimensional Target Scattering Characteristic Characterization Method Based on the Electromagnetic Vortex-Polarization Joint Scattering Matrix
Abstract
1. Introduction
2. Fundamental Properties of Vortex EM Waves
2.1. OAM Characterizes of EM Waves
2.2. SAM Characterization of EM Waves and Polarization Scattering Matrix
3. The EM Vortex Scattering Matrix
3.1. Definition of the EM Vortex Scattering Matrix
3.2. Implication of the Elements in EVSM
4. The EM Vortex-Polarization Joint Scattering Matrix
4.1. Definition of the EM Vortex-Polarization Joint Scattering Matrix
4.2. The Degradation Problem of the EVPJSM
5. Numerical Simulation and Discussion
5.1. Principle of Scattering Coefficient Calculation
5.2. Experimental Setup
5.3. Calculation of the Vortex Scattering Coefficient of the PEC Sphere
5.4. Calculation of the Vortex Scattering Coefficient of the PEC Flat Plate
6. Conclusions
7. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Angular Momentum |
| EM | Electromagnetic |
| EVPJSM | Electromagnetic Vortex-Polarization Joint Scattering Matrix |
| EVSM | Electromagnetic Vortex Scattering Matrix |
| ISAR | Inverse Synthetic Aperture Radar |
| LM | Linear Momentum |
| OAM | Orbital Angular Momentum |
| ORCS | OAM Radar Cross Section |
| PSM | Polarization Scattering Matrix |
| RCS | Radar Cross Section |
| RF | Radio Frequency |
| SAM | Spin Angular Momentum |
| SAR | Synthetic Aperture Radar |
| VNA | Vector Network Analyzer |
References
- Li, C.; Xu, H.; Peng, W.; Han, G.; Feng, X.; Liu, F.; You, D.; Wu, T.; Li, S. Research progress on vortex electromagnetic wave radar. China Basic Sci. 2023, 25, 44–53. [Google Scholar]
- Allen, L.; Beijersbergen, M.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Garcés-Chávez, V.; McGloin, D.; Melville, H.; Sibbett, W.; Dholakia, K. Simultaneous micromanipulation in multiple planes using a self-reconstructing light beam. Lett. Nat. 2002, 419, 145–147. [Google Scholar] [CrossRef] [PubMed]
- Thide, B.; Then, H.; Sjoholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.; Istomin, Y.; Ibragimov, N.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef] [PubMed]
- Bu, X.; Zhang, Z.; Liang, X.; Zeng, Z.; Chen, L.; Tang, H. Scattering characteristics of vortex electromagnetic waves for typical targets. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), New York, NY, USA, 6–9 November 2018. [Google Scholar]
- Bu, X.; Liang, X.; Zhang, Z.; Chen, L.; Tang, H.; Zeng, Z. Scattering characteristics of vortex electromagnetic waves for a wedge. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS), Toyama, Japan, 26–30 August 2018. [Google Scholar]
- Guo, L.; Huang, Q.; Cheng, M.; Li, J.; Liu, S.; Cheng, M. The scattering of vortical electromagnetic waves by a coated sphere. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation and USNC/URSI National Radio Science Meeting, New York, NY, USA, 8–13 July 2018. [Google Scholar]
- Liu, K.; Gao, Y.; Li, X.; Cheng, Y. Target scattering characteristics for OAM-based radar. AIP Adv. 2018, 8, 025002. [Google Scholar] [CrossRef]
- Liu, K.; Liu, H.; Sha, W.; Cheng, Y.; Wang, H. Backward scattering of electrically large standard objects illuminated by OAM beams. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1167–1171. [Google Scholar] [CrossRef]
- Fang, L.; Yan, J.; Zhou, L.; Yang, W.; Chen, B.; Lei, S. Analysis on Scattering Characteristics of an Electrically Large Ship under the Illumination of Vortex Electromagnetic Wave. In Proceedings of the 2022 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Harbin, China, 15–18 August 2022. [Google Scholar]
- Arfan, M.; Ghaffar, A.; Alkanhal, M.; Naz, M.; Alqahtani, A.; Khan, Y. Orbital angular momentum wave scattering from perfect electromagnetic conductor (PEMC) sphere. Optik 2022, 253, 168562. [Google Scholar] [CrossRef]
- Bu, L.; Zhu, Y.; Chen, Y.; Yang, Y.; Zang, Y. Vortex-electromagnetic-wave-based ISAR imaging for high-speed maneuvering targets. Sci. Rep. 2022, 12, 18009. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, H.; Wu, T.; Meng, X.; Li, F. Near-field electromagnetic scattering of Bessel vortex beam by metal target. Acta Phys. Sin. 2023, 72, 100302. [Google Scholar] [CrossRef]
- Wang, H.; Qu, T.; Niu, J.; Wu, J. Scattering Characteristics of Vortex Electromagnetic Waves by Symmetrical Targets. In Proceedings of the 2024 Photonics & Electromagnetics Research Symposium (PIERS), Chengdu, China, 21–25 April 2024. [Google Scholar]
- Sun, M.; Liu, S.; Guo, L. Scattering Field Intensity and Orbital Angular Momentum Spectral Distribution of Vortex Electromagnetic Beams Scattered by Electrically Large Targets Comprising Different Materials. Remote Sens. 2024, 16, 754. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Cheng, X.; Wang, X. Summarization of radar polarization measurement modes. Syst. Eng. Electron. 2013, 35, 1873–1877. [Google Scholar]
- Wang, C.; Yu, W. Comparative analyses of Huynen target decomposition methods. J. Grad. Sch. Chin. Acad. Sci. 2011, 28, 402–409. [Google Scholar]
- Cloude, S.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, S.; Zhao, W.; Peng, X.; Ma, H. Target polarization scattering matrix estimation with conformal MIMO radar. Signal Process. 2023, 210, 109054. [Google Scholar] [CrossRef]
- Ciuca, M.; Vasile, G.; Anghel, A.; Gay, M.; Ciochina, S. Real Representation of the Polarimetric Scattering Matrix for Monostatic Radar. Remote Sens. 2023, 15, 1037. [Google Scholar] [CrossRef]
- Malik, R.; Singh, G.; Dikshit, O.; Yamaguchi, Y. Model-Based Nine-Component Scattering Matrix Power Decomposition. IEEE Geosci. Remote Sens. Lett. 2024, 21, 4008105. [Google Scholar] [CrossRef]
- Maurya, H.; Bhattacharya, A.; Mishra, A.; Panigrahi, R. Hybrid Three-Component Scattering Power Characterization from Polarimetric SAR Data Isolating Dominant Scattering Mechanisms. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4415315. [Google Scholar] [CrossRef]
- Bu, X. Research on Synthetic Aperture Radar Technology Based on Vortex Electromagnetic Waves. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2019. [Google Scholar]
- Yao, A.; Padgett, M. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, X.; Yu, L.; Zhao, X.; Zhang, Y.; Shi, X.; Li, D.; Yang, Q.; Kang, X.; Zhai, W.; et al. Modern Radar Theory and Technology, 2nd ed.; Science Press: Beijing, China, 2023; pp. 42–46. [Google Scholar]
- Mahafza, B.; Elsherbeni, A. MATLAB Simulations for Radar Systems Design, 11th ed.; Electronic Industry Press: Beijing, China, 2016; pp. 345–346. [Google Scholar]

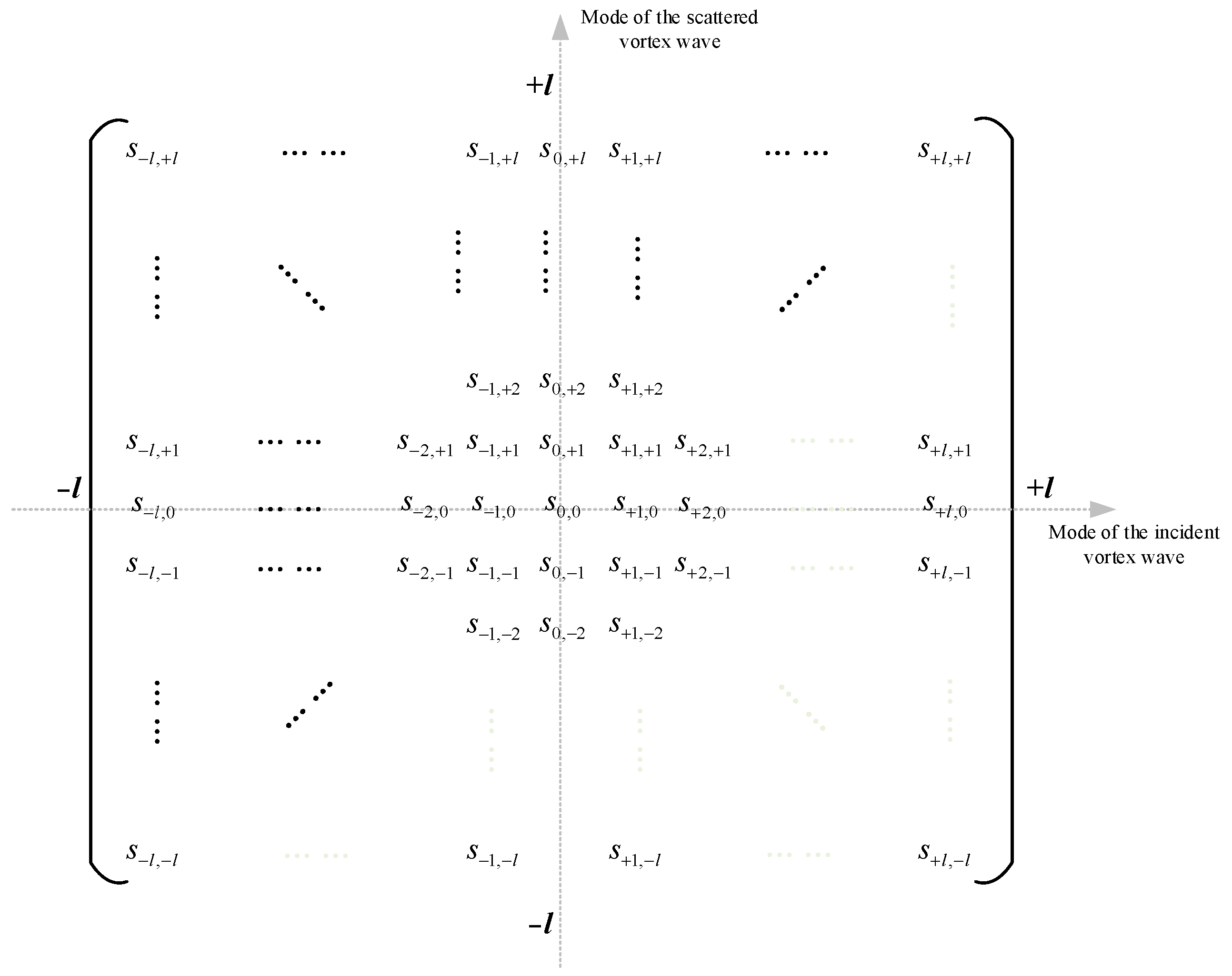
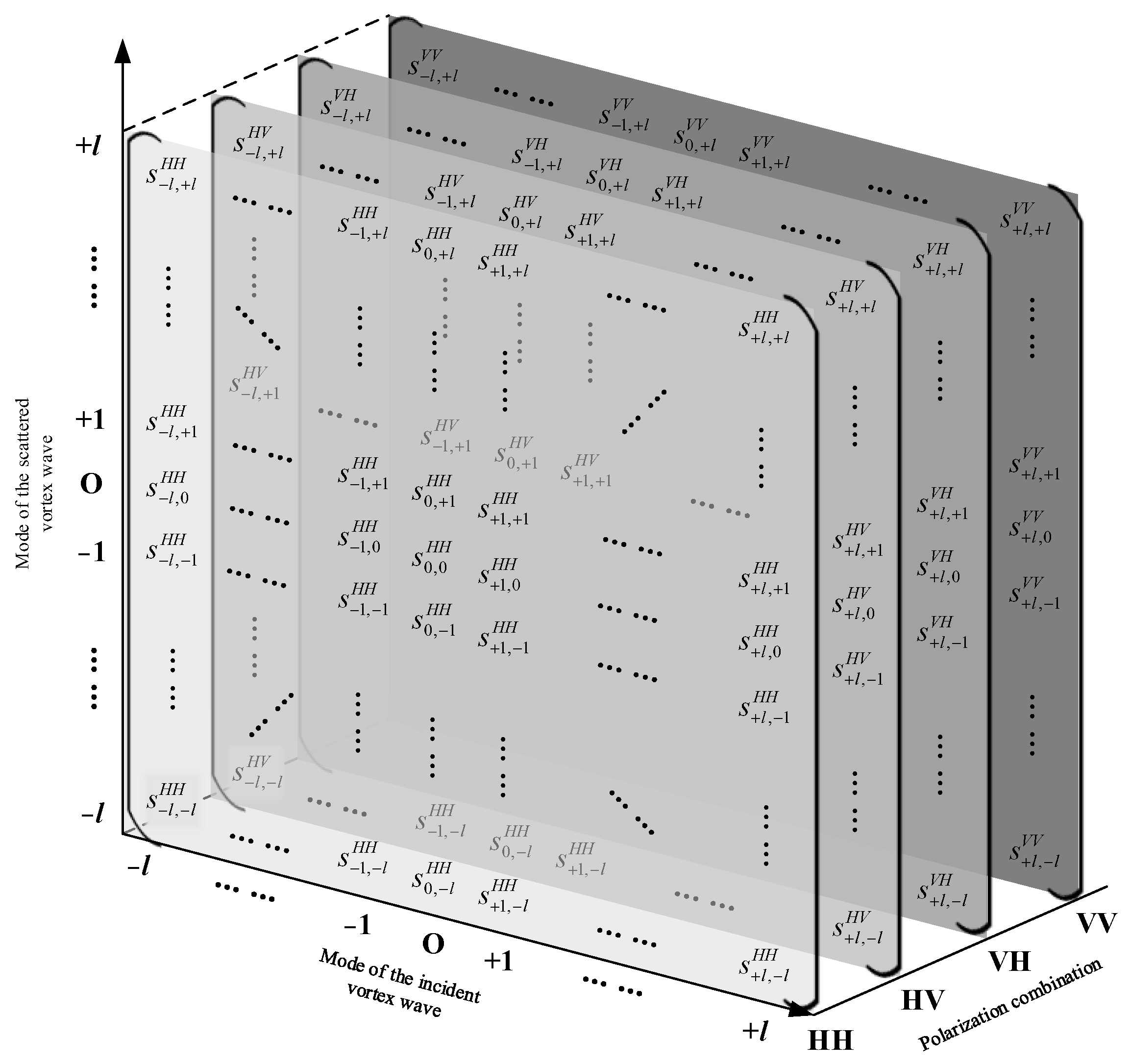
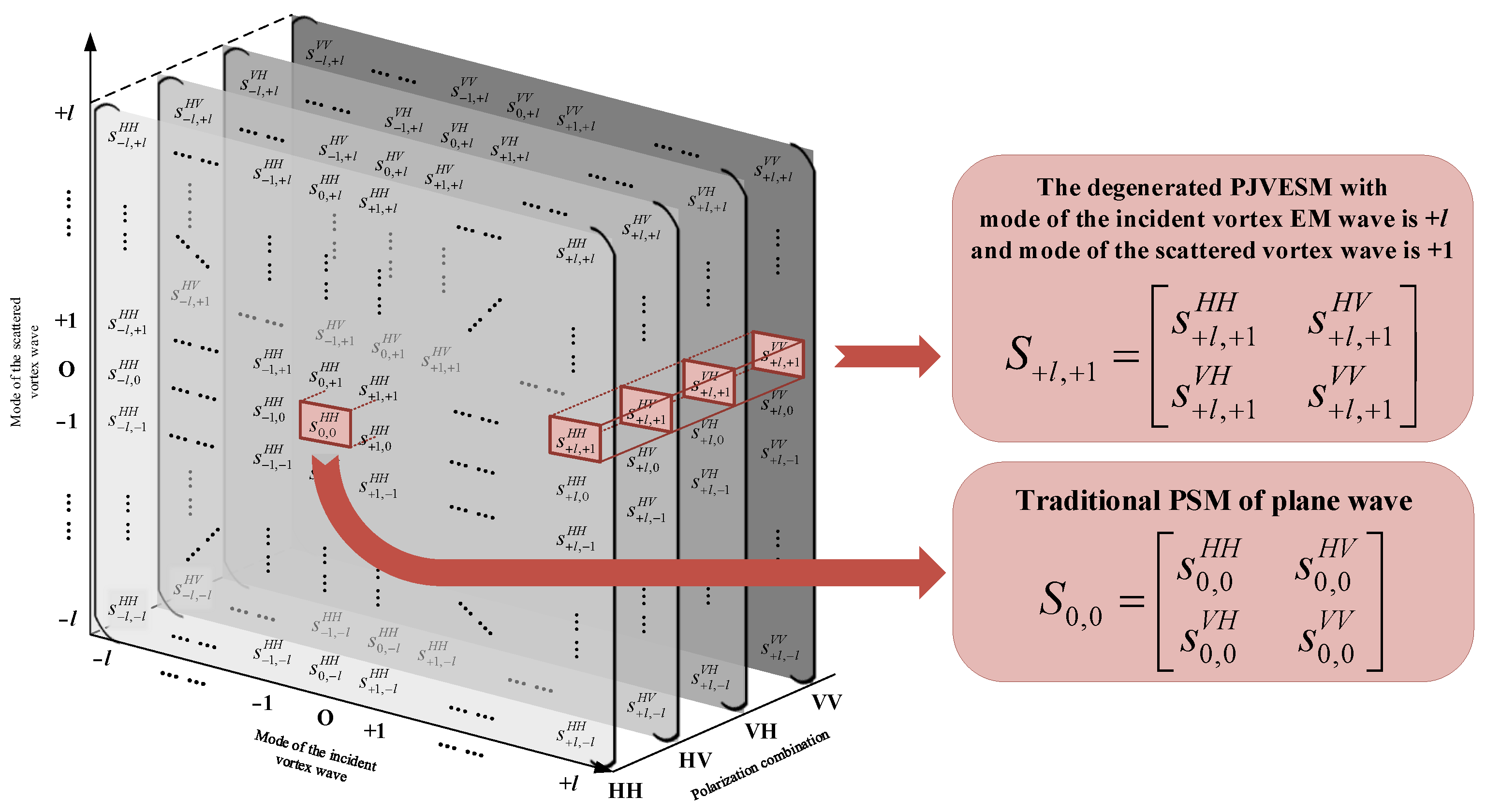
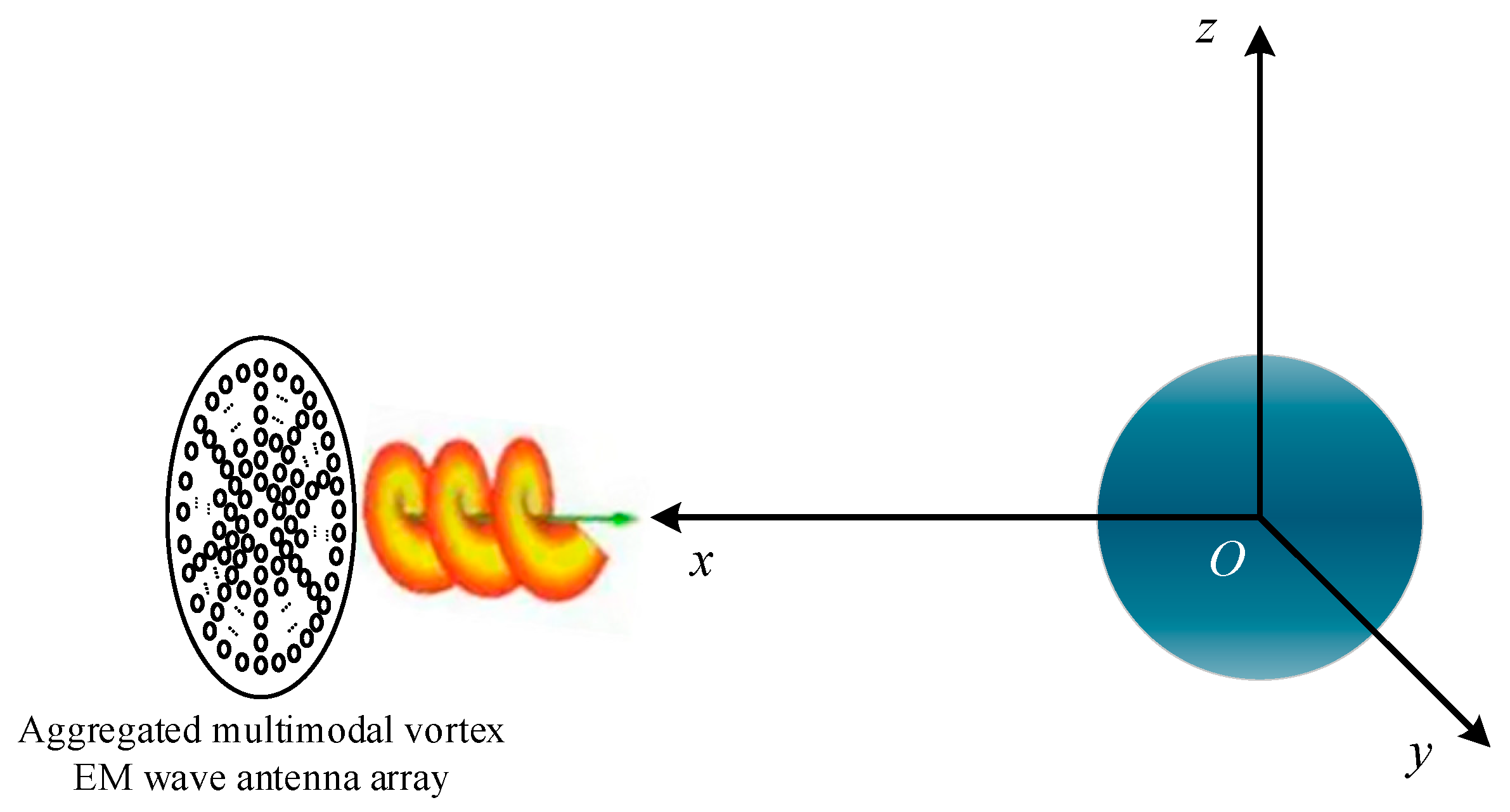
| Number of the Planar Area | Submatrix Symbolic Representation | Located Quadrant | Mode of Incident Wave | Mode of Scattered Wave |
|---|---|---|---|---|
| I | Quadrant I | Positive mode (+) | Positive mode (+) | |
| II | Quadrant II | Negative mode (−) | Positive mode (+) | |
| III | Quadrant III | Negative mode (−) | Negative mode (−) | |
| IV | Quadrant IV | Positive mode (+) | Negative mode (−) |
| Name of Parameter | Value | |
|---|---|---|
| Distance between antennas and target | 5 m | |
| OAM | Mode of incident fields | +1, +2, +3 |
| Mode of scattered fields | 0, +1, +2, +3 | |
| Mode combinations in simulation | [+1, 0], [+1, +1], [+1, +2], [+1, +3], [+2, 0], [+2, +1], [+2, +2], [+2, +3], [+3, 0], [+3, +1], [+3, +2], [+3, +3] | |
| SAM | Polarization of incident fields | H |
| Polarization of scattered fields | H, V | |
| Polarization combinations in simulation | [H, H], [H, V] | |
| Name of Parameter | Value |
|---|---|
| Center frequency | 10 GHz |
| SAM polarization mode | Horizontal polarization (H) |
| Field size | 0.4 m × 0.4 m |
| Sampling points of the field | 41 × 41 |
| OAM mode | +1, +2, +3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, Z.; Wu, T.; Cheng, X. A New Dimensional Target Scattering Characteristic Characterization Method Based on the Electromagnetic Vortex-Polarization Joint Scattering Matrix. Electronics 2025, 14, 3346. https://doi.org/10.3390/electronics14173346
Liu Y, Zhang Z, Wu T, Cheng X. A New Dimensional Target Scattering Characteristic Characterization Method Based on the Electromagnetic Vortex-Polarization Joint Scattering Matrix. Electronics. 2025; 14(17):3346. https://doi.org/10.3390/electronics14173346
Chicago/Turabian StyleLiu, Yixuan, Zhuo Zhang, Tao Wu, and Xinger Cheng. 2025. "A New Dimensional Target Scattering Characteristic Characterization Method Based on the Electromagnetic Vortex-Polarization Joint Scattering Matrix" Electronics 14, no. 17: 3346. https://doi.org/10.3390/electronics14173346
APA StyleLiu, Y., Zhang, Z., Wu, T., & Cheng, X. (2025). A New Dimensional Target Scattering Characteristic Characterization Method Based on the Electromagnetic Vortex-Polarization Joint Scattering Matrix. Electronics, 14(17), 3346. https://doi.org/10.3390/electronics14173346






