1. Introduction
Human beings can incrementally acquire, accumulate, update, and utilize knowledge from the ever-changing environments throughout their lifespan. This ability is referred to as continual learning [
1]. While machine learning, especially deep learning, has made significant strides in various tasks within natural language processing (NLP) and computer vision (CV), endowing machine learning systems with this ability remains a long-standing challenge. This difficulty primarily stems from catastrophic forgetting [
2], where an intelligent agent typically experiences a substantial decline in performance on previously learned tasks when learning new ones. This phenomenon is rooted in the plasticity–stability dilemma [
3].
To address catastrophic forgetting, many strategies have been proposed, including replay-based, regularization-based, and parameter isolation-based approaches [
1]. These methods strike a good balance between the plasticity and stability of agents and mitigate the phenomenon of catastrophic forgetting. Nevertheless, existing methods for mitigating catastrophic forgetting typically only control the extent of performance decline and struggle to achieve incremental performance improvement.
Recent work extends applications of continual learning to graph data, particularly within graph neural networks (GNNs), a field referred to as continual graph learning [
4,
5,
6,
7,
8]. To address the catastrophic forgetting problem in continual graph learning, several recent studies undertake preliminary explorations and report promising results [
9,
10,
11,
12,
13,
14,
15]. Despite recent advancements, addressing catastrophic forgetting in continual graph learning remains challenging as the structural information introduces additional complexity across various aspects of continual graph learning, including scenario settings, task types, and anti-forgetting strategies. Moreover, they all fail to improve model performance incrementally.
Although many continual graph learning works explicitly consider structural information to develop topological structure-aware methods, such as TWP [
10] and PDGNNs [
16], they rarely handle connections across different graphs. More precisely, these connections are called inter-task edges [
17] in multi-task continual learning scenarios (e.g., class incremental and task incremental settings) or inter-stage edges in single-task scenarios (e.g., sample-incremental and domain-incremental settings). SEA-ER [
18] argues that inter-task edges induce structural shifts and catastrophic forgetting and introduce a structure–evolution–aware replay method to mitigate these shifts. IncreGNN [
19] separately samples replay nodes from those connected by inter-task edges and those without such connections, thereby incorporating inter-task edges into continual graph learning for link prediction. TACO [
20] explicitly retrieves and retains inter-task edges by merging the previous reduced graph with the new task subgraph via a node-mapping table, reconnecting new-to-old edges during combination. These preserved inter-task edges are carried through the coarsening and proxy graph generation steps to maintain each node’s evolving receptive field. Nevertheless, they do not investigate how connections between nodes in different tasks or stages affect model performance. Ref. [
17] conducts experiments on node-level tasks under task incremental settings with and without considering inter-task edges. The results show that the inter-task edges introduce contradictory factors for model performance, and the conditions under which they provide benefits versus drawbacks remain uncertain.
This paper explores incremental performance improvement by investigating the influence of inter-stage edges on knowledge transfer. Specifically, we utilize inter-stage edges as an explicit pathway for knowledge transfer in continual graph learning. Through this pathway, we propose to reframe node classification tasks as graph classification tasks to achieve efficient knowledge transfer in sample incremental scenarios of continual graph learning. Moreover, we present a knowledge-augmented replay method that can augment and supplement old knowledge with new knowledge while preserving it, thereby incrementally improving overall performance and overcoming catastrophic forgetting. We validate its effectiveness in a real-world application. Drawing on the experimental results, we further investigate the relationship between the two metrics and identify the key factor to incremental performance improvement. The contributions of this paper are summarized as follows:
Knowledge-augmented replay: We investigate the influence of inter-stage edges on model performance in the sample-incremental scenario of continual graph learning and propose a knowledge-augmented replay method for node classification in this scenario. It leverages inter-stage edges and evolving subgraphs of reappearing nodes as pathways for effective knowledge transfer. It preserves prior knowledge while integrating new knowledge, simultaneously reinforcing and augmenting existing knowledge to overcome catastrophic forgetting, thereby achieving incremental performance improvement and yielding results on par with full retraining but with fewer resources.
A real-world application: We demonstrate the practical effectiveness of the proposed method through validation in Ethereum phishing scam detection. To the best of our knowledge, this is the first study aimed at addressing catastrophic forgetting and improving performance incrementally in Ethereum phishing scam detection using continual graph learning.
Key factor to incremental performance improvement: We explore the relationship between the average accuracy and average forgetting based on the experimental results. Furthermore, we identify the key factor to incremental performance improvement, laying a foundation for convergence analysis in broader continual learning contexts.
The rest of this paper is organized as follows:
Section 2 reviews related work.
Section 3 provides the necessary preliminaries, including the notations used, definitions, and problem formalization. The methodology is detailed in
Section 4, and the experiments are presented in
Section 5.
Section 6 discusses the key to incremental performance improvement in continual graph learning from a knowledge perspective. Finally,
Section 7 concludes the paper.
3. Preliminaries
We present the definitions of key concepts and the problem formulation in this section.
Table 1 summarizes the key notations used in this paper.
3.1. Definitions
Dynamic Network: A dynamic network is represented by , where and are the set of vertices and edges at time t, respectively. Specifically, , where is the incremental network between time and t, with and representing the sets of vertex changes and edge changes, respectively. Consequently, , . Additionally, if the network is attributed, where and denote the adjacency matrix and node feature matrix of the network at time t, respectively. Correspondingly, , where and represent the adjacency matrix and node feature matrix of the incremental network between time and t, respectively.
Graph Neural Networks: A graph neural network is a general neural network designed to capture the dependencies between nodes in graph-structured data. It propagates information across nodes in the graph and learns embeddings that encode graph structures and node features through message passing. The representation of a node
v in the
layer is defined as follows:
where
denotes the representation of node
v at the
layer,
is the set consisting of all neighboring nodes of node
v.
and
denote the aggregation function and update function, respectively. The specific form of the aggregation function varies across GNN architectures and may include operations such as sum, attention, mean, or max pooling. The aggregated representations are typically passed through an update function, which may involve linear transformations and non-linear activation functions, to produce the final representation of each node in the
layer. Representative GNN models include GCNs [
42], GraphSAGE [
44], GATs [
43], and GINs [
45].
3.2. Problem Formalization
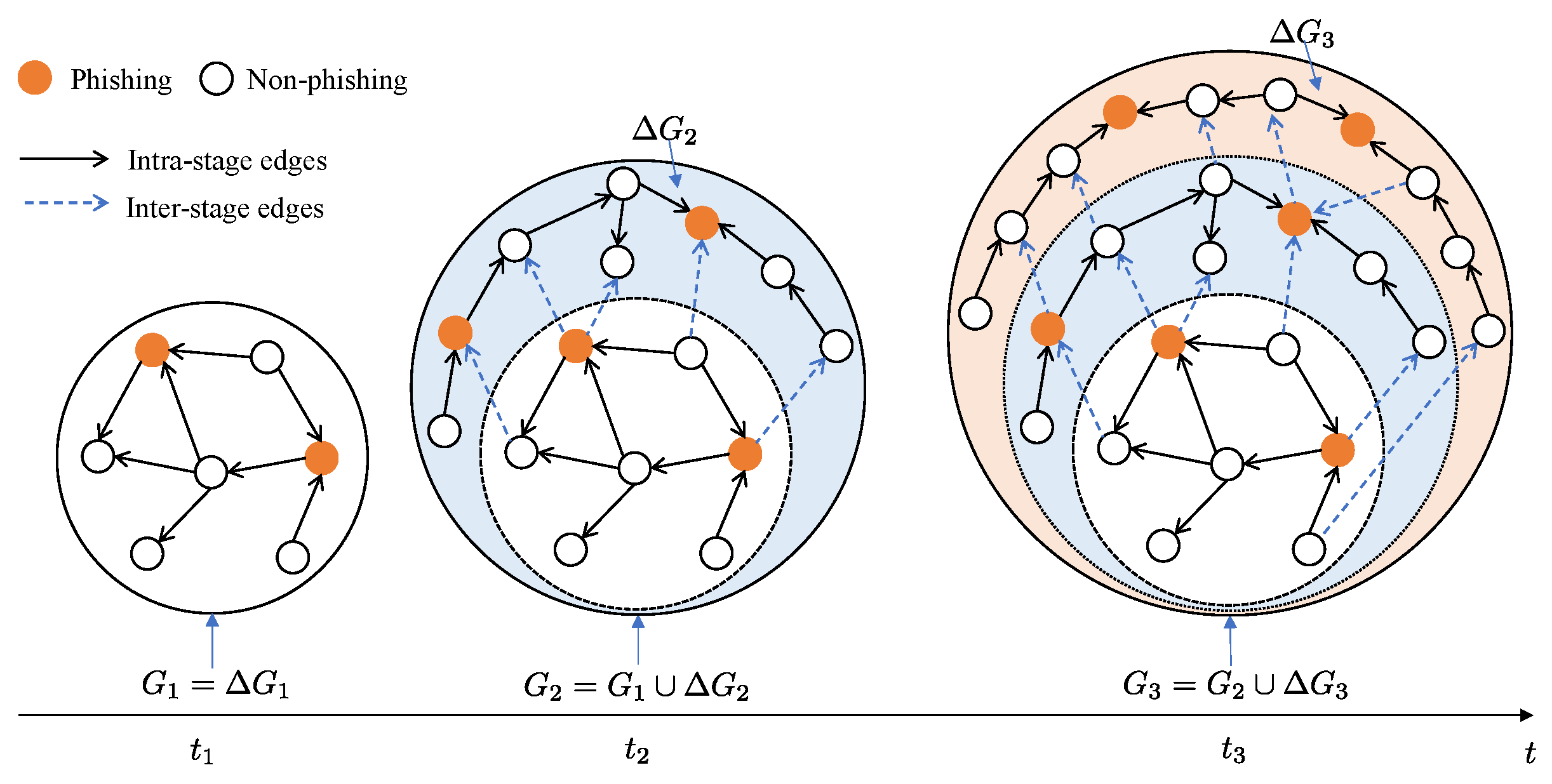
As shown in
Figure 1, in the evolving Ethereum transaction network (ETN) is denoted by
, where
is the snapshot of the network at time
, and
. The term
is the incremental transaction network (ITN) between time
and
(stage
n). We aim to train a sequence of GNN models
for corresponding snapshots
to continuously detect phishing nodes within the sample incremental setting of continual graph learning, incrementally improving the model performance as the network evolves, and to eliminate catastrophic forgetting throughout this process. In this process, each subsequent model
is trained using the previous model
as its initial state.
Notably, we employ the term “inter-stage edges” rather than “inter-task edges” in this work, as the task is single and constant—detecting newly added phishing nodes as the network evolves. In other continual graph learning scenarios with multiple tasks, “inter-task edges” is more appropriate.
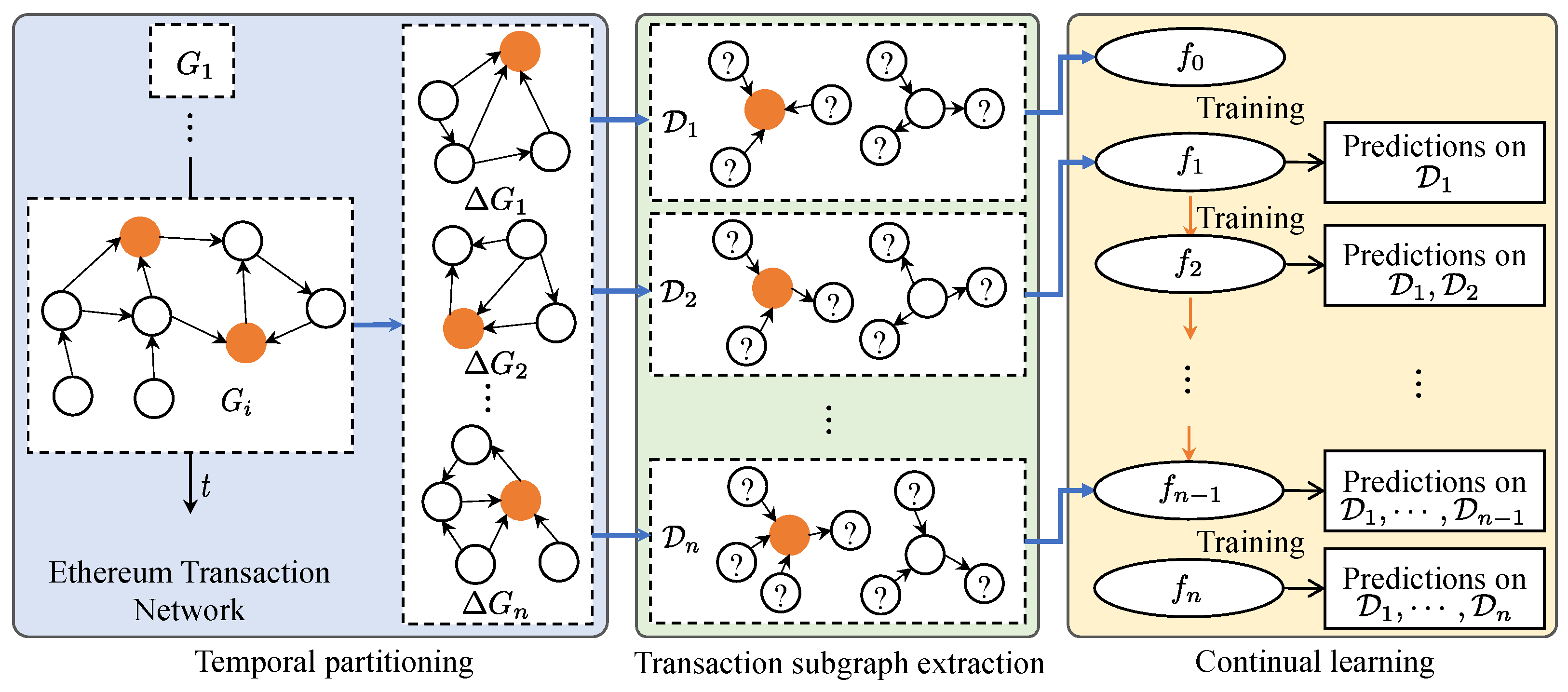
4. Methodology
Figure 2 depicts the proposed approach, which consists of three steps, namely temporal partitioning, transaction subgraph extraction, and continual training.
4.1. Temporal Partitioning
Temporal partitioning involves splitting the entire ETN into multiple ITNs to accommodate the continual learning setting. Since each transaction is associated with a specific timestamp, the most straightforward and logical partitioning method is based on the chronological order of timestamps. Additionally, the ETN can be partitioned according to equal time intervals or by an equal number of phishing nodes. Specifically, the temporal partitioning is formalized as follows.
Temporal Partitioning: Let be the snapshot of the ETN at time t. Choosing a strictly increasing sequence of timestamps . For each , define the incremental transaction network by , and . Temporal partitioning splits the ETN into a sequence of incremental transaction networks .
Since the ETN is a weighted directed multigraph, there may be multiple directed transactions between any two accounts at different times. Consequently, an account may be associated with multiple timestamps. We designate the timestamp that an account is first involved in a transaction as the basis for chronological order. After partitioning the ETN, multiple ITN are obtained.
4.2. Transaction Subgraph Extraction
Phishing scam detection in Ethereum is essentially a typical node classification task. However, in real-world ETN, there is a significant class imbalance between phishing nodes and non-phishing nodes: the number of phishing nodes is typically orders of magnitude smaller than the number of non-phishing nodes. This imbalance makes it highly challenging to conduct effective node classification for phishing detection in the ETN. To address this challenge, we propose transforming the node classification task into a graph classification task by introducing k-order transaction subgraphs (k-TSGs).
k-order subgraphs: The
k-order subgraphs
centered at a node
v is defined as
,
, where
is the graph distance (hop) between nodes
u and
v, as shown in
Figure 3.
Given the extremely small proportion of phishing accounts and our goal to detect them across the entire ETN, we aim for the datasets to include all known phishing accounts. Therefore, we extract the k-TSGs of all phishing accounts in each ITN as positive samples. Next, we randomly select an equal number of k-TSGs from non-phishing accounts in the corresponding ITN as negative samples. In this manner, we can obtain multiple datasets for subsequent continual learning, with each dataset being class-balanced. This paper uses the first-order transaction subgraphs (1-TSGs) of nodes as the samples for graph classification.
4.3. Continual Learning
After obtaining a sequence of class-balanced datasets, we can continuously perform phishing scam detection in the ETN through continual learning with graph classification. During this process, various strategies for continual learning can be implemented. We introduce a knowledge-augmented replay (KAR) method for continual graph learning.
4.3.1. Knowledge-Augmented Replay
Evidence from [
66] suggests that phishing nodes exhibit distinct features and behavior patterns compared to non-phishing nodes. For better clarification, we adopt the theoretical framework of distributional separability.
Let and be the distributions of newly added phishing and non-phishing nodes in , respectively. and are the embedding of nodes u and v produced by , respectively. Let be any chosen separability measure (e.g., distance, divergence, margin) between the two distributions of newly added phishing and non-phishing nodes in . If increases with i, the classifier’s decision boundary can better separate the two classes.
As the network evolves, the differences between phishing and non-phishing nodes tend to become more pronounced. For example, from times to , a phishing account A typically accumulates larger increases in its neighbor count, degrees, and transaction amount than a representative non-phishing node B. As a result, the separability measure between their class-conditional feature distributions grows over time, i.e., .
Nevertheless, an increase in the separability between the newly added phishing and non-phishing nodes in alone does not guarantee that knowledge acquired on current stage will positively transfer back to earlier stages because the classifier is optimized solely to maximize . It may relocate its decision boundary to suit only the new data, thereby misclassifying earlier samples and suffering catastrophic forgetting.
By contrast, knowledge-augmented replay enriches the distribution by taking union with samples in memory buffer, i.e., and . Let and be the distributions of all phishing and non-phishing nodes in , respectively. Define as the separability of and . These two distributions incorporate both newly added and replay samples from earlier stages, encouraging the model to learn a decision boundary that simultaneously maximizes separability on both new and historical distributions. i.e., .
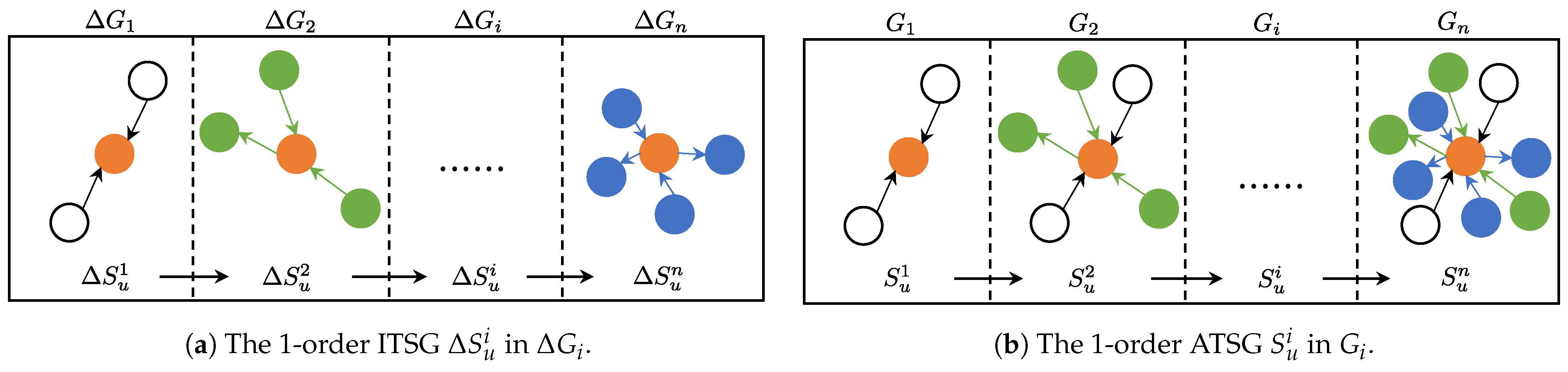
In this paper, we track the activity of all known phishing accounts across ITNs and store the reappearing phishing nodes in the memory buffer. Additionally, to preserve the class balance, we randomly sample an equal number of reappearing non-phishing nodes from earlier ITNs to store in the buffer. As the ETN evolves, the features and structures of these reappearing accounts change, motivating a shift from node classification to graph classification. We therefore introduce evolutionary transaction subgraphs (ETSGs) to capture these differences, which are crucial for continual learning.
4.3.2. Evolutionary Transaction Subgraph
Unlike representing all transactions formed by many nodes over a period of time as a network, we describe all transactions associated with a specific node over a given period as a graph. Consequently, ETSGs depict the evolution process of a node over time. Specifically, ETSGs include incremental transaction subgraphs (ITSGs) and accumulative transaction subgraphs (ATSGs), which are formalized as follows.
Incremental /Accumulative Transaction Subgraph: In a dynamic transaction network , let be the incremental transaction network between time and , and be the snapshot up to . Given a node and a pre-defined rule , the incremental transaction subgraph of u is defined as , where , and includes all endpoints of edges in . The accumulative transaction subgraph of is defined as , where , and contains all endpoints of edges in . returns the set of transactions in G that involve node u according to rule . In this paper, we define to extract all edges incident to u, and we refer to the resulting subgraph as the first-order transaction subgraph.
Figure 4a,b illustrate the first-order ITSG and first-order ATSG, respectively. ITSGs (
) capture a node’s incremental transactions within a specific time period, whereas ATSGs (
) represent all transactions associated with that node up to the current time. Formally,
.
As the patterns of phishing and non-phishing nodes become increasingly distinct over time, retaining the 1-ATSGs of reappearing phishing and non-phishing nodes provides more discriminative examples. By replaying these examples during the current stage, the model can learn more discriminative representations, thereby improving its performance.
4.3.3. Overall Process
Algorithm 1 delineates an overall procedure for continual graph learning using the KAR method.
| Algorithm 1 Continual Graph Learning with KAR Method |
| Input: Incremental Transaction Network , previous model |
| Output: Performance matrix |
- 1:
Initialization: all initialized to the empty set - 2:
for to n do - 3:
Assemble & simplify: - 4:
Extract nodes: - 5:
Balanced sampling: - 6:
- 7:
for to do - 8:
, - 9:
- 10:
end for - 11:
, - 12:
- 13:
- 14:
Subgraph & feature extraction: - 15:
for all do - 16:
- 17:
for all do - 18:
- 19:
end for - 20:
end for - 21:
Dataset & train: - 22:
- 23:
for to i do - 24:
- 25:
end for - 26:
end for
|
Given a timestamp , we extract the ITN and assemble the cumulative snapshot , which comprises all transactions up to . Initially, the snapshot is a multigraph. We simplify the multigraph into a simple graph (still denoted by for convenience) by merging parallel edges and summing their transaction amounts. This simplification preserves the main node features of the ETN while avoiding the additional complexity of handling multi-edge structures during GNN message passing.
At each stage
i, we first extract phishing and non-phishing nodes from the ITN
, distinguishing nodes newly added in
from those reappearing from earlier ITNs. We then construct the class-balanced central node set
by balanced sampling, selecting equal numbers of phishing and non-phishing nodes. The memory buffer
is populated with the reappearing phishing nodes and an equal number of non-phishing nodes. Next, for every central node
, we extract its 1-ATSG
from the simplified snapshot
and compute node features for each node
. The collection
constitutes the dataset
, which we use to train the GNN model and evaluate its performance under continual learning settings. Further implementation details are given in
Section 5.
5. Experiments
We conduct extensive experiments to evaluate the performance of the proposed method on detecting Ethereum phishing scams.
5.1. Data
We construct the ETN dataset for continual graph learning based on ETN data on XBlock (
https://xblock.pro/#/dataset/13, accessed on 15 March 2025), which contains 2,973,489 addresses, 13,551,303 transactions, and 1165 labeled phishing addresses. This transaction network is composed of 13 connected components, where a connected component is a network in which all nodes are reachable from each other through (un)directed edges. We select the largest component, which contains 2,973,382 addresses, 13,551,214 transactions, and 1157 labeled phishing addresses, to construct the continual graph learning datasets.
Table 2 summarizes the statistics of this dataset.
Although node features are not strictly required for graph classification tasks, they can provide valuable information that enables GNNs to more effectively capture patterns and features within the graph structure. In particular, we extract the following node features:
Node labels: Each node is labeled to indicate whether it represents a phishing or non-phishing entity. Although phishing scam detection in Ethereum is fundamentally a node classification task, these node labels can also serve as features when reformulating the problem as a graph classification task.
The number of neighbors: A neighbor of a given node is any node reachable from it. First-order neighbors are directly connected to the given node, while higher-order neighbors are reached through one or more intermediate nodes. For instance, second-order neighbors are connected via one intermediate node, and k-order neighbors are connected through 1 intermediaries. In this paper, we consider the number of first-order neighbors as a node feature.
In-degree: The number of edges directed towards a node, indicating how many edges terminate at that node. In the ETN, in-degree represents the number of incoming transactions an account receives from other accounts.
Out-degree: The number of edges originating from a node, indicating how many edges start from that node. In the ETN, out-degree reflects the number of outgoing transactions from an account to other accounts.
Total degree: The sum of in-degree and out-degree, representing the total number of edges connected to a node, regardless of direction. In the ETN, the total degree corresponds to the number of transactions associated with an account.
In-strength: In a weighted graph, in-strength is the sum of the weights of all incoming edges to a node, serving as the weighted counterpart of in-degree. It captures the total influence or flow that a node receives from its neighbors. In the ETN, it refers to the total amount of Ether received by an account.
Out-strength: In a weighted graph, out-strength is the sum of the weights of all outgoing edges from a node, representing the weighted counterpart of out-degree. It reflects the total influence or flow that a node exerts on its neighbors. In the ETN, it denotes the total amount of Ether sent by an account.
Total strength: The sum of in-strength and out-strength, representing the total weighted connections of a node. It quantifies the overall influence the node exerts and receives within the network. In the ETN, it refers to the total amount of Ether involved in an account’s transactions.
5.2. ETN Partition
Following the chronological order, we propose partitioning the ETN based on the principle of an approximately equal number of phishing accounts. Specifically, we first sort all 1157 phishing accounts according to their first timestamps and then allocate them into 10 ITNs on average (i.e., 116 for the first 7 ITNs and 115 for the last 3 ITNs).
Defining the first timestamp of a phishing node
is
), and the first ITN contains all transactions between the beginning timestamp of the ETN (denoted by
) and the timestamp
. The second ITN contains all transactions between the timestamp
and
, and so forth. The last ITN contains all transactions between the timestamp
and the last timestamp (denoted as
). In this way, we derive 10 ITNs (
) by partitioning the ETN
, along with the distribution of phishing node across these ITNs, as detailed in
Table 3.
Note that the above partitioned ITNs include the inter-stage edges. To further investigate the influence of inter-stage edges on continual learning performance, we also perform continual learning without inter-stage edges.
5.3. Datasets Construction
5.3.1. Central Node Set Construction
After obtaining ITNs, we construct a corresponding class-balanced dataset for each ITN . Since we transform the node classification into a graph classification task, we first determine the central node set of . Under the KAR method, the central node set is the union of the phishing central node set and the central non-phishing node set .
To maximize the presence of phishing examples in the dataset, we incorporate all phishing nodes into the central node set. Therefore, . Furthermore, the phishing central node set comprises both newly added and reappearing phishing central nodes, denoted by and , respectively. Particularly, , and .
The reappearing phishing central nodes are those that were newly added in earlier ITNs and then reappear in . Formally, for each , let be the set of phishing nodes newly added in that reappear in . Then the total reappearing phishing node set is .
Analogously, the central non-phishing node set is partitioned into newly added and reappearing subsets, denoted by and , respectively. Since non-phishing nodes far outnumber phishing nodes, we maintain a consistent distribution of phishing and non-phishing nodes within the central node set by uniformly sampling from the corresponding pools of non-phishing candidates.
Specifically, we obtain the newly added central non-phishing node set by uniformly sampling a subset such that . For the reappearing central non-phishing nodes, we first randomly sample with for each and then aggregate . In this way, we obtain the central node set .
To illustrate, we present a concrete example of central node set construction. As shown in
Table 3,
contains 158 phishing nodes in total: 116 newly added (
) and 42 reappearing (
), of which 8 reappear from
(
) and 34 reappear from
(
). Accordingly, the phishing central node set also contains 158 phishing nodes (
).
Next, we randomly sample 116 non-phishing nodes from the newly added non-phishing node set so that . Similarly, we randomly sample 8 non-phishing nodes from the reappearing non-phishing node pool in () and 34 from the corresponding pool in (), thereby matching the distribution of reappearing phishing nodes. Consequently, the central node set in the third stage contains 316 central nodes in total ().
5.3.2. Subgraph and Node Feature Extraction
We then extract subgraphs and compute node features for each node contained within each subgraph. Specifically, we extract 1-ATSG from each snapshot for each central node and compute the node features of each node . The resulting dataset comprises all such extracted 1-ATSGs.
Additionally, we include naïve and retraining strategies for evaluation. The naïve approach simply fine-tunes the model on each new ITN without any forgetting mitigation, serving as the lower bound for continual learning performance. In contrast, the retraining method retrains the model from scratch on the accumulated date at every stage, thereby establishing an upper bound. The main difference between these two methods and the KAR method lies in the construction of the central node set and the extraction of subgraphs.
Taking stage 3 as an example, introduces 116 newly added phishing nodes. Under the naïve strategy, the phishing central node set consists solely of these 116 nodes. By contrast, the retraining approach aggregates all newly added phishing nodes from stages 1 through 3—totaling 348—into the phishing central node set. The sampling procedure for non-phishing central nodes mirrors that of the KAR method. As for subgraph extraction, the naïve approach extracts 1-ITSGs from , whereas the retraining method extracts 1-ATSGs from .
For the scenario in which inter-stage edges are removed, we extract 1-ITSGs from for the central nodes under the naïve method, and 1-ITSGs from for the central nodes under both the KAR and retraining methods.
5.4. Experimental Settings
5.4.1. Models
We conduct experiments using the following GNNs.
GCN [
42]: The GCN uses convolutional operations on graph data to aggregate information from neighboring nodes through a first-order approximation of spectral convolution.
GAT [
43]: The GAT employs attention mechanisms to assign different weights to the edges connecting a node to its neighbors, enabling more flexible and context-aware feature aggregation in graph neural networks.
GATv2 [
67]: GATv2 improves upon the original GAT by using a dynamic attention mechanism that better captures the importance of neighboring nodes, resulting in more accurate and expressive attention weights.
GIN [
45]: The GIN improves the expressiveness of graph neural networks by using sum aggregation, which closely approximates the Weisfeiler–Lehman graph isomorphism test, making it capable of distinguishing a wider variety of graph structures.
All four models share a common blueprint: two stacked graph convolutional layers (each followed by a nonlinear activation and 50% dropout); a global pooling operation that collapses node embeddings into a single graph-level vector; and a final linear classifier that produces the output logits.
In the GCN variant, both convolutional layers are implemented as GCNConv modules that project node features into a d-dimensional latent space, each followed by a ReLU activation. The GAT and GATv2 versions replace these with attention-based convolutions: the first layer employs eight parallel heads, each producing a d-dimensional output that is concatenated into a -dimensional representation and subjected to ELU activation and dropout, before a single-head projection back to d dimensions; the only difference between them is the use of GATConv versus GATv2Conv. The GIN model instead uses two GINConv layers, each internally parameterized by an MLP that applies a linear map to d dimensions, batch normalization, a ReLU, and a second linear layer with ReLU. After each convolution, global sum pooling yields two d-dimensional graph summaries that are concatenated into a -dimensional embedding and passed through a two-layer MLP head with a -unit hidden layer, ReLU activation, and 50% dropout prior to the final classification.
5.4.2. Training
We train the aforementioned GNN models using the following parameters: the proportion of the training set within each dataset (), the number of neurons in the hidden layers (d), the maximum number of epochs (m), the learning rate (), and the batch size (b). Specifically, we set to 0.7, d to 32, m to (100, 300, 500), to (0.001, 0.003, 0.005), and b to 32. All datasets are randomly shuffled before being split into training and test sets.
Training is conducted on a server equipped with an NVIDIA V100 GPU with 16GB of GPU memory. The models are implemented in PyTorch v2.1.2, with the GNNs constructed using the PyTorch Geometric library.
5.4.3. Evaluation
We assess the overall performance and degree of forgetting of the models using the average accuracy (ACC) and backward transfer (BWT), respectively, as defined in [
68].
where
n is the number of all stages, and
refers to the test performance on the
stage after training on the
stage.
ACC describes the overall performance of a continual learning model across all datasets after sequentially training on all n stages. BWT measures the extent to which a model forgets previously learned knowledge. Therefore, we use overall performance and average accuracy interchangeably, as well as backward transfer and average forgetting.
5.5. Results
5.5.1. Overall Performance
Table 4 compares the average accuracy and average forgetting of four GNNs after training on all 10 datasets across two scenarios. It shows that retaining inter-stage edges significantly improves model’s overall performance and backward transfer compared to removing them.
In the scenario without inter-stage edges, nearly all models exhibit catastrophic forgetting across all three methods, as indicated by the negative backward transfer values, with the exception of the retraining-o method using a GIN. However, in the scenario with inter-stage edges, both the KAR and retraining methods eliminate catastrophic forgetting for all models. Particularly, the KAR method achieves performance comparable to the retraining method.
An intriguing observation is that, in the scenario without inter-stage edges, the replay-o method unexpectedly underperforms compared to the naïve-o method. A reasonable explanation is the high proportion of recurring nodes in the ETN, resulting in a significant number of inter-stage edges between ITNs. When inter-stage edges are removed, phishing nodes lose substantial transactional information, making their 1-TSGs less distinguishable from those of non-phishing nodes. The replay-o method introduces more of these indistinguishable samples, which paradoxically leads to worse performance compared to the naïve-o method.
5.5.2. Stage-Wise Average Accuracy
We also compare the average accuracy of four GNNs using three methods under two scenarios of each stage, as shown in
Figure 5. The plots demonstrate that retaining inter-stage edges allow the model to incrementally improve overall performance or maintain stability, while removing inter-stage edges causes the model’s overall performance to decline sharply over time and eventually stabilize.
When inter-stage edges are removed, all methods experience a sharp decline in average accuracy over time, particularly during the initial stages. The naïve-o and replay-o methods eventually stabilize around 50%, while the retraining-o method performs slightly better, stabilizing at 60%. Conversely, when inter-stage edges are retained, all methods exhibit an incremental increase in average accuracy over time, except for those using the GIN model, which remain stable or show a slight decrease. Specifically, the KAR and retraining methods reach or exceed 90%, consistently delivering the best performance. The KAR method achieves results comparable to the retraining method while using less memory.
These results highlight that removing inter-stage edges hinders knowledge transfer, leading to a gradual decline in overall performance. In contrast, retaining inter-stage edges facilitates knowledge transfer, promoting improvements in overall performance over time.
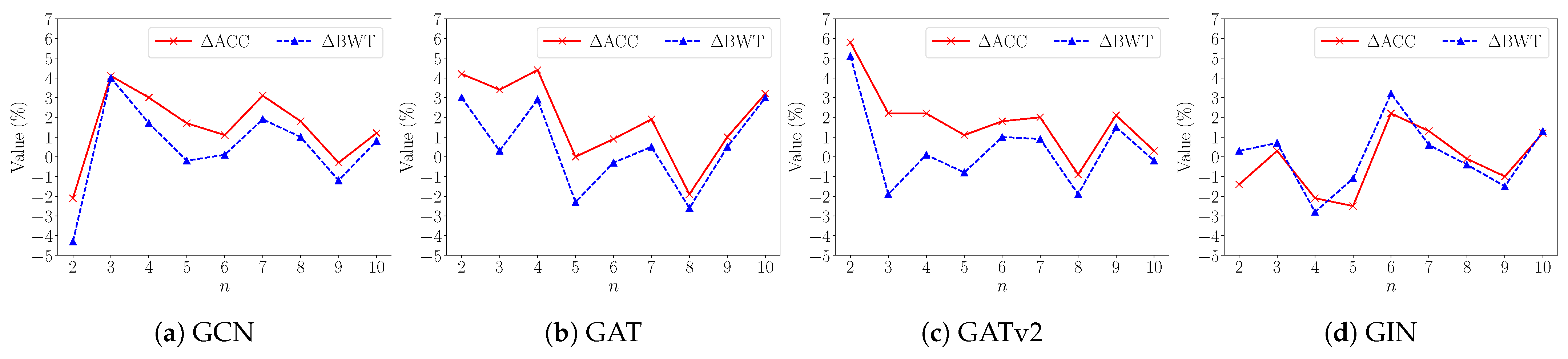
5.5.3. Stage-Wise Average Forgetting
Figure 6 plots the results of the stage-wise average forgetting mechanisms of four GNNs using three methods across two scenarios. Each method generally shows stronger positive backward transfer when inter-stage edges are retained compared to when they are removed. Furthermore, in conjunction with stage-wise average accuracy, the results reveal that incremental performance improvement does not necessarily coincide with positive backward transfer values.
When inter-stage edges are removed, the naïve-o and replay-o methods consistently exhibit negative backward transfer values across all stages, indicating persistent catastrophic forgetting. The retraining-o method shows predominantly positive backward transfer, remaining stable or with slight fluctuations around zero in most cases.
In contrast, when inter-stage edges are retained, both the KAR and retraining methods show predominantly positive backward transfer values that are significantly above zero, with the exception of their implementations using the GIN model. This outcome suggests positive knowledge transfer in most cases, effectively overcoming catastrophic forgetting. Notably, the KAR method achieves performance comparable to the retraining method while using less memory. The naïve method displays considerable fluctuations, with only a few stages showing positive backward transfer values, but catastrophic forgetting remains prevalent in most stages.
5.5.4. Comparison with Existing Methods
We further compare the proposed method with several existing baselines, EWC [
53], LwF [
52], and TWP [
10], under a unified training protocol, using a maximum of 300 epochs, a batch size of 32, and a learning rate of
.
Table 5 presents the results under two scenarios.
As shown in
Table 5, in the scenario of removing inter-stage edges, the Replay-o method confers no clear advantage: the Retraining-o method achieves the best results in most cases, while the replay-o method lags behind or at best matches other methods. Moreover, all approaches exhibit negative backward transfer values in this setting, indicating persistent forgetting of prior knowledge. In contrast, when inter-stage edges are preserved, every method attains substantially improved backward transfer—most values turn positive—and the KAR method not only matches or slightly exceeds the retraining method in average accuracy across all four GNNs but also surpasses established baselines (EWC, LwF, TWP) on both accuracy and forgetting metrics. These results underscore the critical importance of maintaining inter-stage connectivity in the Ethereum transaction network for continuous and effective phishing detection.
5.6. Determinants of Performance Improvement
From the results of stage-wise average accuracy and stage-wise average forgetting, we observe that performance improvement does not necessarily require positive backward transfer values, thereby somewhat contradicting our intuition.
Figure 7 depicts the changes in average accuracy and forgetting values of the KAR method across different stages.
Figure 7 demonstrates that the variations in backward transfer closely mirror those in average accuracy, with their trends remaining consistent in most cases. However, certain exceptions to this alignment are observed. To further investigate this effect, we explore the mathematical relationship between them starting from their definitions.
According to Equations (2) and (3), we have
Therefore,
can be expressed as a function of
. In other words, we have
where
is the average initial performance over all known
n stages.
To uncover the relationship between the changes in overall performance and backward transfer, we define
as the change in overall performance after training on
stage, compared to the performance after training on the
stage in the continual learning process. According to Equation (
6), we obtain the following equation:
This equation can be further simplified to the following one:
where
represents the change in backward transfer after training on the
stage, compared to the backward transfer after training on the
stage.
Equation (
8) indicates that overall performance change is primarily influenced by the variation in backward transfer, alongside its value and the initial performance of each stage.
5.6.1. Backward Transfer
In the early stages of continual learning, both the value of backward transfer and the initial performance of each stage have a notable influence on overall performance changes. This is particularly evident in cases where positive changes in backward transfer do not necessarily lead to improvements in overall performance. A clear example of this can be observed in the naive-o method, as shown in
Figure 5d and
Figure 6d.
When , the naïve-o method exhibits a large negative backward transfer value, indicating substantial forgetting. Although there is a positive change in backward transfer from stages two to three, this improvement is insufficient to offset the negative impact of the large negative backward transfer and the continuously declining initial performance, leading to a further decrease in overall performance. This highlights the critical role of both backward transfer and initial performance in the early stages of continual learning.
5.6.2. Initial Performance
Figure 5 and
Figure 6 also reveal the significant influence of initial performance in early stages on overall performance changes. For highly discriminative models such as GINs, the initial performance at the beginning tends to be high, as shown in
Figure 5d. According to Equation (
8), this can negatively impact overall performance. If changes in backward transfer and its values fail to offset the gap between the initial performance of new stages and the average initial performance of previous stages, overall performance declines. For example, in the naïve method, both the backward transfer value and its change are negative, which exacerbates this decline. In contrast, less discriminative models such as GCNs, GATs, and GATv2 exhibit lower initial performance in the early stages. In the sample-incremental setting of this study, a lower starting performance proves beneficial for improving overall performance, particularly when the introduction of new samples reinforces the model’s inductive bias, as observed when inter-stage edges are retained.
5.6.3. Backward Transfer Change
As the number of stage increases, the influence of backward transfer variation on performance becomes progressively stronger. In the limit, as the number of stages approaches infinity, overall performance change is governed solely by the change in backward transfer.
The relationship between the average accuracy and backward transfer indicates that predominantly negative backward transfer values do not necessarily result in a continuous performance decline. For example, in the naïve method, the backward transfer values are negative most of the time due to the absence of forgetting-resistant strategies. However, by retaining inter-stage edges, both phishing samples and non-phishing samples preserve most transaction information, maintaining the primary pattern distinction between them. As a result, the initial performance across stages differs slightly, preventing sharp drops in overall performance and even allowing for gradual improvement.
Similarly, predominantly positive backward transfer values do not guarantee incremental performance improvement. In the retraining-o method, the backward transfer values are generally positive due to the accumulation of data from all prior stages, indicating no forgetting. However, the removal of inter-stage edges causes a significant loss of transaction information, disrupting the pattern distinction between phishing and non-phishing nodes. Consequently, subsequent stages fail to enhance the patterns from earlier ones, and the initial performance on new stages is substantially lower than the average initial performance of previous stages, thereby negatively impacting overall performance.
5.7. Convergence
5.7.1. Performance Perspective
In deep learning, convergence refers to the state where the training process stabilizes, typically characterized by the loss function, model parameters, gradient norms, or validation error reaching a steady state or approaching an optimal value. It can also be reflected in the stabilization of model performance metrics, such as accuracy, which exhibit no further improvement as training progresses. Currently, the convergence of deep learning is predominantly studied through the lens of loss function optimization via stochastic gradient descent, with limited focus on alternative approaches. In this work, we assess convergence from the perspective of average accuracy and backward transfer. Specifically, we define the convergence in continual learning from the changes in average accuracy and backward transfer.
5.7.2. -k Bounded Convergence
Considering the changes in overall performance and backward transfer as functions of n, and given their bounded ranges (), it is impossible that these changes exhibit a strictly monotonic increase or decrease over the long term as n grows. Instead, they can only fluctuate within their respective ranges.
To formalize this, we introduce two thresholds and k to define -k bounded convergence, where continual learning is considered converge when backward transfer variation or overall performance variation falls below a specified threshold over k consecutive stages, rather than requiring the variation to strictly reach zero. This allows for more flexibility in determining convergence based on task-specific requirements. Since different scenarios prioritize different metrics, we separately define convergence based on overall performance and backward transfer.
Specifically, continual learning is considered to converge on average accuracy at t stage if . Similarly, it converges on backward transfer at t stage if . As the change in overall performance with increasing stages is primarily influenced by variations in backward transfer, it is generally sufficient to use either of these two metrics to assess convergence.
5.7.3. Convergence in KAR Method
In the sample incremental scenario examined in this paper, as shown in
Figure 5 and
Figure 6, the introduction of new samples initially exerts a pronounced impact on previous stages, leading to substantial changes in both overall performance and backward transfer. As
n increases, the influence of new samples on earlier stages gradually diminishes, resulting in smaller variations in overall performance and backward transfer, eventually stabilizing with minor fluctuations around zero. This indicates that, in this sample-incremental setting, the variations in average accuracy and backward transfer will ultimately converge to a relatively stable state over time. To explain this, we further explore the key factors influencing convergence, building on their respective definitions.
According to Equation (
2), we obtain
Since
, Equation (
9) can be simplified to the following one:
Similarly, according to Equation (3), we have
Since
, Equation (
11) can be simplified to
Equations (
10) and (
12) suggest that the convergence of continual learning process is predominantly influenced by the term
, thereby representing the change in performance on the
stage after training on the
stage relative to the
stage. This term quantifies the extent to which performance on the
stage is affected by additional training on the
stage, thereby reflecting the influence of newly acquired knowledge on previously learned knowledge.
Let , , and . The term represents the cumulative influence of learning the stage on all preceding stages. Furthermore, quantifies the average influence on average accuracy, while captures the average influence on backward transfer.
In this paper, we identify two primary factors that influence convergence: uncertainties arising from random sampling and significant shifts in phishing patterns. The KAR method effectively preserves prior knowledge by retaining inter-stage edges and evolutionary subgraphs of reoccurring phishing nodes. When phishing patterns remain stable, learning at a new stage typically has a positive effect on earlier stages, with the magnitude of this effect gradually diminishing and eventually stabilizing around zero. However, this influence can fluctuate irregularly due to random sampling uncertainties. For instance, if a stage’s sampling disproportionately includes exceptional non-phishing nodes, the impact of learning this new stage on prior stages may be more pronounced than usual.
When excluding random sampling uncertainties, significant changes in phishing patterns at a later stage—if not captured by the node features—may cause substantial fluctuations in the influence on prior stages, even if the model has already converged at an earlier stage. In cases where the phishing patterns of subsequent stages differ significantly from those of earlier stages, learning the new stage may negatively affect prior stages, leading to a decline in overall performance. However, if the phishing patterns of later stages align with those of earlier stages, the model’s performance may gradually recover and eventually converge to a new stable state. Consequently, convergence in continual learning may not be a one-time event but rather a multi-stage process.
5.7.4. Convergence in Broader Contexts
In broader continual learning scenarios, the convergence of continual learning may depend on the relationships between tasks, model capacity, and anti-forgetting strategies. Specifically, similar or complementary tasks encourage positive transfer, supporting convergence, while unrelated tasks can lead to interference and hinder stability. High-capacity models (e.g., with a large number of parameters) better accommodate new information without overwriting prior knowledge, whereas limited-capacity models may struggle to represent both old and new tasks, slowing or even preventing convergence. Effective anti-forgetting strategies, such as replay methods or regularization techniques, help maintain learned representations and stabilize performance. In scenarios where these factors are misaligned or inadequately addressed, the convergence of continual learning becomes uncertain and warrants further discussion.
6. Discussion
6.1. A Knowledge Perspective
The core of the KAR method lies in the ability of knowledge learned from later stages to supplement or augment the knowledge acquired from earlier stages, thereby facilitating incremental improvement in overall performance. In deep learning, knowledge takes various forms and is represented through different carriers, including data samples, data distributions, embeddings, and model parameters, all of which form a hierarchical structure.
In graph theory [
69], nodes serve as the fundamental elements. Edges, subgraphs, and entire graphs are all defined based on nodes and their relationships. As such, nodes can be considered the smallest unit of knowledge within graph data. In knowledge graphs, for example, nodes often represent specific entities, each containing attribute information. A node representing a cat, for instance, might include attributes such as breed, fur color, and other relevant details. This attribute information constitutes the knowledge associated with the node and is commonly expressed in the form of a triplet: “node–attribute–attribute value.”
However, the knowledge encapsulated within a single node is often isolated. In most cases, knowledge is organized and represented in a systematic, hierarchical, or networked manner to facilitate understanding, usage, and reasoning. Consequently, nodes can also represent abstract categories or concepts, with their relationships to entity-specific nodes expressing more complex knowledge. For example, in a knowledge graph, a node might represent the concept of “animal”, and through its relationship to the node representing “cat”, it can convey the knowledge “a cat is an animal”. In this case, the node becomes a component of a more intricate knowledge structure, with triplets of the form “node–relationship–node” serving as fundamental building blocks of such organized knowledge.
In this paper, a node represents an account, which encompasses various details such as account type, permissions, registration time, address, and public/private key pairs. However, this information alone is insufficient for identifying phishing accounts. To extract the necessary knowledge for phishing detection, we require interaction data (transactions) between accounts. The more comprehensive the transactions, the clearer the distinction between phishing and non-phishing accounts, enabling the model to learn more discriminative representations and thereby improving performance. To this end, the KAR method utilizes transaction subgraphs as a fundamental knowledge structure to capture account transaction behaviors. By retaining inter-stage edges and the 1-ATSGs of reoccurring phishing accounts, the method preserves more transactions. This approach not only addresses catastrophic forgetting but also strengthens the differentiation between phishing and non-phishing accounts. As new stages are introduced, the model can continuously refine and update its knowledge, resulting in a gradual improvement in overall performance.
6.2. Applicability of KAR
The KAR method is not confined to Ethereum phishing detection; it can be extended to a wider range of cryptocurrency anomaly detection applications, including anti-money laundering and fraud detection. Additionally, the Ethereum transaction network is a multigraph, whereas simple graphs (i.e., graphs without multiple edges between two nodes and self-loops) do not exhibit reoccurring nodes, making it impossible to identify important nodes. However, alternative approaches can be used to assess node importance. In graph theory, metrics such as degree and centrality are commonly employed to gauge the significance of nodes. In deep learning, node importance can be evaluated based on its contribution to the learning task, which can be quantified through factors such as loss function values, gradients, and model parameters. The specific metrics and methods for evaluating node importance vary according to the task and application context.
On the other hand, knowledge is not solely confined to being expressed through subgraphs. In continual graph learning scenarios involving multiple tasks, such as task incremental and class incremental settings, samples from a particular class can be represented by one or multiple prototypes. When a new sample belonging to an existing class appears, its similarity to the prototype of the known class can be measured using Euclidean distance or cosine similarity, allowing the prototype to be updated or augmented. When a new class emerges, a new prototype is added to the existing set of prototypes. This approach enables the model to retain knowledge from previous tasks while simultaneously learning from new ones. The concept of prototypes can also be interpreted from a graph perspective. If the prototype of a class is viewed as a central node, each sample from that class can be seen as a child node connected to the prototype by their similarity, forming a subgraph. The greater the number of representative samples, the richer the information, and the more accurately the prototype can represent the class.
In general continual learning settings, data often lack clear relationships. However, relationships can be discovered or constructed, such as temporal relationships in scenarios with time-series (e.g., video analysis, action recognition, object tracking) and spatial relationships in tasks like multi-view learning or 3D reconstruction. Images can also be linked through similarity measures; for instance, ref. [
70] uses the RBF kernel to compute pairwise similarities and generate random graphs that capture relational structures. However, how these relational structures are effectively leveraged to incrementally enhance model performance in general continual learning remains an open question.
7. Conclusions
In this work, we address the challenge of incremental performance improvement in sample-incremental continual graph learning for node classification tasks, with a focus on leveraging inter-stage edges as a pathway for explicit knowledge transfer. We propose a knowledge-augmented replay method, KAR, to use these edges to reinforce learned patterns across stages, effectively mitigating catastrophic forgetting and achieving incremental performance improvement by consolidating previously acquired knowledge while integrating new information. Experimental results on Ethereum phishing scam detection validate KAR’s effectiveness, achieving performance comparable to retraining with lower resource requirements. Additionally, we analyze the role of backward transfer variation in long-term performance changes and introduce -k bounded convergence as a practical criterion for assessing the convergence of continual learning.
Looking forward, our findings on knowledge augmentation provide a foundation for preserving and enhancing knowledge in evolving graph structures for incremental performance improvement. This approach has potential applicability beyond Ethereum phishing detection, extending to cryptocurrency anomaly detection and even other various continual graph learning scenarios. Further research could explore adapting knowledge augmentation to other continual learning settings. Further refinement of the -bounded convergence criterion may also facilitate standardization in convergence assessment, supporting sustained model performance across dynamic data landscapes.