Dynamic Task Scheduling Based on Greedy and Deep Reinforcement Learning Algorithms for Cloud–Edge Collaboration in Smart Buildings
Abstract
1. Introduction
- (1)
- Ignoring container compatibility constraints: Most existing studies assume that edge nodes have homogeneous computing resources and default tasks can be flexibly migrated to any node for execution, without fully considering issues such as container constraints in actual deployment [13]. In actual deployment, the functions and operation logics of each container application are independent, and tasks can only run within the appropriate application containers. For example, the video transcoding task relies on containers of specific codec libraries, while the data analysis task requires containers that are adapted to dedicated algorithm frameworks.
- (2)
- It is difficult to balance global optimization and real-time performance: Global optimization algorithms based on reinforcement learning and other techniques require global state modeling and complex calculations, resulting in high decision delay [14], making it difficult to deal with sudden scenarios such as fire alarms in smart buildings. Although heuristic algorithms are fast, they can easily obtain local optimal solutions [15]. For example, greedy algorithms are prone to cause resource imbalance and cannot take into account global optimization requirements such as energy consumption, delay, and the resource utilization rate.
- (3)
- Difficulty in adapting to dynamic environments: Mainstream algorithms such as particle swarm optimization and gray Wolf optimization [16] and other meta-heuristic algorithms lack environmental perception and learning capabilities. In complex scenarios such as dynamic fluctuations in the resource status of smart buildings, they are prone to fall into local optima and have difficulty dynamically adjusting strategies, resulting in task scheduling lagging behind real-time demands and being unable to efficiently respond to real-time changes in the system status.
- A task-scheduling system model with container compatibility constraints is developed for the typical application scenario of smart buildings. Under the assumption of static container deployment, the model jointly considers task characteristics, real-time requirements, and edge node resource status to optimize the overall task latency and energy consumption. Additionally, a timeout penalty mechanism based on each task’s maximum tolerable delay is introduced to ensure the timeliness of critical tasks.
- A two-stage dynamic task scheduling mechanism is proposed: In the first stage, a Resource-Aware Cost-Driven Greedy scheduling algorithm (RACDG) is designed to make rapid offloading decisions at edge nodes. In the second stage, the Proximal Policy Optimization algorithm based on Action Mask (AMPPO) is introduced to optimize the task-scheduling strategy based on the global state of the system, mask illegal actions, improve the global scheduling performance, and adapt to the dynamic task load changes in the smart building.
- A simulation environment for the smart building scenario is established to simulate real conditions such as dynamic arrival of tasks according to the Poisson process, heterogeneous edge node resources, and limited deployment of application containers. Moreover, a variety of representative scheduling algorithms are selected for comparative experiments. The experimental results show that the proposed algorithm can significantly improve the task completion rate under high-load conditions, reduce system delay and energy consumption, and demonstrate good scheduling robustness and practical application potential.
2. Related Work
2.1. Cloud–Edge Collaborative Computing
2.2. Task-Scheduling Algorithm
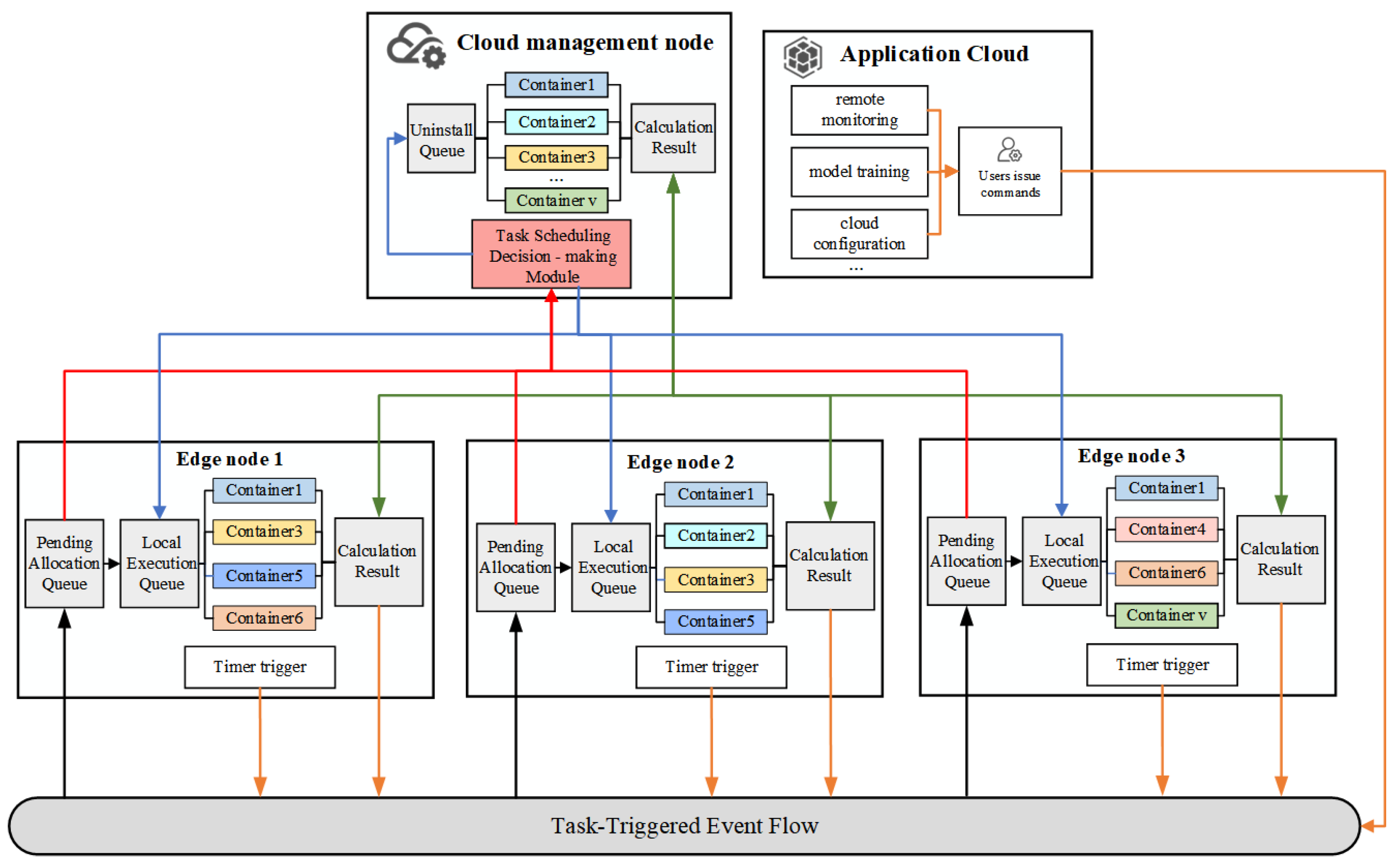
3. System Model and Problem Definition
3.1. System Model
3.1.1. Task Model
3.1.2. Decision-Making Model
3.1.3. Delay Model
3.1.4. Energy Consumption Model
3.2. Optimization Objective
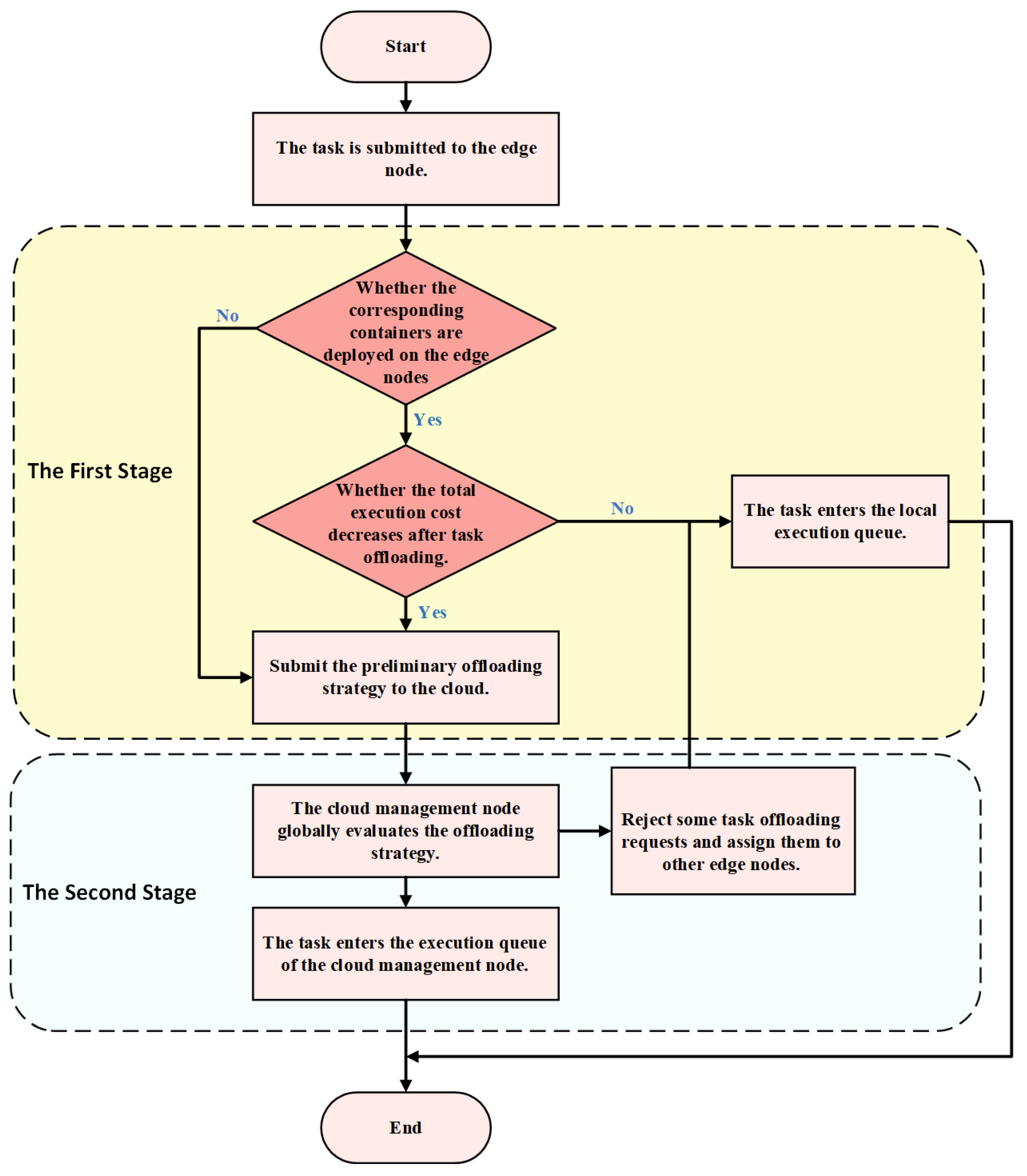
4. Greedy and Deep Reinforcement Learning-Based Task Scheduling Algorithm
4.1. Problem Decomposition
4.2. Distributed Edge Node Decision Phase
| Algorithm 1: Greedy scheduling algorithm based on a resource-aware cost-driven approach. |
 |
4.3. Cloud Management Node Decision Phase
4.3.1. Markov Decision Process Modeling
4.3.2. PPO Dynamic Scheduling Algorithm Based on Action Mask
| Algorithm 2: PPO dynamic scheduling algorithm based on action masks. |
 |
- (1)
- Initialization Stage: At the beginning of each episode, the policy network, value network, and memory are randomly initialized. These operations are independent of the number of tasks or episodes; hence, the time complexity for this stage is .
- (2)
- Environment State and Task Queue Generation: At the start of each episode, the system’s environment state is reset, and the resource states of all edge nodes and the cloud are initialized. This operation involves resetting the state of the system, and its time complexity is . Following this, the algorithm collects the tasks to be offloaded and generates the task allocation queue for the cloud. Assuming there are T tasks per episode, the time complexity for generating the task queue is .
- (3)
- Task Scheduling Loop:The policy network generates action probabilities based on the current task attributes and resource states. The computational complexity of this process depends on the network architecture (e.g., the number of layers and parameters), and is denoted as . Subsequently, for each task to be scheduled, the algorithm traverses all nodes to verify whether they contain available containers and satisfy the number of nodes; the complexity of this action masking step is thus . After filtering through the mask, the algorithm executes the offloading decision and calculates the task’s delay, energy consumption, and timeout penalties to generate rewards. Since each task requires individual computation, the time complexity for this part is . Finally, the state transition data is stored in the memory, which incurs a constant-time cost of . Therefore, the overall time complexity of the task-scheduling loop is , Here, the action masking cost is relatively negligible compared to policy inference and can therefore be incorporated into the overall scheduling complexity.
- (4)
- Policy Update: At the end of each episode, data is sampled from the memory, and the PPO algorithm is used to update the policy and value network parameters. The complexity of PPO typically depends on the network layers, so its time complexity is . The time complexity of the operation to clear the memory is .
5. Simulation and Analysis
5.1. Simulation Settings
- (1)
- Edge-first strategy (EF): All tasks are preferentially executed on local edge nodes. If edge resources are insufficient, the tasks are discarded;
- (2)
- Cloud-First strategy (CF): All tasks are, by default, offloaded to the cloud for execution;
- (3)
- Random Selection strategy (RS): In each scheduling round, tasks are randomly assigned to either the cloud or edge nodes for execution;
- (4)
- RACDG: a resource-aware cost-driven greedy algorithm proposed in Section 4 as the first-stage solution of this work;
- (5)
- PSO [36]: this algorithm is a task-offloading strategy based on particle swarm optimization for industrial IoT environment, aiming to minimize the delay and energy consumption of task processing.
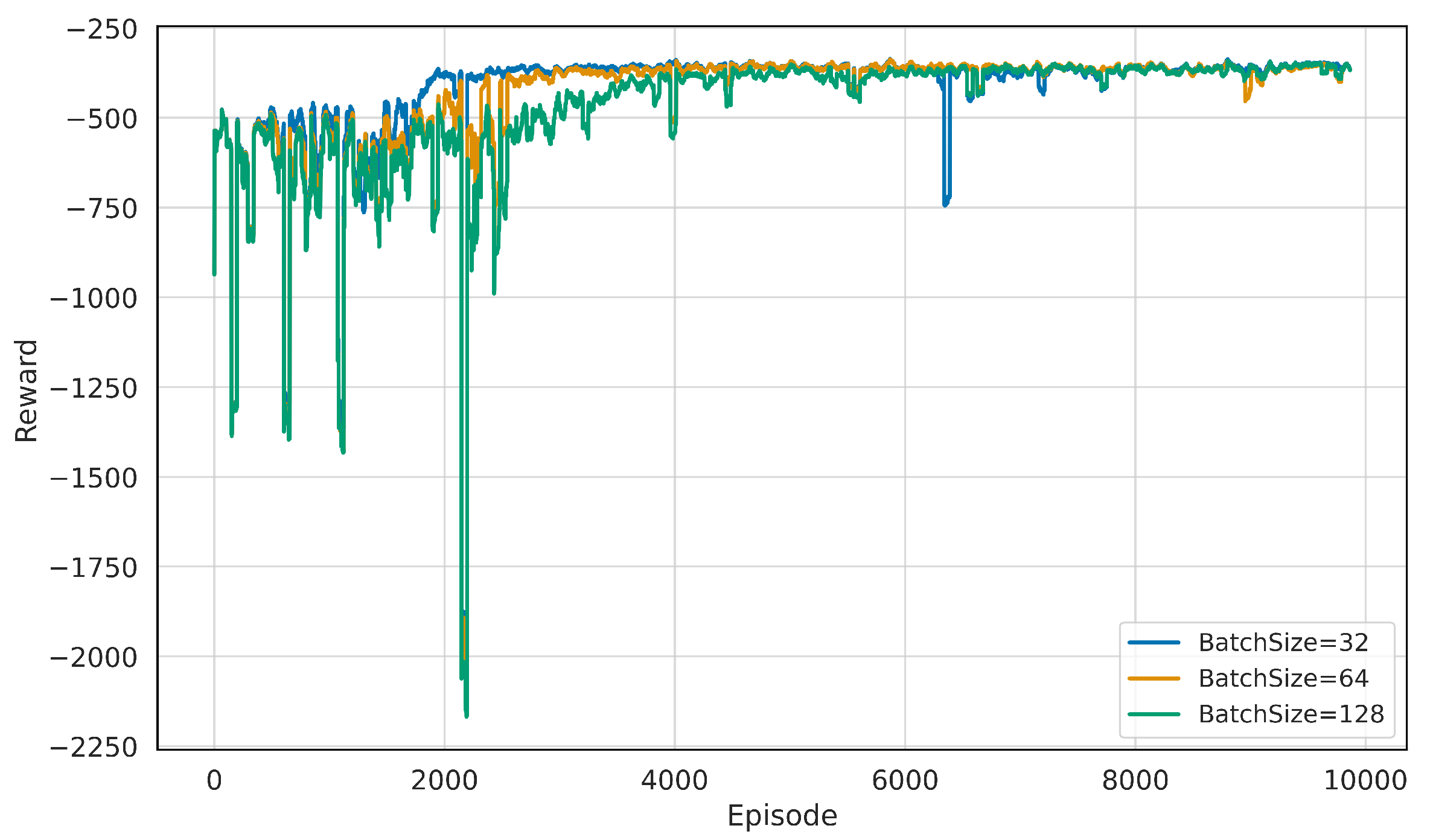
5.2. Model Hyperparameter Settings and Training Cost Analysis
5.2.1. Hyperparameter Settings
5.2.2. Training Cost Analysis
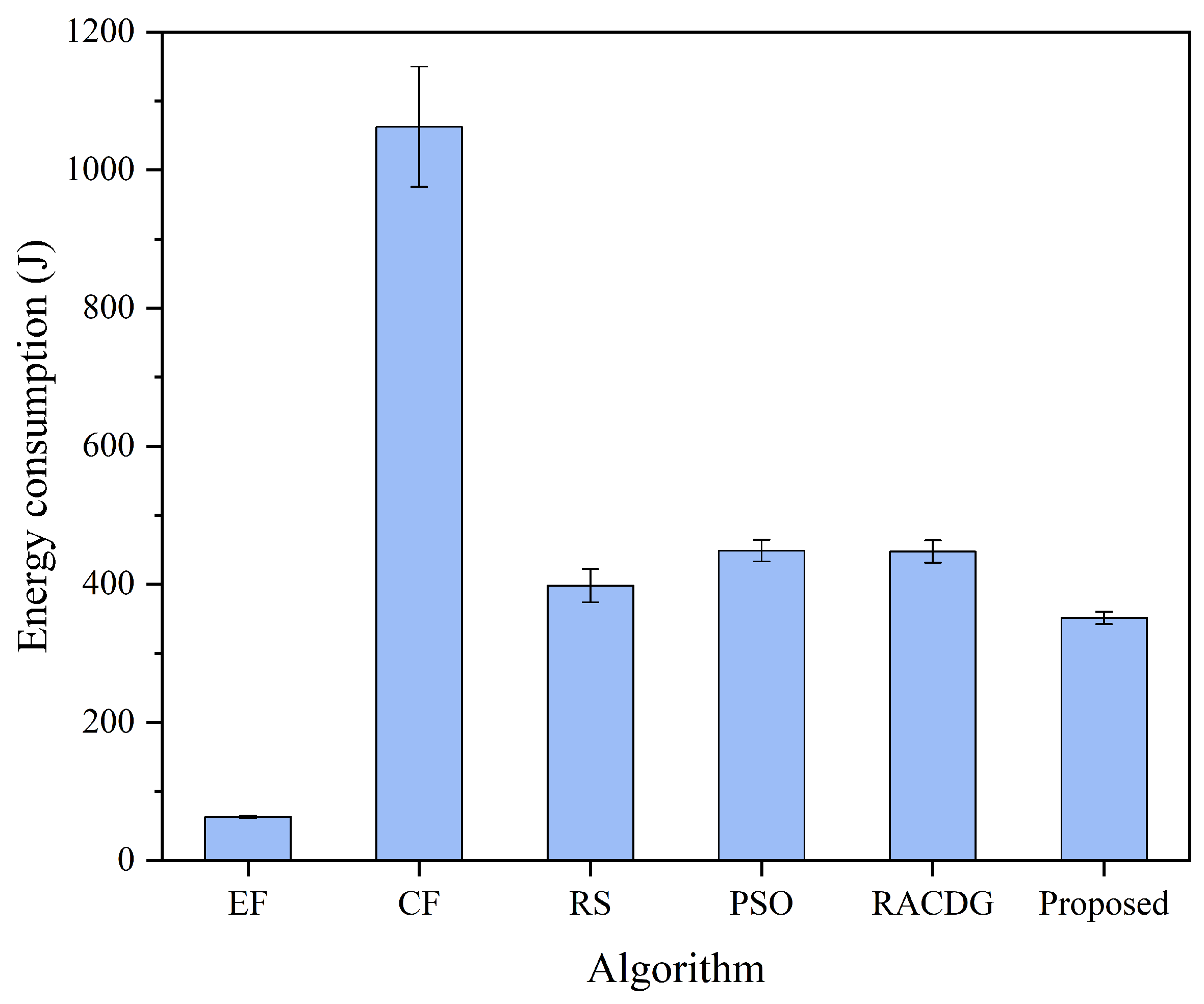
5.3. Experimental Results and Analysis
- Total Time: Refers to the cumulative time taken for all tasks from their arrival in the system to the completion of execution, measured in seconds (s).
- Total Energy Consumption: Refers to the sum of computational and communication energy consumed during the execution of all tasks, measured in joules (J).
- On-Time completion rate of tasks: Refers to the proportion of tasks completed within their maximum tolerable latency. It is defined as .
5.3.1. Overall Performance Comparison
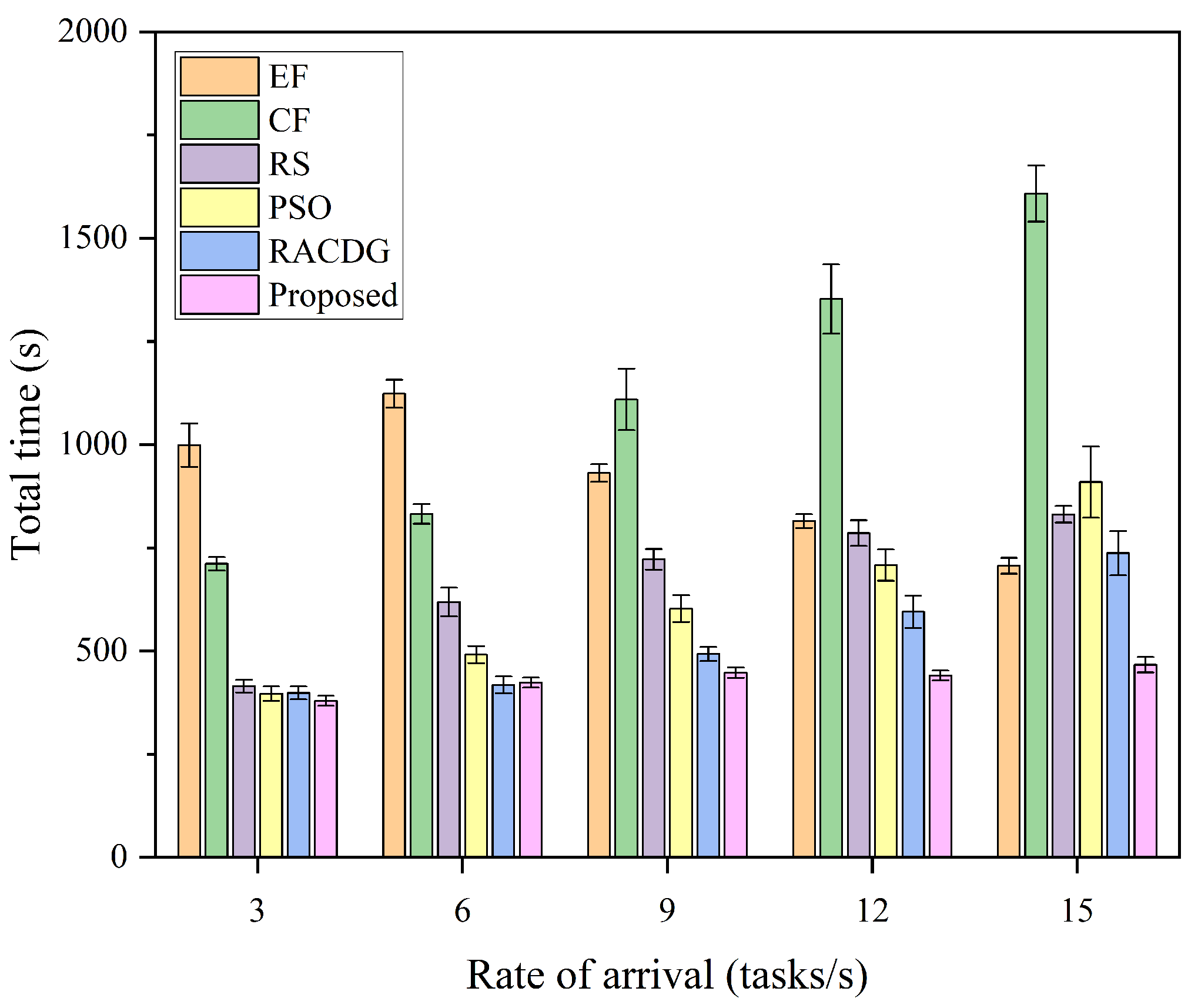
5.3.2. Performance Analysis Under Different Mission Arrival Rates
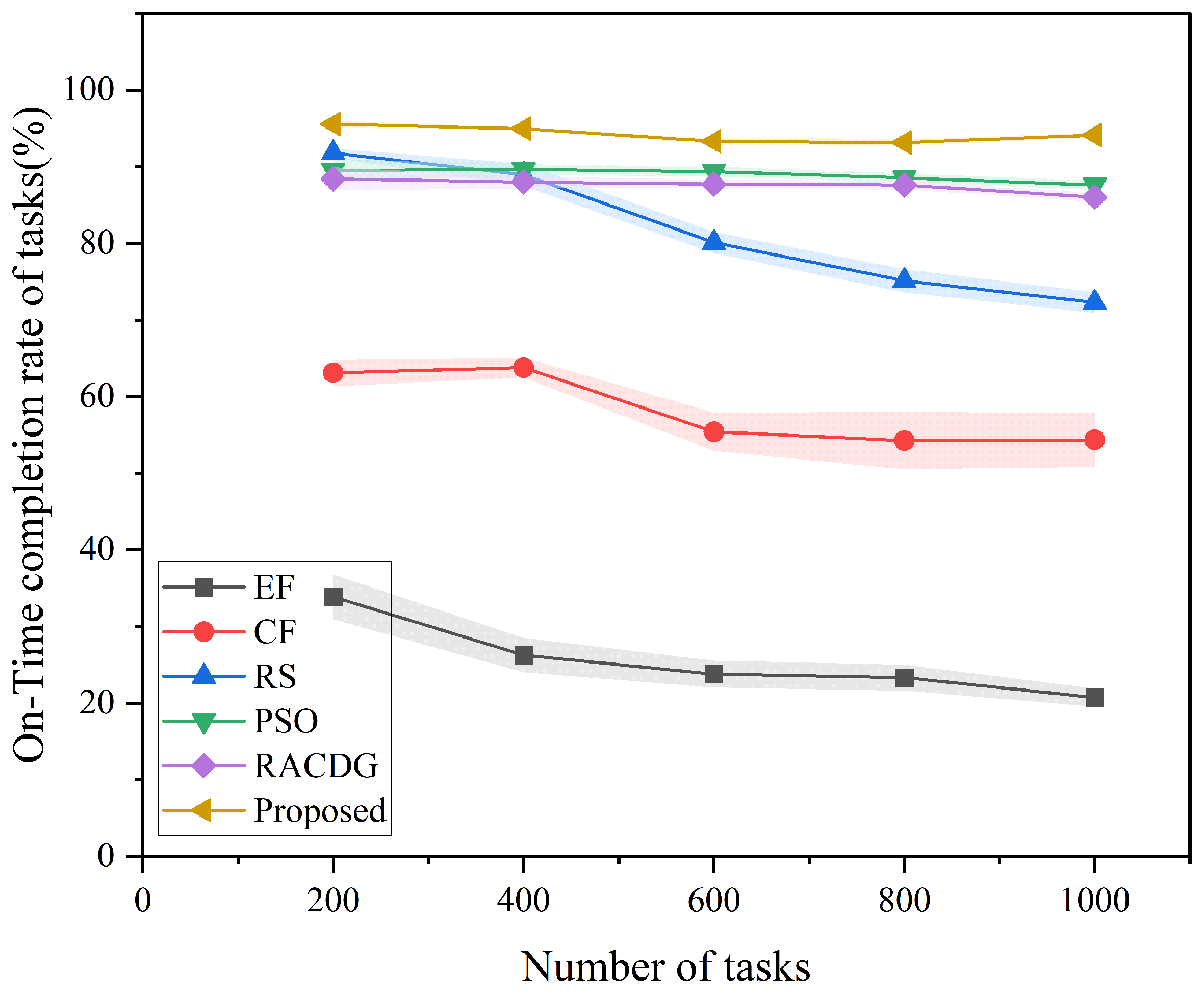
5.3.3. Performance Analysis by Total Number of Tasks
5.4. Time Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haiyirete, X.; Zhang, W.; Gao, Y. Evolving Trends in Smart Building Research: A Scientometric Analysis. Buildings 2024, 14, 3023. [Google Scholar] [CrossRef]
- Apanaviciene, R.; Vanagas, A.; Fokaides, P.A. Smart Building Integration into a Smart City (SBISC): Development of a New Evaluation Framework. Energies 2020, 13, 2190. [Google Scholar] [CrossRef]
- Doukari, O.; Seck, B.; Greenwood, D.; Feng, H.; Kassem, M. Towards an Interoperable Approach for Modelling and Managing Smart Building Data: The Case of the CESI Smart Building Demonstrator. Buildings 2022, 12, 362. [Google Scholar] [CrossRef]
- Ghaffarianhoseini, A.; Berardi, U.; AlWaer, H.; Chang, S.; Halawa, E.; Ghaffarianhoseini, A.; Clements-Croome, D. What Is an Intelligent Building? Analysis of Recent Interpretations from an International Perspective. Archit. Sci. Rev. 2015, 59, 338–357. [Google Scholar] [CrossRef]
- Jayanetti, A.; Halgamuge, S.; Buyya, R. Deep Reinforcement Learning for Energy and Time Optimized Scheduling of Precedence-Constrained Tasks in Edge–Cloud Computing Environments. Future Gener. Comput. Syst. 2022, 137, 14–30. [Google Scholar] [CrossRef]
- Premsankar, G.; Di Francesco, M.; Taleb, T. Edge Computing for the Internet of Things: A Case Study. IEEE Internet Things J. 2018, 5, 1275–1284. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, H.; Wang, T.; Tang, M. A Fast and Efficient Task Offloading Approach in Edge-Cloud Collaboration Environment. Electronics 2024, 13, 313. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Mishra, S.K. A Survey on Task Scheduling in Edge-Cloud. SN Comput. Sci. 2025, 6, 217. [Google Scholar] [CrossRef]
- Song, C.; Zheng, H.; Han, G.; Zeng, P.; Liu, L. Cloud Edge Collaborative Service Composition Optimization for Intelligent Manufacturing. IEEE Trans. Ind. Inform. 2023, 19, 6849–6858. [Google Scholar] [CrossRef]
- Zhang, W.; Tuo, K. Research on Offloading Strategy for Mobile Edge Computing Based on Improved Grey Wolf Optimization Algorithm. Electronics 2023, 12, 2533. [Google Scholar] [CrossRef]
- Zhu, S.; Zhao, M.; Zhang, Q. Multi-objective Optimal Offloading Decision for Multi-user Structured Tasks in Intelligent Transportation Edge Computing Scenario. J. Supercomput. 2022, 78, 17797–17825. [Google Scholar] [CrossRef]
- Su, X.; An, L.; Cheng, Z.; Weng, Y. Cloud-edge collaboration-based bi-level optimal scheduling for intelligent healthcare systems. Future Gener. Comput. Syst. 2023, 141, 28–39. [Google Scholar] [CrossRef]
- Urblik, L.; Kajati, E.; Papcun, P.; Zolotová, I. Containerization in Edge Intelligence: A Review. Electronics 2024, 13, 1335. [Google Scholar] [CrossRef]
- Thodoroff, P.; Li, W.; Lawrence, N. Benchmarking Real-Time Reinforcement Learning. In Proceedings of NeurIPS Workshop on Pre-Registration in Machine Learning; 2022; Volume 181, pp. 26–41. Available online: https://proceedings.mlr.press/v181/thodoroff22a.html (accessed on 6 November 2024).
- Wang, Y. Review on Greedy Algorithm. Theor. Nat. Sci. 2023, 14, 233–239. [Google Scholar] [CrossRef]
- Nujhat, N.; Haque, S.F.; Sarker, S. Task Offloading Exploiting Grey Wolf Optimization in Collaborative Edge Computing. J. Cloud Comput. 2024, 13, 1. [Google Scholar] [CrossRef]
- Shu, W.; Yu, H.; Zhai, C.; Feng, X. An Adaptive Computing Offloading and Resource Allocation Strategy for Internet of Vehicles Based on Cloud-Edge Collaboration. IEEE Trans. Intell. Transp. Syst. 2024, 1–10. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, J.; Bao, X.; Liu, C.; Yuan, P.; Zhang, X.; Wang, S. Dependent Task Offloading Mechanism for Cloud–Edge–Device Collaboration. J. Netw. Comput. Appl. 2023, 216, 103656. [Google Scholar] [CrossRef]
- Hao, T.; Zhan, J.; Hwang, K.; Gao, W.; Wen, X. AI-oriented Workload Allocation for Cloud-Edge Computing. In Proceedings of the 2021 IEEE/ACM 21st International Symposium on Cluster, Cloud and Internet Computing (CCGrid), Melbourne, Australia, 10–13 May 2021; pp. 555–564. [Google Scholar] [CrossRef]
- Xiao, Z.; Shu, J.; Jiang, H.; Lui, J.C.; Min, G.; Liu, J.; Dustdar, S. Multi-Objective Parallel Task Offloading and Content Caching in D2D-Aided MEC Networks. IEEE Trans. Mob. Comput. 2023, 22, 6599–6615. [Google Scholar] [CrossRef]
- Jia, L.W.; Li, K.; Shi, X. Cloud Computing Task Scheduling Model Based on Improved Whale Optimization Algorithm. Wirel. Commun. Mob. Comput. 2021, 13, 4888154. [Google Scholar] [CrossRef]
- Song, F.; Xing, H.; Luo, S.; Zhan, D.; Dai, P.; Qu, R. A Multiobjective Computation Offloading Algorithm for Mobile-Edge Computing. IEEE Internet Things J. 2020, 7, 8780–8799. [Google Scholar] [CrossRef]
- Wang, M.; Shi, S.; Gu, S.; Gu, X.; Qin, X. Q-learning Based Computation Offloading for Multi-UAV-Enabled Cloud-Edge Computing Networks. IET Commun. 2020, 14, 2481–2490. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, B.; Wang, J.; Jiang, D.; Li, D. Integrating Deep Reinforcement Learning with Pointer Networks for Service Request Scheduling in Edge Computing. Knowl.-Based Syst. 2022, 258, 109983. [Google Scholar] [CrossRef]
- Sellami, B.; Hakiri, A.; Ben Yahia, S.; Berthou, P. Energy-aware Task Scheduling and Offloading Using Deep Reinforcement Learning in SDN-enabled IoT Network. Comput. Netw. 2022, 210, 108957. [Google Scholar] [CrossRef]
- Tang, T.; Li, C.; Liu, F. Collaborative Cloud-Edge-End Task Offloading with Task Dependency Based on Deep Reinforcement Learning. Comput. Commun. 2023, 209, 78–90. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, K.; Ling, C. COPSA: A Computation Offloading Strategy Based on PPO Algorithm and Self-Attention Mechanism in MEC-Empowered Smart Factories. J. Cloud Comput. 2024, 13, 153. [Google Scholar] [CrossRef]
- Liu, K.; Yang, W. Task Offloading and Resource Allocation Strategies Based on Proximal Policy Optimization. In Proceedings of the 6th International Conference on Natural Language Processing (ICNLP), Xi’an, China, 22–24 March 2024; pp. 693–698. [Google Scholar] [CrossRef]
- Feng, X.; Yi, L.; Wang, L.B. An Efficient Scheduling Strategy for Collaborative Cloud and Edge Computing in System of Intelligent Buildings. J. Adv. Comput. Intell. Intell. Inform. 2023, 27, 948–958. [Google Scholar] [CrossRef]
- Shen, Z.; Lu, X.L. An Edge Computing Offloading Method Based on Data Compression and Improved Grey Wolf Algorithm in Smart Building Environment. Appl. Res. Comput. 2024, 41, 3311–3316. [Google Scholar] [CrossRef]
- Wang, Y. Design and Application of Cloud-Edge Collaborative Management Components for Smart Buildings. Master’s Thesis, Zhejiang University, Hangzhou, China, 2022. [Google Scholar] [CrossRef]
- Tang, B.; Luo, J.; Obaidat, M.S.; Li, H. Container-based Task Scheduling in Cloud-Edge Collaborative Environment Using Priority-aware Greedy Strategy. Clust. Comput. 2023, 26, 3689–3705. [Google Scholar] [CrossRef]
- Zhang, W.; Wen, Y.; Guan, K.; Kilper, D.C.; Luo, H.; Wu, D.O. Energy-Optimal Mobile Cloud Computing Under Stochastic Wireless Channel. IEEE Trans. Wirel. Commun. 2013, 12, 4569–4581. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Tang, C.; Liu, C.; Chen, W.; You, S.D. Implementing Action Mask in Proximal Policy Optimization (PPO) Algorithm. ICT Express 2020, 6, 200–203. [Google Scholar] [CrossRef]
- You, Q.; Tang, B. Efficient Task Offloading Using Particle Swarm Optimization Algorithm in Edge Computing for Industrial Internet of Things. J. Cloud Comput. 2021, 10, 41. [Google Scholar] [CrossRef]
- Engstrom, L.; Ilyas, A.; Santurkar, S.; Tsipras, D.; Janoos, F.; Rudolph, L.; Madry, A. Implementation Matters in Deep RL: A Case Study on PPO and TRPO. In Proceedings of the International Conference on Learning Representations (ICLR), Addis Ababa, Ethiopia, 26–30 April 2020; Available online: https://openreview.net/forum?id=r1etN1rtPB (accessed on 10 December 2024).









| Symbols | Description | Value |
|---|---|---|
| n | Edge Node Number | 5 |
| Edge Node Maximum Compute Resources | [3, 15] GHz | |
| Cloud Node Maximum Compute Resources | 100 GHz | |
| Edge Node Maximum Bandwidth Resources | [10, 20] MHz | |
| Cloud Node Maximum Bandwidth Resources | 100 MHz | |
| Task Compute Size | cycles | |
| Task Data Size | [1, 50] MB | |
| Container Type | 14 | |
| Task Maximum Tolerance Time | [0.1, 5] s | |
| Edge Node n to Cloud Node Channel Gain | ||
| Transmission power of edge nodes | [0.1, 1] W | |
| Gaussian white noise | W | |
| b | Chip structure coefficient in energy consumption model | |
| Total time coefficient | 0.5 | |
| Total energy coefficient | 0.5 | |
| Timeout penalty coefficient | 5, 2, 0.5 |
| Symbols | Description | Value |
|---|---|---|
| Learning Rate | 0.001 | |
| Discount Factor | 0.99 | |
| Clip Range | 0.2 | |
| GAE Hyperparameter | 0.95 | |
| Value Function Loss Coefficient | 0.5 | |
| Entropy Regularization Term Coefficient | 0.01 | |
| S | Sample Batch Size | 64 |
| Algorithm | EF | CF | RS | PSO | RACDG | Proposed |
|---|---|---|---|---|---|---|
| Time complexity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; He, J. Dynamic Task Scheduling Based on Greedy and Deep Reinforcement Learning Algorithms for Cloud–Edge Collaboration in Smart Buildings. Electronics 2025, 14, 3327. https://doi.org/10.3390/electronics14163327
Yang P, He J. Dynamic Task Scheduling Based on Greedy and Deep Reinforcement Learning Algorithms for Cloud–Edge Collaboration in Smart Buildings. Electronics. 2025; 14(16):3327. https://doi.org/10.3390/electronics14163327
Chicago/Turabian StyleYang, Ping, and Jiangmin He. 2025. "Dynamic Task Scheduling Based on Greedy and Deep Reinforcement Learning Algorithms for Cloud–Edge Collaboration in Smart Buildings" Electronics 14, no. 16: 3327. https://doi.org/10.3390/electronics14163327
APA StyleYang, P., & He, J. (2025). Dynamic Task Scheduling Based on Greedy and Deep Reinforcement Learning Algorithms for Cloud–Edge Collaboration in Smart Buildings. Electronics, 14(16), 3327. https://doi.org/10.3390/electronics14163327





