A Configurable Parallel Architecture for Singular Value Decomposition of Correlation Matrices

Abstract

Singular value decomposition (SVD) plays a critical role in signal processing, image analysis, and particularly in MIMO channel estimation, where it enables spatial multiplexing and interference mitigation. This study presents a configurable parallel architecture for computing SVD on 4 × 4 and 8 × 8 correlation matrices using the Jacobi algorithm with Givens rotations, optimized via CORDIC. Exploiting algorithmic parallelism, the design achieves low-latency performance on a Virtex-5 FPGA, with processing times of 5.29 µs and 24.25 µs, respectively, while maintaining high precision and efficient resource usage. These results confirm the architecture’s suitability for real-time wireless systems with strict latency demands, such as those defined by the IEEE 802.11n standard.

1. Introduction

Singular value decomposition (SVD) is a mathematical algorithm that transforms the information in a matrix into a more manageable form for other mathematical analysis techniques [1]. SVD algorithms are applied in various fields such as digital communications, signal processing, and image processing. In all these areas, the execution time of the SVD algorithm is crucial in the design process of any application involving information processing [2]. This paper explores parallel architectures that execute the SVD algorithm to minimize processing time and assess its effectiveness in reduced range generic channel estimation for MIMO systems [3].

Although several hardware implementations of SVD have been proposed, many fail to achieve an ideal balance between low-latency performance and efficient resource utilization, particularly within power- and area-constrained embedded systems. The present work addresses this gap by introducing a configurable parallel architecture, optimized for both speed and resource usage, thereby ensuring suitability for real-time applications in embedded environments.

One of the main challenges in implementing SVD practically is its computational cost, especially in real-time execution or resource-constrained environments such as embedded systems or reconfigurable platforms. To overcome this, alternative methods have been developed for efficient hardware-based computation [4]. The Jacobi algorithm is one of the most robust and parallelization-friendly approaches. When combined with the CORDIC algorithm, it avoids computationally expensive operations such as square roots and divisions, relying instead on additions, subtractions, and bit-shifting operations [5].

This research introduces a parallel architecture for the singular value decomposition of a correlation matrix involving two variants: 4 × 4 and 8 × 8 matrix sizes. The SVD algorithm used in our experiments is the one proposed by Forsythe et al. [6], along with the “Coordinate Rotation Digital Computer” (CORDIC) algorithm presented by Volder in 1959 [7]. CORDIC is used for intermediate information processing as part of the main algorithm. The proposed parallel architecture reduces the overall processing speed. Similar work includes hardware implementations of SVD algorithms. For instance [8], a variation of a parallel SVD algorithm was implemented to compute the SVD for a set of post-fault Jacobians on a MasPar MP-1 and IBM SP2. A two-sided rotation Jacobi SVD algorithm was used to compute the SVD [9] on a Virtex-II FPGA, with results showing the maximum clock rate and using the CORDIC Intellectual Property (IP) from XILINX for the inverse tangent function and vector rotation function for the SVD array. Various digital architectures for hardware implementation of SVD and CORDIC algorithms were proposed using VHDL and Xilinx tools [10]. A hardware VLSI architecture for steering matrix computation using a hardware-optimized SVD algorithm with a Givens rotation unit was described [11]. A programmable architecture to perform QRD and SVD with variable precision was also presented [12].

The proposed configurable SVD architecture exhibits strong adaptability beyond conventional MIMO systems, particularly in sensor-based biomedical monitoring and human–device interaction. Its ability to efficiently process multichannel signals in real time makes it suitable for physiological assessment using wearable or embedded sensor arrays. Recent studies have demonstrated that SVD-based decomposition can enhance the extraction of vital signs such as respiration and heartbeat from radar signals, even under noisy conditions, supporting its use in bioelectromagnetic field analysis [13]. Additionally, optimized SVD implementations on embedded platforms have proven effective for real-time signal processing in biomedical systems, including inertial sensing and Kalman filtering [14].

Furthermore, antenna array configurations such as 4 × 4 and 8 × 8 MIMO—commonly deployed in Wi-Fi and 5G systems to enhance throughput and coverage—share spatial acquisition principles that are transferable to biomedical contexts. For example, compact 8 × 8 MIMO designs have been proposed for 5G terminals, demonstrating high isolation and efficiency across sub-6 GHz bands [15]. The proposed architecture can be reconfigured to operate over such array structures, supporting efficient signal separation and feature extraction in both communication and physiological domains.

The proposed configurable SVD architecture is well-suited for signal classification and anomaly detection when integrated with soft computing techniques. For instance, Versaci et al. [16] demonstrated a fuzzy similarity-based classifier for estimating delaminations in CFRP plates using eddy current testing, highlighting how physical signal processing can be combined with intelligent classification methods. Similarly, SVD-based feature extraction has proven effective in anomaly detection for multivariate time series, such as satellite telemetry and sensor diagnostics [17], and in structural health monitoring to isolate damage-sensitive features from noisy data [18]. These findings support the extension of the architecture to applications requiring robust signal decomposition and intelligent decision-making, including biomedical diagnostics and smart material analysis.

Recent advances in intelligent fault diagnosis for industrial machinery highlight the relevance of SVD-based architectures in sensor-driven monitoring systems. Brusa et al. [19] demonstrate the use of SVD combined with explainable AI for vibration-based fault detection in rotating equipment, enabling real-time classification and interpretability. Similarly, Singh et al. [20] review AI techniques—including SVD—for anomaly detection in motors and gearboxes, emphasizing its role in feature extraction and dimensionality reduction. These studies support the transferability of our architecture to embedded industrial applications, where low-latency processing and scalable integration with sensor interfaces are essential.

This paper is organized as follows: Section 2 describes the SVD algorithm used in this research; Section 3 explains the proposed parallel architecture; Section 4 presents the results and observations from implementing the proposed algorithms in very-high-speed hardware description language (VHDL) using an FPGA model Virtex-5 XC5VLX20T. Finally, Section 5 discusses our conclusions.

2. The SVD Algorithm

The SVD is a real-valued matrix decomposition $M ϵ C_{m\times n}$, which involves its factorization into three matrices, as shown below:

$$M=U\sum V^T$$

(1)

where $U ϵ C_{m\times m}$ and ${V ϵ C}_{n\times n}$ are usually called the left and right singular vectors of $M$, respectively; $\sum$ $ϵ C_{m\times n}$ is a diagonal matrix whose diagonal elements are the singular values of $M$.

2.1. SVD of Correlation Matrices

The SVD has been successfully applied in correlation or symmetric matrices [21], leading us to rewrite Equation (1) as follows in Equation (2):

$$M=U\sum U^T$$

(2)

By manipulating matrices $U$ and $\sum$, we obtain the following expression:

$$U=[u_1,u_2,\dots ,u_n]$$

(3)

$$\sum =diag\left[{\sigma }_1,{\sigma }_2,\dots {\sigma }_n\right]$$

(4)

where $u_n$ is the $n$-th singular vector, and σn is the $n$-th singular value of the matrix $M$. Applying the SVD algorithm to correlation matrices simplifies the calculation of the largest element in the upper or lower diagonal matrix, thereby streamlining the factorization process.

2.2. SVD Using Jacobi’s Algorithm

The Jacobi algorithm is widely used for computing SVDs because of its stability and suitability for parallelization in hardware descriptions. The algorithm uses a sequence of rotations to derive the diagonal matrix of singular values. This is achieved using a rotation matrix $J (i, j,\theta ).$ A crucial step in Jacobi’s method is identifying the element with the largest contribution in the matrix $M$, i.e., locating indices (i, j) where this data resides, satisfying 1 ≤ i < j ≤ n. Subsequently, the algorithm determines the rotation angle, as given by Equation (5); estimates the sine and cosine; and finally formulates the rotation matrix, $J(i, j, \theta )$, as shown in Equation (6).

$$\theta ={\displaystyle \frac{1}{2}}arctan\left({\displaystyle \frac{{2m}_{ij}}{m_{jj}-m_{ii}}}\right)$$

(5)

$$J(i,j,\theta )=\left[\begin{array}{cccccc}c& \dots & 0& s& \dots & 0\\ ⋮& \ddots & ⋮& ⋮& \dots & ⋮\\ 0& 0& 1& 0& \dots & 0\\ -s& 0& 0& c& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& \dots & 0& 0& \dots & 1\end{array}\right]$$

(6)

where $c=cos\left(\theta \right)$, and $s=sen\left(\theta \right)$. Equation (7) illustrates the process required to achieve the factorization of $M$.

$$M^{\prime }=J^{T}M J$$

(7)

where $M$ is the input matrix, i.e., the matrix that needs to be decomposed; $J$ is $J(i,j,\theta )$; JT is the transpose of the Jacobian; and $M^{\prime }$ is the estimated matrix containing the eigenvalues. In (8) we show the simplified version of the complete estimation of values:

$$M^{\prime }=\left[\begin{array}{cc}c& -s\\ s& c\end{array}\right]\left[\begin{array}{cc}{m}_{ii}& m_{ij}\\ m_{ji}& m_{jj}\end{array}\right]\left[\begin{array}{cc}c& s\\ -s& c\end{array}\right]$$

(8)

The estimation of the eigenvalues involves using Equation (9), where $Ev$ is initialized as an identity matrix.

$${E_v}^{\prime }=E_v J$$

(9)

Parallelism is more apparent in the last two equations, as they can be easily parallelized in any hardware description language, such as VHDL. Matrices of size 4 × 4 require fifteen algorithm calls, while matrices of size 8 × 8 require fifty algorithm calls [22].

2.3. CORDIC Algorith

The elements of the Jacobian matrix can be computed using the following well-known trigonometric equations:

$$c_1={\displaystyle \frac{\left(m_{jj}-m_{ii}\right)}{\sqrt[2]{{{(2m}_{ij}}^2+{(m_{jj}-m_{ii})}^2}}}$$

(10)

$$s_1={\displaystyle \frac{{2m}_{ij}}{\sqrt[2]{{{(2m}_{ij}}^2+{(m_{jj}-m_{ii})}^2}}}$$

(11)

However, for the estimation of the sine and cosine of $\theta /2$, the half-angle equations can be used:

$$sen{\displaystyle \frac{\theta }{2}}=\pm \sqrt[2]{{\displaystyle \frac{1-c_1}{2}}}$$

(12)

$$cos{\displaystyle \frac{\theta }{2}}=\pm \sqrt[2]{{\displaystyle \frac{1+c_1}{2}}}$$

(13)

These operations require the computation of additions, subtractions, powers of two, square roots, and divisions. Implementing these trigonometric functions is costly in terms of hardware resources.

A viable alternative is the CORDIC algorithm, which uses only additions, subtractions, LUTS, and shift operations to estimate the angle [23]. With the right configuration, it can determine the inverse tangent and subsequently the sine and cosine. This algorithm is widely used in the electronic design industry. For example, Xilinx industries use this algorithm in their Xilinx Core Generator, over the ISE Design. Its relevance lies in its low resource consumption; however, it has the following disadvantages: it requires N iterations to converge to the desired value and N iterations for N precision bits [24].

The CORDIC algorithm is based on vector rotation and can be used in Vectorization Mode, where the input is the vector $r= (x,y)$, and the output returns the magnitude $R$ and the angle $\theta$ of the vector [25]. Alternatively, it can be used in Rotation Mode, where an initial rotation vector is proposed and rotated at a given angle, and then the sine and cosine are computed for that input [26]. The equations describing the rotations of the CORDIC algorithm are the following:

$$x_2=x_1\times \mathit{cos}\left(\varnothing \right)-y_1\times sen(\varnothing )$$

(14)

$$y_2=x_1\times \mathit{sen}\left(\varnothing \right)+y_1\times cos(\varnothing )$$

(15)

By factorizing Equations (14) and (15), we obtain the following:

$$x_2=\mathit{cos}\left(\varnothing \right)\left[x_1-y_1\times tan(\varnothing )\right]$$

(16)

$$y_2=\mathit{cos}\left(\varnothing \right)\left[x_1\times tan(\varnothing )+y_1\right]$$

(17)

Instead of performing large rotations, small rotations were proposed, considering that the chosen amount of rotation only uses shift operations, additions, and subtractions. To achieve this, the following variable boundaries were considered:

$$\mathit{tan}\left(\varnothing \right)=\pm 2^i$$

(18)

Therefore, the product by the tangent variable is reduced to shift operations only. The cosine expression becomes constant and can be estimated by the product of the cosines of the selected angles. Consequently, we can reformulate the expressions required by the CORDIC algorithm as follows:

$$x_{i+1}=K_i\left[x_i-y_i\times d_i\times 2^{-i}\right]$$

(19)

$$y_{i+1}=K_i\left[y_i+x_i\times d_i\times 2^{-i}\right]$$

(20)

where $d_i = \pm 1$, and $K_i= cos(tan-12-1)$ *…*$cos(tan-12-i)$. The precision of the result depends on the number of rotations to be used, as well as the number of bits that are being handled.

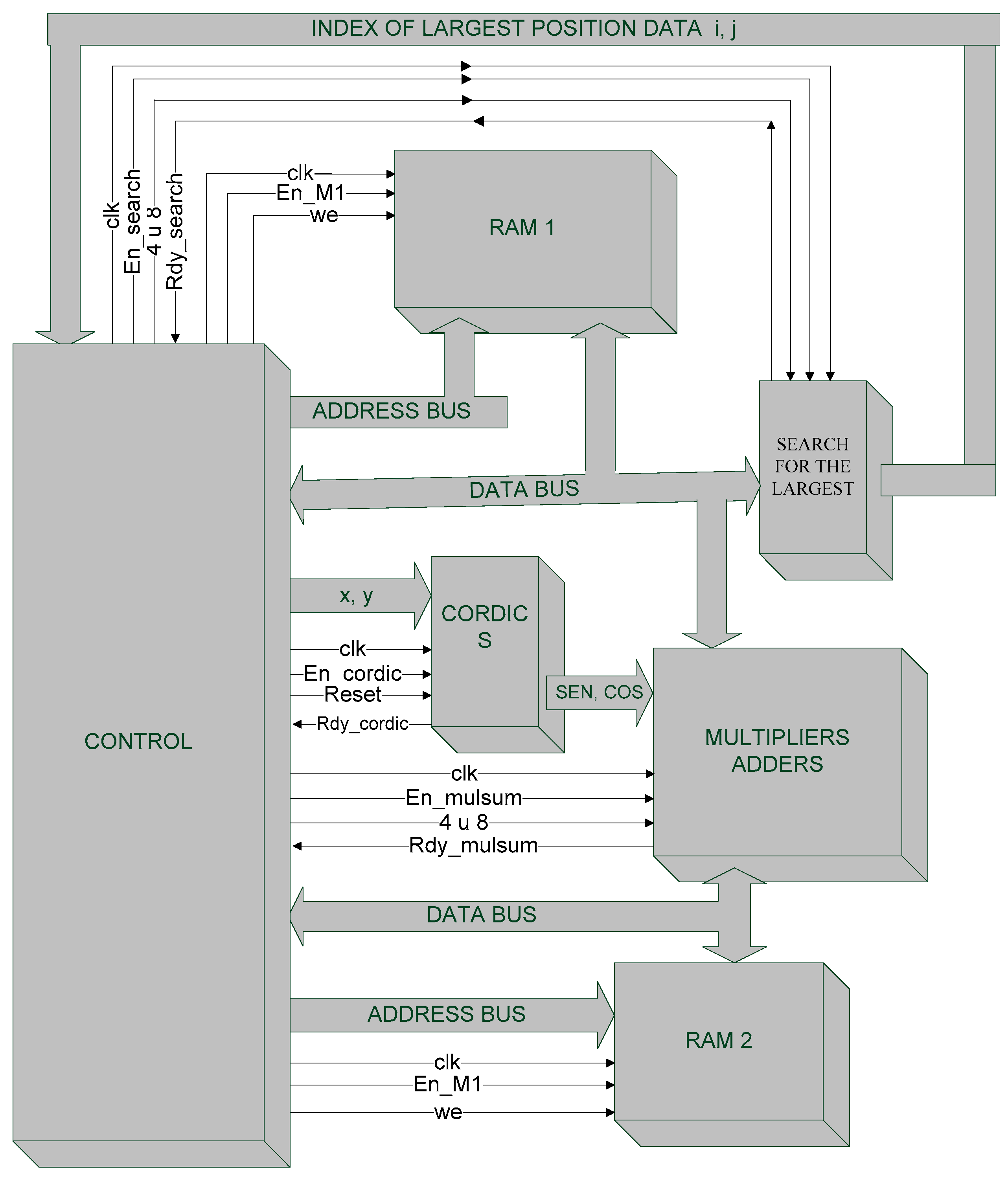
3. Architecture for SVD

The design of the SVD architecture involved analyzing fixed points to find the appropriate dynamic range. We conducted experiments with the CORDIC algorithm, varying bit depths and the number of rotations.

These experiments were executed using MATLAB R2019a software and its fixed point (FI) toolbox. The goal of this experimental analysis was to determine the largest absolute error when reconstructing the original matrix using the eigenvalues and eigenvectors with (7) for matrices of size 8 × 8. We calculated the average of the 100 largest absolute errors, with each average represented as a bar in Figure 1’s analysis of the average absolute error for the SVD algorithm. In all cases, we used one bit for the sign, three bits for the integer part, and the remaining bits for the fraction part. Figure 1’s analysis of the average absolute error for the SVD algorithm shows that for 16-bit words and below, the error is significantly high. So far, we have analyzed the dynamic range to use and the number of iterations for the CORDIC algorithm to apply the SVD algorithm in hardware description language. The FPGA has 18-bit multipliers, so it was decided to use this length to take full advantage of the capacity within the FPGA. The number of iterations for the CORDIC block was selected based on the analysis of the average absolute error shown in Figure 1, while also avoiding the use of more than 13 cycles, which is the maximum number required for the SEARCH block, to avoid extending the pipeline process time. Next, we designed a model based on flow control, allowing several instructions to be executed simultaneously [27].

In Figure 2, the pipeline timing diagram used shows each pipeline stage used in this work, and how data depends on each stage and where the clock cycles required to complete each stage are presented.

Algorithm 1 is the pseudocode that outlines how the Jacobi and CORDIC algorithms work together.

Algorithm 1: Jacobi Meets CORDIC

If enable = 1 and rising edge of clock:

If reset = 1:

Initialize variables and states

Else:

Repeat up to 50 times:

1. Find the pair (i, j) with the largest off-diagonal contribution (using search_mem)

2. Compute the sine and cosine of the corresponding rotation angle (using tg_sen)

3. Apply the rotation:

- Update rows i and j in the original matrix (memo1)

- Update columns i and j (memo2)

- Merge the updated columns back into the original matrix

End repeat

Final outputs:

- eig_val ← most recently computed value

- eig_vec ← most recently computed vector

In the block diagram shown in Figure 3, the configurable architecture for the SVD algorithm over 4 × 4 and 8 × 8 matrices explains the proposed architecture, with each step detailed block by block as follows:

Search for the Largest: This is the first block used by the SVD algorithm. It searches for the element with the greatest contribution within either the upper or lower diagonal matrix due to symmetry. To achieve this, only four blocks have been used as comparators, which can be adjusted according to the size of the matrices (either 4 × 4 or 8 × 8) using the signal 4_or_8. The latency for searching for the largest value is seven cycles for 4 × 4 matrices, and 13 cycles for 8 × 8 matrices. The data travels through the RAM 1 memory bus, controlled by control unit signals. Once the indices for the largest element are found, the Rdy_search signal is activated, and data is transferred to the control block.

CORDICS: This architectural block performs scaling operations with the input data to compute the angle of the vector at any point in the Cartesian plane. The internal process involves 26-bit-length words. First, the angle is computed using a CORDIC in vectorization mode. Later, the sine and cosine parameters are computed in rotation mode. The output is limited to 18 bits and is sent to the multipliers adder’s block. When the data is ready, the Rdy_cordic signal is activated.

RAM 1 and 2: These are Random Access Memories (RAMs). RAM 1 stores the data for the matrix being factorized and, during the process, also stores the eigenvalues obtained. RAM 2 initially contains a unitary diagonal matrix, but after the algorithm called, it also stores intermediate eigenvectors as needed. The data bus and address sizes are configured to work with eight data values per clock cycle.

Control: This block is the fundamental component of the design model, controlling every process and all information flow among blocks. The input should include the size of the matrices and other necessary information for proper operation.

To further enhance the system’s adaptability to uncertainties in physical measurements, recent studies on intuitionistic fuzzy divergence provide promising methods for evaluating mechanical stress states in steel plates subjected to biaxial loads [1]. These approaches, which integrate FEM-based modeling with fuzzy logic, could benefit from a high-speed SVD engine to accelerate real-time inversion and anomaly segmentation. By combining these fuzzy modeling techniques with our architecture’s dynamic range and error management capabilities, the system may become well-suited for applications in non-destructive testing and structural health monitoring [16].

4. Implementation

The proposed architecture was designed using Active-HDL 8.1 for simulation processes and Xilinx ISE Design Suite 13.2_1 for synthesis and implementation.

Table 1. FPGA resource utilization summary.

Number of Slice Registers:	3416 out of 12,480   27%
Number of Slice LUTS	9729 out of 12,480   77%
Number of DSP48Es	16 out of 24   66%
Multipliers	Multiplier = 16 18 × 18 bit

, FPGA resource utilization summary, presents a summary of the resources being used with the proposed architecture.

We conducted a power analysis using the Xilinx XPower Analyzer tool. The results, obtained at an ambient temperature of 50 °C, are summarized in

Table 2. Summary of power consumption.

On-Chip	Power (W)
Clocks	0.075
Logic	0.012
Signals	0.044
DSPs	0.002
IOs	0.001
Leakage	0.322
Total	0.456

, summary of power consumption.

The proposed architecture achieved a working speed of 130.41 MHz, requiring 3163 cycles for 8 × 8 matrices and 690 cycles for 4 × 4 matrices.

Table 3. Implementation results of SVD architectures.

Work	Frequency (MHz)	Slices/LUTs/Registers	Latency/Time	Bits	Data Type	Matrix Size	Latency Per Matrix Size/MHz	Scalability/Remarks
[4] 1CPP	Not specified	Not specified	14 ms	Not specified	Real	6 × 7	Not specified	Parallel SIMD, lacks hardware details
[4] 2CPP	Not specified	Not specified	18 ms	Not specified	Real	6 × 7	Not specified	Similar to above
[5] ESVD_12bits	7.4	8531	Not specified	12	Real	4 × 4	Not specified	Fixed architecture, no scalability
[6] 25bitsFixedP	148	2609 Slices	Not specified	25	Real	2 × 2	Not specified	High frequency, small matrix size
[6] 25bitsFloating	35	4648 Slices	Not specified	25	Real	2 × 2	Not specified	Lower frequency, fixed architecture
[11] VLSI	149	Not specified	3.3 µs	16	Complex	4 × 4	Not specified	ASIC-based, high-speed design
[12] MDU-II	272	Not specified	15.8 µs	32	Complex	4 × 4	Not specified	ASIC, good frequency but higher latency
[12] MDU-I	133	Not specified	11.6 µs	32	Complex	4 × 4	Not specified	ASIC, moderate performance
Timofte et al. (2017) [28]	~100	Not specified	Not specified	Not specified	Real/CORDIC	Variable	Not specified	Systolic array, moderate time efficiency
Ma et al. (2006) [9]	133	Not specified	11.6 µs	32	Complex	4 × 4	Not specified	Uses Xilinx CORDIC IP, fixed-size architecture
Szecówka & Malinowski [10]	148	2609 Slices	3.3 µs	16	Complex	4 × 4	Not specified	Fixed architecture, no scalability
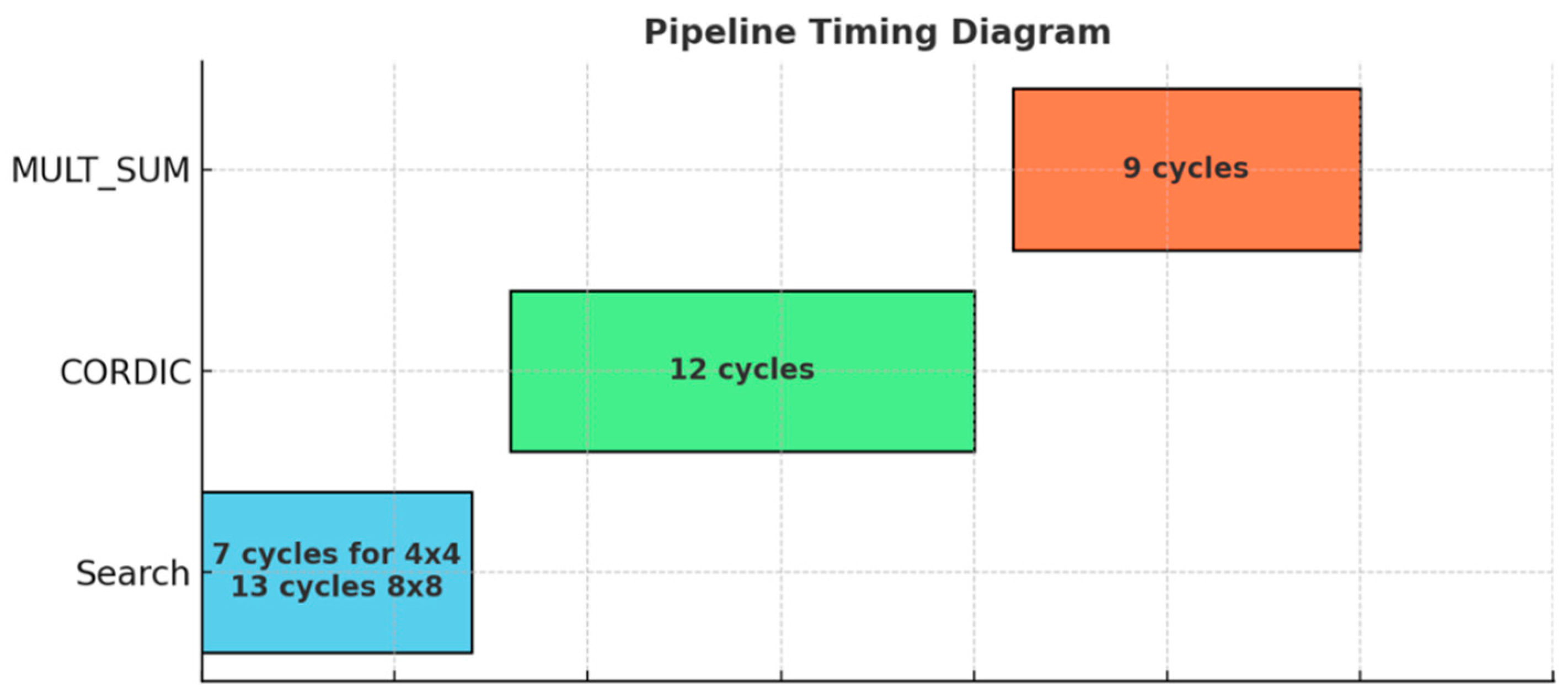
This Work 1 (4 × 4)	130.41	9729 LUTs/3416 Registers	5.29 µs	18	Real	4 × 4	0.189	High scalability (configurable for 4 × 4/8 × 8 matrices)
This Work 2 (8 × 8)	130.41	9729 LUTs/3416 Registers	24.25 µs	18	Real	8 × 8	0.0412	High scalability (configurable for 4 × 4/8 × 8 matrices)

, implementation results of SVD architectures, shows a comparative with related works. The first two comparisons involve 6 × 7 matrices processed over a long duration using parallel SIMD machines. The next three benchmarks were conducted on FPGAs, showing only the maximum working frequency without providing the number of cycles required for the SVD. The next three comparisons are ASIC designs, and only the reference [11] shows improved processing speed, but the work [12] can also calculate the QR decomposition. For a more accurate comparison, it would be necessary to implement the architecture in an ASIC design, such as using Design Compiler. The work of Timofte et al. [28] lacks sufficient implementation details, Ma et al. (2006) [9] achieve 11.6 µs latency with higher bit precision (32 bits), and Szecówka and Malinowski [10] offer faster performance but with reduced resolution (16 bits); none of these architectures support configurability for both 4 × 4 and 8 × 8 matrix sizes. In contrast, the proposed architecture stands out with its reconfigurable design, competitive latency, and efficient resource utilization, making it highly suitable for real-time embedded applications.

Recent developments in single photon avalanche diode (SPAD) interfaces have emphasized the need for ultra-low-latency and low-power digital processing to support high-speed photonic sensing. Pullano et al. [29] proposed an electronic interface for SPADs using pole-zero compensation techniques to minimize quenching and recovery times, achieving sub-10 ns response performance. These constraints align with the strengths of the proposed configurable SVD architecture, which offers efficient matrix decomposition and low-latency multichannel processing. As a future extension, the architecture may be adapted to operate as a digital backend for SPAD-based systems, enabling real-time signal extraction and classification in quantum or photonic sensing environments. This integration would support AI-assisted spatiotemporal modeling of photon events, bridging optical front-end precision with scalable embedded processing.

The proposed architecture can also be extended to support non-destructive defect detection, particularly in applications involving subsurface anomaly characterization. For example, Versaci et al. [30] demonstrated the use of eddy current modeling and FEM-based energy functional analysis to identify defects in CFRP plates. A fast SVD engine, like the one presented in this study, could accelerate real-time inversion algorithms and anomaly segmentation by enabling rapid matrix factorization during iterative reconstruction.

Parallel architecture is well-suited for solving inverse problems in bioimpedance systems, which often rely on iterative solvers and matrix decompositions. The low-latency SVD engine could be integrated into Electrical Impedance Tomography (EIT) frameworks to accelerate the reconstruction of conductivity maps. Previous studies have demonstrated that FEM-based models, when combined with deep learning classifiers, benefit significantly from fast matrix operations. Consequently, this architecture is a promising candidate for real-time bioimpedance analysis in wearable or clinical settings [31].

The proposed parallel SVD architecture is well-suited for neuromuscular signal analysis, particularly EMG applications requiring fast preprocessing and artifact removal. Studies have shown that SVD is effective for suppressing cardiac interference in trunk EMG signals, outperforming ICA and traditional filters in both time and frequency domains [32]. Additionally, low-latency hardware implementations are essential for real-time acquisition and classification, as demonstrated in wearable EMG systems using novel electrode designs [33]. By integrating the SVD engine into AI-assisted pipelines—such as convolutional or recurrent neural network classifiers—the architecture enables rapid feature extraction and segmentation of motor unit activity, supporting clinical and rehabilitative applications.

Although the number of iterations depends primarily on the cyclic sweep count required for convergence, and not solely on the matrix size [34], Jacobi algorithms typically require O(n²) sweeps per iteration to sufficiently reduce off-diagonal elements. However, the actual number of iterations until convergence is highly data-dependent, influenced by the matrix’s spectral properties and conditioning [35]. For hardware implementations, using a fixed iteration count—such as 15 or 50—is a practical compromise that simplifies control logic and resource allocation. Nonetheless, this approach may sacrifice numerical precision for speed, especially in cases where adaptive iteration control would yield more accurate results.

Furthermore, the proposed parallel SVD architecture is well-suited for miniaturization and integration into portable or home-based biomedical monitoring systems. Its low-latency and scalable structure enables real-time signal processing under constrained power and size conditions. A natural evolution toward ASIC implementation is feasible, beginning with FPGA-based prototyping using VHDL modeling. As demonstrated in Lane and Sahafi [36], the ASIC design flow typically starts with simulation and synthesis on FPGA platforms, allowing early-stage functional validation and iterative refinement. This flexibility is a key advantage of FPGA development, enabling the transition to optimized ASIC architectures with reduced power consumption and silicon area—ideal for embedded biomedical applications.

5. Conclusions

Singular value decomposition (SVD) on 4 × 4 and 8 × 8 correlation matrices: By utilizing the inherent parallelism of the Jacobi method and optimizing trigonometric operations with the CORDIC algorithm, the proposed design achieves low processing times of 5.29 µs and 24.25 µs for 4 × 4 and 8 × 8 matrices, respectively, using a Virtex-5 FPGA.

The proposed architecture shows competitive performance in speed, resource usage, and power consumption compared to similar FPGA-based or ASIC-based SVD implementation. Additionally, its configurability allows it to adapt to different matrix sizes without changing the core processing model, making it suitable for dynamic applications. These results confirm the suitability of this architecture for real-time MIMO systems, especially those adhering to IEEE 802.11n standards [37], where channel estimation must be performed within strict latency constraints.

Recent advances in hybrid deep learning architecture have demonstrated the potential of combining temporal and spatial modeling for intelligent signal monitoring. For instance, Pratticò et al. [38] proposed an integrated framework based on LSTM and U-Net models for electrical absorption analysis using sensor networks, highlighting the effectiveness of deep recurrent and convolutional structures in capturing spatiotemporal dynamics. In this context, the proposed configurable SVD architecture can serve as a robust preprocessing stage for feature extraction, dimensionality reduction, and noise suppression. As a future extension, the system may incorporate deep learning modules—such as recurrent and convolutional neural networks—to enable AI-assisted monitoring of electrical absorption phenomena with spatial–temporal variability, leveraging matrix decomposition as a foundational layer for intelligent decision making.

Future work will focus on porting the architecture to ASIC for enhanced performance and energy efficiency, extending its scalability to larger matrices, and evaluating its integration into more advanced communication protocols or adaptive systems, including 5G and AI-assisted reconfigurable platforms.

Beyond its application in real-time MIMO systems, singular value decomposition (SVD) is crucial in many high-impact scientific and engineering domains, where efficient matrix factorization is essential. In data analytics and machine learning, SVD is fundamental for dimensionality reduction techniques such as principal component analysis (PCA) [39], which are widely used for feature extraction, data compression, and noise reduction in high-dimensional environments such as genomics, environmental monitoring, and computer vision [40]. Recommender systems also leverage SVD for collaborative filtering and matrix completion to infer user preferences from sparse data matrices, enabling personalized services on platforms such as Netflix and Amazon [41].

Reduced precision in MIMO systems has significant implications for channel state information (CSI) estimation, directly impacting the performance of related applications. First, low-resolution quantization introduces quantization noise, which degrades CSI fidelity, especially in high signal-to-noise ratio (SNR) regimes where estimation errors dominate over thermal noise [42]. Additionally, bias in linear estimators such as least squares (LS) and minimum mean square error (MMSE) arises due to systematic distortion from quantization [43]. Finally, in fast-fading or highly correlated environments, such as RIS-assisted MIMO systems, reduced precision fails to capture subtle channel variations, leading to poor tracking of channel dynamics [44].

In natural language processing (NLP), latent semantic analysis (LSA) applies SVD to term-document matrices to reveal latent semantic structures and improve tasks such as document clustering, topic modeling, and semantic similarity estimation [45]. In image and signal processing, SVD supports low-rank approximations for tasks such as lossy image compression, background subtraction, and denoising, with increasing use in real-time systems due to dedicated hardware acceleration [46].

Moreover, with the rise of intelligent, low-latency platforms such as 5G communication systems, edge computing, and autonomous embedded devices, there is a growing demand for efficient SVD computation at the hardware level. The architecture presented in this work is well positioned to meet these requirements, enabling scalable, reconfigurable, and energy efficient integration of SVD within AI-enhanced communication protocols and adaptive digital signal processing pipelines.