Multi-Variable Evaluation via Position Binarization-Based Sparrow Search
Abstract
1. Introduction
- (1)
- A novel stochastic binarization mechanism using Gaussian-perturbed sigmoid mapping to mitigate premature convergence;
- (2)
- A unified framework integrating BSSA with SVM classifiers to simultaneously optimize feature cardinality and accuracy;
- (3)
- Extensive validation across 12 UCI datasets demonstrating statistically significant improvements in accuracy, computation time, and feature reduction.
2. Background
2.1. Continuous Sparrow Search Algorithm
2.2. Related Work
3. The Position Binarization Based Binary Sparrow Search Algorithm
3.1. Method
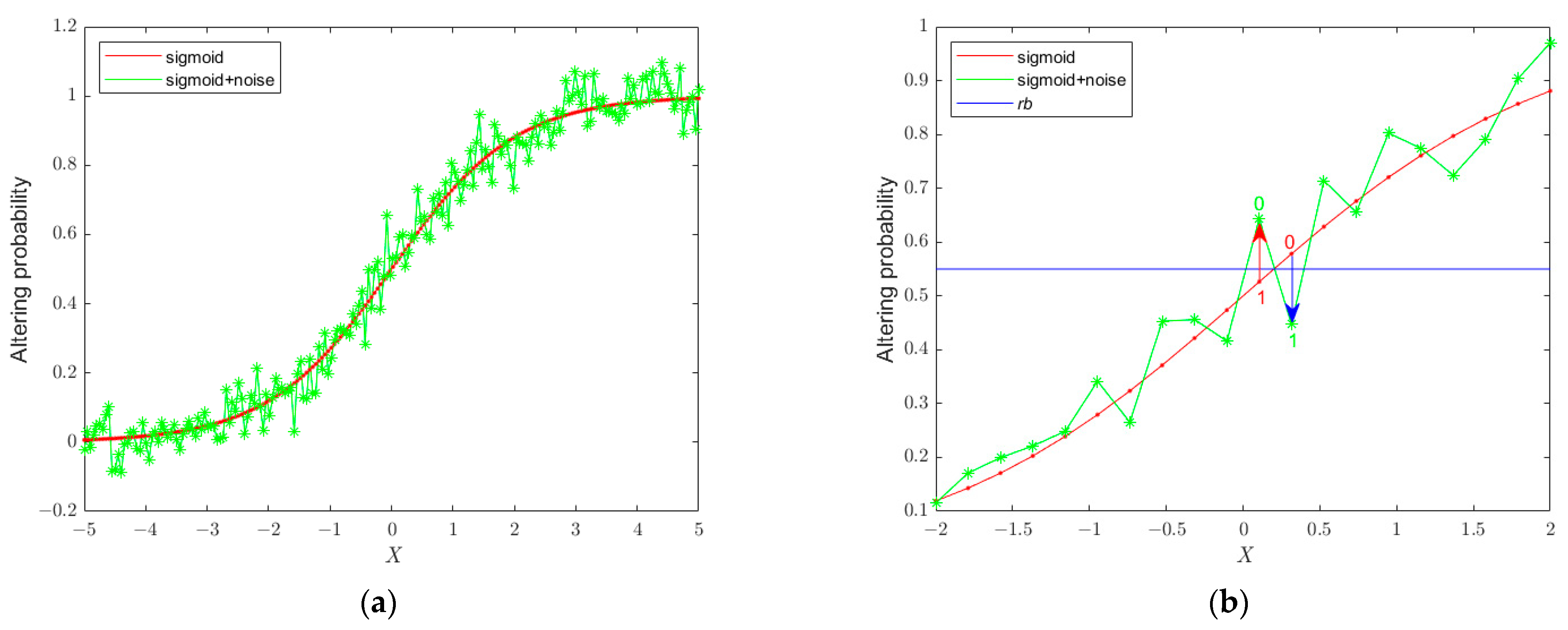
3.1.1. The Updated Position Binarization
3.1.2. The Updated Position Binarization Based on a Small Perturbation
3.1.3. The BSSA Framework
| Algorithm 1: The position binarization-based Sparrow Search Algorithm |
| Input: N: the number of sparrows : maximum number of iterations AV: the alarm value SN: the number of sparrows observed to be at risk PN: the number of producers σ: perturbation Output: the optimal location of the population the global optimal fitness value Initialize a population of N sparrows and set the corresponding parameters; Calculate the fitness value of each sparrow ; , ; , fP = f; t = 0; While (t < ) Sort the fitness values to identify the present best positions , it is the best fitness and the worst positions ; AV = random (0,1); for j = 1: PN Compute the new position of the jth sparrow using Equation (1); end for for j = (PN + 1): N Compute the new position of the jth sparrow using Equation (2); end for for j = 1: SN Compute the new position of the jth sparrow using Equation (3); end for for j = 1: N Calculate the changing probability by using Equation (4); Using Equation (5), obtain the binary solution; Get the current new location ; Calculate the changing probability with perturbation by using Equation (6); Using Equation (7) obtain the binary solution; Get the current new location ; Calculate the fitness value of and the fitness value of ; If , update the new position and ; If , update the new position and ; end for t = t + 1; end while return , |
3.2. Computation Complexity Analysis
- (1)
- The computation complexity of Population Initialization is O(N D);
- (2)
- The computation complexity of Position Update Mechanisms, including Sigmoid transformation, Gaussian noise injection, and threshold-based binarization, is O(N D);
- (3)
- Because its L2 regularization inherently penalizes model complexity, mitigating overfitting when evaluating sparse feature subsets, the SVM classifier is employed for evaluating the feature subset selected by BSSA. Assuming SVM classifier training on the selected feature subset (size k ≤ D) with M training samples, the computation complexity of fitness evaluation is O(N M2 k).
4. Multi-Variable Evaluation Using Position Binarization-Based Sparrow Optimization Algorithm
5. Experimental Results and Discussion
5.1. Data Description
| No. | Dataset | Features | Samples | Classes |
|---|---|---|---|---|
| 1 | BreastEW | 30 | 569 | 2 |
| 2 | Clean1 | 166 | 476 | 2 |
| 3 | forest | 27 | 198 | 8 |
| 4 | KrvskpEW | 36 | 3196 | 2 |
| 5 | WaveformEW | 40 | 5000 | 3 |
| 6 | glass | 9 | 214 | 6 |
| 7 | dermatology | 33 | 366 | 6 |
| 8 | lung-cancer | 55 | 366 | 3 |
| 9 | Z-Alizideh | 49 | 140 | 2 |
| 10 | sonarEW | 60 | 208 | 2 |
| 11 | LUNG2 | 3312 | 203 | 2 |
| 12 | PRO | 6033 | 102 | 2 |
| Algorithm | Parameter | Value (s) |
|---|---|---|
| all algorithms | Population size | 40 |
| The number of iterations | 100 | |
| BPSO | Learn the factors c1 and c2 | c1 = c2 = 2 |
| Constriction factor k | 0.729 | |
| Inertial factor | Dynamic | |
| Acceleration constants in PSO | [2,2] | |
| Inertia w in PSO | [0.9,0.6] | |
| The optimal solution (a) | It is decreasing linearly from 2 to 0 | |
| BGWOA | Collaborative coefficient vector (A) | [−a,a] |
| Collaborative coefficient vector (C) | Random value [0,2] | |
| Step size scaling factor () | ||
| BCSA | Probability of being discovered by the host () | |
| Step size scaling factor ( | ||
| Search agents’ number | 8 | |
| BWOA | Search domain | [0,1] |
| α parameter in the fitness function | 0.99 | |
| β parameter in the fitness function | 0.01 | |
| The number of discoverers | 20% | |
| BSSA | Detecting the number of endangered sparrows | 10% |
| Safe threshold | 0.8 | |
| Perturbation σ | 0.2 |
5.2. Evaluation Criteria
5.3. Experimental Results
5.3.1. Classification Performance and Statistical Significance
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 0.11 | 0.23 | 0.20 | 0.18 | 0.09 |
| 2 | Clean1 | 0.33 | 0.08 | 0.44 | 0.06 | 0.01 |
| 3 | forest | 0.68 | 24.16 | 0.32 | 0.06 | 0.04 |
| 4 | KrvskpEW | 0.16 | 0.43 | 0.12 | 0.07 | 0.08 |
| 5 | WaveformEW | 0.22 | 0.21 | 0.30 | 0.29 | 0.16 |
| 6 | Glass | 0.73 | 0.24 | 0.16 | 0.26 | 0.05 |
| 7 | dermatology | 0.47 | 0.03 | 0.32 | 0.03 | 0.01 |
| 8 | lung-cancer | 0.55 | 0.23 | 0.38 | 0.33 | 0.04 |
| 9 | Z-Alizideh | 0.10 | 0.23 | 0.29 | 0.24 | 0.10 |
| 10 | sonarEW | 0.06 | 0.08 | 0.11 | 0.08 | 0.03 |
| 11 | LUNG2 | 0.21 | 0.24 | 0.23 | 0.24 | 0.19 |
| 12 | PRO | 0.08 | 0.28 | 0.25 | 0.04 | 0.03 |
| average | 0.31 | 2.2 | 0.26 | 0.16 | 0.07 |
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 0.11 | 0.18 | 0.19 | 0.12 | 0.02 |
| 2 | Clean1 | 0.32 | 0.07 | 0.41 | 0.05 | 0.00 |
| 3 | forest | 0.61 | 23.80 | 0.23 | 0.04 | 0.01 |
| 4 | KrvskpEW | 0.03 | 0.09 | 0.08 | 0.05 | 0.02 |
| 5 | WaveformEW | 0.21 | 0.21 | 0.29 | 0.27 | 0.01 |
| 6 | Glass | 0.69 | 0.05 | 0.11 | 0.21 | 0.03 |
| 7 | dermatology | 0.41 | 0.02 | 0.29 | 0.02 | 0.01 |
| 8 | lung-cancer | 0.52 | 0.21 | 0.31 | 0.32 | 0.07 |
| 9 | Z-Alizideh | 0.18 | 0.18 | 0.22 | 0.23 | 0.05 |
| 10 | sonarEW | 0.05 | 0.06 | 0.10 | 0.07 | 0.02 |
| 11 | LUNG2 | 0.20 | 0.21 | 0.21 | 0.21 | 0.17 |
| 12 | PRO | 0.06 | 0.24 | 0.22 | 0.03 | 0.02 |
| average | 0.28 | 2.11 | 0.22 | 0.14 | 0.04 |
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 0.15 | 0.36 | 0.24 | 0.19 | 0.13 |
| 2 | Clean1 | 0.38 | 0.12 | 0.45 | 0.07 | 0.06 |
| 3 | forest | 0.71 | 24.21 | 0.34 | 0.06 | 0.27 |
| 4 | KrvskpEW | 0.23 | 0.60 | 0.20 | 0.12 | 0.09 |
| 5 | WaveformEW | 0.24 | 0.23 | 0.31 | 0.31 | 0.23 |
| 6 | Glass | 0.77 | 0.37 | 0.17 | 0.30 | 0.07 |
| 7 | dermatology | 0.48 | 0.05 | 0.33 | 0.31 | 0.01 |
| 8 | lung-cancer | 0.59 | 0.50 | 0.40 | 0.35 | 0.07 |
| 9 | Z-Alizideh | 0.22 | 0.30 | 0.30 | 0.27 | 0.19 |
| 10 | sonarEW | 0.26 | 0.15 | 0.13 | 0.12 | 0.09 |
| 11 | LUNG2 | 0.23 | 0.23 | 0.23 | 0.27 | 0.20 |
| 12 | PRO | 0.10 | 0.32 | 0.31 | 0.06 | 0.03 |
| average | 0.36 | 2.29 | 0.28 | 0.2 | 0.12 |
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 0.011 | 0.013 | 0.008 | 0.012 | 0.006 |
| 2 | Clean1 | 0.01 | 0.005 | 0.005 | 0.032 | 0.003 |
| 3 | forest | 0.021 | 0.016 | 0.030 | 0.025 | 0.010 |
| 4 | KrvskpEW | 0.030 | 0.061 | 0.035 | 0.040 | 0.020 |
| 5 | WaveformEW | 0.220 | 0.058 | 0.041 | 0.003 | 0.011 |
| 6 | Glass | 0.003 | 0.006 | 0.004 | 0.023 | 0.004 |
| 7 | dermatology | 0.077 | 0.093 | 0.052 | 0.063 | 0.056 |
| 8 | lung-cancer | 0.003 | 0.002 | 0.004 | 0.052 | 0.001 |
| 9 | Z-Alizideh | 0.018 | 0.029 | 0.022 | 0.020 | 0.016 |
| 10 | sonarEW | 0.009 | 0.009 | 0.047 | 0.003 | 0.005 |
| 11 | LUNG2 | 0.089 | 0.048 | 0.034 | 0.067 | 0.012 |
| 12 | PRO | 0.030 | 0.059 | 0.065 | 0.037 | 0.013 |
| average | 0.043 | 0.033 | 0.029 | 0.031 | 0.013 |
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA |
|---|---|---|---|---|---|
| 1 | BreastEW | 0.00593 | 0.000561 | 2.81 × 10−6 | 3.32 × 10−6 |
| 2 | Clean1 | 1.82 × 10−10 | 0.000985 | 5.88 × 10−8 | 8.64 × 10−9 |
| 3 | forest | 0.0781 | 0.000515 | 0.00119 | 0.0000344 |
| 4 | KrvskpEW | 7.95 × 10−7 | 0.0431 | 0.000821 | 0.0796 |
| 5 | WaveformEW | 0.0431 | 0.04312 | 0.000655 | 0.0431 |
| 6 | Glass | 0.0171 | 0.00314 | 0.140 | 0.000801 |
| 7 | dermatology | 0.138 | 0.0431 | 0.0356 | 0.0461 |
| 8 | lung-cancer | 0.00377 | 0.000653 | 0.000647 | 0.231 |
| 9 | Z-Alizideh | 0.000431 | 0.000801 | 0.000650 | 0.00377 |
| 10 | sonarEW | 0.00356 | 0.00314 | 0.00759 | 0.0431 |
| 11 | LUNG2 | 0.000650 | 0.000655 | 0.000803 | 0.0146 |
| 12 | PRO | 0.0109 | 0.00687 | 0.000623 | 0.114 |
5.3.2. Feature Selection Efficiency
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 16 | 13.6 | 12 | 15 | 10 |
| 2 | Clean1 | 77.24 | 97.2 | 94 | 67 | 66.10 |
| 3 | forest | 21.79 | 11 | 14.6 | 16 | 6.40 |
| 4 | KrvskpEW | 20.8 | 10.94 | 30.80 | 27.60 | 10.20 |
| 5 | WaveformEW | 22.7 | 32.54 | 34.40 | 36.40 | 18.67 |
| 6 | Glass | 30.27 | 5.40 | 8.30 | 3 | 5.60 |
| 7 | dermatology | 32.70 | 16.6 | 31.23 | 28 | 12.53 |
| 8 | lung-cancer | 21.13 | 25 | 29 | 29 | 10.67 |
| 9 | Z-Alizideh | 19.03 | 27 | 22.8 | 31 | 8.40 |
| 10 | sonarEW | 21.59 | 30.4 | 32.9 | 23 | 19.67 |
| 11 | LUNG2 | 12.4 | 13.4 | 13.8 | 14.6 | 11.8 |
| 12 | PRO | 11.6 | 13.6 | 10.8 | 11 | 10.8 |
| average | 25.6 | 24.72 | 27.89 | 25.13 | 15.9 |
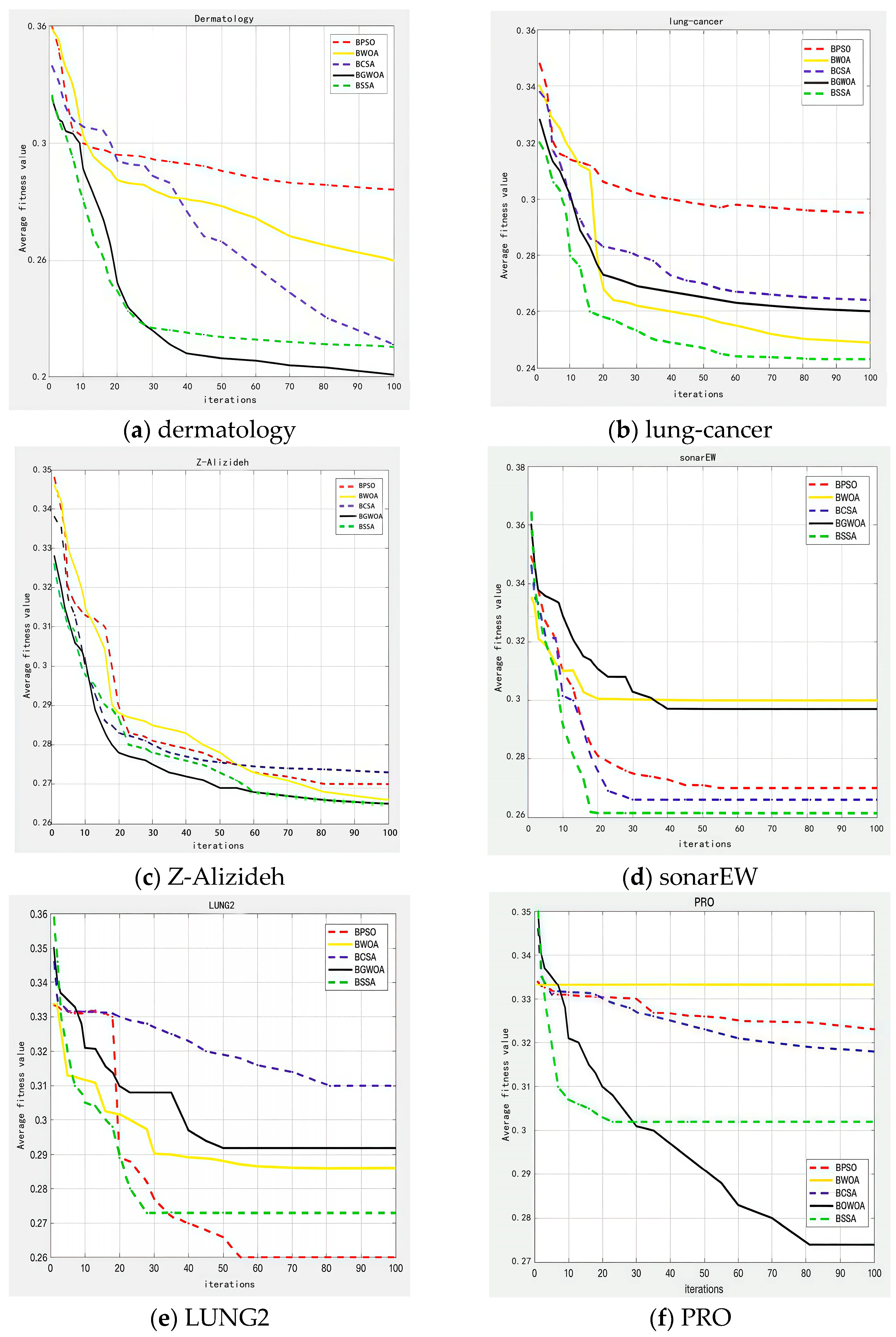
5.3.3. Convergence
5.3.4. Computational Efficiency
| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 1.19 | 0.46 | 8.12 | 1.59 | 1.11 |
| 2 | Clean1 | 2.91 | 2.58 | 7.98 | 1.93 | 1.72 |
| 3 | forest | 21.79 | 24.16 | 15.41 | 1.81 | 1.13 |
| 4 | KrvskpEW | 19.61 | 48.97 | 15.89 | 13.03 | 1.30 |
| 5 | WaveformEW | 33.53 | 305.29 | 43.72 | 86.64 | 1.12 |
| 6 | Glass | 30.27 | 1.46 | 19.98 | 0.55 | 1.20 |
| 7 | dermatology | 33.70 | 1.44 | 16.33 | 0.56 | 1.21 |
| 8 | lung-cancer | 21.13 | 1.50 | 10.19 | 0.49 | 1.06 |
| 9 | Z-Alizideh | 1.564 | 2.48 | 19.71 | 0.06 | 1.22 |
| 10 | sonarEW | 1.09 | 4.46 | 15.43 | 0.05 | 4.11 |
| 11 | LUNG2 | 18.09 | 11.73 | 16.36 | 14.36 | 11.05 |
| 12 | PRO | 16.17 | 9.78 | 7.61 | 13.02 | 13.92 |
| average | 16.75 | 34.53 | 16.39 | 11.17 | 3.35 |
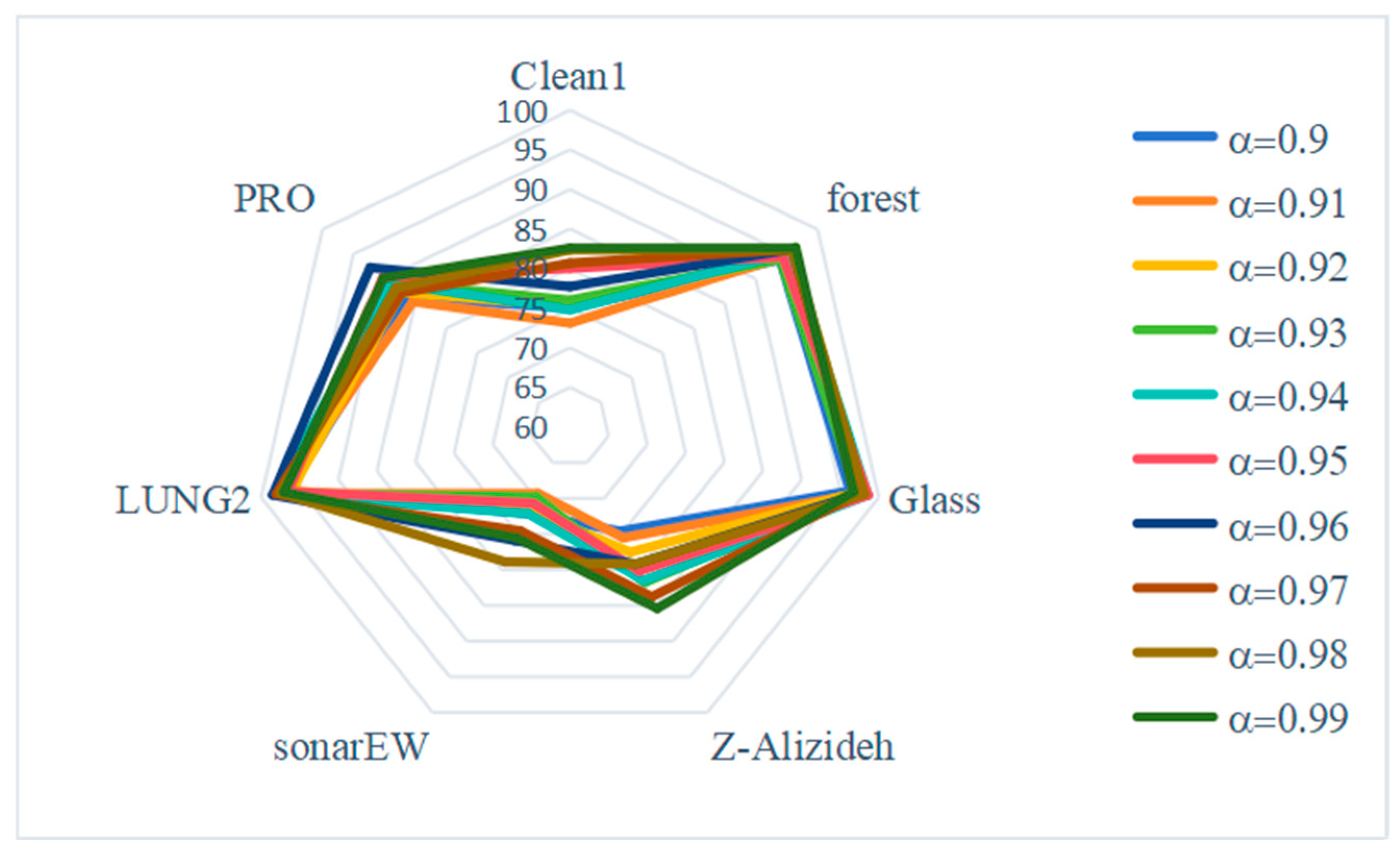
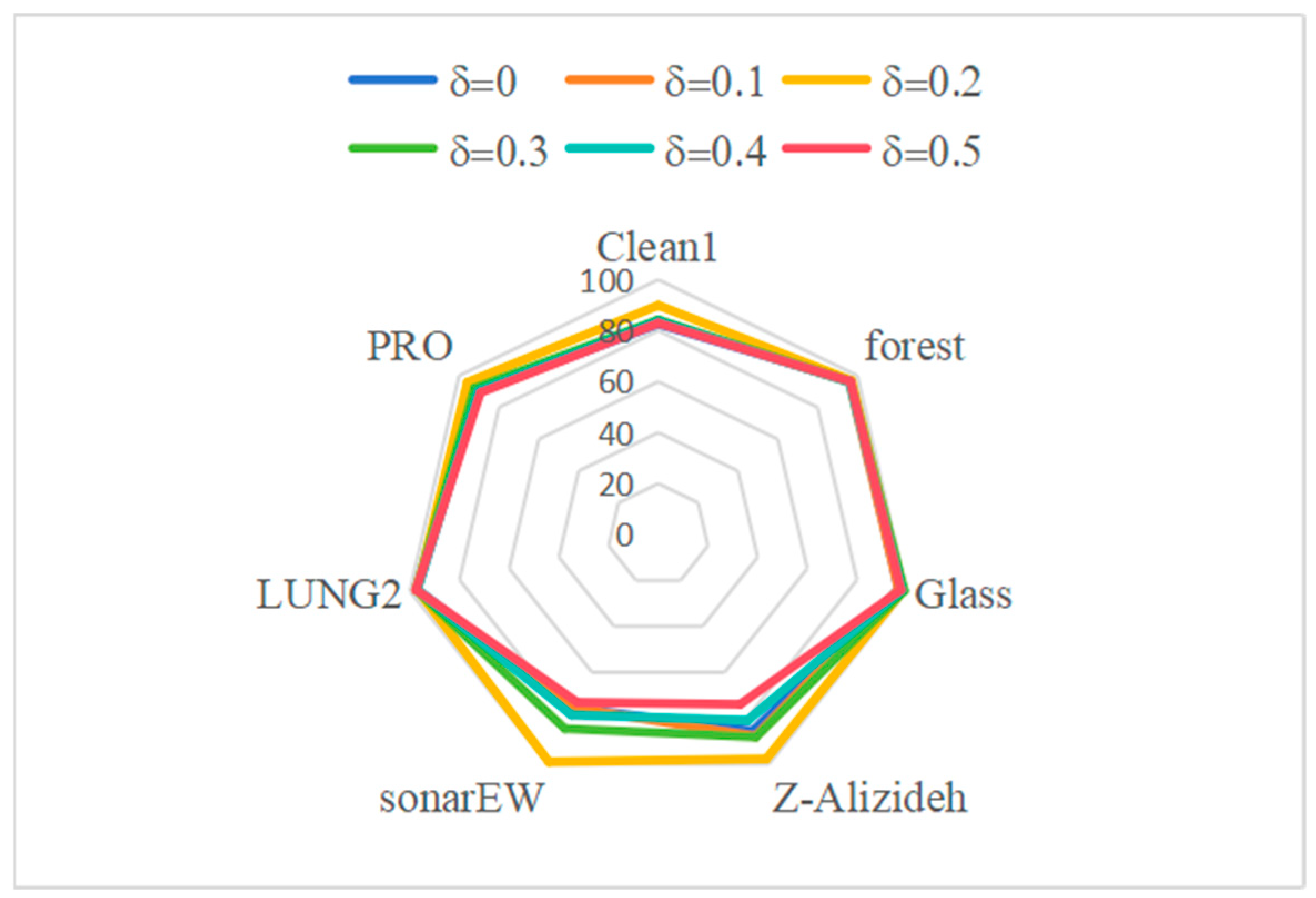
5.4. Sensitivity Analysis of Parameters
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khine, A.H.; Wettayaprasit, W.; Duangsuwan, J. A new word embedding model integrated with medical knowledge for deep learning-based sentiment classification. Artif. Intell. Med. 2024, 148, 102758. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhu, P. Online group streaming feature selection based on fuzzy neighborhood granular ball rough sets. Expert Syst. Appl. 2024, 249, 123778. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wei, J.M. Feature selection based on measurement of ability to classify subproblems. Neurocomputing 2017, 224, 155–165. [Google Scholar] [CrossRef]
- Li, J.; Luo, T.; Zhang, B.; Chen, M.; Zhou, J. An efficient multi-objective filter–wrapper hybrid approach for high-dimensional feature selection. J. King Saud. Univ-Com. 2024, 36, 2024. [Google Scholar] [CrossRef]
- Gaugel, S.; Reichert, M. Data-driven multi-objective optimization of hydraulic pump test cycles via wrapper feature selection. Cirp. J. Manuf. Sci. Tec. 2024, 50, 14–25. [Google Scholar] [CrossRef]
- Oluwaseun, P.; Keng, H. Ensemble Filter-Wrapper Text Feature Selection Methods for Text Classification. Comput. Mod. Eng. Sci. 2024, 141, 1847–1865. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, J.; Feng, L.; Zhao, C. A survey and experimental study for embedding-aware generative models: Features, models, and any-shot scenarios. J. Process Contr. 2024, 143, 103297. [Google Scholar] [CrossRef]
- An, H.; Yang, J.; Zhang, X.; Ruan, X.; Wu, Y.; Li, S.; Hu, J. A class-incremental learning approach for learning feature-compatible embeddings. Neural Netw. 2024, 180, 106685. [Google Scholar] [CrossRef]
- Sarkar, S.S.; Sheikh, K.H.; Mahanty, A.; Mali, K.; Ghosh, A.; Sarkar, R. A harmony search-based wrapper-filter feature selection approach for microstructural image classification. Integr. Mater. Manuf. Innov. 2021, 10, 1–19. [Google Scholar] [CrossRef]
- Shokooh, T.; Mohammad, H. A binary metaheuristic algorithm for wrapper feature selection. INT J. Comput. Sci. Eng. 2021, 8, 168–172. [Google Scholar]
- Sancho, S.S. Modern meta-heuristics based on nonlinear physics processes: A review of models and design procedures. Phys. Rep. 2016, 655, 1–70. [Google Scholar] [CrossRef]
- Laith, A. Multi-verse optimizer algorithm: A comprehensive survey of its results, variants, and applications. Neural Comput. Appl. 2020, 32, 12381–12401. [Google Scholar] [CrossRef]
- Bolaji, A.L.A.; Al-Betar, M.A.; Awadallah, M.A.; Khader, A.T.; Abualigah, L.M. A comprehensive review: Krill herd algorithm and its applications. Appl. Soft Comput. 2016, 49, 437–446. [Google Scholar] [CrossRef]
- Akinola, O.O.; Ezugwu, A.E.; Agushaka, J.O.; Zitar, R.A.; Abualigah, L. Multiclass feature selection with metaheuristic optimization algorithms: A review. Neural. Comput. Applic. 2022, 34, 19751–19790. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Zhang, H. A Novel Binary Dragonfly Algorithm for Feature Selection. Pattern Recogn. Lett. 2023, 171, 276–283. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Liu, J. A novel multi-objective feature selection algorithm based on improved sparrow search and chaotic local search. Knowl.-Based Syst. 2023, 269, 110694. [Google Scholar] [CrossRef]
- Kumar, R.; Rai, B.; Samui, P. Prediction of mechanical properties of high-performance concrete and ultrahigh-performance concrete using soft computing techniques: A critical review. Struct. Concr. 2025, 26, 1309–1337. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithm in Search, Optimization and Machine Learning; Addison-Wesley: London, UK, 1989; pp. 122–129. [Google Scholar]
- Xue, Y.; Zhu, H.K.; Ferrante, N. A self-adaptive multi-objective feature selection approach for classification problems. Integr. Comput. Aid Eng. 2022, 29, 3–21. [Google Scholar] [CrossRef]
- Zheng, R.; Liu, M.Q.; Zhang, Y.; Wang, Y.L. An optimization method based on improved ant colony algorithm for complex product change propagation path. Intell. Syst. Appl. 2024, 23, 200412. [Google Scholar] [CrossRef]
- Cai, Q.; Zhou, X.; Jie, A.; Zhong, M.; Wang, M.; Wang, H.; Peng, H.; Gao, X.; Zhang, Y.; Wang, Y. Enhancing Artificial Bee Colony Algorithm with Dynamic Best Neighbor-guided Search Strategy. Proceedings of 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Nisar, K.; Soomro, T.R.; Ibrahim, A.A.; Mallah, G.A.; Hassan, N.U.; Rehman, N.U. An improved particle swarm optimization algorithm for data classification. Appl. Sci. 2023, 13, 283. [Google Scholar] [CrossRef]
- Ileberi, E.; Sun, Y. Machine Learning-Assisted Cervical Cancer Prediction Using Particle Swarm Optimization for Improved Feature Selection and Prediction. IEEE Access 2024, 12, 152684–152695. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Contr. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S. A stochastic configuration network based on chaotic sparrow search algorithm. Knowl.-Based Syst. 2021, 220, 106924. [Google Scholar] [CrossRef]
- Li, B.; Wang, H. Multi-objective sparrow search algorithm: A novel algorithm for solving complex multi-objective optimisation problems. Expert Syst. Appl. 2022, 210, 118414. [Google Scholar] [CrossRef]
- Sun, L.; Si, S.; Ding, W. BSSFS: Binary sparrow search algorithm for feature selection. Int. J. Mach. Learn. Cybern. 2023, 14, 2633–2657. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Ap-plications and Trends. IEEE/CAA J. Automatica Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Ahmed Shaban, A.; Ibrahim, I.M. Swarm intelligence algorithms: A survey of modifications and applications. Int. J. Sci. World 2025, 11, 59–65. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Xue, B.; Zhang, M. A survey on swarm intelligence approaches to feature selection in data mining. Swarm Evol. Comput. 2020, 54, 100663. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Z.; Lei, Z.; Wang, R.L.; Wu, Z.; Gao, S. Feature selection with clustering probabilistic particle swarm optimization. Int. J. Mach. Learn. Cybern. 2024, 15, 3599–3617. [Google Scholar] [CrossRef]
- Xiao, X.; Na, X.; Zu, Z.; Ma, H.; Ren, W. A Novel Binary Particle Swarm Optimization Algorithm for Feature Selection. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024; pp. 4386–4391. [Google Scholar] [CrossRef]
- Unler, A.; Murat, A. A discrete particle swarm optimization method for feature selection in binary classification problems. Eur. J. Oper. Res. 2010, 206, 528–539. [Google Scholar] [CrossRef]
- Mirjalili, S.; Hashim, S.Z. BMOA: Binary magnetic optimization algorithm. Int. J. Mach. Learn. Comput. 2012, 2, 204–208. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Pereira, L.A.M.; Rodrigues, D.; Almeida, T.N.S.; Ramos, C.C.O.; Papa, J.P. A binary cuckoo search and its application for feature selection. In Cuckoo Search and Firefly Algorithm; Yang, X.S., Ed.; Springer: New York, NY, USA, 2014; pp. 141–154. [Google Scholar]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H. S-shaped binary whale optimization algorithm for feature selection. In Recent Trends in Signal and Image Processing; Bhattacharyya, S., Mukherjee, A., Bhaumik, H., Eds.; Springer: New York, NY, USA, 2019; pp. 79–87. [Google Scholar]
- Liang, Q.; Chen, B.; Wu, H.; Ma, C.; Li, S. A novel modified sparrow search algorithm with application in side lobe level reduction of linear antenna array. Wirel. Commun. Mob. Comput. 2021, 1, 9915420. [Google Scholar] [CrossRef]
- Chang, D.; Rao, C.; Xiao, X.; Hu, F.; Goh, M. Multiple strategies based Grey Wolf Optimizer for feature selection in performance evaluation of open-ended funds. Swarm Evol. Comput. 2024, 86, 101518. [Google Scholar] [CrossRef]
- Mi, L.N.; Guo, Y.F.; Zhang, M.; Zhuo, X.J. Stochastic resonance in gene transcriptional regulatory system driven by Gaussian noise and Lévy noise. Chaos Solitons Fract. 2022, 167, 113096. [Google Scholar] [CrossRef]
- Mandal, A.K.; Nadim, M.; Saha, H.; Sultana, T.; Hossain, M.D.; Huh, E.N. Feature subset selection for high-dimensional, low sampling size data classification using ensemble feature selection with a wrapper-based search. IEEE Access 2024, 12, 62341–62357. [Google Scholar] [CrossRef]
- Tijjani, S.; Wahab, M.N.A.; Noor, M.H.M. An enhanced particle swarm optimization with position update for optimal feature selection. Expert Syst. Appl. 2024, 247, 123337. [Google Scholar] [CrossRef]
- Markelle, K.; Rachel, L.; Kolby, N. The UCI Machine Learning Repository. 2021. Available online: https://archive.ics.uci.edu (accessed on 13 August 2025).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009; pp. 96–106. [Google Scholar]
- Abdel-Basset, M.; Ding, W.; El-Shahat, D. A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection. Artif. Intell. Rev. 2021, 54, 593–637. [Google Scholar] [CrossRef]
- Bagkavos, D.; Patil, P.N. Improving the Wilcoxon signed rank test by a kernel smooth probability integral transformation. Stat. Probabil. Lett. 2021, 171, 109026. [Google Scholar] [CrossRef]
- Vierra, A.; Razzaq, A.; Andreadis, A. Continuous variable analyses: T-test, Mann–Whitney U, Wilcoxon sign rank. In Handbook for Designing and Conducting Clinical and Translational Research, Translational Surgery; Eltorai, A.E.M., Bakal, J.A., Newell, P.C., Osband, A.J., Eds.; Academic Press: San Diego, CA, USA, 2023; pp. 165–170. [Google Scholar] [CrossRef]
- Ohyver, M.; Moniaga, J.V.; Sungkawa, I.; Subagyo, B.E.; Chandra, I.A. The Comparison Firebase Realtime Database and MySQL Database Performance using Wilcoxon Signed-Rank Test. Procedia Comput. Sci. 2019, 157, 396–405. [Google Scholar] [CrossRef]

| No. | Dataset | BPSO | BGWOA | BCSA | BWOA | BSSA |
|---|---|---|---|---|---|---|
| 1 | BreastEW | 88.87 | 78.81 | 80.67 | 79.49 | 97.97 |
| 2 | Clean1 | 67.19 | 83.07 | 56.51 | 88.42 | 89.92 |
| 3 | forest | 90.33 | 98.99 | 68.37 | 94.87 | 96.98 |
| 4 | KrvskpEW | 94.19 | 81.78 | 85.71 | 90.13 | 98.72 |
| 5 | WaveformEW | 78.91 | 76.50 | 73.29 | 75.38 | 99.32 |
| 6 | Glass | 70.00 | 78.21 | 84.54 | 73.81 | 98.6 |
| 7 | dermatology | 77.97 | 98.36 | 68.37 | 97.26 | 95.61 |
| 8 | lung-cancer | 71.55 | 80.95 | 61.82 | 66.67 | 89.91 |
| 9 | Z-Alizideh | 90.28 | 78.19 | 71.32 | 76.67 | 97.70 |
| 10 | sonarEW | 93.57 | 94.20 | 89.18 | 92.68 | 98.99 |
| 11 | LUNG2 | 93.12 | 79.89 | 81.84 | 89.24 | 97.05 |
| 12 | PRO | 80.33 | 60.02 | 64.09 | 83.23 | 95.80 |
| average | 83.03 | 82.41 | 73.81 | 83.99 | 96.11 | |
| W/L/T | 12/0/0 | 10/2/0 | 12/0/0 | 12/0/0 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, J.; Gu, X.; Sun, D.; Zhu, J.; Wang, S. Multi-Variable Evaluation via Position Binarization-Based Sparrow Search. Electronics 2025, 14, 3312. https://doi.org/10.3390/electronics14163312
Hua J, Gu X, Sun D, Zhu J, Wang S. Multi-Variable Evaluation via Position Binarization-Based Sparrow Search. Electronics. 2025; 14(16):3312. https://doi.org/10.3390/electronics14163312
Chicago/Turabian StyleHua, Jiwei, Xin Gu, Debing Sun, Jinqi Zhu, and Shuqin Wang. 2025. "Multi-Variable Evaluation via Position Binarization-Based Sparrow Search" Electronics 14, no. 16: 3312. https://doi.org/10.3390/electronics14163312
APA StyleHua, J., Gu, X., Sun, D., Zhu, J., & Wang, S. (2025). Multi-Variable Evaluation via Position Binarization-Based Sparrow Search. Electronics, 14(16), 3312. https://doi.org/10.3390/electronics14163312






