Adaptive Learning Gain-Based Robust Attitude Control for Satellites with Time-Varying External Disturbances
Abstract
1. Introduction
- An ALG-based attitude control method is developed for nonlinear satellite dynamics subject to unknown and time-varying external disturbances.
- The proposed controller guarantees that tracking errors remain within prescribed performance bounds without requiring any prior knowledge of disturbance magnitudes or extensive gain tuning.
- A self-updating gain mechanism is introduced that dynamically increases the control gain in the presence of large tracking errors and reduces it as errors decrease, thereby preventing excessive control input and improving efficiency.
2. Satellite Dynamics
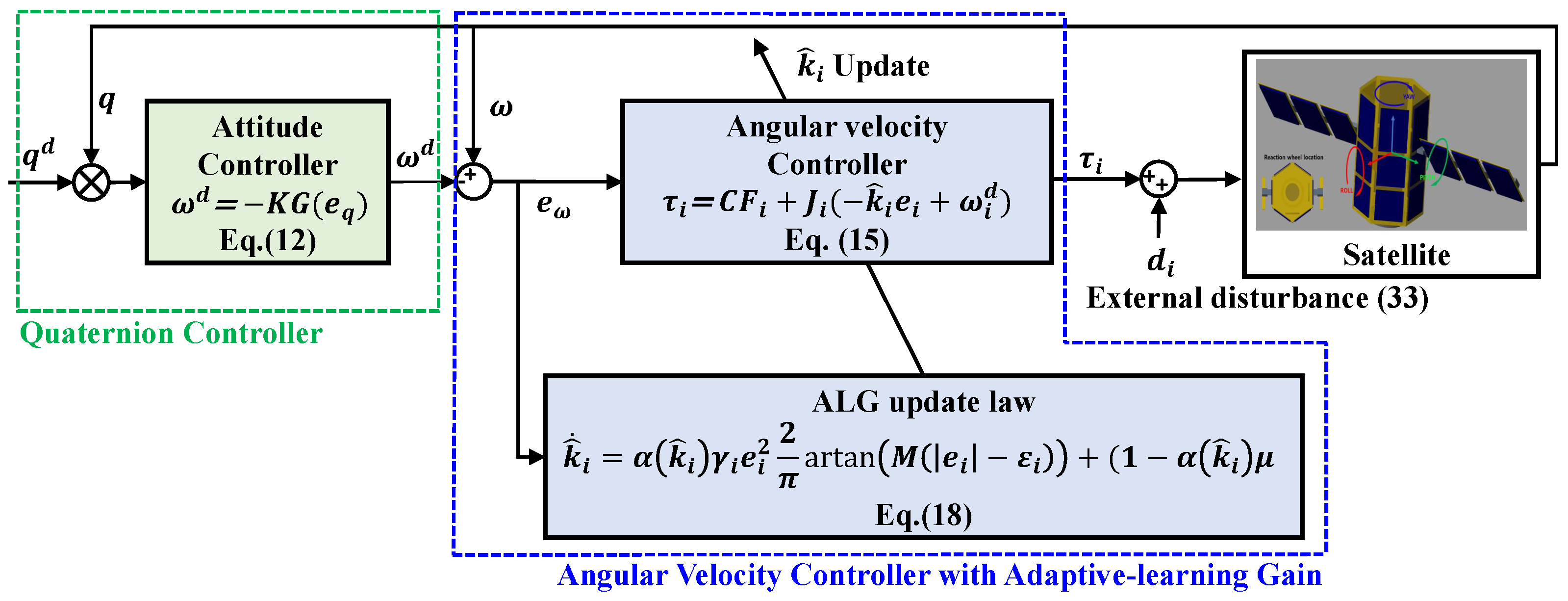
3. Control Methodology
3.1. Conventional Quaternion Controller
3.2. Proposed Angular Velocity Controller with Adaptive-Learning Gain
- Initial gain : Choose a small positive value to avoid excessive control input at startup. If the initial tracking error is expected to be large, a slightly higher initial gain may improve transient behavior while avoiding instability.
- Lower gain bound: A strictly positive lower bound is required to maintain controllability even under mild disturbances. It should reflect the minimal feedback needed to regulate the system dynamics.
- Desired bound : This constant value defines the steady-state bound for each tracking error. It should be selected based on the resolution and physical limits of the system (e.g., sensor accuracy and actuator bandwidth). If chosen too small, the gain may diverge due to infeasibility. Practical selection often involves trial runs using fixed-gain controllers or user-defined specifications provided by industrial clients.
- Gain adaptation rate γ: The parameter γ governs the responsiveness of the gain update when the tracking error exceeds the desired bound. A larger value of γ leads to faster adaptation but may induce chattering or aggressive control. It should be selected by considering the trade-off between responsiveness and control smoothness.
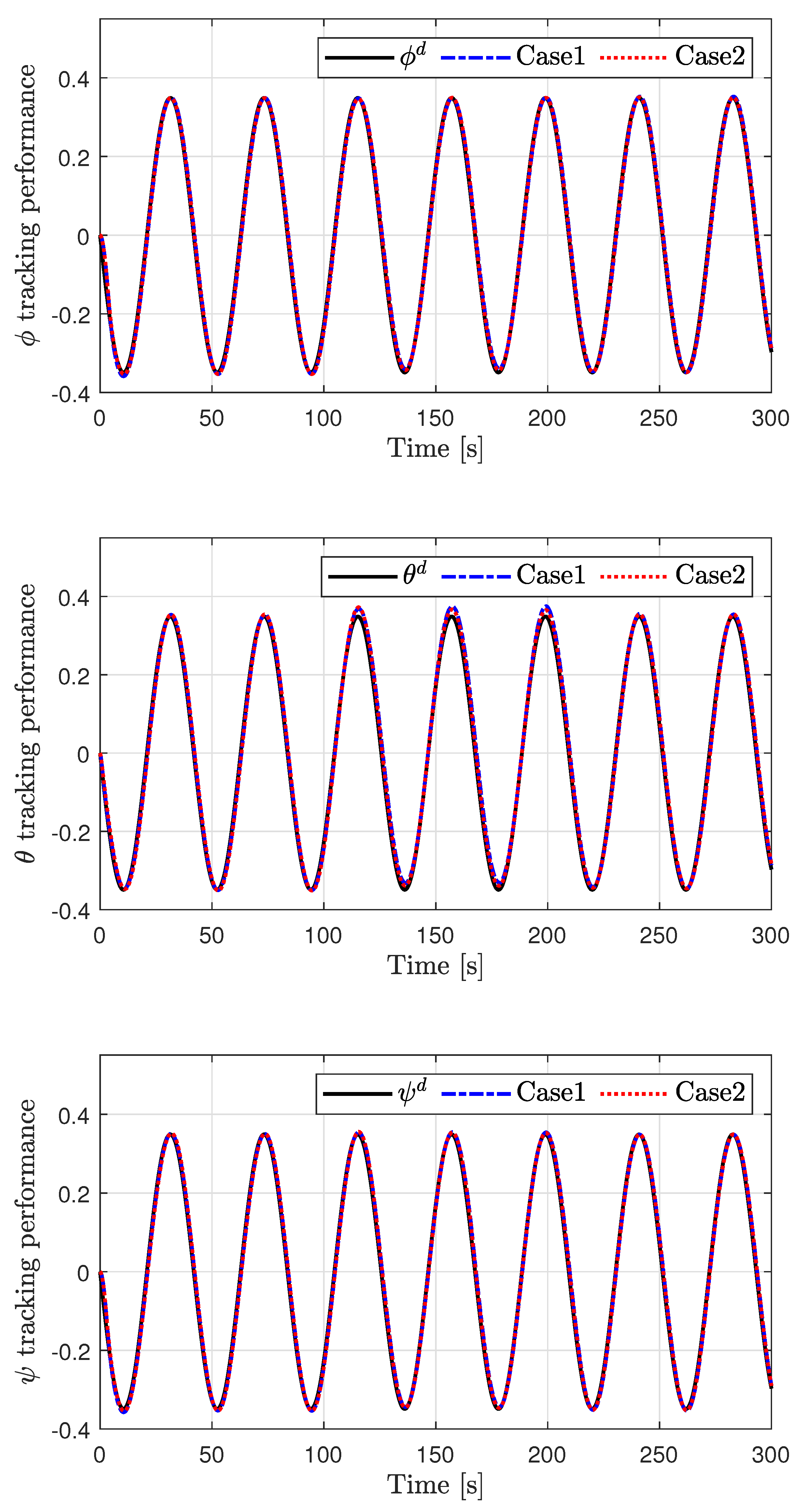
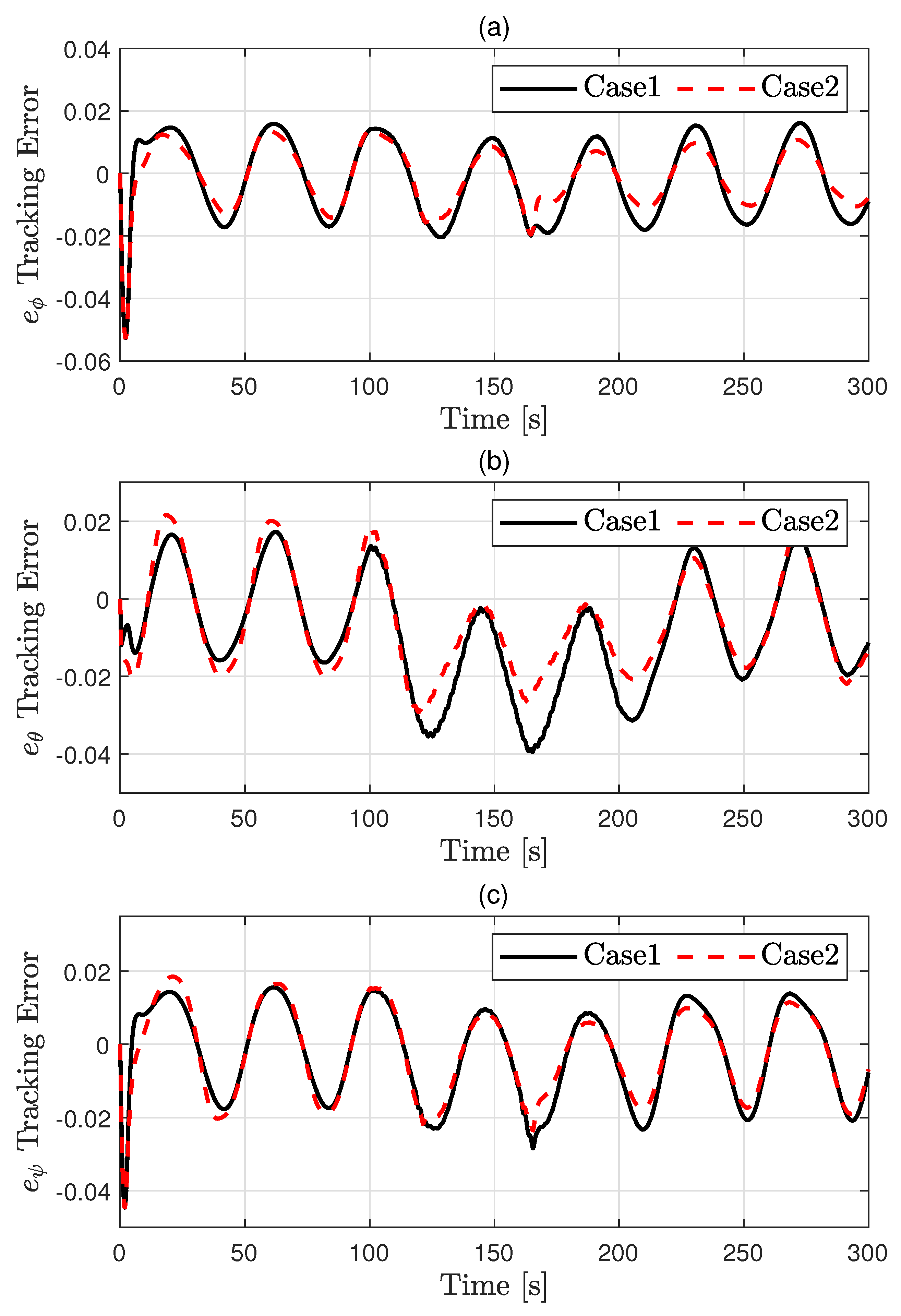
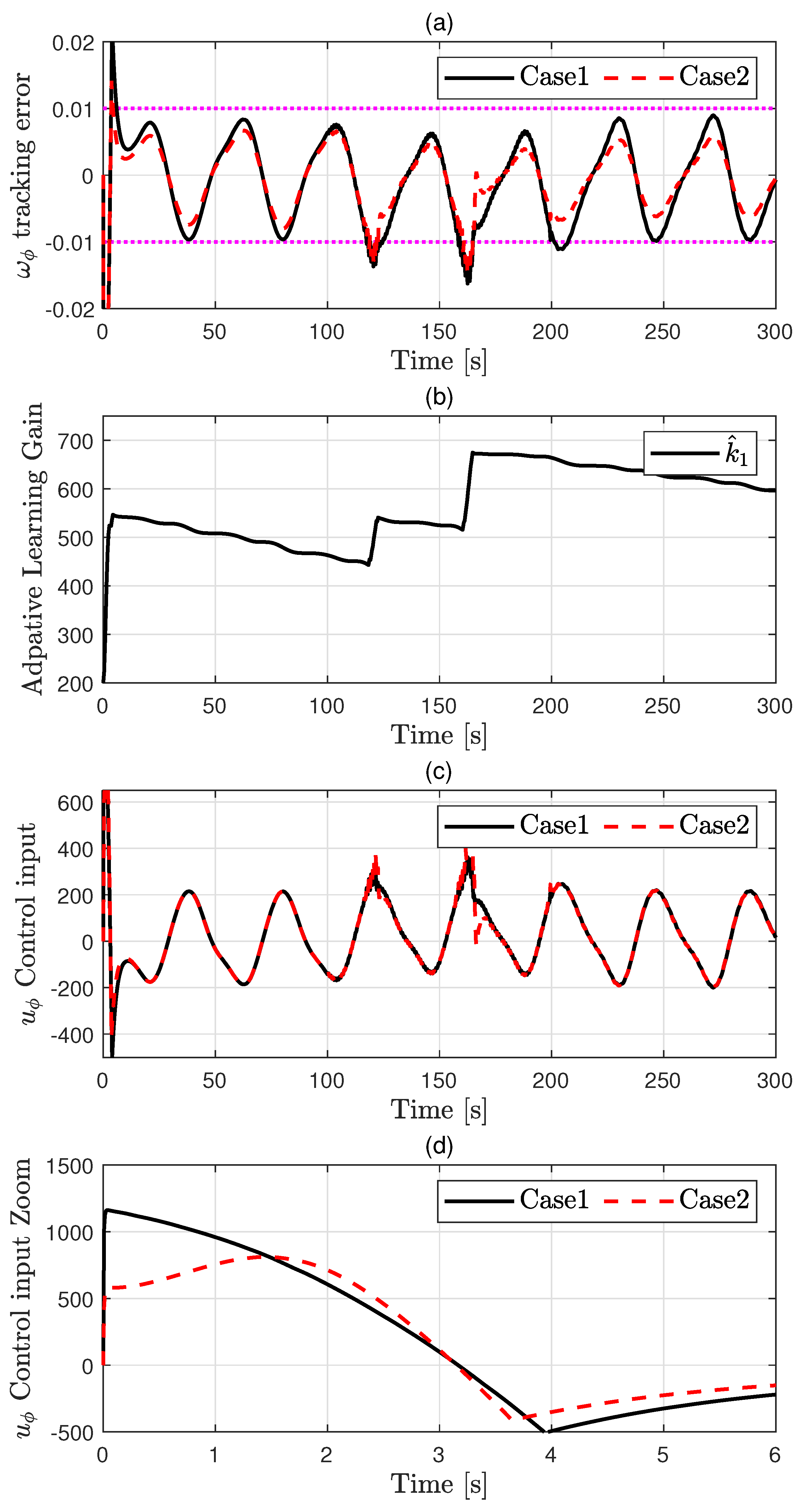
4. Simulation Results and Discussion
- Case 1: Conventional controller with fixed gains. This case uses a well-tuned control strategy with fixed and relatively high gain values, which serve as a performance benchmark. The control gains were configured as , and
- Case 2: Proposed ALG-based controller. In this case, the control gains are adaptively adjusted in real time according to the magnitude of the tracking error. The following parameter settings were used:
- –
- Initial gains: ;
- –
- Learning rates: , , ;
- –
- Slope factor for arctan: ;
- –
- Desired tracking performance bounds: ;
- –
- Minimum gain values: ;
- –
- Residual gain increment: .
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Fajardo, I.; Lidtke, A.A.; Bendoukha, S.A.; Gonzalez-Llorente, J.; Rodríguez, R.; Morales, R.; Faizullin, D.; Matsuoka, M.; Urakami, N.; Kawauchi, R.; et al. Design, Implementation, and Operation of a Small Satellite Mission to Explore the Space Weather Effects in LEO. Aerospace 2019, 6, 108. [Google Scholar] [CrossRef]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satellite Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Soufi, O.; Belouadha, F.Z. An intelligent deep learning approach to spacecraft attitude control: The case of satellites. J. Franklin Inst. 2024, 361, 107078. [Google Scholar] [CrossRef]
- Yang, C.; Fan, Z.; Lu, W.; Gao, H. Uncertain iterative optimal attitude control method for periodic satellite with reliability constraint. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6461–6473. [Google Scholar] [CrossRef]
- Li, Y.; Ye, D.; Sun, Z. Robust finite time control algorithm for satellite attitude control. Aerospace Sci. Technol. 2017, 68, 46–57. [Google Scholar] [CrossRef]
- Hu, Q.; Li, B.; Zhang, Y. Robust attitude control design for spacecraft under assigned velocity and control constraints. ISA Trans. 2013, 52, 480–493. [Google Scholar] [CrossRef]
- Wie, B.; Weiss, H.; Arapostathis, A. Quaternion feedback regulator for spacecraft eigenaxis rotations. J. Guid. Control Dyn. 1989, 12, 375–380. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, L.; Cheng, Y.; Ying, K. A performance evaluation approach for satellite attitude control system in tracking mode. Appl. Sci. 2024, 14, 2867. [Google Scholar] [CrossRef]
- Jiang, Y.; Hu, Q.; Ma, G. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures. ISA Trans. 2010, 49, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Zhang, H.; Wang, Z. Hybrid adaptive control of spacecraft attitude with input saturation and external disturbance. J. Guid. Control Dyn. 2019, 42, 642–649. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, Y.; Ling, K.-V.; Ding, F. Hybrid two-stage identification-based nonlinear MPC strategy for satellite attitude control. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 1–15. [Google Scholar] [CrossRef]
- Zhang, X.; Zong, Q.; Tian, B.; Liu, W. Continuous robust fault-tolerant control and vibration suppression for flexible spacecraft without angular velocity. Int. J. Robust Nonlinear Control 2019, 29, 3915–3935. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Fu, M. Review on the developments of sliding function and adaptive gain in sliding mode control. J. Autom. Intell. 2025. accepted for publication. [Google Scholar] [CrossRef]
- Ross, I.M.; Sekhavat, P.; Fleming, A.; Gong, Q. Optimal feedback control: Foundations, examples, and experimental results for a new approach. J. Guid. Control Dyn. 2008, 31, 307–321. [Google Scholar] [CrossRef]
- Xiao, B.; Hu, Q.; Zhang, Y. Finite-time attitude tracking of spacecraft with fault-tolerant capability. IEEE Trans. Control Syst. Technol. 2015, 23, 1338–1349. [Google Scholar] [CrossRef]
- Li, B.; Hu, Q.; Ma, G. Extended state observer based robust attitude control of spacecraft with input saturation. Aerospace Sci. Technol. 2016, 50, 173–182. [Google Scholar] [CrossRef]
- Xiao, Y.; Ye, D.; Sun, Z. Observer-based continuous finite-time attitude control for rigid–flexible coupling satellites. Int. J. Control 2019, 92, 2667–2680. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, G.; Sun, Y.; Li, C. Observer-based prescribed performance attitude control for flexible spacecraft with actuator saturation. ISA Trans. 2019, 89, 84–95. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Disturbance-observer-based robust backstepping attitude stabilization of spacecraft under input saturation and measurement uncertainty. IEEE Trans. Ind. Electron. 2017, 64, 7994–8002. [Google Scholar] [CrossRef]
- Blanchini, F.; Parisini, T.; Pellegrino, F.A.; Pin, G. High-gain adaptive control: A derivative-based approach. IEEE Trans. Autom. Control 2009, 54, 2164–2169. [Google Scholar] [CrossRef]
- Khalil, H.K. High-gain observers in feedback control: Application to permanent magnet synchronous motors. IEEE Control Syst. Mag. 2017, 37, 25–41. [Google Scholar]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Fuentes-Aguilar, R.Q.; Chairez, I. Adaptive tracking control of state constraint systems based on differential neural networks: A barrier Lyapunov function approach. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5390–5401. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Karras, G.C.; Heshmati-Alamdari, S.; Kyriakopoulos, K.J. Trajectory tracking with prescribed performance for underactuated underwater vehicles under model uncertainties and external disturbances. IEEE Trans. Control Syst. Technol. 2017, 25, 429–440. [Google Scholar] [CrossRef]
- Yang, X.; Deng, W.; Yao, J. Neural adaptive dynamic surface asymptotic tracking control of hydraulic manipulators with guaranteed transient performance. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7339–7349. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Zhu, W.; Deng, W.; Zhao, X.; Yao, J. Adaptive motion control for electro-hydraulic servo systems with appointed-time performance. IEEE/ASME Trans. Mechatronics 2024. early access. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Deng, W.; Yao, J. Command filtered adaptive tracking control of nonlinear systems with prescribed performance under time-variant parameters and input delay. Int. J. Robust Nonlinear Control 2023, 33, 2840–2860. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Shin, D.; Chung, C.C. High-gain disturbance observer-based backstepping control with output tracking error constraint for electro-hydraulic systems. IEEE Trans. Control Syst. Technol. 2015, 23, 787–795. [Google Scholar] [CrossRef]
- Jung, J.-W.; Leu, V.Q.; Do, T.D.; Kim, E.-K.; Choi, H.H. Adaptive PID speed control design for permanent magnet synchronous motor drives. IEEE Trans. Power Electron. 2015, 30, 900–908. [Google Scholar] [CrossRef]
- Lee, J.Y.; Jin, M.; Chang, P.H. Variable PID gain tuning method using backstepping control with time-delay estimation and nonlinear damping. IEEE Trans. Ind. Electron. 2014, 61, 6975–6985. [Google Scholar] [CrossRef]
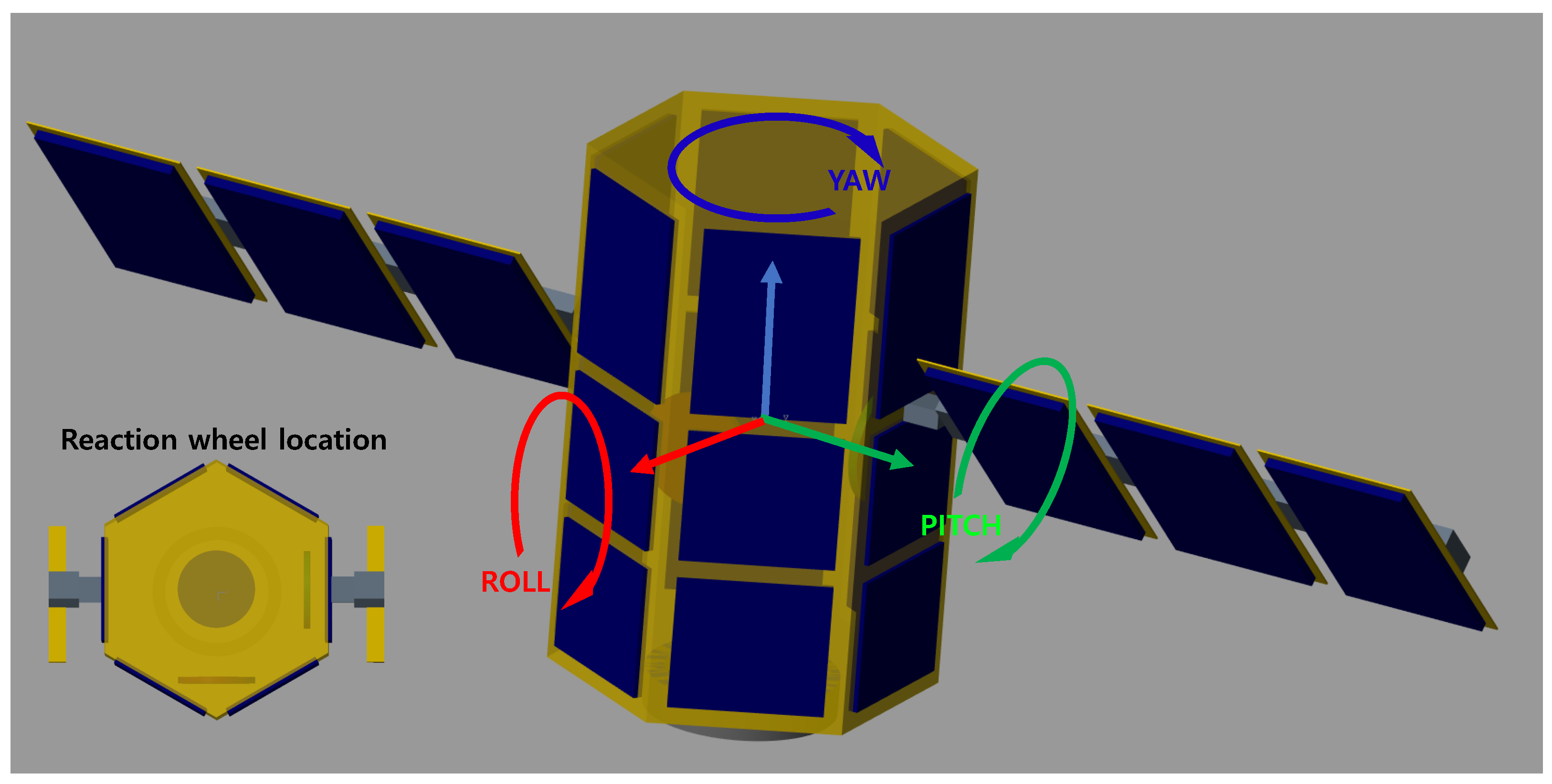



| Symbol | Description | Unit | Value |
|---|---|---|---|
| m | Mass of the satellite body | kg | 20 |
| Moment of inertia about roll axis (p) | kg·m2 | 55 | |
| Moment of inertia about pitch axis (q) | kg·m2 | 14 | |
| Moment of inertia about yaw axis (r) | kg·m2 | 49 | |
| Moment of inertia of each reaction wheel | kg·m2 | 0.0029 | |
| Radius of the reaction wheel | m | 0.18 | |
| Height of the reaction wheel | m | 0.06 | |
| q | Attitude quaternion of the satellite | - | - |
| Angular velocity of the satellite | rad/s | - | |
| Desired angular velocity | rad/s | - | |
| External disturbance torque along axis i | Nm | Defined in Equation (33) | |
| Control torque applied along axis i | Nm | Computed by Equation (15) | |
| Maximum torque output of each wheel pair | Nm | 1.0 |
| Scenario | Method | [rad/s] | [rad/s] | [rad/s] |
|---|---|---|---|---|
| 1, t = [0, 100] | Case 1 | 0.0217 | 0.0084 | 0.0173 |
| Case 2 | 0.0204 | 0.0114 | 0.0167 | |
| 2, t = [100, 200] | Case 1 | 0.0056 | 0.0076 | 0.0055 |
| Case 2 | 0.0041 | 0.0106 | 0.0073 | |
| 3, t = [200, 300]) | Case 1 | 0.0056 | 0.0043 | 0.0055 |
| Case 2 | 0.0042 | 0.0052 | 0.0074 |
| Axis | Case 1 [mNm] | Case 2 [mNm] |
|---|---|---|
| 1161.70 | 811.58 | |
| 279.40 | 138.41 | |
| 1008.60 | 503.61 |
| Scenario | Method | Mean [mNm] | Mean [mNm] | Mean [mNm] |
|---|---|---|---|---|
| 1, t = [0, 100] | Case 1 | 142.76 | 30.80 | 116.44 |
| Case 2 | 135.42 | 30.75 | 105.70 | |
| 2, t = [100, 200] | Case 1 | 121.13 | 54.22 | 106.78 |
| Case 2 | 122.28 | 54.38 | 106.20 | |
| 3, t = [200, 300] | Case 1 | 128.12 | 37.46 | 118.54 |
| Case 2 | 127.14 | 36.61 | 119.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, S. Adaptive Learning Gain-Based Robust Attitude Control for Satellites with Time-Varying External Disturbances. Electronics 2025, 14, 3298. https://doi.org/10.3390/electronics14163298
You S. Adaptive Learning Gain-Based Robust Attitude Control for Satellites with Time-Varying External Disturbances. Electronics. 2025; 14(16):3298. https://doi.org/10.3390/electronics14163298
Chicago/Turabian StyleYou, Sesun. 2025. "Adaptive Learning Gain-Based Robust Attitude Control for Satellites with Time-Varying External Disturbances" Electronics 14, no. 16: 3298. https://doi.org/10.3390/electronics14163298
APA StyleYou, S. (2025). Adaptive Learning Gain-Based Robust Attitude Control for Satellites with Time-Varying External Disturbances. Electronics, 14(16), 3298. https://doi.org/10.3390/electronics14163298






