Abstract
This paper presents a blind source separation (BSS)-based framework for joint communication and sensing (JCAS) in in-band full-duplex (IBFD) multiple-input multiple-output (MIMO) systems operating under time-varying channel conditions. Conventionally, self-interference (SI) in IBFD systems is a major obstacle to recovering the signal of interest (SOI). Under the JCAS paradigm, however, this high-power SI signal presents an opportunity for efficient sensing. Since each transceiver node has access to the original SI signal, its environmental reflections can be exploited to estimate channel conditions and detect changes, without requiring dedicated radar waveforms. We propose a blind source separation (BSS)-based framework to simultaneously perform self-interference cancellation (SIC) and extract sensing information in IBFD MIMO settings. The approach applies the Fast Independent Component Analysis (FastICA) algorithm in dynamic scenarios to separate the SI and SOI signals while enabling simultaneous signal recovery and channel estimation. Simulation results quantify the trade-off between estimation accuracy and channel dynamics, demonstrating that while FastICA is effective, its performance is fundamentally limited by a frame size optimized for the rate of channel variation. Specifically, in static channels, the signal-to-residual-error ratio (SRER) exceeds 22 dB with 500-symbol frames, whereas for moderately time-varying channels, performance degrades significantly for frames longer than 150 symbols, with SRER dropping below 4 dB.
1. Introduction
The relentless growth of mobile data traffic and the expansion into millimeter-wave (mmWave) frequencies demand transformative advances in wireless technology to overcome spectrum scarcity [1,2]. In-band full-duplex (IBFD) communication is a highly promising technique for enhancing spectral efficiency, as it allows a transceiver to transmit and receive simultaneously on the same frequency band [3,4]. However, the primary obstacle in realizing IBFD systems is the powerful self-interference (SI) signal, i.e., the leakage from the node’s own transmitter into its receiver, which can be orders of magnitude stronger than the desired signal of interest (SOI) from a remote user.
Conventionally viewed as a detriment, SI finds a novel purpose within the emerging paradigm of joint communication and sensing (JCAS) [5]. The JCAS framework reinterprets the high-power SI signal as an invaluable “signal of opportunity” for environmental sensing. This dual-functionality is critical for next-generation applications, such as autonomous vehicle navigation, smart city infrastructure, and indoor localization, where real-time environmental awareness is as important as high-speed data links [6]. Since the waveform of the SI signal is perfectly known to the transceiver, its reflections off surrounding objects can be exploited to estimate the radio channel, detect environmental changes, and perform radar-like functions without needing dedicated sensing waveforms or hardware (e.g., see [6,7,8,9,10] and the references therein). This dual use of the radio signal promises to significantly improve resource utilization, efficiency, and system functionality.
To realize this dual functionality, the receiver must effectively separate the SOI from the SI and other signals. Blind source separation (BSS) techniques [11], particularly Independent Component Analysis (ICA) [12], are well suited for this task. BSS algorithms can distinguish and separate signals based on their statistical properties, such as statistical independence, making them ideal for untangling the SOI and the reflected SI components in a complex received signal mixture.
1.1. Related Work
The concept of using BSS for signal separation in communication systems is well established. Prior work has explored BSS for various JCAS and full-duplex applications, demonstrating its potential in managing overlapping signals and extracting valuable information [13]. In particular, a sparsity-enhanced source separation scheme is proposed in [14] to mitigate aliasing in joint communication and radar scenarios. Fouda et al. [15] further explored the design of BSS architectures tailored for full-duplex systems, emphasizing the challenges associated with maintaining computational efficiency while managing strong SI signals. Barneto [16] provides insights into waveform and hardware integration strategies, offering a foundational understanding of signal co-design in cellular JCAS systems.
1.2. Contributions
However, these studies primarily assume a stationary or quasi-stationary channel environment. Our work distinguishes itself by explicitly investigating the performance degradation of a BSS-based JCAS framework under continuously time-varying channel conditions. While some adaptive BSS techniques exist [17,18], the performance of the widely used and computationally efficient FastICA algorithm in such dynamic JCAS scenarios has not been systematically quantified. The primary objective of this paper is not to benchmark different BSS algorithms against one another but rather to examine the feasibility and performance implications of applying a BSS-based framework to the integrated communication and sensing scenario in time-varying IBFD MIMO systems. Our key contributions are the following:
- We model a JCAS system where the known SI signal is used for sensing in a time-varying environment.
- We systematically evaluate the system’s sensing (ELMMSE) and communication (SRER) performance as a function of frame size and the rate of channel variation.
- We identify and analyze the fundamental trade-off between statistical reliability (favoring longer frames) and channel stationarity (favoring shorter frames), revealing an optimal frame size that is dependent on channel dynamics.
1.3. Paper Organization
The remainder of this paper is organized as follows. Section 2 introduces the system model for IBFD MIMO with time-varying channels. Section 3 describes the BSS-based channel estimation framework using FastICA. Section 4 presents the simulation setup and analyzes the performance under various channel dynamics. Section 5 concludes this work and outlines future research directions.
1.4. Notations
We use to represent the expectation of the random variable X. Bold letters denote vectors or matrices. represents the Frobenius norm. denotes the Gaussian distribution with mean and variance . represents a generic matrix with n rows and m columns. denotes transpose operation.
2. System Model
As illustrated in Figure 1, we consider an IBFD MIMO system comprising two transceiver nodes, each equipped with n transmit antennas and m receive antennas. Both nodes simultaneously transmit and receive signals over the same frequency band, enabling full-duplex communication. The received signal at each node is composed of multiple components: (1) the SOI, which includes both direct-path and reflected components from the remote node, and (2) the SI signal, which includes direct leakage between the local transmit and receive antennas and reflections from the environment. Unlike conventional channel models developed solely for communication systems (e.g., 3GPP TR 38.901 [19], WINNER II [20], COST 2100 [21]), our framework explicitly incorporates both direct and reflected SI components alongside the SOI. Non-JCAS models typically do not model the loopback SI path created by in-band full-duplex operation, nor do they account for environmental reflections of SI that are crucial for sensing functionality.
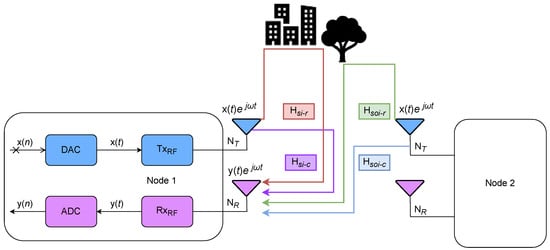
Figure 1.
IBFD MIMO system model with self-interference and environmental reflections.
Crucially, in this work, we consider the impact of time-varying channel conditions, which are characteristic of many realistic wireless environments. The channel properties, including amplitude and phase responses, can change over time due to factors such as user mobility, changes in the environment, and multipath fading. Let denote the time-domain received signal at the l-th receive antenna at time k. It is expressed as
Here, is the additive Gaussian noise. For each node at time k, and are the direct SI and SOI channels, respectively; and denote the reflected channels at the i-th transmit antenna; and and are the SI and SOI signals from the i-th transmit antenna, respectively. Each channel, now explicitly represented as a function of time k, is assumed to have independent, identically distributed (i.i.d.) entries for a given time instant. For convenience, we can rewrite the equation in matrix form at time k as follows:
where , , and . In our model, the channels are explicitly time-dependent. We assume that the direct SI channel, , is relatively stable or can be accurately calibrated, as it corresponds to the fixed geometry of the transceiver hardware. In contrast, the reflected channels, and , are stochastic and time-varying, capturing the dynamic nature of the propagation environment due to mobility and scattering. Note that is the transmitted signal from the same node at time k, implying that is known to the receiver. The direct self-interference channel is also generally known to the receiver and remains relatively stable compared to the reflected channels, although it can still exhibit some time dependency.
We can further rewrite (2) in a form that resembles a canonical BSS model at time k:
where is a composite mixing matrix at time k, defined as
and being the identity matrix of size . Equation (3) represents a key step in our framework. By stacking the known transmitted SI signal with the received signal , we create an augmented observation vector. This transforms the problem into a canonical BSS form where the “sources” are the SI and SOI signals, and the “mixing matrix” contains the channel parameters we wish to estimate. Crucially, because is known, it can serve as a reference signal, anchoring the BSS algorithm and helping to resolve ambiguities in the separation progress, thereby enabling the estimation of both the unknown channel and the unknown signal .
3. BSS-Based Channel Estimation
We now describe the application of the FastICA algorithm [12] to separate the SI and SOI components from the observed signals. For simplicity, we assume , meaning each node has an equal number of transmit and receive antennas. We treat the sum in (6) as the overall channel coefficient of the SOI. The goal is two-fold: (1) to estimate the unknown communication signal for data recovery and (2) to estimate the reflected SI channel for environmental sensing.
3.1. Blind Source Separation for Sensing
The ICA algorithm is founded on the principle that many mixed signals are linear combinations of underlying source signals that are mutually statistically independent and non-Gaussian. In our model, the transmitted BPSK signals are non-Gaussian, satisfying this core requirement. The goal of ICA is to find a linear transformation (an “unmixing” matrix) that, when applied to the observed mixtures, maximizes the statistical independence of the outputs. This process allows us to recover the original source signals, or scaled versions of them. In particular, the FastICA algorithm exploits non-Gaussianity in the received signal mixture to estimate the independent source components iteratively. The algorithm follows the following key steps:
- Preprocessing: The received signal matrix is first centered by subtracting its mean. Then, it is “whitened” using a technique like eigenvalue decomposition. Whitening is a linear transformation that removes any second-order correlations in the data, forcing the components to be uncorrelated and have unit variance. This simplifies the problem for the ICA algorithm, as the unknown mixing matrix is transformed into an orthogonal matrix, reducing the search space and improving convergence speed. It is important to note that for whitening to be effective, the number of samples (i.e., the frame size) must be sufficiently large relative to the number of signal dimensions to allow for the robust estimation of the covariance matrix. In highly dynamic environments, this requirement conflicts with the need for short frames to ensure channel stationarity, establishing a fundamental performance trade-off that we investigate in this paper.
- Iterative Estimation: FastICA iteratively estimates the columns of the unmixing matrix by maximizing a measure of non-Gaussianity called negentropy, i.e., , where G is a non-quadratic function, y is the estimated source, and v is a Gaussian variable with the same variance as y. Negentropy is always non-negative and is zero only for a Gaussian distribution. Therefore, maximizing it drives the estimated source y away from Gaussianity and towards one of the independent source components. For computational simplicity, FastICA maximizes approximations of negentropy using non-quadratic functions such as and .
- Source Recovery: Estimate the unknown channel and signal from the separated components using the known SI signal as a reference. The FastICA update rule for extracing one independent component iswhere is the whitened data, g is the derivative of G, and is normalized after each iteration.
3.2. Performance Metrics
We evaluate the quality of channel estimation using the ergodic linear minimum mean squared error (ELMMSE), which quantifies the average estimation error of the sensed channel:
The communication performance is quantified via the signal-to-residual-error ratio (SRER) of the extracted communication signal:
A higher SRER implies more effective signal separation and cleaner communication signal extraction, directly reflecting the system’s communication performance under the JCAS paradigm. Additionally, we can assess the ELMMSE of the overall SOI channel as
which accounts for both the direct transmission channel between the transmitter and receiver, as well as the reflected and scattered components from the surrounding environment. This channel state information can be leveraged to optimize the transmission schemes (e.g., precoder design in MIMO systems) and to maximize the signal-to-interference-plus-noise ratio (SINR), as follows:
In Section 4, we will also track the number of iterations required for the ICA algorithm to converge, which provides insights into the computational complexity and algorithmic efficiency of the proposed BSS approach under different signal block sizes and channel dynamics.
4. Simulation and Discussion
4.1. Simulation Setup
In this section, we evaluate the sensing and communication performance of the proposed system through numerical simulations based on a practical system model. Each node is equipped with two antennas. The reflected channel is modeled as a Rician channel with , where x is the Rician factor and y is the average channel power. This is because the SI signal reflects off objects near the transceiver, creating a scenario with a dominant line-of-sight (LOS) path alongside multipath components, for which the Rician distribution is the standard model. In contrast, the overall communication channel is modeled as Rayleigh-distributed. This represents a rich, scattering, non-LOS propagation environment, which is typical for communication between two separate nodes in urban settings where obstacles are common, which is consistent with 3GPP TR 38.901 urban microcell assumptions [19]. Our simplified model preserves these key statistical properties while reducing complexity, making it suitable for algorithm-level evaluations of BSS-based JCAS without introducing excessive simulation overhead.
The transmitted signals and are BPSK-modulated, with each symbol randomly chosen from . BPSK is chosen for its simplicity and non-Gaussian nature, which is a prerequisite for ICA, making it an ideal starting point for this analysis. The combined source matrix is defined as , where N denotes the frame size (signal processing block length). The received signal is generated by linearly mixing the source signals through the corresponding channel matrices and adding a Gaussian noise of (20 dB SNR).
To model time-varying channels, and , are initialized once and then linearly perturbed at each time frame. The chosen simulation values for channel variation () and frame size were selected to systematically demonstrate the core trade-off between statistical reliability and channel stationarity in the proposed system. We test three time variation speeds corresponding to = 0, 0.0005, 0.001, where represents an ideal, unchanging channel, and and are selected to model realistic, dynamic mobile environments. The static channel serves as a crucial performance benchmark, showing how the FastICA algorithm performs when its core assumption of a stationary environment is perfectly met. This baseline allows for isolating performance limitations of the algorithm itself versus those caused by channel dynamics. In contrast, the non-zero small variation factors are chosen to be low enough to prevent immediate algorithm failure yet sufficiently high to introduce measurable degradation as the frame size increases. This design clearly demonstrates the existence of an optimal frame size that balances statistical reliability with the rate of channel variation. For each time frame (where is the number of frames), the time-varying channels are computed as
Since the mixing matrix is continuously changing with time, we consider the midpoint mixing matrix for evaluation, as follows:
In cases where the mixing matrix varies sporadically over time, the average mixing matrix offers a more stable approximation than using a single midpoint. The average composite mixing matrix is defined as
The estimated mixing matrix is post-processed via column permutation to resolve inherent ICA ambiguities. The range of frame sizes (50 to 500 symbols) is selected to effectively capture and display the system’s performance across different processing block lengths. The lower bound of 50 tests the system under conditions of limited statistical data, where performance is expected to be poor. The upper bound of 500 is large enough to achieve high performance in a static channel, demonstrating the benefit of having more data when the environment is stable. The step size of 50 provides enough data points to plot a smooth and clear performance curve, allowing for easy visualization of the performance trends and the identification of the optimal frame size regions.
4.2. Simulation Results
Figure 2, Figure 3, Figure 4 and Figure 5 illustrate the system’s performance as a function of frame size under three different time variation speeds. The time variation speeds , , and correspond to static, slowly time-varying, and moderately time-varying channel conditions, respectively. These plots evaluate how well the proposed FastICA-based joint communication and sensing framework performs as the rate of channel change increases.
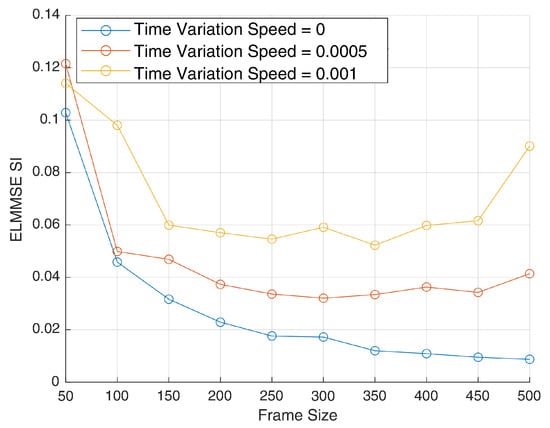
Figure 2.
ELMMSE of channel sensing vs. frame size.
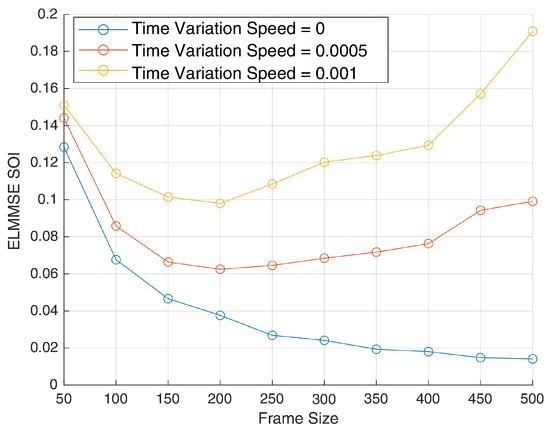
Figure 3.
ELMMSE of channel sensing vs. frame size.
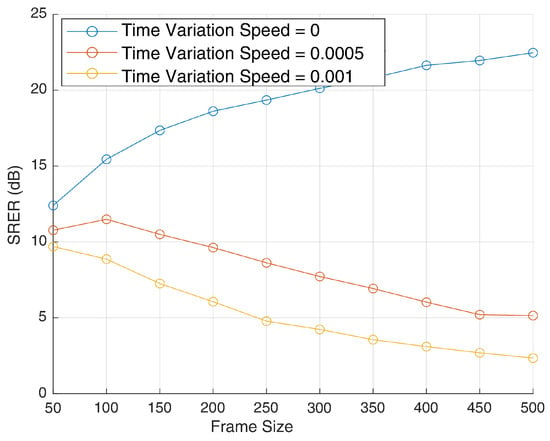
Figure 4.
SRER for SOI in dB vs. frame size.
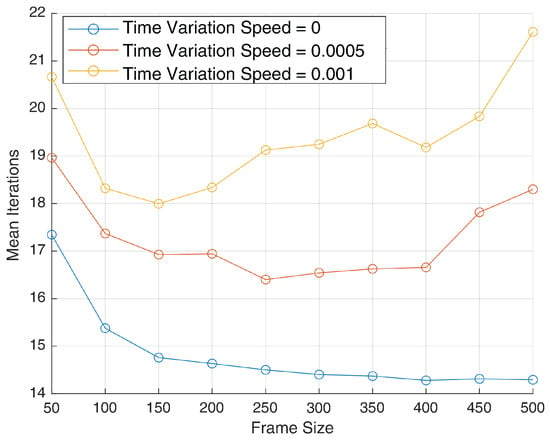
Figure 5.
Number of FastICA iterations required for convergence vs. frame size.
Figure 2 shows the evolution of the ELMMSE for the SI reflection channel across varying frame sizes. In the static case (i.e., ), the estimation error decreases steadily with increasing frame length, reaching approximately 0.01 at 500 symbols. This improvement occurs because longer frames provide more statistical information for the ICA algorithm to exploit. However, for time-varying channels, the behavior is noticeably different. The slowly varying case () shows optimal performance around 200–250 frames, after which the error begins to increase. The moderately varying case () exhibits even more pronounced degradation, with optimal performance occurring around 150 frames. This degradation occurs because the average composite mixing matrix becomes less representative of any individual time frame as the channel varies more significantly over the processing block.
A similar trend is observed in Figure 3, which shows the ELMMSE for the SOI channel . The estimation error decreases rapidly for small-to-moderate frame sizes across all variation speeds but begins to degrade when the channel varies too quickly within a block. In particular, the curve for demonstrates increasing error beyond 200–250 frames, highlighting the fundamental limitation of using batch ICA methods in dynamic environments. The SOI channel estimation appears more sensitive to time variations than the SI channel, likely due to the lack of prior knowledge about the SOI signal structure.
Figure 4 displays the SRER in decibels, which quantifies the quality of the recovered communication signal. The static case () shows a consistent increase in SRER with frame size, reaching over 22 dB by 500 symbols. However, in time-varying scenarios, performance peaks early and then degrades significantly. For , the SRER begins to decline beyond 200 frames, while for , the degradation starts even earlier (around 150 frames) and is more severe, dropping below 4 dB. These results show that while longer frames improve statistical estimation in principle, they also introduce greater inconsistency between the assumed and actual mixing behavior, leading to poorer separation outcomes in dynamic channels.
Figure 5 depicts the average number of iterations required by the FastICA algorithm to converge. In the static case, iteration count decreases from about 15 at small frame sizes to approximately 14 at larger frame sizes, indicating improved convergence efficiency with more data. However, for time-varying cases, convergence behavior is different. The slowly varying case () maintains relatively stable iteration counts around 17–18. The moderately varying case shows the most challenging convergence behavior, requiring over 21 iterations at 500 symbols. The increased convergence time reflects the algorithm’s difficulty in finding a consistent separation solution when the underlying mixing matrix is changing during the processing block.
4.3. Discussion and Insights
The simulation results reveal several important insights for the JCAS system’s design in time-varying environments. A critical trade-off exists for the optimal frame size, which must balance statistical reliability with channel stationarity. For slowly varying channels (), this optimum is around 200–250 symbols, whereas for faster variations (), it shifts to 150–200 symbols, meaning system designers must select frame sizes based on expected channel dynamics. This performance degradation stems from the mismatch between the block-based assumption of FastICA and the continuous evolution of the channel. As the frame size increases, this mismatch becomes more pronounced, leading to errors in both channel estimation and signal separation. Notably, the SOI channel estimation and signal recovery appear more sensitive to time variations than the SI channel estimation, which suggests that leveraging the known SI signal provides some robustness in dynamic environments. Furthermore, the increased iteration count in these scenarios indicates not only convergence difficulties but also higher computational requirements that must be considered for real-time implementation. Ultimately, these results demonstrate the limitations of traditional FastICA for time-varying channels and motivate the development of adaptive BSS algorithms capable of tracking such variations continuously.
5. Conclusions and Future Work
In this work, we proposed and evaluated a blind source separation (BSS)-enabled framework for joint communication and sensing (JCAS) in in-band full-duplex (IBFD) MIMO systems. By exploiting the known self-interference (SI) signal, we demonstrated how it can be repurposed for environmental sensing without requiring dedicated sensing waveforms. The system was formulated as a BSS problem and solved using the FastICA algorithm to achieve simultaneous SI suppression and channel estimation. Through extensive simulations under static and time-varying channel conditions, we evaluated the performance of the proposed framework using various metrics, including signal-to-residual-error ratio (SRER), ergodic linear minimum mean 124 squared error (ELMMSE) for both signal of interest (SOI) and SI channels, and convergence behavior of FastICA. Our results indicate that in static channels (), longer frame sizes consistently improve separation and estimation performance, with SRER exceeding 22 dB at 500-symbol frames and ELMMSE approaching 0.01. However, under time-varying conditions ( and ), performance degrades beyond certain optimal frame lengths. This degradation is due to the mismatch between the assumed stationary mixing matrix and the actual evolving one, which hampers both separation accuracy and algorithm convergence.
The average number of iterations required for convergence also increases significantly in highly dynamic channels, particularly for , highlighting the limitations of conventional FastICA in such settings.
To further enhance the practicality and robustness of the proposed JCAS framework, future research directions include the following:
- Hardware Implementation Considerations: As full-duplex JCAS systems move toward practical deployment, addressing implementation challenges such as I/Q imbalance, phase noise, and nonlinear distortions in the BSS framework becomes crucial.
- Dynamic Frame Size Adaptation: Developing reinforcement learning-based strategies that dynamically adjust processing block lengths based on real-time channel variation estimates could optimize the trade-off between statistical reliability and channel stationarity.
- Multi-User Scenarios: Extending the framework to multi-user MIMO scenarios where multiple communication pairs share the same spectrum while performing distributed sensing presents both theoretical and practical challenges worth exploring.
- Machine Learning Integration: Following recent trends in wireless communications, integrating deep learning approaches such as complex time-domain dilated convolutional recurrent networks could provide superior adaptation to time-varying channels while maintaining reasonable computational complexity.
Overall, the integration of adaptive intelligence and advanced BSS techniques holds significant promise for realizing spectrally efficient, environment-aware wireless networks. As 5G-Advanced and 6G standardization efforts progress, these technologies will play a crucial role in enabling applications ranging from autonomous vehicles to smart city infrastructure.
Author Contributions
Conceptualization, S.L. and T.Y.; methodology, S.L. and T.Y.; software, C.P.; validation, C.P., S.L. and T.Y.; formal analysis, C.P., S.L. and T.Y.; investigation, C.P.; data curation, C.P.; writing—original draft preparation, S.L. and C.P.; writing—review and editing, C.P., S.L. and T.Y.; visualization, C.P.; supervision, S.L. and T.Y.; project administration, S.L. and T.Y.; funding acquisition, S.L. and T.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Embry-Riddle Aeronautical University Internal Faculty Seed Fund (4.04) from The Boeing Center for Aviation and Aerospace Safety (BCAAS).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| MIMO | Multiple-Input Multiple-Output |
| IBFD | In-Band Full Duplex |
| BSS | Blind Source Separation |
| ICA | Independent Component Analysis |
| JCAS | Joint Communication and Sensing |
| SI | Self-Interference |
| SOI | Signal of Interest |
| ELMMSE | Ergodic Linear Minimum Mean Squared Error |
| SRER | Signal-to-Residual-Error Ratio |
| SINR | Signal-to-Interference-Plus-Noise Ratio |
References
- Heath, R.W.; Gonzalez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An overview of signal processing techniques for millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Belgium Completes 5G Spectrum Auction. Available online: https://www.rcrwireless.com/20220725/featured/belgium-completes-final-phase-spectrum-auction (accessed on 19 June 2025).
- Kolodziej, K.E. In-Band Full-Duplex Wireless Systems Handbook; Artech House: Norwood, MA, USA, 2021. [Google Scholar]
- Alves, H.; Riihonen, T.; Suraweera, H.A. Full-Duplex Communications for Future Wireless Networks; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Smida, B.; Alexandropoulos, G.C.; Riihonen, T.; Islam, M.A. In-band full-duplex MIMO systems for simultaneous communications and sensing: Challenges, methods, and future perspectives. arXiv 2024, arXiv:2410.06512. [Google Scholar]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rahman, M.L.; Wu, K.; Huang, X.; Guo, Y.J.; Chen, S.; Yuan, J. Enabling joint communication and radar sensing in mobile networks—A survey. IEEE Commun. Surv. Tutor. 2022, 24, 306–345. [Google Scholar] [CrossRef]
- Fang, X.; Feng, W.; Chen, Y.; Ge, N.; Zhang, Y. Joint communication and sensing toward 6G: Models and potential of using MIMO. IEEE Internet Things J. 2023, 10, 4093–4116. [Google Scholar] [CrossRef]
- Li, S.; Caire, G. On the capacity and state estimation error of “beam-pointing” channels: The binary case. IEEE Trans. Inf. Theory 2023, 69, 5752–5770. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Kobayashi, M.; Wigger, M.; Caire, G. An information-theoretic approach to joint sensing and communication. IEEE Trans. Inf. Theory 2024, 70, 1124–1146. [Google Scholar] [CrossRef]
- Cardoso, J.-F. Blind signal separation: Statistical principles. Proc. IEEE 1998, 86, 2009–2025. [Google Scholar] [CrossRef]
- Bingham, E.; Hyvärinen, A. A fast fixed-point algorithm for independent component analysis of complex valued signals. Int. J. Neural Syst. 2000, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Li, C.; Zhu, L. A comprehensive survey on blind source separation for wireless adaptive processing: Principles, perspectives, challenges and new research directions. IEEE Access 2018, 6, 66685–66708. [Google Scholar] [CrossRef]
- Jin, B.; Sun, J.; Ye, P.; Zhou, F.; Lim, H.; Wu, Q.; Al-Dhahir, N. Data-driven sparsity-based source separation of the aliasing signal for joint communication and radar systems. IEEE Trans. Veh. Technol. 2023, 72, 2161–2174. [Google Scholar] [CrossRef]
- Fouda, M.E.; Shen, C.-A.; Eltawil, A.E. Blind source separation for full-duplex systems: Potential and challenges. IEEE Open J. Commun. Soc. 2021, 2, 1379–1389. [Google Scholar] [CrossRef]
- Baquero Barneto, C. Analysis and Design of Joint Communication and Sensing for Wireless Cellular Networks. Ph.D. Dissertation, Tampere University, Tampere, Finland, 2022. [Google Scholar]
- Li, J.; Zhang, H.; Zhang, J. Fast adaptive BSS algorithm for independent/dependent sources. IEEE Commun. Lett. 2016, 20, 2221–2224. [Google Scholar] [CrossRef]
- Thameri, M.; Abed-Meraim, K.; Belouchrani, A. New algorithms for adaptive BSS. In Proceedings of the 2012 11th International Conference on Information Science, Signal Processing and Their Applications (ISSPA), Montreal, QC, Canada, 2–5 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 590–594. [Google Scholar]
- Zhu, Q.; Wang, C.-X.; Hua, B.; Mao, K.; Jiang, S.; Yao, M. 3GPP TR 38.901 channel model. In The Wiley 5G Reference: The Essential 5G Reference Online; Wiley Press: Hoboken, NJ, USA, 2021; pp. 1–35. [Google Scholar]
- Kyösti, P.; Meinilä, J.; Hentilä, L.; Zhao, X.; Jämsä, T.; Schneider, C.; Narandzić, M.; Milojević, M.; Hong, A.; Ylitalo, J.; et al. IST-4-027756 WINNER II D1.1.2 V1.2 WINNER II Channel Models; WINNER II Consortium: Brussels, Belgium, 2007. [Google Scholar]
- Liu, L.; Oestges, C.; Poutanen, J.; Vainikainen, P.; Sarrazin, J.; Laitinen, M.; Costa, E.; Yin, X.; Wang, Y.; Kivinen, J.; et al. The COST 2100 MIMO channel model. IEEE Wirel. Commun. 2012, 19, 92–99. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).