Wavelet-Based Denoising Strategies for Non-Stationary Signals in Electrical Power Systems: An Optimization Perspective
Abstract
1. Introduction
- This is the first study to consist of a detailed study not only of medical but also of experimental PQD signals, exploring a vast parameter space through 4558 iterations.
- The proposed methodology demonstrates robustness in reference-based and reference-free signal processing scenarios.
- The algorithm was rigorously tested over a wide noise range (1–50 dB) by validating it with synthetically generated signals as well as specific benchmark signals from the literature, demonstrating a reliable performance even in high-noise environments.
- Experimental evaluations using PQD signals further substantiated the effectiveness of the method, highlighting its potential for practical applications.
2. Materials and Method
2.1. Wavelet-Based Denoising Techniques for Signal Processing
- 1.
- Transform: where denotes the DWT.
- 2.
- Thresholding: , where is a thresholding operator (e.g., soft, or hard).
- 3.
- Reconstruction: , yielding the denoised estimate.

2.2. Basic Denoising Procedure
2.3. Denoising Evaluation Metrics
2.4. Denoising Evaluation Test Signals
3. Proposed Denoising Optimization Method
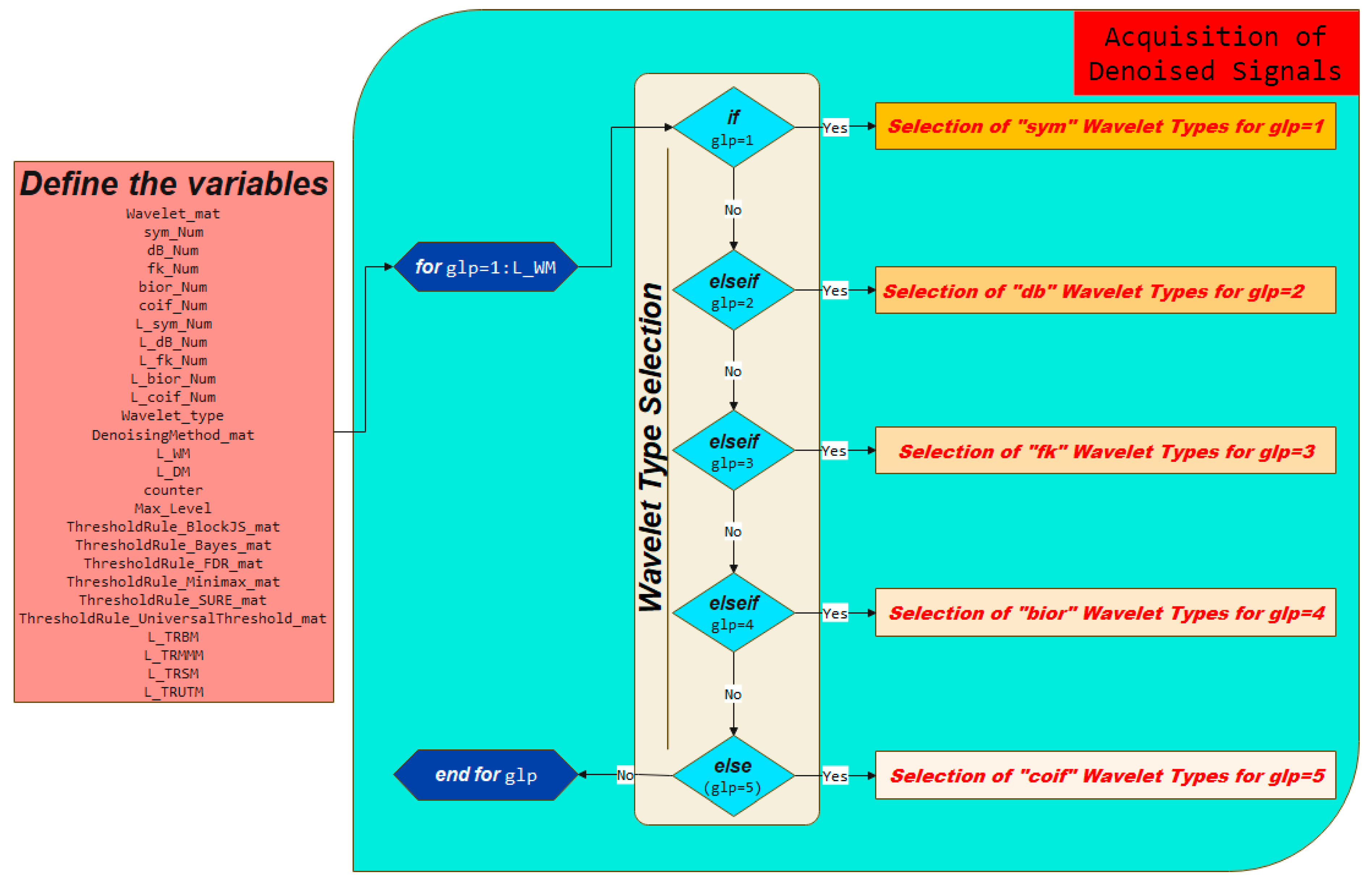
3.1. Defining Variables and Acquisition of Denoised Signals
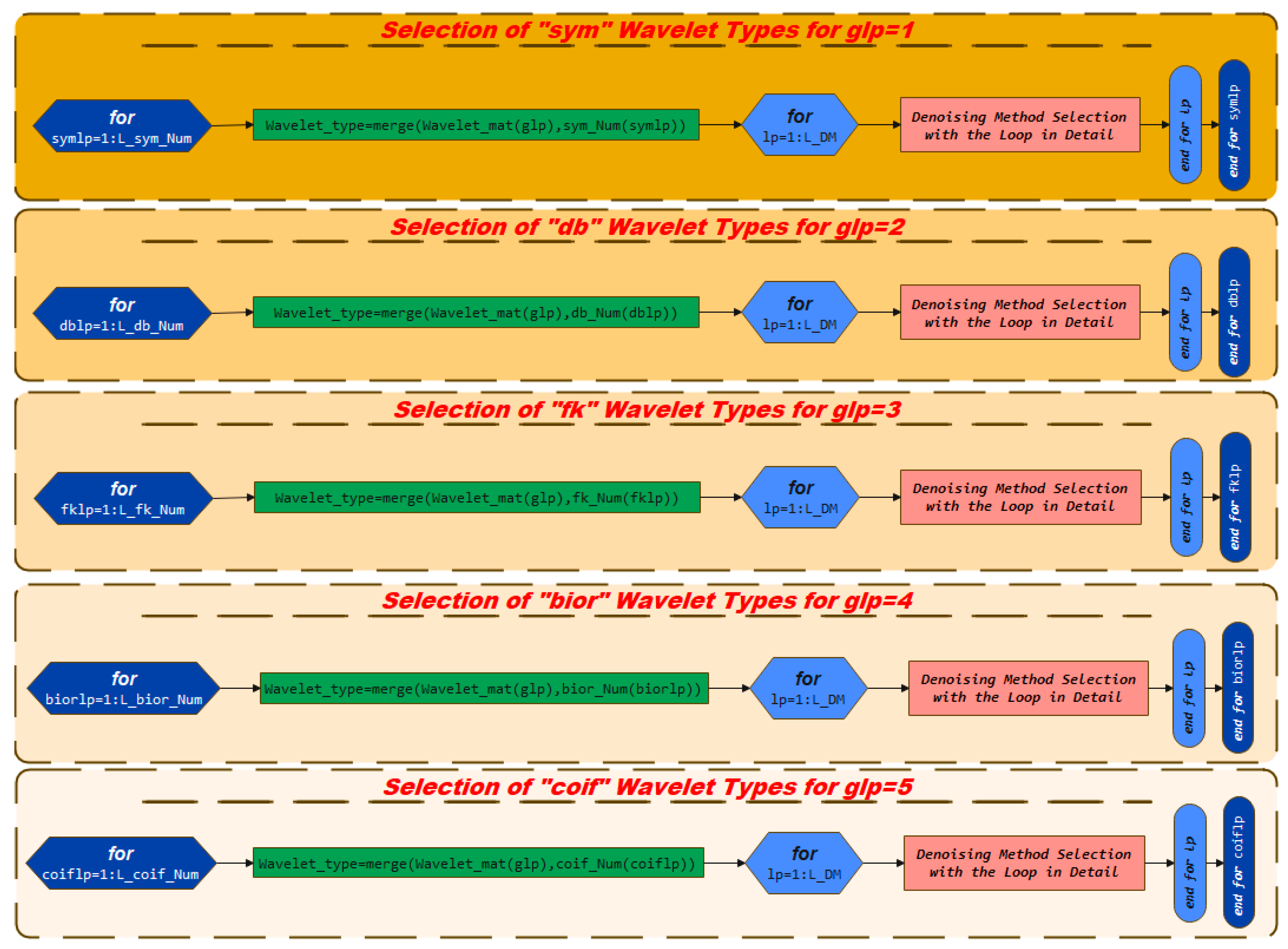
3.2. Selection of Wavelet Types
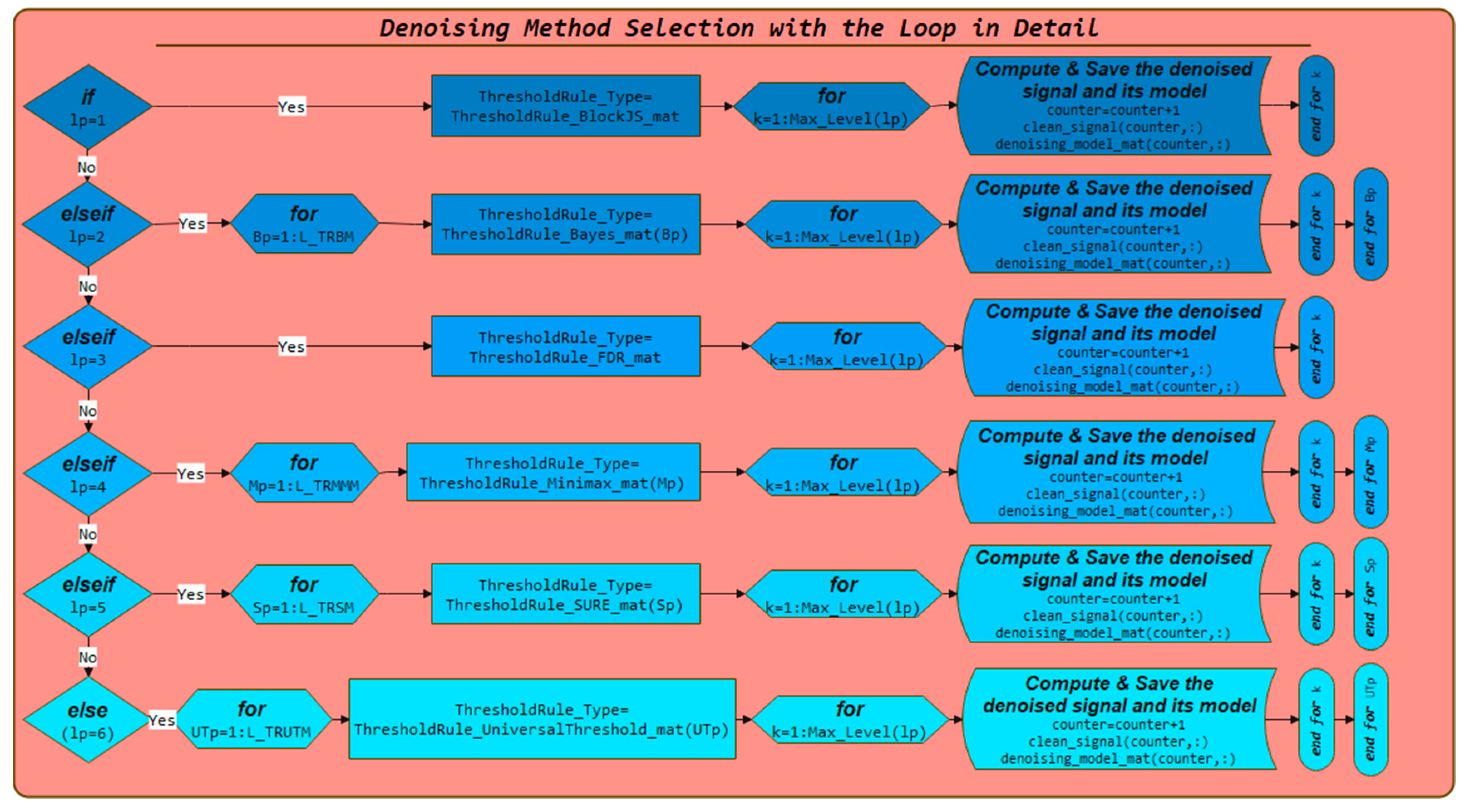
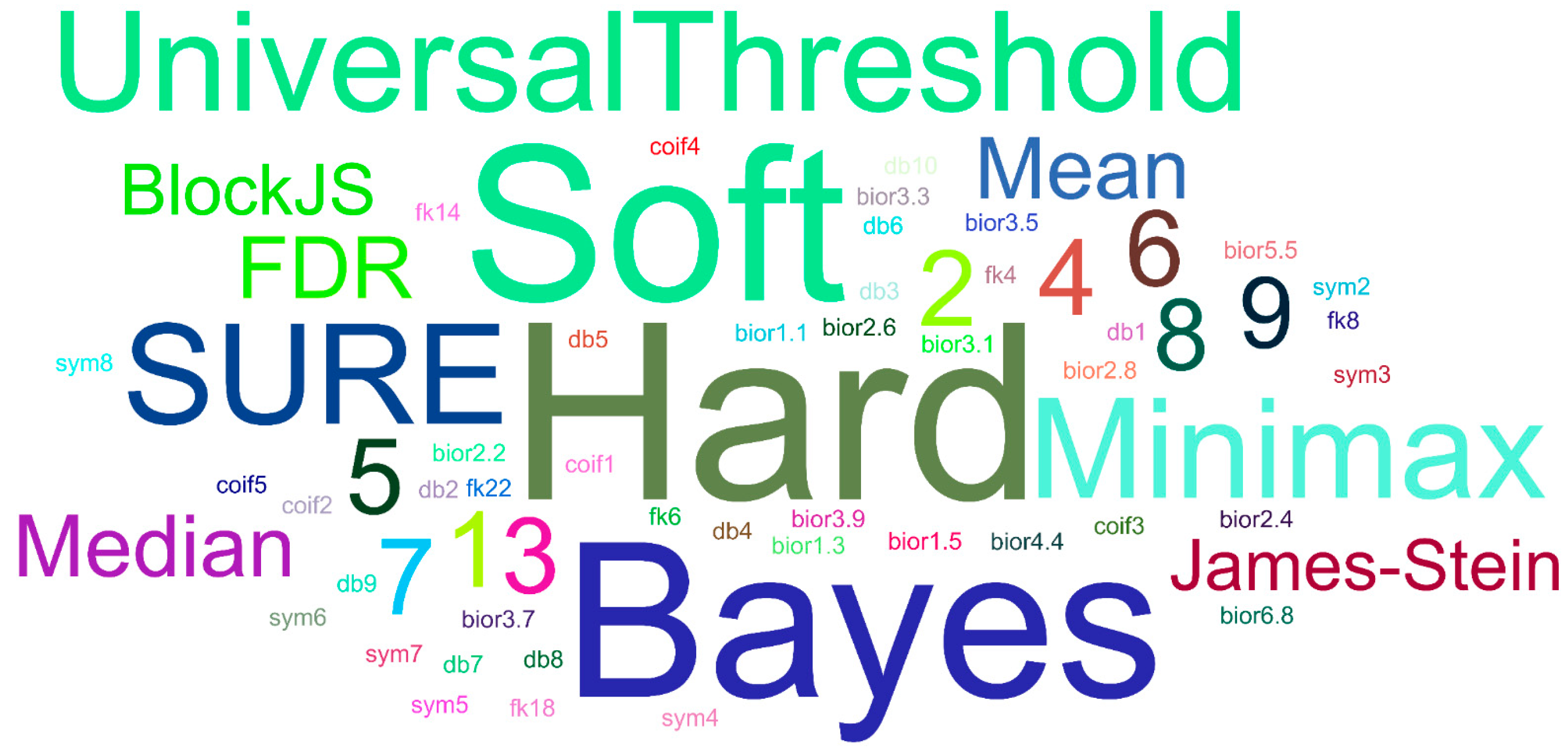
3.3. Denoising Model Selection with the Loop in Detail and Saving
- Appending the new name to the Wavelet_mat array (e.g., Wavelet_mat = [“sym”, …, “new_wlt”]),
- Defining its subtype range in a corresponding vector (like new_wlt_Num = [1,2,3]),
- The glp loop’s conditionals are extended to handle the new branch.
- Similarly, for new denoising methods, such as threshold-free neural filters or transformer-based denoisers, the following changes would suffice:
- Add the new method to DenoisingMethod_mat,
- Define a new threshold rule matrix (if applicable), such as ThresholdRule_DL_mat = [“Soft”, “Hard”, “Learned”],
- Include a maximum decomposition level entry in Max_Level,
- Extend the corresponding loop bounds or switch-case logic if necessary.
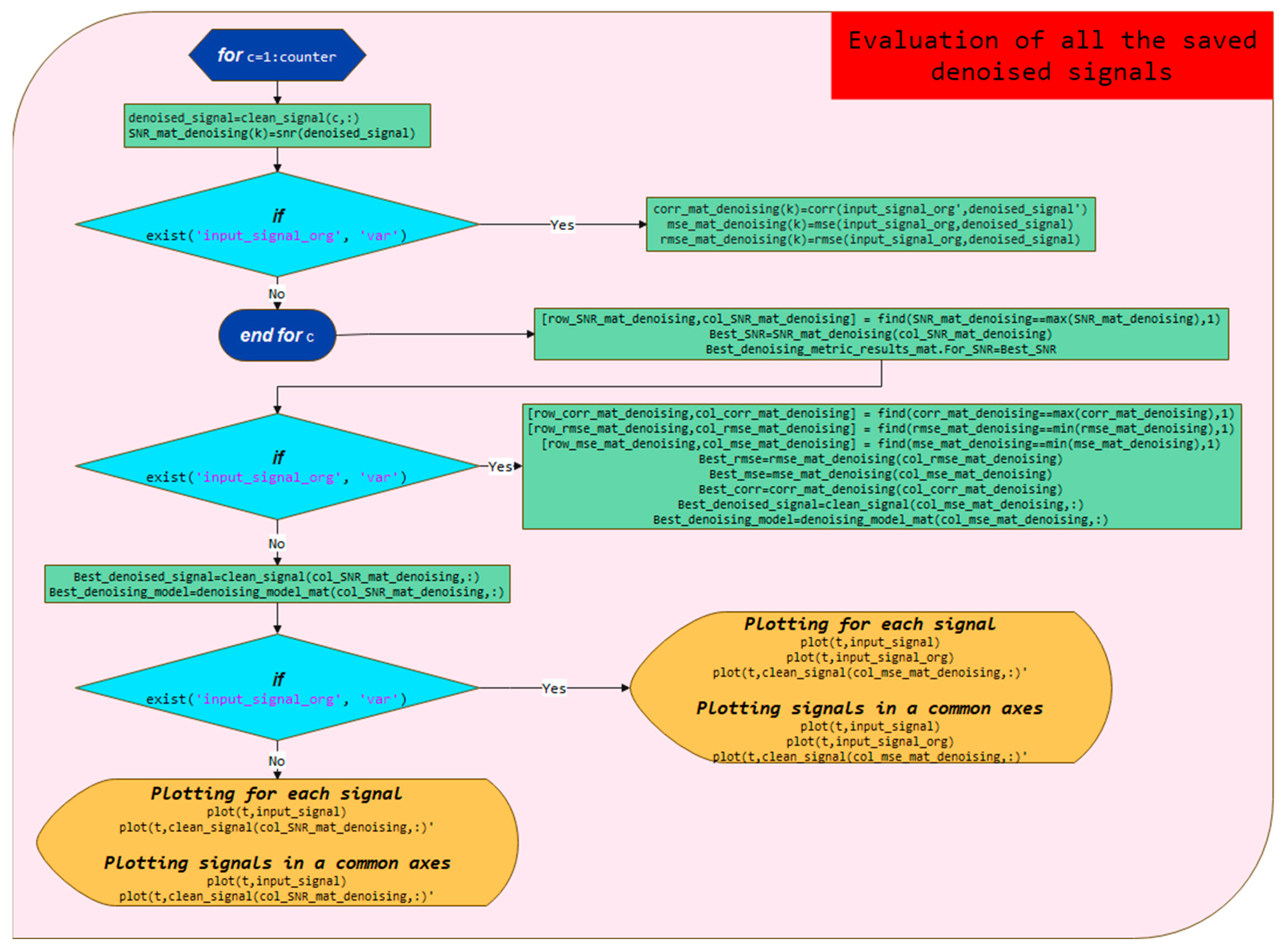
3.4. Evaluation of All the Saved Denoised Signals
4. Results and Discussion
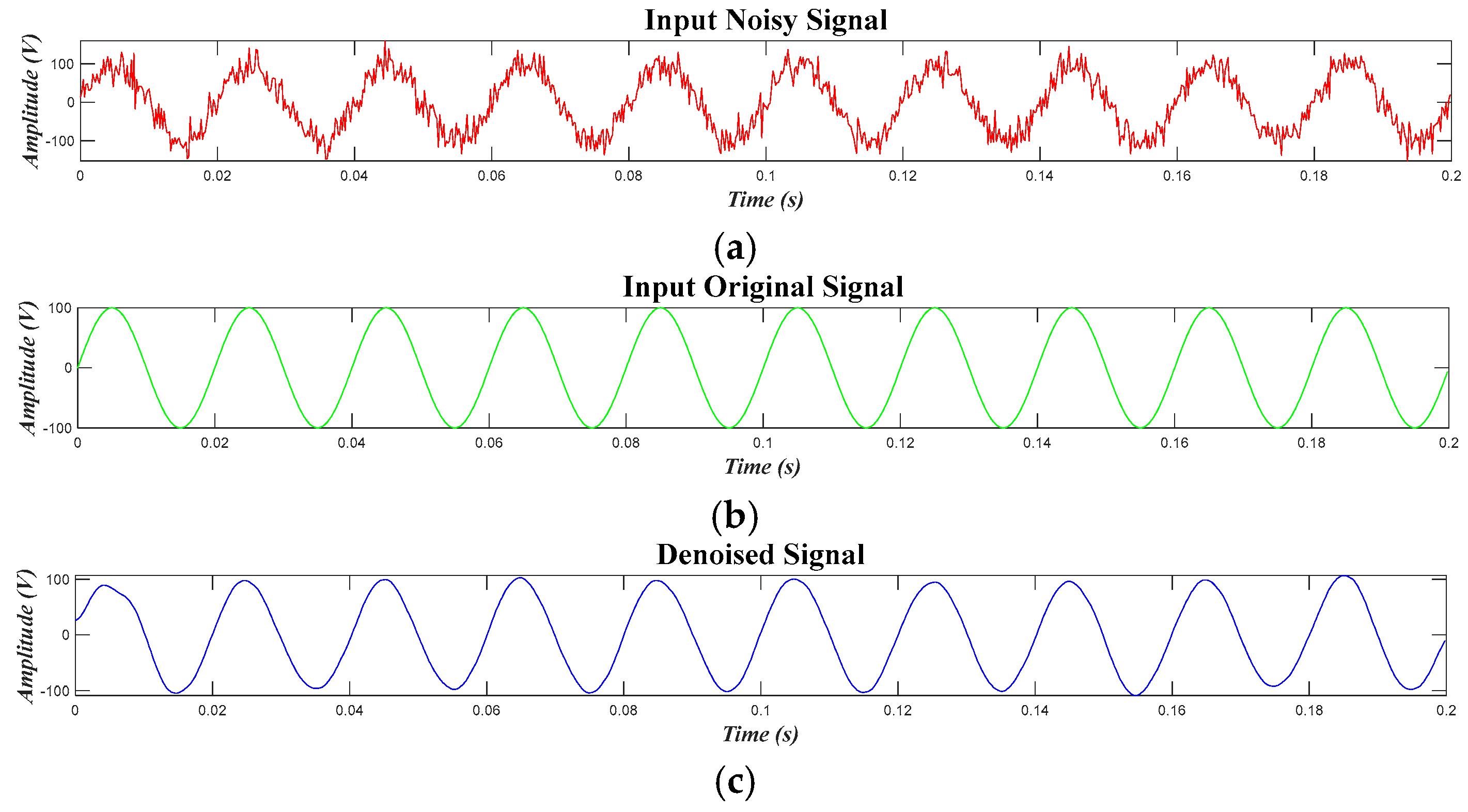
4.1. Results for the Pure Signal, in the Case of the Original Signal
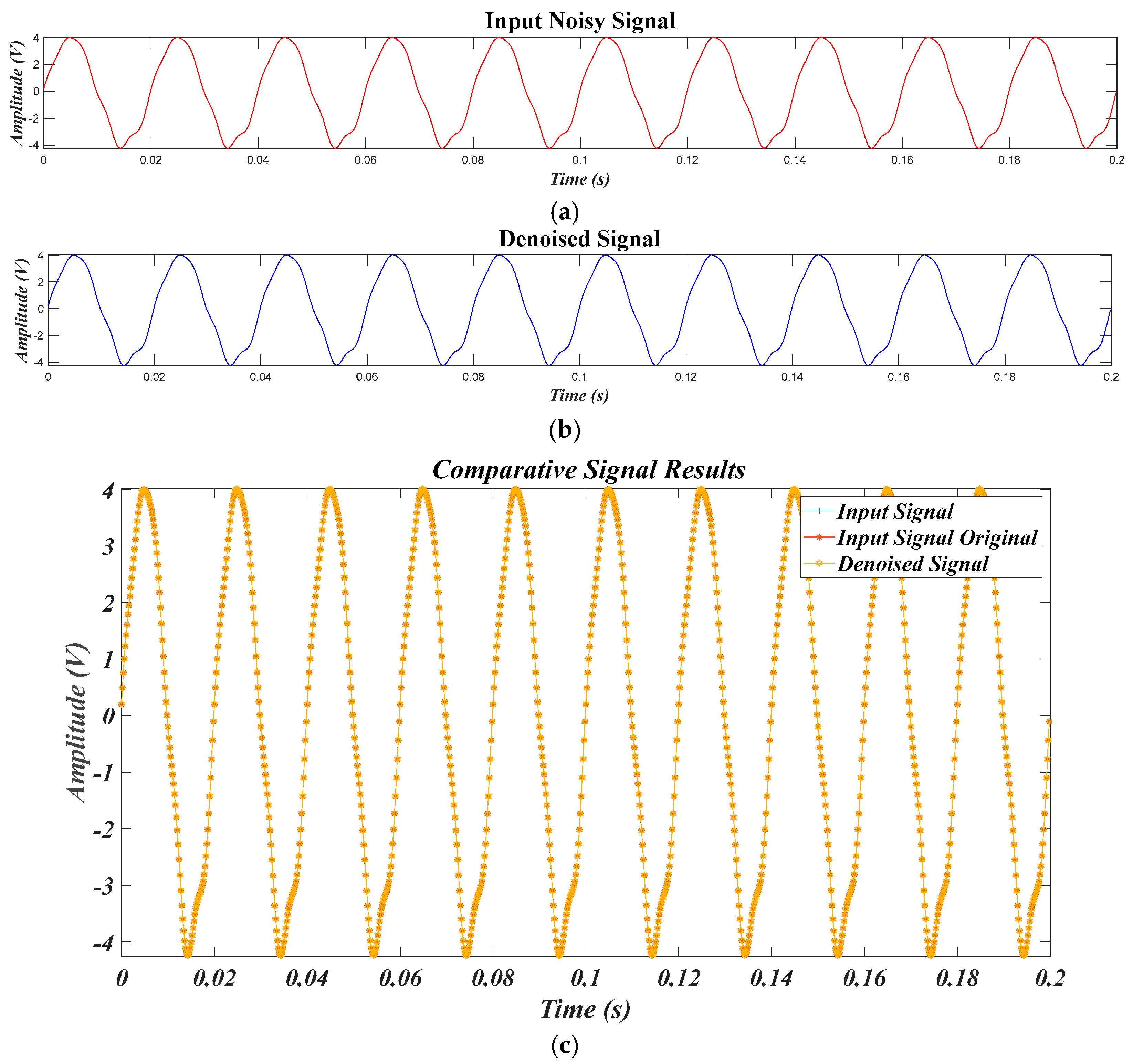
4.2. Results of Test Signals
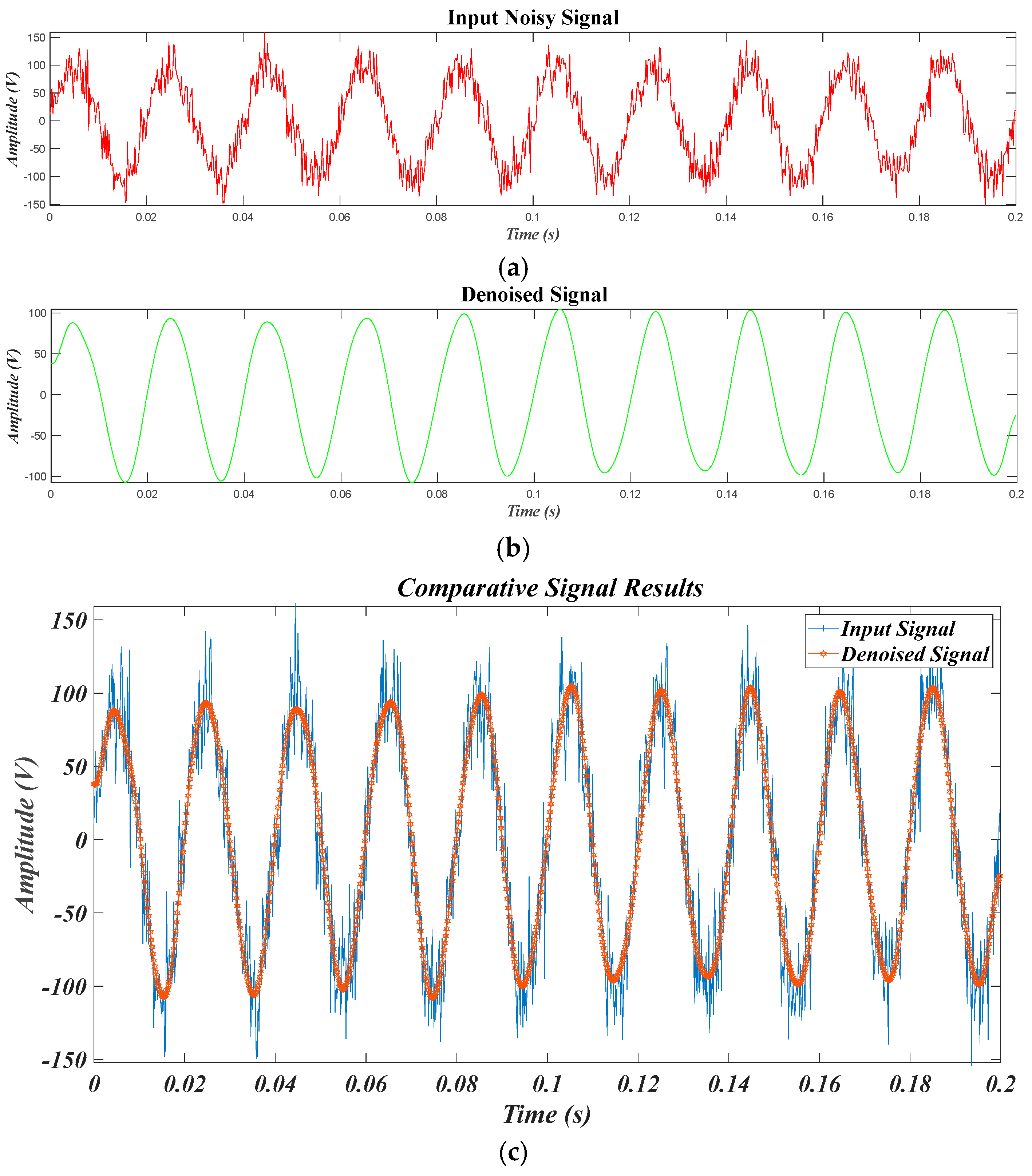
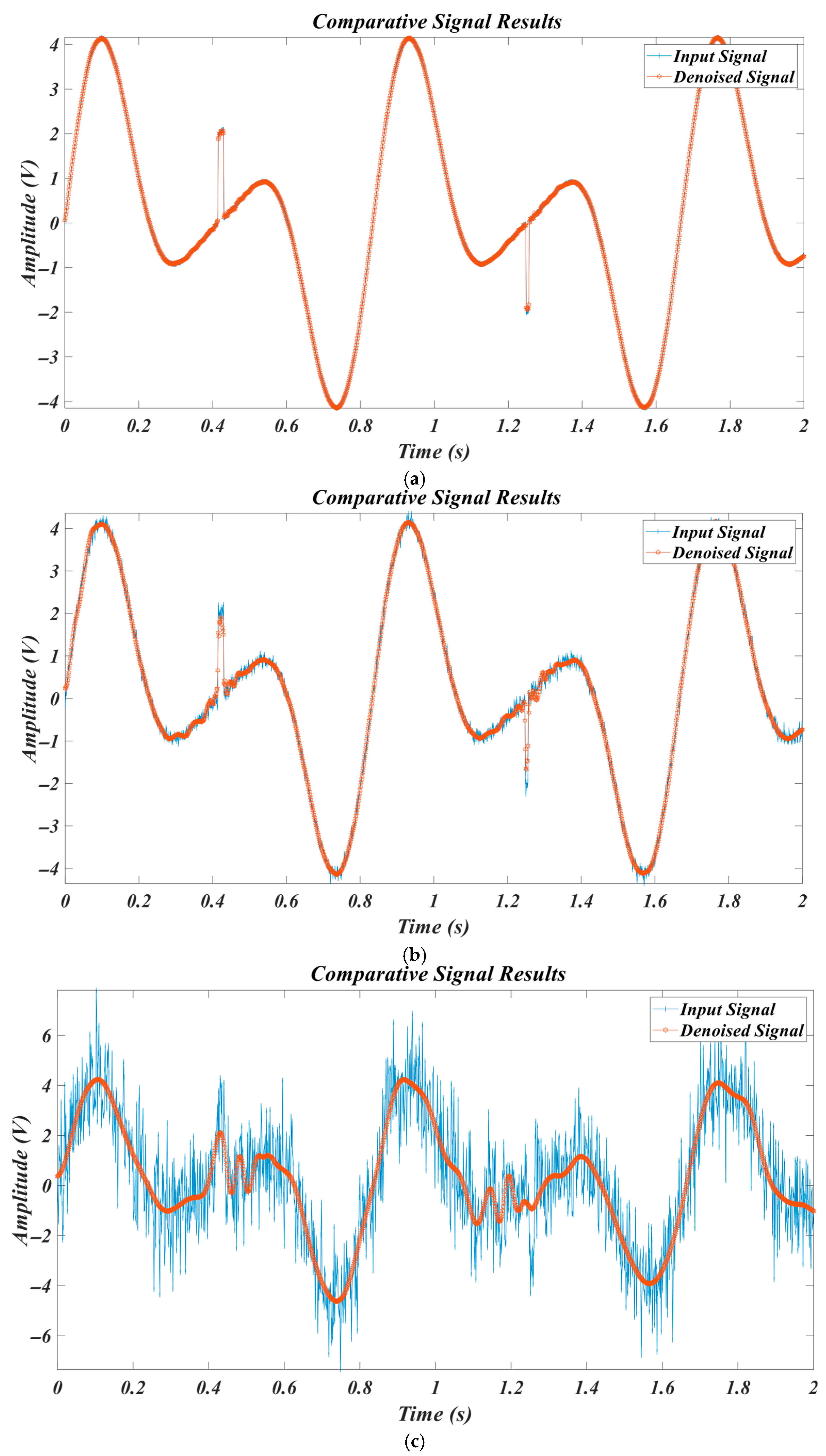
4.2.1. Results for for Different SNR Levels
4.2.2. Results for L3 Signal for Different SNR Levels
4.2.3. Results for for Different SNR Levels
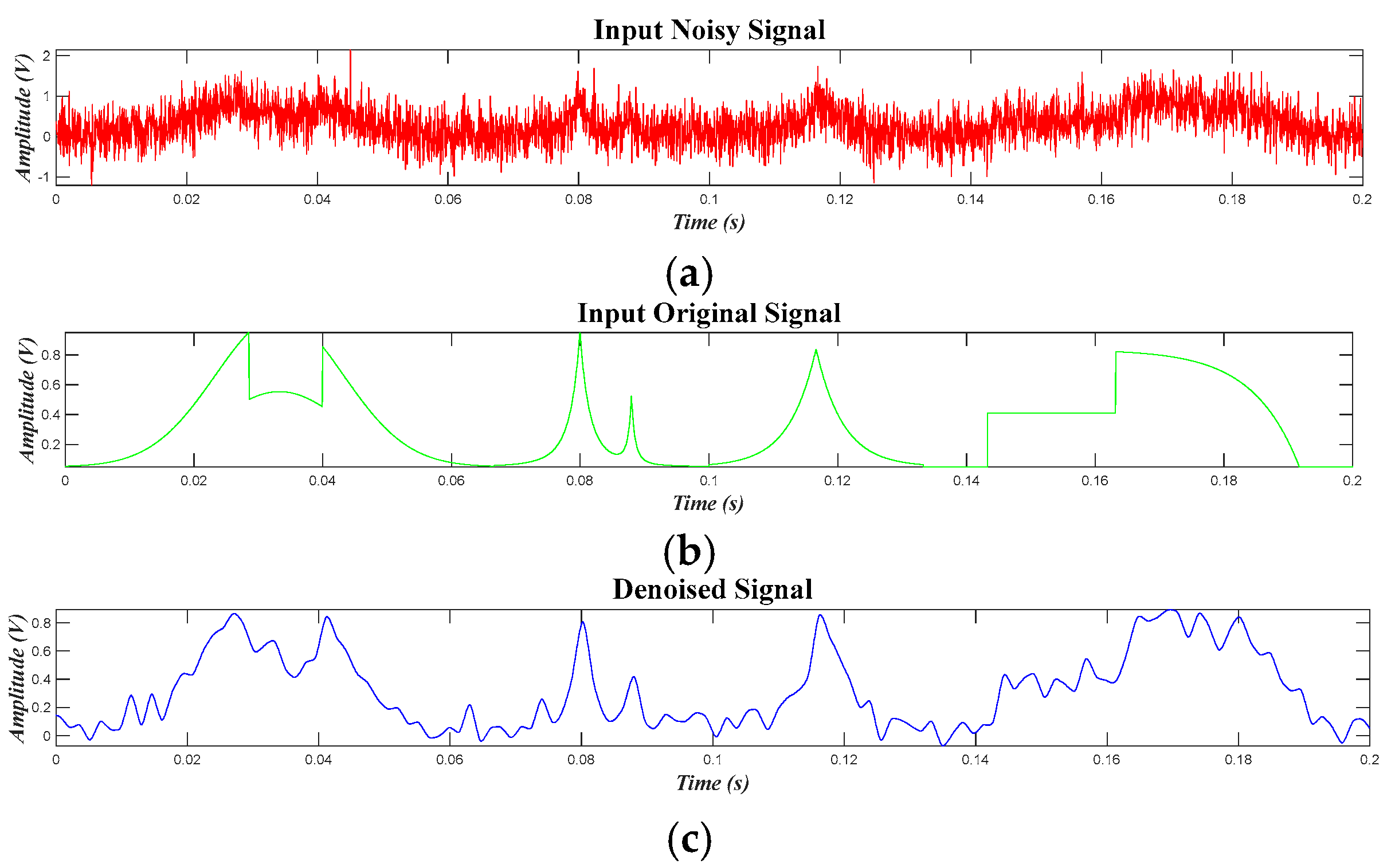
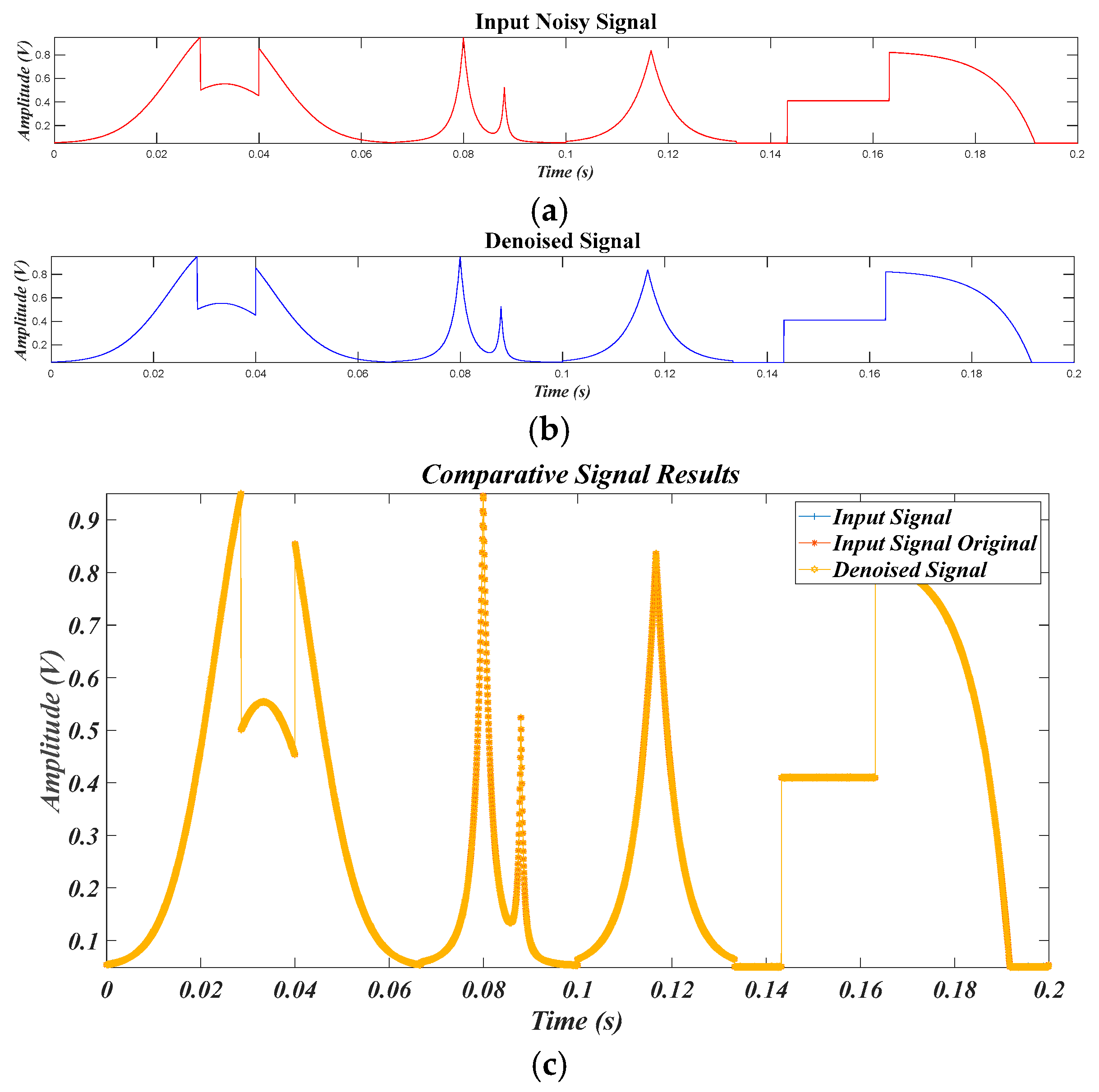
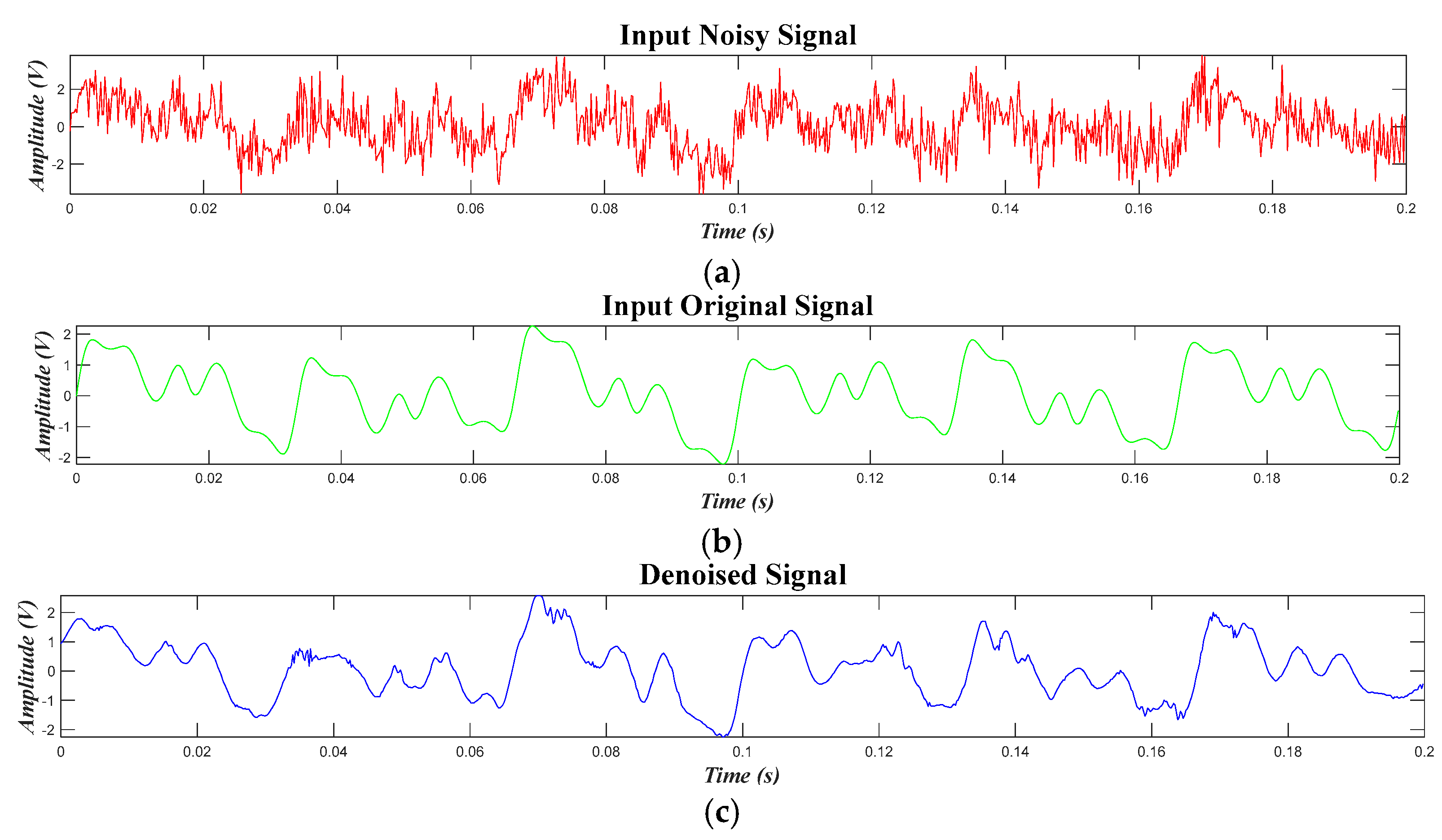
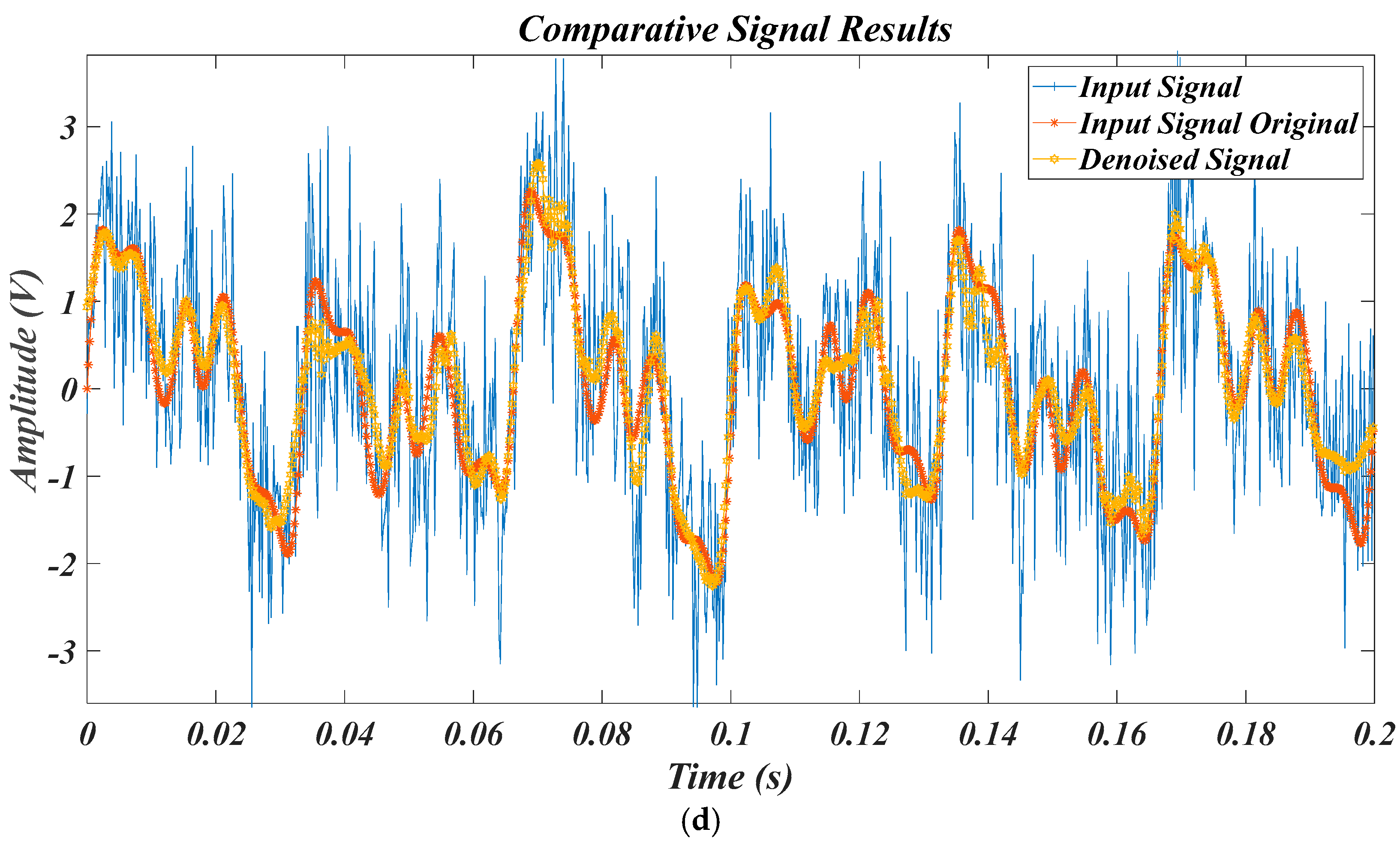
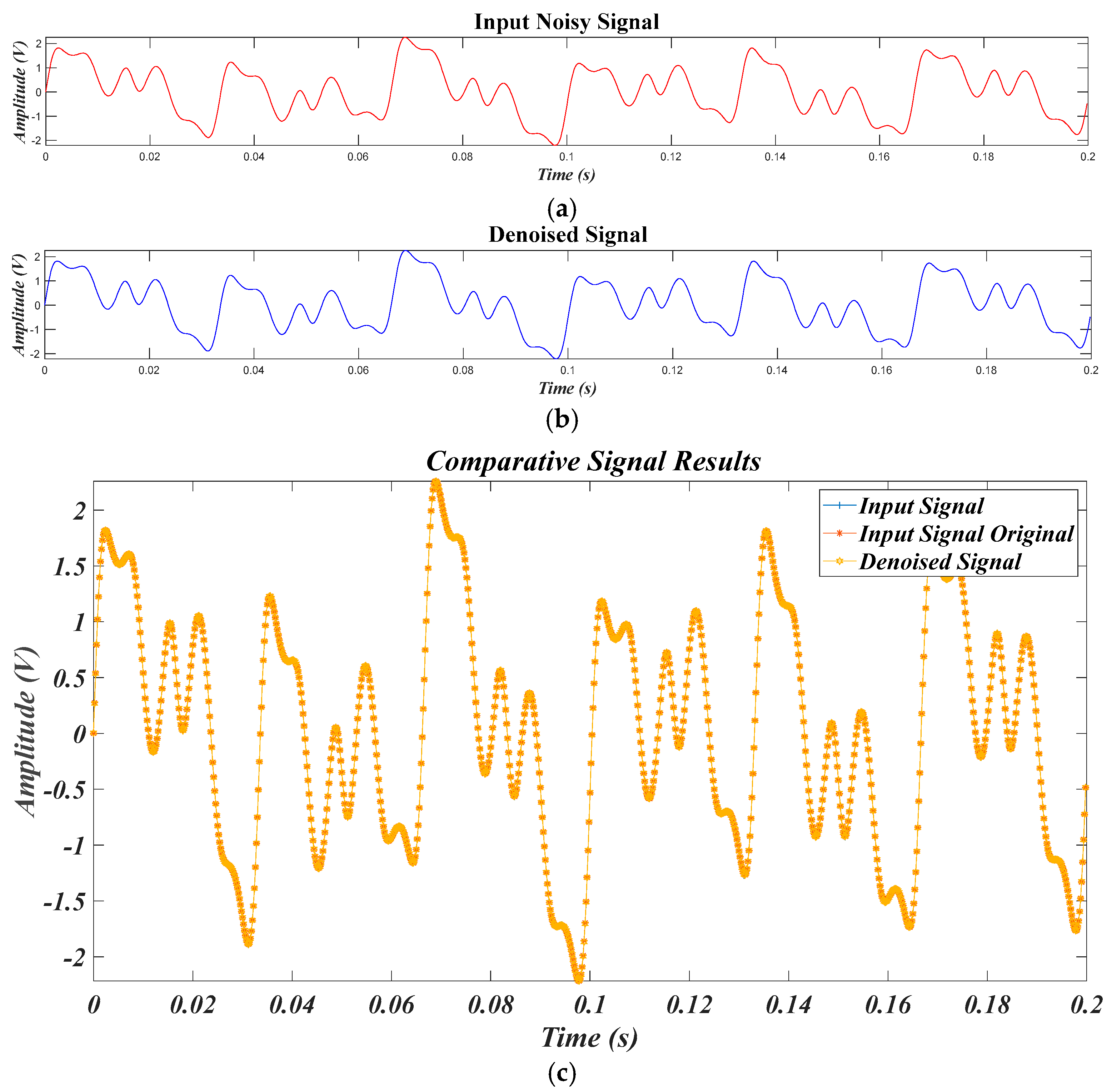
4.3. Results for Synthetic Data of PQDs
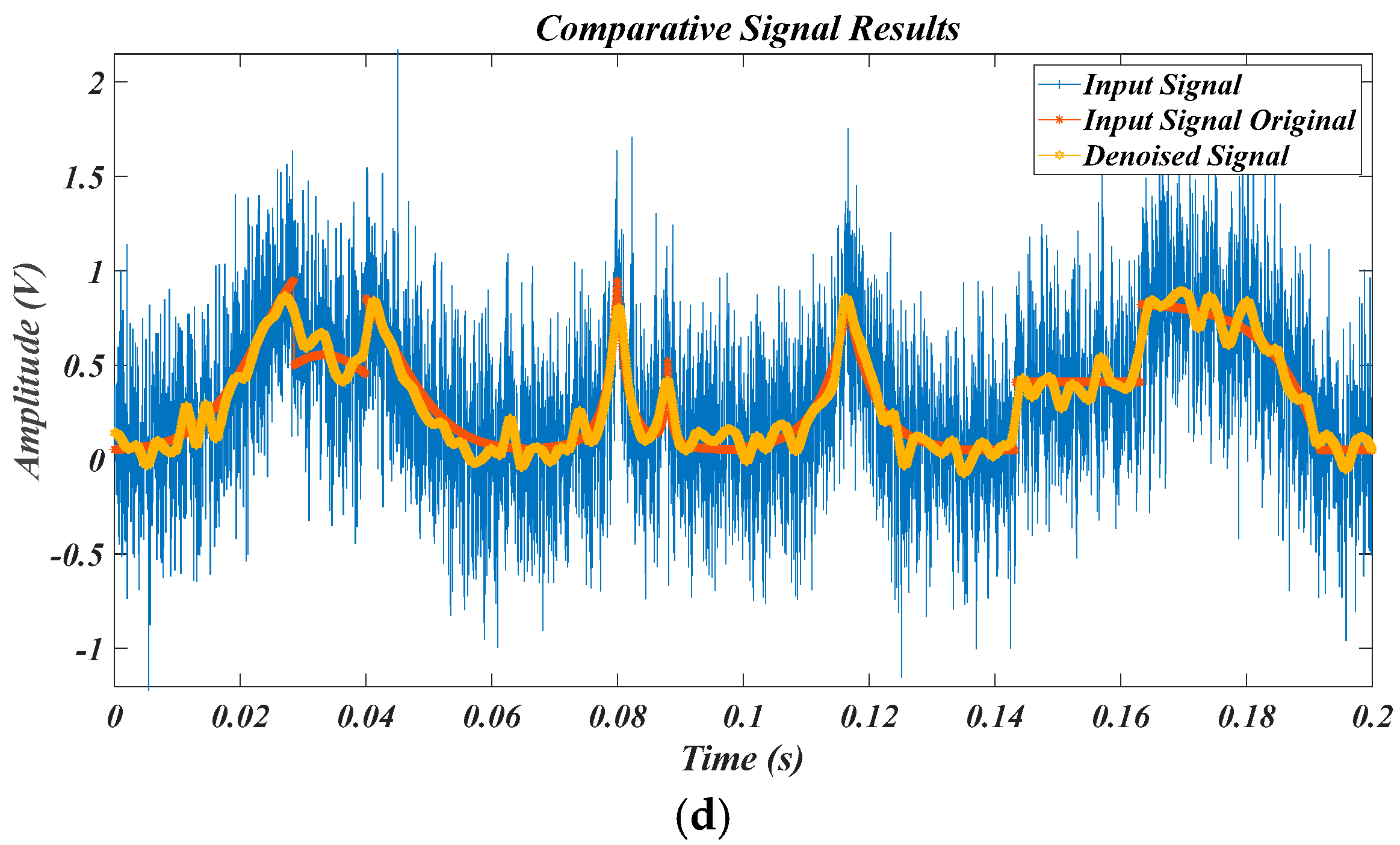
4.4. Results for Experimental Data
4.5. An Application with Classification
4.6. Comparison with Different Hardware Platforms
4.7. Comparison of the Other Methods with the Proposed Method
4.8. Limitations of the Proposed Method
- Performance degradation in extreme noise scenarios: In cases where signals are heavily corrupted by composite or structured noise (e.g., impulsive + Gaussian), the denoising performance may degrade, particularly when the selected wavelet type is not well-suited to the underlying signal morphology.
- Scalability to very large model spaces: Although the algorithm achieves fast execution (~4.86 ms/model), expanding the wavelet families, subtypes, and denoising methods significantly increases the search space. In resource-constrained or real-time environments, this could lead to latency unless additional pruning or parallelization strategies are employed.
- Dependence on predefined parameter sets: The current framework relies on manually defined wavelet families, thresholding rules, and decomposition levels. While modular, performance is still bound by the completeness and granularity of these parameter pools. If novel methods are introduced, additional calibration may be required.
- Thresholding method sensitivity: Certain denoising methods like Bayes, SURE, etc., exhibit high sensitivity to their internal thresholding rule. Minor changes in noise level or signal variance can shift the optimal settings, especially in real-time or biomedical applications.
- Domain-agnostic noise modeling: The current framework performs denoising primarily based on signal waveform analysis without incorporating domain-specific knowledge. However, distinguishing between inherent signal fluctuations and actual noise may require application-aware strategies, especially in fields like biomedical or power systems, where physiological or operational variations can mimic noise. Future work may integrate supervised or hybrid techniques to address this challenge more effectively.
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Correlation coefficient | |
| of the denoised signal | |
| enhancement for the signal | |
| of noisy signal | |
| Grid noise | |
| PQD signal in the type of kth | |
| Noisy test signal | |
| bior | Biorthogonal Spline |
| biorlp | biorlp loop |
| BlockJS | Block James-Stein |
| Bp | Bp loop |
| clean_signal | Denosied signal |
| coiflp | Coif loop |
| col_corr_mat_denoising | Column of corr measurement matrix |
| col_mse_mat_denoising | Column of the MSE measurement matrix |
| col_rmse_mat_denoising | Column of the RMSE measurement matrix |
| corr_mat_denoising | Corr measurement matrix |
| db | Daubechies |
| dblp | dblp loop |
| ECG | Electrocardiogram |
| EEG | Electroencephalogram |
| EEMD | Enhanced Empirical Mode Decomposition |
| FDR | False Discovery Rate |
| fklp | fklp loop |
| GANs | Generative Adversarial Networks |
| glp | glp loop |
| input_signal | Input noisy signal |
| input_signal_org | Input original signal |
| InSAR | Interferometric Synthetic Aperture Radar |
| L | Length of signal |
| L_bior_Num | Length of bior_Num |
| L_coif_Num | Length of coif_Num |
| L_db_Num | Length of db_Num |
| L_fk_Num | Length of fk_Num |
| L_sym_Num | Length of sym_Num |
| L_WM | Length of wavelet matrix |
| lp | lp loop |
| Max_Level | Max wavelet level |
| Mp | Mp loop |
| MSE | Mean square error |
| mse_mat_denoising | MSE measurement matrix |
| PCG | Phonocardiography |
| PQD | Power Quality Disturbance |
| RMSE | Root mean square error |
| rmse_mat_denoising | RMSE measurement matrix |
| RNNs | recurrent neural networks |
| row_corr_mat_denoising | Row of corr measurement matrix |
| row_mse_mat_denoising | Row of MSE measurement matrix |
| row_rmse_mat_denoising | Row of RMSE measurement matrix |
| SNR_mat_denoising | SNR measurement matrix |
| Sp | Sp loop |
| SURE | Stein’s Unbiased Risk Estimate |
| sym | Symlets |
| symlp | Sym loop |
| t | time |
| UT | Universal Threshold |
| UTp | UniversalThreshold loop |
| VMD | Variational Mode Decomposition |
| Noisy PQD signal |
References
- Pasti, L.; Walczak, B.; Massart, D.L.; Reschiglian, P. Optimization of signal denoising in discrete wavelet transform. Chemom. Intell. Lab. Syst. 1999, 48, 21–34. [Google Scholar] [CrossRef]
- Sardy, S.; Tseng, P.; Bruce, A. Robust Wavelet Denoising. IEEE Trans. Signal Process. 2001, 49, 1146–1152. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.; Yan, R.; Li, X.; Liu, Y. From heuristic optimization to dictionary learning: A review and comprehensive comparison of image denoising algorithms. IEEE Trans. Cybern. 2014, 44, 1001–1013. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.Y.; Selesnick, I.W. Group-sparse signal denoising: Non-convex regularization, convex optimization. IEEE Trans. Signal Process. 2014, 62, 3464–3478. [Google Scholar] [CrossRef]
- Azzouz, A.; Bengherbia, B.; Wira, P.; Alaoui, N.; Souahlia, A.; Maazouz, M.; Hentabeli, H. An efficient ECG signals denoising technique based on the combination of particle swarm optimisation and wavelet transform. Heliyon 2024, 10, e26171. [Google Scholar] [CrossRef]
- Mei, Y.; Wang, Y.; Zhang, X.; Liu, S.; Wei, Q.; Dou, Z. Wavelet packet transform and improved complete ensemble empirical mode decomposition with adaptive noise based power quality disturbance detection. J. Power Electron. 2022, 22, 1334–1346. [Google Scholar] [CrossRef]
- Narmada, A.; Shukla, M.K. A novel adaptive artifacts wavelet denoising for EEG artifacts removal using deep learning with meta-heuristic approach. Multimed. Tools Appl. 2023, 82, 40403–40441. [Google Scholar] [CrossRef]
- Yue, Y.; Chen, C.; Wu, X.; Zhou, X. An effective electrocardiogram segments denoising method combined with ensemble empirical mode decomposition, empirical mode decomposition, and wavelet packet. IET Signal Process. 2023, 17, e12232. [Google Scholar] [CrossRef]
- Fu, L.; Zhu, T.; Pan, G.; Chen, S.; Zhong, Q.; Wei, Y. Power quality disturbance recognition using VMD-based feature extraction and heuristic feature selection. Appl. Sci. 2019, 9, 4901. [Google Scholar] [CrossRef]
- Chen, M.; Li, Y.; Zhang, X.; Gao, J.; Sun, Y.; Shi, W.; Wei, S. Multiscale convolution and attention based denoising autoencoder for motion artifact removal in ECG signals. In Proceedings of the 7th International Conference on Image and Graphics Processing (ICIGP), Beijing, China, 19–21 January 2024; pp. 442–448. [Google Scholar]
- Chen, M.; Li, Y.; Zhang, L.; Liu, L.; Han, B.; Shi, W.; Wei, S. Elimination of random mixed noise in ECG using convolutional denoising autoencoder with transformer encoder. IEEE J. Biomed. Health Inform. 2024, 28, 1993–2004. [Google Scholar] [CrossRef]
- Khodayar, M.; Regan, J. Deep neural networks in power systems: A review. Energies 2023, 16, 4773. [Google Scholar] [CrossRef]
- Tao, Y.; Xu, B.; Zhang, Y. Refined self-attention transformer model for ECG-based arrhythmia detection. IEEE Trans. Instrum. Meas. 2024, 73, 4007314. [Google Scholar] [CrossRef]
- Ramana, P.V.; Reddy, G.J.; Krishna, V.S.; Reddy, Y.Y.; Reddy, V.V. A hybrid signal denoising approach using wavelet decomposition and neural network-based thresholding. In Proceedings of the 5th International Conference on Trends in Material Science and Inventive Materials (ICTMIM), Kanyakumari, India, 7–9 April 2025; pp. 1400–1404. [Google Scholar] [CrossRef]
- Elouaham, S.; Dliou, A.; Jenkal, W.; Louzazni, M.; Zougagh, H.; Dlimi, S.; Tani, A. Empirical wavelet transform based ECG signal filtering method. J. Electr. Comput. Eng. 2024, 2024, 9050909. [Google Scholar] [CrossRef]
- Nayak, A.B.; Shah, A.; Maheshwari, S.; Anand, V.; Chakraborty, S.; Kumar, T.S. An empirical wavelet transform-based approach for motion artifact removal in electroencephalogram signals. Decis. Anal. J. 2024, 10, 100420. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, K.; Ma, C.; Li, X.; Zhang, J. An improved empirical wavelet transform and its applications in rolling bearing fault diagnosis. Appl. Sci. 2018, 8, 2352. [Google Scholar] [CrossRef]
- Singh, P.; Pradhan, G. Variational mode decomposition based ECG denoising using non-local means and wavelet domain filtering. Australas. Phys. Eng. Sci. Med. 2018, 41, 891–904. [Google Scholar] [CrossRef]
- Edder, A.; Ben-Bouazza, F.E.; Tafala, I.; Manchadi, O.; Jioudi, B. Self attention-driven ECG denoising: A transformer-based approach for robust cardiac signal enhancement. Signals 2025, 6, 26. [Google Scholar] [CrossRef]
- Mishra, A.; Dharahas, G.; Gite, S.; Kotecha, K.; Koundal, D.; Zaguia, A.; Kaur, M.; Lee, H.-N. ECG data analysis with denoising approach and customized CNNs. Sensors 2022, 22, 1928. [Google Scholar] [CrossRef]
- Mohagheghian, F.; Han, D.; Ghetia, O.; Peitzsch, A.; Nishita, N.; Nejad, M.P.S.; Ding, E.Y.; Noorishirazi, K.; Hamel, A.; Otabil, E.M.; et al. Noise reduction in photoplethysmography signals using a convolutional denoising autoencoder with unconventional training scheme. IEEE Trans. Biomed. Eng. 2023, 71, 456–466. [Google Scholar] [CrossRef]
- Caicedo, J.E.; Agudelo-Martínez, D.; Rivas-Trujillo, E.; Meyer, J. A systematic review of real-time detection and classification of power quality disturbances. Prot. Control Mod. Power Syst. 2023, 8, 3. [Google Scholar] [CrossRef]
- Chen, M.; Cheng, Q.; Feng, X.; Zhao, K.; Zhou, Y.; Xing, B.; Tang, S.; Wang, R.; Duan, J.; Wang, J.; et al. Optimized variational mode decomposition algorithm based on adaptive thresholding method and improved whale optimization algorithm for denoising magnetocardiography signal. Biomed. Signal Process. Control 2024, 88, 105681. [Google Scholar] [CrossRef]
- Roy, A.; Satija, U. A novel deep metric learning based state-stable and noise-aware biometric authentication framework using seismocardiogram signals. IEEE Trans. Biom. Behav. Ident. Sci. 2024, 7, 246–255. [Google Scholar] [CrossRef]
- Qin, A.; Mao, H.; Sun, K.; Huang, Z.; Li, X. Cross-domain fault diagnosis based on improved multi-scale fuzzy measure entropy and enhanced joint distribution adaptation. IEEE Sens. J. 2022, 22, 9649–9664. [Google Scholar] [CrossRef]
- Rezazadeh, N.; Perfetto, D.; Polverino, A.; De Luca, A.; Lamanna, G. Guided wave-driven machine learning for damage classification with limited dataset in aluminum panel. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]
- Ding, Y.; Selesnick, I.W. Artifact-Free Wavelet Denoising: Non-convex Sparse Regularization, Convex Optimization. IEEE Signal Process. Lett. 2015, 22, 1364–1368. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Y.; Yildirim, T.; Zhang, J. Signal denoising optimization based on a Hilbert-Huang transform-triple adaptable wavelet packet transform algorithm. Europhys. Lett. 2018, 124, 54002. [Google Scholar] [CrossRef]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L.; Raghuvanshi, D.K. Review of noise removal techniques in ECG signals. Inst. Eng. Technol. 2020, 14, 569–590. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, S.; Li, F.; Tian, S.; Wang, J.; Ding, X.; Gong, R.; Sangaiah, A.K. An Efficient ECG Denoising Method Based on Empirical Mode Decomposition, Sample Entropy, and Improved Threshold Function. Wirel. Commun. Mob. Comput. 2020, 2020, 8811962. [Google Scholar] [CrossRef]
- Wang, G.; Yang, L.; Liu, M.; Yuan, X.; Xiong, P.; Lin, F.; Liu, X. ECG signal denoising based on deep factor analysis. Biomed. Signal Process Control 2020, 57, 101824. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Tripathy, R.K.; Ponnalagu, R.N. Evaluation of Performance Metrics and Denoising of PCG Signal using Wavelet Based Decomposition. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 11–13 December 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Sun, Z.; Xi, X.; Yuan, C.; Yang, Y.; Hua, X. Surface electromyography signal denoising via EEMD and improved wavelet thresholds. Math. Biosci. Eng. 2020, 17, 6945–6962. [Google Scholar] [CrossRef]
- Baldazzi, G.; Solinas, G.; Del Valle, J.; Barbaro, M.; Micera, S.; Raffo, L.; Pani, D. Systematic analysis of wavelet denoising methods for neural signal processing. J. Neural Eng. 2020, 17, 066016. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H. Vibration signal denoising for structural health monitoring by residual convolutional neural networks. Measurement 2020, 157, 107651. [Google Scholar] [CrossRef]
- Sha, D.; Liang, W.; Wu, L. A novel noise reduction method for natural gas pipeline defect detection signals. J. Nat. Gas. Sci. Eng. 2021, 96, 104335. [Google Scholar] [CrossRef]
- Feng, G.; Wei, H.; Qi, T.; Pei, X.; Wang, H. A transient electromagnetic signal denoising method based on an improved variational mode decomposition algorithm. Measurement 2021, 184, 109815. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yan, S.; Shi, W.; Yang, X.; Guo, Y.; Gulliver, T.A. A Novel Underwater Acoustic Signal Denoising Algorithm for Gaussian/Non-Gaussian Impulsive Noise. IEEE Trans. Veh. Technol. 2021, 70, 429–445. [Google Scholar] [CrossRef]
- Prashar, N.; Sood, M.; Jain, S. Design and implementation of a robust noise removal system in ECG signals using dual-tree complex wavelet transform. Biomed. Signal Process. Control 2021, 63, 102212. [Google Scholar] [CrossRef]
- Kaur, C.; Bisht, A.; Singh, P.; Joshi, G. EEG Signal denoising using hybrid approach of Variational Mode Decomposition and wavelets for depression. Biomed. Signal Process. Control 2021, 65, 102337. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, Z.; Zheng, Y.; Ma, P. Recurrent neural networks for atmospheric noise removal from InSAR time series with missing values. ISPRS J. Photogramm. Remote Sens. 2021, 180, 227–237. [Google Scholar] [CrossRef]
- Shi, F. A review of noise removal techniques in ECG signals. In Proceedings of the 2022 IEEE Conference on Telecommunications, Optics and Computer Science (TOCS), Dalian, China, 11–12 December 2022; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2023; pp. 237–240. [Google Scholar] [CrossRef]
- Wang, X.; Chen, B.; Zeng, M.; Wang, Y.; Liu, H.; Liu, R.; Tian, L.; Lu, X. An ECG Signal Denoising Method Using Conditional Generative Adversarial Net. IEEE J. Biomed. Health Inf. 2022, 26, 2929–2940. [Google Scholar] [CrossRef]
- Madan, P.; Singh, V.; Singh, D.P.; Diwakar, M.; Kishor, A. Denoising of ECG signals using weighted stationary wavelet total variation. Biomed. Signal Process. Control 2022, 73, 103478. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Lin, H.; Li, J.; Zhang, F.; Yang, Y. ECG Denoising Method Based on an Improved VMD Algorithm. IEEE Sens. J. 2022, 22, 22725–22733. [Google Scholar] [CrossRef]
- Zhu, M.L.; Zhao, L.L.; Xiao, L. Image Denoising Based on GAN with Optimization Algorithm. Electronics 2022, 11, 2445. [Google Scholar] [CrossRef]
- Jia, N.; Cheng, Y.; Liu, Y.; Tian, Y. Intelligent Fault Diagnosis of Rotating Machines Based on Wavelet Time-Frequency Diagram and Optimized Stacked Denoising Auto-Encoder. IEEE Sens. J. 2022, 22, 17139–17150. [Google Scholar] [CrossRef]
- Yue, G.D.; Xu, Z.; Wang, L.D.; Liu, C.; Zhou, W.J. Vibration analysis for slab track at different train speeds using Bayes wavelet denoising. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit 2017, 231, 892–901. [Google Scholar] [CrossRef]
- Katicha, S.W.; Loulizi, A.; John; Khoury, E.; Asce, M.; Flintsch, G.W. Adaptive False Discovery Rate for Wavelet Denoising of Pavement Continuous Deflection Measurements. J. Comput. Civ. Eng. 2016, 31, 04016049. [Google Scholar] [CrossRef]
- Karim, S.A.A.; Ismail, M.T.; Hasan, M.K.; Sulaiman, J.; Sakidin, H. Denoising using new thresholding method. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MD, USA, 2016. [Google Scholar] [CrossRef]
- Dai, T.; Li, Y. Efficient dual domain image denoising via SURE-based optimization. Int. J. Mach. Learn. Cybern. 2023, 14, 4417–4430. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Ulfarsson, M.O.; Sveinsson, J.R. Hyperspectral Image Denoising Using SURE-Based Unsupervised Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3369–3382. [Google Scholar] [CrossRef]
- Li, J.; Tong, Y.; Guan, L.; Wu, S.; Li, D. A UV-visible absorption spectrum denoising method based on EEMD and an improved universal threshold filter. RSC Adv. 2018, 8, 8558–8568. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- Sørensen, J.S.; Johannesen, L.; Grove, U.S.L.; Lundhus, K.; Couderc, J.P.; Graff, C. A Comparison of IIR and Wavelet Filtering for Noise Reduction of the ECG. Comput. Cardiol. 2010, 37, 489–492. [Google Scholar]
- Yusuf, S.D.; Maduakolam, F.C.; Umar, I.; Loko, Z.A. Analysis of Butterworth Filter for Electrocardiogram De-Noising Using Daubechies Wavelets. SSRG Int. J. Electron. Commun. Eng. 2020, 7, 8–13. [Google Scholar] [CrossRef]
- Jia, Y.; Pei, H.; Liang, J.; Zhou, Y.; Yang, Y.; Cui, Y.; Xiang, M. Preprocessing and Denoising Techniques for Electrocardiography and Magnetocardiography: A Review. Bioengineering 2024, 11, 1109. [Google Scholar] [CrossRef]
- Yadav, O.P.; Ray, S. Analysis of Butterworth and Chebyshev Filters for ECG Denoising Using Wavelets. IOSR J. Electron. Commun. Eng. 2013, 6, 37–44. [Google Scholar] [CrossRef]
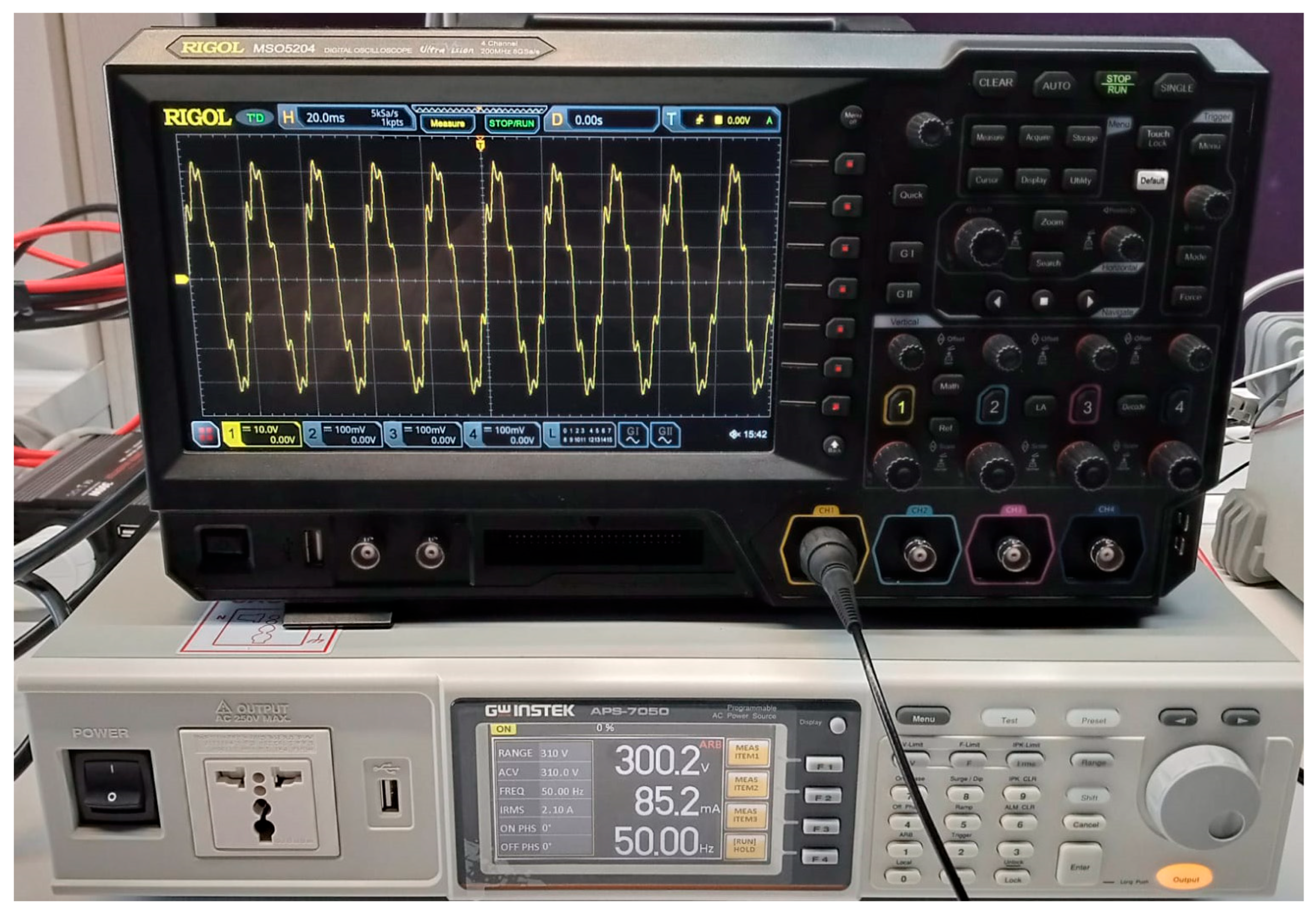



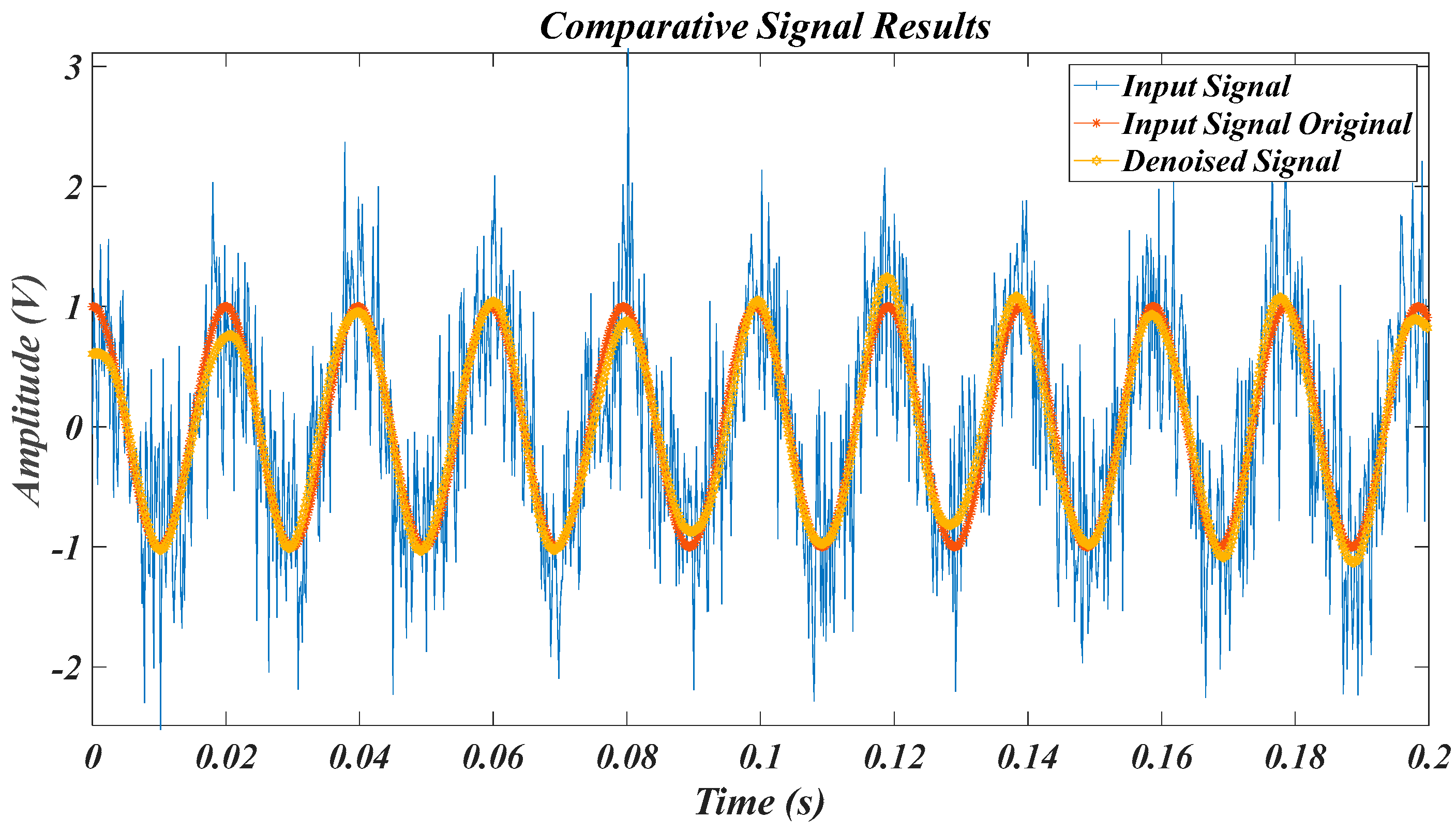
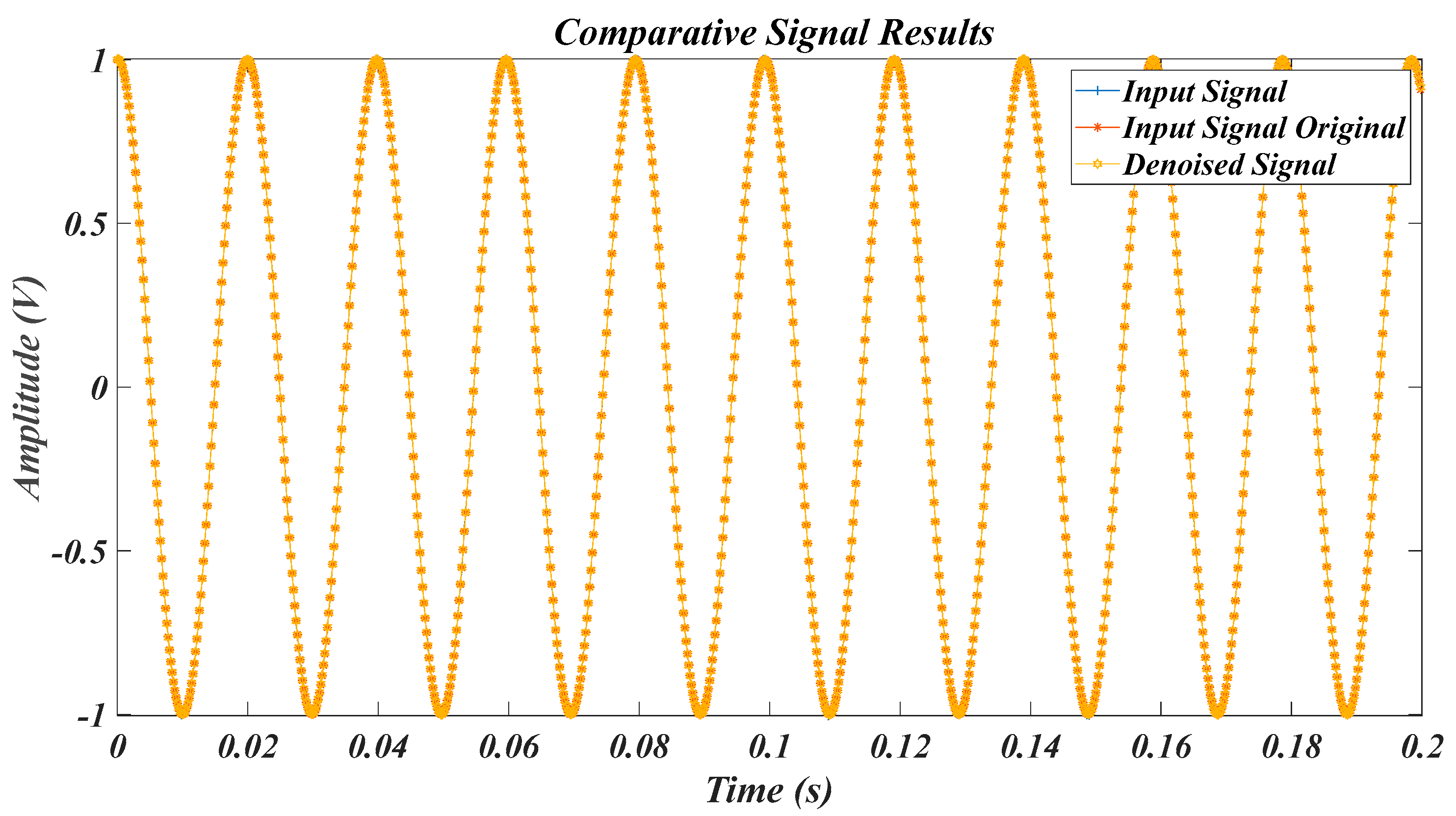
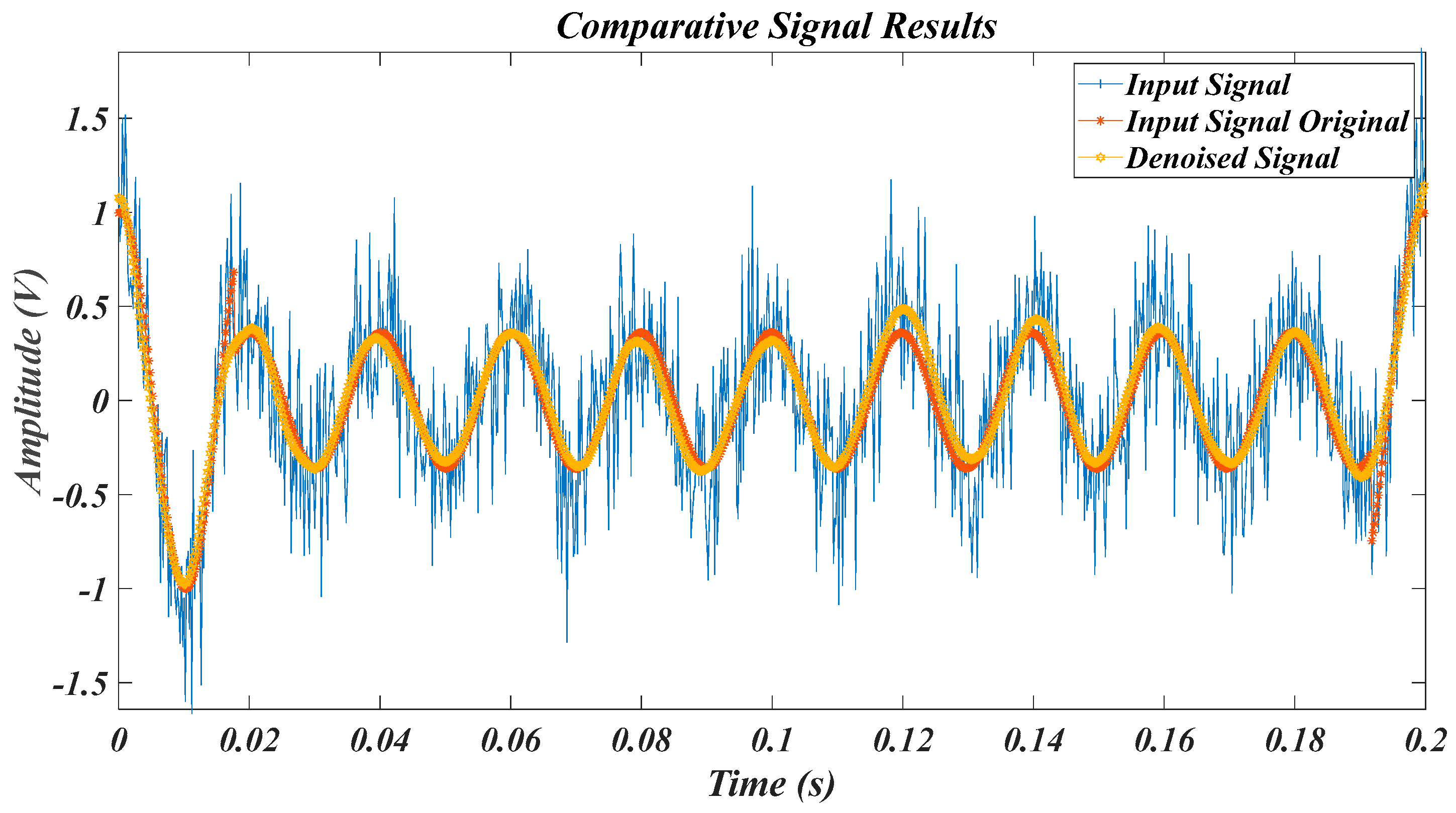
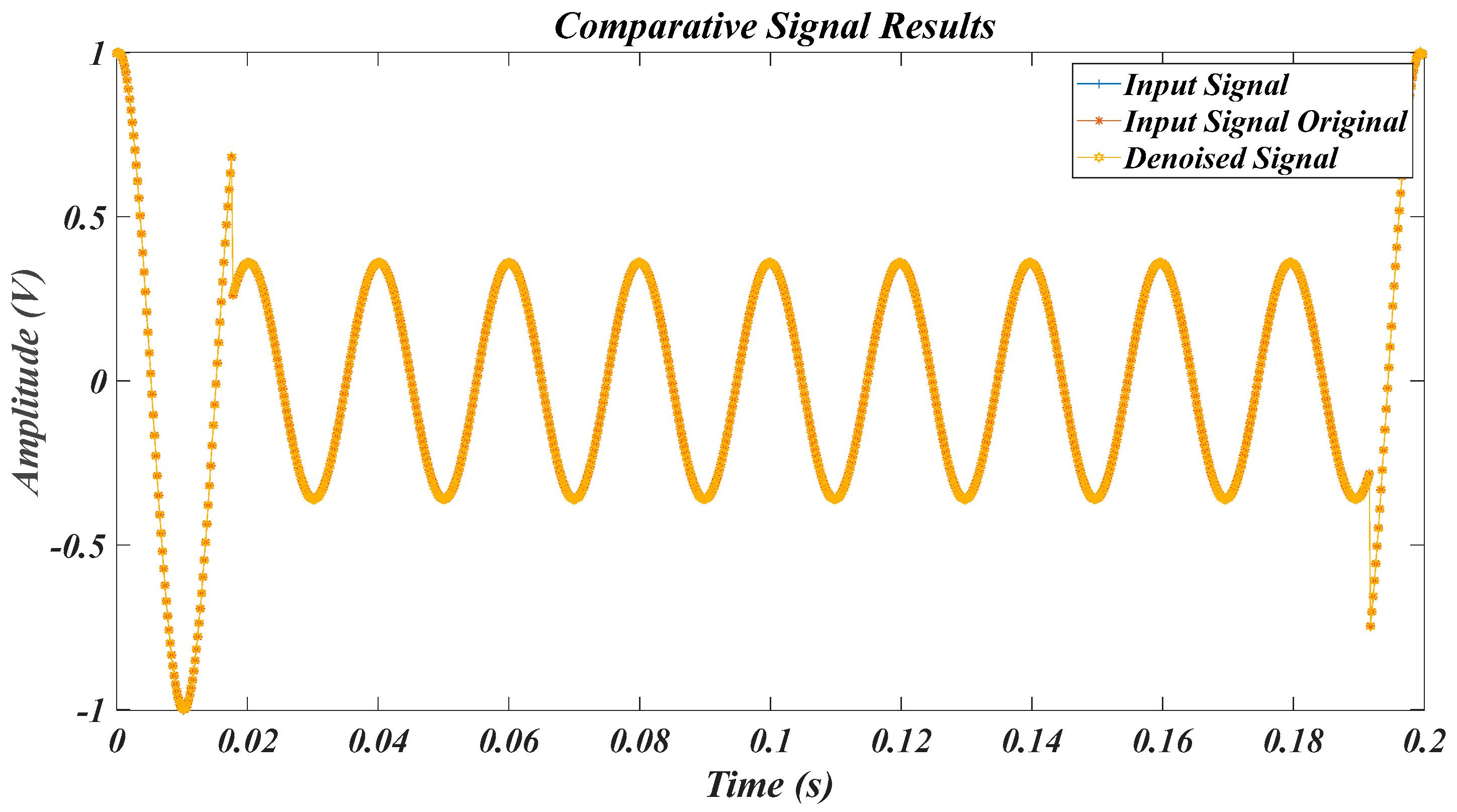
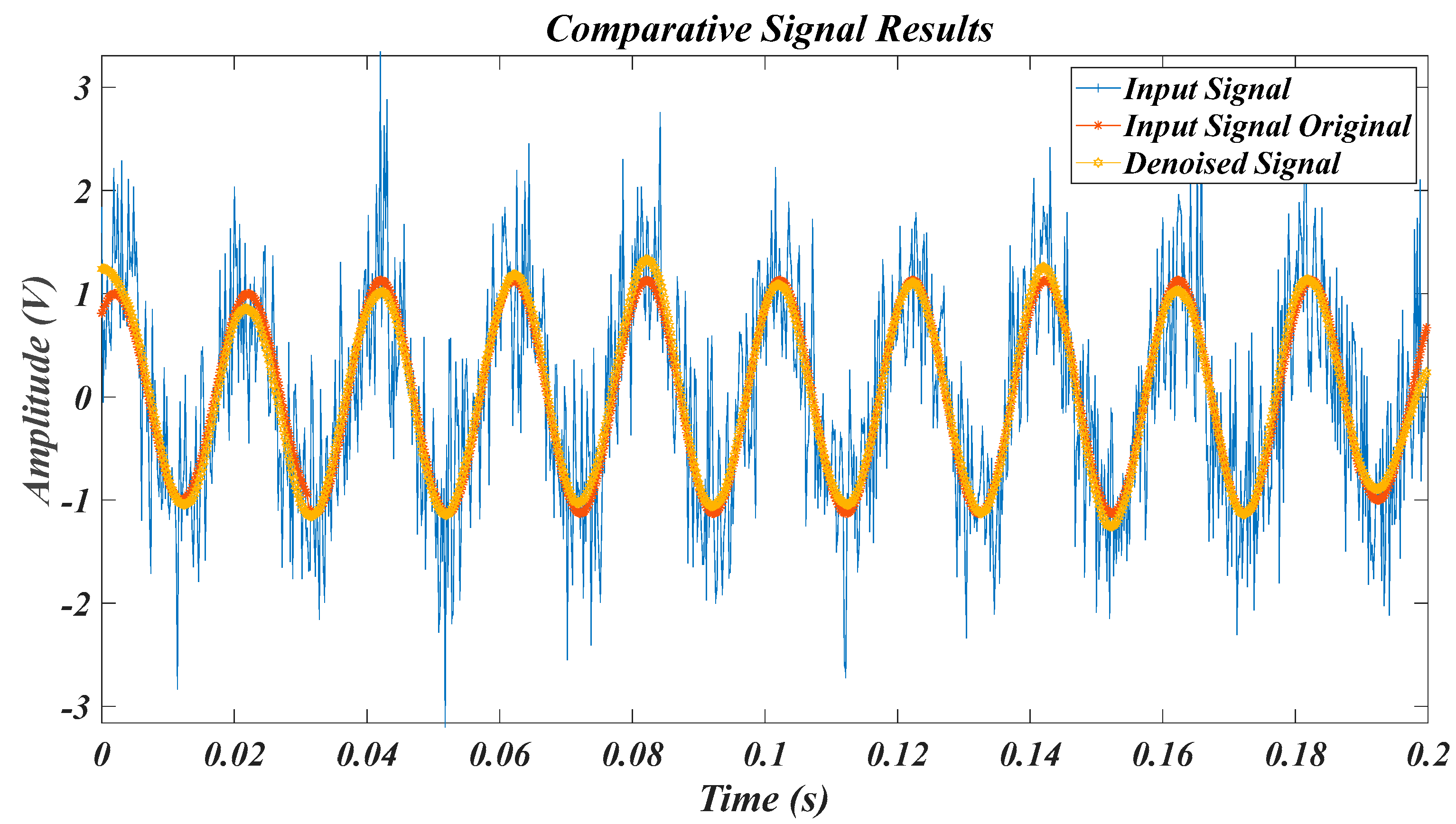
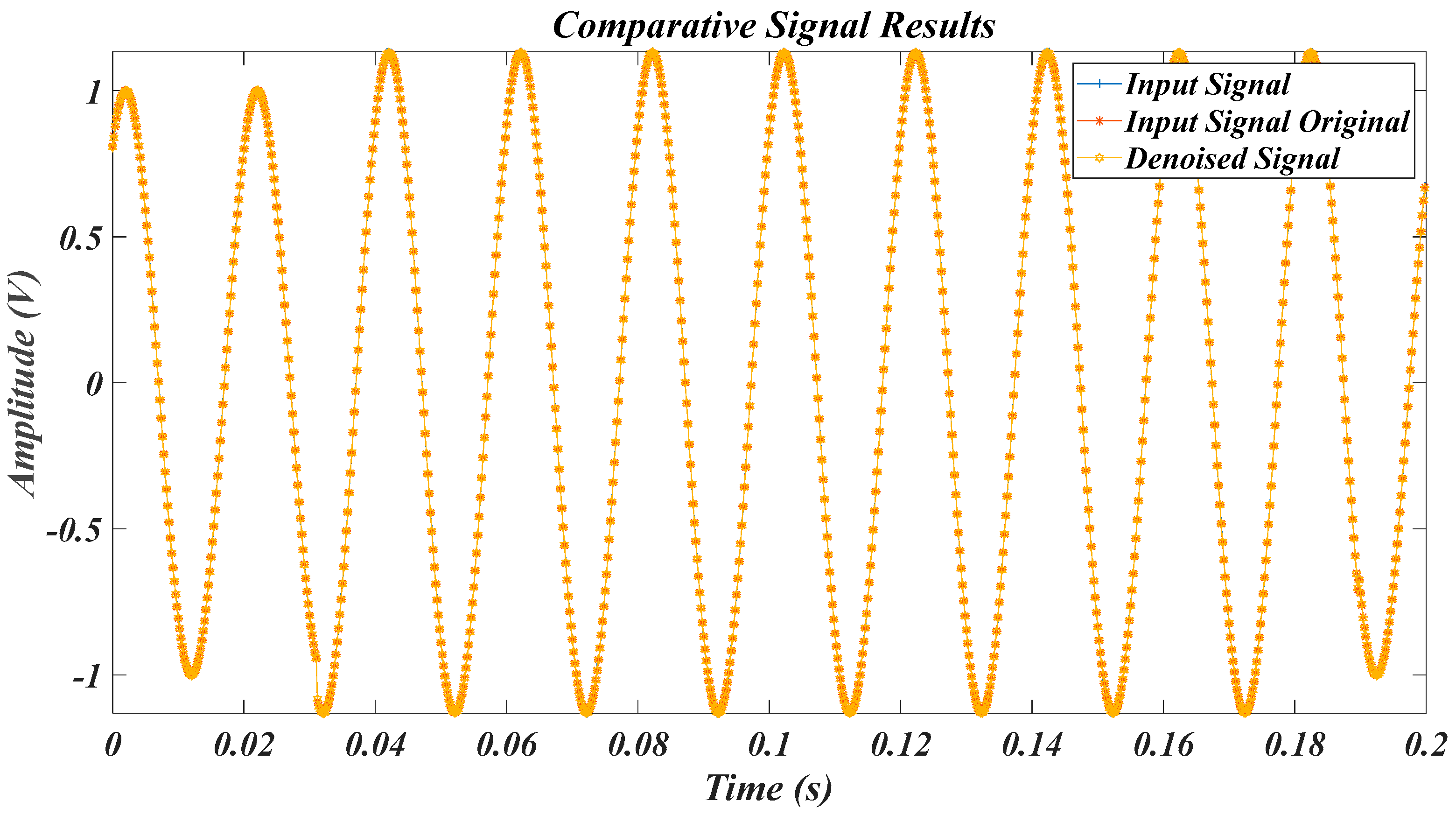
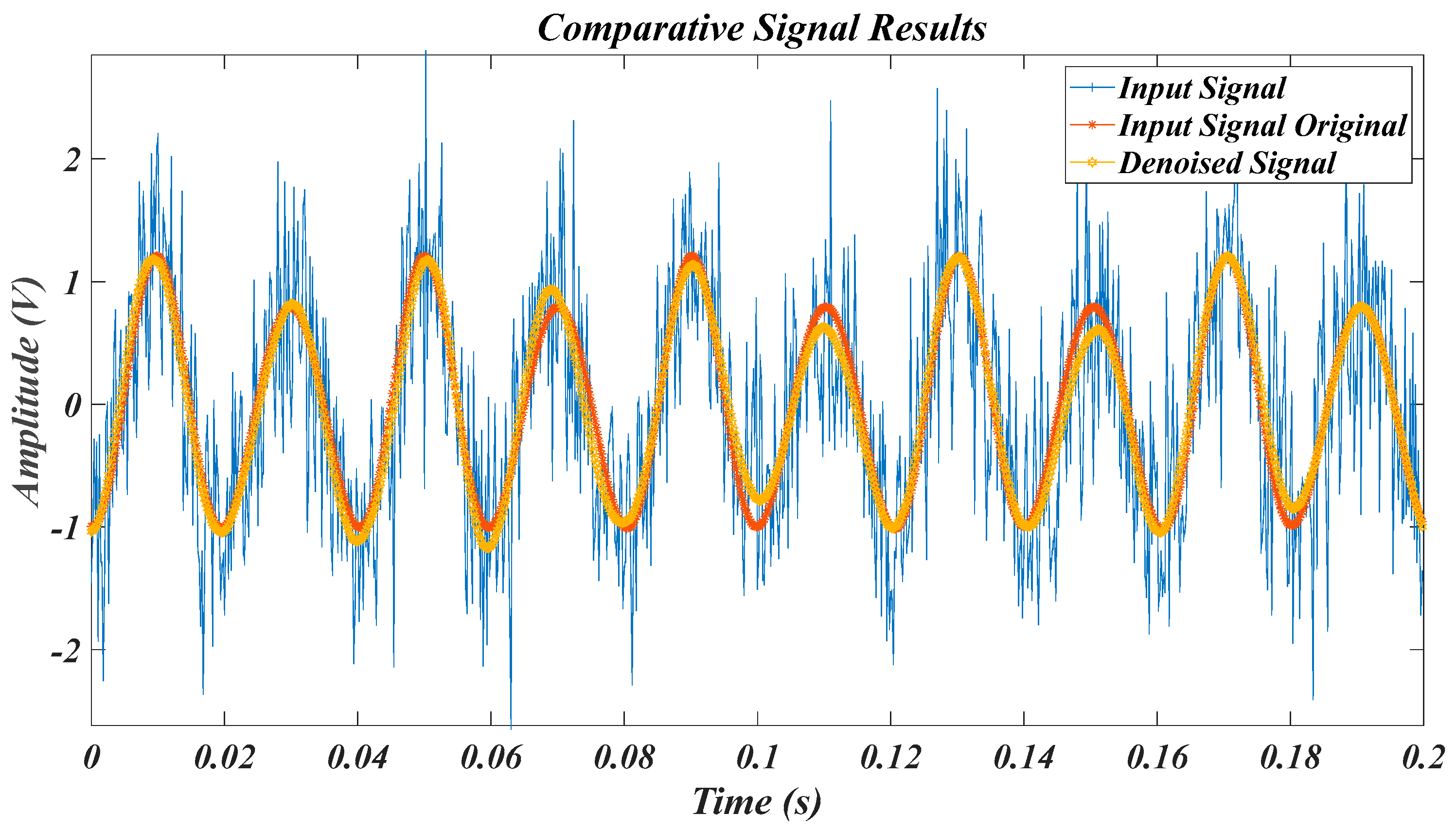
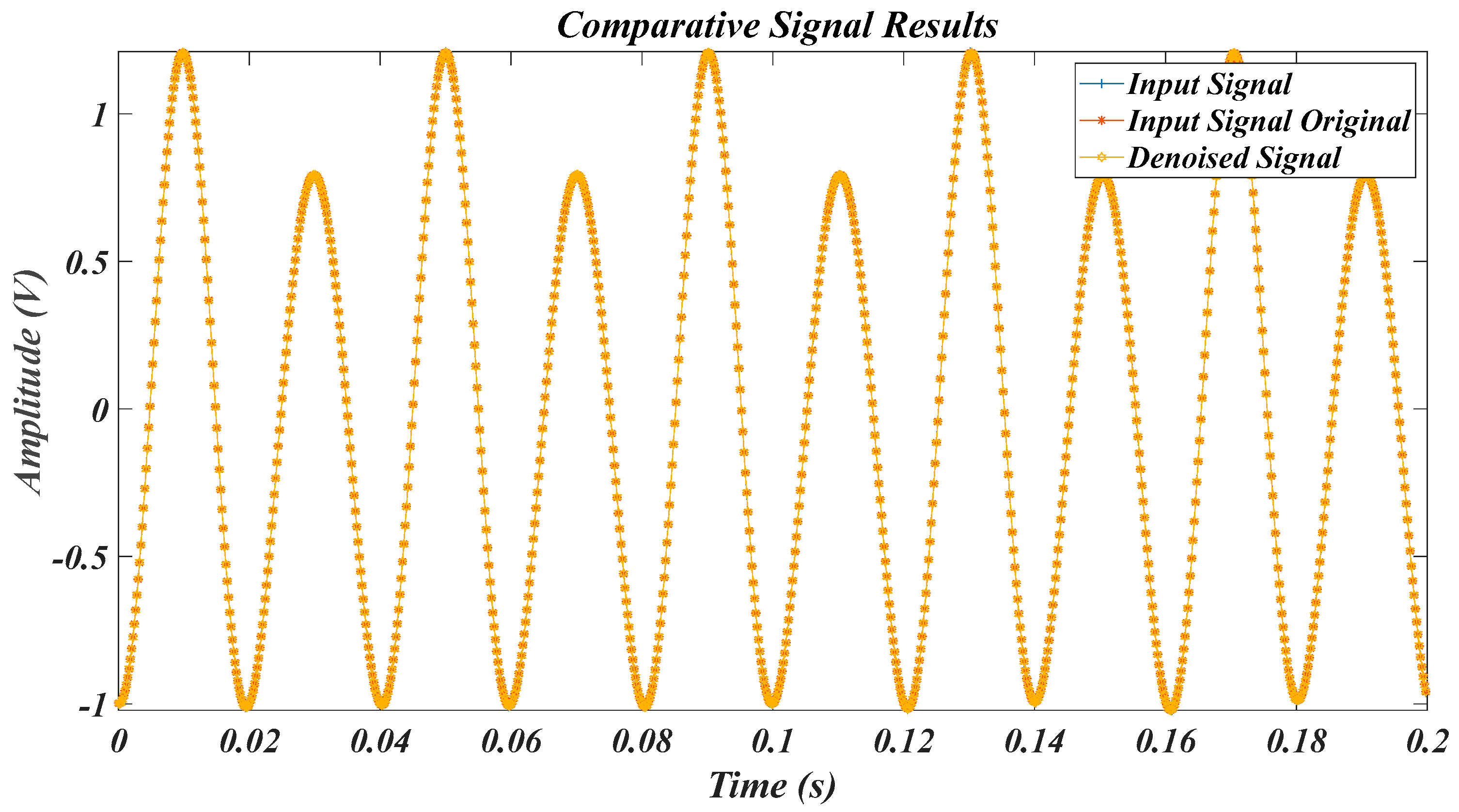
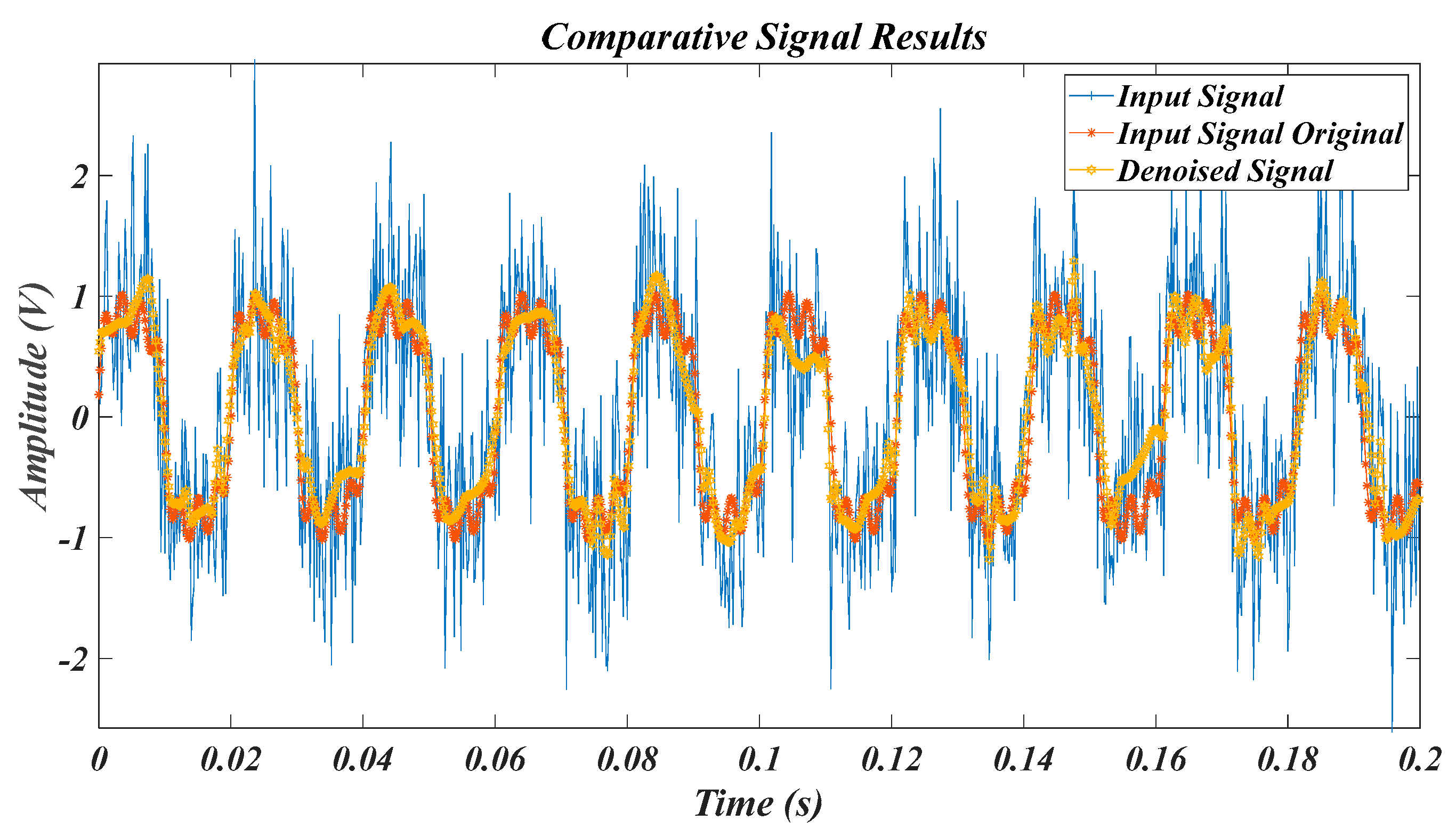
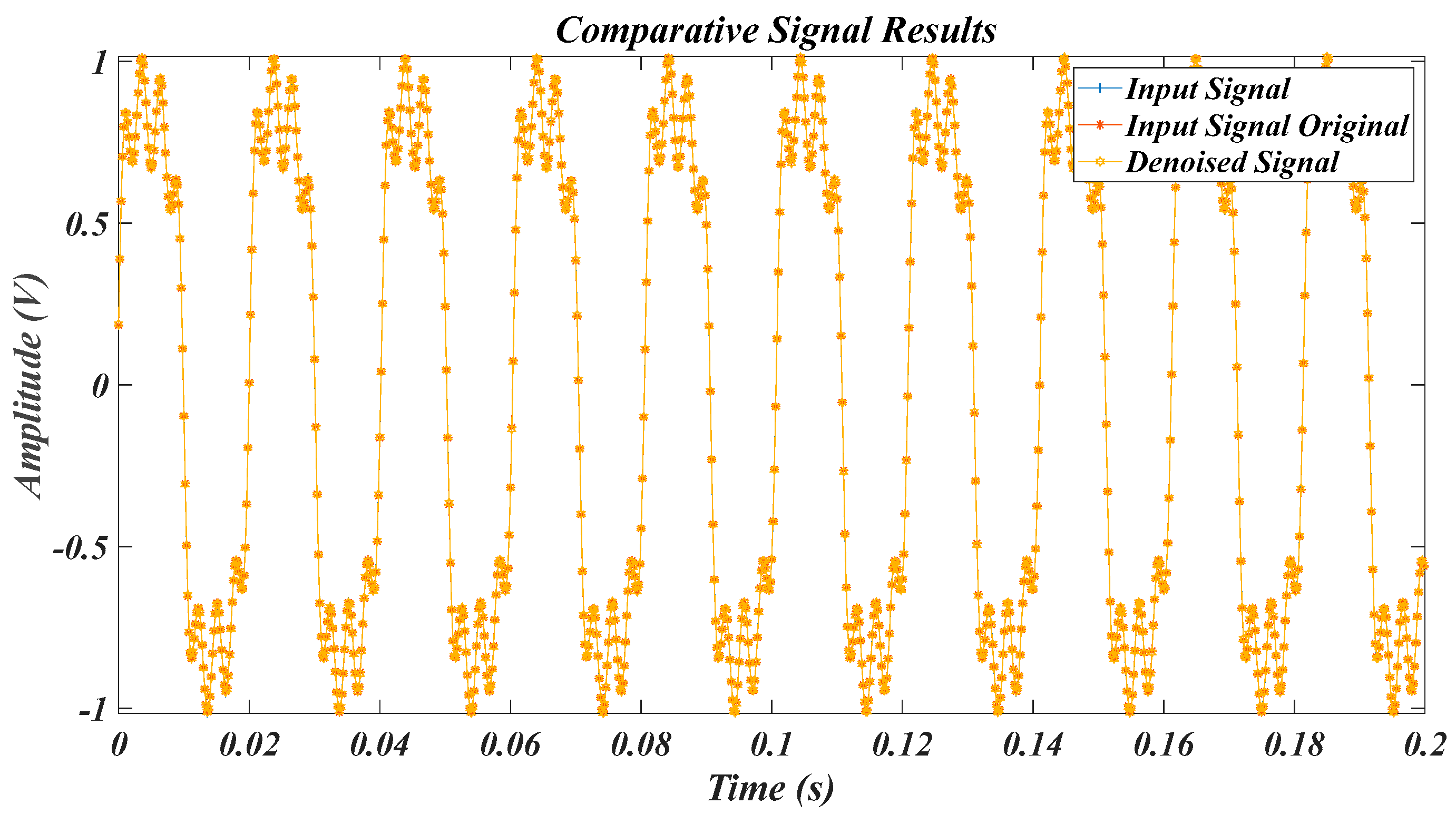
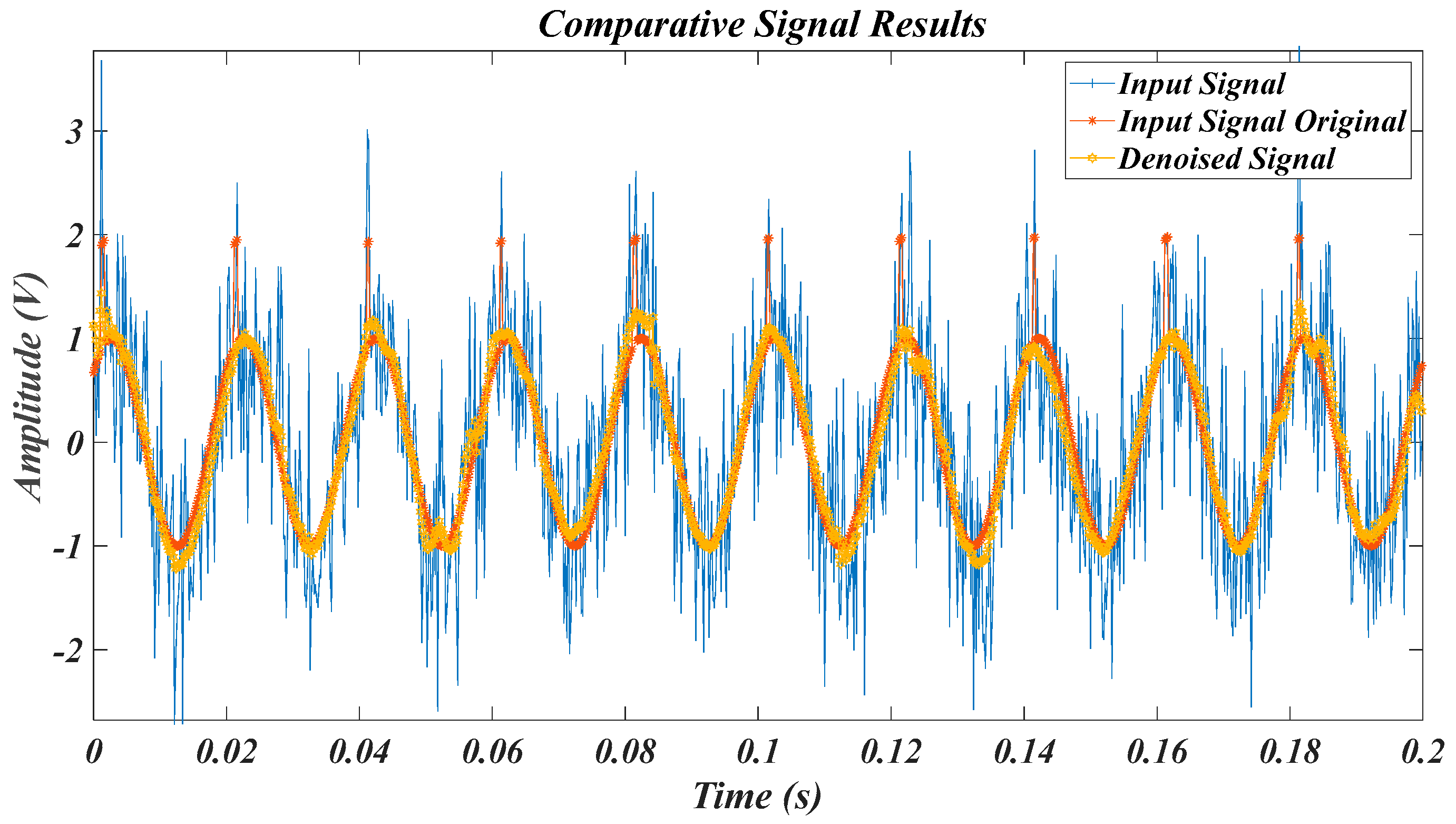
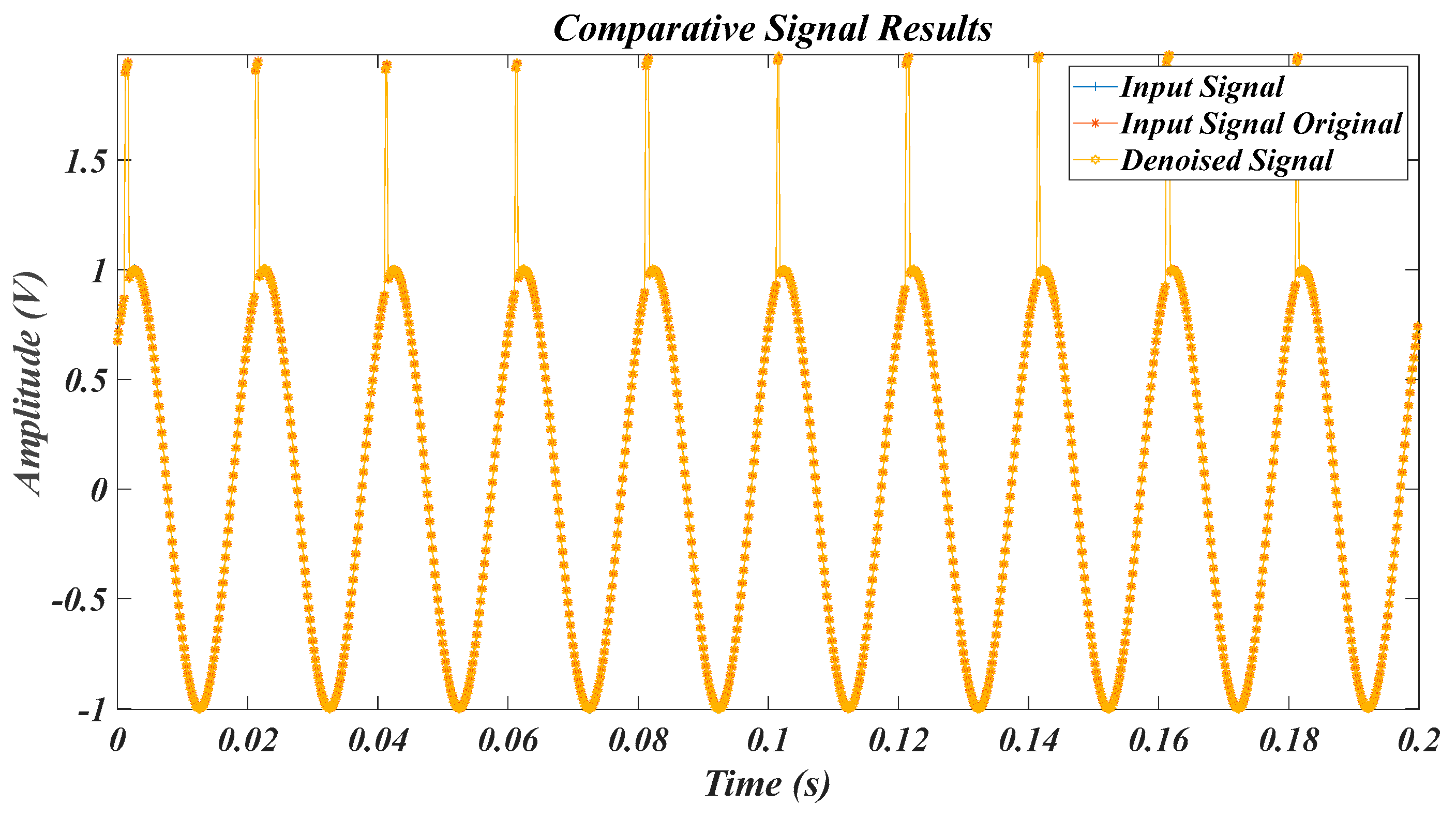
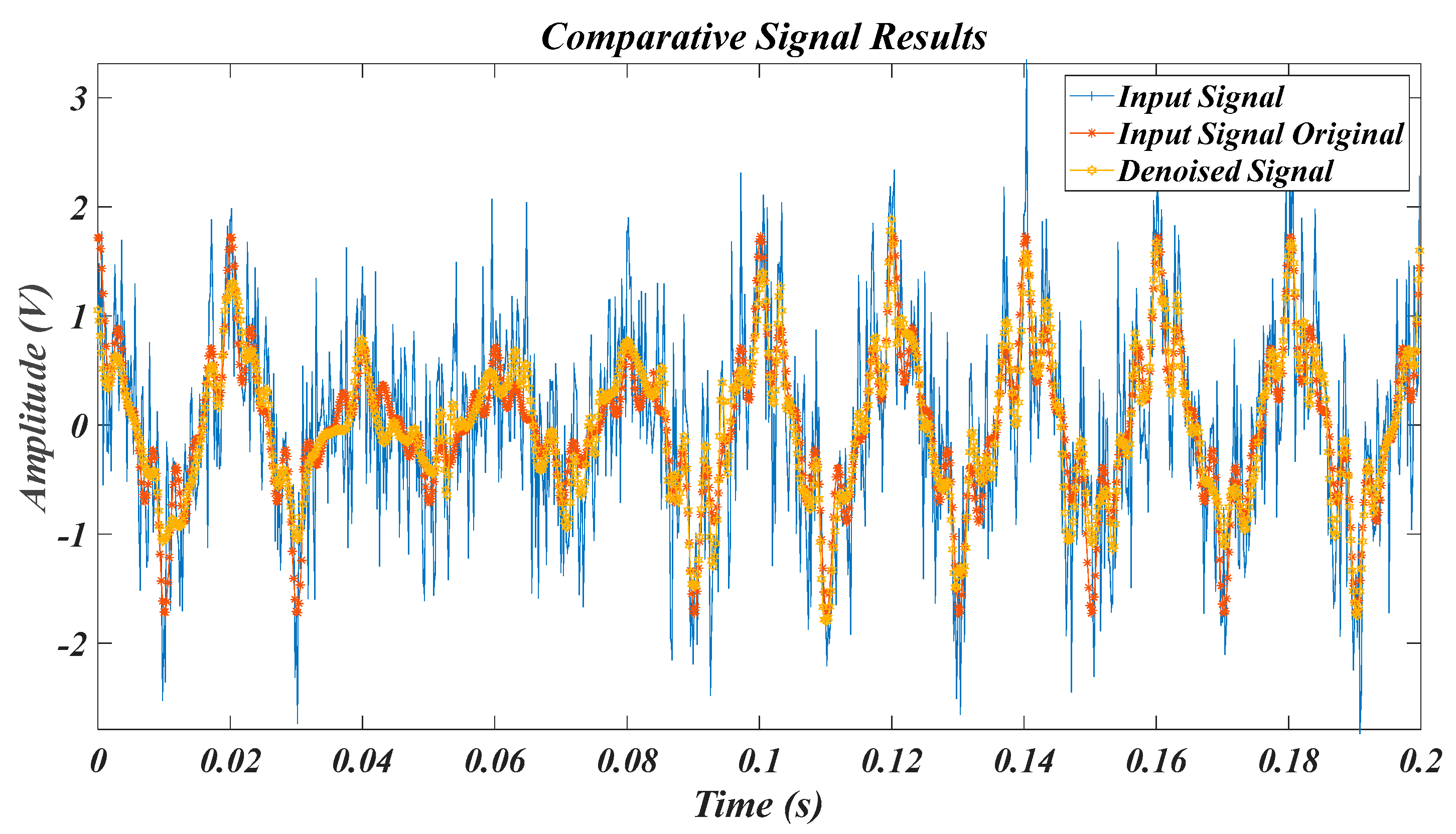
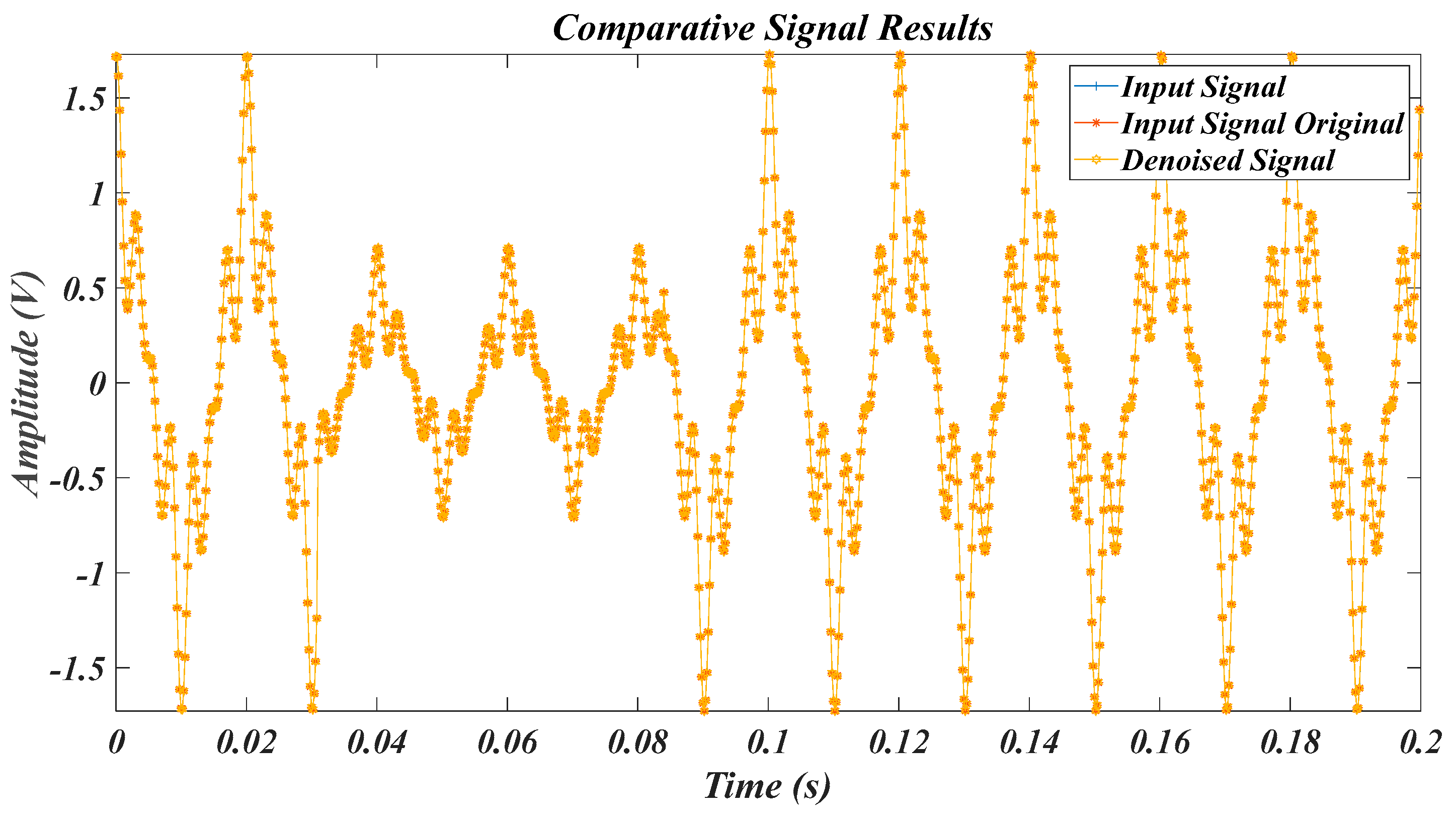
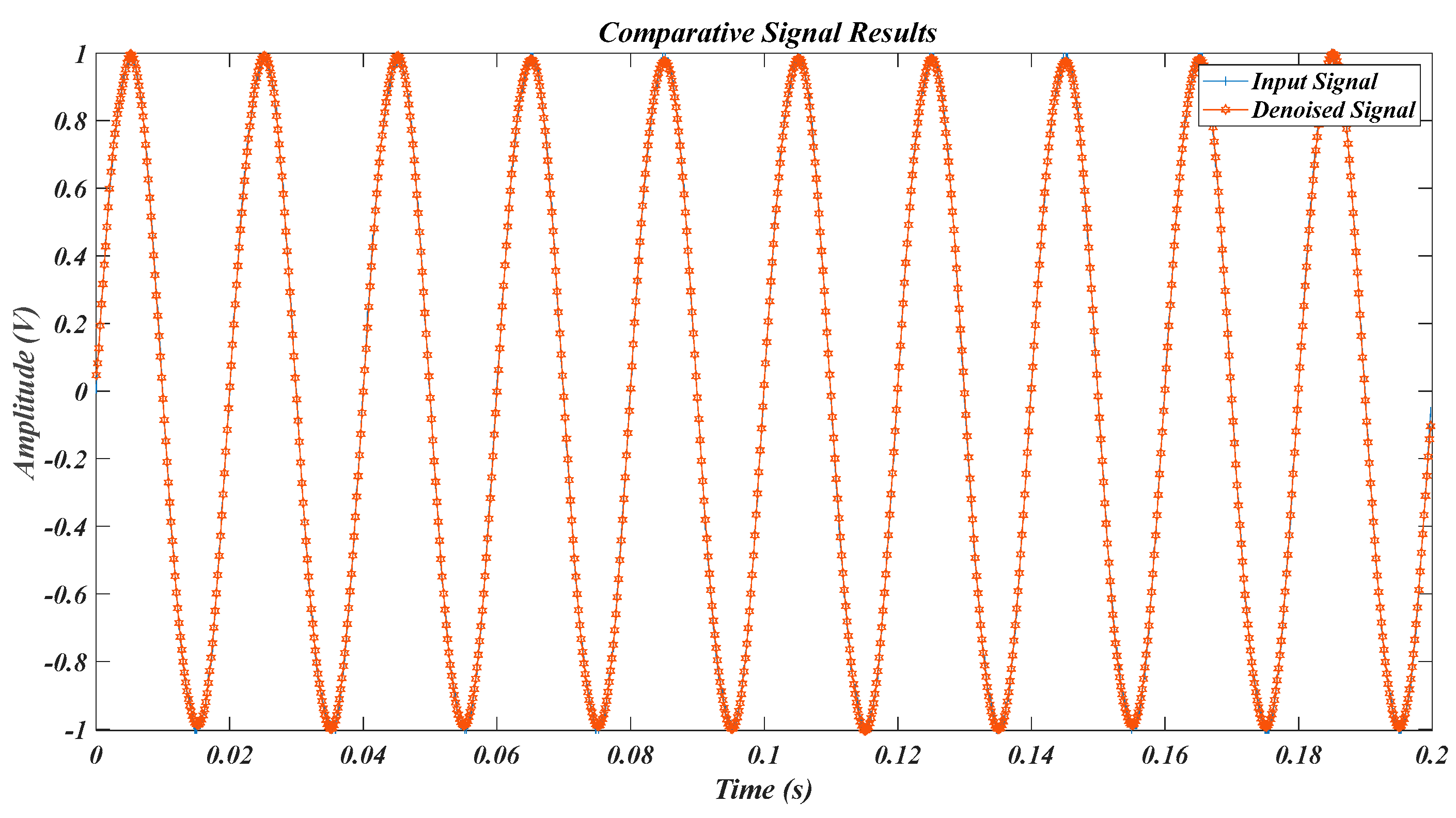
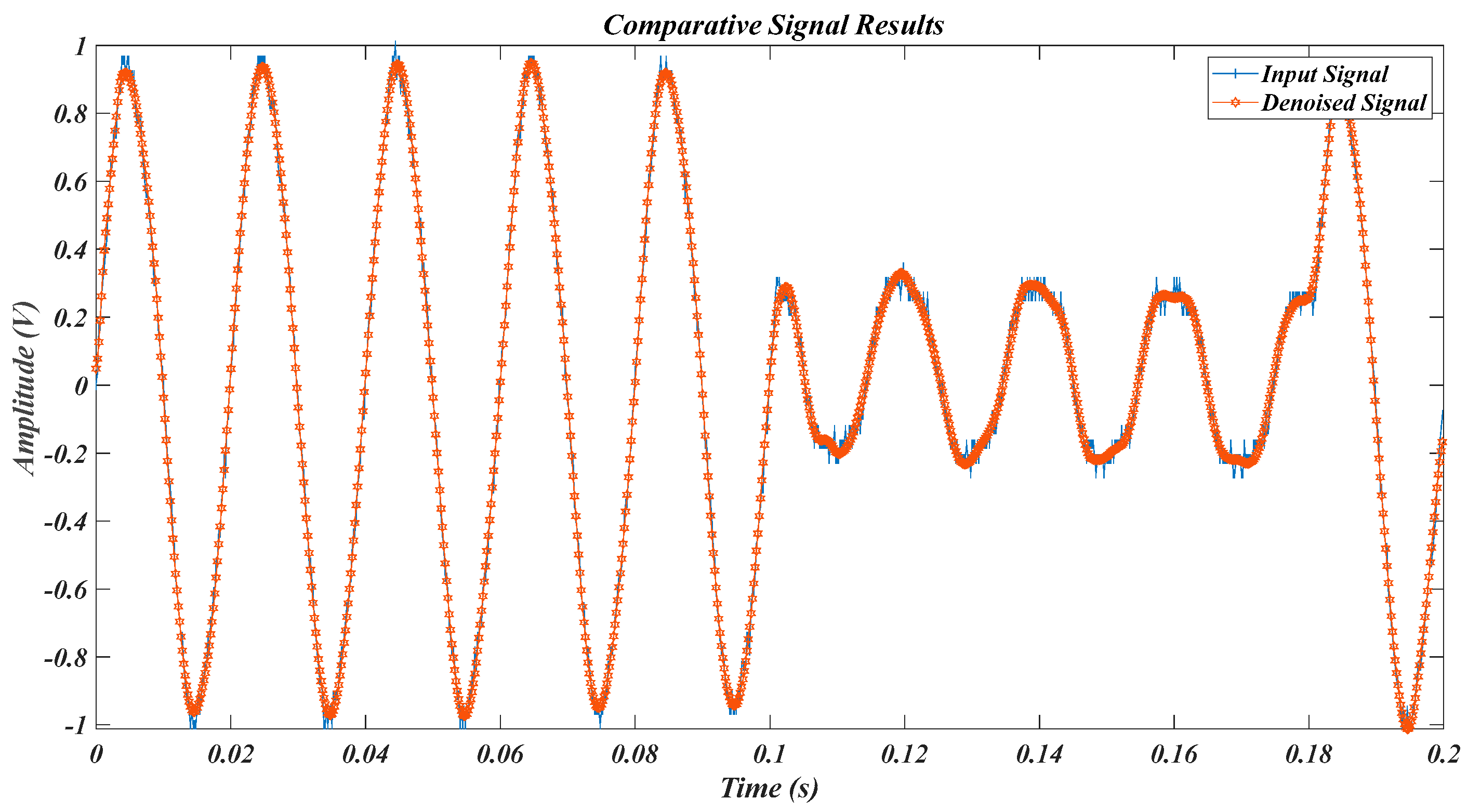
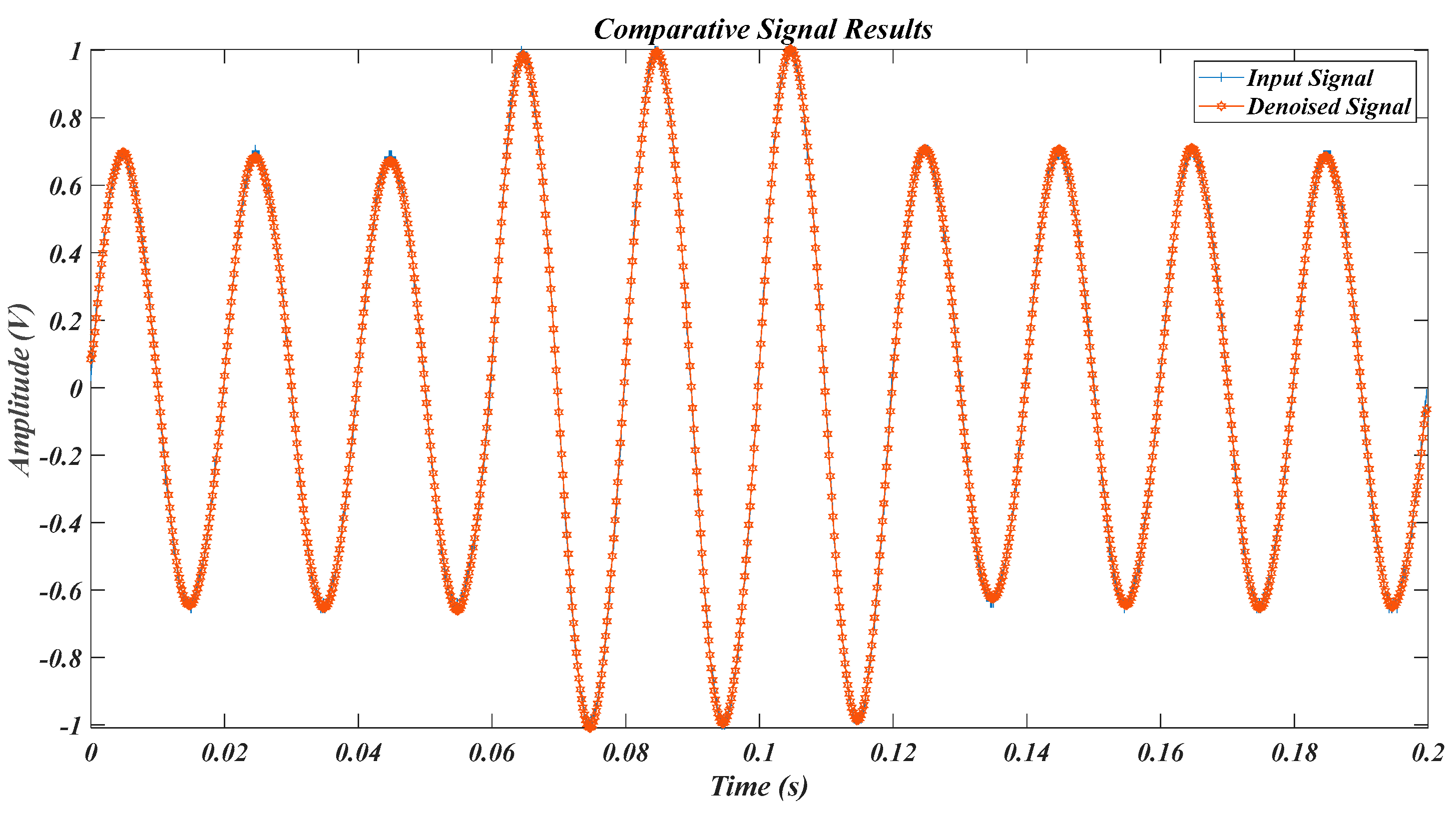
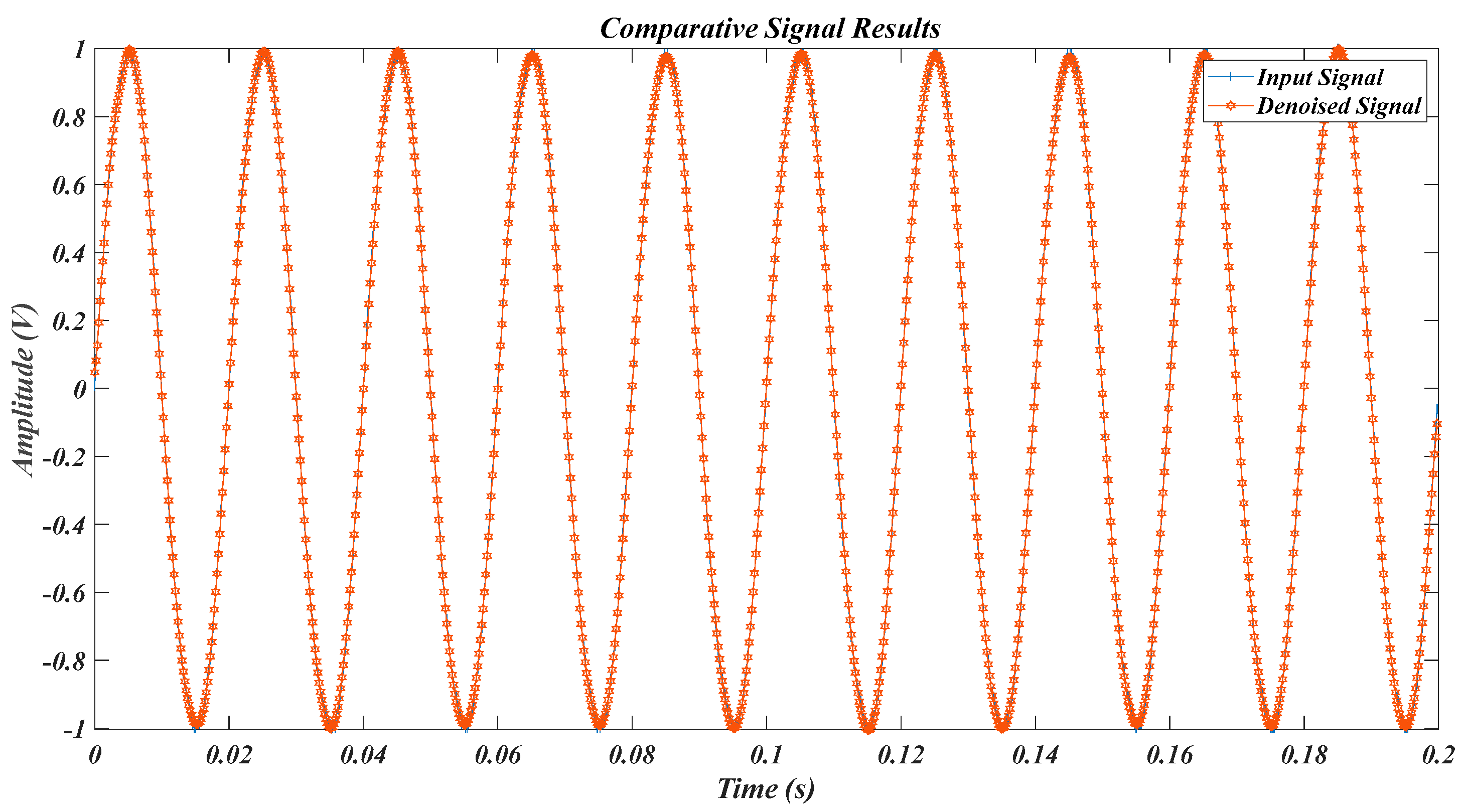

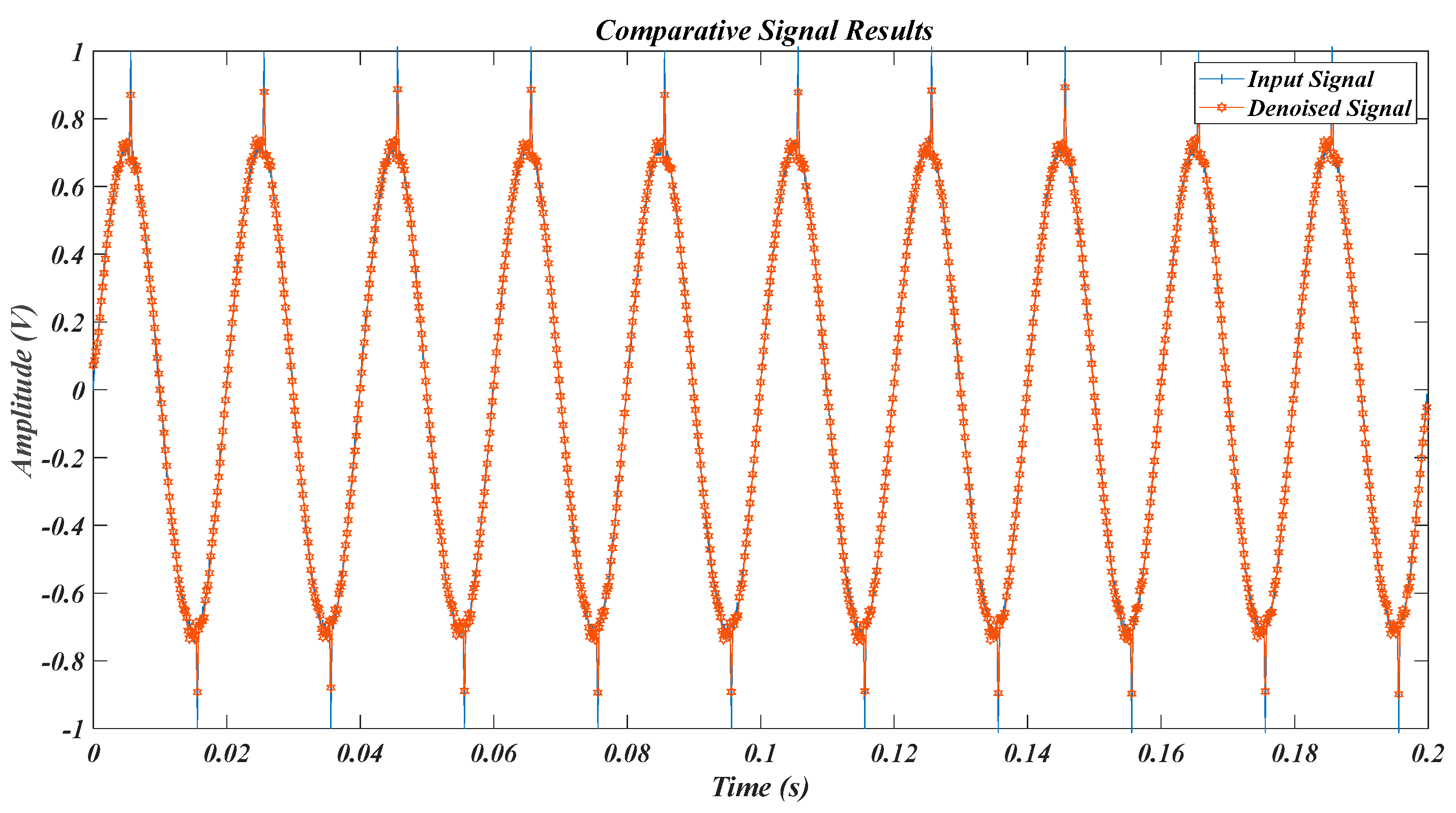
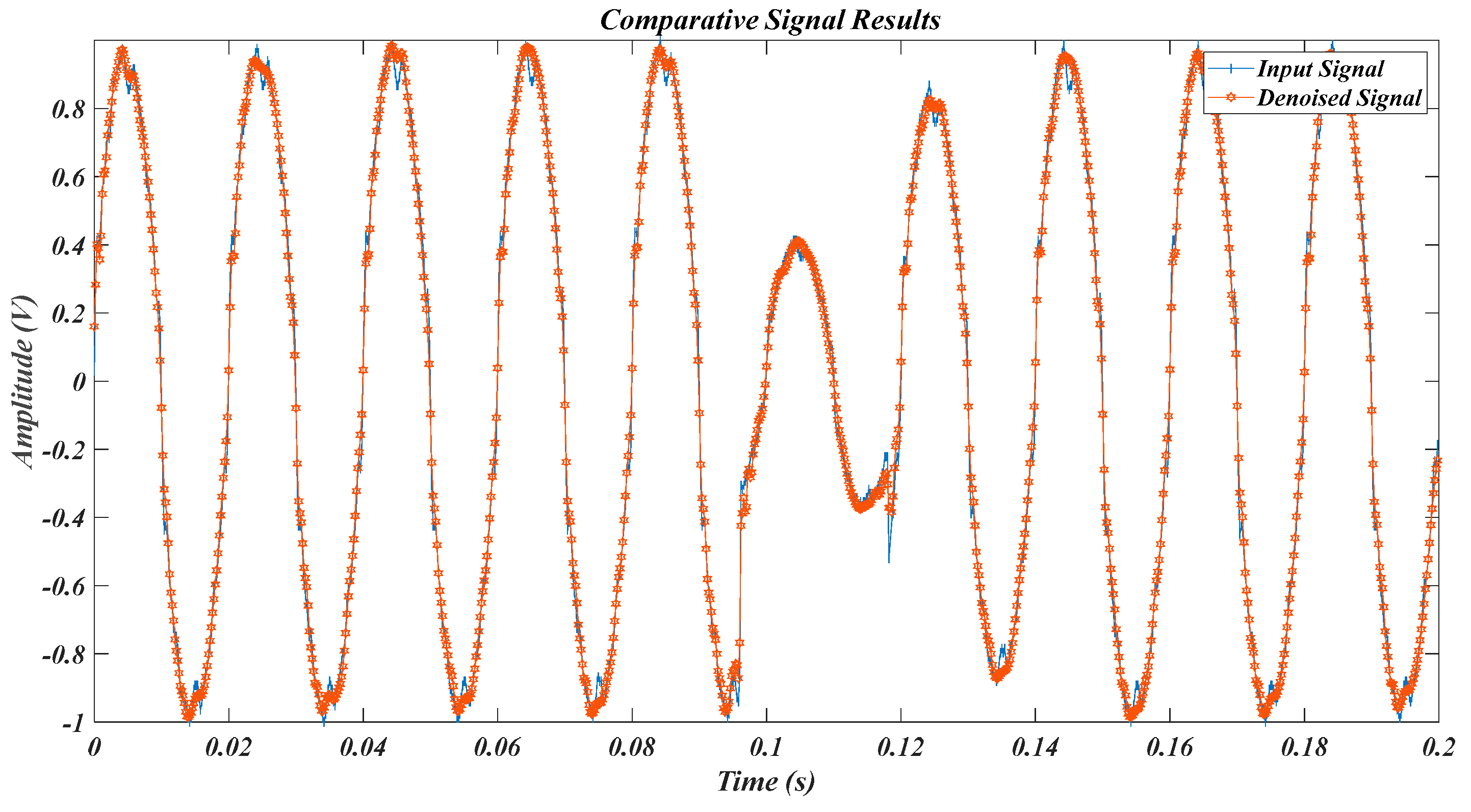
| Test Signal | Label | Test Signal | Label |
|---|---|---|---|
| signal in Table 2 for Equation (1) | L1 | Equation (15) signal in [40] | L4 |
| Equation (11) signal in [36] | L2 | Experimental PQD signals in Table 2 | L5 |
| Arrhythmia data in [54] | L3 |
| Definition | Model Equation | Noisy Model | Parameter | |
|---|---|---|---|---|
| 1 | Pure | |||
| 2 | Sag | | ||
| 3 | Swell | | ||
| 4 | Flicker | | ||
| 5 | Harmonics | |||
| 6 | Spikes | | ||
| 7 | Sag and Harmonics | |
| Variable | Definition | Value |
|---|---|---|
| Wavelet_mat | Wavelet Types | [“sym”, ”db”, ”fk”, ”bior”, ”coif”] |
| sym_Num | Number of Sym Wavelet | [2:1:8] |
| db_Num | Number of db Wavelet | [1:1:10] |
| fk_Num | Number of fk Wavelet | [4, 6, 8, 14, 18, 22] |
| bior_Num | Number of bior Wavelet | [1.1, 1.3, 1.5, 2.2, 2.4, 2.6, 2.8, 3.1, 3.3, 3.5, 3.7, 3.9, 4.4, 5.5, 6.8] |
| coif_Num | Number of coif Wavelet | [1:1:5] |
| DenoisingMethod_mat | Denoising Method Types | [“BlockJS”, ”Bayes”, ”FDR”, ”Minimax”, ”SURE”, ”UniversalThreshold”] |
| wavelet_type | Wavelet Type | merge(Wavelet_mat(i),num2str(sym_Num(symlp))) |
| Max_Level | Maximum Level of Denoising Method | [7, 9] |
| L_DM | Length of DenoisingMethod_mat | 6 |
| L_WM | Length of Wavelet_mat | 5 |
| ThresholdRule_BlockJS_mat | ThresholdRules of BlockJS | [“James-Stein”] |
| ThresholdRule_Bayes_mat | ThresholdRules of Bayes | [“Median”, ”Mean”, ”Soft”, ”Hard”] |
| ThresholdRule_FDR_mat | ThresholdRules of FDR | [“Hard”] |
| ThresholdRule_Minimax_mat | ThresholdRules of Minimax | [“Soft”, ”Hard”] |
| ThresholdRule_SURE_mat | ThresholdRules of SURE | [“Soft”, ”Hard”] |
| ThresholdRule_UniversalThreshold_mat | ThresholdRules of UniversalThreshold | [“Soft”, ”Hard”] |
| L_TRBM | Length of ThresholdRule_Bayes_mat | 4 |
| L_TRMMM | Length of ThresholdRule_Minimax_mat | 2 |
| L_TRSM | Length of ThresholdRule_SURE_mat | 2 |
| L_TRUTM | Length of ThresholdRule_UniversalThreshold_mat | 2 |
| Parameter | Count | Parameter | Count | Parameter | Count | Parameter | Count | Parameter | Count | Parameter | Count |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 516 | FDR | 387 | bior1.5 | 106 | bior5.5 | 106 | db4 | 106 | fk8 | 106 |
| 2 | 516 | Hard | 1935 | bior2.2 | 106 | bior6.8 | 106 | db5 | 106 | sym2 | 106 |
| 3 | 516 | James-Stein | 301 | bior2.4 | 106 | coif1 | 106 | db6 | 106 | sym3 | 106 |
| 4 | 516 | Mean | 387 | bior2.6 | 106 | coif2 | 106 | db7 | 106 | sym4 | 106 |
| 5 | 516 | Median | 387 | bior2.8 | 106 | coif3 | 106 | db8 | 106 | sym5 | 106 |
| 6 | 516 | Minimax | 774 | bior3.1 | 106 | coif4 | 106 | db9 | 106 | sym6 | 106 |
| 7 | 516 | SURE | 774 | bior3.3 | 106 | coif5 | 106 | fk14 | 106 | sym7 | 106 |
| 8 | 473 | Soft | 1548 | bior3.5 | 106 | db1 | 106 | fk18 | 106 | sym8 | 106 |
| 9 | 473 | UniversalThreshold | 774 | bior3.7 | 106 | db10 | 106 | fk22 | 106 | ||
| Bayes | 1935 | bior1.1 | 106 | bior3.9 | 106 | db2 | 106 | fk4 | 106 | ||
| BlockJS | 301 | bior1.3 | 106 | bior4.4 | 106 | db3 | 106 | fk6 | 106 |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 14.475 | 1347.535 | 2.524 | 0.536 | 78.779 | 6.371 | 0.287 | 95.497 | 0.749 | 0.983 | 31.233 |
| 2 | 16.869 | 743.457 | 2.270 | 0.407 | 82.085 | 5.151 | 0.165 | 96.790 | 0.783 | 0.990 | 26.373 |
| 3 | 16.438 | 447.930 | 1.992 | 0.427 | 78.545 | 3.967 | 0.183 | 95.397 | 0.808 | 0.989 | 22.311 |
| 4 | 17.871 | 346.775 | 1.781 | 0.362 | 79.660 | 3.173 | 0.131 | 95.863 | 0.845 | 0.992 | 17.354 |
| 5 | 18.255 | 265.096 | 1.570 | 0.347 | 77.923 | 2.465 | 0.120 | 95.126 | 0.875 | 0.993 | 13.414 |
| 10 | 21.724 | 117.239 | 0.900 | 0.233 | 74.171 | 0.810 | 0.054 | 93.328 | 0.954 | 0.997 | 4.482 |
| 15 | 23.841 | 58.942 | 0.526 | 0.182 | 65.361 | 0.277 | 0.033 | 88.002 | 0.983 | 0.998 | 1.518 |
| 20 | 28.743 | 43.713 | 0.274 | 0.104 | 62.168 | 0.075 | 0.011 | 85.687 | 0.995 | 0.999 | 0.400 |
| 25 | 34.021 | 36.082 | 0.157 | 0.056 | 64.028 | 0.025 | 0.003 | 87.060 | 0.998 | 1.000 | 0.132 |
| 30 | 38.312 | 27.708 | 0.085 | 0.034 | 59.702 | 0.007 | 0.001 | 83.761 | 1.000 | 1.000 | 0.038 |
| 35 | 41.704 | 19.154 | 0.050 | 0.023 | 53.065 | 0.002 | 0.001 | 77.971 | 1.000 | 1.000 | 0.012 |
| 40 | 45.478 | 13.696 | 0.029 | 0.015 | 47.969 | 0.001 | 0.000 | 72.927 | 1.000 | 1.000 | 0.004 |
| 45 | 50.332 | 11.849 | 0.016 | 0.009 | 47.193 | 0.000 | 0.000 | 72.115 | 1.000 | 1.000 | 0.001 |
| 50 | 55.821 | 11.642 | 0.009 | 0.005 | 49.445 | 0.000 | 0.000 | 74.442 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | fk22 | Hard | FDR | 10 | 5 | fk18 | Mean | Bayes | 35 | 3 | fk22 | Mean | Bayes |
| 2 | 7 | fk18 | Soft | Bayes | 15 | 5 | db10 | Soft | Bayes | 40 | 6 | bior6.8 | Hard | Bayes |
| 3 | 6 | fk22 | Hard | FDR | 20 | 3 | fk18 | James-Stein | BlockJS | 45 | 2 | bior6.8 | Hard | FDR |
| 4 | 5 | fk22 | Hard | FDR | 25 | 4 | fk22 | James-Stein | BlockJS | 50 | 2 | coif5 | Hard | FDR |
| 5 | 5 | fk22 | Soft | Bayes | 30 | 4 | fk22 | James-Stein | BlockJS |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 18.173 | 1773.480 | 0.368 | 0.051 | 86.159 | 0.136 | 0.003 | 98.084 | 0.587 | 0.981 | 66.961 |
| 2 | 18.662 | 1766.208 | 0.335 | 0.048 | 85.605 | 0.112 | 0.002 | 97.928 | 0.613 | 0.983 | 60.218 |
| 3 | 18.531 | 826.528 | 0.296 | 0.049 | 83.482 | 0.088 | 0.002 | 97.272 | 0.656 | 0.982 | 49.815 |
| 4 | 19.407 | 546.912 | 0.259 | 0.044 | 82.914 | 0.067 | 0.002 | 97.081 | 0.710 | 0.985 | 38.822 |
| 5 | 20.357 | 408.930 | 0.231 | 0.040 | 82.823 | 0.053 | 0.002 | 97.049 | 0.737 | 0.988 | 34.124 |
| 10 | 23.596 | 162.177 | 0.132 | 0.027 | 79.280 | 0.017 | 0.001 | 95.707 | 0.893 | 0.995 | 11.422 |
| 15 | 27.245 | 94.608 | 0.074 | 0.018 | 75.704 | 0.005 | 0.000 | 94.097 | 0.961 | 0.998 | 3.849 |
| 20 | 31.507 | 65.828 | 0.041 | 0.011 | 73.167 | 0.002 | 0.000 | 92.800 | 0.988 | 0.999 | 1.155 |
| 25 | 36.902 | 53.756 | 0.023 | 0.006 | 74.653 | 0.001 | 0.000 | 93.575 | 0.996 | 1.000 | 0.381 |
| 30 | 40.810 | 40.723 | 0.013 | 0.004 | 71.768 | 0.000 | 0.000 | 92.030 | 0.999 | 1.000 | 0.123 |
| 35 | 45.436 | 33.636 | 0.007 | 0.002 | 69.718 | 0.000 | 0.000 | 90.830 | 1.000 | 1.000 | 0.036 |
| 40 | 49.799 | 27.690 | 0.004 | 0.001 | 68.381 | 0.000 | 0.000 | 90.002 | 1.000 | 1.000 | 0.012 |
| 45 | 54.955 | 24.899 | 0.002 | 0.001 | 68.024 | 0.000 | 0.000 | 89.775 | 1.000 | 1.000 | 0.004 |
| 50 | 59.126 | 20.666 | 0.001 | 0.000 | 65.128 | 0.000 | 0.000 | 87.839 | 1.000 | 1.000 | 0.001 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | db4 | Mean | Bayes | 10 | 7 | sym7 | Mean | Bayes | 35 | 6 | bior4.4 | Median | Bayes |
| 2 | 7 | db5 | Mean | Bayes | 15 | 7 | sym6 | Mean | Bayes | 40 | 6 | coif2 | Median | Bayes |
| 3 | 8 | sym3 | Soft | SURE | 20 | 8 | coif1 | Mean | Bayes | 45 | 9 | bior4.4 | Median | Bayes |
| 4 | 7 | sym3 | Mean | Bayes | 25 | 6 | coif2 | Mean | Bayes | 50 | 8 | sym4 | Median | Bayes |
| 5 | 8 | fk18 | Soft | SURE | 30 | 6 | bior4.4 | Median | Bayes |
| Normal ECG | Abnormal ECG | |||
|---|---|---|---|---|
(dB) | (dB) | (%) | (dB) | (%) |
| 1 | 9.22 | 822 | 8.16 | 716 |
| 5 | 20.01 | 300.2 | 18.10 | 262 |
| 10 | 19.56 | 95.6 | 15.57 | 55.7 |
| 20 | 32.95 | 64.75 | 22.07 | 10.35 |
| 30 | 42.03 | 40.1 | 31.35 | 4.5 |
| 40 | 50.37 | 25.93 | 40.98 | 2.45 |
| 50 | 56.91 | 13.82 | 54.27 | 8.54 |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11.312 | 1031.184 | 0.918 | 0.282 | 69.311 | 0.844 | 0.079 | 90.582 | 0.750 | 0.963 | 28.421 |
| 2 | 13.120 | 556.006 | 0.797 | 0.229 | 71.264 | 0.634 | 0.052 | 91.742 | 0.791 | 0.975 | 23.283 |
| 3 | 11.996 | 299.851 | 0.769 | 0.261 | 66.125 | 0.592 | 0.068 | 88.525 | 0.807 | 0.970 | 20.140 |
| 4 | 14.037 | 250.918 | 0.663 | 0.206 | 68.938 | 0.440 | 0.042 | 90.351 | 0.846 | 0.980 | 15.846 |
| 5 | 14.858 | 197.161 | 0.575 | 0.187 | 67.430 | 0.331 | 0.035 | 89.392 | 0.874 | 0.985 | 12.631 |
| 10 | 19.487 | 94.873 | 0.321 | 0.110 | 65.740 | 0.103 | 0.012 | 88.262 | 0.956 | 0.995 | 4.033 |
| 15 | 24.629 | 64.192 | 0.179 | 0.061 | 65.979 | 0.032 | 0.004 | 88.426 | 0.985 | 0.998 | 1.314 |
| 20 | 28.318 | 41.588 | 0.103 | 0.040 | 61.339 | 0.011 | 0.002 | 85.053 | 0.995 | 0.999 | 0.420 |
| 25 | 32.956 | 31.822 | 0.055 | 0.023 | 57.559 | 0.003 | 0.001 | 81.987 | 0.999 | 1.000 | 0.116 |
| 30 | 36.808 | 22.694 | 0.032 | 0.015 | 53.240 | 0.001 | 0.000 | 78.135 | 1.000 | 1.000 | 0.037 |
| 35 | 41.155 | 17.586 | 0.019 | 0.009 | 51.315 | 0.000 | 0.000 | 76.298 | 1.000 | 1.000 | 0.012 |
| 40 | 45.605 | 14.013 | 0.011 | 0.005 | 50.137 | 0.000 | 0.000 | 75.137 | 1.000 | 1.000 | 0.004 |
| 45 | 49.865 | 10.811 | 0.006 | 0.003 | 45.152 | 0.000 | 0.000 | 69.917 | 1.000 | 1.000 | 0.001 |
| 50 | 55.655 | 11.310 | 0.003 | 0.002 | 47.682 | 0.000 | 0.000 | 72.629 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | db7 | Soft | SURE | 10 | 9 | sym7 | Soft | Bayes | 35 | 3 | sym7 | Mean | Bayes |
| 2 | 5 | fk22 | Soft | SURE | 15 | 3 | fk22 | James-Stein | BlockJS | 40 | 3 | db8 | Median | Bayes |
| 3 | 9 | sym7 | Soft | SURE | 20 | 3 | fk14 | James-Stein | BlockJS | 45 | 2 | coif4 | Hard | FDR |
| 4 | 7 | fk18 | Mean | Bayes | 25 | 3 | fk22 | James-Stein | BlockJS | 50 | 2 | db8 | James-Stein | BlockJS |
| 5 | 3 | coif4 | James-Stein | BlockJS | 30 | 9 | db8 | Mean | Bayes |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11.312 | 1031.184 | 0.918 | 0.282 | 69.311 | 0.844 | 0.079 | 90.582 | 0.750 | 0.963 | 28.421 |
| 2 | 13.120 | 556.006 | 0.797 | 0.229 | 71.264 | 0.634 | 0.052 | 91.742 | 0.791 | 0.975 | 23.283 |
| 3 | 11.996 | 299.851 | 0.769 | 0.261 | 66.125 | 0.592 | 0.068 | 88.525 | 0.807 | 0.970 | 20.140 |
| 4 | 14.037 | 250.918 | 0.663 | 0.206 | 68.938 | 0.440 | 0.042 | 90.351 | 0.846 | 0.980 | 15.846 |
| 5 | 14.858 | 197.161 | 0.575 | 0.187 | 67.430 | 0.331 | 0.035 | 89.392 | 0.874 | 0.985 | 12.631 |
| 10 | 19.487 | 94.873 | 0.321 | 0.110 | 65.740 | 0.103 | 0.012 | 88.262 | 0.956 | 0.995 | 4.033 |
| 15 | 24.629 | 64.192 | 0.179 | 0.061 | 65.979 | 0.032 | 0.004 | 88.426 | 0.985 | 0.998 | 1.314 |
| 20 | 28.318 | 41.588 | 0.103 | 0.040 | 61.339 | 0.011 | 0.002 | 85.053 | 0.995 | 0.999 | 0.420 |
| 25 | 32.956 | 31.822 | 0.055 | 0.023 | 57.559 | 0.003 | 0.001 | 81.987 | 0.999 | 1.000 | 0.116 |
| 30 | 36.808 | 22.694 | 0.032 | 0.015 | 53.240 | 0.001 | 0.000 | 78.135 | 1.000 | 1.000 | 0.037 |
| 35 | 41.155 | 17.586 | 0.019 | 0.009 | 51.315 | 0.000 | 0.000 | 76.298 | 1.000 | 1.000 | 0.012 |
| 40 | 45.605 | 14.013 | 0.011 | 0.005 | 50.137 | 0.000 | 0.000 | 75.137 | 1.000 | 1.000 | 0.004 |
| 45 | 49.865 | 10.811 | 0.006 | 0.003 | 45.152 | 0.000 | 0.000 | 69.917 | 1.000 | 1.000 | 0.001 |
| 50 | 55.655 | 11.310 | 0.003 | 0.002 | 47.682 | 0.000 | 0.000 | 72.629 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | coif5 | James-Stein | BlockJS | 10 | 5 | fk22 | Soft | SURE | 35 | 4 | sym8 | Soft | Bayes |
| 2 | 9 | fk18 | Soft | Bayes | 15 | 5 | coif4 | Median | Bayes | 40 | 4 | db9 | Hard | FDR |
| 3 | 5 | fk22 | James-Stein | BlockJS | 20 | 9 | bior6.8 | Soft | Bayes | 45 | 4 | db10 | Median | Bayes |
| 4 | 6 | fk22 | Hard | Bayes | 25 | 8 | db9 | Hard | FDR | 50 | 6 | db10 | James-Stein | BlockJS |
| 5 | 5 | fk18 | James-Stein | BlockJS | 30 | 4 | sym8 | Soft | Bayes |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 13.628 | 1262.772 | 0.305 | 0.071 | 76.664 | 0.093 | 0.005 | 94.555 | 0.768 | 0.979 | 27.544 |
| 2 | 15.166 | 658.303 | 0.272 | 0.060 | 78.081 | 0.074 | 0.004 | 95.195 | 0.782 | 0.985 | 25.951 |
| 3 | 15.150 | 404.997 | 0.246 | 0.060 | 75.748 | 0.061 | 0.004 | 94.118 | 0.814 | 0.985 | 20.956 |
| 4 | 15.182 | 279.539 | 0.206 | 0.059 | 71.127 | 0.042 | 0.004 | 91.664 | 0.850 | 0.985 | 15.810 |
| 5 | 19.629 | 292.577 | 0.183 | 0.036 | 80.551 | 0.034 | 0.001 | 96.217 | 0.878 | 0.995 | 13.303 |
| 10 | 19.554 | 95.542 | 0.114 | 0.036 | 68.518 | 0.013 | 0.001 | 90.089 | 0.949 | 0.995 | 4.766 |
| 15 | 24.535 | 63.567 | 0.062 | 0.020 | 67.326 | 0.004 | 0.000 | 89.324 | 0.984 | 0.998 | 1.423 |
| 20 | 29.984 | 49.919 | 0.034 | 0.011 | 68.307 | 0.001 | 0.000 | 89.956 | 0.995 | 0.999 | 0.448 |
| 25 | 33.828 | 35.310 | 0.019 | 0.007 | 64.166 | 0.000 | 0.000 | 87.159 | 0.998 | 1.000 | 0.141 |
| 30 | 38.917 | 29.722 | 0.011 | 0.004 | 64.357 | 0.000 | 0.000 | 87.296 | 0.999 | 1.000 | 0.044 |
| 35 | 43.295 | 23.701 | 0.006 | 0.002 | 61.849 | 0.000 | 0.000 | 85.445 | 1.000 | 1.000 | 0.014 |
| 40 | 48.150 | 20.374 | 0.003 | 0.001 | 60.618 | 0.000 | 0.000 | 84.491 | 1.000 | 1.000 | 0.004 |
| 45 | 52.685 | 17.078 | 0.002 | 0.001 | 57.359 | 0.000 | 0.000 | 81.817 | 1.000 | 1.000 | 0.001 |
| 50 | 57.344 | 14.688 | 0.001 | 0.000 | 57.374 | 0.000 | 0.000 | 81.830 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | fk22 | James-Stein | BlockJS | 10 | 5 | sym8 | Mean | Bayes | 35 | 4 | db6 | Median | Bayes |
| 2 | 5 | fk22 | Hard | FDR | 15 | 6 | coif5 | Mean | Bayes | 40 | 4 | db8 | Hard | UT |
| 3 | 6 | coif5 | Soft | Bayes | 20 | 4 | sym7 | Hard | UT | 45 | 7 | coif4 | Median | Bayes |
| 4 | 9 | sym8 | Hard | Bayes | 25 | 4 | sym6 | Median | Bayes | 50 | 3 | bior5.5 | Median | Bayes |
| 5 | 5 | coif5 | Soft | Bayes | 30 | 4 | bior5.5 | Mean | Bayes |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 17.681 | 1668.115 | 0.673 | 0.102 | 84.863 | 0.453 | 0.010 | 97.709 | 0.759 | 0.992 | 30.724 |
| 2 | 16.680 | 733.990 | 0.608 | 0.114 | 81.200 | 0.370 | 0.013 | 96.466 | 0.796 | 0.990 | 24.255 |
| 3 | 16.009 | 433.625 | 0.566 | 0.123 | 78.198 | 0.321 | 0.015 | 95.247 | 0.806 | 0.988 | 22.483 |
| 4 | 20.559 | 413.969 | 0.475 | 0.073 | 84.606 | 0.226 | 0.005 | 97.630 | 0.855 | 0.996 | 16.446 |
| 5 | 19.613 | 292.258 | 0.433 | 0.082 | 81.154 | 0.187 | 0.007 | 96.448 | 0.869 | 0.995 | 14.516 |
| 10 | 23.952 | 139.519 | 0.242 | 0.049 | 79.532 | 0.058 | 0.002 | 95.811 | 0.956 | 0.998 | 4.431 |
| 15 | 26.554 | 77.029 | 0.140 | 0.037 | 73.720 | 0.019 | 0.001 | 93.094 | 0.984 | 0.999 | 1.476 |
| 20 | 30.586 | 52.928 | 0.076 | 0.023 | 69.855 | 0.006 | 0.001 | 90.913 | 0.995 | 1.000 | 0.441 |
| 25 | 36.696 | 46.783 | 0.045 | 0.011 | 74.373 | 0.002 | 0.000 | 93.433 | 0.998 | 1.000 | 0.153 |
| 30 | 39.646 | 32.152 | 0.025 | 0.008 | 67.440 | 0.001 | 0.000 | 89.398 | 0.999 | 1.000 | 0.046 |
| 35 | 43.957 | 25.592 | 0.014 | 0.005 | 65.009 | 0.000 | 0.000 | 87.756 | 1.000 | 1.000 | 0.014 |
| 40 | 47.795 | 19.487 | 0.008 | 0.003 | 58.212 | 0.000 | 0.000 | 82.538 | 1.000 | 1.000 | 0.004 |
| 45 | 51.881 | 15.290 | 0.004 | 0.002 | 55.823 | 0.000 | 0.000 | 80.484 | 1.000 | 1.000 | 0.001 |
| 50 | 58.034 | 16.068 | 0.002 | 0.001 | 60.615 | 0.000 | 0.000 | 84.488 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | fk22 | Soft | Bayes | 10 | 5 | fk22 | Hard | FDR | 35 | 4 | coif4 | Hard | UT |
| 2 | 9 | fk22 | Median | Bayes | 15 | 8 | fk18 | Soft | Bayes | 40 | 5 | sym7 | Median | Bayes |
| 3 | 6 | fk14 | James-Stein | BlockJS | 20 | 5 | sym8 | James-Stein | BlockJS | 45 | 4 | db9 | Mean | Bayes |
| 4 | 8 | fk22 | Soft | Bayes | 25 | 4 | coif4 | Hard | FDR | 50 | 3 | bior6.8 | Hard | UT |
| 5 | 6 | fk22 | Hard | Bayes | 30 | 4 | coif4 | Hard | UT |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15.210 | 1421.003 | 0.650 | 0.124 | 80.947 | 0.422 | 0.015 | 96.370 | 0.734 | 0.985 | 34.242 |
| 2 | 16.242 | 712.119 | 0.572 | 0.110 | 80.773 | 0.327 | 0.012 | 96.303 | 0.782 | 0.988 | 26.418 |
| 3 | 15.647 | 421.561 | 0.511 | 0.118 | 76.960 | 0.261 | 0.014 | 94.692 | 0.811 | 0.987 | 21.762 |
| 4 | 19.009 | 375.237 | 0.449 | 0.080 | 82.207 | 0.202 | 0.006 | 96.834 | 0.853 | 0.995 | 16.541 |
| 5 | 17.836 | 256.725 | 0.406 | 0.091 | 77.459 | 0.165 | 0.008 | 94.919 | 0.876 | 0.993 | 13.285 |
| 10 | 21.865 | 118.650 | 0.234 | 0.058 | 75.408 | 0.055 | 0.003 | 93.952 | 0.950 | 0.997 | 4.964 |
| 15 | 26.766 | 78.438 | 0.128 | 0.033 | 74.399 | 0.016 | 0.001 | 93.446 | 0.984 | 0.999 | 1.506 |
| 20 | 32.002 | 60.008 | 0.072 | 0.018 | 75.131 | 0.005 | 0.000 | 93.816 | 0.995 | 1.000 | 0.475 |
| 25 | 38.275 | 53.100 | 0.040 | 0.009 | 78.139 | 0.002 | 0.000 | 95.221 | 0.998 | 1.000 | 0.148 |
| 30 | 42.229 | 40.762 | 0.023 | 0.006 | 75.831 | 0.001 | 0.000 | 94.158 | 0.999 | 1.000 | 0.048 |
| 35 | 47.040 | 34.401 | 0.013 | 0.003 | 74.730 | 0.000 | 0.000 | 93.614 | 1.000 | 1.000 | 0.014 |
| 40 | 51.500 | 28.751 | 0.007 | 0.002 | 72.605 | 0.000 | 0.000 | 92.495 | 1.000 | 1.000 | 0.004 |
| 45 | 55.398 | 23.107 | 0.004 | 0.001 | 70.432 | 0.000 | 0.000 | 91.258 | 1.000 | 1.000 | 0.002 |
| 50 | 59.120 | 18.241 | 0.002 | 0.001 | 64.279 | 0.000 | 0.000 | 87.240 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | fk22 | James-Stein | BlockJS | 10 | 5 | fk22 | Median | Bayes | 35 | 9 | db9 | Hard | FDR |
| 2 | 5 | fk22 | James-Stein | BlockJS | 15 | 4 | bior6.8 | James-Stein | BlockJS | 40 | 7 | coif5 | James-Stein | BlockJS |
| 3 | 9 | db10 | Soft | SURE | 20 | 4 | coif4 | Soft | UT | 45 | 4 | db10 | James-Stein | BlockJS |
| 4 | 6 | fk22 | Soft | SURE | 25 | 4 | db9 | Median | Bayes | 50 | 3 | db6 | James-Stein | BlockJS |
| 5 | 8 | fk22 | Soft | Bayes | 30 | 7 | db10 | James-Stein | BlockJS |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10.649 | 964.896 | 0.636 | 0.217 | 65.809 | 0.404 | 0.047 | 88.310 | 0.752 | 0.956 | 27.207 |
| 2 | 10.679 | 433.945 | 0.619 | 0.217 | 65.024 | 0.383 | 0.047 | 87.767 | 0.768 | 0.957 | 24.670 |
| 3 | 11.890 | 296.328 | 0.506 | 0.188 | 62.782 | 0.256 | 0.035 | 86.148 | 0.829 | 0.969 | 16.831 |
| 4 | 12.328 | 208.203 | 0.470 | 0.179 | 61.912 | 0.221 | 0.032 | 85.493 | 0.844 | 0.971 | 15.040 |
| 5 | 13.042 | 160.839 | 0.407 | 0.165 | 59.421 | 0.165 | 0.027 | 83.534 | 0.875 | 0.975 | 11.420 |
| 10 | 16.639 | 66.386 | 0.231 | 0.109 | 52.728 | 0.053 | 0.012 | 77.654 | 0.955 | 0.989 | 3.591 |
| 15 | 20.968 | 39.787 | 0.132 | 0.066 | 49.934 | 0.018 | 0.004 | 74.934 | 0.984 | 0.996 | 1.189 |
| 20 | 26.392 | 31.958 | 0.071 | 0.035 | 49.798 | 0.005 | 0.001 | 74.798 | 0.995 | 0.999 | 0.342 |
| 25 | 31.277 | 25.110 | 0.041 | 0.020 | 50.553 | 0.002 | 0.000 | 75.550 | 0.998 | 1.000 | 0.115 |
| 30 | 36.230 | 20.767 | 0.022 | 0.011 | 49.121 | 0.001 | 0.000 | 74.113 | 1.000 | 1.000 | 0.034 |
| 35 | 40.060 | 14.456 | 0.013 | 0.007 | 43.086 | 0.000 | 0.000 | 67.608 | 1.000 | 1.000 | 0.010 |
| 40 | 43.868 | 9.671 | 0.007 | 0.005 | 35.896 | 0.000 | 0.000 | 58.907 | 1.000 | 1.000 | 0.003 |
| 45 | 48.024 | 6.719 | 0.004 | 0.003 | 27.548 | 0.000 | 0.000 | 47.507 | 1.000 | 1.000 | 0.001 |
| 50 | 53.102 | 6.204 | 0.002 | 0.002 | 29.648 | 0.000 | 0.000 | 50.506 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9 | coif2 | Soft | SURE | 10 | 9 | fk14 | Soft | SURE | 35 | 2 | coif5 | James-Stein | BlockJS |
| 2 | 9 | sym7 | Mean | Bayes | 15 | 7 | bior5.5 | Hard | Bayes | 40 | 2 | coif5 | Mean | Bayes |
| 3 | 4 | coif3 | Soft | SURE | 20 | 2 | fk22 | Soft | UT | 45 | 3 | db10 | Mean | Bayes |
| 4 | 6 | sym3 | Mean | Bayes | 25 | 4 | sym6 | Median | Bayes | 50 | 3 | bior5.5 | Median | Bayes |
| 5 | 5 | db9 | Soft | SURE | 30 | 2 | coif5 | James-Stein | BlockJS |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11.886 | 1088.561 | 0.694 | 0.193 | 72.242 | 0.481 | 0.037 | 92.295 | 0.744 | 0.968 | 30.001 |
| 2 | 11.821 | 491.049 | 0.589 | 0.194 | 67.070 | 0.347 | 0.038 | 89.156 | 0.795 | 0.968 | 21.704 |
| 3 | 13.233 | 341.101 | 0.549 | 0.165 | 69.944 | 0.301 | 0.027 | 90.966 | 0.813 | 0.976 | 20.057 |
| 4 | 12.759 | 218.964 | 0.480 | 0.174 | 63.756 | 0.231 | 0.030 | 86.864 | 0.843 | 0.974 | 15.533 |
| 5 | 13.329 | 166.588 | 0.424 | 0.163 | 61.519 | 0.180 | 0.027 | 85.192 | 0.872 | 0.977 | 11.988 |
| 10 | 16.740 | 67.398 | 0.236 | 0.110 | 53.257 | 0.055 | 0.012 | 78.151 | 0.955 | 0.989 | 3.600 |
| 15 | 20.944 | 39.629 | 0.130 | 0.068 | 47.721 | 0.017 | 0.005 | 72.669 | 0.986 | 0.996 | 1.052 |
| 20 | 26.655 | 33.275 | 0.074 | 0.035 | 52.739 | 0.006 | 0.001 | 77.664 | 0.995 | 0.999 | 0.375 |
| 25 | 31.189 | 24.757 | 0.041 | 0.021 | 48.531 | 0.002 | 0.000 | 73.510 | 0.999 | 1.000 | 0.106 |
| 30 | 35.210 | 17.366 | 0.024 | 0.013 | 45.554 | 0.001 | 0.000 | 70.356 | 0.999 | 1.000 | 0.036 |
| 35 | 39.781 | 13.659 | 0.013 | 0.008 | 42.517 | 0.000 | 0.000 | 66.957 | 1.000 | 1.000 | 0.011 |
| 40 | 44.499 | 11.247 | 0.008 | 0.005 | 41.613 | 0.000 | 0.000 | 65.909 | 1.000 | 1.000 | 0.003 |
| 45 | 49.784 | 10.632 | 0.004 | 0.002 | 41.406 | 0.000 | 0.000 | 65.667 | 1.000 | 1.000 | 0.001 |
| 50 | 54.149 | 8.299 | 0.002 | 0.001 | 40.274 | 0.000 | 0.000 | 64.328 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | fk18 | Mean | Bayes | 10 | 4 | db4 | Mean | Bayes | 35 | 2 | bior2.4 | Hard | UT |
| 2 | 6 | fk18 | James-Stein | BlockJS | 15 | 4 | bior4.4 | Mean | Bayes | 40 | 3 | sym4 | Median | Bayes |
| 3 | 5 | coif5 | Mean | Bayes | 20 | 9 | coif2 | Hard | Bayes | 45 | 3 | bior4.4 | Median | Bayes |
| 4 | 9 | fk18 | Mean | Bayes | 25 | 3 | bior2.2 | Hard | UT | 50 | 5 | bior4.4 | Median | Bayes |
| 5 | 7 | fk14 | Mean | Bayes | 30 | 9 | bior2.4 | Median | Bayes |
(%) | (%) | (%) | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.104 | 810.388 | 0.628 | 0.241 | 61.659 | 0.394 | 0.058 | 85.299 | 0.741 | 0.937 | 26.410 |
| 2 | 9.067 | 353.339 | 0.542 | 0.242 | 55.404 | 0.294 | 0.058 | 80.112 | 0.766 | 0.936 | 22.250 |
| 3 | 9.908 | 230.253 | 0.489 | 0.219 | 55.143 | 0.239 | 0.048 | 79.879 | 0.810 | 0.948 | 16.932 |
| 4 | 10.845 | 171.134 | 0.449 | 0.197 | 56.145 | 0.202 | 0.039 | 80.767 | 0.836 | 0.958 | 14.590 |
| 5 | 12.020 | 140.407 | 0.394 | 0.172 | 56.380 | 0.156 | 0.030 | 80.973 | 0.875 | 0.969 | 10.805 |
| 10 | 16.353 | 63.526 | 0.223 | 0.104 | 53.097 | 0.050 | 0.011 | 78.001 | 0.951 | 0.988 | 3.952 |
| 15 | 20.975 | 39.831 | 0.123 | 0.061 | 50.290 | 0.015 | 0.004 | 75.289 | 0.984 | 0.996 | 1.206 |
| 20 | 25.340 | 26.700 | 0.071 | 0.037 | 47.430 | 0.005 | 0.001 | 72.364 | 0.995 | 0.999 | 0.382 |
| 25 | 30.610 | 22.438 | 0.038 | 0.020 | 46.079 | 0.001 | 0.000 | 70.925 | 0.999 | 1.000 | 0.106 |
| 30 | 34.567 | 15.225 | 0.022 | 0.013 | 41.329 | 0.000 | 0.000 | 65.577 | 0.999 | 1.000 | 0.033 |
| 35 | 38.860 | 11.028 | 0.012 | 0.008 | 33.881 | 0.000 | 0.000 | 56.283 | 1.000 | 1.000 | 0.008 |
| 40 | 43.159 | 7.898 | 0.007 | 0.005 | 30.249 | 0.000 | 0.000 | 51.347 | 1.000 | 1.000 | 0.003 |
| 45 | 48.358 | 7.462 | 0.004 | 0.003 | 30.355 | 0.000 | 0.000 | 51.496 | 1.000 | 1.000 | 0.001 |
| 50 | 52.724 | 5.447 | 0.002 | 0.002 | 25.359 | 0.000 | 0.000 | 44.287 | 1.000 | 1.000 | 0.000 |
| SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method | SNR (dB) | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | db6 | Soft | SURE | 10 | 5 | bior6.8 | Soft | SURE | 35 | 4 | db6 | Median | Bayes |
| 2 | 5 | coif4 | Mean | Bayes | 15 | 5 | fk18 | Soft | SURE | 40 | 4 | db8 | Hard | UT |
| 3 | 5 | db10 | Mean | Bayes | 20 | 2 | db10 | Mean | Bayes | 45 | 7 | coif4 | Median | Bayes |
| 4 | 5 | coif5 | Mean | Bayes | 25 | 2 | coif5 | Mean | Bayes | 50 | 3 | bior5.5 | Median | Bayes |
| 5 | 9 | coif4 | Mean | Bayes | 30 | 4 | bior5.5 | Mean | Bayes | 39 | 4 | db8 | Median | Bayes |
| Case | (dB) | (dB) | (dB) | (%) | Case | (dB) | (dB) | (dB) | (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 40.634 | 60.962 | 20.328 | 50.028 | 5 | 16.244 | 18.639 | 2.395 | 14.747 |
| 2 | 38.732 | 56.081 | 17.349 | 44.794 | 6 | 22.522 | 26.106 | 3.583 | 15.909 |
| 3 | 37.522 | 58.226 | 20.703 | 55.176 | 7 | 16.322 | 18.981 | 2.659 | 16.293 |
| 4 | 36.037 | 65.567 | 29.53 | 81.944 |
| Case | Level | Wavelet Type | Threshold Rule | Denoising Method | Case | Level | Wavelet Type | Threshold Rule | Denoising Method |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | db9 | Soft | UniversalThreshold | 5 | 4 | sym2 | Soft | UniversalThreshold |
| 2 | 4 | db8 | Soft | UniversalThreshold | 6 | 5 | fk22 | Soft | UniversalThreshold |
| 3 | 9 | coif5 | Soft | UniversalThreshold | 7 | 5 | fk22 | Soft | UniversalThreshold |
| 4 | 5 | db9 | Soft | UniversalThreshold |
| Dataset | True Positives (Abnormal) | True Negatives (Normal) | False Positives | False Negatives | Accuracy (%) |
|---|---|---|---|---|---|
| Clean | 100% | 100% | 0% | 0% | 100.00 |
| Noisy | 100.00% | 32.41% | 67.59% | 0% | 66.20 |
| Denoised signal with proposed method | 84.44% | 96.81% | 3.19% | 15.56% | 90.63 |
| System No | Hardware Specifications | Execution Time (s) | Description |
|---|---|---|---|
| 1 | Intel Core i7-10700 @ 2.90 GHz, 32 GB RAM | 22.15 | Desktop-class 8-core CPU; reference baseline system. |
| 2 | Intel Core i7-8750H @ 2.20 GHz, 32 GB RAM | 30.85 | Laptop-core CPU; lower base clock, reduced thermal performance. |
| 3 | Intel Xeon W-2223, 64 GB RAM, NVIDIA Quadro P4000 GPU | 12.5 | Multi-threaded Xeon + moderate GPU acceleration via Quadro P4000. |
| 4 | Truba Barbun CUDA Server: 2× Intel Xeon Gold 6148 (40 cores), 2× NVIDIA P100 GPUs, 100 Gbps InfiniBand | 3.8 | High-performance server; GPU-parallelized execution using P100 accelerators. |
| Method | Advantages | Limitations |
|---|---|---|
| SURE | Adapts to signal statistics; balances noise and detail | Sensitive to noise variance; tuning required |
| Bayes | Probabilistic estimation of threshold | Assumes Gaussian noise; may mis-perform in structured noise |
| Minimax Thresholding | Statistically motivated; good for smooth signals | Rigid threshold; not flexible across noise levels |
| BlockJS/FDR | Improved spatial adaptivity; block-level denoising | Complex parameter selection; increased computation |
| Proposed Optimized Framework | Jointly optimizes wavelet parameters; adaptable to various noise types | Requires offline search or initialization; may need real-time tuning |
| Method | Runtime | Key Feature |
|---|---|---|
| EWT [15] | 11.2 ms | Entropy-tracked segments for ECG denoising |
| VMD [18] | 14.3 ms | Optimization-enhanced decomposition for ECG |
| Transformer DL [13] | 14–20 ms | High accuracy, high complexity, GPU required |
| Proposed Method | 4.86 ms | Fast adaptive wavelet framework |
| Criteria | Butterworth/IIR Filtering (with References) | Proposed Optimized Wavelet-Based Framework |
|---|---|---|
| Noise Suppression | Limited under high noise (SNR ≈ 3.1 dB) [55] | High robustness via adaptive thresholding |
| Feature Preservation | May distort the waveforms [56,57] | Maintains morphological integrity |
| Reconstruction Accuracy | High error (MSE ≈ 0.18) [58] | Low error (<0.001) with optimization |
| Computational Performance | Fast in basic form; no adaptation [55,58] | Real-time capable (~4.86 ms per signal window) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akkaya, S. Wavelet-Based Denoising Strategies for Non-Stationary Signals in Electrical Power Systems: An Optimization Perspective. Electronics 2025, 14, 3190. https://doi.org/10.3390/electronics14163190
Akkaya S. Wavelet-Based Denoising Strategies for Non-Stationary Signals in Electrical Power Systems: An Optimization Perspective. Electronics. 2025; 14(16):3190. https://doi.org/10.3390/electronics14163190
Chicago/Turabian StyleAkkaya, Sıtkı. 2025. "Wavelet-Based Denoising Strategies for Non-Stationary Signals in Electrical Power Systems: An Optimization Perspective" Electronics 14, no. 16: 3190. https://doi.org/10.3390/electronics14163190
APA StyleAkkaya, S. (2025). Wavelet-Based Denoising Strategies for Non-Stationary Signals in Electrical Power Systems: An Optimization Perspective. Electronics, 14(16), 3190. https://doi.org/10.3390/electronics14163190







