Electromigration Failures in Integrated Circuits: A Review of Physics-Based Models and Analytical Methods
Abstract
1. Introduction
2. Fundamentals and Physical Phenomena of EM
3. Factors Influencing EM-Induced Failures in ICs
3.1. Current Density and Temperature
3.2. Interconnect Materials
3.3. Microstructure
3.4. Geometric Shape
3.5. Cu Interconnect Process
3.6. EM in Solder Joints
3.7. Pulsed Current and Frequency
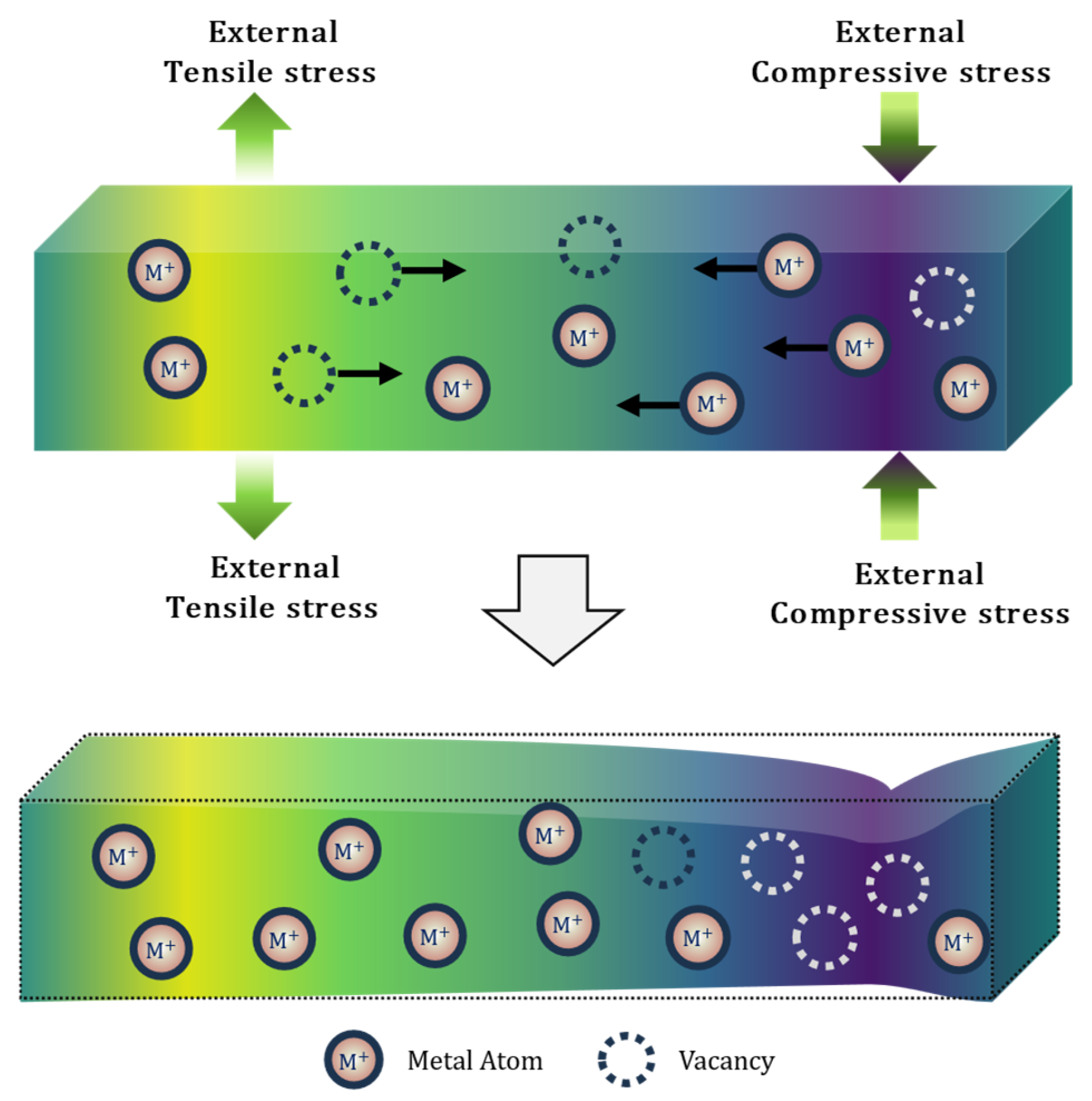
3.8. Mechanical Stress
3.8.1. Stress Gradients Induced by Thermal Expansion Mismatch
3.8.2. Stress Gradients Induced by Non-Uniform Metal Deposition Growth
3.8.3. Stress Gradients Induced by Material Redistribution During EM
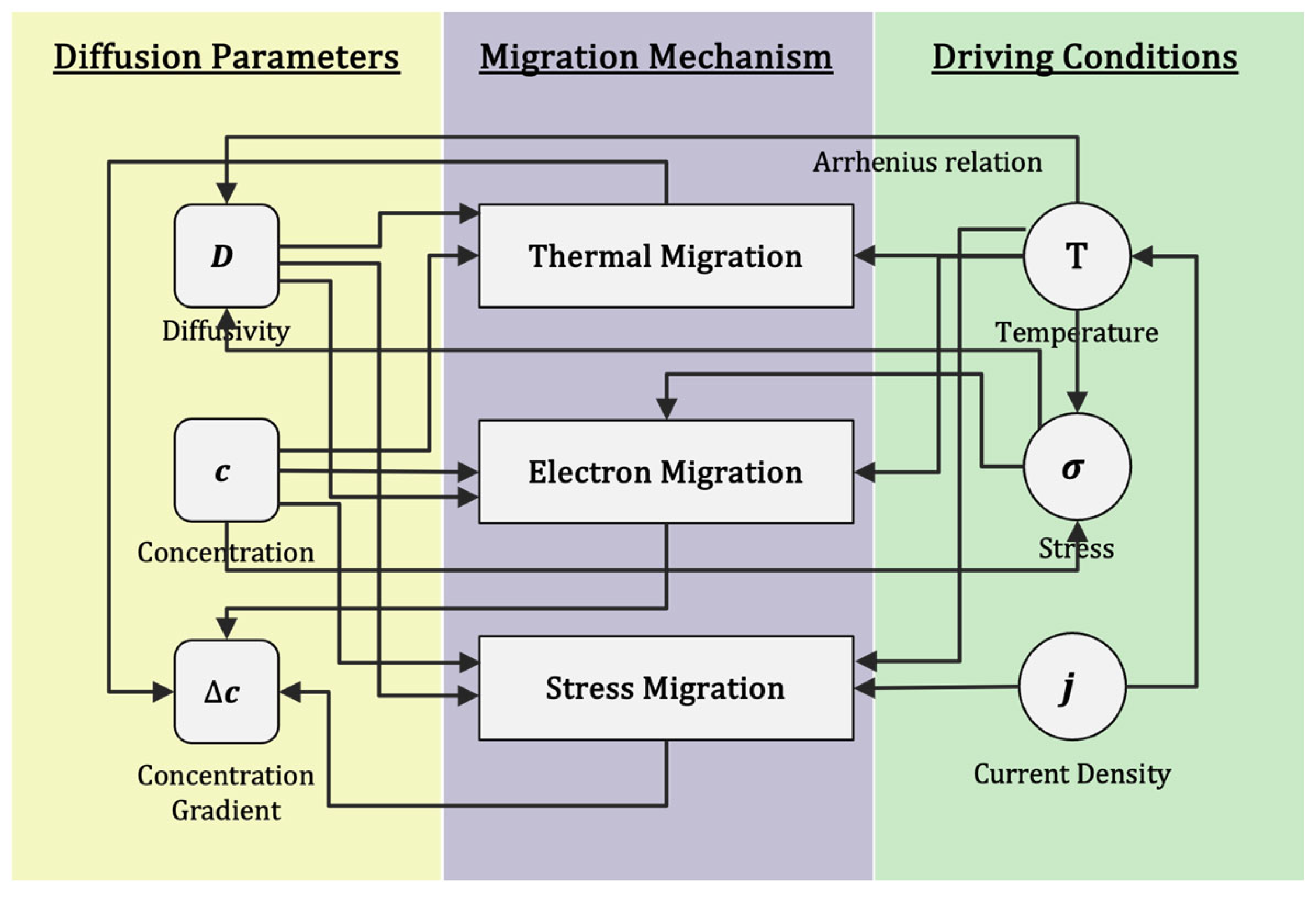
4. Multi-Physics Driving Mechanisms of Atomic Migration
4.1. Electron Migration (EM)
4.2. Thermal Migration (TM)
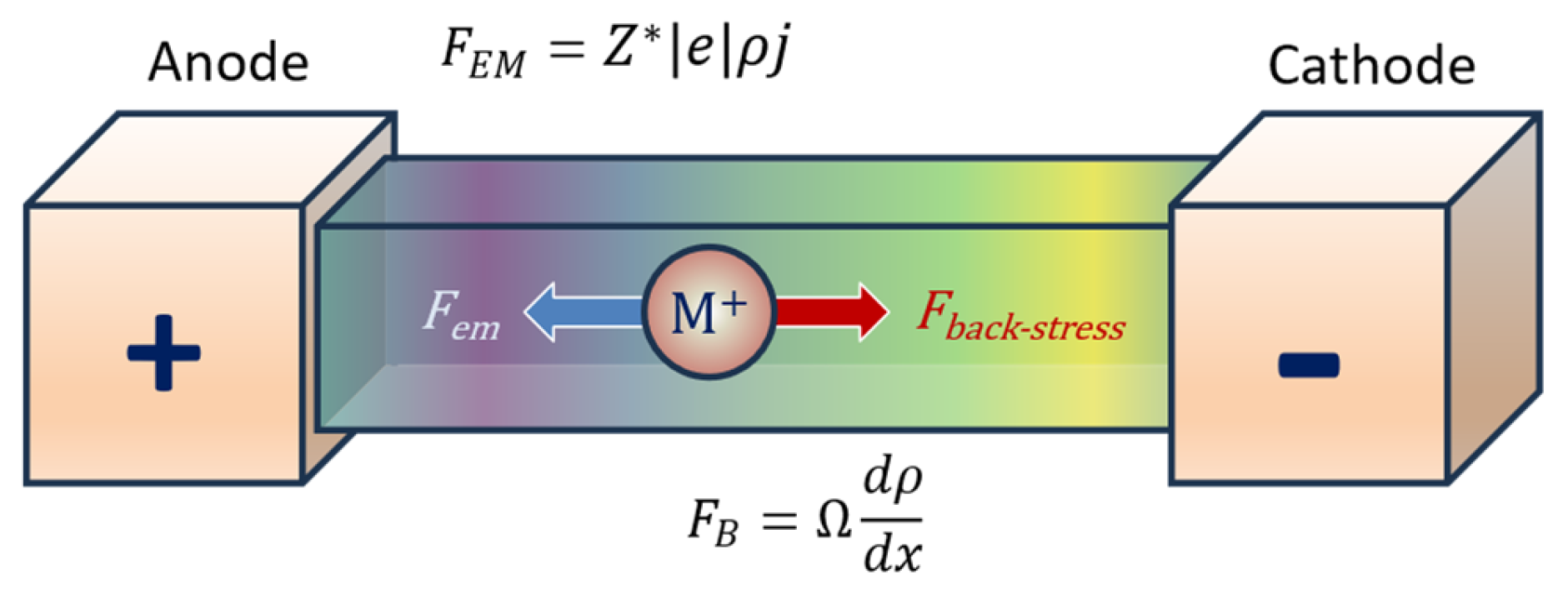
4.3. Stress Migration (SM)
4.4. Coupling Effects in Multi-Physics Migration
5. EM Failure Analysis Models
5.1. Black’s Empirical Model
5.2. Blech Critical Model
5.3. AFD Model
5.4. Korhonen Stress Evolution Model
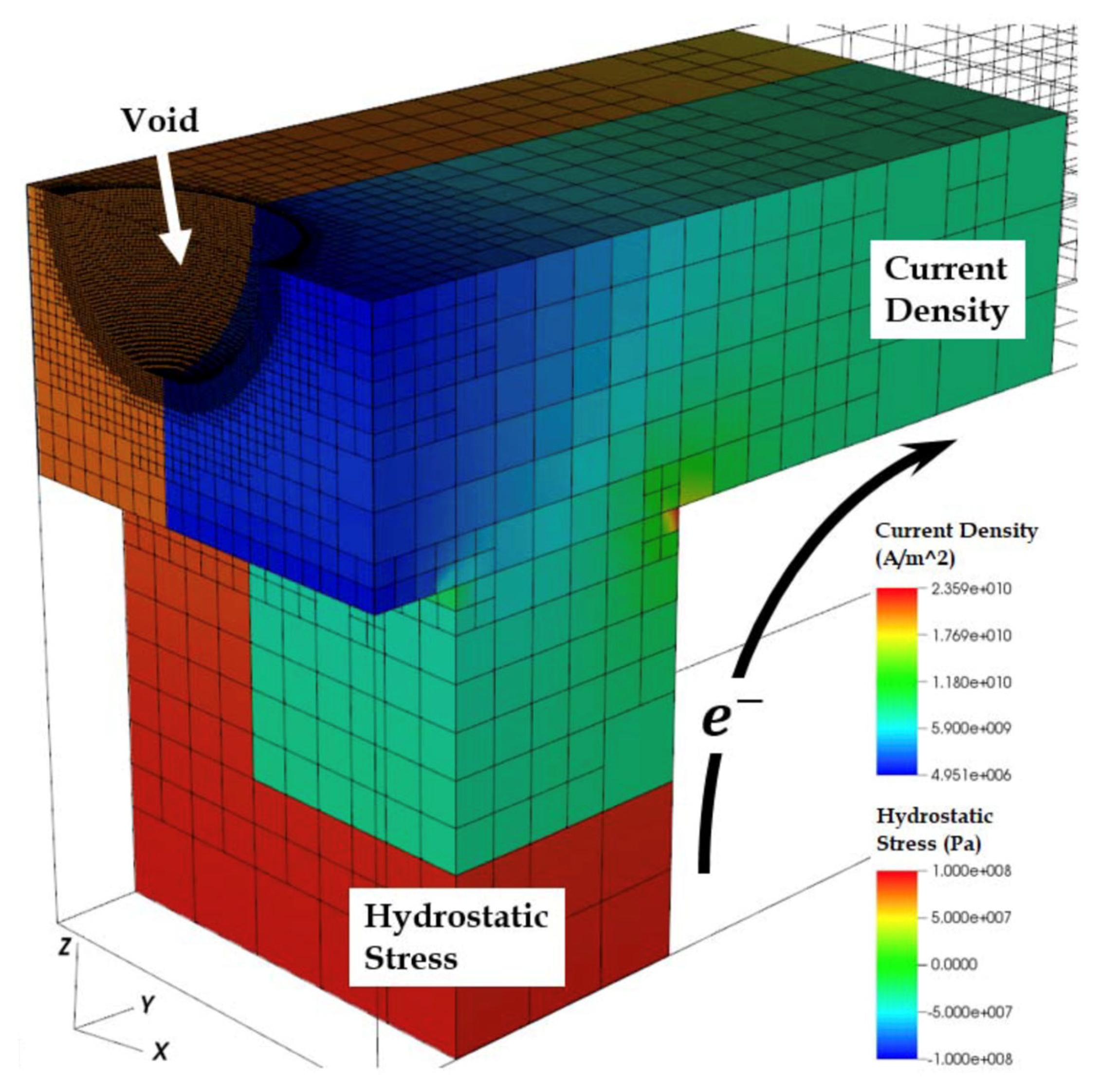
5.5. EM Simulation Methods
5.6. Recent Advances in EM Modeling and Analysis
6. Problems and Challenges
7. Summary and Outlook
Funding
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| AC | Alternating current |
| AFD | Atomic flux divergence |
| Al | Aluminum |
| BCT | Body-centered tetragonal |
| BGA | Ball Grid Array |
| BSDPNs | Backside power delivery networks |
| CMP | Chemical mechanical polishing |
| Co | Cobalt |
| Cu | Copper |
| DC | Direct current |
| EDA | Electronic design automation |
| EM | Electromigration |
| ESD | Electrostatic discharge |
| FEM | Finite element method |
| FEOL | Front-end-of-line |
| GAN | Generative adversarial network |
| IC | Integrated circuit |
| IMC | Intermetallic compound |
| IRDS | International Roadmap for Devices and Systems |
| ITRS | International Technology Roadmap for Semiconductors |
| MTTF | Median time to failure |
| PDN | Power delivery network |
| PINN | Physics-informed neural network |
| RDL | Redistribution layer |
| Ru | Ruthenium |
| SM | Stress migration |
| TM | Thermomigration |
| TSVs | Through-silicon vias |
| UBM | Under Bump Metallization |
References
- d’Heurle, F.M. Electromigration and failure in electronics: An introduction. Proc. IEEE 1971, 59, 1409–1418. [Google Scholar] [CrossRef]
- Colon, J.; Bavarian, B.; Leon, R. Failure of Electronic Equipment by Electromigration. In Proceedings of the CORROSION 2002, Denver, CO, USA, 7–12 April 2002; pp. 1–6. [Google Scholar]
- Arzt, E.; Kraft, O.; Spolenak, R.; Joo, Y.-C. Physical Metallurgy of Electromigration: Failure Mechanisms in Miniaturized Conductor Lines/Metallphysik der Elektromigration: Ausfallsmechanismen in miniaturisierten Leiterbahnen. Int. J. Mater. Res. 1996, 87, 934–942. [Google Scholar] [CrossRef]
- Chiu, M.-C.; Tsai, M.-Y.; Wang, S.-B.; Lin, Y.-S.; Liang, C.-L. Applications of Ni and Ag metallizations at the solder/Cu interfaces in advanced high-power automobile interconnects: An electromigration study. Surf. Coat. Technol. 2024, 484, 130828. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.; Zhifeng, Y.; Yao, Y. Interfacial Fracture Caused by Electromigration at Copper Interconnects. J. Electron. Packag. 2023, 146, 011007. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, P. A multi-phase-field model of void crossing grain boundary under electromigration-induced anisotropic surface diffusion in interconnects. Eur. J. Mech.—A/Solids 2024, 106, 105305. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, P. Multi-phase-field simulation of the void crossing grain boundary under electromigration-induced anisotropic surface diffusion in (110)-oriented interconnects. Appl. Phys. A 2025, 131, 235. [Google Scholar] [CrossRef]
- Lau, J.; Fan, X. Design Rules for Preventing Electromigration Failure. In Hybrid Bonding, Advanced Substrates, Failure Mechanisms, and Thermal Management for Chiplets and Heterogeneous Integration; Lau, J., Fan, X., Eds.; Springer Nature: Singapore, 2025; pp. 491–558. [Google Scholar]
- Wang, S.; Feng, J.; Wang, W.; Wu, P.; Wen, J.; Yang, D.; Huang, Y.; Tian, R.; Wang, S.; Tian, Y. Isothermal aging and electromigration reliability of Cu pillar bumps interconnections in advanced packages monitored by in-situ dynamic resistance testing. J. Mater. Res. Technol. 2024, 32, 937–954. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, Z.; Ye, Z.; Pan, X. Theoretical Understanding of Electromigration-Related Surface Diffusion and Current-Induced Force in Ag–Pd Systems. ACS Omega 2024, 9, 29576–29584. [Google Scholar] [CrossRef]
- Hou, Y.-S.; Lin, C.-Y. Characterization of ESD-induced electromigration on CMOS metallization in on-chip ESD protection circuit. Jpn. J. Appl. Phys. 2024, 63, 02SP58. [Google Scholar] [CrossRef]
- Li, W.; Guo, L.; Li, D.; Liu, Z.-Q. Research Overview on the Electromigration Reliability of SnBi Solder Alloy. Materials 2024, 17, 2848. [Google Scholar] [CrossRef]
- Gee, S.; Kelkar, N.; Huang, J.; Tu, K.-N. Lead-Free and PbSn Bump Electromigration Testing. In Proceedings of the ASME 2005 Pacific Rim Technical Conference and Exhibition on Integration and Packaging of MEMS, NEMS, and Electronic Systems collocated with the ASME 2005 Heat Transfer Summer Conference, San Francisco, CA, USA, 17–22 July 2005; pp. 1313–1321. [Google Scholar]
- 2015 International Technology Roadmap for Semiconductors (ITRS); Semiconductor Industry Association: Washington, DC, USA, 2015.
- Oates, A.S. Strategies to Ensure Electromigration Reliability of Cu/Low-k Interconnects at 10 nm. ECS J. Solid State Sci. Technol. 2015, 4, N3168. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Qin, Z.; Lu, R.; Chen, R. Interconnect electromigration modeling based on chemical mechanical polishing process variation. Microelectron. Reliab. 2025, 172, 115809. [Google Scholar] [CrossRef]
- Yao, Y.; An, Y.; Tu, K.N.; Liu, Y. Electromigration failure induced by interdiffusion between Al trace and Cu seed layer in the immortal microbump in three-dimensional integrated circuit. J. Mater. Res. Technol. 2025, 36, 6400–6408. [Google Scholar] [CrossRef]
- Sbrana, C.; Catania, A.; Paliy, M.; Pascoli, S.D.; Strangio, S.; Macucci, M.; Iannaccone, G. Design Criteria of High-Temperature Integrated Circuits Using Standard SOI CMOS Process up to 300 °C. IEEE Access 2024, 12, 57236–57249. [Google Scholar] [CrossRef]
- Yao, Y.; Lu, Z.; An, Y.; Tu, K.N.; Liu, Y. Counteracting Effect of Sn Grain Orientation on Current Crowding in Electromigration Failures of Solder Joints. Electron. Mater. Lett. 2025, 21, 134–143. [Google Scholar] [CrossRef]
- Yao, Y.; An, Y.; Tu, K.N.; Liu, Y. Coupling effect between electromigration and joule heating on the failure of ball grid array in 3D integrated circuit technology. J. Mater. Res. Technol. 2024, 28, 3573–3582. [Google Scholar] [CrossRef]
- Hou, T.; Najm, F.N.; Wong, N.; Chen, H.B. Novel Partitioning-Based Approach for Electromigration Assessment With Neural Networks. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2025. Early access. [Google Scholar] [CrossRef]
- IEEE. More Moore; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2024. [Google Scholar]
- Rothe, S.; Lienig, J. Combined Modeling of Electromigration, Thermal and Stress Migration in AC Interconnect Lines. In Proceedings of the 2023 International Symposium on Physical Design, Virtual Event, 26–29 March 2023; pp. 107–114. [Google Scholar]
- Fiks, V.B. On the mechanism of the mobility of ions in metals. Sov. Phys.-Solid State 1959, 1, 14–28. [Google Scholar]
- Lienig, J.; Thiele, M. Fundamentals of Electromigration-Aware Integrated Circuit Design, 2nd ed.; Springer International Publishing: Cham, Switzerland, 2025. [Google Scholar]
- Wei, C.C.; Liu, P.C.; Chen, C.; Tu, K.N. Electromigration-induced Pb and Sn whisker growth in SnPb solder stripes. J. Mater. Res. 2008, 23, 2017–2022. [Google Scholar] [CrossRef][Green Version]
- Lin, M.; Jou, N.; Liang, J.W.; Su, K.C. Effect of multiple via layout on electromigration performance and current density distribution in copper interconnect. In Proceedings of the 2009 IEEE International Reliability Physics Symposium, Montreal, QC, Canada, 26–30 April 2009; pp. 844–847. [Google Scholar]
- Huntington, H.B.; Grone, A.R. Current-induced marker motion in gold wires. J. Phys. Chem. Solids 1961, 20, 76–87. [Google Scholar] [CrossRef]
- Fischer, A.H.; Glasow, A.V.; Penka, S.; Ungar, F. Electromigration failure mechanism studies on copper interconnects. In Proceedings of the IEEE 2002 International Interconnect Technology Conference (Cat. No.02EX519), Burlingame, CA, USA, 5 June 2002; pp. 139–141. [Google Scholar]
- Tan, C.M.; Roy, A. Electromigration in ULSI interconnects. Mater. Sci. Eng. R Rep. 2007, 58, 1–75. [Google Scholar] [CrossRef]
- Li, B.; Christiansen, C.; Badami, D.; Yang, C.-C. Electromigration challenges for advanced on-chip Cu interconnects. Microelectron. Reliab. 2014, 54, 712–724. [Google Scholar] [CrossRef]
- Hau-Riege, C.S. An introduction to Cu electromigration. Microelectron. Reliab. 2004, 44, 195–205. [Google Scholar] [CrossRef]
- Ho, P.S.; Huntington, H.B. Electromigration and void observation in silver. J. Phys. Chem. Solids 1966, 27, 1319–1329. [Google Scholar] [CrossRef]
- Huntington, H.B. Effect of driving forces on atom motion. Thin Solid Film. 1975, 25, 265–280. [Google Scholar] [CrossRef]
- Duryea, T.W.; Huntington, H.B. The driving force for electromigration of an atom adsorbed on simple metal surface. Surf. Sci. 1988, 199, 261–281. [Google Scholar] [CrossRef]
- Black, J.R. Electromigration—A brief survey and some recent results. IEEE Trans. Electron Devices 1969, 16, 338–347. [Google Scholar] [CrossRef]
- Cui, H.; Liu, X.; Deng, D. Factors influencing electromigration in metal interconnects. Trans. China Weld. Inst. 2018, 39, 29–32+130. [Google Scholar]
- Huang, J.S.; Yeh, E.C.C.; Zhang, Z.B.; Tu, K.N. The effect of contact resistance on current crowding and electromigration in ULSI multi-level interconnects. Mater. Chem. Phys. 2003, 77, 377–383. [Google Scholar] [CrossRef]
- Sherby, O.D.; Simnad, M.T. Prediction of atomic mobility in metallic systems. Trans. Am. Soc. Metals 1961, 54, 227–240. [Google Scholar]
- Sullivan, T.D. Thermal dependence of voiding in narrow aluminum microelectronic interconnects. Appl. Phys. Lett. 1989, 55, 2399–2401. [Google Scholar] [CrossRef]
- House, D.; Keyser, J.C. Foundations of Physically Based Modeling and Animation; AK Peters/CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Zhang, X.J.; Ji, H.; Nie, B.J. Electromigration analysis of FinFETs considering self-heating effects. Appl. Electron. Tech. 2019, 45, 53–60. [Google Scholar] [CrossRef]
- Ames, I.; d’Heurle, F.M.; Horstmann, R.E. Reduction of Electromigration in Aluminum Films by Copper Doping. IBM J. Res. Dev. 1970, 14, 461–463. [Google Scholar] [CrossRef]
- Kawasaki, H.; Hu, C.K. An electromigration failure model of tungsten plug contacts/vias for realistic lifetime prediction. In Proceedings of the 1996 Symposium on VLSI Technology, Digest of Technical Papers, Honolulu, HI, USA, 11–13 June 1996; pp. 192–193. [Google Scholar]
- Liu, X.Y.; Adams, J.B. Grain-boundary segregation in Al–10%Mg alloys at hot working temperatures. Acta Mater. 1998, 46, 3467–3476. [Google Scholar] [CrossRef]
- Liu, C.L.; Liu, X.Y.; Borucki, L.J. Defect generation and diffusion mechanisms in Al and Al–Cu. Appl. Phys. Lett. 1999, 74, 34–36. [Google Scholar] [CrossRef]
- Liu, X.Y.; Liu, C.L.; Borucki, L.J. A new investigation of copper’s role in enhancing Al–Cu interconnect electromigration resistance from an atomistic view. Acta Mater. 1999, 47, 3227–3231. [Google Scholar] [CrossRef]
- Sen, F.G.; Aydinol, M.K. Atomistic simulation of self-diffusion in Al and Al alloys under electromigration conditions. J. Appl. Phys. 2008, 104, 073510. [Google Scholar] [CrossRef]
- Tu, K.N. Recent advances on electromigration in very-large-scale-integration of interconnects. J. Appl. Phys. 2003, 94, 5451–5473. [Google Scholar] [CrossRef]
- Lee, W.W.; Ho, P.S. Low-Dielectric-Constant Materials for ULSI Interlayer-Dielectric Applications. MRS Bull. 1997, 22, 19–27. [Google Scholar] [CrossRef]
- Christou, A. Electromigration and Electronic Device Degradation; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Lienig, J. Introduction to electromigration-aware physical design. In Proceedings of the 2006 International Symposium on Physical Design, San Jose, CA, USA, 9–12 April 2006; pp. 39–46. [Google Scholar]
- Fang, J.-S.; Chen, G.-S.; Chang, C.-C.; Hsiao, C.-N.; Chen, W.-C.; Cheng, Y.-L. Understanding electromigration failure behaviors of narrow cobalt lines and the mechanism of reliability enhancement for extremely dilute alloying of manganese oxide. J. Alloys Compd. 2024, 970, 172591. [Google Scholar] [CrossRef]
- Fang, J.-S.; Su, T.-H.; Cheng, Y.-L.; Chen, G.-S. Synergistic enhancement of adhesion and electromigration reliability of cobalt via super-diluted (0.06 at.%) tungsten alloying as next-generation interconnect materials. Microelectron. Reliab. 2024, 158, 115427. [Google Scholar] [CrossRef]
- Chehadi, Z.; Daubriac, R.; Lu, L.; Huet, K.; Tokei, Z.; Cancellara, L.; Cristiano, F.; Thuries, L. Investigation of the enlargement of Ru grains and failure modes analysis in microsecond UV laser annealing. In Proceedings of the 2024 IEEE International Interconnect Technology Conference (IITC), San Jose, CA, USA, 3–6 June 2024; pp. 1–3. [Google Scholar]
- Wu, F.; Zhang, J.; Wu, Y.; Zheng, Z.; Wang, L.; Qiao, K. Research progress on electromigration in integrated circuit interconnect wires. Semicond. Technol. 2004, 29, 15–21, 38. [Google Scholar] [CrossRef]
- Gangulee, A.; d’Heurle, F.M. Effect of Alloy Additions on Electromigration Failures in Thin Aluminum Films. Appl. Phys. Lett. 1971, 19, 76–77. [Google Scholar] [CrossRef]
- Chen, K.; Wang, Z.; Wang, C.; Zhang, D.W. Enhanced thermal stability of Ru interconnects using h-BN as barrier layers. In Proceedings of the 2025 9th IEEE Electron Devices Technology & Manufacturing Conference (EDTM), Hong Kong, China, 9–12 March 2025; pp. 1–3. [Google Scholar]
- Huang, J.-Z.; Tsao, P.-C.; Chang, E.-C.; Jiang, Z.-K.; Ni, I.C.; Li, S.-W.; Chan, Y.-C.; Yang, S.-Y.; Lee, M.-H.; Shue, S.-L.; et al. Improving the electromigration life of advanced interconnects through graphene capping. ACS Appl. Nano Mater. 2023, 6, 12479–12485. [Google Scholar] [CrossRef]
- Shin, K.W.; Cho, Y.; Nam, S.-G.; Jung, A.; Lee, E.-K.; Lee, C.-S.; Lee, M.-H.; Shin, H.-J.; Byun, K.-E. Graphene capping of Cu back-end-of-line interconnects reduces resistance and improves electromigration lifetime. ACS Appl. Nano Mater. 2023, 6, 4170–4177. [Google Scholar] [CrossRef]
- Choi, Y.W.; Cohen, M.L. Resonantly enhanced electromigration forces for adsorbates on graphene. Phys. Rev. Lett. 2022, 129, 206801. [Google Scholar] [CrossRef]
- Koch, R.H.; Lloyd, J.R.; Cronin, J. 1fNoise and grain-boundary diffusion in aluminum and aluminum alloys. Phys. Rev. Lett. 1985, 55, 2487–2490. [Google Scholar] [CrossRef]
- Kwieciński, J.; Wyrzykowski, J.W. Investigation of grain boundary self-diffusion at low temperatures in polycrystalline aluminium by means of the dislocation spreading method. Acta Metall. Mater. 1991, 39, 1953–1958. [Google Scholar] [CrossRef]
- Lin, M. A Thermodynamic Framework for Damage Mechanics of Microelectronic Packaging Materials. Doctoral Dissertation, University at Buffalo, State University of New York, Buffalo, NY, USA, 2009. [Google Scholar]
- Butrymowicz, D.B.; Manning, J.R.; Read, M.E. Diffusion in copper and copper alloys. Part I. Volume and surface self-diffusion in copper. J. Phys. Chem. Ref. Data 1973, 2, 643–656. [Google Scholar] [CrossRef]
- Divinski, S.; Ribbe, J.; Schmitz, G.; Herzig, C. Grain boundary diffusion and segregation of Ni in Cu. Acta Mater. 2007, 55, 3337–3346. [Google Scholar] [CrossRef]
- Surholt, T.; Herzig, C. Grain boundary self-diffusion in Cu polycrystals of different purity. Acta Mater. 1997, 45, 3817–3823. [Google Scholar] [CrossRef]
- Rosenberg, R. Reliability of Copper Metallization; NASA/NEPP Tech. Rep.; NASA/NEPP: Greenbelt, MD, USA, 2010.
- Herzig, C.; Divinski, S.V. Grain boundary diffusion in metals: Recent developments. Mater. Trans. 2003, 44, 14–27. [Google Scholar] [CrossRef]
- Kraatz, K.H.; Frohberg, G.; Wever, H. Thermo- and electromigration in high purity cobalt. Phys. Status Solidi A 1979, 52, 149–159. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, X.; Tsurekawa, S. Diffusion in copper/cobalt systems under high magnetic fields. Materials 2021, 14, 3104. [Google Scholar] [CrossRef]
- Simon, A.H.; Bolom, T.; Niu, C.; Baumann, F.H.; Hu, C.; Parks, C.; Nag, J.; Kim, H.; Lee, J.Y.; Yang, C.; et al. Electromigration comparison of selective CVD cobalt capping with PVD Ta(N) and CVD cobalt liners on 22nm-groundrule dual-damascene Cu interconnects. In Proceedings of the 2013 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 14–18 April 2013; pp. 3F.4.1–3F.4.6. [Google Scholar]
- Beyne, S.; Pedreira, O.V.; Oprins, H.; De Wolf, I.; Tokei, Z.; Croes, K. Electromigration activation energies in alternative metal interconnects. IEEE Trans. Electron. Devices 2019, 66, 5278–5283. [Google Scholar] [CrossRef]
- Shang, S.-L.; Zhou, B.-C.; Wang, W.Y.; Ross, A.J.; Liu, X.L.; Hu, Y.-J.; Fang, H.-Z.; Wang, Y.; Liu, Z.-K. A comprehensive first-principles study of pure elements: Vacancy formation and migration energies and self-diffusion coefficients. Acta Mater. 2016, 109, 128–141. [Google Scholar] [CrossRef]
- Angsten, T.; Mayeshiba, T.; Wu, H.; Morgan, D. Elemental vacancy diffusion database from high-throughput first-principles calculations for fcc and hcp structures. New J. Phys. 2014, 16, 15018. [Google Scholar] [CrossRef]
- Dyment, F.; Balart, S.; Lugo, C.; Pérez, R.A.; Di Lalla, N.; Iribarren, M.J. Ru self-diffusion and Ru diffusion in Al. Defect Diffus. Forum 2005, 237–240, 402–407. [Google Scholar] [CrossRef]
- Pedreira, O.V.; Stucchi, M.; Gupta, A.; Gonzalez, V.V.; Van Der Veen, M.; Lariviere, S.; Wilson, C.J.; Tokei, Z.; Imec, K.C. Metal reliability mechanisms in ruthenium interconnects. In Proceedings of the 2020 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 28 April–30 May 2020. [Google Scholar]
- Vaidya, S.; Sheng, T.T.; Sinha, A.K. Linewidth dependence of electromigration in evaporated Al-0.5%Cu. Appl. Phys. Lett. 1980, 36, 464–466. [Google Scholar] [CrossRef]
- Kinsbron, E. A model for the width dependence of electromigration lifetimes in aluminum thin-film stripes. Appl. Phys. Lett. 1980, 36, 968–970. [Google Scholar] [CrossRef]
- Cho, J.; Thompson, C.V. Grain size dependence of electromigration-induced failures in narrow interconnects. Appl. Phys. Lett. 1989, 54, 2577–2579. [Google Scholar] [CrossRef]
- Ogurtani, T.O.; Oren, E.E. Computer simulation of void growth dynamics under the action of electromigration and capillary forces in narrow thin interconnects. J. Appl. Phys. 2001, 90, 1564–1572. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Wang, J.Y.; Yang, Y.T. Research progress on electromigration reliability of copper interconnects. Microelectron. Int. 2007, 24, 364–368, 373. [Google Scholar]
- Spolenak, R.; Kraft, O.; Arzt, E. Effects of alloying elements on electromigration. Microelectron. Reliab. 1998, 38, 1015–1020. [Google Scholar] [CrossRef]
- Cheng, Y.-L.; Chang, W.-Y.; Wang, Y.-L. Line-width dependency on electromigration performance for long and short copper interconnects. J. Vac. Sci. Technol. B 2010, 28, 973–977. [Google Scholar] [CrossRef]
- Khoo, K.; Tashiro, S.; Onuki, J. Influence on the Electro-Migration Resistance by Line Width and Average Grain Size along the Longitudinal Direction of Very Narrow Cu Wires. Mater. Trans. 2010, 51, 1183–1187. [Google Scholar] [CrossRef]
- Lin, M.H.; Chang, K.P.; Su, K.C.; Wang, T. Effects of width scaling and layout variation on dual damascene copper interconnect electromigration. Microelectron. Reliab. 2007, 47, 2100–2108. [Google Scholar] [CrossRef]
- Blech, I.A. Electromigration in thin aluminum films on titanium nitride. J. Appl. Phys. 1976, 47, 1203–1208. [Google Scholar] [CrossRef]
- Gao, G. Research on Chip-Level Electromigration Analysis and Electromigration-Friendly Routing. Master’s Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Nguyen, H.V.; Salm, C.; Wenzel, R.; Mouthaan, A.J.; Kuper, F.G. Simulation and experimental characterization of reservoir and via layout effects on electromigration lifetime. Microelectron. Reliab. 2002, 42, 1421–1425. [Google Scholar] [CrossRef][Green Version]
- Uekubo, M.; Oku, T.; Nii, K.; Murakami, M.; Takahiro, K.; Yamaguchi, S.; Nakano, T.; Ohta, T. WNx diffusion barriers between Si and Cu. Thin Solid Film. 1996, 286, 170–175. [Google Scholar] [CrossRef]
- Karppinen, J. Reliability Assessment of Electronic Assemblies Under Multiple Interacting Loading Conditions. Doctoral Thesis, School of Electrical Engineering, Aalto University, Espoo, Finland, 2013. [Google Scholar]
- Rahman, M.K.; Musa, A.M.M.; Neher, B.; Patwary, K.A.; Rahman, M.A.; Islam, M.S. A review of the study on the electromigration and power electronics. J. Electron. Cool. Therm. Control 2016, 6, 19–31. [Google Scholar] [CrossRef]
- Zhang, P.; Xue, S.; Wang, J. New challenges of miniaturization of electronic devices: Electromigration and thermomigration in lead-free solder joints. Mater. Des. 2020, 192, 108726. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, W.; Li, Y.; Tamura, N.; Chen, K. In situ synchrotron study of electromigration induced grain rotations in Sn solder joints. Sci. Rep. 2016, 6, 24418. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Chen, P.; Liu, J.; Hu, A.; Li, M. Effect of Co-W and Co-Fe-W diffusion barriers on the reliability of the solder/Cu interface during reflow conditions. Electron. Mater. Lett. 2024, 20, 517–524. [Google Scholar] [CrossRef]
- Yang, S.-C.; Su, H.-C.; Tu, K.-N.; Chen, C. Unraveling the effect of Sn crystallographic orientation on electromigration-induced intermetallic compounds formations in Cu/Ni/SnAg/Ni/Cu microbumps. J. Alloys Compd. 2025, 1021, 179631. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, K.; Zhang, C.; Huo, F.; Gao, Y. Study on the electromigration organization and mechanical properties of Sn2.5Ag0.7Cu0.1RE/Cu solder joints. Metals 2025, 15, 75. [Google Scholar] [CrossRef]
- Lin, H.-W.; Lu, J.-L.; Hu, C.-C.; Tu, K.N.; Chen, C. To suppress tin whisker growth by using (100)-oriented copper. J. Mater. Res. Technol. 2025, 35, 3217–3225. [Google Scholar] [CrossRef]
- Chang, Y.-W.; Cheng, Y.; Helfen, L.; Xu, F.; Tian, T.; Scheel, M.; Di Michiel, M.; Chen, C.; Tu, K.-N.; Baumbach, T. Electromigration mechanism of failure in flip-chip solder joints based on discrete void formation. Sci. Rep. 2017, 7, 17950. [Google Scholar] [CrossRef]
- Attari, V.; Ghosh, S.; Duong, T.; Arroyave, R. On the interfacial phase growth and vacancy evolution during accelerated electromigration in Cu/Sn/Cu microjoints. Acta Mater. 2018, 160, 185–198. [Google Scholar] [CrossRef]
- Tao, J.; Cheung, N.W.; Hu, C. Metal electromigration damage healing under bidirectional current stress. IEEE Electron Device Lett. 1993, 14, 554–556. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, J.F.; Cheung, N.W.; Chenming, H. Modeling and characterization of electromigration failures under bidirectional current stress. IEEE Trans. Electron Devices 1996, 43, 800–808. [Google Scholar] [CrossRef]
- Pierce, D.G.; Brusius, P.G. Electromigration: A review. Microelectron. Reliab. 1997, 37, 1053–1072. [Google Scholar] [CrossRef]
- Wu, W.; Yuan, J.S. Skin effect of on-chip copper interconnects on electromigration. Solid-State Electron. 2002, 46, 2269–2272. [Google Scholar] [CrossRef]
- Yao, W.; Cemal, B. Skin effect and material degradation of lead-free solder joint under AC. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, 30 May–1 June 2012; pp. 408–412. [Google Scholar]
- Ceric, H.; Selberherr, S. Electromigration in submicron interconnect features of integrated circuits. Mater. Sci. Eng. R Rep. 2011, 71, 53–86. [Google Scholar] [CrossRef]
- Sukharev, V.; Kteyan, A.; Huang, X. Postvoiding Stress Evolution in Confined Metal Lines. IEEE Trans. Device Mater. Reliab. 2016, 16, 50–60. [Google Scholar] [CrossRef]
- Larisa, K.; Baranowski, S.P.; Mike, C.B.; Spooner, T.; Elliott, L.; Brooke, L.; James, R.L. Thermally induced stresses and electromigration failure. In Proceedings of the Proc.SPIE, San Jose, CA, USA, 20–25 September 1992; pp. 154–163. [Google Scholar]
- Breiland, W.G.; Lee, S.R.; Koleske, D.D. Effect of diffraction and film-thickness gradients on wafer-curvature measurements of thin-film stress. J. Appl. Phys. 2004, 95, 3453–3465. [Google Scholar] [CrossRef]
- Cacho, F.; Federspiel, X. 1-Modeling of electromigration phenomena. In Electromigration in Thin Films and Electronic Devices; Kim, C.-U., Ed.; Woodhead Publishing: Cambridge, UK, 2011; pp. 3–44. [Google Scholar]
- Balluffi, R.W. Grain boundary diffusion mechanisms in metals. Metall. Trans. B 1982, 13, 527–553. [Google Scholar] [CrossRef]
- Kirchheim, R. Stress and electromigration in Al-lines of integrated circuits. Acta Metall. Mater. 1992, 40, 309–323. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M.; Prager, W. Theory of Elastic Stability, Second Edition. J. Appl. Mech. 1962, 29, 220–221. [Google Scholar] [CrossRef]
- Sarychev, M.E.; Zhitnikov, Y.V.; Borucki, L.; Liu, C.L.; Makhviladze, T.M. A new, general model for mechanical stress evolution during electromigration. Thin Solid Film. 2000, 365, 211–218. [Google Scholar] [CrossRef]
- Korhonen, M.A.; Bo/rgesen, P.; Tu, K.N.; Li, C.Y. Stress evolution due to electromigration in confined metal lines. J. Appl. Phys. 1993, 73, 3790–3799. [Google Scholar] [CrossRef]
- Tan, C.M.; Roy, A. Investigation of the effect of temperature and stress gradients on accelerated EM test for Cu narrow interconnects. Thin Solid Film. 2006, 504, 288–293. [Google Scholar] [CrossRef]
- Basaran, C.; Lin, M.; Ye, H. A thermodynamic model for electrical current induced damage. Int. J. Solids Struct. 2003, 40, 7315–7327. [Google Scholar] [CrossRef]
- Rovitto, M. Electromigration Reliability Issue in Interconnects for Three-Dimensional Integration Technologies. Ph.D. Thesis, Technische Universität Wien, Wien, Austria, 2016. [Google Scholar]
- Kumar, P.; Sorbello, R.S. Linear response theory of the driving forces for electromigration. Thin Solid Film. 1975, 25, 25–35. [Google Scholar] [CrossRef]
- Schaich, W.L. Driving forces for electromigration by linear response. Phys. Rev. B 1976, 13, 3360–3367. [Google Scholar] [CrossRef]
- Sham, L.J. Microscopic theory of the driving force in electromigration. Phys. Rev. B 1975, 12, 3142–3149. [Google Scholar] [CrossRef]
- Yin, L.M.; Zhang, X.P. Electromigration in micro-interconnections of electronic packaging. Chin. J. Electron. 2008, 36, 1160–1164. [Google Scholar]
- Schwarzenberger, A.P.; Ross, C.A.; Evetts, J.E.; Greer, A.L. Electromigration in the presence of a temperature gradient: Experimental study and modelling. J. Electron. Mater. 1988, 17, 473–478. [Google Scholar] [CrossRef]
- Guo, W.; Li, Z.; Zhu, H.; Zhang, W.; Ji, Y.; Sun, Y.; Shen, G. Temperature gradient impact on electromigration failure in VLSI metallization. In Proceedings of the Fourteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium (Cat. No.98CH36195), San Diego, CA, USA, 10–12 March 1998; pp. 122–127. [Google Scholar]
- Nguyen, H.V.; Salm, C.; Krabbenborg, B.; Weide-Zaage, K.; Bisschop, J.; Mouthaan, A.J.; Kuper, F.G. Effect of thermal gradients on the electromigration life-time in power electronics. In Proceedings of the 2004 IEEE International Reliability Physics Symposium, Proceedings, Phoenix, AZ, USA, 25–29 April 2004; pp. 619–620. [Google Scholar]
- Chen, C.; Tong, H.M.; Tu, K.N. Electromigration and Thermomigration in Pb-Free Flip-Chip Solder Joints. Annu. Rev. Mater. Res. 2010, 40, 531–555. [Google Scholar] [CrossRef]
- Huang, J.R.; Tsai, C.M.; Lin, Y.W.; Kao, C.R. Pronounced electromigration of Cu in molten Sn-based solders. J. Mater. Res. 2008, 23, 250–257. [Google Scholar] [CrossRef]
- Tu, K.-N. Solder Joint Technology; Springer: New York, NY, USA, 2007; Volume 117. [Google Scholar]
- Tu, K.N. Reliability challenges in 3D IC packaging technology. Microelectron. Reliab. 2011, 51, 517–523. [Google Scholar] [CrossRef]
- Choobineh, L.; Jones, J.; Jain, A. Experimental and numerical investigation of interdie thermal resistance in three-dimensional integrated circuits. J. Electron. Packag. 2017, 139, 020908. [Google Scholar] [CrossRef]
- Matsumoto, K.; Ibaraki, S.; Sueoka, K.; Sakuma, K.; Kikuchi, H.; Orii, Y.; Yamada, F. Experimental thermal resistance evaluation of a three-dimensional (3D) chip stack. In Proceedings of the Management Symposium (SEMI-THERM), San Jose, CA, USA, 20–24 March 2011; pp. 125–130. [Google Scholar]
- Tian, W.; Gao, R.; Gu, L.; Ji, H.; Zhou, L. Three-dimensional integrated fan-out wafer-level package micro-bump electromigration study. Micromachines 2023, 14, 1255. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, W.; Wang, H.; Zhang, X.; Shao, W.; Zhou, B.; Shi, Y.; Gong, W.; Deng, R.; Zhao, J.; et al. Electrothermal reliability analysis of electromigration in 3-D TSV-RDL interconnects. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 157–165. [Google Scholar] [CrossRef]
- Athikulwongse, K.; Pathak, M.; Lim, S.K. Exploiting die-to-die thermal coupling in 3D IC placement. In Proceedings of the DAC ‘12: The 49th Annual Design Automation Conference 2012, San Francisco, CA, USA, 3–7 June 2012; pp. 741–746. [Google Scholar]
- Cher Ming, T.; Guan, Z.; Zhenghao, G. Dynamic study of the physical processes in the intrinsic line electromigration of deep-submicron copper and aluminum interconnects. IEEE Trans. Device Mater. Reliab. 2004, 4, 450–456. [Google Scholar] [CrossRef]
- Black, J.R. Mass Transport of Aluminum by Momentum Exchange with Conducting Electrons. In Proceedings of the 6th Annual Reliability Physics Symposium (IEEE), Los Angeles, CA, USA, 6–8 November 1967; pp. 148–159. [Google Scholar]
- Black, J.R. Electromigration failure modes in aluminum metallization for semiconductor devices. Proc. IEEE 1969, 57, 1587–1594. [Google Scholar] [CrossRef]
- Shatzkes, M.; Lloyd, J.R. A model for conductor failure considering diffusion concurrently with electromigration resulting in a current exponent of 2. J. Appl. Phys. 1986, 59, 3890–3893. [Google Scholar] [CrossRef]
- Blair, J.C.; Ghate, P.B.; Haywood, C.T. Concerning electromigration in thin films. Proc. IEEE 1971, 59, 1023–1024. [Google Scholar] [CrossRef]
- Attardo, M.J.; Rosenberg, R. Electromigration Damage in Aluminum Film Conductors. J. Appl. Phys. 1970, 41, 2381–2386. [Google Scholar] [CrossRef]
- Wu, K.; Bradley, R.M. Theory of electromigration failure in polycrystalline metal films. Phys. Rev. B 1994, 50, 12468–12488. [Google Scholar] [CrossRef]
- Blair, J.C.; Ghate, P.B.; Haywood, C.T. Electromigration-induced failures in aluminum film conductors. Appl. Phys. Lett. 1970, 17, 281–283. [Google Scholar] [CrossRef]
- JESD22-A104F.01; Temperature Cycling. JEDEC Solid State Technology Association: Arlington, VA, USA, 2023.
- IPC-9701B; Thermal Cycling Test Method for Fatigue Life Characterization of Surface Mount Attachments. IPC—Association Connecting Electronics Industries: Bannockburn, IL, USA, 2022.
- Cui, H.; Tian, W.; Zhang, Y.; Chen, Z. The study of the reliability of complex components during the electromigration process. Micromachines 2023, 14, 499. [Google Scholar] [CrossRef]
- Ruiz, C.; Hashemian, S.F.; Liao, H. Reliability prediction via accelerated testing with imperfectly controlled conditions. In Proceedings of the 2024 Annual Reliability and Maintainability Symposium (RAMS), Albuquerque, NM, USA, 22–25 January 2024; pp. 1–6. [Google Scholar]
- Lloyd, J.R. New models for interconnect failure in advanced IC technology. In Proceedings of the 2008 15th International Symposium on the Physical and Failure Analysis of Integrated Circuits, Singapore, 7–11 July 2008; pp. 1–7. [Google Scholar]
- Huang, X.; Kteyan, A.; Tan, S.X.D.; Sukharev, V. Physics-Based Electromigration Models and Full-Chip Assessment for Power Grid Networks. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 1848–1861. [Google Scholar] [CrossRef]
- Chaudhuri, A.; van Dijk, M.; Jaeschke, J.; Oppermann, H. Investigation of Electromigration in Fine-Pitch Copper Interconnects Through Simulation and Analysis. Available online: https://www.comsol.fr/paper/download/1277231/Investigation%20of%20Electromigration%20in%20Fine-Pitch%20Copper%20Interconnects%20Through%20Simulation%20and%20Analysis.pdf (accessed on 22 July 2025).
- Lacerda de Orio, R. Electromigration Modeling and Simulation. Ph.D. Thesis, Technische Universität Wien, Wien, Austria, 2010. [Google Scholar]
- Dalleau, D.; Weide-Zaage, K. Three-Dimensional Voids Simulation in chip Metallization Structures: A Contribution to Reliability Evaluation. Microelectron. Reliab. 2001, 41, 1625–1630. [Google Scholar] [CrossRef]
- Hua, Y.; Basaran, C.; Hopkins, D.C. Numerical simulation of stress evolution during electromigration in IC interconnect lines. IEEE Trans. Compon. Packag. Technol. 2003, 26, 673–681. [Google Scholar] [CrossRef]
- Clement, J.J.; Thompson, C.V. Modeling electromigration-induced stress evolution in confined metal lines. J. Appl. Phys. 1995, 78, 900–904. [Google Scholar] [CrossRef]
- Clement, J.J. Reliability analysis for encapsulated interconnect lines under dc and pulsed dc current using a continuum electromigration transport model. J. Appl. Phys. 1997, 82, 5991–6000. [Google Scholar] [CrossRef]
- Zhao, H.; Tan, S.X.D. Postvoiding FEM analysis for electromigration failure characterization. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 2483–2493. [Google Scholar]
- Chu, L.; Shi, J.; De Cursi, E.S. Monte carlo-based stochastic finite element model for electromigration in the interfaces of SAC solder and Cu conductors with uncertainties in boundary conditions. J. Electron. Mater. 2022, 51, 3173–3187. [Google Scholar] [CrossRef]
- Dong, C.; Huang, P.; Zhang, J. Finite-element simulation of a phase-field model for inclusion electromigration in {110}-oriented single crystal metal interconnects due to interface diffusion anisotropy. Appl. Phys. A 2022, 128, 617. [Google Scholar] [CrossRef]
- Zhang, Y.; Anicode, S.V.K.; Fan, X.; Madenci, E. Peridynamic modeling of void nucleation and growth in metal lines due to electromigration in a finite element framework. Comput. Methods Appl. Mech. Eng. 2023, 414, 116183. [Google Scholar] [CrossRef]
- Jin, W.; Chen, L.; Sadiqbatcha, S.; Peng, S.; Tan, S.X.D. EMGraph: Fast Learning-Based Electromigration Analysis for Multi-Segment Interconnect Using Graph Convolution Networks. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 919–924. [Google Scholar]
- Lamichhane, S.; Lu, H.; Tan, S.X.D. BPINN-EM-post: Stochastic electromigration damage analysis in the post-void phase based on bayesian physics-informed neural network. arXiv 2025, arXiv:2503.17393. [Google Scholar] [CrossRef]
- Tan, S.X.D.; Amrouch, H.; Kim, T.; Sun, Z.; Cook, C.; Henkel, J. Recent advances in EM and BTI induced reliability modeling, analysis and optimization (invited). Integration 2018, 60, 132–152. [Google Scholar] [CrossRef]
- Sun, Z.; Demircan, E.; Shroff, M.D.; Cook, C.; Tan, S.X.D. Fast Electromigration Immortality Analysis for Multisegment Copper Interconnect Wires. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 3137–3150. [Google Scholar] [CrossRef]
- Najm, F.N.; Sukharev, V. Electromigration simulation and design considerations for integrated circuit power grids. J. Vac. Sci. Technol. B 2020, 38, 063204. [Google Scholar] [CrossRef]
- Zahedmanesh, H.; Ciofi, I.; Zografos, O.; Badaroglu, M.; Croes, K. A Novel System-Level Physics-Based Electromigration Modelling Framework: Application to the Power Delivery Network. In Proceedings of the 2021 ACM/IEEE International Workshop on System Level Interconnect Prediction (SLIP), Munich, Germany, 4 November 2021; pp. 1–7. [Google Scholar]
- Sadasiva, S.; Vaitheeswaran, P.; Subbarayan, G. A phase field computational procedure for electromigration with specified contact angle and diffusional anisotropy. Comput. Mech. 2020, 66, 373–390. [Google Scholar] [CrossRef]
- Li, Y.; Fu, G.; Wan, B.; Yan, X.; Zhang, W.; Li, W. Phase-Field Modelling of Lead-Free Solder Joint Void Growth Under Thermal-Electrical Coupled Stress. J. Electron. Mater. 2022, 51, 259–272. [Google Scholar] [CrossRef]
- Wu, X.-W.; Chen, M.; Ke, L.-L. An electro-thermo-mechanical coupling phase-field model of defect evolution induced by electromigration in interconnects. Int. J. Mech. Sci. 2025, 285, 109792. [Google Scholar] [CrossRef]
- Chen, L.; Tan, S.X.D.; Sun, Z.; Peng, S.; Tang, M.; Mao, J. A Fast Semi-Analytic Approach for Combined Electromigration and Thermomigration Analysis for General Multisegment Interconnects. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 350–363. [Google Scholar] [CrossRef]
- Chen, H.B.; Tan, S.X.D.; Huang, X.; Kim, T.; Sukharev, V. Analytical Modeling and Characterization of Electromigration Effects for Multibranch Interconnect Trees. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 1811–1824. [Google Scholar] [CrossRef]
- Chen, H.B.; Tan, S.X.D.; Peng, J.; Kim, T.; Chen, J. Analytical Modeling of Electromigration Failure for VLSI Interconnect Tree Considering Temperature and Segment Length Effects. IEEE Trans. Device Mater. Reliab. 2017, 17, 653–666. [Google Scholar] [CrossRef]
- Shohel, M.A.A.; Chhabria, V.A.; Evmorfopoulos, N.; Sapatnekar, S.S. Analytical Modeling of Transient Electromigration Stress based on Boundary Reflections. In Proceedings of the 2021 IEEE/ACM International Conference on Computer Aided Design (ICCAD), Munich, Germany, 1–4 November 2021; pp. 1–8. [Google Scholar]
- Cook, C.; Sun, Z.; Demircan, E.; Shroff, M.D.; Tan, S.X.D. Fast Electromigration Stress Evolution Analysis for Interconnect Trees Using Krylov Subspace Method. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 969–980. [Google Scholar] [CrossRef]
- Axelou, O.; Evmorfopoulos, N.; Floros, G.; Stamoulis, G.; Sapatnekar, S.S. A Novel Semi-Analytical Approach for Fast Electromigration Stress Analysis in Multi-Segment Interconnects. In Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design, San Diego, CA, USA, 30 October–3 November 2022; p. 27. [Google Scholar]
- Stoikos, P.; Floros, G.; Garyfallou, D.; Evmorfopoulos, N.; Stamoulis, G. A Fast Semi-Analytical Approach for Transient Electromigration Analysis of Interconnect Trees Using Matrix Exponential. In Proceedings of the 28th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 16–19 January 2023; pp. 1–6. [Google Scholar]
- Jin, W.; Sadiqbatcha, S.; Sun, Z.; Zhou, H.; Tan, S.X.D. EM-GAN: Data-Driven Fast Stress Analysis for Multi-Segment Interconnects. In Proceedings of the 2020 IEEE 38th International Conference on Computer Design (ICCD), Hartford, CT, USA, 18–21 October 2020; pp. 296–303. [Google Scholar]
- Jin, W.; Peng, S.; Tan, S.X.D. Data-Driven Electrostatics Analysis based on Physics-Constrained Deep learning. In Proceedings of the 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 1382–1387. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Hou, T.; Zhen, P.; Ji, Z.; Chen, H.-B. A Deep Learning Framework for Solving Stress-based Partial Differential Equations in Electromigration Analysis. ACM Trans. Des. Autom. Electron. Syst. 2023, 28, 57. [Google Scholar] [CrossRef]
- Jin, W.; Chen, L.; Lamichhane, S.; Kavousi, M.; Tan, S.X.-D. HierPINN-EM: Fast Learning-Based Electromigration Analysis for Multi-Segment Interconnects Using Hierarchical Physics-Informed Neural Network. In Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design, San Diego, CA, USA, 30 October–3 November 2022; p. 28. [Google Scholar]


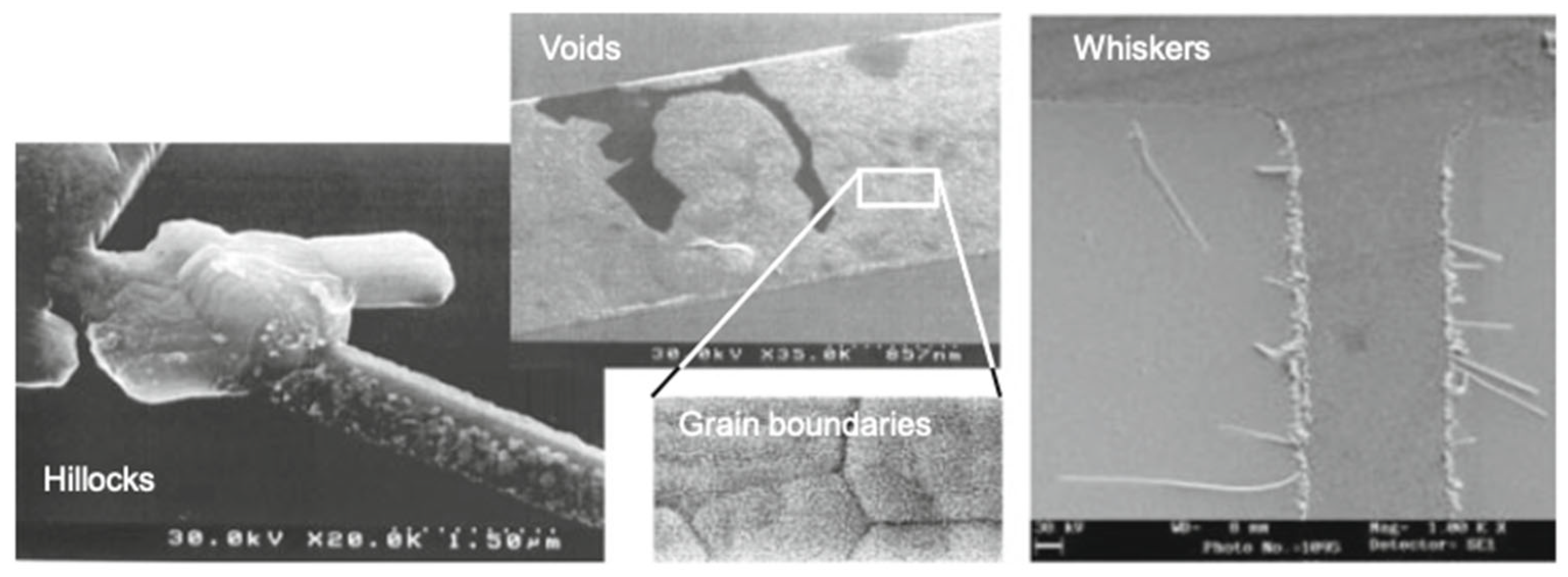
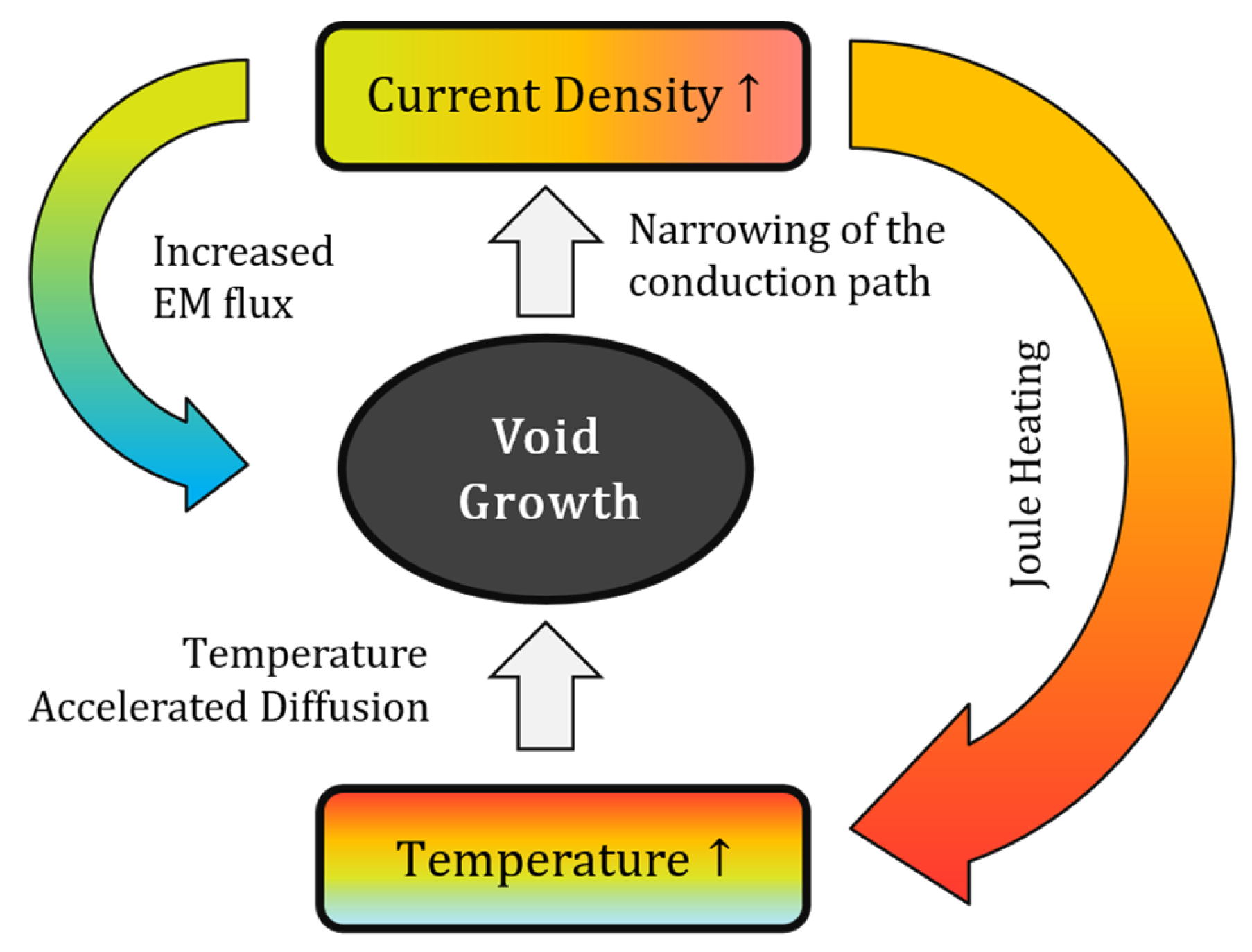
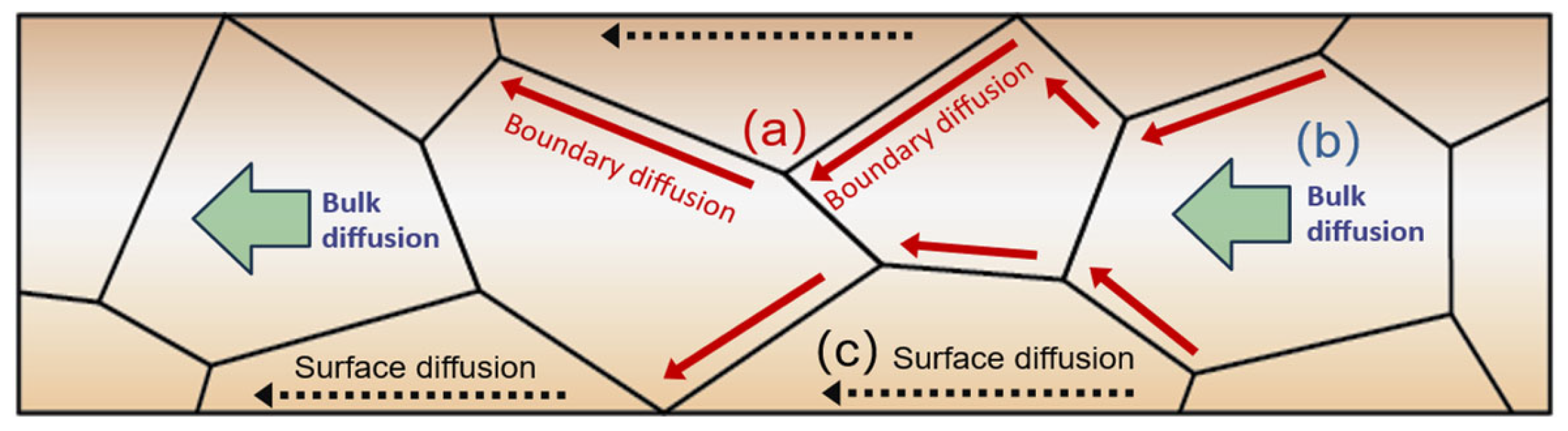





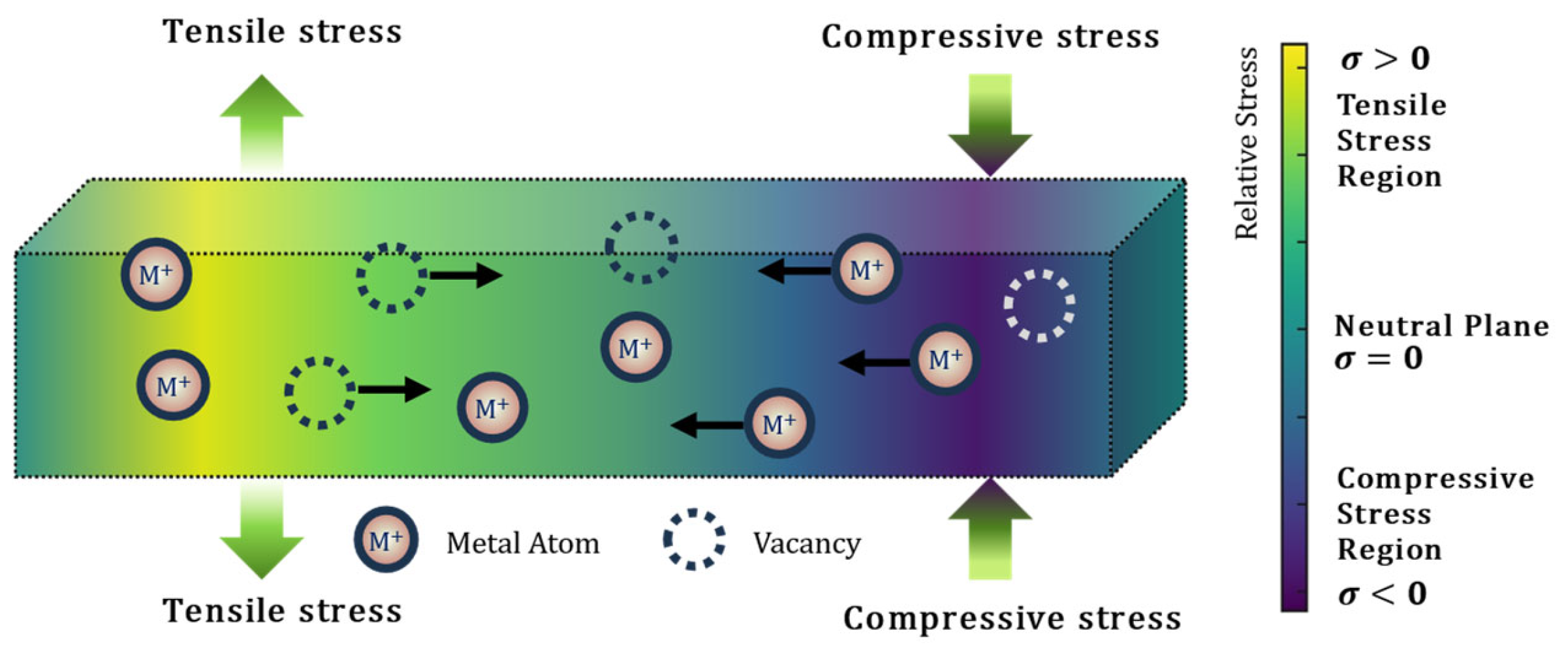

| Material | EM Lifetime (Relative) | Advantages | Disadvantages |
|---|---|---|---|
| Aluminum (Al) | Low (baseline) | Mature process; low cost | Poor EM resistance; high resistivity at nanoscale |
| Copper (Cu) | ~10× better than Al | Low resistivity; good mechanical properties | Susceptible to EM below 20 nm; needs complex barriers |
| Cobalt (Co) | ~2×–5× better than Cu | High EM reliability; simple barrier or barrierless; good adhesion; all-wet process | Higher resistivity; integration complexity |
| Ruthenium (Ru) | ≥2× better than Co | Short mean free path; high EM resistance; barrierless integration; stable at high T | Higher resistivity; deposition challenges |
| Ta/Ti/W (barrier) | Indirect benefit via EM pathways | Industry standard; robust diffusion blocking; strong adhesion | Thick (~5–10 nm); adds resistance; scaling limitations below 5 nm |
| Graphene (barrier) | Superior atomic-level blocking | Atomically thin; impermeable to Cu; low interface resistance; minimizes scattering | Immature integration; conformality and adhesion need further optimization |
| Graphene (capping) | 2×–78× improvement when capped | Suppresses surface diffusion; enhances EM life and current density | Integration complexity; non-load-bearing; variability by synthesis route |
| Metal | Bulk Diffusion (eV) | Grain Boundary Diffusion (eV) | Surface Diffusion (eV) | Reference |
|---|---|---|---|---|
| Al | ~1.2 | 0.7~0.9 | ~0.8 | [25,62,63,64] |
| Cu | ~2.2 | 0.8~1.2 | ~0.8 | [25,65,66,67,68] |
| Co | ~2.8 | 1.1~1.3 | 1.0~1.7 | [69,70,71,72] |
| Ru | >3 | ~1.8 | ~1.0 | [73,74,75,76,77] |
| Method | Speedup | Error Margin | Limitations | Applicable Scale |
|---|---|---|---|---|
| FastEM [172] | 60–100× | <0.5% | Stress evolution only | Large-scale interconnect trees |
| Matrix-Exp + EKS [174] | Up to 268× | ≈0.5% | High eigendecomposition cost | Full-chip PDN with arbitrary trees |
| AEKS-MOR [173] | 10–100× | <0.5% | Requires spectral sparsity and Krylov basis | Industrial-scale power networks |
| EM-GAN [175] | ~10 | ~6.6% (NRMSE) | Needs pre-solved datasets; low generalization | Fixed multi-branch layouts |
| PINN [177] | 3–10× | Varies | Sensitive to BC and long-range temporal accuracy | Simple PDE domains |
| HierPINN-EM [179] | N/A | 79× over EMGraph | Model complexity due to hierarchical decoupling | Arbitrary multi-segment topologies |
| BPINN-EM-Post [160] | 65–240× | Very low (statistical) | Post-void only; requires variation modeling | Layouts with process randomness |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, P.; Mao, L.-F.; Shen, W.-H.; Yan, Y.-L. Electromigration Failures in Integrated Circuits: A Review of Physics-Based Models and Analytical Methods. Electronics 2025, 14, 3151. https://doi.org/10.3390/electronics14153151
Cheng P, Mao L-F, Shen W-H, Yan Y-L. Electromigration Failures in Integrated Circuits: A Review of Physics-Based Models and Analytical Methods. Electronics. 2025; 14(15):3151. https://doi.org/10.3390/electronics14153151
Chicago/Turabian StyleCheng, Ping, Ling-Feng Mao, Wen-Hao Shen, and Yu-Ling Yan. 2025. "Electromigration Failures in Integrated Circuits: A Review of Physics-Based Models and Analytical Methods" Electronics 14, no. 15: 3151. https://doi.org/10.3390/electronics14153151
APA StyleCheng, P., Mao, L.-F., Shen, W.-H., & Yan, Y.-L. (2025). Electromigration Failures in Integrated Circuits: A Review of Physics-Based Models and Analytical Methods. Electronics, 14(15), 3151. https://doi.org/10.3390/electronics14153151







