Gecko-Inspired Robots for Underground Cable Inspection: Improved YOLOv8 for Automated Defect Detection
Abstract
1. Introduction
- Gecko-Inspired Quadruped Robot Design:A novel quadruped robot is developed, inspired by the gecko’s flexible spine and multi-joint limb structure. By combining biologically inspired mechanics with Denavit–Hartenberg-based kinematic modeling and zero-impact gait trajectory planning, the robot achieves stable adaptive locomotion in constrained and irregular underground cable environments.
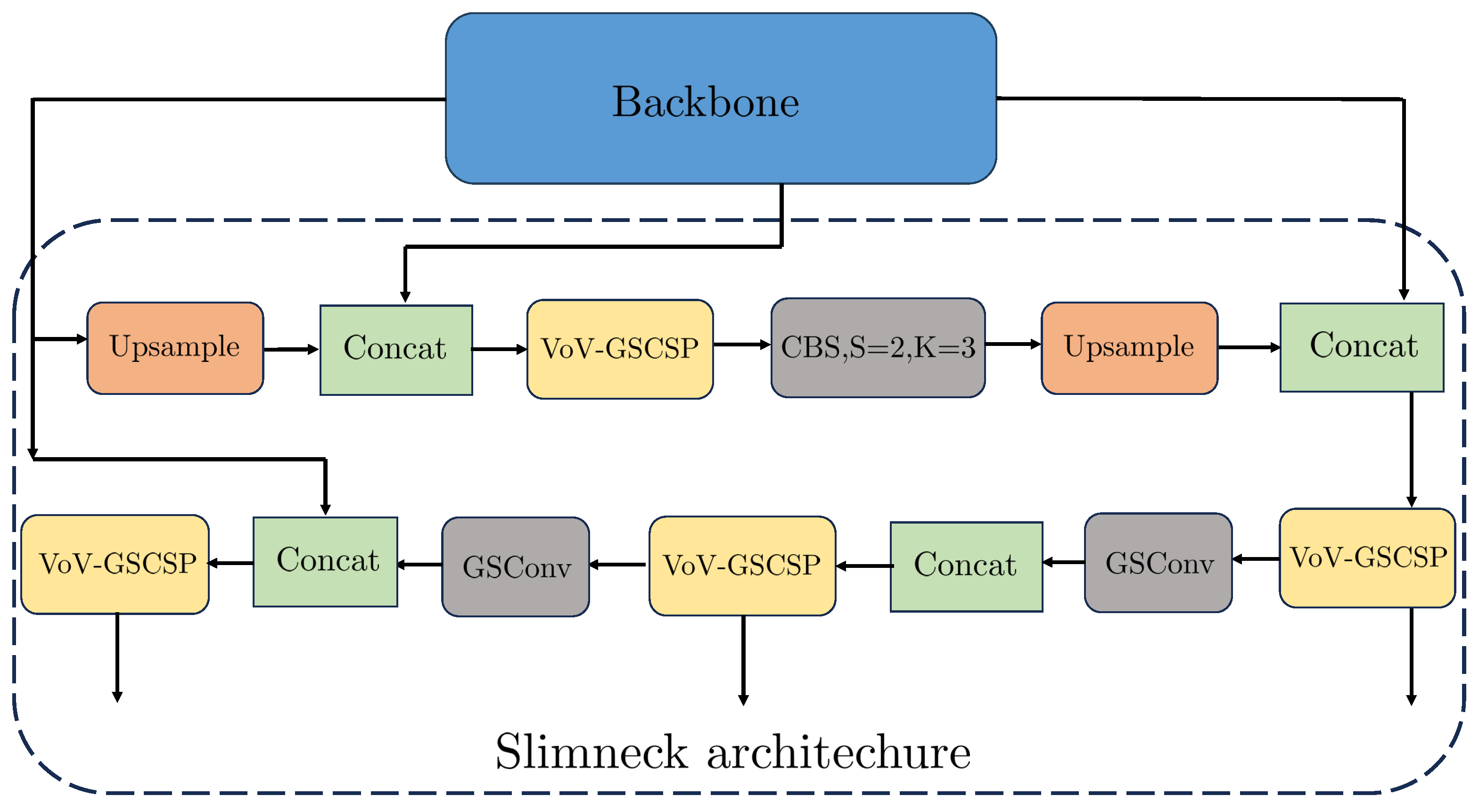
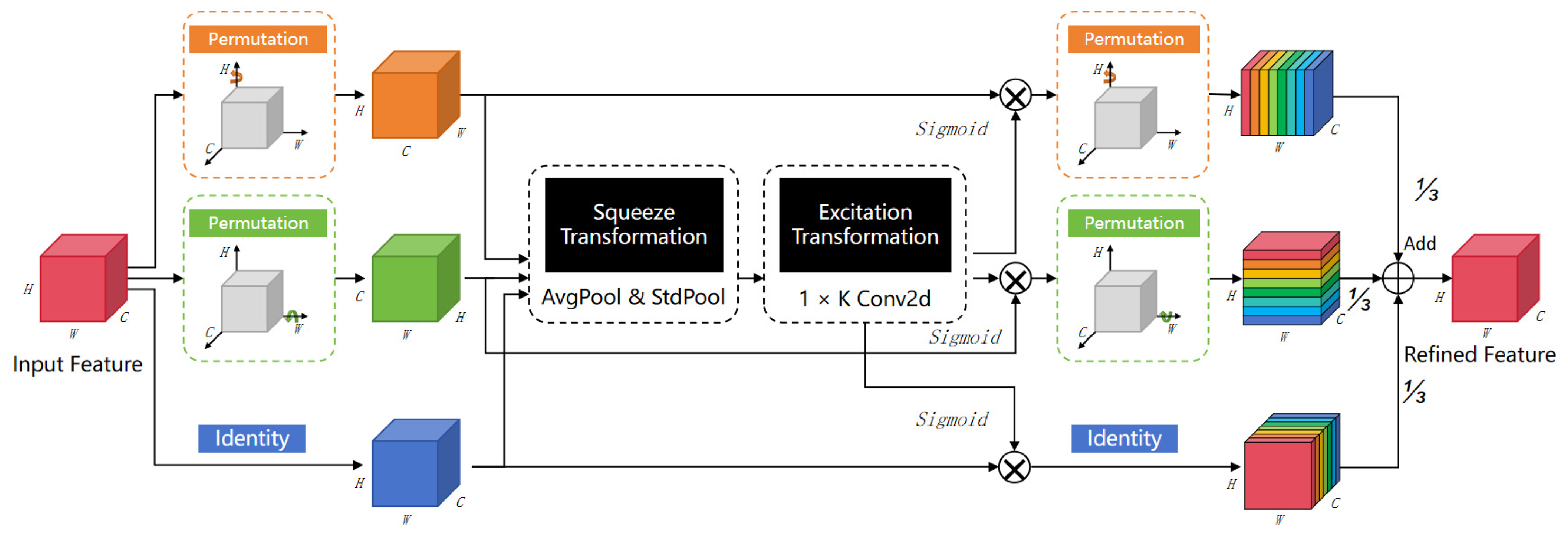
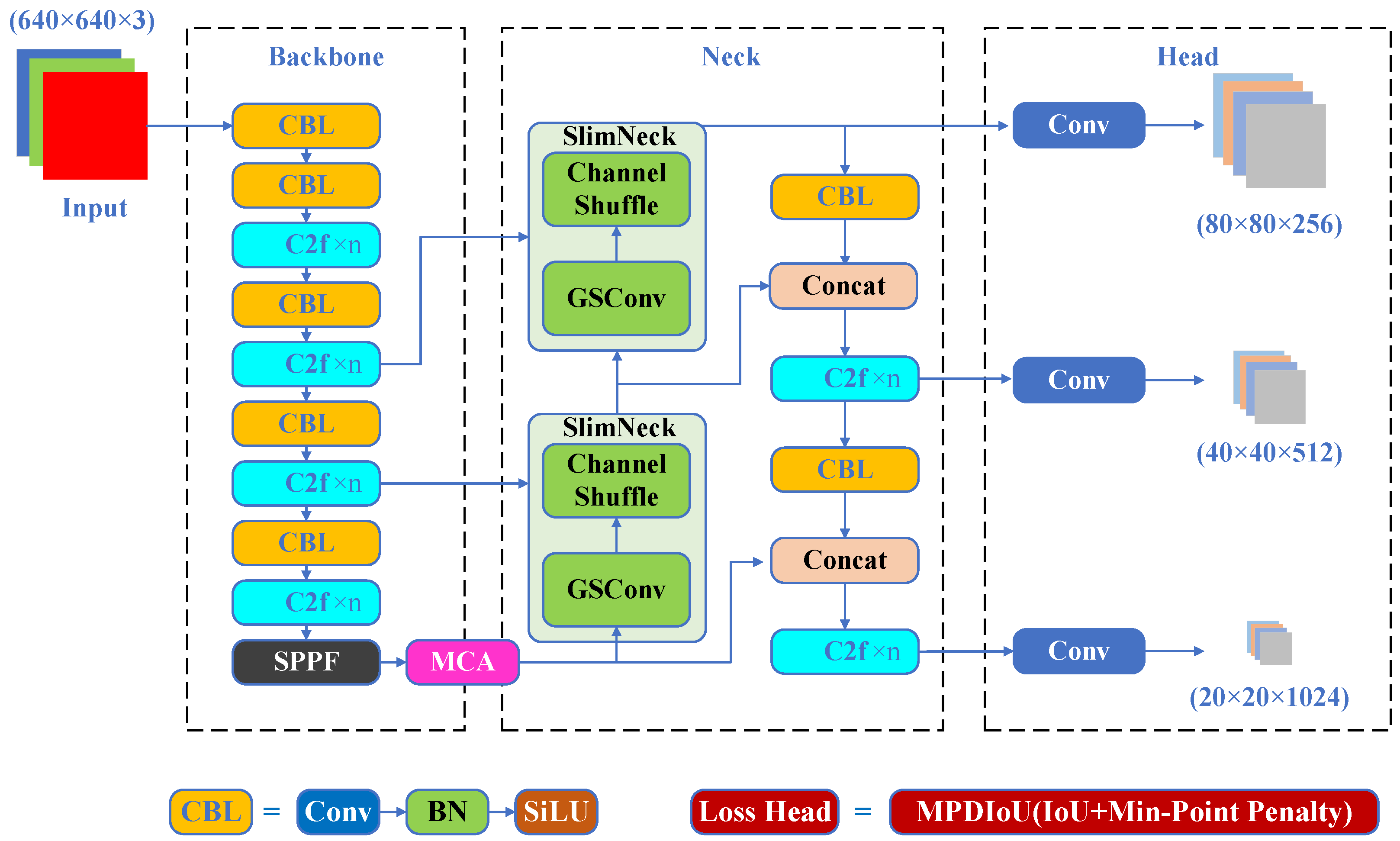
- Improved Lightweight Vision Framework Based on YOLOv8:To improve the performance of defect detection in complex underground environments, we propose an enhanced YOLOv8-based object detection model. This framework includes three novel modules: (1) SlimNeck, a lightweight neck architecture designed to efficiently aggregate multi-scale features using GSConv and VoV-GSCSP structures; (2) MCA, which introduces coordinate attention along the channel, width, and height dimensions to strengthen feature discrimination; and (3) MPDIoU loss, which introduces a geometric penalty based on the shortest point-to-point distance between predicted and ground-truth boxes, thus improving localization accuracy.
2. Related Works
2.1. Currently Underground Cable Inspection Robots
2.2. Gecko-Inspired Climbing Robots
2.3. Three-Dimensional Image Acquisition and Analysis for Underground Cables
3. Methodology
3.1. Kinematic Modeling of a Quadruped Robot
Note: The components , , and represent the 3D position of the foot in the base frame and are obtained from the last column of the full transformation matrix.
Note: For simplification, we define shorthand notations such as or , e.g., , , etc.
3.2. Image Dataset Preparation and Modular Detection Enhancements
3.2.1. Image Collection
3.2.2. Data Augmentation
3.2.3. Enhancement Algorithms
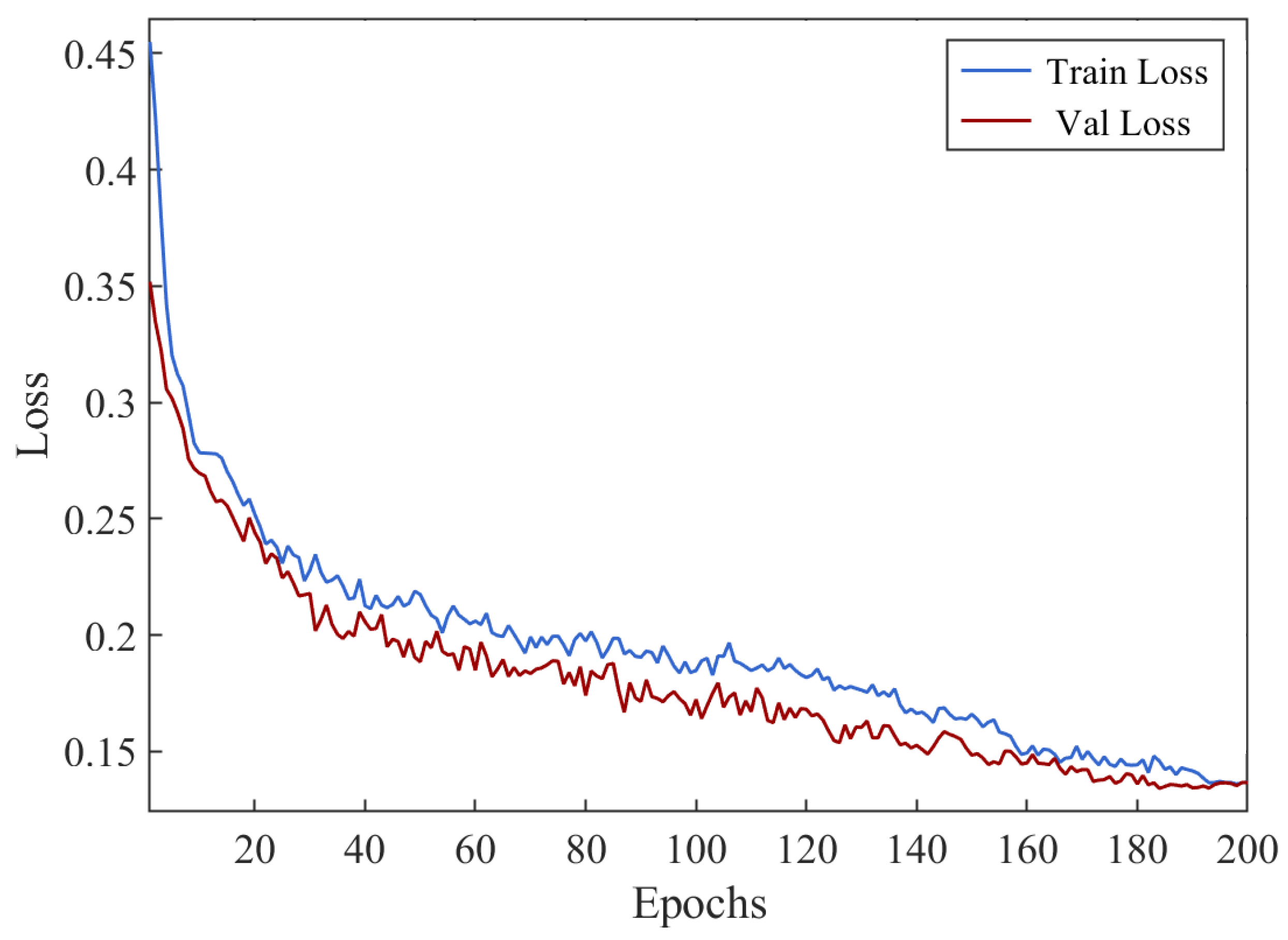
3.2.4. Model Accuracy Analysis
4. Experiment
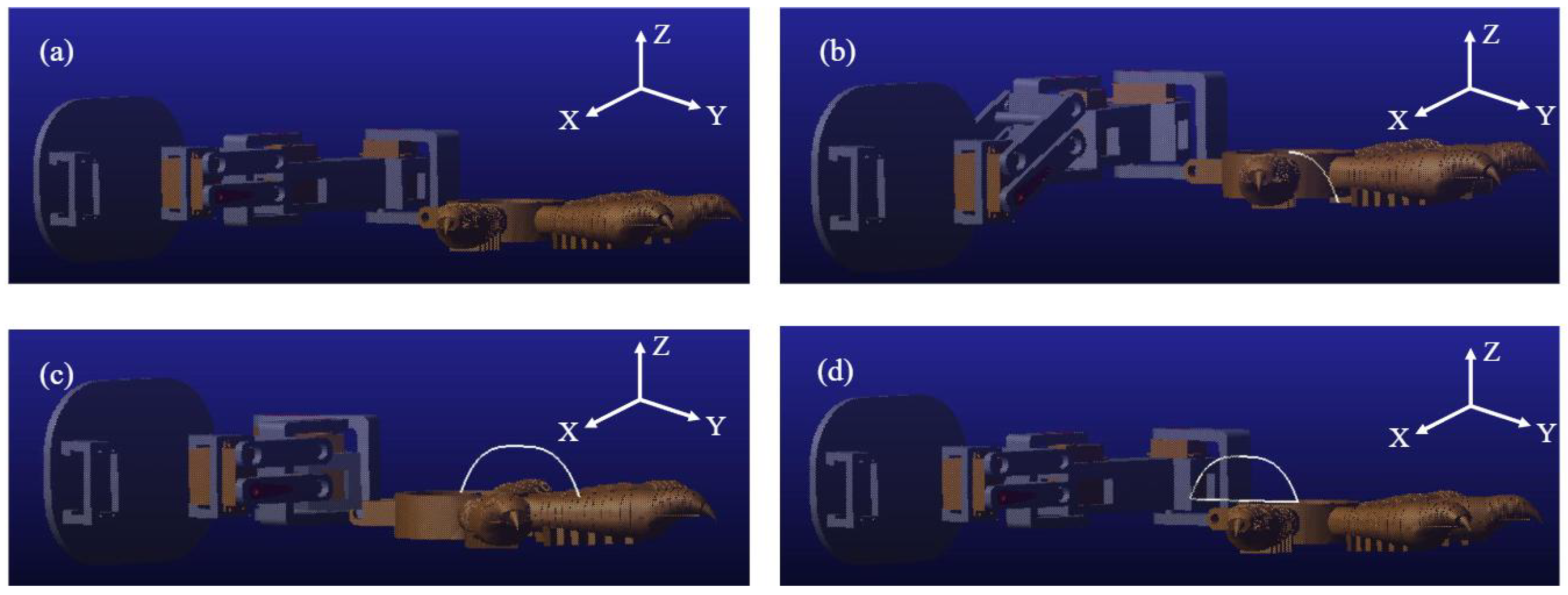
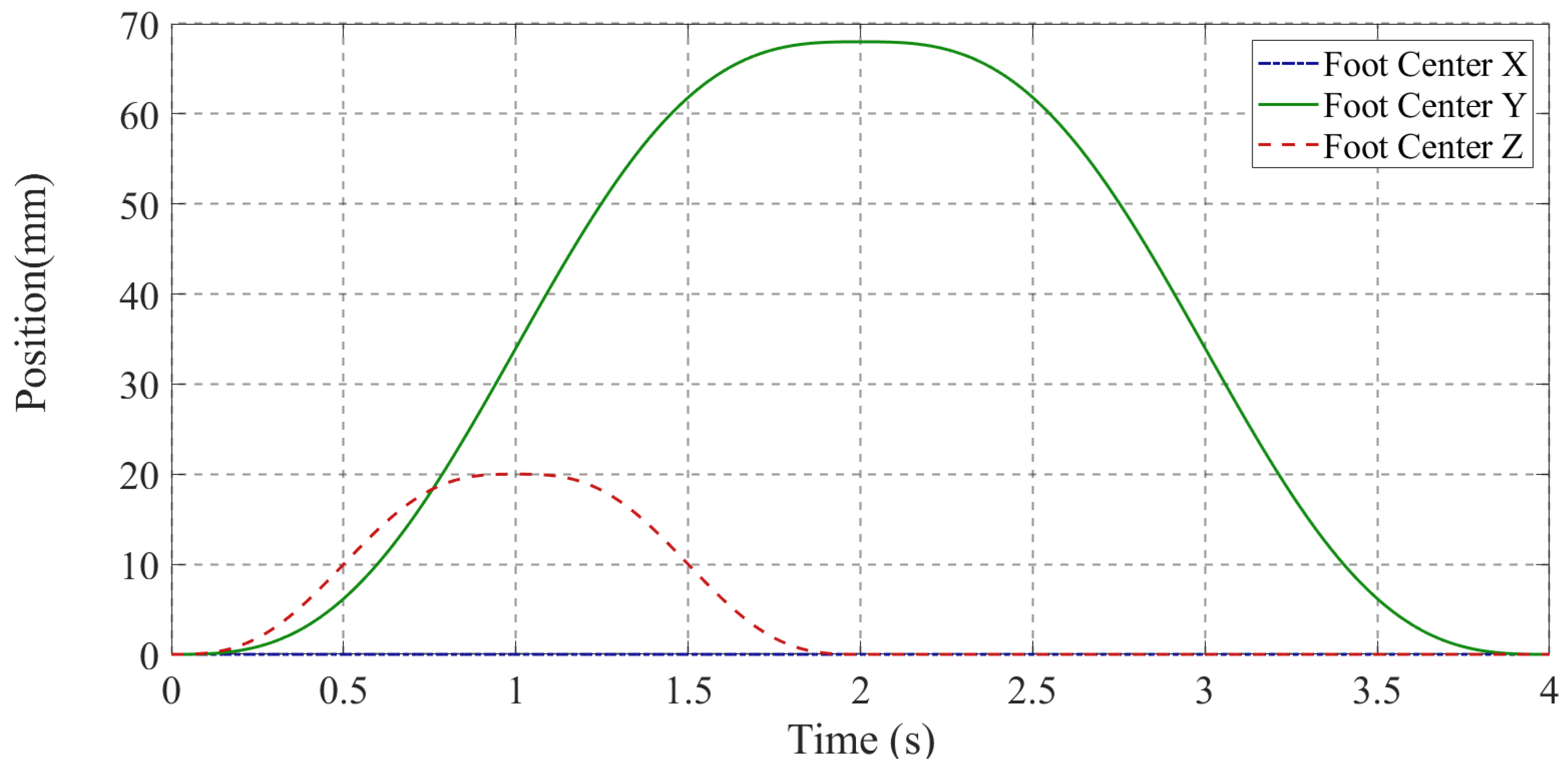
4.1. Kinematic Simulation Experiment
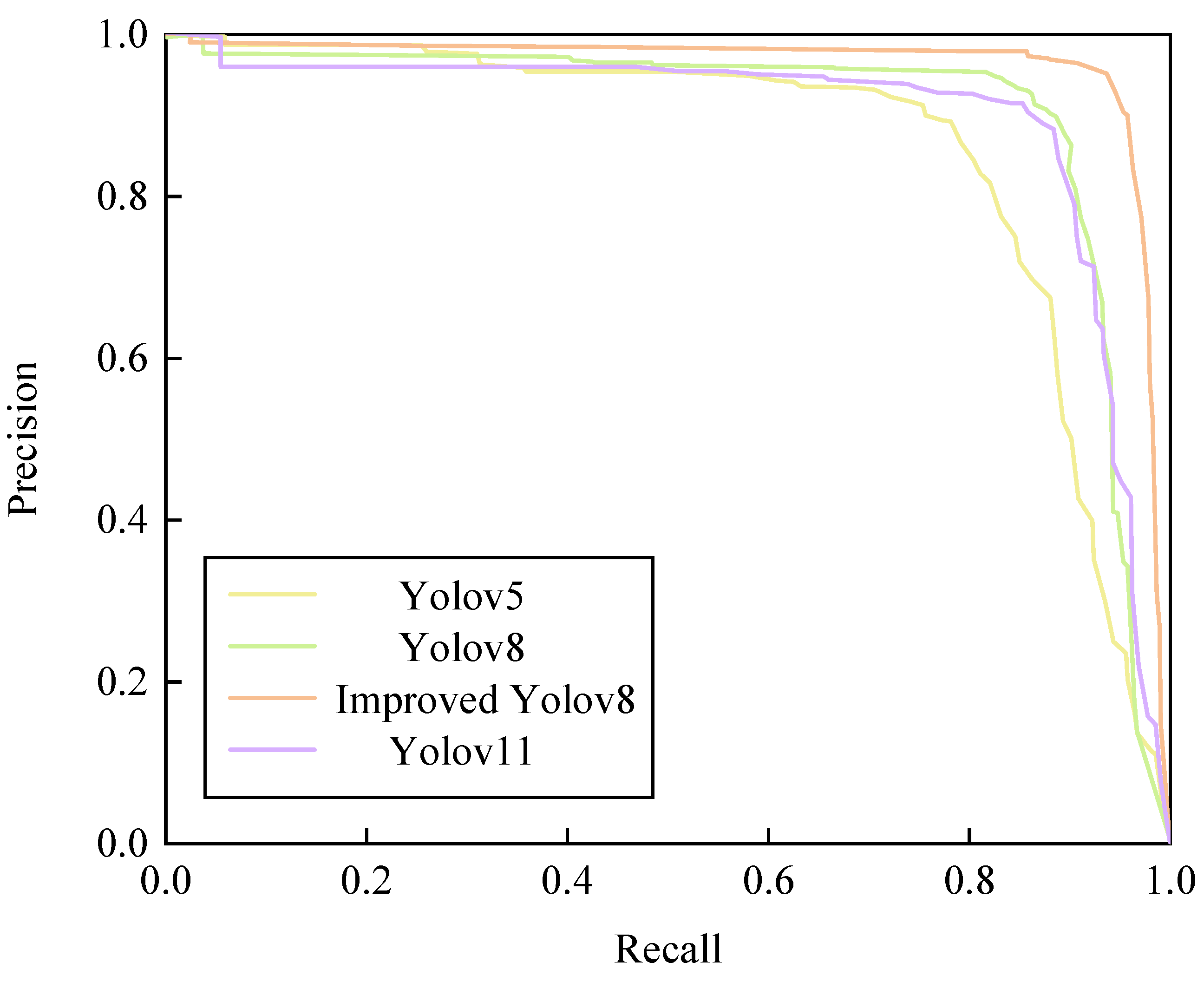
4.2. Cable Defect Identification Model Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yangí, L.; Yang, G.; Liu, Z.; Chang, Y.; Jiang, B.; Awad, Y.; Xiao, J. Wall-climbing robot for visual and GPR inspection. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 1004–1009. [Google Scholar]
- Raut, H.K.; Baji, A.; Hariri, H.H.; Parveen, H.; Soh, G.S.; Low, H.Y.; Wood, K.L. Gecko-inspired dry adhesive based on micro–nanoscale hierarchical arrays for application in climbing devices. ACS Appl. Mater. Interfaces 2018, 10, 1288–1296. [Google Scholar] [CrossRef]
- Hegde, N.; Samantaray, R.R.; Kamble, S.J. Automated Robotic System for Pipeline Health Assessment. In Proceedings of the 2025 International Conference on Intelligent and Innovative Technologies in Computing, Electrical and Electronics (IITCEE), Bangalore, India, 16–17 January 2025. [Google Scholar] [CrossRef]
- Bian, S.; Xu, F.; Wei, Y.; Kong, D. A Novel Type of Wall-Climbing Robot with a Gear Transmission System Arm and Adhere Mechanism Inspired by Cicada and Gecko. Appl. Sci. 2021, 11, 4137. [Google Scholar] [CrossRef]
- Mello, C., Jr.; Gonçalves, E.M.; Estrada, E.; Oliveira, G.; Souto, H., Jr.; Almeida, R.; Botelho, S.; Santos, T.; Oliveira, V. TATUBOT–Robotic System for Inspection of Undergrounded Cable System. In Proceedings of the 2008 IEEE Latin American Robotic Symposium, Salvador, Brazil, 29–30 October 2008; pp. 170–175. [Google Scholar] [CrossRef]
- Zheng, Z.; Yuan, X.; Huang, H.; Yu, X.; Ding, N. Mechanical Design of a Cable Climbing Robot for Inspection on a Cable-Stayed Bridge. In Proceedings of the 2018 13th World Congress on Intelligent Control and Automation (WCICA), Changsha, China, 4–8 July 2018; pp. 1680–1684. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, H.; Zheng, H.; Fan, S.; Liu, Z. An Intelligent Inspection Robot for Underground Cable Trenches Based on Adaptive 2D-SLAM. Machines 2022, 10, 1011. [Google Scholar] [CrossRef]
- Chen, G.; Lin, T.; Lodewijks, G.; Ji, A. Design of an Active Flexible Spine for Wall Climbing Robot Using Pneumatic Soft Actuators. J. Bionic Eng. 2023, 20, 530–542. [Google Scholar] [CrossRef]
- Schmidt, D.; Berns, K. Climbing robots for maintenance and inspections of vertical structures—A survey of design aspects and technologies. Robot. Auton. Syst. 2013, 61, 1288–1305. [Google Scholar] [CrossRef]
- Chen, M.; Li, Q.; Wang, S.; Zhang, K.; Chen, H.; Zhang, Y. Single-Leg Structural Design and Foot Trajectory Planning for a Novel Bioinspired Quadruped Robot. Complexity 2021, 2021, 6627043. [Google Scholar] [CrossRef]
- Feng, X.; Han, Q.; Qiu, B.; Ji, A. Design of a Gecko-Inspired Flexible Foot Using Shape Memory Alloys. J. Nanjing Univ. Aeronaut. Astronaut. 2023, 55, 427–436. (In Chinese) [Google Scholar]
- Wang, Z.; Feng, Y.; Wang, B.; Yuan, J.; Zhang, B.; Song, Y.; Wu, X.; Li, L.; Li, W.; Dai, Z. Device for Measuring Contact Reaction Forces during Animal Adhesion Landing/Takeoff from Leaf-like Compliant Substrates. Biomimetics 2024, 9, 141. [Google Scholar] [CrossRef]
- Haomachai, W.; Dai, Z.; Manoonpong, P. Transition Gradient From Standing to Traveling Waves for Energy-Efficient Slope Climbing of a Gecko-Inspired Robot. IEEE Robot. Autom. Lett. 2024, 9, 2423–2430. [Google Scholar] [CrossRef]
- Li, B.; Wang, X.; Yu, S.; Mei, T. Structure of Gecko Inspired Flexible Foot and Control System. Res. Prepr. 2011, 22, 897–900. [Google Scholar]
- Yu, Z.; Fu, J.; Ji, Y.; Zhao, B.; Ji, A. Design of a Variable Stiffness Gecko-Inspired Foot and Adhesion Performance Test on Flexible Surface. Biomimetics 2022, 7, 125. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Chi, Y.; Sun, J.; Huang, T.H.; Maghsoudi, O.H.; Spence, A.; Zhao, J.; Su, H.; Yin, J. Leveraging elastic instabilities for amplified performance: Spine-inspired high-speed and high-force soft robots. Sci. Adv. 2020, 6, eaaz6912. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Xu, L.; Chen, S.; Xu, H.; Cheng, G.; Li, T.; Yang, Q. Design and realization of a bio-inspired wall climbing robot for rough wall surfaces. In Proceedings of the Intelligent Robotics and Applications: 12th International Conference, ICIRA 2019, Shenyang, China, 8–11 August 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 47–59. [Google Scholar]
- Chen, D.; Zhang, Q.; Wang, L.; Zu, Y. Design and realization of a kind of rough wall climbing robot. J. Harbin Eng. Univ. 2012, 33, 209–213. [Google Scholar]
- Beck, H.K.; Schultz, J.T.; Clemente, C.J. A Bio-Inspired Robotic Climbing Robot to Understand Kinematic and Morphological Determinants for an Optimal Climbing Gait. Bioinspiration Biomimetics 2022, 17, 016005. [Google Scholar] [CrossRef]
- Qiu, J.; Ji, A.; Zhu, K.; Han, Q.; Wang, W.; Qi, Q.; Chen, G. A Gecko-Inspired Robot with a Flexible Spine Driven by Shape Memory Alloy Springs. Soft Robot. 2023, 10, 713–723. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Ballesteros-Escamilla, M.; Chairez, I.; Luviano, A. Output Second-Order Sliding-Mode Control for a Gecko Biomimetic Climbing Robot. J. Bionic Eng. 2019, 16, 633–646. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Z.; Kang, H.; Tang, Y. 3D vision technologies for a self-developed structural external crack damage recognition robot. Autom. Constr. 2024, 159, 105262. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Jie, Y.; Zhao, C.; Zhang, Z. Dual-Frequency Lidar for Compressed Sensing 3D Imaging Based on All-Phase Fourier Transform. J. Opt. Photonics Res. 2023, 1, 74–81. [Google Scholar] [CrossRef]
- Xiao, F.; Chu, S.; Guo, X.; Zhang, Y.; Huang, R. Enhanced path planning for robot navigation in Gaussian noise environments with YOLO v10 and depth deterministic strategies. Discov. Artif. Intell. 2025, 5, 44. [Google Scholar] [CrossRef]
- Liu, G.; Jin, C.; Ni, Y.; Yang, T.; Liu, Z. UCIW-YOLO: Multi-category and high-precision obstacle detection model for agricultural machinery in unstructured farmland environments. Expert Syst. Appl. 2025, 294, 128686. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, K.; Liu, C.; Chen, L. Bi2F-YOLO: A novel framework for underwater object detection based on YOLOv7. Intell. Mar. Technol. Syst. 2025, 3, 9. [Google Scholar] [CrossRef]
- Bhagwat, A.; Dutta, S.; Saha, D.; Reddy, M.J.B. An online 11 kV distribution system insulator defect detection approach with modified YOLOv11 and MobileNetV3. Sci. Rep. 2025, 15, 15691. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, G.; Cao, H.; Hu, K.; Wang, Q.; Deng, Y.; Gao, J.; Tang, Y. Geometry-Aware 3D Point Cloud Learning for Precise Cutting-Point Detection in Unstructured Field Environments. J. Field Robot. 2025; early view. [Google Scholar] [CrossRef]
- Hou, S.; Dong, B.; Wang, H.; Wu, G. Inspection of surface defects on stay cables using a robot and transfer learning. Autom. Constr. 2020, 119, 103382. [Google Scholar] [CrossRef]
- Magdy, A.; Moustafa, M.S.; Ebied, H.M.; Tolba, M.F. Lightweight faster R-CNN for object detection in optical remote sensing images. Sci. Rep. 2025, 15, 16163. [Google Scholar] [CrossRef]
- Gelu-Simeon, M.; Mamou, A.; Saint-Georges, G.; Alexis, M.; Sautereau, M.; Mamou, Y.; Simeon, J. Deep learning model applied to real-time delineation of colorectal polyps. BMC Med. Inform. Decis. Mak. 2025, 25, 206. [Google Scholar] [CrossRef] [PubMed]
- Terven, J.; Córdova-Esparza, D.M.; Romero-González, J.A. A Comprehensive Review of YOLO Architectures in Computer Vision: From YOLOv1 to YOLOv8 and YOLO-NAS. Mach. Learn. Knowl. Extr. 2023, 5, 1680–1716. [Google Scholar] [CrossRef]
- Varghese, R.; Sambath, M. YOLOv8: A Novel Object Detection Algorithm with Enhanced Performance and Robustness. In Proceedings of the 2024 International Conference on Advances in Data Engineering and Intelligent Computing Systems (ADICS), Chennai, India, 18–19 April 2024. [Google Scholar] [CrossRef]
- Biswal, P.; Mohanty, P.K. Kinematic and Dynamic Modeling of a Quadruped Robot. In Proceedings of the Machines, Mechanism and Robotics, Ischia, Italy, 1–3 June 2022; Kumar, R., Chauhan, V.S., Talha, M., Pathak, H., Eds.; Springer: Singapore, 2022; pp. 369–378. [Google Scholar]
- Patil, A.; Kulkarni, M.; Aswale, A. Analysis of the inverse kinematics for 5 DOF robot arm using D-H parameters. In Proceedings of the 2017 IEEE International Conference on Real-time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 688–693. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Wang, S.; He, Y. Gait Control Strategy of a Hydraulic Quadruped Robot Based on Foot-End Trajectory Planning Algorithm. J. Mech. Eng. 2013, 49, 39–44. [Google Scholar] [CrossRef]
- Roboflow, S. Cable Surface Defect Detection Dataset. 2025. Available online: https://universe.roboflow.com/seok-6suvt/-q5ecy (accessed on 23 June 2025).
- Ogino, Y.; Shoji, Y.; Toizumi, T.; Ito, A. ERUP-YOLO: Enhancing Object Detection Robustness for Adverse Weather Condition by Unified Image-Adaptive Processing. In Proceedings of the 2025 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Tucson, AZ, USA, 26 February–6 March 2025; pp. 8597–8605. [Google Scholar] [CrossRef]
- Kaur, P.; Khehra, B.S.; Mavi, E.B.S. Data Augmentation for Object Detection: A Review. In Proceedings of the 2021 IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Lansing, MI, USA, 9–11 August 2021; pp. 537–543. [Google Scholar] [CrossRef]
- Uddin, A.F.M.S.; Qamar, M.; Mun, J.; Lee, Y.; Bae, S.H. GaussianMix: Rethinking Receptive Field for Efficient Data Augmentation. Appl. Sci. 2025, 15, 4704. [Google Scholar] [CrossRef]
- Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; Yang, Y. Random Erasing Data Augmentation. arXiv 2017, arXiv:1708.04896. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Wei, H.; Liu, Z.; Zhan, Z.; Ren, Q. Slim-neck by GSConv: A lightweight-design for real-time detector architectures. J. Real Time Image Process. 2024, 21, 62. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Y.; Cheng, Z.; Song, Z.; Tang, C. MCA: Multidimensional collaborative attention in deep convolutional neural networks for image recognition. Eng. Appl. Artif. Intell. 2023, 126, 107079. [Google Scholar] [CrossRef]
- Zhou, N.; Gao, D.; Zhu, Z. YOLOv8n-SMMP: A Lightweight YOLO Forest Fire Detection Model. Fire 2025, 8, 183. [Google Scholar] [CrossRef]
- Ma, S.; Xu, Y. MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression. arXiv 2023, arXiv:2307.07662. [Google Scholar]
- Alqahtani, D.K.; Cheema, A.; Toosi, A.N. Benchmarking Deep Learning Models for Object Detection on Edge Computing Devices. arXiv 2024, arXiv:2409.16808. [Google Scholar]
- Lankarani, H.; Nikravesh, P. Continuous contact force models for impact analysis in multibody systems. Nonlinear Dyn. 1994, 5, 193–207. [Google Scholar] [CrossRef]
- Flores, P.; Ambrósio, J.; Claro, J.; Lankarani, H. Influence of the contact-impact force model on the dynamic response of multi-body systems. Proc. Inst. Mech. Eng. K 2006, 220, 21–34. [Google Scholar] [CrossRef]













| Joint Angle () | Joint Distance () | Link Length () | Link Twist () |
|---|---|---|---|
| 0 | |||
| 0 | |||
| 0 | |||
| 0 | |||
| 0 |
| Parameter | Value | Unit |
|---|---|---|
| Stiffness | 2855 | N/mm |
| Force Exponent | 1.5 | – |
| Damping | 5 | N·s/mm |
| Penetration Depth | 0.1 | mm |
| Static Friction Coefficient | 0.8 | – |
| Dynamic Friction Coefficient | 0.6 | – |
| Friction Transition Velocity | 1 | mm/s |
| Stiction Transition Velocity | 10 | mm/s |
| Parameter | Value |
|---|---|
| Epochs | 200 |
| Batch Size | 16 |
| Momentum | 0.937 |
| Initial Learning Rate | 0.01 |
| Learning Rate Schedule | Dynamic |
| Weight Decay | 0.0005 |
| Optimizer | SGD |
| Model | Precision | Recall | F1-Score | Model Size (MB) | FPS |
|---|---|---|---|---|---|
| YOLOv5 | 0.728 | 0.875 | 0.795 | 5.03 | 70.2 |
| YOLOv8 | 0.895 | 0.923 | 0.909 | 5.95 | 76.6 |
| YOLOv8-Improved | 0.900 | 0.970 | 0.933 | 5.78 | 82.1 |
| YOLOv11 | 0.802 | 0.916 | 0.855 | 5.24 | 74.7 |
| Faster R-CNN | 0.899 | 0.827 | 0.860 | 108.9 | 59.8 |
| SSD | 0.877 | 0.807 | 0.840 | 90.6 | 65.3 |
| Model | Precision | Recall | F1-Score | Model Size (MB) | FPS |
|---|---|---|---|---|---|
| YOLOv8 | 0.895 | 0.923 | 0.909 | 5.95 | 76.6 |
| YOLOv8-Slimneck | 0.898 | 0.888 | 0.9061 | 5.75 | 80.6 |
| YOLOv8-MCA | 0.896 | 0.932 | 0.9240 | 5.96 | 77.2 |
| YOLOv8-MPDIoU | 0.895 | 0.965 | 0.9189 | 5.95 | 78.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, D.; Honarvar Shakibaei Asli, B. Gecko-Inspired Robots for Underground Cable Inspection: Improved YOLOv8 for Automated Defect Detection. Electronics 2025, 14, 3142. https://doi.org/10.3390/electronics14153142
Guan D, Honarvar Shakibaei Asli B. Gecko-Inspired Robots for Underground Cable Inspection: Improved YOLOv8 for Automated Defect Detection. Electronics. 2025; 14(15):3142. https://doi.org/10.3390/electronics14153142
Chicago/Turabian StyleGuan, Dehai, and Barmak Honarvar Shakibaei Asli. 2025. "Gecko-Inspired Robots for Underground Cable Inspection: Improved YOLOv8 for Automated Defect Detection" Electronics 14, no. 15: 3142. https://doi.org/10.3390/electronics14153142
APA StyleGuan, D., & Honarvar Shakibaei Asli, B. (2025). Gecko-Inspired Robots for Underground Cable Inspection: Improved YOLOv8 for Automated Defect Detection. Electronics, 14(15), 3142. https://doi.org/10.3390/electronics14153142






