Image-Based Adaptive Visual Control of Quadrotor UAV with Dynamics Uncertainties
Abstract
1. Introduction
- (1)
- Image moment features are applied to a controller design process, eliminating the need for real-time depth estimation and reducing system control complexity.
- (2)
- The corresponding torque controller is derived based on quadrotor dynamics rather than the traditional PD controller to enhance the responsiveness of the IBVS strategy.
- (3)
- An adaptive estimation algorithm for the mass and inertia matrix is designed to address unknown system dynamics parameters, and it is integrated into the IBVS controller to guarantee system robustness under uncertainties.
2. Problem Statement and Preliminaries
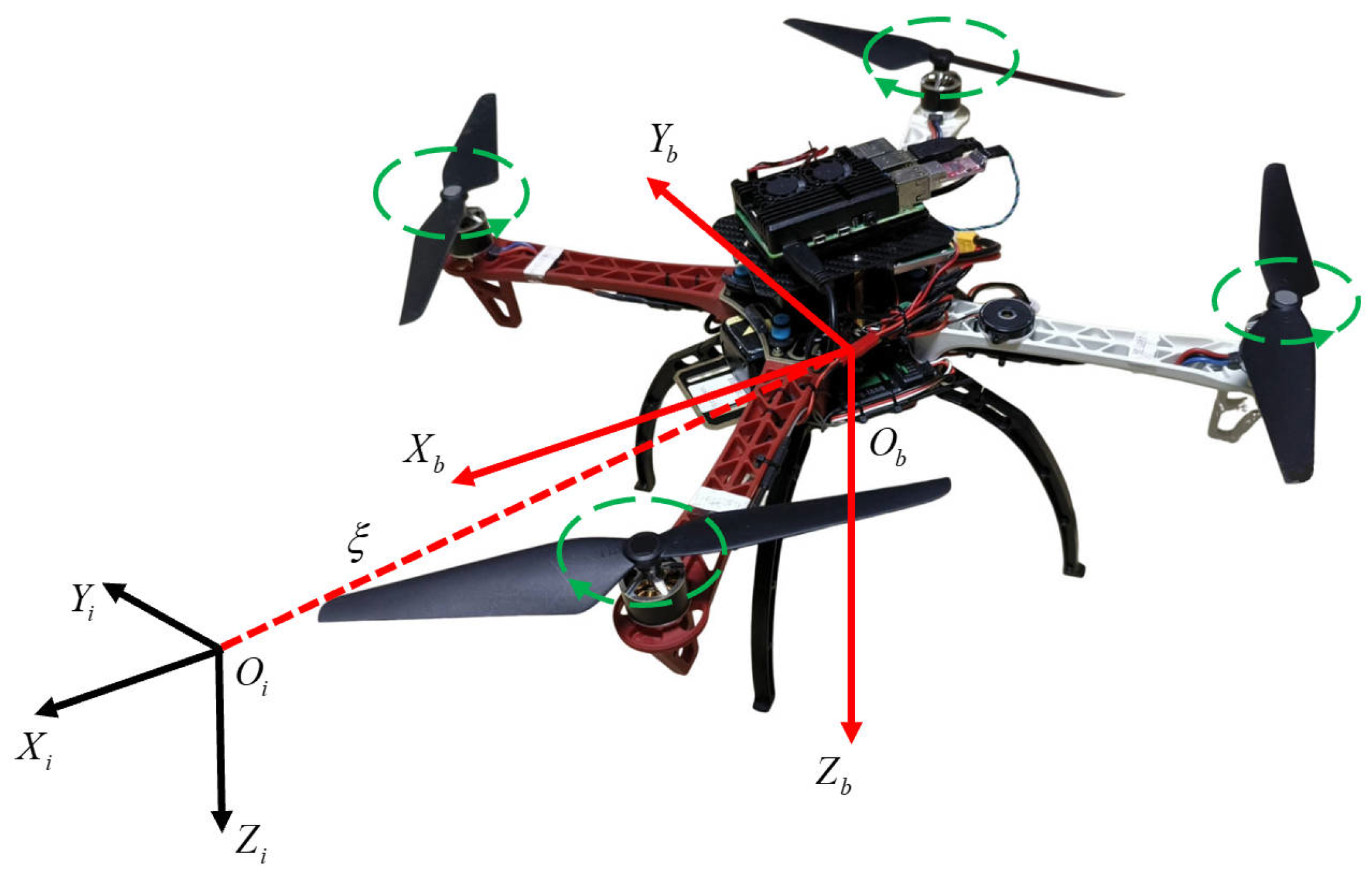
2.1. Quadrotor Model
2.2. Perspective Projection Model
2.3. Image Moment Features
3. Adaptive Controller Design
3.1. Image-Based Quadrotor Dynamics
3.2. Backstepping Controller Design Considering Unknown Mass
4. Torque Controller Design
4.1. Desired Angular Velocity
4.2. Controller Design Considering Uncertainty in Moment of Inertia
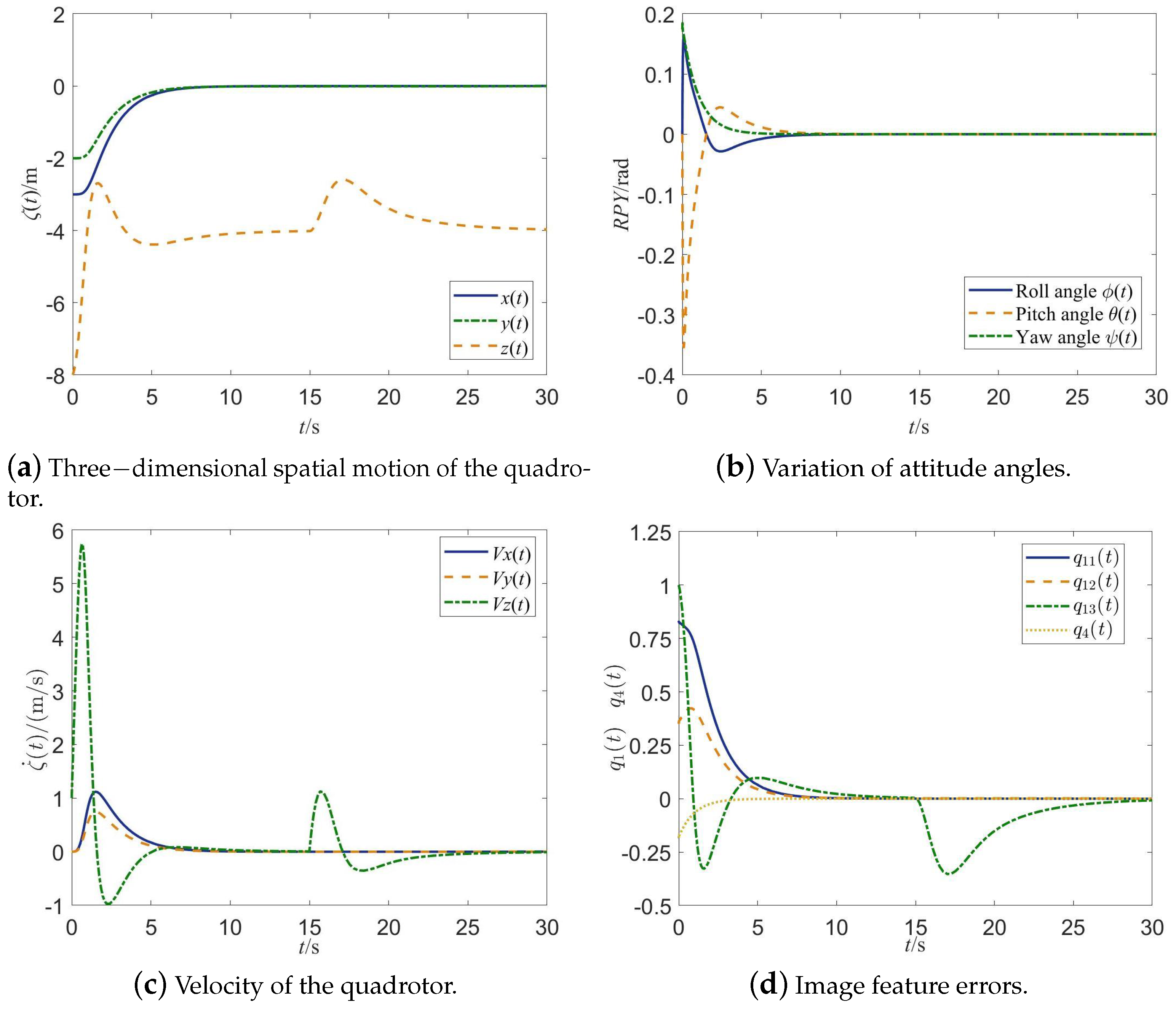
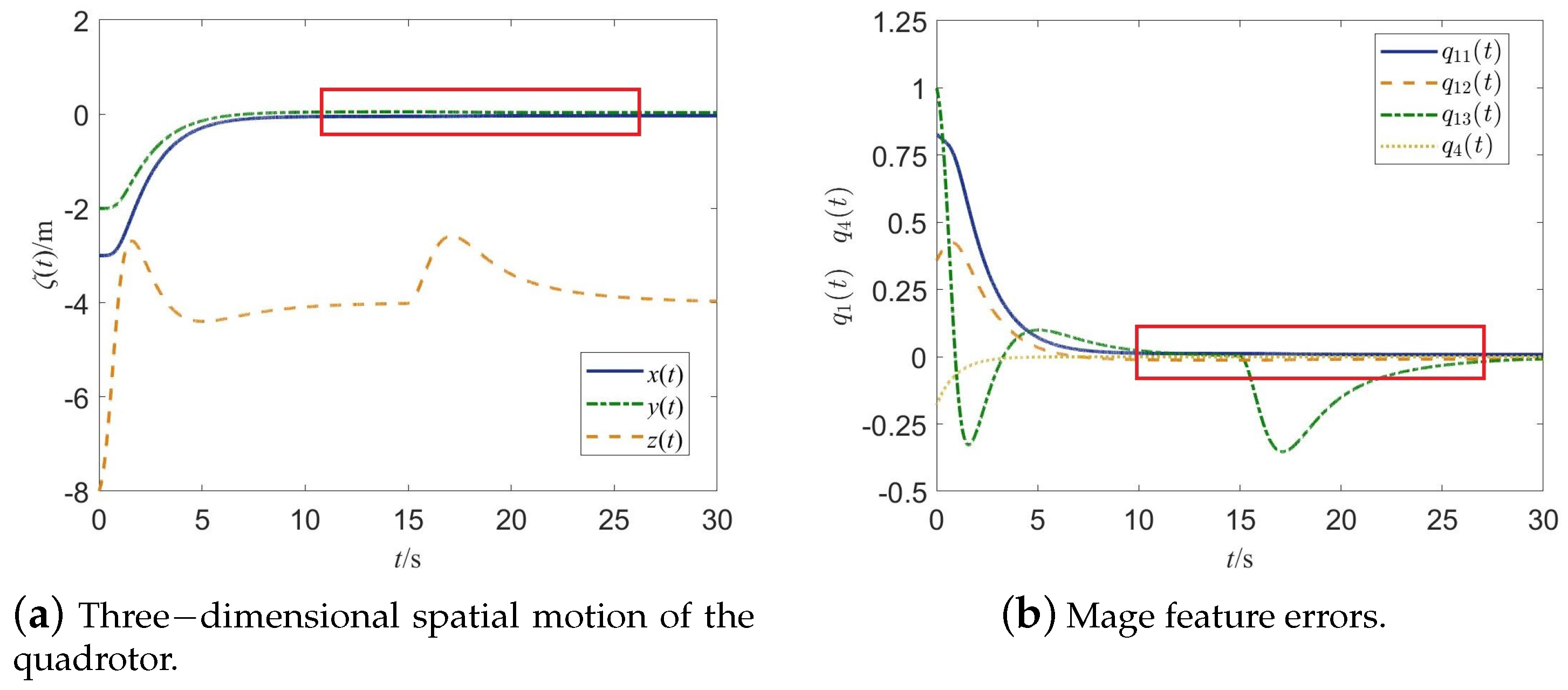
5. Performance Tests
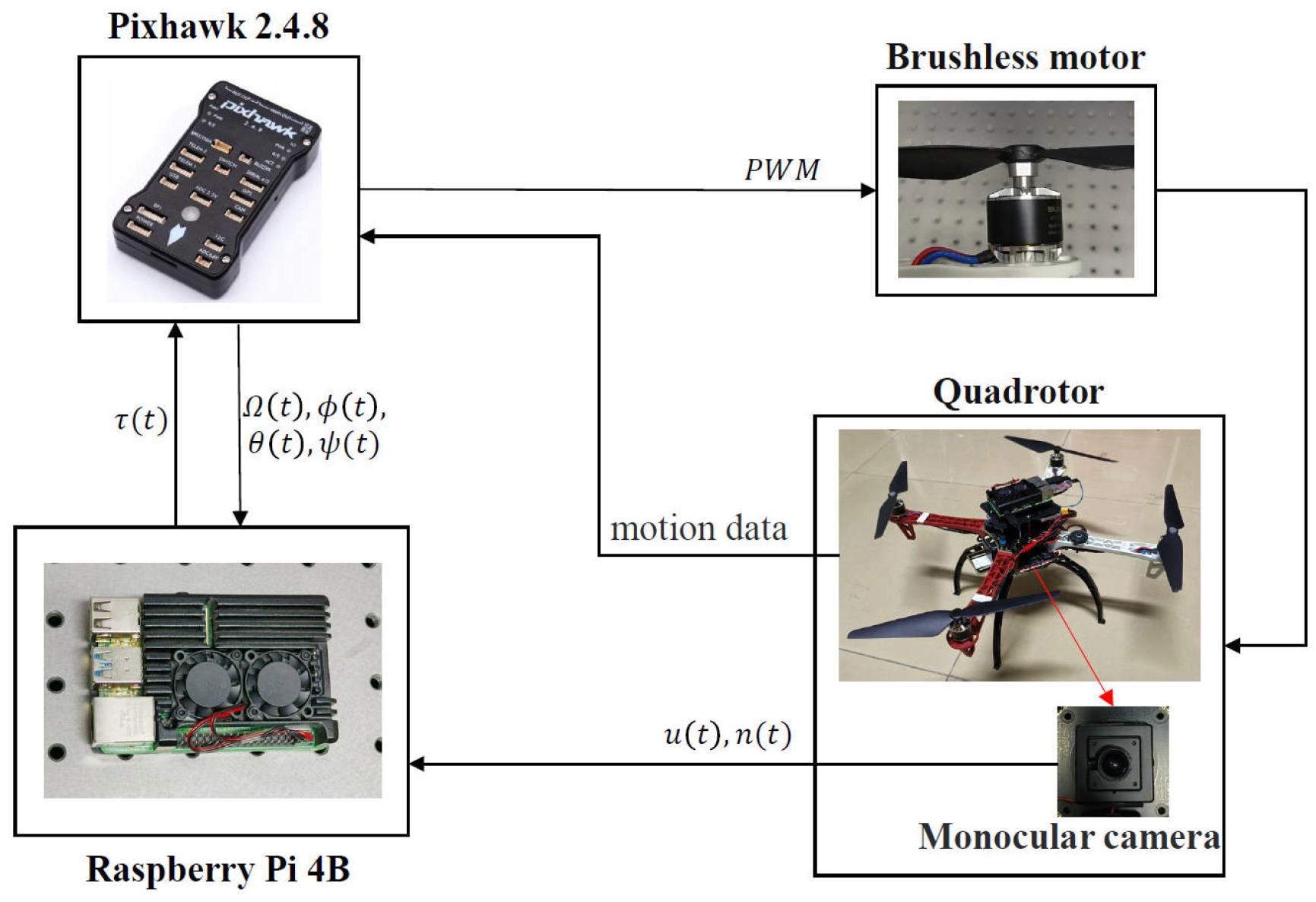
5.1. Hardware System Platform
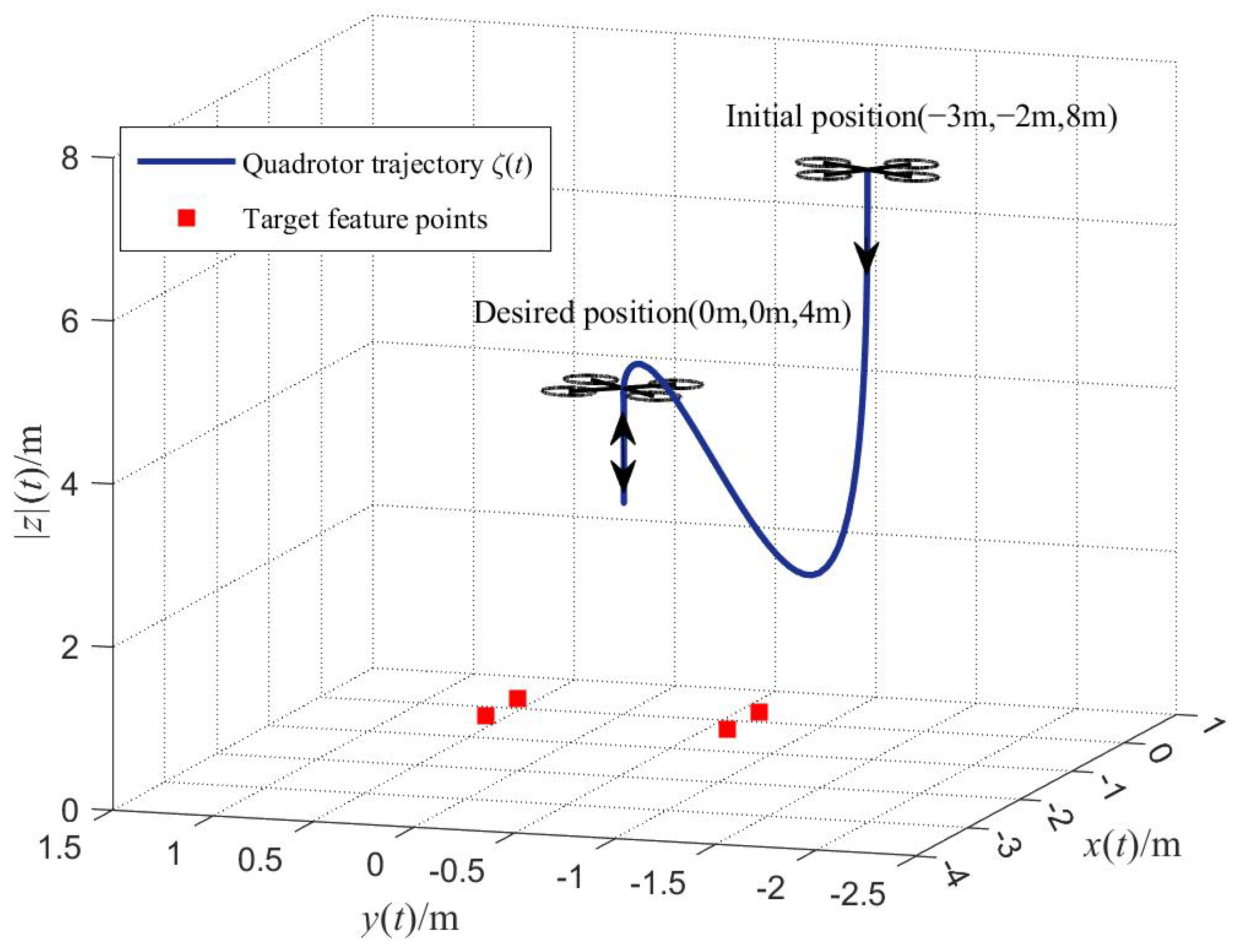
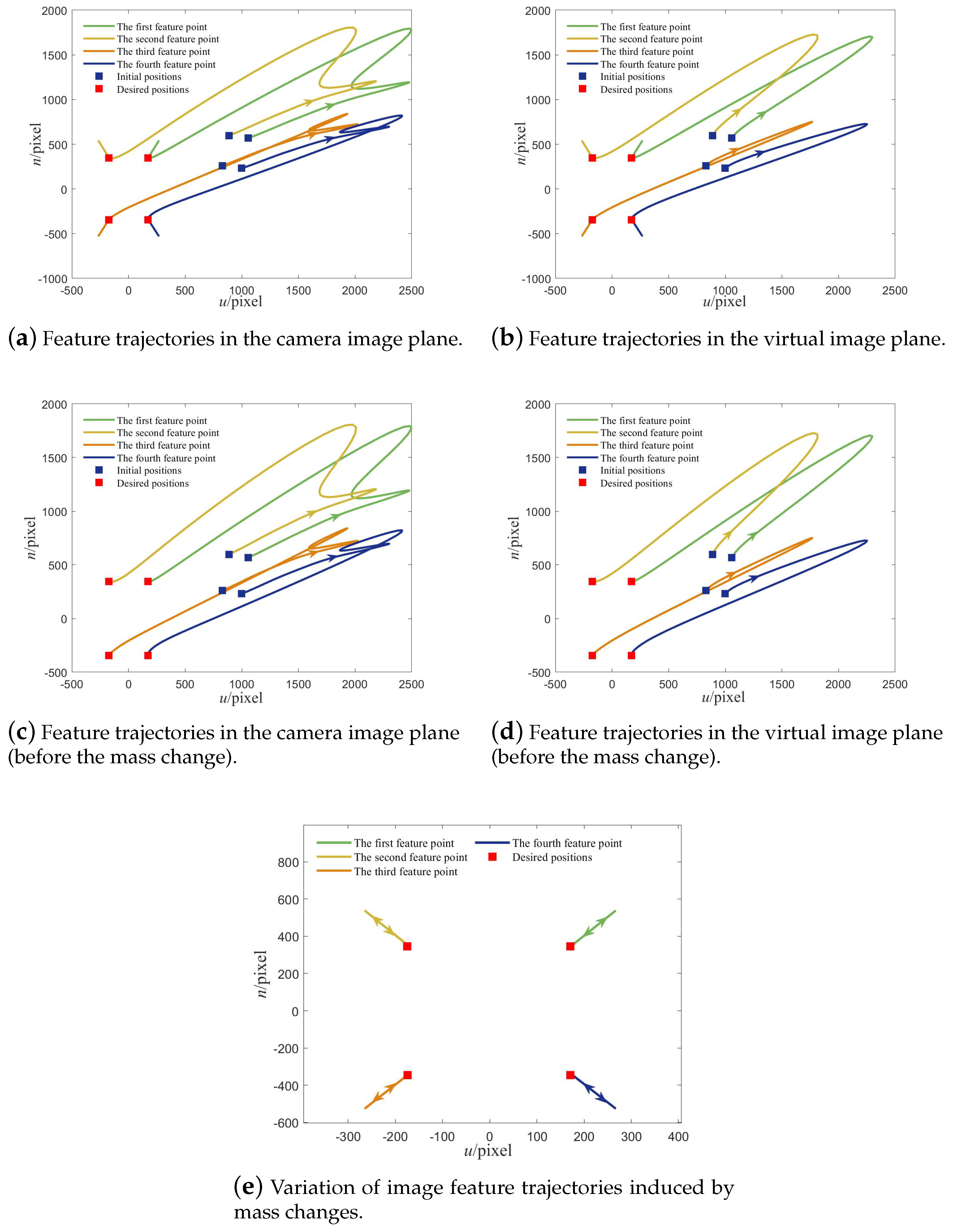
5.2. Performance Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Chen, J.; He, X. An adaptive composite disturbance rejection for attitude control of the agricultural quadrotor UAV. ISA Trans. 2022, 129, 564–579. [Google Scholar] [CrossRef] [PubMed]
- Lal, R.; Prabhakar, P. Time-Optimal Multi-Quadrotor Trajectory Planning for Pesticide Spraying. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7965–7971. [Google Scholar]
- Chen, G.; Peng, P.; Zhang, P.; Dong, W. Risk-Aware Trajectory Sampling for Quadrotor Obstacle Avoidance in Dynamic Environments. IEEE Trans. Ind. Electron. 2023, 70, 12606–12615. [Google Scholar] [CrossRef]
- Ben Abdi, S.; Debilou, A.; Guettal, L.; Guergazi, A. Robust trajectory tracking control of a quadrotor under external disturbances and dynamic parameter uncertainties using a hybrid P-PID controller tuned with ant colony optimization. Aerosp. Sci. Technol. 2025, 160, 110053. [Google Scholar] [CrossRef]
- Qin, C.; Yu, Q.; Go, H.S.H.; Liu, H.H.T. Perception-Aware Image-Based Visual Servoing of Aggressive Quadrotor UAVs. IEEE/ASME Trans. Mechatron. 2023, 28, 2020–2028. [Google Scholar] [CrossRef]
- Guenard, N.; Hamel, T.; Mahony, R. A Practical Visual Servo Control for an Unmanned Aerial Vehicle. IEEE Trans. Robot. 2008, 24, 331–340. [Google Scholar] [CrossRef]
- Zheng, D. Image-based Visual Serving of a Quadrotor UAV. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2018. [Google Scholar]
- Jiang, D.; Li, G.; Sun, Y.; Hu, J.; Yun, J.; Liu, Y. Manipulator grabbing position detection with information fusion of color image and depth image using deep learning. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 10809–10822. [Google Scholar] [CrossRef]
- Miao, Z.; Zhong, H.; Wang, Y.; Zhang, H.; Tan, H.; Fierro, R. Low-Complexity Leader-Following Formation Control of Mobile Robots Using Only FOV-Constrained Visual Feedback. IEEE Trans. Ind. Inform. 2022, 18, 4665–4673. [Google Scholar] [CrossRef]
- Hamel, T.; Mahony, R. Visual servoing of an under-actuated dynamic rigid-body system: An image-based approach. IEEE Trans. Robot. Autom. 2002, 18, 187–198. [Google Scholar] [CrossRef]
- Bourquardez, O.; Mahony, R.; Guenard, N.; Chaumette, F.; Hamel, T.; Eck, L. Image-Based Visual Servo Control of the Translation Kinematics of a Quadrotor Aerial Vehicle. IEEE Trans. Robot. 2009, 25, 743–749. [Google Scholar] [CrossRef]
- Jabbari, H.; Oriolo, G.; Bolandi, H. Dynamic IBVS control of an underactuated UAV. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 1158–1163. [Google Scholar]
- Jabbari, H.; Oriolo, G.; Bolandi, H. An adaptive scheme for image-based visual servoing of an underactuated UAV. Int. J. Robot. Autom. 2014, 29, 92–104. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, H.; Wang, J.; Chen, S.; Chen, W.; Liang, X. Image-Based Visual Servoing of a Quadrotor Using Virtual Camera Approach. IEEE/ASME Trans. Mechatron. 2017, 22, 972–982. [Google Scholar] [CrossRef]
- Sönmez, S.; Rutherford, M.J.; Valavanis, K.P. A Survey of Offline- and Online-Learning-Based Algorithms for Multirotor Uavs. Drones 2024, 8, 116. [Google Scholar] [CrossRef]
- Lei, W.; Li, C.; Chen, M.Z.Q. Robust Adaptive Tracking Control for Quadrotors by Combining PI and Self-Tuning Regulator. IEEE Trans. Control Syst. Technol. 2019, 27, 2663–2671. [Google Scholar] [CrossRef]
- Tang, M.; Lau, V.K.N. Online Identification and Temperature Tracking Control for Furnace System with a Single Slab and a Single Heater Over the Wirelessly Connected IoT Controller. IEEE Internet Things J. 2024, 11, 6730–6747. [Google Scholar] [CrossRef]
- Eschmann, J.; Albani, D.; Loianno, G. Data-Driven System Identification of Quadrotors Subject to Motor Delays. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 8095–8102. [Google Scholar]
- Böhm, C.; Brommer, C.; Hardt-Stremayr, A.; Weiss, S. Combined System Identification and State Estimation for a Quadrotor UAV. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 585–591. [Google Scholar]
- Noormohammadi-Asl, A.; Esrafilian, O.; Ahangar Arzati, M.; Taghirad, H.D. System identification and H∞-based control of quadrotor attitude. Mech. Syst. Signal Process. 2020, 135, 106358. [Google Scholar] [CrossRef]
- Zou, Y.; Meng, Z. Immersion and Invariance-Based Adaptive Controller for Quadrotor Systems. IEEE Trans. Syst. Man. Cybern. Syst. 2019, 49, 2288–2297. [Google Scholar] [CrossRef]
- Liu, Y.C.; Ou, T.W. Non-linear adaptive tracking control for quadrotor aerial robots under uncertain dynamics. IET Control Theory Appl. 2021, 15, 1126–1139. [Google Scholar] [CrossRef]
- Liang, W.; Chen, Z.; Yao, B. Geometric Adaptive Robust Hierarchical Control for Quadrotors with Aerodynamic Damping and Complete Inertia Compensation. IEEE Trans. Ind. Electron. 2022, 69, 13213–13224. [Google Scholar] [CrossRef]
- Xie, H.; Lynch, A.F.; Low, K.H.; Mao, S. Adaptive Output-Feedback Image-Based Visual Servoing for Quadrotor Unmanned Aerial Vehicles. IEEE Trans. Control Syst. Technol. 2020, 28, 1034–1041. [Google Scholar] [CrossRef]
- Imran, I.H.; Wood, K.; Montazeri, A. Adaptive Control of Unmanned Aerial Vehicles with Varying Payload and Full Parametric Uncertainties. Electronics 2024, 13, 347. [Google Scholar] [CrossRef]
- Lin, J.; Miao, Z.; Wang, Y.; Hu, G.; Wang, X.; Wang, H. Error-State LQR Geofencing Tracking Control for Underactuated Quadrotor Systems. IEEE/ASME Trans. Mechatron. 2024, 29, 1146–1157. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, J.; Dou, J.; Wen, B. A fuzzy adaptive backstepping control based on mass observer for trajectory tracking of a quadrotor UAV. Int. J. Adapt. Control Signal Process. 2018, 32, 1675–1693. [Google Scholar] [CrossRef]
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2007. [Google Scholar]
- Chaumette, F. Image moments: A general and useful set of features for visual servoing. IEEE Trans. Robot. 2004, 20, 713–723. [Google Scholar] [CrossRef]
- Lu, M.; Chen, H.; Lu, P. Perception and Avoidance of Multiple Small Fast Moving Objects for Quadrotors with Only Low-Cost RGBD Camera. IEEE Robot. Autom. Lett. 2022, 7, 11657–11664. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Montoya-Cháirez, J.; Pérez-Alcocer, R.; Moreno-Valenzuela, J. Experimental Parameter Identifications of a Quadrotor by Using an Optimized Trajectory. IEEE Access 2020, 8, 167355–167370. [Google Scholar] [CrossRef]
- Yao, Z.; Yi, W. Curvature aided Hough transform for circle detection. Expert Syst. Appl. 2016, 51, 26–33. [Google Scholar] [CrossRef]



| Parameter | Value | Units |
|---|---|---|
| Wheelbase | 450 | mm |
| Empty weight | 1.493 | kg |
| Loadable capacity | 0.5 | kg |
| Motor diameter | 22 | mm |
| Camera resolution | 1920 × 1080 | pixel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Huang, B.; Chen, Y.; Ye, G.; Lai, G. Image-Based Adaptive Visual Control of Quadrotor UAV with Dynamics Uncertainties. Electronics 2025, 14, 3114. https://doi.org/10.3390/electronics14153114
Guo J, Huang B, Chen Y, Ye G, Lai G. Image-Based Adaptive Visual Control of Quadrotor UAV with Dynamics Uncertainties. Electronics. 2025; 14(15):3114. https://doi.org/10.3390/electronics14153114
Chicago/Turabian StyleGuo, Jianlan, Bingsen Huang, Yuqiang Chen, Guangzai Ye, and Guanyu Lai. 2025. "Image-Based Adaptive Visual Control of Quadrotor UAV with Dynamics Uncertainties" Electronics 14, no. 15: 3114. https://doi.org/10.3390/electronics14153114
APA StyleGuo, J., Huang, B., Chen, Y., Ye, G., & Lai, G. (2025). Image-Based Adaptive Visual Control of Quadrotor UAV with Dynamics Uncertainties. Electronics, 14(15), 3114. https://doi.org/10.3390/electronics14153114






