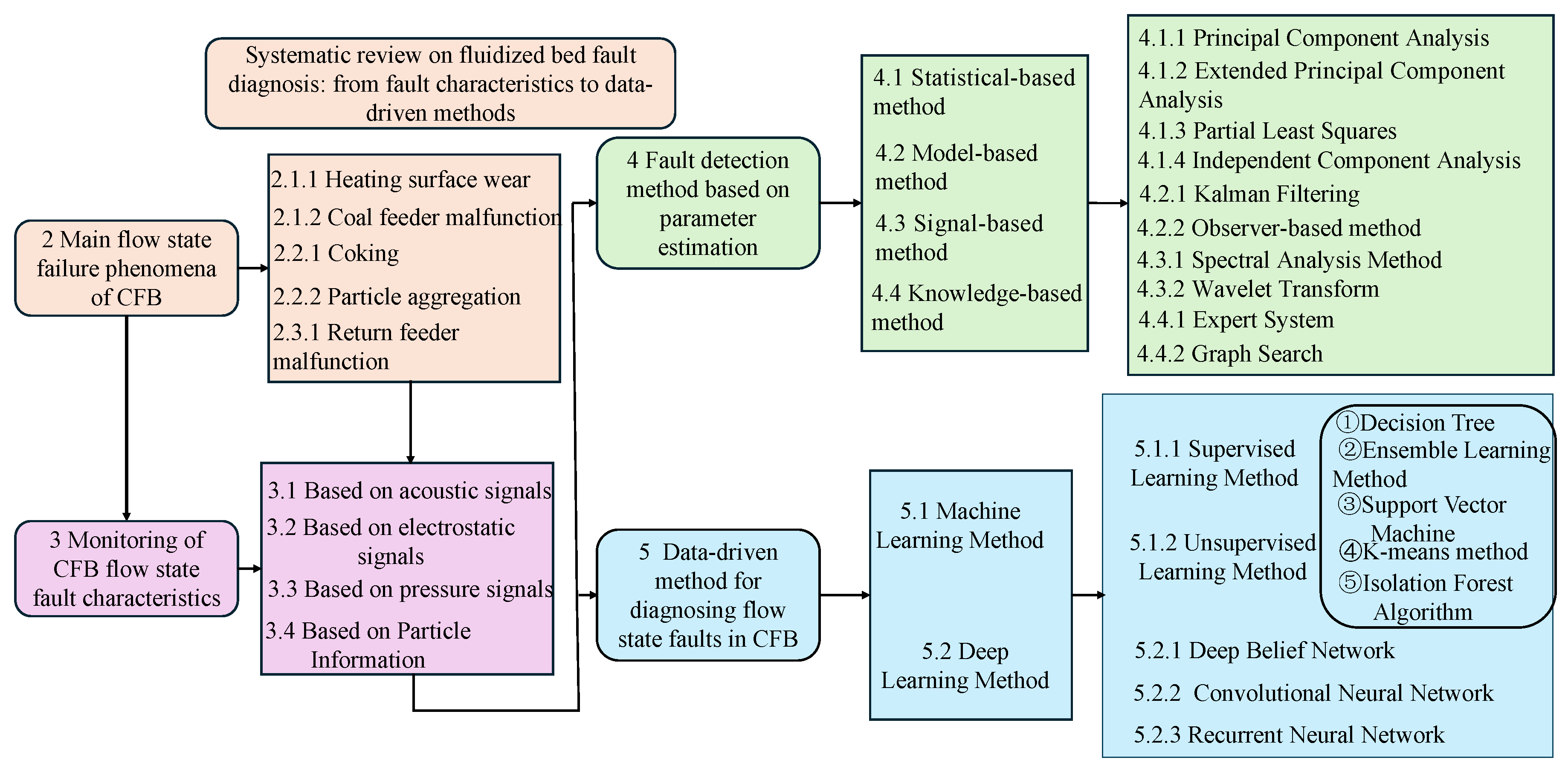
Systematic Review on Fluidized Bed Fault Diagnosis: From Fault Characteristics to Data-Driven Methods
Abstract
1. Introduction
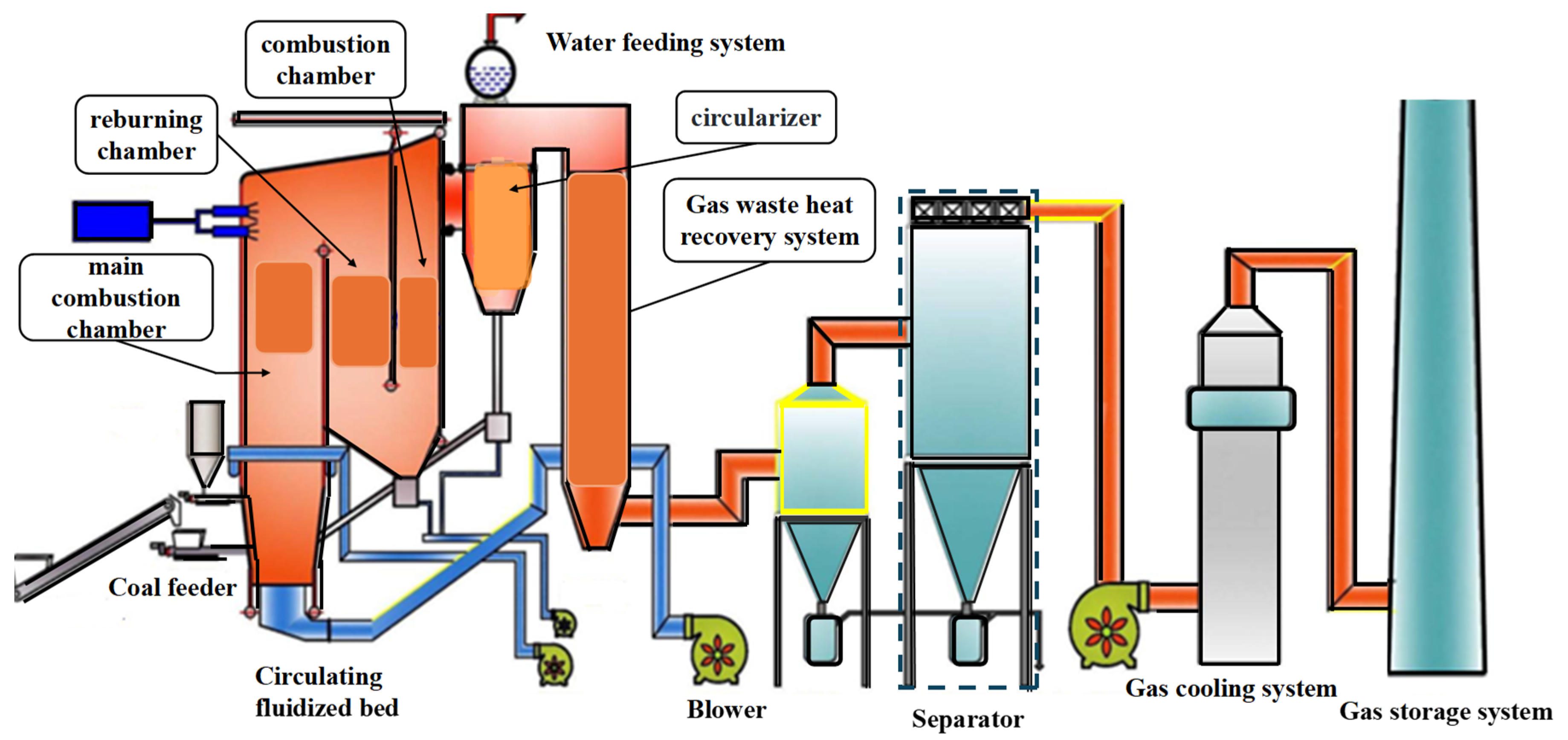
2. Main Flow State Failure Phenomena of CFB
2.1. Deterministic Faults
2.1.1. Heating Surface Wear
2.1.2. Coal Feeder Malfunction
2.2. Statistical Faults
2.2.1. Coking
2.2.2. Particle Aggregation
2.3. Composite Faults
Return Feeder Malfunction
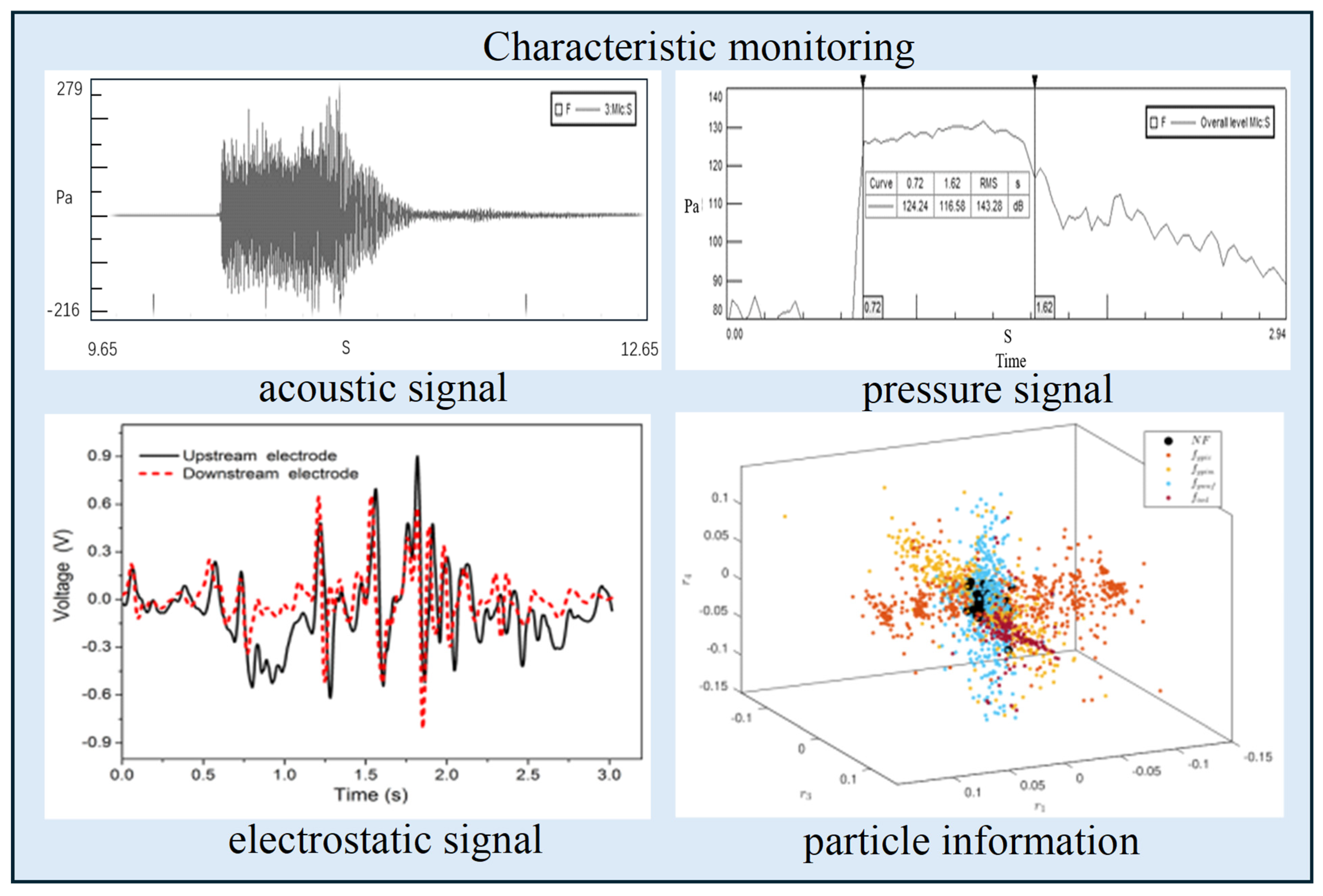
3. Monitoring of CFB Flow State Fault Characteristics
3.1. Fault Monitoring Based on Acoustic Signals
3.2. Fault Monitoring Based on Electrostatic Signal
3.3. Fault Monitoring Based on Pressure Signals
3.4. Fault Monitoring Based on Particle Information
4. Fault Detection Method Based on Parameter Estimation
4.1. Statistic-Based Method
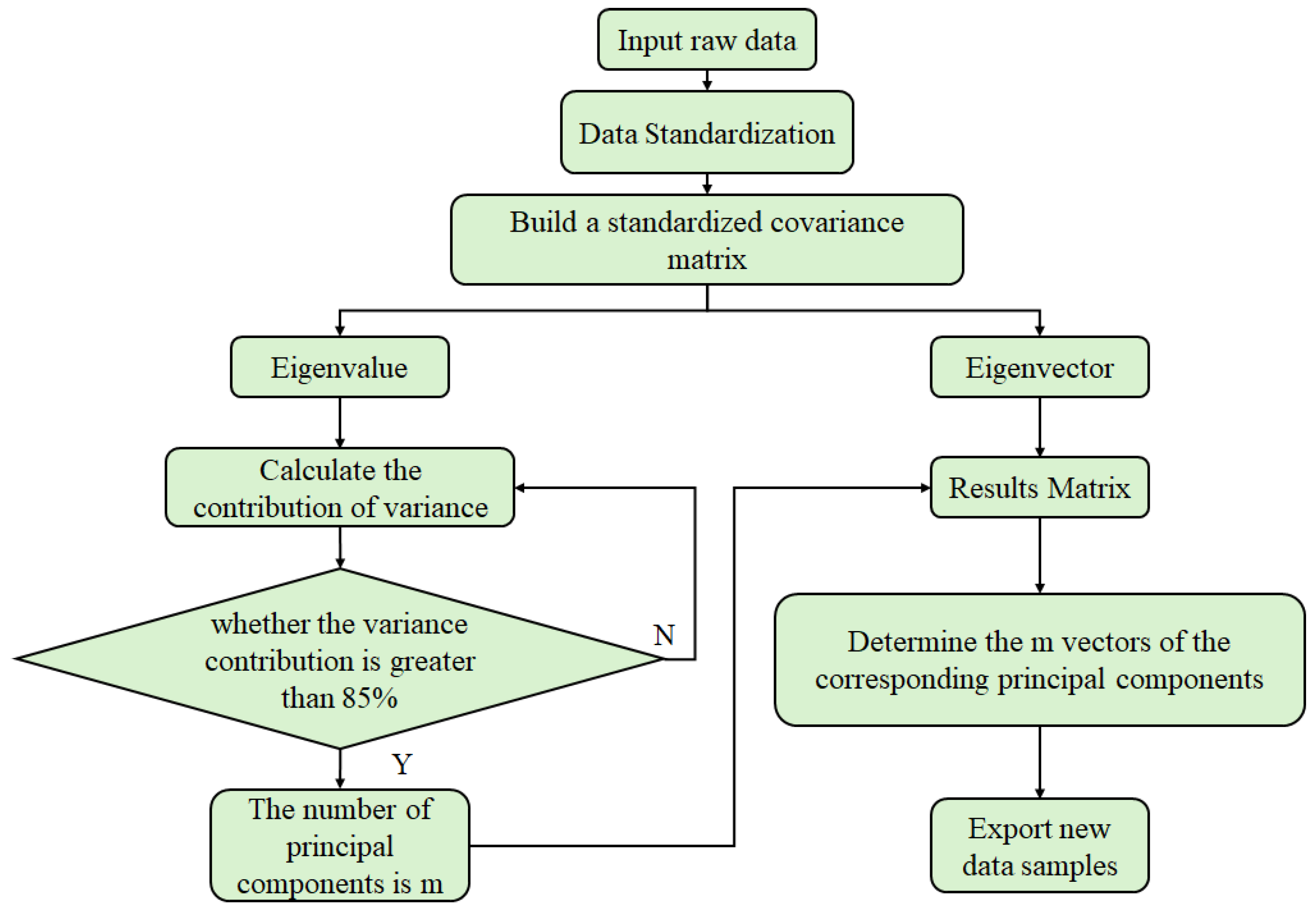
4.1.1. Principal Component Analysis
4.1.2. Extended Principal Component Analysis
4.1.3. Partial Least Squares
4.1.4. Independent Component Analysis
4.2. Model-Based Method
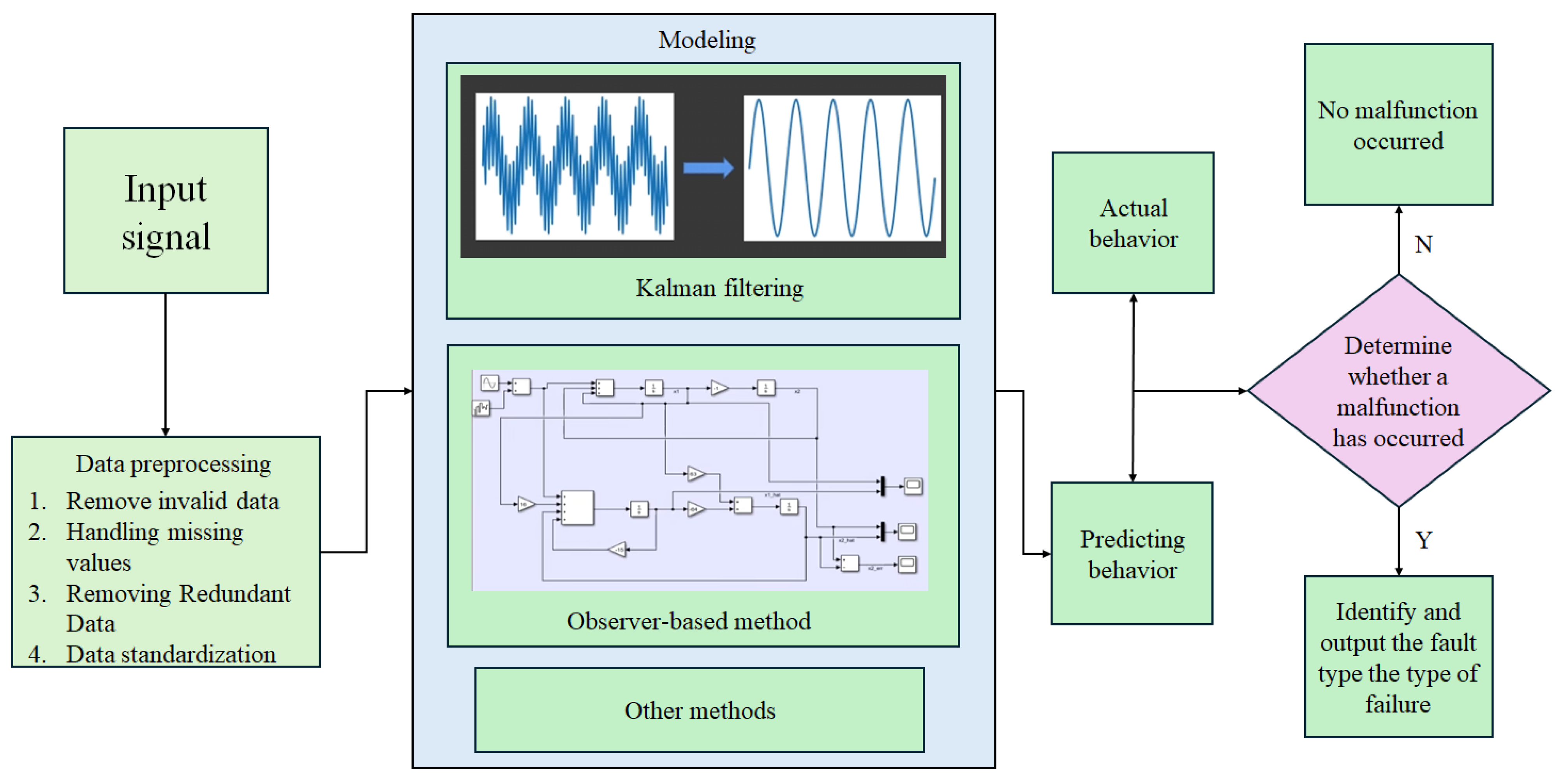
4.2.1. Kalman Filtering
4.2.2. Observer-Based Method
4.3. Signal-Based Method
4.3.1. Spectral Analysis Method
4.3.2. Wavelet Transform
4.4. Knowledge-Based Method
4.4.1. Expert System
4.4.2. Graph Search
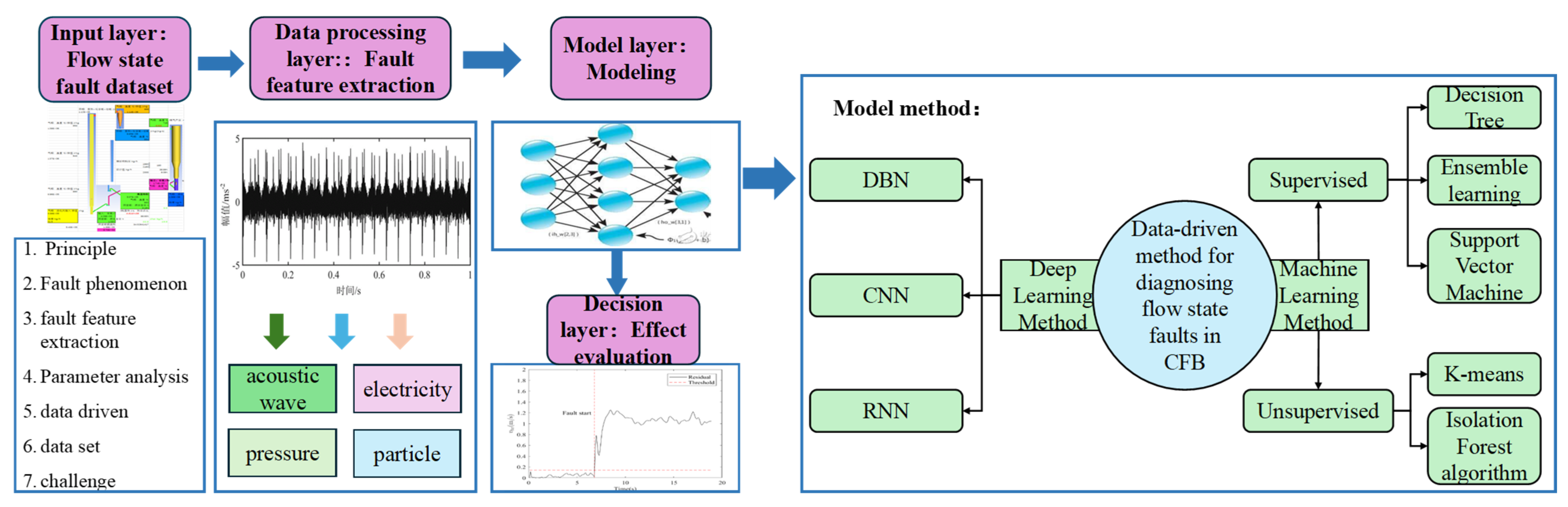
5. Data-Driven Method for Diagnosing Flow State Faults in CFB
5.1. Machine Learning Method
5.1.1. Supervised Learning Method
5.1.2. Unsupervised Learning Method
5.2. Deep Learning Method
5.2.1. Deep Belief Network
5.2.2. Convolutional Neural Network
5.2.3. Recurrent Neural Network
5.3. Summary of This Chapter
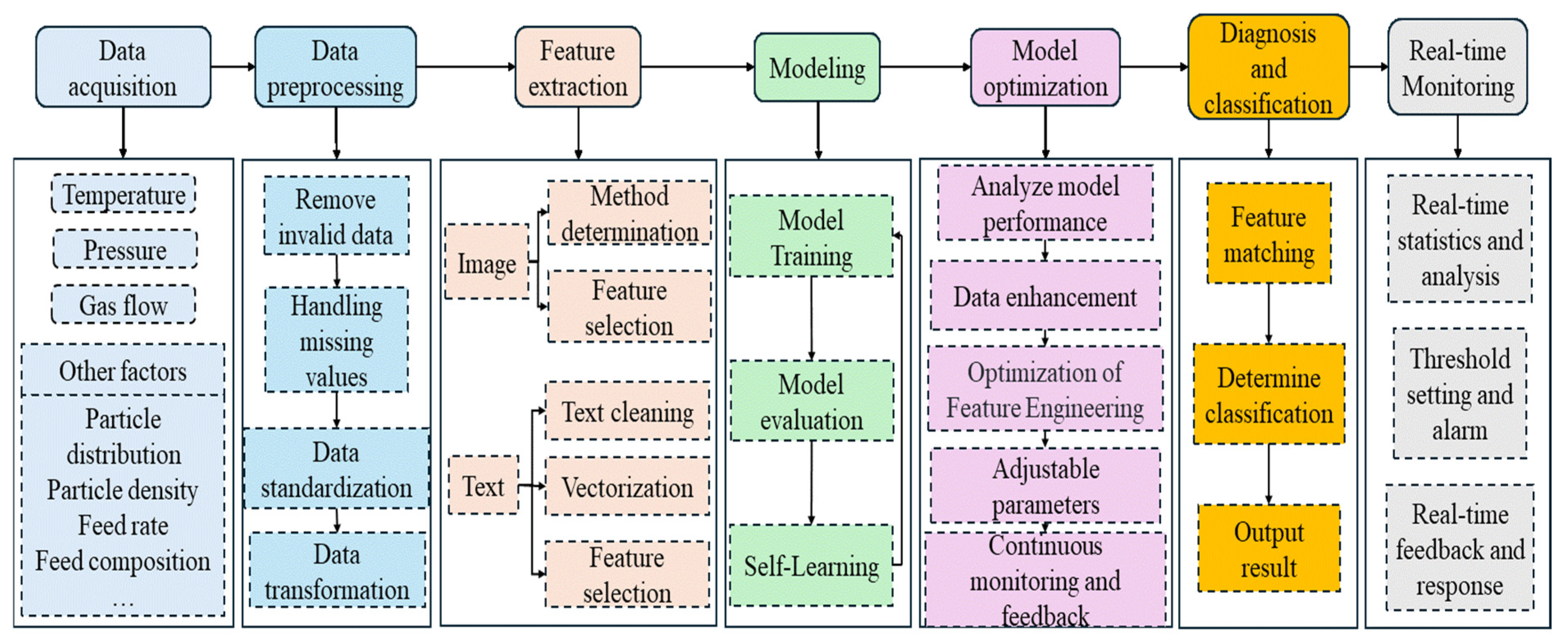
6. Acquisition of Dataset
6.1. Numerical Model
6.1.1. Flow Model
6.1.2. Coupled Model
6.2. Dataset
6.3. Experimental Measuring
6.3.1. Fiber Optic Probe Technology
6.3.2. Ultrasonic Doppler Velocimetry Technology
6.3.3. Laser Doppler Velocimetry Technology
6.3.4. Particle Image Velocimetry Technology
6.3.5. Process Tomography Technology
7. Challenges and Future Prospects
7.1. Challenge
7.1.1. Obtaining High-Quality Datasets
7.1.2. Real-Time and Security of Data
7.1.3. Lack of Standard Datasets
7.1.4. Explanatory Nature of the Model
7.1.5. Timeliness Analysis of Early Warning
7.2. Future Prospects
7.2.1. Construction and Management of High-Quality Datasets
7.2.2. Building Standard Dataset
7.2.3. Focus on Developing Interpretable Models
7.2.4. The Combination of Digital Twin Technology
7.2.5. Developing More Efficient Algorithms
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Lyu, J.; Yue, G. A review on research and development of CFB combustion technology in China. Powder Technol. 2023, 414, 118090. [Google Scholar] [CrossRef]
- Khan, F.; Alauddin, M.; Imtiaz, S.; Ahmed, S.; Amyotte, P. Integrating process dynamics in data-driven models of chemical processing systems. Process Saf. Environ. Prot. 2023, 174, 158–168. [Google Scholar]
- Zaki, M.; Gani, A.; Mamat, R.; Nizar, M.; Rosdi, S.; Yana, S.; Sarjono, R. Analysis of technological developments and potential of biomass gasification as a viable industrial process: A review. Chem. Environ. Eng. 2023, 8, 100439. [Google Scholar]
- Wu, J.; Li, W. Analysis and prevention of 660 MW supercritical circulating fluidized bed boiler water wall wear and leakage. Autom. Appl. 2024, 65, 311–313. [Google Scholar]
- Yu, G. The Practical Challenges and Solutions of the Waste Gas Monitoring System for Circulating Fluidized Bed Boilers in Chemical Enterprises. China Equip. Eng. 2024, 9, 196–198. [Google Scholar]
- Yuan, Y.; Zhao, X. Efficiency enhancement practice of desulfurization system in circulating fluidized bed boiler furnace. Boil. Manuf. 2024, 3, 31–32+35. [Google Scholar]
- Song, Y. Fault analysis and modification of chain coal feeder for 660MW supercritical circulating fluidized bed boiler. Manuf. Upgrad. Today 2023, 1, 101–104. [Google Scholar]
- Yang, L. Analysis of Coal Blockage in Coal Feeding System of Circulating Fluidized Bed Boiler. Technol. Innov. Appl. 2020, 32, 117–119. [Google Scholar]
- Liu, L. Exploring the causes and countermeasures of coking accidents in CFB boilers. Large Scale 2024, 47, 104–108. [Google Scholar]
- Zhang, M. Analysis of Causes and Countermeasures of Coking in Circulating Fluidized Bed Boilers. Appl. IC 2020, 37, 78–79. [Google Scholar]
- Wang, J.; Qi, H.; Gu, X.; Feng, L. Research progress on agglomeration mechanism and fluidization characteristics of viscous particles. Chin. J. Process Eng. 2019, 19, 55–63. [Google Scholar]
- Yang, N.; Zhou, Y. A new technology for measuring the moisture distribution of particle aggregates in fluidized beds. CIESC J. 2014, 65, 3878–3883. [Google Scholar]
- Wang, S.; Hu, X.; Liu, N.; Liu, H. Flow Behavior of Nanoparticle Agglomerates in a Fluidized Bed Simulated with Porous-Structure-Based Drag Laws. Nanomaterials 2024, 14, 1057. [Google Scholar] [CrossRef]
- Cai, J.; Wang, P. Analysis of Overtemperature of the Return Shell of Supercritical Circulating Fluidized Bed Boiler. Power Syst. Eng. 2021, 37, 25–27+31. [Google Scholar]
- Zhang, C.; Liu, B. Research on Factors Influencing Bed Temperature and Load of CFB Boiler. Clean Coal Technol. 2020, 26, 181–183. [Google Scholar]
- Xie, C.; Zhang, R.; Bhola, J. Research on fault detection and identification methods of nonlinear dynamic process based on ICA. Nonlinear Eng. 2022, 11, 13–19. [Google Scholar] [CrossRef]
- Jia, S.; Chen, Z. Analysis of Abnormal Causes and Countermeasures for the Return System of 660 MW Supercritical Circulating Fluidized Bed Boiler. Ind. Boil. 2023, 6, 53–57. [Google Scholar]
- Wu, H.; Chen, Y.; Wang, J.; Lin, W. Agglomeration-monitoring method for a fluidized bed with multiacoustic sensors. Ind. Eng. Chem. Res. 2019, 58, 19531–19544. [Google Scholar] [CrossRef]
- Zhao, Z.; Pang, J. Real-time Monitoring of Fluidized Bed Agglomerating based on Improved Adaboost Algorithm. J. Phys. Conf. Ser. 2021, 1924, 012026. [Google Scholar]
- Yan, Y.; Qi, B.; Zhang, W.; Li, X. Experimental Investigations Into Bubble Characteristics in a Fluidized Bed Through Electrostatic Imaging. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar]
- Yan, Y.; Hu, Y.; Wang, L.; Qian, X.; Zhang, W.; Reda, K.; Wu, J.; Zheng, G. Electrostatic sensors—Their principles and applications. Measurement 2021, 169, 108506. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, J.; Hou, J.; Zhang, W.; Wu, S. Early risk warning method for fluidized beds using generalized extremum distribution of pressure fluctuation. Process Saf. Environ. Prot. 2021, 156, 29–42. [Google Scholar]
- Gao, Z.; Wang, J.; Liu, Z.; Wei, Y.; Wang, J.; Mao, Y. Effects of different inlet structures on the flow field of cyclone separators. Powder Technol. 2020, 372, 519–531. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Y.; Kolehmainen, J.; Kevrekidis, I.G.; Ozel, A.; Sundaresan, S. Development of data-driven filtered drag model for industrial-scale fluidized beds. Chem. Eng. Sci. 2021, 230, 116235. [Google Scholar]
- Widuch, A.; Grochowalski, J.; Sładek, S.; Melka, B.; Nowak, M.; Klimanek, A.; Andrzejczyk, M.; Klajny, M.; Czarnowska, L.; Hernik, B. Technique for reducing erosion in large-scale circulating fluidized bed units. Powder Technol. 2023, 426, 118651. [Google Scholar] [CrossRef]
- Li, Y.; Ma, T.; Zhou, Q.; Chen, X. Microscale drag model considering the effect of interface between dense and dilute phases for gas-solid suspensions at moderate Reynolds numbers. Int. J. Multiph. Flow 2022, 157, 104270. [Google Scholar]
- Chen, Y.; Kong, L.; Wang, W. Dynamics Study of Particle Mesoscale Structure in Gas Solid Fluidization. CIESC J. 2022, 73, 2486–2495. [Google Scholar]
- Chen, Y.; Xia, Y. Study on the influence of grid size on identifying particle agglomeration characteristics in the riser of a circulating fluidized bed. J. Energy Chem. 2023, 44, 52–59. [Google Scholar]
- Lu, Y.; Kang, P.; Yang, L.; Hu, X.E.; Chen, H.; Zhang, R.; Zhou, Y.J.; Luo, X.; Wang, J.; Yang, Y. Multi-scale characteristics and gas-solid interaction among multiple beds in a dual circulating fluidized bed reactor system. Chem. Eng. J. 2020, 385, 123715. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Gao, F. Review of Recent Research on Data-Based Process Monitoring. Ind. Eng. Chem. Res. 2013, 52, 3543–3562. [Google Scholar] [CrossRef]
- He, Y.; Lin, Y.; Yuan, Z.; Wu, C.; Gou, C.; Li, C. Abnormal working condition detection in chemical processes based on PCA-SVDD. Chin. J. Process Eng. 2022, 22, 970–978. [Google Scholar]
- Jolliffe, I. Principal component analysis. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1094–1096. [Google Scholar]
- Zhang, B.; Zhang, Y.; Wu, Z. Multi-Model Modeling of CFB Boiler Bed Temperature System Based on Principal Component Analysis. IEEE Access 2020, 8, 389–399. [Google Scholar] [CrossRef]
- Fan, M. Research on the Application of Machine Learning in the Field of Chemical Process Fault Detection. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2023. [Google Scholar]
- de Carvalho Michalski, M.A.; de Souza, G.F.M. Comparing PCA-based fault detection methods for dynamic processes with correlated and Non-Gaussian variables. Expert Syst. Appl. 2022, 207, 117989. [Google Scholar] [CrossRef]
- Zhang, A.; Guo, J.; Li, Y. Method for selecting kernel principal components in KPCA based on fault detection. Comput. Appl. Softw. 2021, 38, 60–66+85. [Google Scholar]
- Simmini, F.; Rampazzo, M.; Peterle, F.; Susto, G.A.; Beghi, A. A Self-Tuning KPCA-Based Approach to Fault Detection in Chiller Systems. IEEE Trans. Control Syst. Technol. 2021, 30, 1359–1374. [Google Scholar] [CrossRef]
- Xia, Z.; Gao, Y.; Wang, D. Matrix time series statistical monitoring and inference based on 2DPCA. Chin. J. Eng. Math. 2023, 40, 41–54. [Google Scholar]
- Guerfel, M.; Messaoud, H. On the use of DPCA in process fault detection and identification. In Proceedings of the 2024 International Conference on Control, Automation and Diagnosis (ICCAD), Paris, France, 17 May 2024; pp. 1–6. [Google Scholar]
- Dai, J.; Liang, B. Application of Partial Least Squares Method in System Fault Diagnosis. J. Harbin Inst. Technol. 2020, 52, 156–164. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Aljunaid, M.; Tao, Y.; Shi, H. A Novel Mutual Information and Partial Least Squares Approach for Quality-Related and Quality-Unrelated Fault Detection. Processes 2021, 9, 166. [Google Scholar] [CrossRef]
- Li, J. Fault Diagnosis Method Based on Improved Partial Least Squares Method and Contribution Graph. Master’s Thesis, Bohai University, Jinzhou, China, 2021. [Google Scholar]
- Jie, J.; Kong, X.; Luo, J.; Li, Q. Quality related fault diagnosis based on improved and efficient partial least squares. J. Control Theory Appl. 2020, 37, 2645–2653. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [PubMed]
- Billor, N.; Yi, Y.; Ekstrom, A.; Zheng, J. CW_ICA: An efficient dimensionality determination method for independent component analysis. Sci. Rep. 2024, 14, 143. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Guo, J.; Li, Y. Fault detection and diagnosis based on DICA. J. Shenyang Univ. (Nat. Sci.) 2022, 34, 290–297. [Google Scholar]
- Lv, Z.; Lu, T. Chemical process monitoring based on adaptive independent component analysis. J. Beijing Univ. Chem. Technol. (Nat. Sci. Ed.) 2019, 46, 64–71. [Google Scholar]
- Zhang, X.; Qi, J.; Tao, C.; Fu, S.; Guo, M.; Ruan, Y. Research progress, challenges, and trends in cloud removal from optical remote sensing images. J. Geod. Geoinf. Sci. 2025, 54, 603–620. [Google Scholar]
- Zhang, K.; Hu, X.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced Fault Diagnosis for Lithium-Ion Battery Systems: A Review of Fault Mechanisms, Fault Features, and Diagnosis Procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Lei, Y.; Zhao, J.; Li, Z. Overview of the Application of Kalman Filter in Equipment Fault Prediction. Ordnance Ind. Autom. 2024, 43, 16–20. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Fluids Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Yan, K.; Li, W.; Wang, K.I.K.; Ma, J.; Jin, Q. Edge-Enabled Two-Stage Scheduling Based on Deep Reinforcement Learning for Internet of Everything. IEEE Internet Things J. 2023, 10, 3295–3304. [Google Scholar] [CrossRef]
- Cho, S.; Choi, M.; Gao, Z.; Moan, T. Fault detection and diagnosis of a blade pitch system in a floating wind turbine based on Kalman filters and artificial neural networks. Renew. Energy 2021, 169, 1–13. [Google Scholar] [CrossRef]
- Hu, Y.; Han, X.; Xie, A.; Yan, X.; Wang, X.; Pei, C. Quadratic-Kalman-Filter-Based Sensor Fault Detection Approach for Unmanned Aerial Vehicles. IEEE Sens. J. 2022, 22, 18669–18683. [Google Scholar]
- Afshar, S.; Germ, F.; Morris, K. Extended Kalman filter based observer design for semilinear infinite-dimensional systems. IEEE Trans. Autom. Control 2022, 69, 3631–3646. [Google Scholar] [CrossRef]
- Liu, G.; Gao, B.; Zhang, J.; Wang, S. Estimation of State of Charge (SOC) of Lithium ion Batteries Using Unscented Kalman Filter Method. Battery Bimon. 2021, 51, 270–274. [Google Scholar]
- Zhou, H.; Meng, E.; Han, D.; Yang, G.; Xu, G. Overview of Particle Filter Target Tracking Algorithms. Comput. Eng. Appl. 2019, 55, 8–17+59. [Google Scholar]
- Jeong, H.; Park, B.; Park, S.; Min, H.; Lee, S. Fault detection and identification method using observer-based residuals. Reliab. Eng. Syst. Saf. 2018, 184, 27–40. [Google Scholar] [CrossRef]
- Vijay, P.; Tadé, M.O.; Shao, Z. Adaptive observer based approach for the fault diagnosis in solid oxide fuel cells. J. Process Control 2019, 84, 101–114. [Google Scholar] [CrossRef]
- Bernardi, E.; Adam, E.J. Observer-based fault detection and diagnosis strategy for industrial processes. J. Frankl. Inst. 2020, 357, 10054–10081. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: Tamil Nadu, India, 1999. [Google Scholar]
- Pang, M.; Yang, X.; Li, P.; Chen, P.; Niu, Q. A Novel Mine Cage Safety Monitoring Algorithm Utilizing Visible Light. Sensors 2020, 20, 3920. [Google Scholar] [CrossRef]
- Zhang, B. Fault and vibration diagnosis of coal mine spiral drum coal washing machine based on spectrum analysis. Coal Mine Mach. 2024, 45, 175–179. [Google Scholar]
- Chang, Y.; Zou, Z.; Guan, C.; Huang, Y.; Feng, W.; Zhao, D. A new spectrum analyzer based on Ethernet communication and its application in monitoring chemical equipment. CIESC J. 2013, 64, 4656–4661. [Google Scholar]
- Zhao, J.; Yu, F.; Zhang, L. Remote collaborative diagnosis system for chemical machinery equipment faults based on wavelet transform. Autom. Instrum. 2021, 10, 89–92. [Google Scholar]
- Meng, Y.; Zhao, L.; Jiang, Z.; Lv, Y.; Wang, H. Bearing Fault Diagnosis Combining Wavelet Transform and Attention Mechanism. J. Vib. Meas. Diagn. 2025, 45, 430–437+616. [Google Scholar]
- Malla, P.; Coburn, W.; Keegan, K.; Yu, X.H. Power system fault detection and classification using wavelet transform and artificial neural networks. In International Symposium on Neural Networks; Advances in Neural Networks–ISNN 2019; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Astrom, K.J.; Bergman, S. Fault detection in boiling water reactors by noise analysis. In Technical Reports; Department of Automatic Control, Lund Institute of Technology: Knoxville, TN, USA, 1983. [Google Scholar]
- Yang, X.; Zhu, C. Industrial Expert Systems Review: A Comprehensive Analysis of Typical Applications. IEEE Access 2024, 12, 88558–88584. [Google Scholar] [CrossRef]
- Matsuzaka, Y.; Yashiro, R. AI-based computer vision techniques and expert systems. AI 2023, 3, 289–302. [Google Scholar] [CrossRef]
- Sarabi, S.; Han, Q.; de Vries, B.; Romme, A.G.L.; Almassy, D. The Nature-Based Solutions Case-Based System: A hybrid expert system. J. Environ. Manag. 2022, 324, 116413. [Google Scholar] [CrossRef]
- Mahdavifar, S.; Ghorbani, A.A. DeNNeS: Deep embedded neural network expert system for detecting cyber attacks. Neural Comput. Appl. 2020, 32, 14753–14780. [Google Scholar] [CrossRef]
- Starr, A.; Zhao, Y.; Dong, A. Neural network-based parametric system identification: A review. Int. J. Syst. Sci. 2023, 54, 2676–2688. [Google Scholar] [CrossRef]
- Kranakis, E. A Survey of the Impact of Knowledge on the Competitive Ratio in Linear Search. Stab. Saf. Secur. Distrib. Syst. 2024, 14931, 22–38. [Google Scholar]
- Zaitsev, O.V.; Kruchkov, R.L. Predictive Diagnostic and State Classification of the Inertial Navigation System Using ML. In Proceedings of the 2024 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 8–14 September 2024; pp. 236–241. [Google Scholar]
- Hu, D.; Ji, Z.; Xu, D.; Liu, J.; Liu, C. Transformer Fault Diagnosis Based on PCA-ISO-SVM. Inn. Mong. Electr. Power 2025, 1–8. [Google Scholar]
- Frank, P.M. Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: A survey and some new results. Automatica 1990, 26, 459–474. [Google Scholar] [CrossRef]
- Thomson, W.T. On-line current monitoring for fault diagnosis in induction motors using spectral analysis. IEEE Trans. Ind. Electron. 1999, 46, 392–398. [Google Scholar]
- Wu, C. Research on Process Fault Recognition Based on Improved Deep Learning Model. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2019. [Google Scholar]
- Yan, W.; Wang, J.; Lu, S.; Zhou, M.; Peng, X. A Review of Real-Time Fault Diagnosis Methods for Industrial Smart Manufacturing. Processes 2023, 11, 369. [Google Scholar] [CrossRef]
- Yang, G.; Xu, W.; Wei, Y.; Deng, Q. Overview of input features for machine learning based fault recognition algorithms for rotating machinery. J. Xihua Univ. (Nat. Sci. Ed.) 2024, 1–16. [Google Scholar]
- Zhang, J.; Liu, Y.; Wang, X. Fault diagnosis method for blast furnace based on trajectory distance partition decision tree. J. Control Decis. 2024, 40, 1533–1540. [Google Scholar]
- Qi, C.; Zhang, Y.; Cheng, Y. Mechanical rotor fault diagnosis based on DPSO-BP. Mach. Tool Hydraul. 2022, 50, 194–199. [Google Scholar]
- Avelin, A.; Widarsson, B.; Dahlquist, E.; Lilja, R. Time based data reconciliation and decision support for a CFB boiler. IFAC Proc. Vol. 2009, 42, 338–343. [Google Scholar] [CrossRef]
- Li, Z.H.; Zhang, Y.; Abu-Siada, A.; Chen, X.; Li, Z.; Xu, Y.; Zhang, L.; Tong, Y. Fault Diagnosis of Transformer Windings Based on Decision Tree and Fully Connected Neural Network. Energies 2021, 14, 1531. [Google Scholar] [CrossRef]
- Castellanos, M.B.; Serpa, A.L.; Biazussi, J.L.; Verde, W.M.; Sassim, N.D.S.D.A. Fault identification using a chain of decision trees in an electrical submersible pump operating in a liquid-gas flow. J. Pet. Sci. Eng. 2019, 184, 106490. [Google Scholar] [CrossRef]
- Kherif, O.; Benmahamed, Y.; Teguar, M.; Boubakeur, A.; Ghoneim, S.S. Accuracy Improvement of Power Transformer Faults Diagnostic Using KNN Classifier with Decision Tree Principle. IEEE Access 2021, 9, 81693–81701. [Google Scholar] [CrossRef]
- Zhou, S.; Wei, C.; Li, P.; Liu, A.; Chang, W.; Xiao, Y. A Text-Driven Aircraft Fault Diagnosis Model Based on Word2vec and Stacking Ensemble Learning. Aerospace 2021, 8, 357. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J. Integrated Learning Methods: A Review of Research. J. Yunnan Univ. (Nat. Sci. Ed.) 2018, 40, 1082–1092. [Google Scholar]
- Li, Y.; Ye, Y. Fault diagnosis of multiple wind turbines based on CNN ensemble learning. Ind. Eng. J. 2022, 25, 136–143. [Google Scholar]
- Li, K.; Wen, X.; Wang, J. NOx emission predicting for coal-fired boilers based on ensemble learning methods and optimized base learners. Energy 2023, 264, 126171. [Google Scholar]
- Eskandari, A.; Milimonfared, J.; Aghaei, M. Line-line fault detection and classification for photovoltaic systems using ensemble learning model based on I-V characteristics. Sol. Energy 2020, 211, 354–365. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Access 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Jia, C.; Jiang, T. A Review of Research on Granular Support Vector Machines. J. Tianjin Univ. Technol. 2024, 40, 57–66. [Google Scholar]
- Guan, X. Modeling and Control of Circulating Fluidized Bed Boiler Combustion System Based on Support Vector Machine. Master’s Thesis, Southeast University, Nanjing, China, 2015. [Google Scholar]
- Ma, H.; Niu, P.; Li, G.; Ma, Y.; Chen, G.; Zhang, X. Research on NOx emission characteristics of circulating fluidized bed boiler based on support vector machine and fruit fly optimization algorithm. J. Chin. Soc. Power Eng. 2013, 33, 267–271. [Google Scholar]
- Venkata, S.K.; Rao, S. Fault Detection of a Flow Control Valve Using Vibration Analysis and Support Vector Machine. Electronics 2019, 8, 1062. [Google Scholar] [CrossRef]
- Zhang, S. Research on Mechanical Equipment Fault Diagnosis Based on Support Vector Machine. Adhesion 2021, 47, 129–132. [Google Scholar]
- Chen, Y.; Zhang, L.; Wang, G. SMOTE-ENN-Based Imbalanced Data Classification for Fault Diagnosis in Industrial Processes. IEEE Trans. Ind. Inform. 2022, 18, 3327–3336. [Google Scholar]
- Ye, Z.; Yu, J.; Huang, Y. Cost-sensitive weighted SVM for class-imbalance fault diagnosis with industrial applications. Mech. Syst. Signal Process. 2021, 149, 107175. [Google Scholar]
- Wang, S.; Liu, Q.; Zhu, E. Focal Loss Deep Neural Networks for Fault Diagnosis of Imbalanced Industrial Data. IEEE/ASME Trans. Mechatron. 2023, 28, 482–493. [Google Scholar]
- Zhou, X.; Liang, W.; Shimizu, S.; Ma, J.; Jin, Q. Siamese Neural Network Based Few-Shot Learning for Anomaly Detection in Industrial Cyber-Physical Systems. IEEE Trans. Ind. Inform. 2021, 17, 5790–5798. [Google Scholar] [CrossRef]
- Yuan, J.; Feng, Q.; Liu, Q.; Zhang, P.; Jiang, X.; Liu, J. Health monitoring of switch rails based on long-term monitoring system and unsupervised learning. Railw. Stand. Des. 2024, 1–12. [Google Scholar] [CrossRef]
- Zeng, X. Credit risk assessment of listed companies based on improved k-means clustering algorithm. J. Sci. Teach. Coll. Univ. 2024, 44, 20–25. [Google Scholar]
- Chen, H. Correlation analysis between student behavior data and academic performance based on K-means algorithm. China Sci. Technol. Inf. 2024, 23, 86–88. [Google Scholar]
- Zhou, X.; Liang, W.; Kevin, I.; Wang, K.; Yang, L.T. Deep Correlation Mining Based on Hierarchical Hybrid Networks for Heterogeneous Big Data Recommendations. IEEE Trans. Comput. Soc. Syst. 2021, 8, 171–178. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, J.; Wang, C.; Sun, Z.; Lan, X.; Gao, K.; Zhu, J. Particle aggregation characteristics of gas-solid circulating fluidized bed based on k-means machine learning method. Chem. Ind. Eng. Prog. 2024, 44, 625–634. [Google Scholar]
- Chen, G.; Liu, Y.; Ge, Z. K-means Bayes algorithm for imbalanced fault classification and big data application. J. Process Control 2019, 81, 54–64. [Google Scholar] [CrossRef]
- Li, H.; Zhao, H. Linux log anomaly detection method based on improved isolated forest algorithm. Command. Control Simul. 2024, 46, 114–118. [Google Scholar]
- Jiang, J.; Li, T.; Chang, C.; Yang, C.; Liao, L. Fault diagnosis method for lithium-ion batteries in electric vehicles based on isolated forest algorithm. J. Energy Storage 2022, 50, 104177. [Google Scholar] [CrossRef]
- Wang, J.; Nie, C. A review of research and development of data analysis methods. Comput. Telecommun. 2024, 04, 20–25. [Google Scholar]
- Kang, T.; Yao, J.; Jin, M.; Yang, S.; Duong, T. A Novel Improved Cuckoo Search Algorithm for Parameter Estimation of Photovoltaic (PV) Models. Energies 2018, 11, 1060. [Google Scholar] [CrossRef]
- Cui, Q.; Feng, G.; Xu, X. Q-Learning-Based Robust Control for Nonlinear Systems with Mismatched Perturbations. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1–6. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Li, F.; Li, J.; Kong, L. Energy consumption scheduling of assembly line workshop based on ultra-low standby state of machine tools. Control Decis. 2021, 36, 143–151. [Google Scholar]
- He, Y.; Zhang, C.; Yuan, L.; Xiang, S. Analog Circuit Incipient Fault Diagnosis Method Using DBN Based Features Extraction. IEEE Access 2018, 6, 23053–23064. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, X.; Liang, W.; Zeng, Z.; Yan, Z. Deep-Learning-Enhanced Multitarget Detection for End–Edge–Cloud Surveillance in Smart IoT. IEEE Internet Things J. 2021, 8, 12588–12596. [Google Scholar] [CrossRef]
- Rao, J.; Yuan, X.; Gu, Y.; Ye, L.; Wang, K.; Wang, Y. Online Adaptive Modeling Framework for Deep Belief Network-Based Quality Prediction in Industrial Processes. Ind. Eng. Chem. Res. 2021, 60, 15208–15218. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on Cyclic Spectral Coherence and Convolutional Neural Networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Gupta, J.; Pathak, S.; Kumar, G. Deep Learning (CNN) and Transfer Learning: A Review. J. Phys. Conf. Ser. 2022, 2273, 012029. [Google Scholar] [CrossRef]
- Chen, X.; Xu, G.; Xu, X.; Jiang, H.; Tian, Z.; Ma, T. Multicenter Hierarchical Federated Learning with Fault-Tolerance Mechanisms for Resilient Edge Computing Networks. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 47–61. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Hu, Y.; Liang, W.; Ma, J.; Jin, Q. Variational LSTM Enhanced Anomaly Detection for Industrial Big Data. IEEE Trans. Ind. Inform. 2021, 17, 3469–3477. [Google Scholar] [CrossRef]
- Zhang, Q.; Huang, T.; Tang, X.; Zhao, S.; Lu, X. A novel fault diagnosis method based on CNN and LSTM and its application in fault diagnosis for complex systems. Artif. Intell. Rev. 2021, 55, 1289–1315. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, D.; Song, Y.; Gao, S.; Li, Y. Application of Multiscale Learning Neural Network Based on CNN in Bearing Fault Diagnosis. J. Signal Process. Syst. 2019, 91, 1205–1217. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Kevin, I.; Wang, K.; Wang, H.; Yang, L.T.; Jin, Q. Deep-Learning-Enhanced Human Activity Recognition for Internet of Healthcare Things. IEEE Internet Things J. 2020, 7, 6429–6438. [Google Scholar] [CrossRef]
- Chen, H. Research on Data-Driven Methods for Fault Detection and Diagnosis in Dynamic Chemical Processes. Master’s Thesis, Guangdong Normal University of Technology, Guangzhou, China, 2023. [Google Scholar]
- Wang, Y. Research on Chemical Process Fault Monitoring and Diagnosis Based on Autoencoder and Gated Loop Unit. Master’s Thesis, Beijing University of Chemical Technology, Beijing, China, 2024. [Google Scholar]
- Dietterich, T.G. Overfitting and undercomputing in machine learning. ACM Comput. Surv. 1995, 27, 326–327. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. Proc. SODA 2007, 1027–1035. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 2002, 86, 2278–2324. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. arXiv 2014, arXiv:1409.3215. [Google Scholar] [CrossRef]
- Yu, L.; Shao, X.; Wei, Y.; Zhou, K. Intelligent Land-Vehicle Model Transfer Trajectory Planning Method Based on Deep Reinforcement Learning. Sensors 2018, 18, 2905. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, Y.; Zhang, Y.; Zhao, Y. Fiber-optic sensors based on Vernier effect. Measurement 2021, 167, 108451. [Google Scholar] [CrossRef]
- Halkare, P.; Punjabi, N.; Wangchuk, J.; Nair, A.; Kondabagil, K.; Mukherji, S. Bacteria functionalized gold nanoparticle matrix based fiber-optic sensor for monitoring heavy metal pollution in water. Sens. Actuators B Chem. 2019, 281, 643–651. [Google Scholar] [CrossRef]
- Gandhi, M.A.; Chu, S.; Senthilnathan, K.; Babu, P.R.; Nakkeeran, K.; Li, Q. Recent Advances in Plasmonic Sensor-Based Fiber Optic Probes for Biological Applications. Appl. Sci. 2019, 9, 949. [Google Scholar] [CrossRef]
- Taşkın, A.F.; Uludağ, Y.; Ayranci, I. Analysis of core velocity in the presence of solids using UDV and improved model for cloud height in stirred tanks. Chem. Eng. Sci. 2024, 285, 119508. [Google Scholar]
- Fang, L.; Liu, Y.; Wang, S.; Zhao, J.; Faraj, Y.; Tian, M.; Wei, Z. Dual-modality UDV-PIV system for measurement of solid-liquid flow in sewage facilities. Flow Meas. Instrum. 2021, 82, 102063. [Google Scholar] [CrossRef]
- Key, N.L.; Gooding, W.J. Leveraging LDV techniques for the investigation of unsteady turbomachinery flows. Aeronaut. J. 2019, 123, 1919–1937. [Google Scholar] [CrossRef]
- Pasch, S.; Leister, R.; Gatti, D.; Örlü, R.; Frohnapfel, B.; Kriegseis, J. Measurements in a Turbulent Channel Flow by Means of an LDV Profile Sensor. Flow Turbul. Combust. 2023, 113, 195–213. [Google Scholar] [CrossRef]
- Scharnowski, S.; Bross, M.; Kähler, C.J. Accurate turbulence level estimations using PIV/PTV. Exp. Fluids 2018, 60, 1–12. [Google Scholar] [CrossRef]
- Kozlowski, E.; Rymarczyk, T.; Klosowski, G.; Niderla, K. Logistic Regression for Machine Learning in Process Tomography. Sensors 2019, 19, 3400. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X.; Liu, A.; Hu, C. A Latency and Coverage Optimized Data Collection Scheme for Smart Cities Based on Vehicular Ad-hoc Networks. Sensors 2017, 17, 888. [Google Scholar] [CrossRef]
- Lundgren, A.; Jung, D. Data-Driven Fault Diagnosis Analysis and Open-Set Classification of Time-Series Data. Control Eng. Pract. 2022, 121, 105006. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, Z.; Yang, S.; Shao, H. A Novel Blockchain Framework for Industrial IoT Edge Computing. Sensors 2020, 20, 2061. [Google Scholar] [CrossRef] [PubMed]
- Rong, H.; Zhang, H.; Xiao, S.; Li, C.; Hu, C. Optimizing energy consumption for data centers. Renew. Sustain. Energy Rev. 2016, 58, 674–691. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; She, J.; Yan, Z.; Wang, K. Two-Layer Federated Learning with Heterogeneous Model Aggregation for 6G Supported Internet of Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5308–5317. [Google Scholar] [CrossRef]

| Fault Type | Representative Cases | Characteristics | Applicable Methods |
|---|---|---|---|
| Deterministic faults | Heating surface wear; Coal feeder malfunction | Clear physical characteristics; can be directly determined through thresholds or rules | Signal-based method (Wavelet Transform, spectral analysis method); model-based method |
| Statistical faults | Coking; Particle aggregation | The early features are weak; identification through statistical analysis of process parameters is required | PCA, ICA, time series analysis (RNN; LSTM), isolation forest |
| Composite faults | Return feeder malfunction | Combine certainty and randomness; multi-source data fusion diagnosis is required | Ensemble learning; multimodal deep learning (CNN + GRU) |
| Method | Applicable Scenarios | Advantage | Limitation | Applicable Fault Types | Accuracy | Recall |
|---|---|---|---|---|---|---|
| PCA | Data dimensionality reduction | Excellent dimensionality reduction effect; strong ability to remove redundant information; high computational efficiency | Poor ability to handle nonlinear relationships; susceptible to noise influence [77] | Heating surface wear (2.1.1) Particle agglomeration (2.2.2) | 85–92% [33] | 78–85% [33] |
| PLS | Suitable for situations with a small sample size and a large number of variables | Strong ability to handle multicollinearity; wide applicability [41] | Sensitive to outliers; weak model interpretability | Coal feeder malfunction (2.1.2) System air leakage (2.3.1) | 80–87% [42] | 75–83% [42] |
| ICA | Commonly used in scenarios such as voice separation and electroencephalogram (EEG) signal processing | Strong blind source separation capability; strong ability to extract independent features; high flexibility [45] | Complex in calculation; sensitive to noise; the convergence is influenced by multiple factors | Stochastic faults (2.2) Sensor faults | 83–90% [16] | 79–86% [16] |
| Kalman filtering | Suitable for real-time systems such as target tracking, navigation, etc. | Good real-time property; capable of dynamically updating the estimation results; highly efficacious for linear Gaussian systems [52] | Poor performance under nonlinear and non-Gaussian conditions | Return feeder blockage (2.3.1) | 89–95% [55] | 85–91% [55] |
| Observer-based methods | Commonly used for state estimation in control systems or complex equipment | Simple to implement; strong real-time detection capability for status changes; high robustness [78] | High dependence on model accuracy; parameter selection relies on professional knowledge | Return feeder blockage (2.3.1); heating surface wear (2.1.1) | 87–93% [61] | 84–89% [61] |
| Spectral analysis method | Suitable for frequency characteristic analysis of periodic signals, such as mechanical vibration and motor noise analysis | Accurate identification of signal characteristics; intuitive analysis results [79] | Poor processing effect on non-stationary signals | Vibration-related faults | 82–88% [64] | 76–84% [64] |
| Wavelet Transform | Suitable for non-stationary signal processing, such as transient signal analysis and image processing | Capable of capturing both time and frequency information simultaneously, suitable for multi-resolution analysis | The algorithm complexity is high, and suitable wavelet basis functions need to be selected | Sudden coking (2.2.1) | 86–92% [66] | 81–88% [66] |
| Expert System | Applicable to fields with clear empirical rules | Integrate domain knowledge, have clear logic, and are easy to expand | Relying on expert experience makes it difficult to build a rule base and handle dynamic changes | Most of the faults | 78–85% [73] | 72–80% [73] |
| Graph search | Suitable for path planning and optimal solution search, such as navigation, scheduling, and other problems | Guaranteed optimal solution | High algorithm complexity and high computational resource consumption | System air leakage (2.3.1) | 84–90% [75] | 80–87% [75] |
| Category | Method | Advantage | Disadvantage | Accuracy | Recall |
|---|---|---|---|---|---|
| Machine learning method | Decision tree | Intuitive structure and low data requirements | Easy to overfit [129] | 82–89% [85] | 78–85% [85] |
| Ensemble learning | High accuracy and stability | The process of model training and parameter tuning is complex | 88–94% [91] | 85–91% [91] | |
| Support Vector Machine | Strong generalization ability and can avoid local optimal solutions | when the amount of data is large, it is time-consuming and sensitive to parameters | 86–93% [96] | 83–89% [96] | |
| K-means | Simple and efficient | Easy to become stuck in local optimal solutions [130] | 80–87% [106] | 75–83% [106] | |
| Deep learning method | DBN | Strong feature extraction ability [131] | Slow model training speed and sensitivity to parameters | 87–94% [116] | 84–90% [116] |
| CNN | Superior performance in image processing, capable of automatically extracting features [132] | High data demand and poor robustness to location changes | 90–96% [119] | 88–93% [119] | |
| RNN | Has memory ability | Difficult to handle long sequences and complex training processes [133] | 85–92% [122] | 82–88% [122] |
| Method | Advantage | Disadvantage | Applicable Scenarios |
|---|---|---|---|
| Fiber optic probe technology | High measurement accuracy, suitable for micro particle detection; miniaturization of probe, suitable for local measurement | Limited measurement range; easy to be worn by particles; high installation and alignment requirements | Microscopic particle size measurement; local concentration and velocity measurement, suitable for particle beds, gas–solid reactors, and laboratory research |
| UDV technology | Non-contact measurement; suitable for velocity field measurement of multiphase flow; strong penetration ability, can be used in opaque media | Low spatial resolution; sensitive to the acoustic properties of the medium, which may affect measurement accuracy | Gas–liquid flow monitoring; Measurement of flow velocity distribution inside pipelines; liquid solid or gas–liquid flow analysis in the fields of chemical engineering, energy, and environmental protection |
| LDV technology | High spatial and temporal resolution; non-contact measurement; suitable for high-speed flow measurement | Restricted by transparency; high requirements for laser path; high equipment cost | Analysis of high-speed flow and turbulence characteristics; accurate velocity measurement in transparent media, such as combustion processes, droplet injection, and flow separation scenarios |
| PIV technology | Visualize the velocity field and provide two-dimensional or even three-dimensional flow field distribution information; suitable for high-resolution and complex flow measurements | Complex data processing; high requirements for particle tracking performance and image quality; high hardware cost | Research on multiphase flow field distribution; flow characteristic analysis in cyclone separators, stirred reactors, and environmental simulations, as well as fundamental research requiring global flow field data |
| PT technology | Capable of providing global multiphase distribution information; suitable for dynamic monitoring; widely applicable, including gas–solid and gas–liquid flow scenarios | Low resolution; the imaging quality depends on the reconstruction algorithm; the measurement time is relatively long | Multiphase distribution monitoring in industrial equipment; process monitoring and optimization of flow in reactors, conveying pipelines, and storage tanks; state detection and diagnosis in energy and chemical production |
| Method Type | Example Methods | Lead Time | Best For | Limitations |
|---|---|---|---|---|
| Statistical method | PCA | 1–5 h [33] | Slow wear degradation | Misses sudden faults |
| Model-based | Kalman filter | 5–30 min [55] | Real-time state estimation | Requires accurate physics model |
| Signal-based | Wavelet transform | 1–60 s [68] | Transient anomalies | No fault prediction |
| Machine learning | SVM | 10–30 min [97] | Trend-based faults | Needs historical data |
| Deep learning | CNN/RNN | 5–60 min [122] | Early subtle anomalies | Computationally intensive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Huang, Y.; Ai, Y.; Wang, G.; Singh, J. Systematic Review on Fluidized Bed Fault Diagnosis: From Fault Characteristics to Data-Driven Methods. Electronics 2025, 14, 3043. https://doi.org/10.3390/electronics14153043
Liu J, Huang Y, Ai Y, Wang G, Singh J. Systematic Review on Fluidized Bed Fault Diagnosis: From Fault Characteristics to Data-Driven Methods. Electronics. 2025; 14(15):3043. https://doi.org/10.3390/electronics14153043
Chicago/Turabian StyleLiu, Jinjin, Yibin Huang, Yandi Ai, Gang Wang, and Jenisha Singh. 2025. "Systematic Review on Fluidized Bed Fault Diagnosis: From Fault Characteristics to Data-Driven Methods" Electronics 14, no. 15: 3043. https://doi.org/10.3390/electronics14153043
APA StyleLiu, J., Huang, Y., Ai, Y., Wang, G., & Singh, J. (2025). Systematic Review on Fluidized Bed Fault Diagnosis: From Fault Characteristics to Data-Driven Methods. Electronics, 14(15), 3043. https://doi.org/10.3390/electronics14153043






