A Novel Method for Predicting Landslide-Induced Displacement of Building Monitoring Points Based on Time Convolution and Gaussian Process
Abstract
1. Introduction
2. Deep Learning Methods
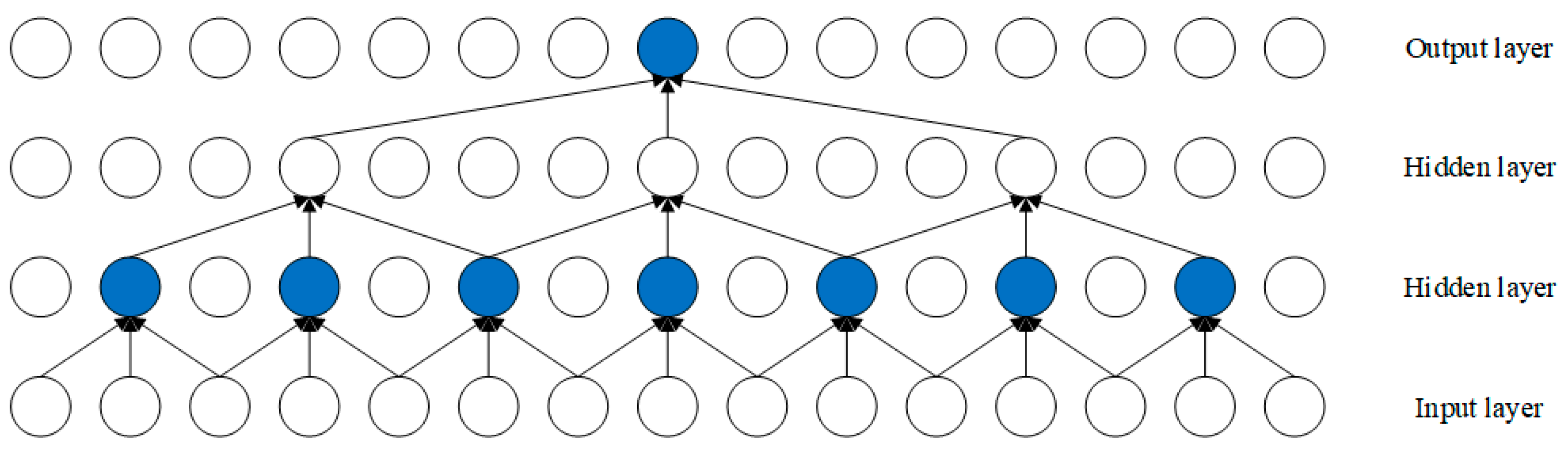
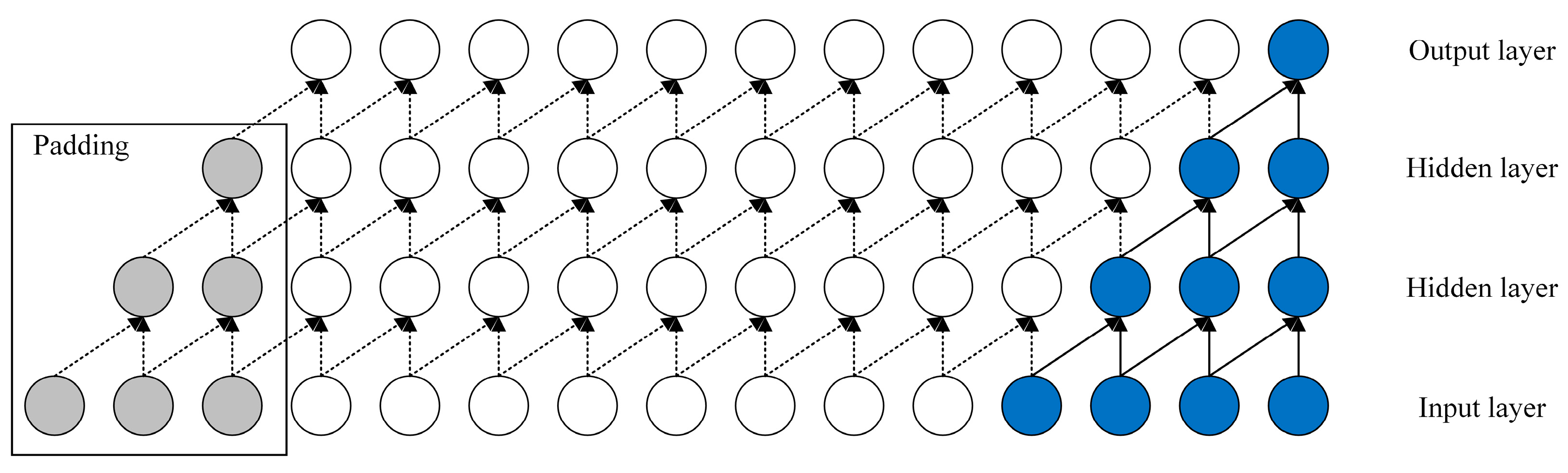
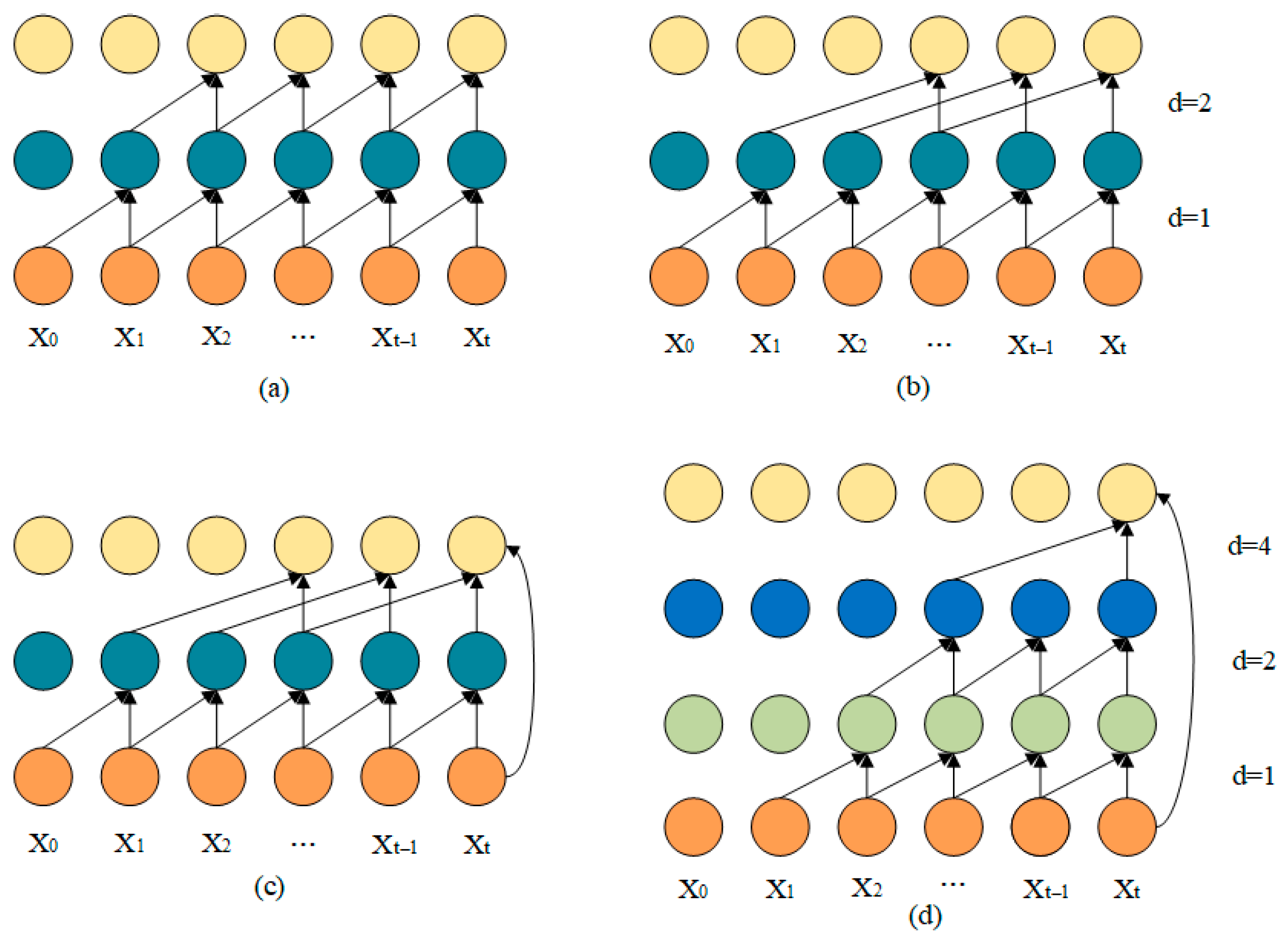
2.1. Temporal Convolutional Network (TCN)
2.2. Gaussian Process Regression (GPR)
3. Case Study
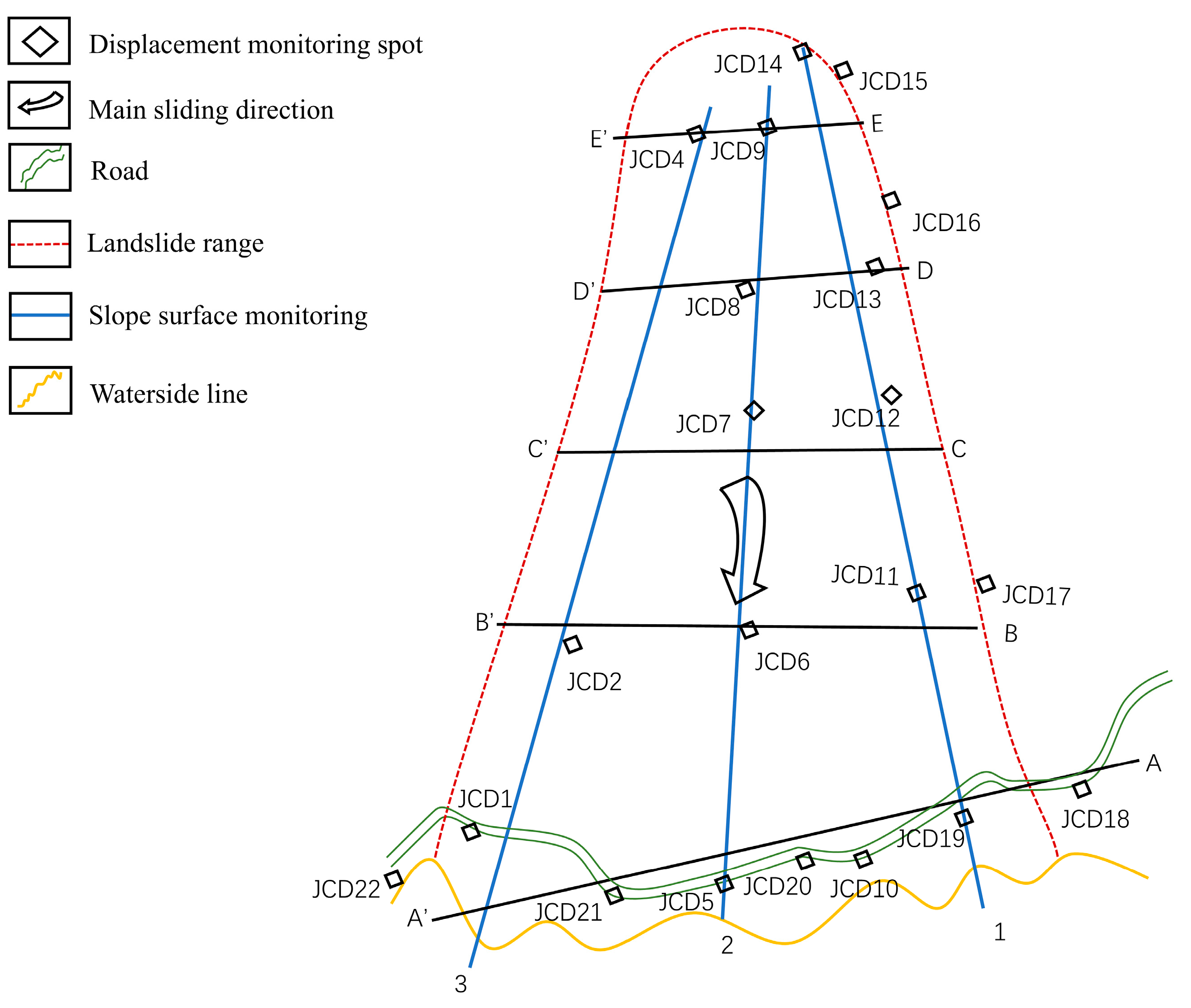
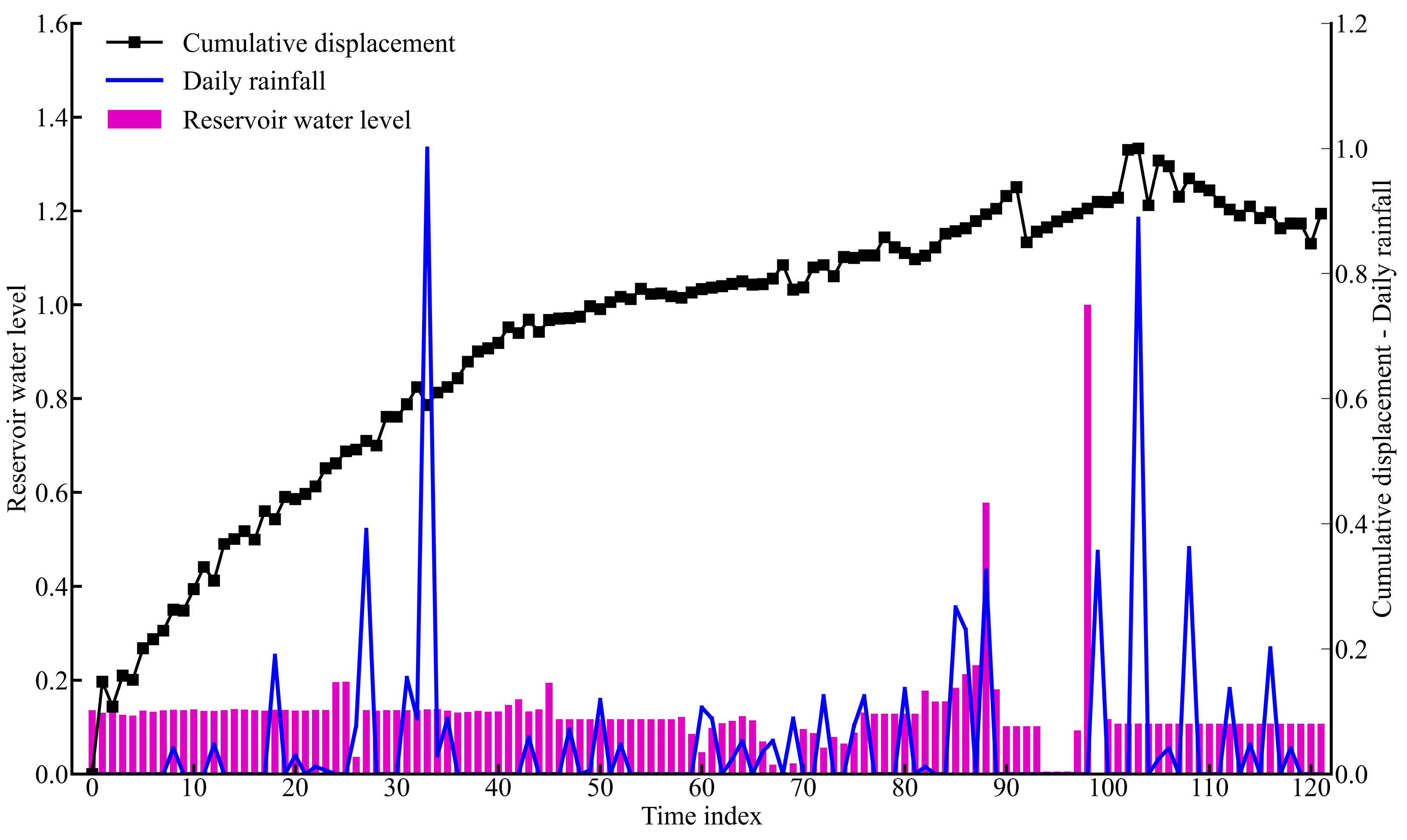
3.1. Engineering Overview
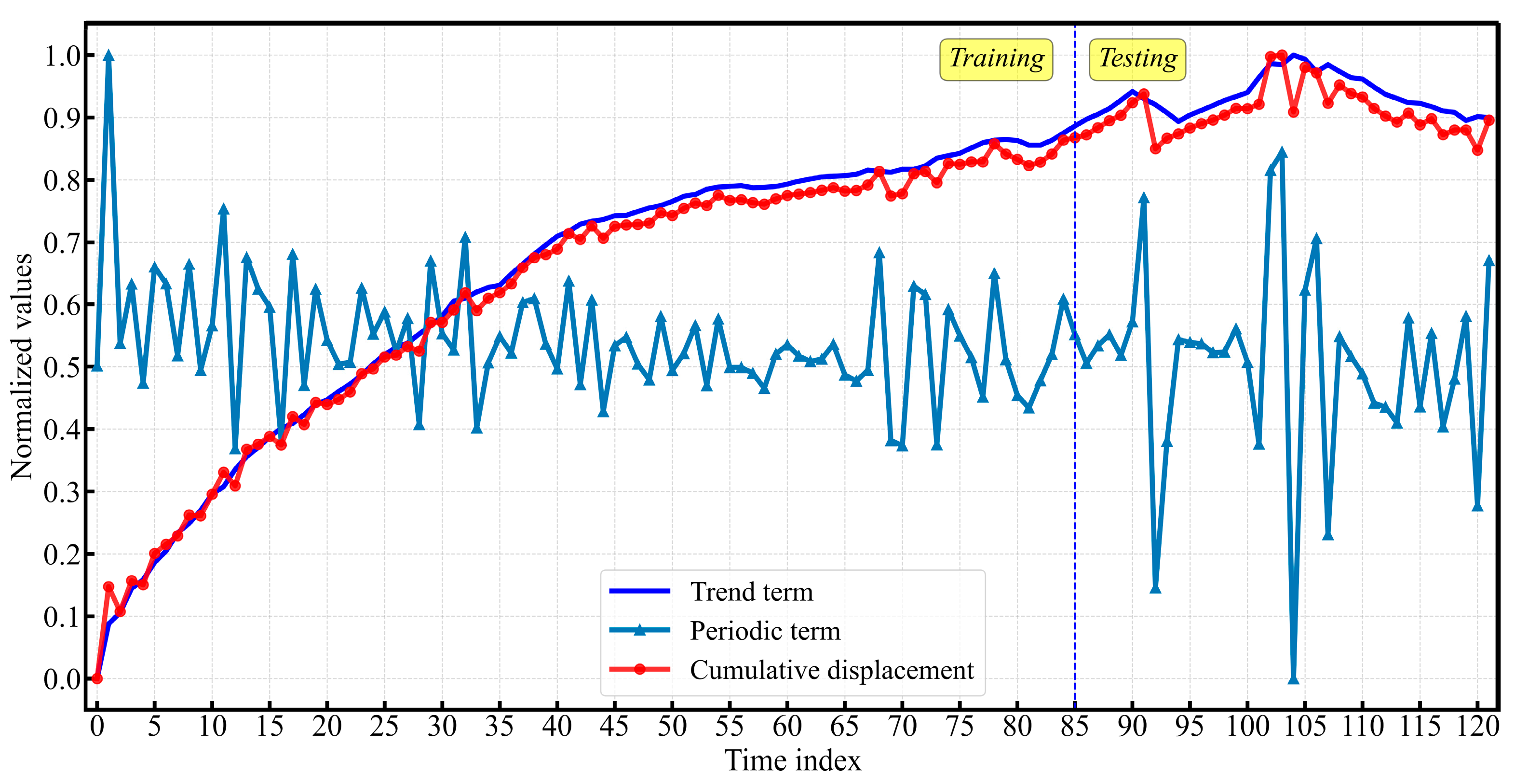
3.2. Cumulative Displacement Decomposition
3.3. Variational Mode Decomposition (VMD)
3.4. Forecasting Metrics
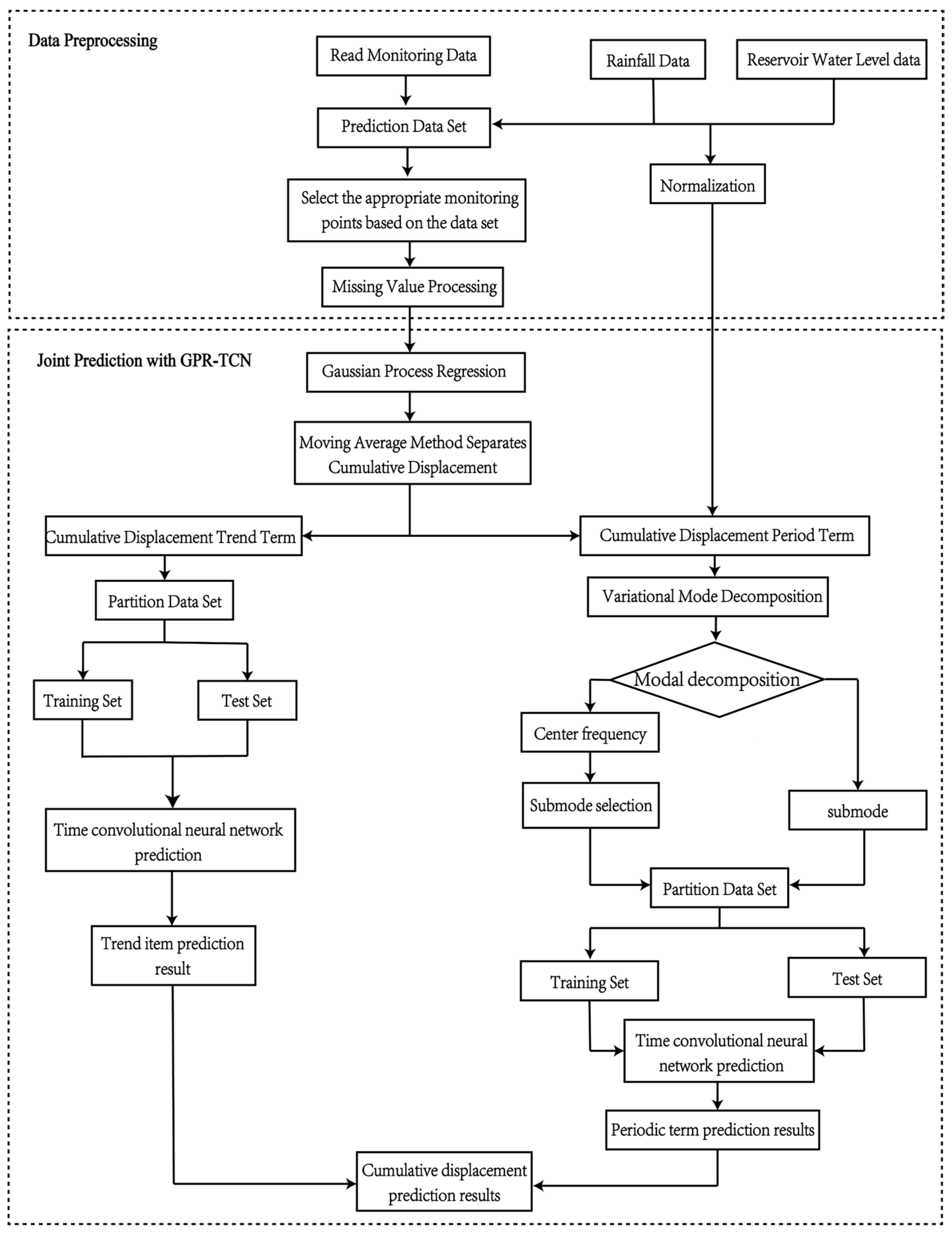
3.5. Gauss Time Convolutional Neural Network Joint Model
4. Forecast Result
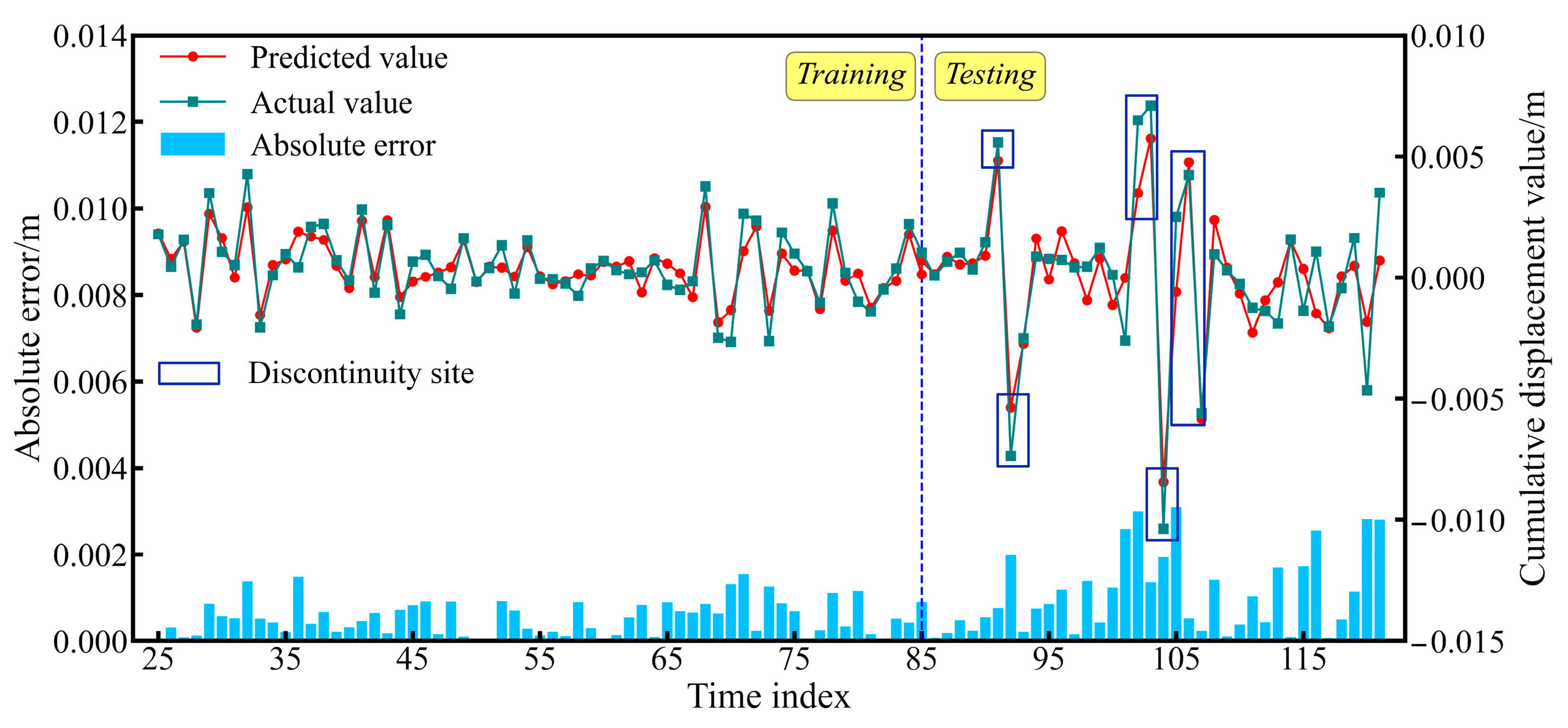
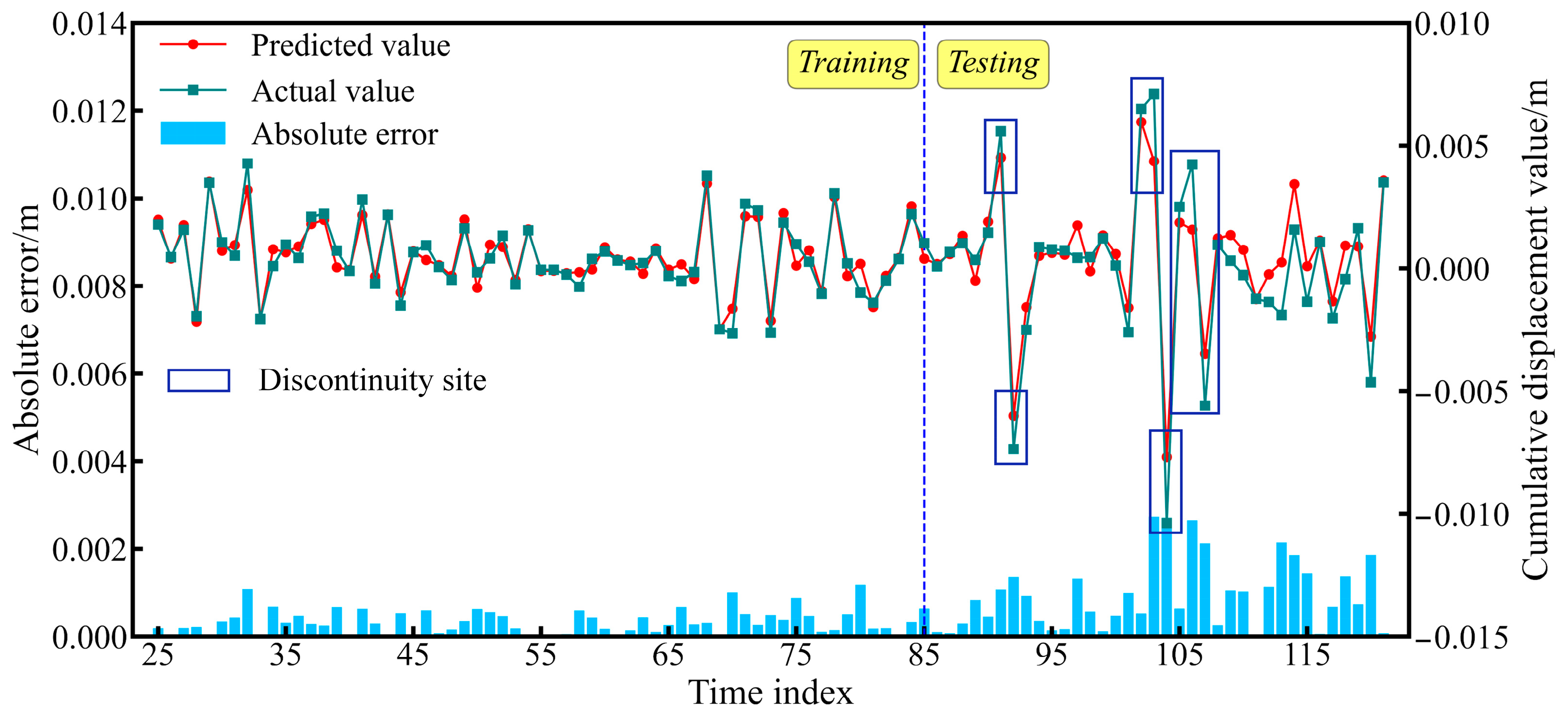
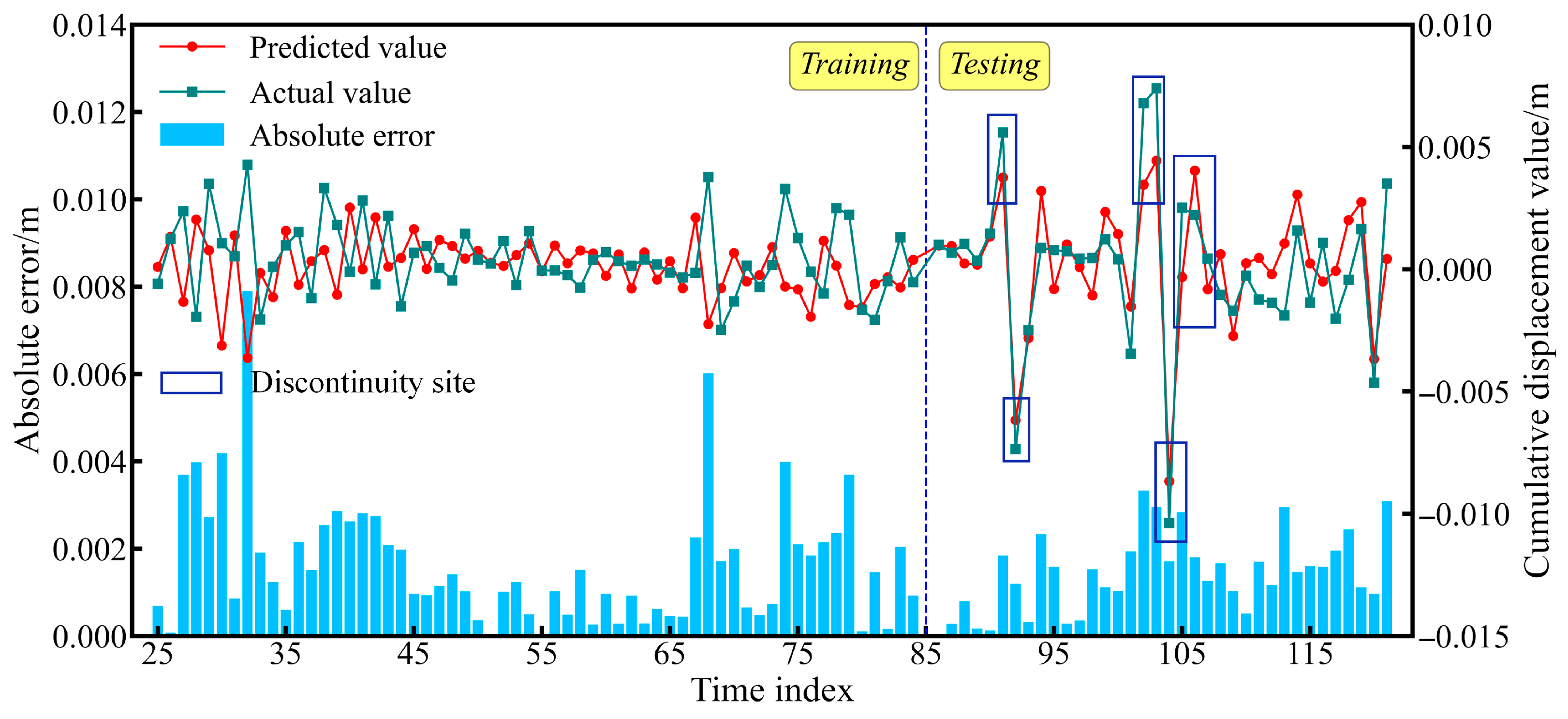
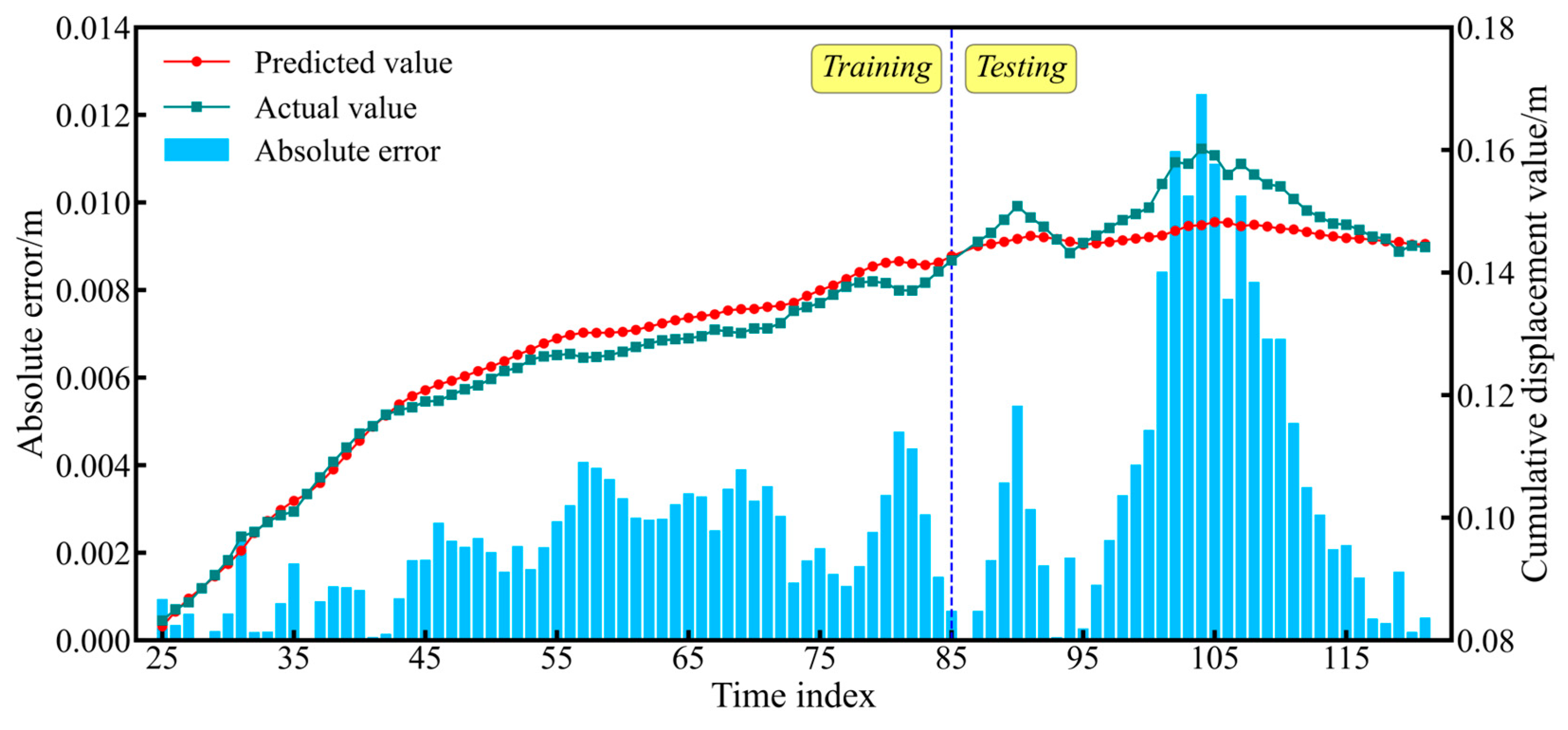
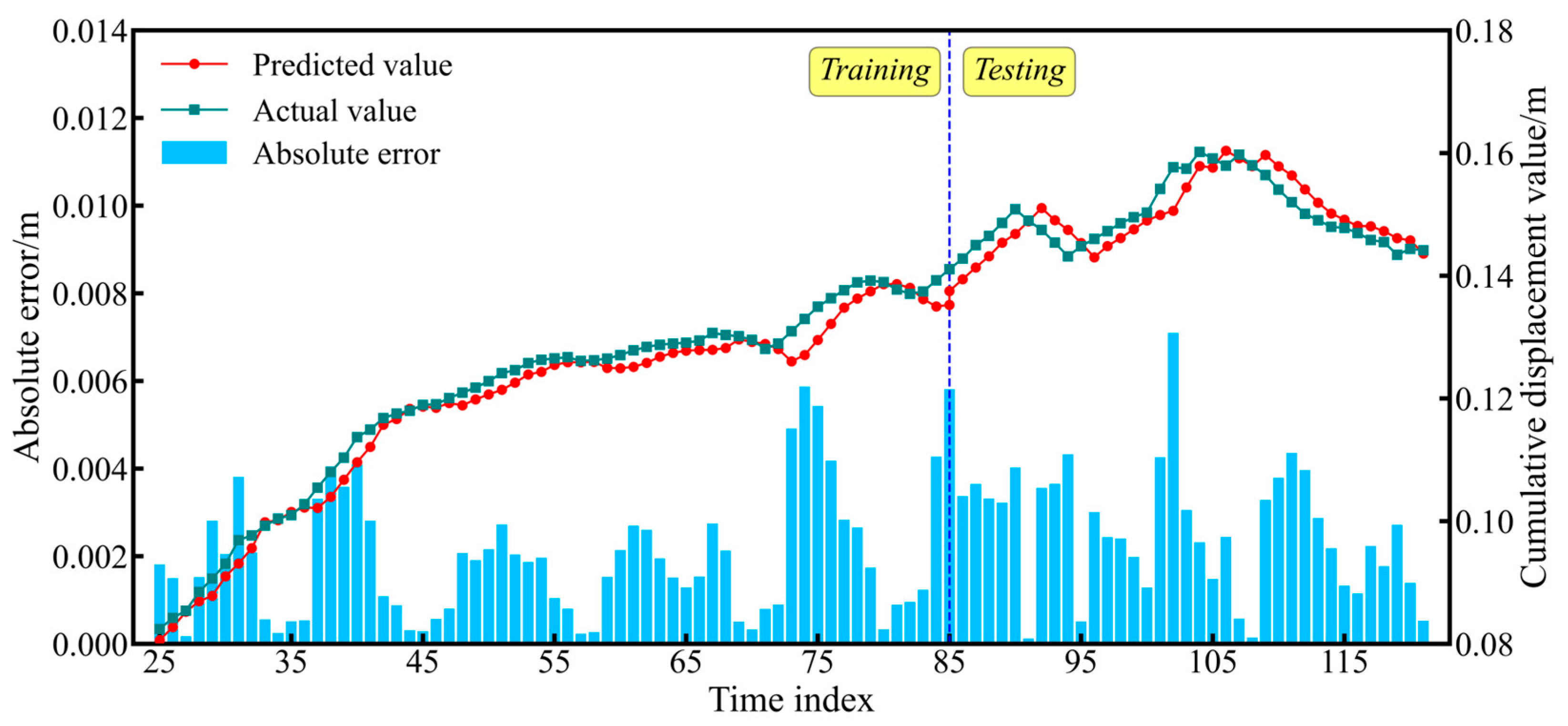
4.1. Fluctuating Term Prediction Results
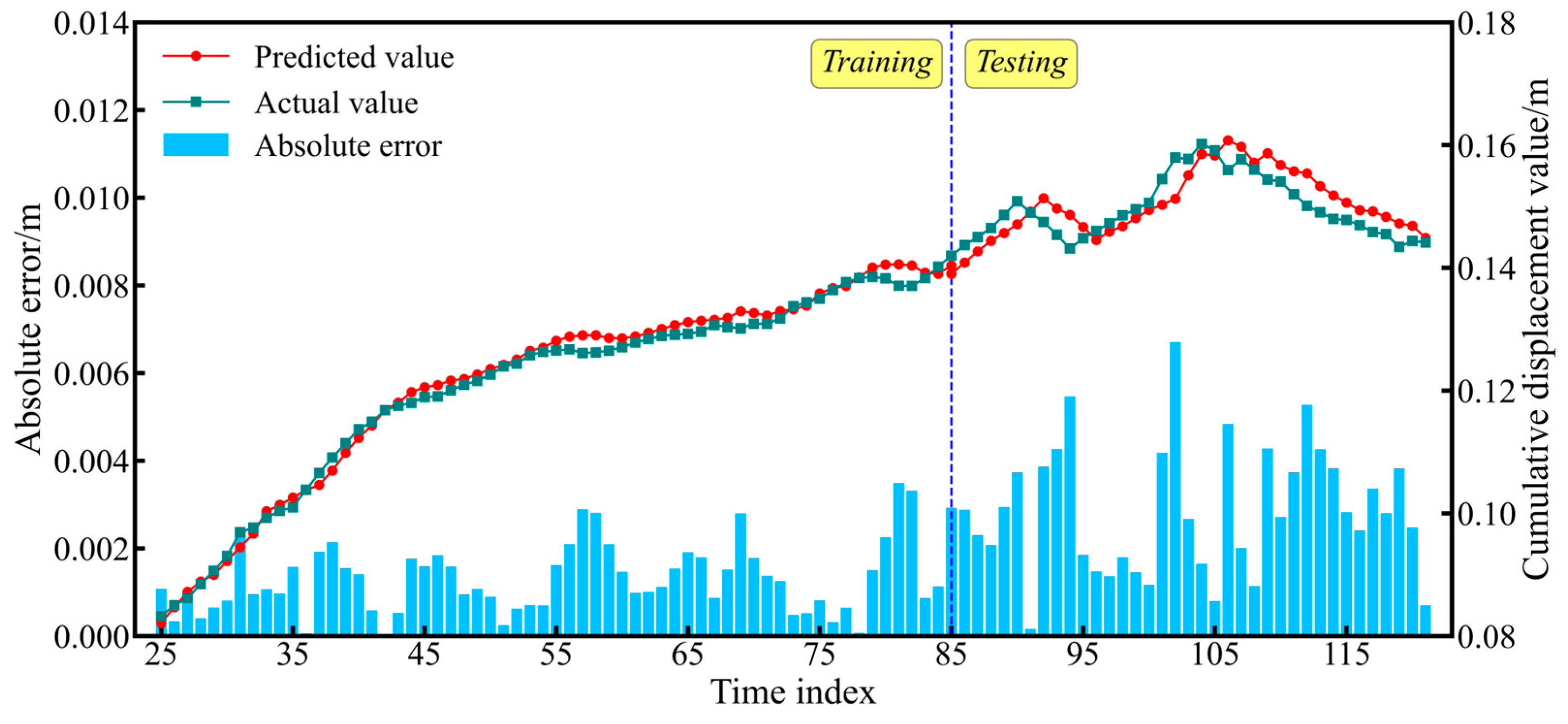
4.2. Trend Item Prediction Result
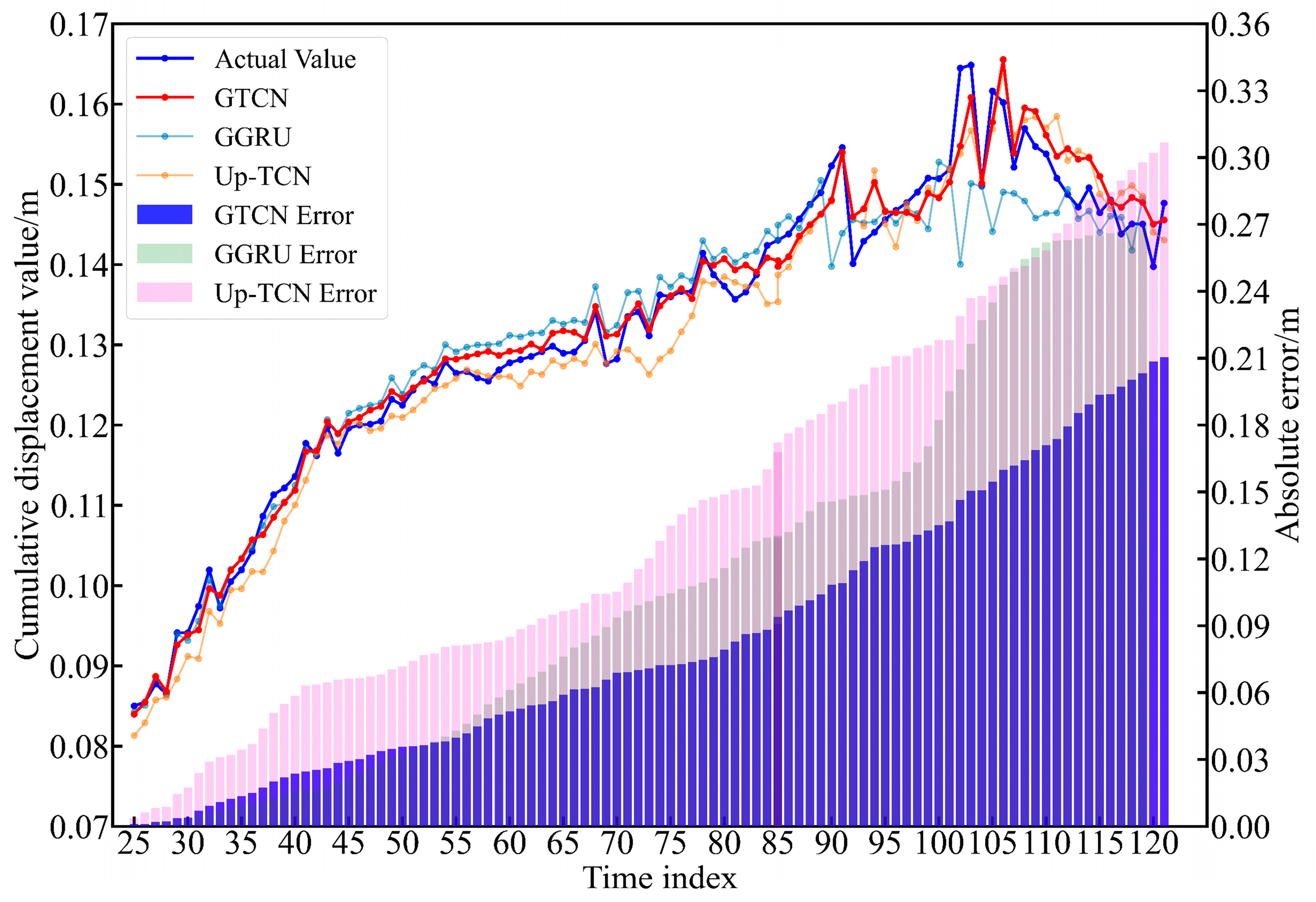
4.3. Cumulative Displacement Prediction Results
5. Discussion
6. Conclusions
- (1)
- To address cumulative errors in historical data, a multi-dimensional spatiotemporal data one-dimensional reconstruction method is proposed. Based on VMD, periodic components are decomposed into submodal components (IMFs). Experiments demonstrate that VMD-decomposed IMFs are more suitable as prediction targets for TCN models. When integrated with multi-source covariates (standardized rainfall, reservoir water levels, etc.), the model’s prediction accuracy improves by 15.6%. This strategy significantly enhances compatibility with heterogeneous data and feature representation capability.
- (2)
- Through systematic comparison using four metrics, the GTCN demonstrates comprehensive advantages over baseline models: compared to Gated Recurrent Unit (GRU) models, the mean square error (MSE) was reduced by 114.2% and the mean absolute error (MAE) decreased by 33.3%; compared to the UP-TCN, the coefficient of determination (R2) improved by 1.02%. The root mean square error (RMSE) fluctuation range narrows to ±0.03 × 10−2, verifying model stability.
- (3)
- The GTCN excels in high-data-integrity scenarios, though its periodic component prediction accuracy is 9.8% lower than that of the GRU due to high-frequency oscillations. Notably, the GRU exhibits overfitting in trend-term predictions due to a limited test set size. The GPR imputation method quantifies uncertainty through covariance kernel functions, reducing imputation errors by 64.7% compared to piecewise constant interpolation in data mutation regions (e.g., abrupt reservoir drawdown). This model provides a theoretically reliable and practically applicable solution for landslide displacement prediction with missing values.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Niu, X.; Ma, J.; Wang, Y.; Zhang, J.; Chen, H.; Tang, H. A novel decomposition-ensemble learning model based on ensemble empirical mode decomposition and recurrent neural network for landslide displacement prediction. Appl. Sci. 2021, 11, 4684. [Google Scholar] [CrossRef]
- Wang, F.-W.; Zhang, Y.-M.; Huo, Z.-T.; Matsumoto, T.; Huang, B.-L. The July 14, 2003 Qianjiangping landslide, three gorges reservoir, China. Landslides 2004, 1, 157–162. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Huning, L.S.; Chiang, F.; Sadegh, M.; Vahedifard, F.; Mazdiyasni, O.; Moftakhari, H.; Mallakpour, I. How do natural hazards cascade to cause disasters? Nature 2018, 561, 458–460. [Google Scholar] [CrossRef] [PubMed]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Han, L.; Chen, L.; Wang, L. Slope stability prediction using ensemble learning techniques: A case study in Yunyang County, Chongqing, China. J. Rock Mech. Geotech. Eng. 2022, 14, 1089–1099. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.; Zhou, C. Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 2017, 218, 173–186. [Google Scholar] [CrossRef]
- Du, J.; Yin, K.; Lacasse, S. Displacement prediction in colluvial landslides, Three Gorges Reservoir, China. Landslides 2013, 10, 203–218. [Google Scholar] [CrossRef]
- Shihabudheen, K.V.; Pillai, G.N.; Peethambaran, B. Prediction of landslide displacement with controlling factors using extreme learning adaptive neuro-fuzzy inference system (ELANFIS). Appl. Soft Comput. 2017, 61, 892–904. [Google Scholar] [CrossRef]
- Li, G.; Sun, Y.; Qi, C. Machine learning-based constitutive models for cement-grouted coal specimens under shearing. Int. J. Min. Sci. Technol. 2021, 31, 813–823. [Google Scholar] [CrossRef]
- Farnood Ahmadi, F.; Farsad Layegh, N. Integration of artificial neural network and geographical information system for intelligent assessment of land suitability for the cultivation of a selected crop. Neural Comput. Appl. 2015, 26, 1311–1320. [Google Scholar] [CrossRef]
- Wang, J.; Nie, G.; Gao, S.; Wu, S.; Li, H.; Ren, X. Landslide deformation prediction based on a GNSS time series analysis and recurrent neural network model. Remote Sens. 2021, 13, 1055. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Wang, K.; Li, K.; Zhou, L.; Hu, Y.; Cheng, Z.; Liu, J.; Chen, C. Multiple convolutional neural networks for multivariate time series prediction. Neuro-Comput. 2019, 360, 107–119. [Google Scholar] [CrossRef]
- Rossi, A.; Hagenbuchner, M.; Scarselli, F.; Tsoi, A.C. A Study on the effects of recursive convolutional layers in convolutional neural networks. Neurocomputing 2021, 460, 59–70. [Google Scholar] [CrossRef]
- Basiri, M.E.; Nemati, S.; Abdar, M.; Cambria, E.; Acharya, U.R. ABCDM: An attention-based bidirectional CNN-RNN deep model for sentiment analysis. Future Gener. Comput. Syst. 2021, 115, 279–294. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, J.; Li, F.; Han, S.; Qin, L.; Li, Q. Landslide Risk Prediction Model Using an Attention-Based Temporal Convolutional Network Connected to a Recurrent Neural Network. IEEE Access 2022, 10, 37635–37645. [Google Scholar] [CrossRef]
- Luo, X.; Gan, W.; Wang, L.; Chen, L.; Ma, E. A deep learning prediction model for structural deformation based on temporal convolutional networks. Comput. Intell. Neurosci. 2021, 2021, 8829639. [Google Scholar] [CrossRef]
- Huang, D.; He, J.; Song, Y.; Guo, Z.; Huang, X.; Guo, Y. Displacement Prediction of the Muyubao Landslide Based on a GPS Time-Series Analysis and Temporal Convolutional Network Model. Remote Sens. 2022, 14, 2656. [Google Scholar] [CrossRef]
- Pigott, T.D. A review of methods for missing data. Educ. Res. Eval. 2001, 7, 353–383. [Google Scholar] [CrossRef]
- Enders, C.K. Applied Missing Data Analysis; Guilford Publications: New York, NY, USA, 2022. [Google Scholar]
- Little, R.J.; Rzubin, D.B. Statistical Analysis with Missing Data; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Somasundaram, R.; Nedunchezhian, R. Missing value imputation using refined mean substitution. Int. J. Comput. Sci. Issues 2012, 9, 306. [Google Scholar]
- Little, R.J. Regression with missing X’s: A review. J. Am. Stat. Assoc. 1992, 87, 1227–1237. [Google Scholar] [CrossRef]
- Zhang, K.; Gonzalez, R.; Huang, B.; Ji, G. Expectation–maximization approach to fault diagnosis with missing data. IEEE Trans. Ind. Electron. 2014, 62, 1231–1240. [Google Scholar] [CrossRef]
- Barber, C.; Bockhorst, J.; Roebber, P. Auto-regressive HMM inference with incomplete data for short-horizon wind forecasting. Adv. Neural Inf. Process. Syst. 2010, 23, 136–144. [Google Scholar]
- Wojtowicz, A.; Żywica, P.; Stachowiak, A.; Dyczkowski, K. Solving the problem of incomplete data in medical diagnosis via interval modeling. Appl. Soft Comput. 2016, 47, 424–437. [Google Scholar] [CrossRef]
- Aye, S.A.; Heyns, P. An integrated Gaussian process regression for prediction of remaining useful life of slow speed bearings based on acoustic emission. Mech. Syst. Signal Process. 2017, 84, 485–498. [Google Scholar] [CrossRef]
- Wang, Y.; Chaib-Draa, B. An online Bayesian filtering framework for Gaussian process regression: Application to global surface temperature analysis. Expert Syst. Appl. 2017, 67, 285–295. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Williams, C.; Rasmussen, C. Gaussian processes for regression. Adv. Neural Inf. Process. Syst. 1995, 8, 514–520. [Google Scholar]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Chu, W.; Ghahramani, Z.; Williams, C.K. Gaussian processes for ordinal regression. J. Mach. Learn. Res. 2005, 6, 1019–1041. [Google Scholar]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using Gaussian process regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of different machine learning methods and deep-learning convolutional neural networks for landslide detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Man, T.; Zhang, P.; Ge, Z.; Galindo-Torres, S.A.; Hill, K.M. Friction-dependent rheology of dry granular systems. Acta Mech. Sin. 2023, 39, 722191. [Google Scholar] [CrossRef]
- Zhang, X.; Du, D.; Man, T.; Ge, Z.; Huppert, H.E. Particle clogging mechanisms in hyporheic exchange with coupled lattice Boltzmann discrete element simulations. Phys. Fluids 2024, 36, 013312. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhong, H.; Li, Y.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Tang, L.; Zhang, W.; Lacasse, S.; Liu, H.; Gao, L. Efficient reliability analysis of earth dam slope stability using extreme gradient boosting method. Acta Geotech. 2020, 15, 3135–3150. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Armaghani, D.J.; Zhang, W.; Li, C.; Zhu, S.; Tarinejad, R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geosci. Front. 2021, 12, 101091. [Google Scholar] [CrossRef]
- Ching, J.; Phoon, K.-K. Transformations and correlations among some clay parameters—The global database. Can. Geotech. J. 2014, 51, 663–685. [Google Scholar] [CrossRef]
- Amagu, C.A.; Zhang, C.; Sainoki, A.; Sugimoto, K.; Shimada, H.; Dzimunya, N.; Sinkala, P.; Kodama, J.-I. Analysis of excavation-induced effect of a rock slope using 2-dimensional back analysis method: A case study for clay-bearing interbedded rock slope. Geotech. Geol. Eng. 2024, 42, 6315–6337. [Google Scholar] [CrossRef]

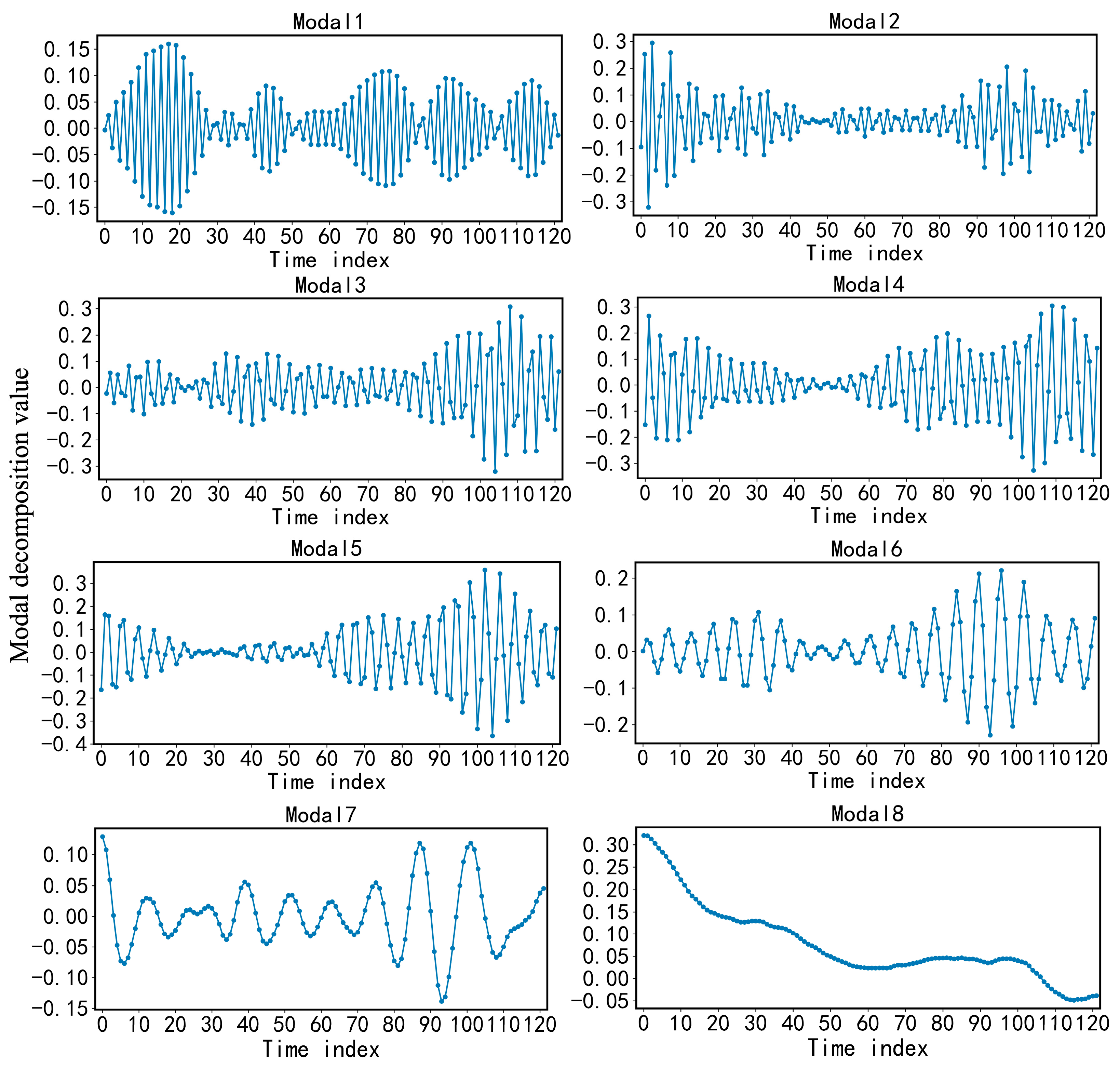
| Number of Modal Decomposition | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Center frequency value | 0.007 | 0.324 | 0.359 | 0.377 | 0.413 | 0.431 | 0.465 |
| MSE (×10−4) | RMSE (×10−2) | R2 (%) | MAE (×10−2) | |
|---|---|---|---|---|
| GTCN | 0.011 | 0.1 | 70.94 | 0.07 |
| GGRU | 0.007 | 0.08 | 81.20 | 0.06 |
| UP-TCN | 0.043 | 0.21 | −35.70 | 0.16 |
| MSE (×10−4) | RMSE (×10−2) | R2 (%) | MAE (×10−2) | |
|---|---|---|---|---|
| GTCN | 0.053 | 0.10 | 70.94 | 0.07 |
| GGRU | 0.147 | 0.38 | 95.12 | 0.28 |
| UP-TCN | 0.060 | 0.25 | 98.41 | 0.19 |
| Prediction Model | |||
|---|---|---|---|
| UP-TCN | GTCN | GGRU | |
| MSE (×10−4) | 0.11 | 0.07 | 0.15 |
| RMSE (×10−2) | 0.33 | 0.27 | 0.38 |
| R2 (%) | 96.88 | 97.88 | 95.84 |
| MAE (×10−2) | 0.26 | 0.21 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zeng, X.; Shi, Y.; Liu, J.; Xie, L.; Xu, Y.; Liu, J. A Novel Method for Predicting Landslide-Induced Displacement of Building Monitoring Points Based on Time Convolution and Gaussian Process. Electronics 2025, 14, 3037. https://doi.org/10.3390/electronics14153037
Wang J, Zeng X, Shi Y, Liu J, Xie L, Xu Y, Liu J. A Novel Method for Predicting Landslide-Induced Displacement of Building Monitoring Points Based on Time Convolution and Gaussian Process. Electronics. 2025; 14(15):3037. https://doi.org/10.3390/electronics14153037
Chicago/Turabian StyleWang, Jianhu, Xianglin Zeng, Yingbo Shi, Jiayi Liu, Liangfu Xie, Yan Xu, and Jie Liu. 2025. "A Novel Method for Predicting Landslide-Induced Displacement of Building Monitoring Points Based on Time Convolution and Gaussian Process" Electronics 14, no. 15: 3037. https://doi.org/10.3390/electronics14153037
APA StyleWang, J., Zeng, X., Shi, Y., Liu, J., Xie, L., Xu, Y., & Liu, J. (2025). A Novel Method for Predicting Landslide-Induced Displacement of Building Monitoring Points Based on Time Convolution and Gaussian Process. Electronics, 14(15), 3037. https://doi.org/10.3390/electronics14153037







