Abstract
Dual-active bridge (DAB) converters have emerged as a preferred topology in electric vehicle charging and energy storage applications, owing to their structurally symmetric configuration and intrinsic galvanic isolation capabilities. However, conventional triple-phase shift (TPS) control strategies face significant challenges in maintaining high efficiency across ultra-wide output voltage and load ranges. To exploit the inherent structural symmetry of the DAB topology, a symmetric optimization strategy based on triple-phase shift (SOS-TPS) is proposed. The method specifically targets the forward buck operating mode, where an optimization framework is established to minimize the root mean square (RMS) current of the inductor, thereby addressing both switching and conduction losses. The formulation explicitly incorporates zero-voltage switching (ZVS) constraints and operating mode conditions. By employing the Karush–Kuhn–Tucker (KKT) conditions in conjunction with the Lagrange multiplier method (LMM), the refined control trajectories corresponding to various power levels are analytically derived, enabling efficient modulation across the entire operating range. In the medium-power region, full-switch ZVS is inherently satisfied. In the low-power operation, full-switch ZVS is achieved by introducing a modulation factor λ, and a selection principle for λ is established. For high-power operation, the strategy transitions to a conventional single-phase shift (SPS) modulation. Furthermore, by exploiting the inherent symmetry of the DAB topology, the proposed method reveals the symmetric property of modulation control. The modulation strategy for the forward boost mode can be efficiently derived through a duty cycle and voltage gain mapping, eliminating the need for re-derivation. To validate the effectiveness of the proposed SOS-TPS strategy, a 2.3 kW experimental prototype was developed. The measured results demonstrate that the method ensures ZVS for all switches under the full load range, supports ultra-wide voltage conversion capability, substantially suppresses RMS current, and achieves a maximum efficiency of 97.3%.
1. Introduction
Dual-active bridge (DAB) converters have gained widespread adoption in medium- and high-power systems, owing to their structural symmetry, inherent galvanic isolation, extended soft-switching capability, versatile power control, compact design, and ease of digital implementation. They are particularly well-suited for use in DC microgrids [1,2], automotive power systems [3,4], and energy storage systems [5].
Ensuring consistently high efficiency over a broad span of input and output voltage conditions remains a critical design target in such applications. For converters utilizing wide-bandgap (WBG) devices, achieving ZVS for all power switches is essential, as they substantially reduce switching losses—particularly at elevated switching frequencies where such losses become more pronounced [6]. Furthermore, ZVS contributes to improved electromagnetic compatibility (EMC) and system reliability by mitigating high dv/dt transients during switching events.
To extend the ZVS range and accommodate wide variations in input and output voltages, two primary approaches have been investigated, which include topological modifications [7,8] and modulation strategy enhancements. While topological changes can expand operating boundaries, they often introduce increased circuit complexity, higher cost, and reduced system reliability. As a result, modulation-based techniques are generally preferred in practical implementations due to their lower overhead and greater adaptability. DAB converters commonly employ phase-shift modulation schemes. Although certain strategies utilize asymmetric duty cycles [9,10,11], they often result in unbalanced switching stress and reduced transformer utilization. In contrast, symmetric duty cycle modulation offers better current sharing and improved transformer efficiency. Modulation approaches for DAB converters are generally categorized by theirs degree of freedom (DOFs), including single-phase shift (SPS) with one DOF, dual-phase shift (DPS) or extended-phase shift (EPS) with two DOFs, and triple-phase shift (TPS) offering three DOFs. Among these, SPS remains the most prevalent due to its straightforward control logic and ease of hardware realization [12]. However, it exhibits severe limitations—particularly when there is a significant deviation of the voltage conversion ratio from its nominal value—where the loss of ZVS leads to reduced efficiency [13,14,15]. In contrast, DPS, EPS, and TPS provide enhanced flexibility through additional control parameters. These advanced modulation schemes have been applied to various optimization objectives, including the minimization of current stress [16,17,18,19,20,21,22,23,24,25,26,27,28,29], the suppression of circulating power [30,31,32], and the reduction in the root mean square (RMS) current [33,34,35,36,37], thereby improving the overall performance of DAB converters under wide-ranging operating conditions.
An enhanced power regulation method employing EPS modulation was developed to suppress peak current, thereby achieving notable improvements in efficiency, particularly within the medium-power operating region [19]; however, its performance remains suboptimal under light-load conditions [37]. A particle swarm optimization (PSO)-based EPS scheme was developed to optimize current stress [25], and full-range ZVS with enhanced efficiency was achieved using an AI-based EPS approach in another study [38]. Nevertheless, both [25,38] rely on artificial intelligence algorithms, which suffer from limited online computation capability and poor portability, making them unsuitable for practical engineering applications. In the context of DPS modulation, ZVS conditions have been analyzed in several studies. Zhao et al. concentrated on the comprehensive reduction in different categories of power dissipation to enhance overall system efficiency [39], while Liu et al. emphasized reducing surge currents and improving system stability [40]. However, neither of these solutions achieve ZVS across the full-load range.
A current stress optimization strategy based on dual-phase shift (CSO-DPS) was proposed to alleviate current stress in both the buck and boost operation modes. However, its ZVS capability remained limited. Under conventional DPS control, at least one switch pair in the DAB converter was subjected to hard switching during high-power operation. In addition, methods leveraging magnetizing current were also explored to enable wide-range ZVS and mitigate current stress [20,22]. While effective, these approaches introduce additional complexity in transformer design, posing challenges for practical implementation.
With its superior modulation flexibility, the TPS control enables comprehensive performance optimization over a broad operating range. A TPS-based current stress reduction approach was introduced in [16]. In [27], a reactive power controller based on TPS was innovatively introduced to reduce inductor current across all load conditions by optimizing reactive power. However, its full-range ZVS performance was not thoroughly investigated. In [41], a TPS-based strategy was proposed to minimize current stress under varying DC-link voltages. While it achieved minimal current stress at light loads, full ZVS was not guaranteed for all switches. The strategy presented in [21] realized ZVS for all six power switches under medium-load conditions and full-switch ZVS under both light and heavy loads, while maintaining nearly optimal peak inductor currents in both the buck and boost modes. Nonetheless, two switches still failed to achieve ZVS under medium load, resulting in elevated switching losses. In [23], artificial intelligence (AI)-based methods were employed to build current stress prediction models from simulation datasets. Despite its effectiveness, this approach requires extensive simulation or experimental data and a separate optimization process for each operating condition, leading to high complexity and limited real-time applicability. TPS-based current stress optimization was also investigated, but this method failed to achieve ZVS for two switches in the medium-power region, as shown in [26]. A three-level phase-shift control scheme was presented in to minimize reactive power and improve conversion efficiency across a wide operational range [30]. In addition, a unified optimal modulation strategy (UOMS) was developed to suppress circulating power, thereby achieving full-range ZVS and reduced root mean square (RMS) current. Nevertheless, the effectiveness of UOMS remains constrained to certain operating points, limiting its general applicability [32].
Given that conduction losses increase proportionally with the squared magnitude of the RMS current, minimizing RMS current is essential for improving overall energy efficiency [37]. In [28], the authors investigated the correlation between current stress and RMS current minimization under TPS control and proposed an associated optimization method. However, the manuscript does not provide a detailed analysis of ZVS, and the relatively low switching frequency raises concerns about the strategy’s effectiveness at higher frequencies. While studies [33,34] have investigated RMS and efficiency optimization, their analyses were tailored to specific device configurations and lacked generalized analytical modulation expressions, limiting their applicability to broader operating conditions. A global optimal condition (GOC) for minimizing the RMS current across the entire power range was proposed, but ZVS performance was not considered in the analysis [35]. However, it neglected the evaluation of ZVS characteristics. To address RMS current, another approach grounded in fundamental harmonic analysis was proposed, yet ZVS could not be achieved by two switches under moderate and low load levels [37]. Moreover, under light-load conditions, none of the six switches achieved ZVS [16,30,35]. In [29], the authors propose a method that dynamically sets the ZVS current threshold to achieve ZVS for power switches while maintaining a low inductor current. However, under low-power conditions with high output voltage, ZVS can be achieved for only two switches, and under medium-power conditions, ZVS is limited to six switches. To improve ZVS operation and attain high efficiency across the full-load range, nonlinear modeling techniques were utilized to more accurately capture the switching behavior [42]. Nevertheless, these methods typically depend on offline lookup tables, which are unsuitable for real-time control and impose substantial computational requirements, thereby limiting their feasibility in practical implementations [33,34,42].
To address the limitations identified in prior studies, this paper proposes a symmetric optimization strategy based on triple-phase shift for DAB converters (SOS-TPS). The proposed methodology is designed to ensure full-range ZVS and reduced RMS current while maintaining high efficiency under diverse operating scenarios. First, among the eight operating modes capable of forward power transfer, three are selected for further analysis based on their optimization potential. Using the Karush–Kuhn–Tucker (KKT) conditions and the Lagrange multiplier method (LMM), the optimal combination of control variables is derived for minimizing the RMS current in the forward buck mode under low- and medium-power conditions. To facilitate full-switch ZVS at low power, a modulation factor λ is introduced, balancing soft-switching and current stress. For high-power operation, the strategy transitions to conventional SPS modulation, which inherently satisfies ZVS and maintains low RMS current. Second, exploiting the structural symmetry of the DAB topology, the proposed approach reveals a key modulation feature: once the analytical framework is established for the forward buck mode, the corresponding control law for the forward boost mode can be directly obtained via variable transformation, eliminating the need for repetitive derivation. Third, most existing modulation strategies are only effective under specific operating conditions and tend to fail when the voltage conversion ratio between the input and output varies significantly. In contrast, the proposed SOS-TPS strategy remains applicable across the full-load range and large voltage conversion ratios, maintaining both low RMS current and full-switch ZVS as its optimization objectives. Fourth, due to its closed-form analytical expressions, the proposed modulation strategy supports real-time computation and exhibits high portability, making it more suitable for practical engineering implementation. Finally, the proposed SOS-TPS strategy is experimentally verified to demonstrate its correctness and practical effectiveness.
2. Analysis Modeling and Operational Analysis of DAB Converters
2.1. Operational Mechanism of DAB Converters
As illustrated in Figure 1, the DAB converter comprises two full-bridge (FB) stages, FB1 and FB2, interconnected through a high-frequency transformer with a turns ratio of n:1. The voltage conversion ratio is expressed as k = V1/(nV2), where k > 1 indicates operation in buck mode, and k < 1 corresponds to boost mode. Given the inherent structural symmetry of the DAB converter, the control strategies optimized for k > 1 and k < 1 are expected to exhibit corresponding symmetrical characteristics when V1 remains constant.
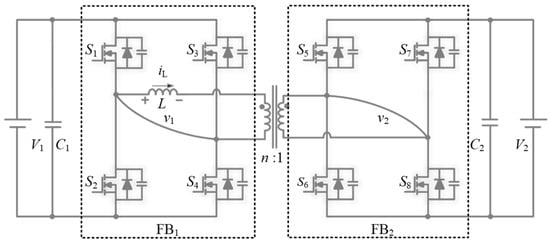
Figure 1.
Topology of the DAB converter.
Figure 2 presents the representative waveforms of a DAB converter operating under the TPS modulation scheme. In this context, D1 and D2 denote the duty cycles of the voltage waveforms on the primary and secondary sides, respectively, while Φ signifies the phase shift between their waveform centers. These three modulation parameters—D1, D2, and Φ—are collectively defined as the Dcontrol and are restricted to the interval [0, 1]. The switching period is represented by Ts, with its associated frequency fs, and the half-period is defined as Ths = Ts/2. The inductor current, along with the voltages v1 and v2, exhibit waveform variations dependent on D1, D2, and Φ, which subsequently affect both the RMS value of the leakage inductor current and the average power transferred from the primary to the secondary side.
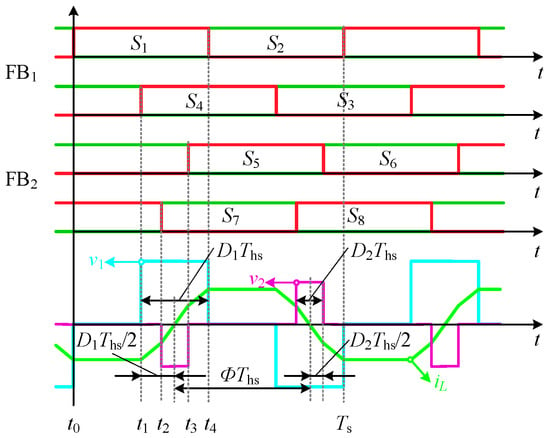
Figure 2.
Triple phase-shift modulation waveforms of a DAB.
2.2. Classification and Selection of TPS Modes in DAB Converters
Depending on the specific combination of D1, D2, and Φ, a DAB converter can operate in eight distinct modulation modes under the TPS control scheme. Figure 3 depicts the representative voltage and current waveforms for each TPS mode. As presented in Section 2.3 of [43], the normalized transmitted power expressions, operating ranges, and mode constraints for each modulation mode can be obtained, along with the normalized inductor current values at each switching instant for modes D, F, and G.
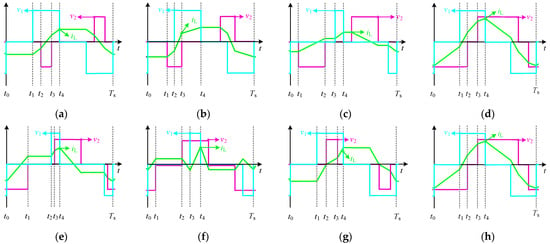
Figure 3.
Typical voltage and current waveforms under eight TPS modulation modes. (a) Mode A. (b) Mode B. (c) Mode C. (d) Mode D. (e) Mode E. (f) Mode F. (g) Mode G. (h) Mode H.
This study focuses on optimizing forward power transfer of the DAB converter under both buck and boost conditions. Based on Figure 3, the normalized inductor currents for each modulation mode, and Equation (1), the actual RMS inductor current Irms is computed. To facilitate further analysis, the square of the RMS current is normalized using Equation (2), and the normalized RMS current Inrms2 for each modes are summarized in Table 1.

Table 1.
Normalized root mean square current values for modes D, F, and G.
2.3. Symmetry of DAB Converters
Taking mode D as an example, the DAB converter operates under condition a. By interchanging the primary and secondary DC voltages, as well as the duty cycles of the AC voltages on both sides while keeping the phase shift Φ unchanged, b is obtained. The normalized transferred power of the DAB converter depends solely on the Dcontrol vector; thus, pa = pb. As shown in Figure 4, the waveforms of a and b are symmetric with respect to the red axis. The current values at the same time instants tx (x = 0, 1, 2, 3, 4) are identical, indicating that the actual normalized root mean square current values under operating conditions a and b are equal, as also supported by Equation (2).
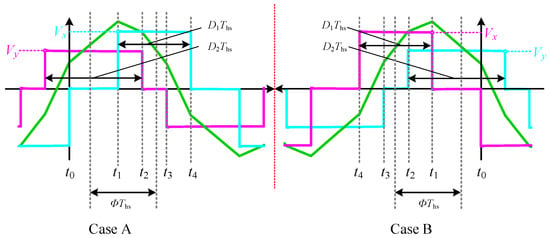
Figure 4.
Operating waveforms under operating conditions a and b.
Generalizing this symmetry, consider the DAB converter operating under condition c in mode D (Table 2), where V1 = Vm and V2 = Vn, with Vm/Vn maintained as 1/k. The ratio of the normalized RMS current values of operating conditions a and c can be derived as follows:

Table 2.
Circuit parameters under three operating conditions.
It is demonstrated that interchanging the DC voltages on the primary and secondary sides, swapping the duty cycles of the transformer AC voltages, and maintaining the phase shift ensures the same normalized power transfer. Moreover, the variation trends of the normalized RMS current with respect to normalized power are consistent across both cases. Based on this, the optimization strategy for forward buck mode can be directly extended to the forward boost case simply by swapping D1 and D2 and replacing k with 1/k.
For mode F, let the control vector take configuration a, where D1, D2, and Φ satisfy the constraints of the mode. Its symmetric counterpart operates under b, which essentially corresponds to mode G. The original and symmetric configurations show similar trends in the normalized RMS current variation, with respect to transferred power.
3. Principle of Proposed SOS-TPS
In the forward buck power transfer mode, the optimization problems for modes F and D are formulated with the RMS current as the objective, subject to mode-specific constraints. First, the optimal control trajectory is obtained by minimizing the RMS current using the Karush–Kuhn–Tucker (KKT) conditions and the Lagrange multiplier method (LMM). Then, the switching current is analyzed to validate or refine the ZVS conditions, leading to the final optimized operating trajectory.
3.1. Modulation Strategy in the Low-Power Range When k > 1
Under light-load conditions in buck mode, the DAB converter operates optimally in mode F. To characterize the relationship among normalized RMS current, normalized transmitted power, and duty cycle boundaries, a Lagrange function is constructed as follows:
Here, λ serves as the Lagrange multiplier associated with the equality constraint, while μ1 corresponds to the multiplier for the inequality constraint. By computing the partial derivatives of the Lagrange function Lf, the following expressions are derived:
By solving (6), the optimal Dcontrol can be written as:
It can be concluded that, for any specified normalized power p and voltage conversion ratio k, there exists a feasible combination of duty cycles D1, D2, and Φ that satisfies the operational constraints. The mathematical relationship among these variables is expressed as:
According to (7), switches S3–S8 fail to achieve ZVS. To address this, a small amount of reactive power is introduced. For mode F, it is always true that iL(t2) > iL(t3); therefore, enforcing iL(t2) + iL(t3) = 0 not only ensures the required polarity for ZVS at t2 and t3 but also provides sufficient magnitude to completely discharge the SiC MOSFETs junction capacitance. Based on the condition iL(t2) + iL(t3) = 0, the following expression can be derived:
According to (9) and the constraints of mode F, it can be deduced that k D1 < D2 < 1. To control the amplitude of iLn(t2), a modulation factor λ is introduced such that 0 < λ < 1 and D2 = λ + kD1 (1 − λ). Thus, the normalized current iLn(t2) can be rewritten as:
The value of λ affects both iLn(t2) and Inrms2. Figure 5a,b illustrate the relationships between the normalized transferred power p and the normalized RMS current Inrms2, as well as those between p and the normalized current stress iLn(t2), respectively, for λ = 0.1, 0.3, 0.5, and 0.7. As shown in Figure 5, for a given transferred power, both Inrms2 and iLn(t2) increase with increasing λ. In practice, a larger iLn(t2) facilitates the realization of ZVS but leads to a higher Inrms2. Therefore, a trade-off in selecting λ is necessary. In this study, λ = 0.5 is adopted.
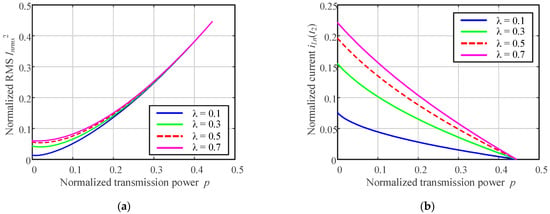
Figure 5.
Influence of λ on the normalized RMS current Inrms2 and the normalized inductor current iLn(t2). (a) Variation of Inrms2 with normalized transmitted power p. (b) Variation of iLn(t2) with normalized transmitted power p.
The normalized transferred power range of mode F is [0, 2(k − 1)/k2]. The final optimal Dcontrol for mode F is given by:
3.2. Modulation Strategy in Medium-Power Range When k > 1
In the buck mode operation of the DAB converter, mode D is selected as the optimal solution. The Lagrange function is formulated to describe the relationship between the normalized RMS current Inrms2, normalized transmitted power p, and duty cycle constraints within the selected switching mode as follows:
Here, λ represents the weight of the equality constraint, while μ1 and μ2 denote the weights of the inequality constraints. By taking the partial derivative of the Lagrange function Lf, the following results can be obtained:
By jointly analyzing (12) and (13), the optimal combination is determined as follows:
When the voltage conversion ratio k > 1, mode D inherently satisfies the current conditions iL(t0) > 0 and iL(t2) < iL(t3) throughout its operation. Therefore, the full ZVS conditions for mode D are designated as iL(t1) < 0 and iL(t2) > 0. By incorporating the ZVS constraints and mode boundary conditions for mode D, the following relation is derived:
Based on (14), a functional relationship among the normalized transferred power p, duty cycle D1, and phase shift Φ in mode D can be established. Taking k = 1.5 as an example, the three-dimensional surface and its two-dimensional projection are depicted in Figure 6. Additionally, as shown in Figure 6, the feasible region of the control variables (D1, Φ) is bounded by the quadrilateral DCIH. The optimal control trajectory remains within this region and gradually approaches the red zone as the transferred power increases. The optimal control trajectory lies entirely within this region and gradually approaches the red area as power increases. According to (14) and (15), the normalized power range for mode D is given by [2(k − 1)/k2, 2(1 − k2 + k(k2 − 1)1/2)], point L corresponds to the minimum normalized transmitted power pL = 2(k − 1)/k2, while point M represents the maximum, given by pM= 2(1 − k2 + k(k2 − 1)1/2).
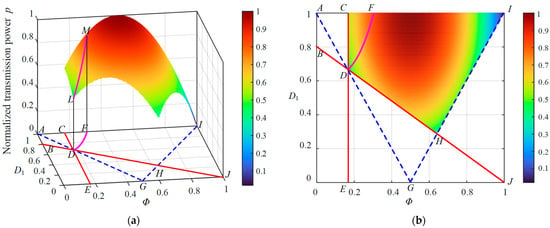
Figure 6.
Optimized operating path in the medium region for k > 1. (a) Three-dimensional visualization of the optimized path. (b) Two-dimensional projection of the optimized path.
The above analysis confirms that for k = 1.5, the optimal trajectory of mode D remains within its ZVS constraints and feasible operating domain. To further investigate the applicability of this trajectory for other k > 1 conditions, the polarity relationship between iLn(t1) and iLn(t2) under different values of k and normalized power p is analyzed based on mode D constraints and Equation (14), as shown in Figure 7.
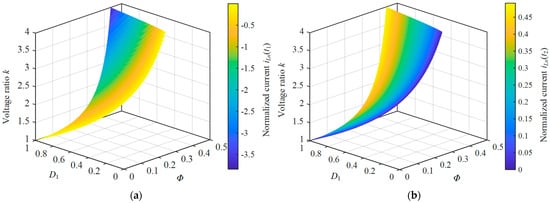
Figure 7.
Variation of iLn(t1) and iLn(t2) with respect to D1, Φ and k. (a) iLn(t1). (b) iLn(t2).
Figure 7 illustrates the feasible solution space of the D1 − Φ domain that satisfies both the mode D operational constraints and the condition given in Equation (13). As shown in the 3D color maps, the conditions iLn(t1) < 0 and iLn(t2) > 0 are consistently satisfied, indicating that the derived optimal trajectory enables ZVS for all switches. It is evident from Figure 7a,b that this polarity relation holds within the range of 1 < k < 4. In fact, by combining Equation (14) with the mode D operational constraints, it can be generally proven that the optimal trajectory ensures full-switch ZVS for any k > 1.
3.3. Modulation Strategy in the High-Power Range When k > 1
Under high-power conditions, the DAB converter operates with conventional single-phase shift (SPS) modulation, and the control variable combination is defined as follows:
Figure 8 illustrates the variation in control parameters D1, D2, and Φ with respect to the normalized transmitted power p. When 0 < p < 2(k − 1)/k2, the converter operates in mode F, and all three parameters (D1, D2, and Φ) increase monotonically with p. At p = 2(k − 1)/k2, D2 reaches one and remains constant thereafter. As p increases further within the range 2(k − 1)/k2 < p < 2(1 − k2 + k(k2 − 1)1/2), the system transitions into mode D, where D2 and Φ continue to increase. When p = 2(1 − k2 + k(k2 − 1)1/2), D1 reaches one and the control scheme evolves into SPS modulation, with the transmitted power solely increasing with Φ. Throughout the entire process, variations in D1, D2, and Φ are continuous without abrupt changes, ensuring smooth transitions between operating modes.
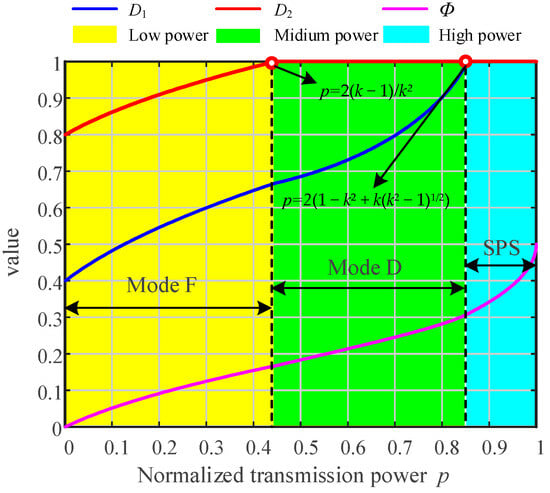
Figure 8.
Variation in D1, D2, and Φ with normalized transmission power p.
3.4. Synopsis of the SOS-TPS Strategy for DAB Converters
As concluded in Section 2.3, the modulation strategy for the forward boost mode can be systematically derived from its buck-mode counterpart by exploiting the inherent structural symmetry of the DAB converter. A summary of the derived results is provided in Table 3.

Table 3.
The SOS-TPS modulation strategy across the full-power range in forward buck and boost modes.
4. Comparative Analysis of ZVS Range and RMS Current in Existing Schemes
Due to the intrinsic symmetry of the DAB converter, the buck and boost modes exhibit similar characteristics under forward power transfer. Therefore, this section provides a comparative analysis of the ZVS range and RMS current performance in buck mode for the SPS [12], GOC [35], UOMS [32] and the proposed SOS-TPS modulation strategies.
4.1. ZVS Range
Figure 9 depicts the two-dimensional operating regions of normalized power p versus the voltage conversion ratio k under SPS, GOC, and UOMS modulation strategies. The green curve marks the transition boundary between partial and full ZVS under SPS modulation. Full-switch ZVS is only achievable when p lies above the curve; in the low-power region, only four switches can achieve ZVS.
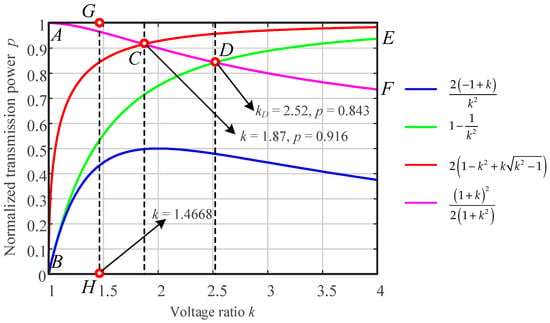
Figure 9.
ZVS region mapping of various modulation strategies.
The blue and red curves jointly define the power regions under GOC modulation. Although the area below the blue curve achieves RMS current minimization, all six switches operate in ZCS, leading to significant turn-on losses under high-frequency conditions, thus limiting efficiency improvement.
The blue and magenta curves define the power regions of the UOMS modulation strategy. Experimental validation on a prototype with k = 1.4668 (operating along line GH) demonstrates that full-switch ZVS can be achieved across the entire load range while maintaining a low RMS current. However, theoretical analysis indicates that when k > 2.52, the DAB converter should transition to SPS in the high-power region. Since SPS cannot achieve full-switch ZVS in region DEF, the applicability of the UOMS modulation strategy is limited to k < kD.
Here, the blue curve defines the low-power boundary. Using the SOS-TPS modulation strategy, full-switch ZVS is achieved in the low-power region while maintaining a low RMS current. In the medium-power region below the red curve, the proposed strategy preserves the RMS current minimization characteristics. For the high-power region, the control naturally transitions to SPS modulation. Overall, the proposed method theoretically enables full-switch ZVS and low RMS current across the entire load range for any k > 1, overcoming the efficiency and applicability limitations of existing modulation strategies.
4.2. RMS Current
A comparative evaluation of the SPS, GOC, Unified, and proposed SOS-TPS modulation strategies is conducted under identical operating conditions to verify the efficiency improvement achieved by the proposed method. In this section, the RMS current is calculated using MATLAB R2020a based on the parameters listed in Table 4.

Table 4.
Design specifications of the DAB converter experimental platform.
Figure 10 illustrates the variation in the normalized RMS current Inrms2 with respect to the normalized transferred power p. In the range 0 < p < 0.3, the Inrms2 values of the SOS-TPS and Unified strategies are slightly higher than that of GOC, primarily due to the introduction of a small amount of reactive power to achieve full-switch ZVS. However, both are significantly lower than that of SPS, which maintains a relatively high Inrms2 throughout the range 0 < p < 0.65. In the range 0.65 < p < 0.75, all four strategies yield comparable RMS current levels. Between 0.75 < p < 0.96, the Unified scheme exhibits a noticeably higher Inrms2 than the other three, which remain nearly identical. At p = 0.96, the UOMS transitions to SPS. For 0.96 < p < 1, all four strategies converge to the same RMS current level as they operate in the SPS mode.
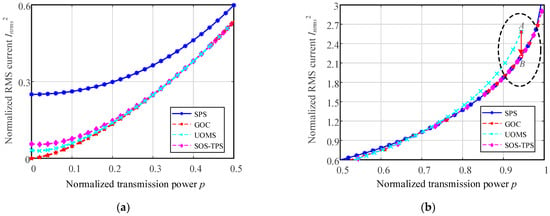
Figure 10.
Normalized RMS current Inrms2 versus normalized transferred power p. (a) 0 < p < 0.5. (b) 0.5 < p < 1.
5. Experimental Verification
To validate the feasibility of the proposed control strategy, as illustrated in Figure 11, an experimental platform based on a DAB converter is established. This section first presents typical operating waveforms and ZVS performance of the SOS-TPS strategy under both buck and boost modes across different power levels. Then, the applicability of SOS-TPS under a wide voltage conversion ratio is demonstrated. Finally, the RMS current and efficiency across the full-power range are compared for SPS, GOC, UOMS, and the proposed SOS-TPS under the forward buck operating mode. According to the aforementioned symmetry characteristics, the DAB converter exhibits similar trends in RMS current and efficiency under the forward boost mode.
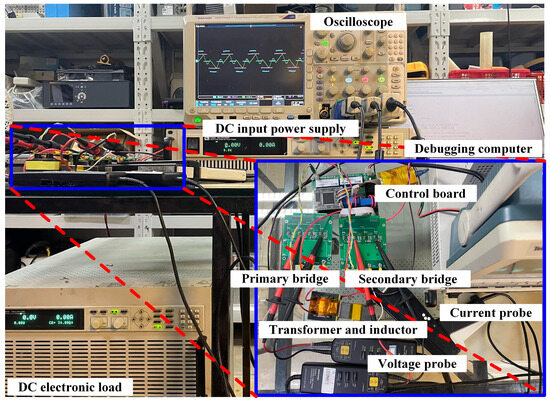
Figure 11.
Experimental setup of the DAB platform.
5.1. Experimental Verification with k > 1
Figure 12, Figure 13 and Figure 14 illustrate the experimental waveforms of the proposed SOS-TPS modulation strategy with a voltage conversion ratio of k = 1.5 (V1 = 80 V, V2 = 53.33 V). The results demonstrate a high degree of consistency between the measured transformer voltage and inductor current waveforms and the theoretical predictions when the DAB converter operates in mode F at 78 W, mode D at 392 W, and SPS modulation at 470 W.

Figure 12.
Experimental waveforms at low power (78 W) using SOS-TPS (V1 = 80 V, V2 = 53.33 V). (a) The waveforms of the voltages and current during operation. (b) Switching waveforms of S1 and S3. (c) Switching waveforms of S5 and S7.

Figure 13.
Experimental waveforms at medium power (392 W) using SOS-TPS (V1 = 80 V, V2 = 53.33 V). (a) The waveforms of the voltages and current during operation. (b) Switching waveforms of S1 and S3. (c) Switching waveforms of S5 and S7.

Figure 14.
Experimental waveforms at high power (470 W) using SOS-TPS (V1 = 80 V, V2 = 53.33 V). (a) The waveforms of the voltages and current during operation. (b) Switching waveforms of S1 and S3. (c) Switching waveforms of S5 and S7.
Figure 15 presents the experimental waveform of the proposed SOS-TPS modulation strategy with a voltage conversion ratio of k = 3 (V1 = 80 V, V2 = 26.66 V). When operating in mode D at an output power of 221 W, the DAB converter demonstrates successful ZVS across all switches. These results confirm that the SOS-TPS modulation strategy maintains full-switch ZVS capability even under high voltage conversion ratio conditions.
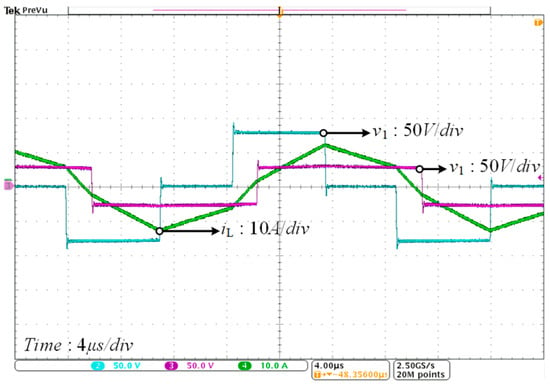
Figure 15.
Experimental waveforms at medium power (221 W) using SOS-TPS (V1 = 80 V, V2 = 26.66 V).
5.2. Experimental Verification with k < 1
The experimental waveforms of the proposed SOS-TPS modulation strategy with a voltage conversion ratio of k = 0.667 (V1 = 80 V, V2 = 120 V) are shown in Figure 16. The results demonstrate that when the converter operates in mode G with an output power of 176 W, mode D with 823 W, and in SPS mode with 1058 W, the transformer voltage and inductor current waveforms closely match the theoretical analysis. Moreover, all switches of the DAB converter successfully achieve ZVS.

Figure 16.
Experimental waveforms using SOS-TPS (V1 = 80 V, V2 = 120 V). (a) Mode G (176 W). (b) Mode D (823 W). (c) SPS (1058 W).
The experimental waveforms of the proposed SOS-TPS modulation strategy with a voltage conversion ratio of k = 1/3 (V1 = 80 V, V2 = 240 V) are shown in Figure 17. When the DAB converter operates in mode D with an output power of 2000 W, all switches successfully achieve ZVS, validating the capability of the SOS-TPS strategy to realize full-switch ZVS even under low-k conditions.
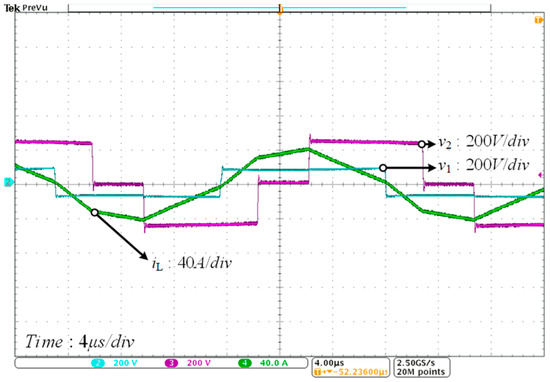
Figure 17.
Experimental waveforms at medium power (2000 W) using SOS-TPS (V1 = 80 V, V2 = 240 V).
5.3. RMS Current and Efficiency
As illustrated in Figure 18a, the RMS current increases with output power p, exhibiting good agreement with the theoretical analysis. Figure 18b presents the measured efficiency across different output power levels. In the low-power region, UOMS and SOS-TPS achieve noticeably higher efficiency compared to GOC and SPS, with GOC slightly outperforming SPS, consistent with theoretical predictions. In the medium-power region, UOMS, GOC, and SOS-TPS maintain marginally higher efficiency than SPS. However, due to the relatively higher RMS current, the efficiency of UOMS slightly decreases in the medium-to-high power range. Near full-load, all strategies converge to SPS modulation, resulting in nearly identical efficiency. In summary, the proposed SOS-TPS enables full-range ZVS and a consistently low RMS current, thereby achieving high efficiency across the entire load range.
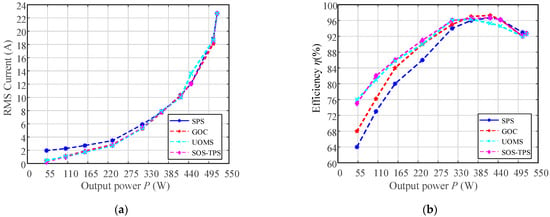
Figure 18.
RMS current and efficiency versus output power p. (a) RMS current versus output power p. (b) Efficiency versus output power p.
6. Conclusions
To address the efficiency limitations of traditional triple-phase shift (TPS) control with ultra-wide voltage conversion ratios and full-load conditions, a symmetric optimized strategy for TPS (SOS-TPS) is proposed based on the structural symmetry of the dual-active bridge (DAB) topology. By employing the Karush–Kuhn–Tucker (KKT) conditions and the Lagrange multiplier method, optimal control trajectories are derived for different power regions: in the low-power region, a modulation factor is introduced to achieve both a low RMS current and full-switch ZVS; in the medium-power region, RMS current minimization is adopted, inherently ensuring ZVS; and in the high-power region, the control naturally transitions to single phase-shift (SPS) modulation while maintaining full-switch ZVS and a low RMS current. Leveraging the intrinsic symmetry of the DAB converter, the control strategy for the forward boost mode can be directly obtained from the buck mode via duty ratio and voltage ratio mapping without additional analysis. Compared to existing modulation schemes, SOS-TPS enables full-switch ZVS and a low RMS current across a wider voltage conversion range and full-load conditions. By jointly optimizing switching and conduction losses, the proposed strategy ensures high efficiency throughout the entire operating range, offering an effective solution for enhancing the performance of high-power-density power electronic systems.
Author Contributions
Conceptualization, L.C.; methodology, L.C.; visualization, L.C.; project administration, Y.Z.; validation, X.W.; writing—review and editing, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by the National Key R&D Program of China (Grant No. 2022YFF0706202).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
All authors thank the editors, referees, and officers of Electronics for their valuable suggestions and help.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DAB | Dual-active bridge (converter) |
| TPS | Triple-phase shift modulation |
| SOS-TPS | Symmetric optimization strategy based on triple-phase shift |
| RMS | Root mean square |
| ZVS | Zero-voltage switching |
| KKT | Karush–Kuhn–Tucker (conditions) |
| LMM | Lagrange multiplier method |
| SPS | Single-phase shift modulation |
| DPS | Dual-phase shift modulation |
| EPS | Extended-phase shift modulation |
| DOFs | Degree of freedoms |
| WBG | Wide bandgap |
| EMC | Electromagnetic compatibility |
| UOMS | Unified optimal modulation strategy |
| GOC | Global optimal condition |
| RL | Reinforcement learning |
| ANN | Artificial neural network |
| AI | Artificial intelligence |
| PSO | Particle swarm optimization |
| FIS | Fuzzy inference system |
References
- Hou, N.; Li, Y.W. A Tunable Power Sharing Control Scheme for the Output-Series DAB DC-DC System With Independent or Common Input Terminals. IEEE Trans. Power Electron. 2019, 34, 9386–9391. [Google Scholar] [CrossRef]
- Tian, J.; Zhuo, C.; Wang, F.; Deng, H. Dual-Side Asymmetric Duty Modulation Based on Accurate Soft-Switching Characteristics Modeling for DAB-Based DC Microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3146–3160. [Google Scholar] [CrossRef]
- Gou, Y.; Zhuo, F.; Wang, F.; Yu, K.; Zhan, C.; Xia, B. Lifetime Estimation of SiC Power Modules in DAB Converter Over Wide-Load Range Considering the Temperature-Dependent Characteristics. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 156–171. [Google Scholar] [CrossRef]
- Tian, J.; Zhuo, C.; Wang, F.; Deng, H. An RMS Current Minimization Method for Three-Level ANPC-DAB-Based Distributed Energy Storage System With Full Operation ZVS. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2388–2405. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.; Du, S.; Dang, H.; Deng, Z.; Chen, H. A T-Type DAB-Based Isolated DC-DC-AC Three-Port Converter With High Power Efficiency. IEEE Trans. Power Electron. 2023, 38, 14178–14194. [Google Scholar] [CrossRef]
- Shah, S.S.; Iyer, V.M.; Bhattacharya, S. Exact Solution of ZVS Boundaries and AC-Port Currents in Dual Active Bridge Type DC-DC Converters. IEEE Trans. Power Electron. 2019, 34, 5043–5047. [Google Scholar] [CrossRef]
- Pan, X.; Rathore, A.K. Novel Bidirectional Snubberless Naturally Commutated Soft-Switching Current-Fed Full-Bridge Isolated DC/DC Converter for Fuel Cell Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 2307–2315. [Google Scholar]
- Xu, G.; Sha, D.; Xu, Y.; Liao, X. Hybrid-Bridge-Based DAB Converter With Voltage Match Control for Wide Voltage Conversion Gain Application. IEEE Trans. Power Electron. 2018, 33, 1378–1388. [Google Scholar] [CrossRef]
- Xu, D.H.; Zhao, C.H.; Fan, H.F. A PWM plus phase-shift control bidirectional DC-DC converter. IEEE Trans. Power Electron. 2004, 19, 666–675. [Google Scholar] [CrossRef]
- Mahdavifard, M.; Mazloum, N.; Zahin, F.; KhakparvarYazdi, A.; Abasian, A.; Khajehoddin, S.A. An Asymmetrical DAB Converter Modulation and Control Systems to Extend the ZVS Range and Improve Efficiency. IEEE Trans. Power Electron. 2022, 37, 12774–12792. [Google Scholar] [CrossRef]
- Wang, M.; Wei, S.; Mou, D.; Wu, P. Research on Efficient Single-Sided Asymmetric Modulation Strategy for Dual Active Bridge Converters in Wide Voltage Range. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5738–5748. [Google Scholar] [CrossRef]
- Krismer, F.; Kolar, J.W. Accurate Small-Signal Model for the Digital Control of an Automotive Bidirectional Dual Active Bridge. IEEE Trans. Power Electron. 2009, 24, 2756–2768. [Google Scholar] [CrossRef]
- Bai, H.; Mi, C. Eliminate Reactive Power and Increase System Efficiency of Isolated Bidirectional Dual-Active-Bridge DC-DC Converters Using Novel Dual-Phase-Shift Control. IEEE Trans. Power Electron. 2008, 23, 2905–2914. [Google Scholar] [CrossRef]
- Zhao, B.; Yu, Q.; Sun, W. Extended-Phase-Shift Control of Isolated Bidirectional DC-DC Converter for Power Distribution in Microgrid. IEEE Trans. Power Electron. 2012, 27, 4667–4680. [Google Scholar] [CrossRef]
- Yu, H.; Hang, L.; Zheng, X.; He, Z.; He, Y.; Shen, L.; Shao, C.; Zeng, P.; Wu, Q.; Yang, X.; et al. Globally Unified ZVS and Quasi-Optimal Minimum Conduction Loss Modulation of DAB Converters. IEEE Trans. Transp. Electrif. 2022, 8, 3989–4000. [Google Scholar] [CrossRef]
- Hou, N.; Song, W.S.; Wu, M.Y. Minimum-Current-Stress Scheme of Dual Active Bridge DC-DC Converter With Unified Phase-Shift Control. IEEE Trans. Power Electron. 2016, 31, 8552–8561. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Y.; Li, Z.; Lei, W. Unified Triple-Phase-Shift Control to Minimize Current Stress and Achieve Full Soft-Switching of Isolated Bidirectional DC-DC Converter. IEEE Trans. Ind. Electron. 2016, 63, 4169–4179. [Google Scholar] [CrossRef]
- Gu, Q.; Yuan, L.; Nie, J.; Sun, J.; Zhao, Z. Current Stress Minimization of Dual-Active-Bridge DC-DC Converter Within the Whole Operating Range. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 129–142. [Google Scholar] [CrossRef]
- An, F.; Song, W.; Yang, K.; Luo, S.; Feng, X. Optimised power control and balance scheme for the output parallel dual-active-bridge DC-DC converters in power electronic traction transformer. IET Power Electron. 2019, 12, 2295–2303. [Google Scholar] [CrossRef]
- Li, L.; Xu, G.; Xiong, W.; Liu, D.; Su, M. An Optimized DPS Control for Dual-Active-Bridge Converters to Secure Full-Load-Range ZVS With Low Current Stress. IEEE Trans. Transp. Electrif. 2022, 8, 1389–1400. [Google Scholar] [CrossRef]
- Li, J.; Luo, Q.M.; Mou, D.; Wei, Y.Q.; Zhang, X.Y. Comprehensive Optimization Modulation Scheme of Low Current Level and Wide ZVS Range for Dual Active Bridge Converter With Dead-Zone Control. IEEE Trans. Power Electron. 2022, 37, 2731–2748. [Google Scholar] [CrossRef]
- Chaurasiya, S.; Singh, B. A Load Adaptive Hybrid DPS Control for DAB to Secure Minimum Current Stress and Full ZVS Operation Over Wide Load and Voltage Conversion Ratio. IEEE Trans. Ind. Appl. 2023, 59, 1901–1911. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Lin, F.; Sun, C.; Mao, K. Artificial-Intelligence-Based Triple Phase Shift Modulation for Dual Active Bridge Converter With Minimized Current Stress. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4430–4441. [Google Scholar] [CrossRef]
- Tian, J.; Wang, F.; Zhuo, F.; Cui, X.; Yang, D. An Optimal Primary-Side Duty Modulation Scheme With Minimum Peak-to-Peak Current Stress for DAB-Based EV Applications. IEEE Trans. Ind. Electron. 2023, 70, 6798–6808. [Google Scholar] [CrossRef]
- Jia, D.; Wang, D. Current Stress Minimization Based on Particle Swarm Optimization for Dual Active Bridge DC-DC Converter. Actuators 2024, 13, 421. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.; Han, Z.; Zhang, C. DAB unified ZVS control strategy with optimal current stress in full power range under TPS control. IET Power Electron. 2024, 17, 2405–2415. [Google Scholar] [CrossRef]
- Naseem, H.; Seok, J.-K. Reactive Power Controller for Single Phase Dual Active Bridge DC–DC Converters. IEEE Access 2023, 11, 141537–141546. [Google Scholar] [CrossRef]
- Zhang, L.; Tu, C.; Xiao, F.; Liu, B.; Li, P. Intrinsic Regularity Analysis and Optimization Control of Current Stress and RMS for Dual-Active Bridge Converter. Electronics 2024, 13, 4802. [Google Scholar] [CrossRef]
- Gong, L.; Jin, X.; Xu, J.; Deng, Z.; Li, H.; Soeiro, T.B.; Wang, Y. A Dynamic ZVS-Guaranteed and Seamless-Mode-Transition Modulation Scheme for the DAB Converter That Maximizes the ZVS Range and Lowers the Inductor RMS Current. IEEE Trans. Power Electron. 2022, 37, 13119–13134. [Google Scholar] [CrossRef]
- Shi, H.; Wen, H.; Chen, J.; Hu, Y.; Jiang, L.; Chen, G. Minimum-Reactive-Power Scheme of Dual-Active-Bridge DC-DC Converter With Three-Level Modulated Phase-Shift Control. IEEE Trans. Ind. Appl. 2017, 53, 5573–5586. [Google Scholar] [CrossRef]
- Shi, H.; Wen, H.; Chen, J.; Hu, Y.; Jiang, L.; Chen, G.; Ma, J. Minimum-Backflow-Power Scheme of DAB-Based Solid-State Transformer With Extended-Phase-Shift Control. IEEE Trans. Ind. Appl. 2018, 54, 3483–3496. [Google Scholar] [CrossRef]
- Li, S.; Yuan, X.; Wang, Z.; Wang, K.; Zhang, Y.; Wu, X. A Unified Optimal Modulation Strategy for DAB Converters to Tradeoff the Backflow Power Reduction and All ZVS in the Full Operating Range. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5701–5723. [Google Scholar] [CrossRef]
- Krismer, F.; Kolar, J.W. Closed Form Solution for Minimum Conduction Loss Modulation of DAB Converters. IEEE Trans. Power Electron. 2012, 27, 174–188. [Google Scholar] [CrossRef]
- Everts, J.; Krismer, F.; Van den Keybus, J.; Driesen, J.; Kolar, J.W. Optimal ZVS Modulation of Single-Phase Single-Stage Bidirectional DAB AC-DC Converters. IEEE Trans. Power Electron. 2014, 29, 3954–3970. [Google Scholar] [CrossRef]
- Tong, A.; Hang, L.; Li, G.; Jiang, X.; Gao, S. Modeling and Analysis of a Dual-Active-Bridge-Isolated Bidirectional DC/DC Converter to Minimize RMS Current With Whole Operating Range. IEEE Trans. Power Electron. 2018, 33, 5302–5316. [Google Scholar] [CrossRef]
- Li, J.; Luo, Q.; Mou, D.; Wei, Y.; Sun, P.; Du, X. A Hybrid Five-Variable Modulation Scheme for Dual-Active-Bridge Converter With Minimal RMS Current. IEEE Trans. Ind. Electron. 2022, 69, 336–346. [Google Scholar] [CrossRef]
- Xie, H.; Cai, F.; Jiang, J.; Li, D. A Fundamental Harmonic Analysis-Based Optimized Scheme for DAB Converters With Lower RMS Current and Wider ZVS Range. IEEE Trans. Transp. Electrif. 2023, 9, 4045–4058. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Lin, F.; Sun, C.; Mao, K. Artificial-Intelligence-Based Hybrid Extended Phase Shift Modulation for the Dual Active Bridge Converter With Full ZVS Range and Optimal Efficiency. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5569–5581. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W. Efficiency Characterization and Optimization of Isolated Bidirectional DC-DC Converter Based on Dual-Phase-Shift Control for DC Distribution Application. IEEE Trans. Power Electron. 2013, 28, 1711–1727. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, Z.Q.; Stone, D.A.; Foster, M.P.; Chu, W.Q.; Urquhart, I.; Greenough, J. Novel Dual-Phase-Shift Control With Bidirectional Inner Phase Shifts for a Dual-Active-Bridge Converter Having Low Surge Current and Stable Power Control. IEEE Trans. Power Electron. 2017, 32, 4095–4106. [Google Scholar] [CrossRef]
- Yan, Y.; Luo, Q.; Luo, T.; Li, J.; Xiong, J.; Xiao, H. Current Stress Optimized Strategy for the Dual-Active-Bridge Converter With Triple-Phase-Shift and Variable DC-Link Voltage Control. IEEE Trans. Power Electron. 2025, 40, 8344–8355. [Google Scholar] [CrossRef]
- Zhang, J.; Sha, D.; Song, K. Single-Phase Single-Stage Bidirectional DAB AC-DC Converter With Extended ZVS Range and High Efficiency. IEEE Trans. Power Electron. 2023, 38, 3803–3811. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Y.; Wang, X.; Zhang, D. An Enhanced Integrated Optimization Strategy for Wide ZVS Operation and Reduced Current Stress Across the Full Load Range in DAB Converters. Appl. Sci. 2025, 15, 7413. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).