Brush Stroke-Based Writing Trajectory Control Model for Robotic Chinese Calligraphy
Abstract
1. Introduction
- By decomposing and refining each writing process, the commonly used control methods and models for “xingbi”, “zhuanbitiaofeng” and “zhebi” are analyzed and built.
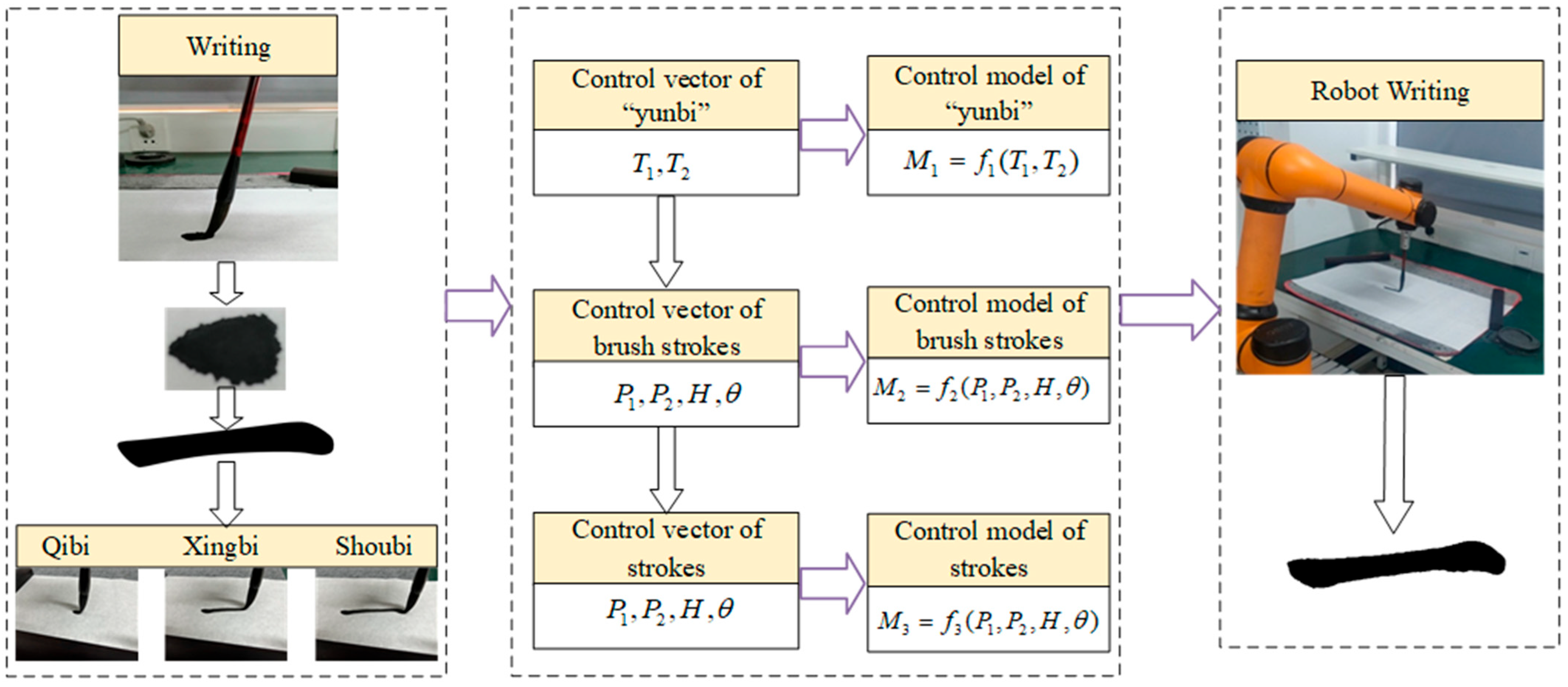
- Based on the existing CCD-BSM, the writing trajectory control models and methods of calligraphy robots are studied and established. According to the writing rules of brush, the corresponding description and representation of the three steps of “qibi”, “yunbi” and “shoubi” are given.
- The fine-grained writing trajectory control models that adhere to the rules of brush calligraphy are proposed. The experimental results show that compared with other models the proposed model has better performance in both basic strokes and Chinese characters with good generalization and robustness.
2. Related Works
- Based on Bézier curve and B-Spline curve
- 2.
- Based on learning control and optimal control
- 3.
- Based on deep learning
3. Methods and Models
3.1. Control Method of “Yunbi”
3.1.1. Control Model for “Xingbi”
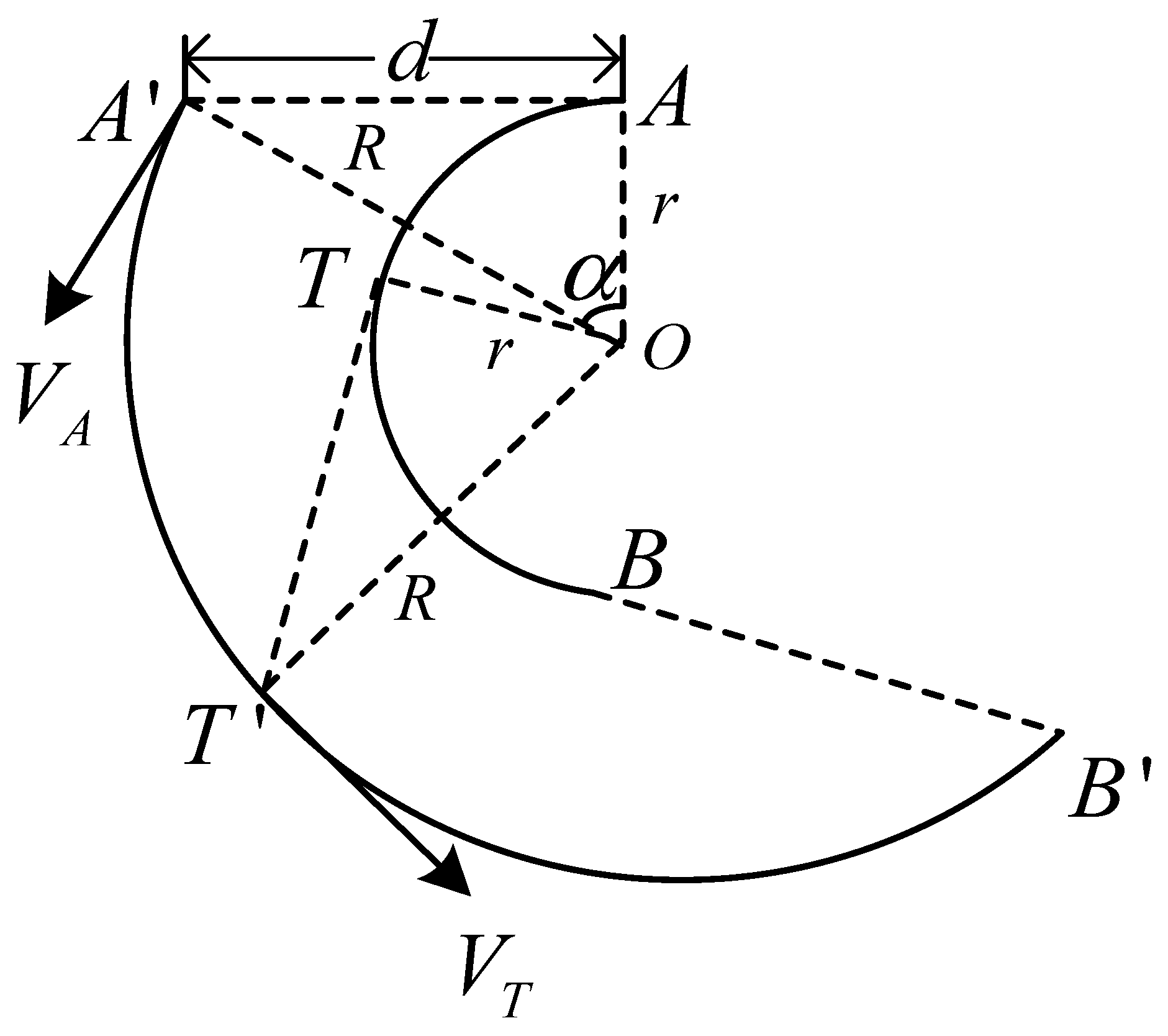
3.1.2. Control Model for “Zhuanbitiaofeng”
3.1.3. Control Model for “Zhebi”
3.2. Control Method of the Brush Stroke Model
3.3. Writing Trajectory Control Models of Strokes
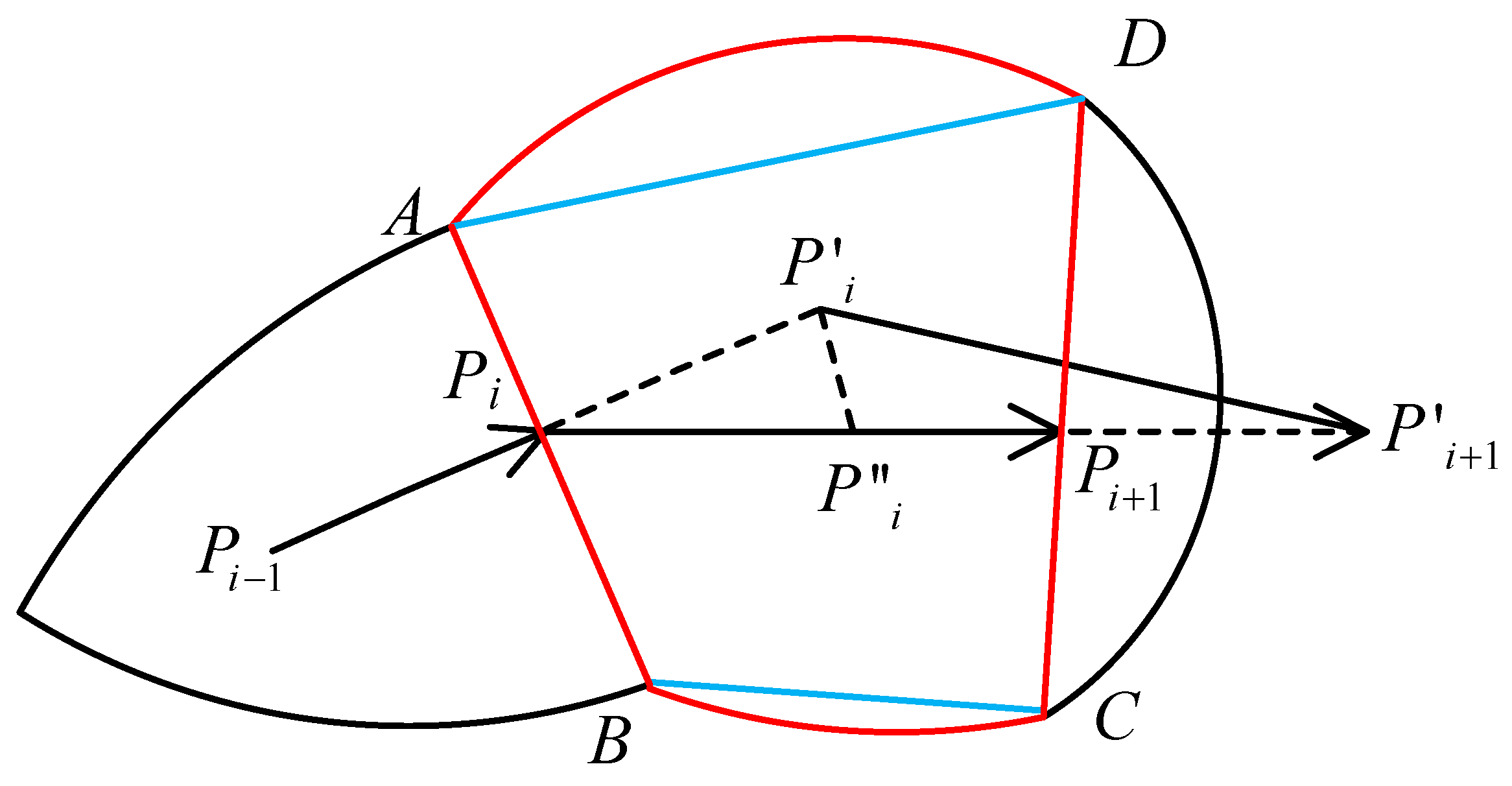
3.3.1. Control Model During the Phase of Stroke Execution
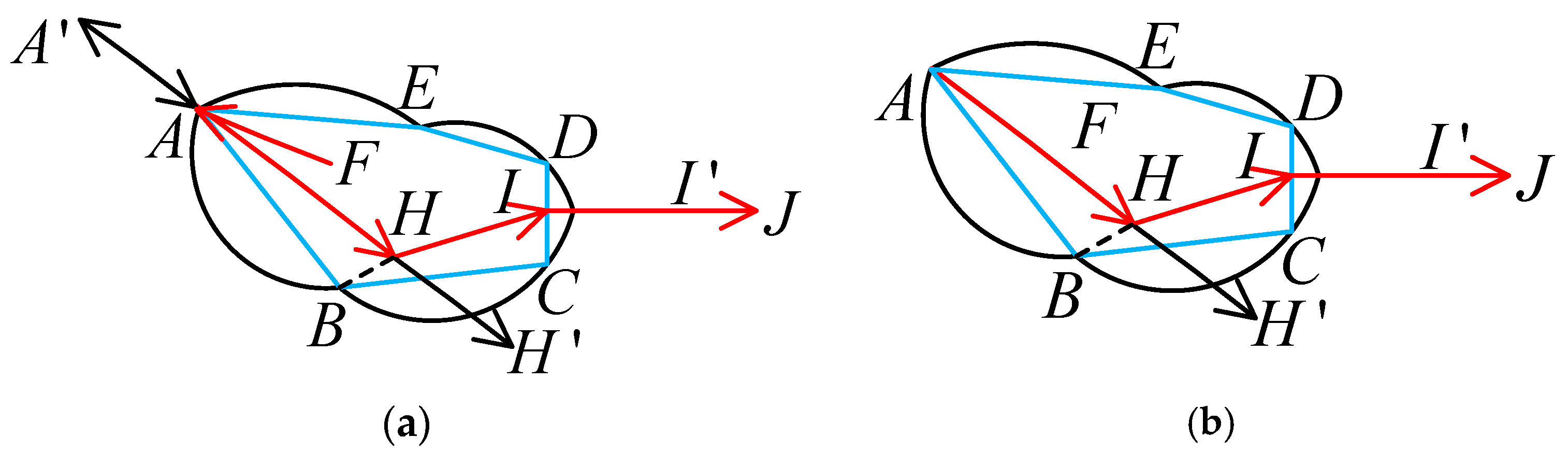
3.3.2. Control Model During the Phase of Stroke Initiation
- “Nifengrubi”
- 2.
- “Shunfengrubi” forward-tip entry
3.3.3. Control Model During the Phase of Stroke Termination
- “Changfengshoubi”—Hidden-Tip Termination
- 2.
- “Loufengshoubi”—Exposed-Tip Termination
4. Experimental Results and Discussion
4.1. Experimental Hardware System
4.2. Robot Writing Test
4.2.1. Writing Test of Basic Strokes
4.2.2. Writing Test of Chinese Characters
4.2.3. Writing Test with Different Brush Pen
4.3. Performance Evaluation
4.3.1. Writing Speed Evaluation
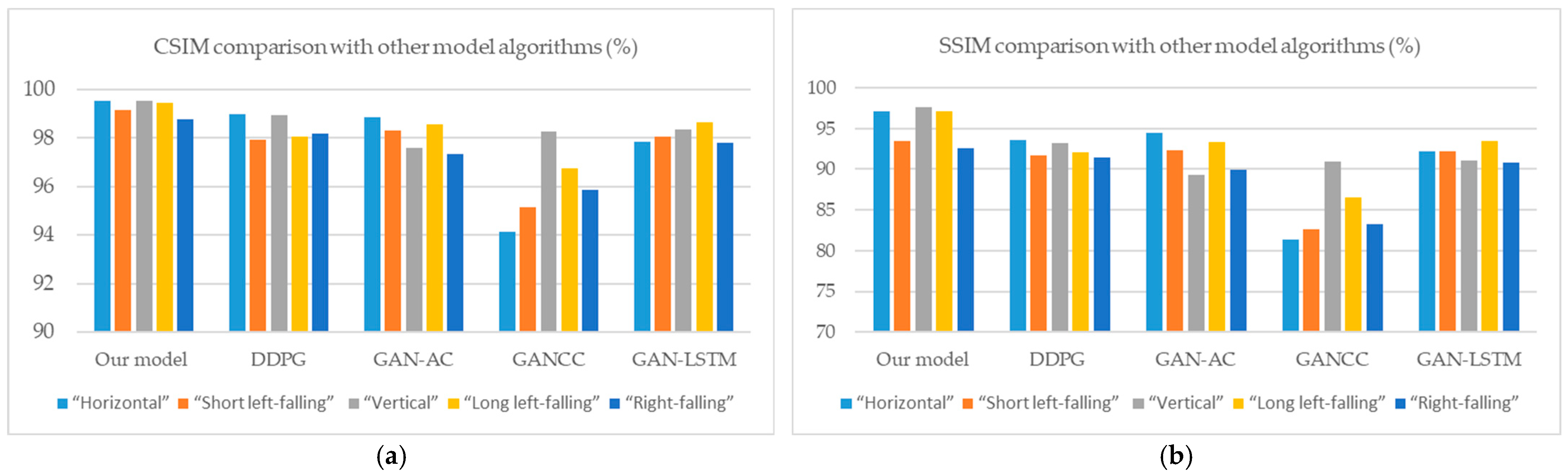
4.3.2. Comparison with Other Model Algorithms
4.3.3. Writing Similarity Evaluation
4.4. Ablation Study
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCD-BSM | Composite-curve-dilation brush stroke model |
| CSIM | Cosine similarity |
| SSIM | Structural similarity index measure |
| DOF | Degree of freedom |
References
- Guo, D.M.; Min, H.S. Survey of calligraphy robot. Control Decis. 2022, 37, 1665–1674. [Google Scholar] [CrossRef]
- Lin, T.T.; She, J. Future Ink: The Collision of AI and Chinese Calligraphy. ACM J. Comput. Cult. Herit. 2025, 18, 1–17. [Google Scholar] [CrossRef]
- Zingrebe, D.S.; Gülzow, J.M. Robotic Writing of Arbitrary Unicode Characters Using Paintbrushes. Robotics 2023, 12, 72. [Google Scholar] [CrossRef]
- Bai, T.; Guo, C. Parallel calligraphy robot: Framework and system implementation. IEEE J. Radio Freq. Identif. 2022, 7, 163–167. [Google Scholar] [CrossRef]
- Mao, Z.; Suzuki, S. Machine learning-enhanced soft robotic system inspired by rectal functions to investigate fecal incontinence. Bio Des. Manuf. 2025, 8, 482–494. [Google Scholar] [CrossRef]
- Aksan, E.; Pece, F.; Hilliges, O. Deepwriting: Making digital ink editable via deep generative modeling. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, Montreal, QC, Canada, 21–26 April 2018. [Google Scholar] [CrossRef]
- Adamik, M.; Goga, J. Fast robotic pencil drawing based on image evolution by means of genetic algorithm. Robot. Auton. Syst. 2022, 148, 103912. [Google Scholar] [CrossRef]
- Karimov, A.; Strelnikov, M. Physically Motivated Model of a Painting Brush for Robotic Painting and Calligraphy. Robotics 2024, 13, 94. [Google Scholar] [CrossRef]
- Wen, Y.; Pagilla, P. A 3D path following control scheme for robot manipulators. IFAC Pap. 2020, 53, 9968–9973. [Google Scholar] [CrossRef]
- Zhenyu, X.; Fujioka, H. Modeling and manipulating dynamic font-based hairy brush characters using control-theoretic B-spline approach. IFAC Pap. OnLine 2020, 53, 4731–4736. [Google Scholar] [CrossRef]
- Peng, Y.H.; Yang, X.Y. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst. Appl. 2025, 264, 125878. [Google Scholar] [CrossRef]
- Chao, F.; Lin, G. An LSTM Based Generative Adversarial Architecture for Robotic Calligraphy Learning System. Sustainability 2020, 12, 9092. [Google Scholar] [CrossRef]
- Wu, R.; Zhou, C. GANCCRobot: Generative adversarial nets based chinese calligraphy robot. Inf. Sci. 2020, 516, 474–490. [Google Scholar] [CrossRef]
- Wu, R.; Zhou, C. Integration of an actor-critic model and generative adversarial networks for a Chinese calligraphy robot. Neurocomputing 2020, 388, 12–23. [Google Scholar] [CrossRef]
- Xiao, Y.; Lei, W. CS-GAN: Cross-structure generative adversarial networks for Chinese calligraphy translation. Knowl.-Based Syst. 2021, 229, 107334. [Google Scholar] [CrossRef]
- Liang, D.; Liang, D. A robot calligraphy writing method based on style transferring algorithm and similarity evaluation. Intell. Serv. Rob. 2020, 13, 137–146. [Google Scholar] [CrossRef]
- Zhou, P.; Zhao, Z. An end-to-end model for Chinese calligraphy generation. Multimed. Tools Appl. 2021, 80, 6737–6754. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y. Intelligent Chinese calligraphy beautification from handwritten characters for robotic writing. Vis. Comput. 2019, 35, 1193–1205. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y. Generative adversarial networks based motion learning towards robotic calligraphy synthesis. CAAI T. Intell. Techno. 2024, 9, 452–466. [Google Scholar] [CrossRef]
- Guo, D.M.; Ye, L. CCD-BSM: Composite-curve-dilation brush stroke model for robotic Chinese calligraphy. Appl. Intell. 2023, 53, 14269–14283. [Google Scholar] [CrossRef]
- Wang, Y.; Min, H. Robot calligraphy system based on brush modeling. CAAI Trans. Intell. Syst. 2021, 16, 707–716. [Google Scholar] [CrossRef]
- Li, J.; Min, H.S.; Zhou, H.T. Robot Brush-Writing System of Chinese Calligraphy Characters. In Proceedings of the International Conference on Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019. [Google Scholar] [CrossRef]
- Yan, G.; Guo, D.M.; Min, H.S. Robot calligraphy based on footprint model and brush trajectory extraction. In Proceedings of the 7th International Conference on Cognitive Systems and Signal Processing, Fuzhou, China, 18–20 November 2023. [Google Scholar] [CrossRef]
- Mueller, S.; Huebel, N.; Waibel, M. Robotic calligraphy—Learning how to write single strokes of Chinese and Japanese characters. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013. [Google Scholar] [CrossRef]
- Lin, H.I.; Chen, X. Calligraphy brush trajectory control of by a robotic arm. Appl. Sci. 2020, 10, 8694. [Google Scholar] [CrossRef]
- Berio, D.; Calinon, S.; Leymarie, F.F. Generating calligraphic trajectories with model predictive control. In Proceedings of the 43rd Graphics Interface Conference, Edmonton, AB, Canada, 16–19 May 2017. [Google Scholar]
- Wu, R.; Chao, F. Internal model control structure inspired robotic calligraphy system. IEEE Trans. Ind. Inf. 2023, 20, 2600–2610. [Google Scholar] [CrossRef]
- Berio, D.; Leymarie, F.F. Interactive generation of calligraphic trajectories from Gaussian mixtures. In Mixture Models and Applications; Springer Nature: Cham, Switzerland, 2020; pp. 23–38. [Google Scholar]
- Berio, D.; Calinon, S.; Leymarie, F.F. Learning dynamic graffiti strokes with a compliant robot. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016. [Google Scholar] [CrossRef]
- Huebel, N.; Mueggler, E.; Waibel, M. Towards robotic calligraphy. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; Deng, X. Robot calligraphy using pseudospectral optimal control in conjunction with a novel dynamic brush model. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar] [CrossRef]
- Ma, Z.; Su, J. Aesthetics evaluation for robotic Chinese calligraphy. IEEE Trans. Cogn. Dev. Syst. 2016, 9, 80–90. [Google Scholar] [CrossRef]



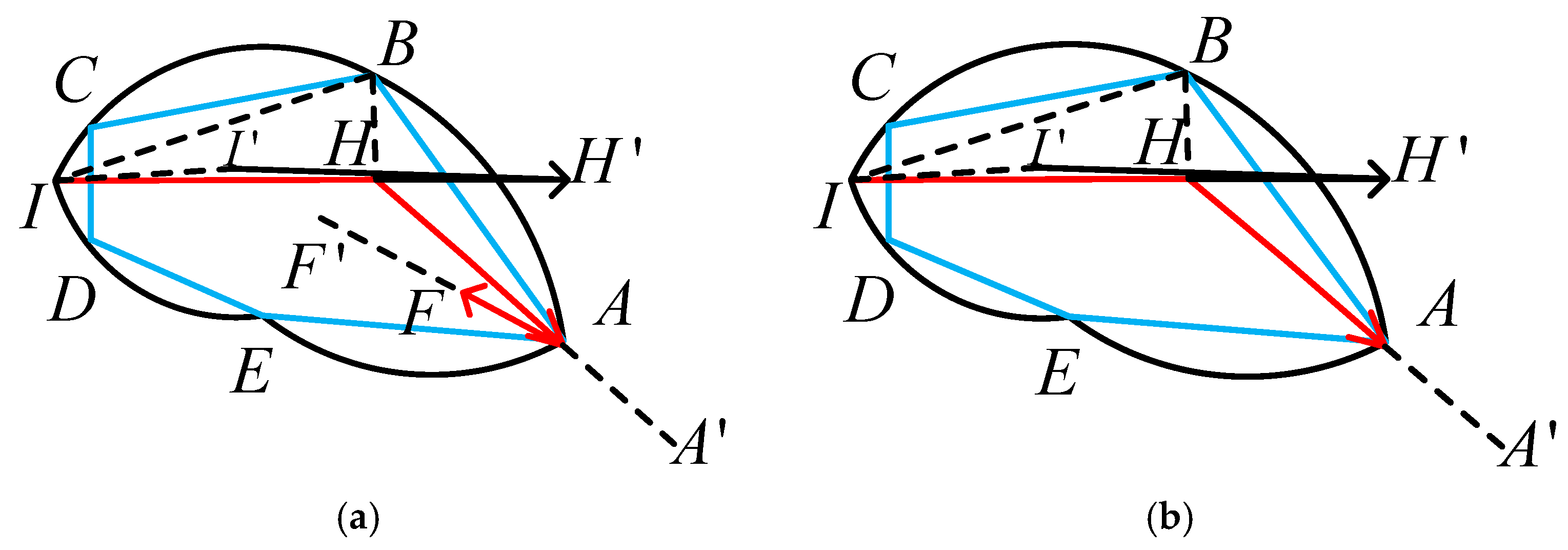







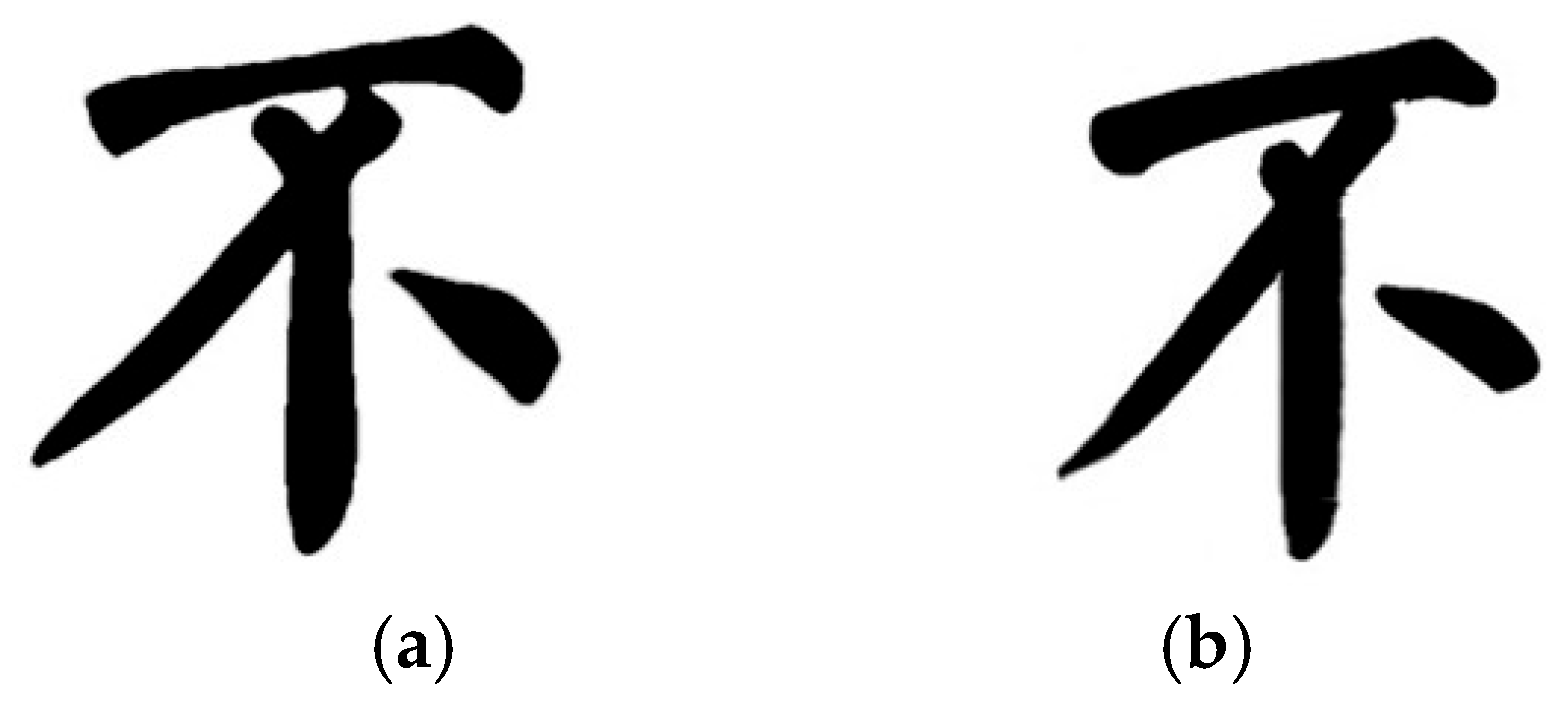





| Strokes | Maximum Speed | Minimum Speed | Range of Variation |
|---|---|---|---|
| “Horizontal” | 22.87 | 21.32 | 1.55 |
| “Short left-falling” | 20.15 | 19.54 | 0.61 |
| “Vertical” | 20.28 | 19.81 | 0.47 |
| “Long left-falling” | 21.66 | 20.23 | 1.43 |
| “Right-falling” | 22.72 | 20.95 | 1.77 |
| System, Model | “Horizontal” | “Short Left-Falling” | “Vertical” | “Long Left-Falling” | “Right-Falling” |
|---|---|---|---|---|---|
| Our model | 99.52 | 99.17 | 99.54 | 99.46 | 98.76 |
| DDPG | 98.97 | 97.94 | 98.95 | 98.04 | 98.17 |
| GAN-AC | 98.85 | 98.31 | 97.61 | 98.58 | 97.34 |
| GANCC | 94.13 | 95.15 | 98.28 | 96.77 | 95.87 |
| GAN-LSTM | 97.86 | 98.06 | 98.37 | 98.66 | 97.80 |
| System, Model | “Horizontal” | “Short Left-Falling” | “Vertical” | “Long Left-Falling” | “Right-Falling” |
|---|---|---|---|---|---|
| Our model | 97.17 | 93.44 | 97.57 | 97.11 | 92.55 |
| DDPG | 93.56 | 91.66 | 93.23 | 92.14 | 91.39 |
| GAN-AC | 94.43 | 92.35 | 89.33 | 93.32 | 89.94 |
| GANCC | 81.39 | 82.59 | 90.90 | 86.55 | 83.23 |
| GAN-LSTM | 92.18 | 92.21 | 91.03 | 93.41 | 90.85 |
| Strokes | CSIM_Max | CSIM_Min | CSIM_Avg | SSIM_Max | SSIM_Min | SSIM_Avg |
|---|---|---|---|---|---|---|
| “Horizontal” | 99.81 | 99.34 | 99.52 | 97.79 | 96.95 | 97.17 |
| “Short left-falling” | 99.31 | 99.06 | 99.17 | 94.32 | 93.16 | 93.44 |
| “Vertical” | 99.88 | 99.40 | 99.54 | 98.06 | 97.27 | 97.57 |
| “Long left-falling” | 99.72 | 99.29 | 99.46 | 97.40 | 96.69 | 97.11 |
| “Right-falling” | 99.01 | 98.33 | 98.76 | 93.56 | 92.20 | 92.55 |
| Characters | CSIM_Max | CSIM_Min | CSIM_Avg | SSIM_Max | SSIM_Min | SSIM_Avg |
|---|---|---|---|---|---|---|
| “bu” | 90.19 | 84.09 | 86.61 | 66.51 | 62.10 | 63.81 |
| “qu” | 95.89 | 86.08 | 88.73 | 73.32 | 64.94 | 68.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Fang, W.; Yang, W. Brush Stroke-Based Writing Trajectory Control Model for Robotic Chinese Calligraphy. Electronics 2025, 14, 3000. https://doi.org/10.3390/electronics14153000
Guo D, Fang W, Yang W. Brush Stroke-Based Writing Trajectory Control Model for Robotic Chinese Calligraphy. Electronics. 2025; 14(15):3000. https://doi.org/10.3390/electronics14153000
Chicago/Turabian StyleGuo, Dongmei, Wenjun Fang, and Wenwen Yang. 2025. "Brush Stroke-Based Writing Trajectory Control Model for Robotic Chinese Calligraphy" Electronics 14, no. 15: 3000. https://doi.org/10.3390/electronics14153000
APA StyleGuo, D., Fang, W., & Yang, W. (2025). Brush Stroke-Based Writing Trajectory Control Model for Robotic Chinese Calligraphy. Electronics, 14(15), 3000. https://doi.org/10.3390/electronics14153000





