Abstract
With the rapid growth of urban populations and the expansion of metro networks, accurate energy consumption prediction has become a critical task for optimizing metro operations and supporting low-carbon city development. Traditional statistical and machine learning methods often struggle to model the complex, nonlinear, and time-varying nature of metro energy data. To address these challenges, this paper proposes MTMM, a novel hybrid model that integrates the multi-head attention mechanism of the Transformer with the efficient, state-space-based Mamba architecture. The Transformer effectively captures long-range temporal dependencies, while Mamba enhances inference speed and reduces complexity. Additionally, the model incorporates multivariate energy features, leveraging the correlations among different energy consumption types to improve predictive performance. Experimental results on real-world data from the Guangzhou Metro demonstrate that MTMM significantly outperforms existing methods in terms of both MAE and MSE. The model also shows strong generalization ability across different prediction lengths and time step configurations, offering a promising solution for intelligent energy management in metro systems.
1. Introduction
With the accelerated pace of global urbanization, urban transportation systems face increasingly severe challenges. The continuous growth of urban populations has rendered traditional transportation modes progressively inadequate to meet rising travel demands, exacerbating issues of traffic congestion, air pollution, and energy consumption [1]. To address these pressing concerns, rail transit systems—particularly metro networks—have emerged as indispensable components of modern urban transportation infrastructure, distinguished by their efficiency, environmental sustainability, and operational reliability. Metro systems demonstrate exceptional passenger throughput capabilities while effectively alleviating surface traffic pressure and enhancing overall urban mobility. An illustration of metro energy prediction and smart dispatch is shown in Figure 1.
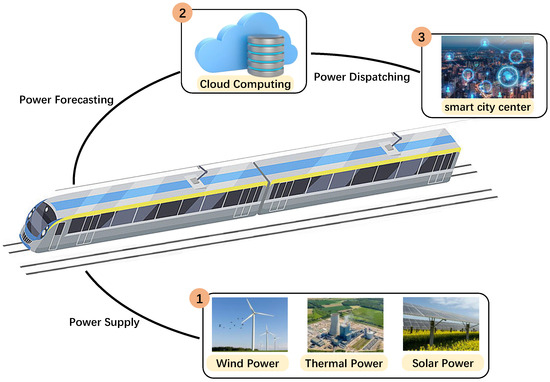
Figure 1.
An illustration of metro energy prediction and smart dispatch.
Globally, metro systems have evolved into primary transportation solutions for major metropolitan areas. According to the International Energy Agency (IEA), rail transit has become a pivotal strategy for global carbon emission reduction and energy conservation [2]. Electrified rail systems exhibit significantly lower energy consumption per passenger-kilometer compared to private vehicles and aircraft, establishing them as one of the most energy-efficient transportation modalities. The combination of high capacity and operational punctuality positions metro systems as crucial enablers for mitigating urban congestion, reducing carbon footprints, and advancing sustainable development goals [3].
The energy consumption of metro systems primarily stems from train traction, station lighting, ventilation, and air conditioning operations. Notably, metro energy demands involve not only the power consumption of operational trains but also the electrical requirements of station facilities including climate control, lighting, and other infrastructure [4]. In many major cities, metro systems have become one of the primary energy consumers in public transportation systems [5]. For metro operators, accurate energy consumption prediction and optimization have become critical for enhancing operational efficiency, reducing energy costs, and achieving sustainable development. For instance, studies indicate that station air conditioning and lighting systems result in a major rate of total energy consumption, particularly during peak hours and extreme weather conditions, leading to elevated energy demands [6,7]. Consequently, precise energy prediction enables operators to rationally allocate resources and minimize energy waste, while also supporting carbon reduction targets and providing data-driven insights for energy-efficient retrofits to address energy security and environmental challenges [8].
Current methods for predicting metro energy consumption mainly fall into three categories: statistical methods, traditional algorithms, and deep learning techniques. Statistical approaches perform well in simple scenarios but show clear limitations when dealing with complex nonlinear relationships [9]. Machine learning methods better capture intricate feature interactions but still face challenges such as overfitting and sensitivity to noisy data [10]. Deep learning models excel in handling sequential data but demand large datasets, high data quality, and substantial computational resources [11]. Consequently, hybrid models that combine the strengths of multiple methods have emerged as a key direction for enhancing prediction accuracy and robustness. Through strategies such as feature extraction, data cleaning, and deep learning architecture optimization, the accuracy of metro energy consumption forecasting can be significantly improved, providing more precise data support for energy optimization and operational scheduling in metro systems.
This paper proposes a novel metro energy consumption prediction framework, the hybrid Mamba–Transformer Metro Energy Consumption Prediction Model (MTMM), which innovatively integrates the Transformer’s multi-head self-attention mechanism with Mamba [12]. Mamba (a selective state space model) is a new type of sequence prediction model proposed in 2023. Drawing on the state space model in control theory, Mamba can quickly model long-sequence features with linear time complexity. The MTMM effectively captures complex temporal dependencies and nonlinear interactions among various types of energy consumption data. Experiments conducted on data from the Guangzhou metro demonstrate that the proposed method significantly outperforms advanced techniques on accuracy and robustness. Further analysis validates the effectiveness of multivariate input modeling and confirms that MTMM generalizes well across different time steps and prediction horizons.
2. Related Work
In recent years, artificial intelligence has experienced rapid development [13,14,15,16,17,18,19,20,21]. With rail transit increasingly becoming the preferred urban mobility solution, the energy consumption of metro stations has gained growing prominence within the building sector. Consequently, enhancing energy utilization efficiency and carbon emission control in metro stations has emerged as a crucial challenge for achieving sustainable development in transportation infrastructure [22]. The formulation of efficient strategies and their implementation are particularly vital for achieving emission reduction targets in metro systems [23]. Within this context, establishing accurate energy consumption prediction mechanisms has become fundamental, serving as the cornerstone for intelligent energy management technologies including safety monitoring, demand response, and optimized control, while providing robust support for green and efficient metro operations [24,25].
2.1. Statistical-Based Energy Consumption Prediction
Statistical methods regarding energy consumption prediction primarily focus on data accumulation, hypothesis testing, explanatory analysis, visualization, and correlation studies. Among these methods, regression models [26,27,28,29] are the most commonly applied in energy prediction tasks. However, traditional time series models have limitations in handling nonlinear patterns, exhibiting weaknesses such as poor nonlinear fitting capability, strong dependence on historical data, and high model complexity.
To address the limitations of single models, Yuan et al. [30] proposed a hybrid forecasting approach that combines Fractional ARIMA (ARFIMA) with Least Squares Support Vector Machines (LSSVMs), successfully applying this complementary method. In another study focused on the seasonal differences in heating system energy consumption, Tingting Fang and colleagues [31] developed a hybrid model by integrating meteorological linear regression with SARIMA. Using hourly meteorological data from Finland, their experiments demonstrated that the model achieved better prediction accuracy compared to existing methods, highlighting its practical applicability.
2.2. Machine Learning-Based Energy Consumption Prediction
By simulating human learning processes, these algorithms acquire new knowledge and skills while continuously optimizing their performance through restructuring existing knowledge frameworks. Divina et al. [32] conducted comparative experiments between statistical and machine learning approaches for time series forecasting, evaluating their performance in short-term electricity consumption prediction tasks. Their study utilized a five-and-a-half-year electricity consumption dataset spanning 13 buildings, demonstrating the superior predictive capabilities of machine learning methods in this context.
Furthermore, Y. Chen et al. [33] employed Support Vector Regression (SVR) models for building electricity load forecasting, incorporating environmental temperature and baseline load information to enhance model performance. A. Bogomolov et al. applied Random Forest Regression (RFR) [34] for energy consumption prediction. Research indicates that such methods can construct complex decision boundaries even with low-dimensional feature spaces [35].
Nevertheless, existing machine learning approaches remain prone to severe overfitting when handling highly complex variable correlations or large-scale datasets. When overfitting occurs, models lose their capacity for accurate long-term energy consumption forecasting, significantly limiting practical generalization capabilities.
2.3. Deep Learning-Based Energy Consumption Prediction
Benefiting from continuous advancements in computational capabilities, deep learning techniques have gained widespread adoption across multiple industries due to their powerful nonlinear mapping capacities and adaptive learning mechanisms.
Series forecasting faces multiple technical challenges, including the multidimensional complexity of data structures, significant heterogeneity among functional zones, and noise interference in sensor-collected data. To overcome these obstacles, researchers have achieved a series of breakthroughs in feature engineering and signal processing techniques [36,37,38,39,40,41,42,43]. The approach of one research team decomposes the original load signals, then builds independent LSTM models to predict each component. In the domain of renewable energy forecasting, Wang’s group [44] developed an EMD–Elman hybrid model that outperforms conventional methods. Mao’s team [45] pioneered a selective feature screening method by integrating entropy weighting with gray relational analysis, significantly enhancing cold load prediction accuracy in high-dimensional feature spaces. Torres and colleagues [46] introduced the Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), which improves noise robustness and convergence while preserving the physical interpretability of mode components, offering clear advantages over traditional EMD techniques [47].
Regarding deep learning architectures, the Transformer model, introduced in 2017 [48], fundamentally transformed sequence modeling by completely abandoning recurrent and convolutional structures. This architecture has achieved outstanding results in time series analysis and computer vision tasks [49]. On the application front, Guo et al. [50] successfully applied the Transformer’s self-attention mechanism to spatiotemporal graph neural networks, greatly improving traffic flow prediction accuracy. Xu and collaborators [51] designed a purely encoder-based Transformer framework, providing a novel approach for extracting spatiotemporal features.
For energy prediction in transportation systems, Lei et al. [52] constructed an Artificial Neural Network (ANN) model to predict energy use and efficiency in the transport sector of developing countries, using Morocco as a case study. Sahraei et al. [53] employed Multivariate Adaptive Regression Splines (MARS) to model and predict Turkey’s transport energy demand based on multiple factors, identifying the best predictive model. Hoxha et al. [54] propose a machine learning stacking ensemble method to predict Turkey’s transport energy demand, comparing multiple algorithms and developing integrated models to boost prediction accuracy.
To address the complexities in metro energy prediction, this paper proposes an enhanced Transformer model integrated with feature extraction techniques and optimized via Mamba architecture. Compared to existing approaches, the proposed model demonstrates significant improvements in Mean Squared Error (MSE) and Mean Absolute Error (MAE) metrics, effectively enhancing prediction accuracy and robustness for metro energy systems.
3. Method
This study proposes a subway energy consumption prediction model based on a hybrid attention mechanism. Mamba is capable of modeling global features with linear time complexity. In large-scale sequence prediction tasks, compared with Transformer, Mamba has obvious advantages in training and inference speed. However, Mamba relies on a hidden state to transmit features and is relatively dependent on the sequence order of the sequence, which may lead to state decay during training and reduce the model’s ability to fit features. Therefore, we have designed a Transformer–Mamba hybrid structure, which combines the advantages of both to achieve accurate prediction of subway power consumption.
Specifically, the multi-head attention mechanism of the Transformer is employed to capture multi-scale features from time series power consumption data, enabling the modeling of variation patterns in multi-source heterogeneous features under diverse spatial and temporal conditions. Furthermore, by integrating the Mamba architecture—characterized by low latency, high throughput, and strong parallelism—we designed a hybrid Mamba–Transformer Metro Energy Consumption Prediction Model (MTMM), as shown in Figure 2.
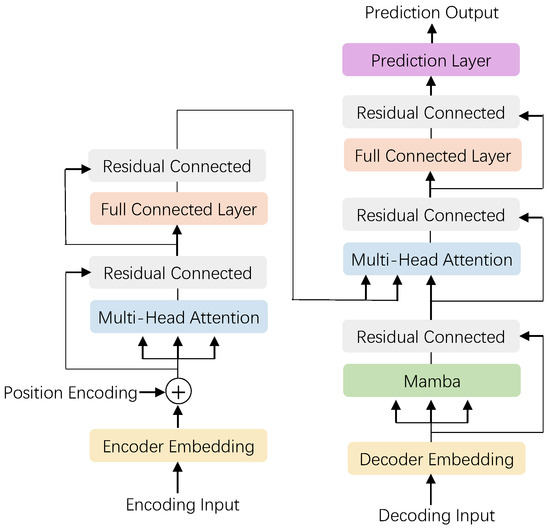
Figure 2.
The structure of MTMM.
3.1. Transformer Attention
To address the nonlinear and time-varying characteristics of load data, this paper employs the Transformer model for feature extraction. Compared with conventional models such as LSTM and GRU, the Transformer is more effective in capturing temporal dependencies within sequences. One limitation of LSTM and GRU networks lies in their encoding process, where, at most, a single hidden state is propagated to the decoding layer, leading to partial information loss. For load prediction tasks, which are typically characterized by high volatility, it is essential to fully utilize the hidden features extracted from earlier time steps. To overcome the limitations of information retention in LSTM and GRU, researchers have proposed attention-based methods that compute the dependencies between input and output sequences using self-attention mechanisms. Unlike recurrent networks, self-attention can model dependencies between any two positions in a sequence, regardless of their distance. The Transformer architecture not only incorporates the self-attention mechanism but also employs deeper network structures, making it more proficient at modeling long-range temporal dependencies. Therefore, by feeding extracted features into the Transformer layer, the model can effectively capture temporal dependencies inherent in the load data.
Each position in the input sequence is projected into a query, key, and value vector. An output vector is then obtained through dot-product operations, followed by a weighted summation.
where denotes the attention output, softmax is the normalization function, and represents the dimensionality of the key vectors.
This paper introduces an innovative enhancement to the conventional self-attention mechanism through a multi-head attention approach. Specifically, the feature vector at each position in the input sequence is divided into H independent sub-vectors. Each of these sub-vector groups undergoes separate attention weight computation and feature extraction. As illustrated in the architecture diagram in Figure 3, this parallel processing framework enables the model to simultaneously capture features at various levels of abstraction, significantly improving its ability to represent features and integrate information.
Figure 3.
The structure of the attention block in Transformer.
Regarding the encoder design, the system employs a stack of N identical modular layers to transform the sequence into higher-level vector representations. Each encoding layer consists of two essential components: a multi-head attention sublayer supporting parallel computation of attention heads and a fully connected feedforward neural network sublayer. It is important to note that, for the I-th encoding layer, the output of the multi-head attention sublayer can be mathematically expressed as follows:
In the multi-head attention mechanism, the symbols are defined as follows: represents the operation of concatenating feature vectors along their dimensions; refers to the output of the i-th independent attention head; and is the output projection matrix responsible for integrating the feature representations from all attention heads. Each attention head, , is generated by training three specific parameter matrices: the query transformation matrix , the key transformation matrix , and the value transformation matrix . These matrices respectively transform the original input into distributed representations.
The feedforward neural network (FFN), a core component of the encoder, applies a nonlinear transformation independently to the features at each position in the sequence. This design, which introduces a multi-layer perceptron with complex mappings, effectively enlarges the model’s representational capacity. The mathematical formulation of this sublayer is expressed as follows:
In this mathematical expression, the parameters are defined as follows: ReLU (Rectified Linear Unit) represents the nonlinear activation function; and are weight matrices that are automatically optimized during model training; and and denote the bias vectors that the network learns autonomously.
3.2. Mamba Attention
Although the Transformer architecture has demonstrated excellent performance and broad application potential in sequential modeling, its core attention mechanism faces inherent limitations. Specifically, when processing long sequences, the computational complexity grows exponentially with sequence length, leading to significantly increased inference time and a rapid expansion in the number of parameters. To address this challenge, recent research has introduced a novel sequence prediction framework called Mamba, which is based on state space modeling (SSMs). This approach achieves a breakthrough in computational efficiency while maintaining high prediction accuracy, modeling with linear time complexity and significantly enhancing the ability to fit long-range dependencies. The Mamba model innovatively integrates deep neural networks with principles from control theory, with its key advancement lying in the selective state space (S6) architecture. This design employs differentiable parameterization to enable dynamic adjustment of the state transition and output matrices. Figure 4 and Figure 5 clearly illustrate the revolutionary structural improvements of Mamba compared to traditional state space models.
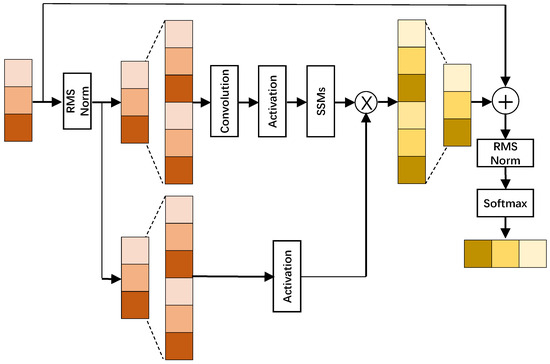
Figure 4.
Illustration of Mamba structure.

Figure 5.
Illustration of SSM structure.
Traditional state space models describe the internal evolution of system states using differential equations and regulate output responses through latent state variables. Mathematically, this can be constructed as
Here, denotes the latent state of the system at time t, and represents the input signal at that time. The model parameters include three learnable matrices: , , and . Considering that real-world applications, such as energy consumption prediction, typically involve discrete-time data, the continuous model is discretized using zero-order hold combined with a fixed sampling interval :
Specifically, the Mamba model first generates two separate components: x and z. A one-dimensional convolution is then performed on x, followed by a SiLU activation function to produce . The structured state matrix A is predefined, while the matrices B and C are obtained by applying linear transformations to . The computation of involves adding a parameter to the result of a broadcasted linear transformation of , followed by applying the Softplus function. The final discrete matrices and are derived through a discretization process. As a result, B, C, and become functions of the input sequence. Although A is independent of the input, the transformation introduces a data-dependent aspect. This mechanism allows Mamba to adapt its behavior based on the input, effectively constructing a dynamic and input-selective model.
4. Experiment
4.1. Implementation Details
This study utilizes energy consumption monitoring data from the Guangzhou Metro. The dataset includes records from 16 metro lines in Guangzhou, categorized into four main types: traction energy consumption, power for lighting and other uses, line losses, and total energy consumption. We constructed data spanning 450 days from January 2020 to December 2021. Among them, 80% of the dataset (from January 2020 to August 2021) was used for model training, and 20% of the data (from September 2021 to December 2021) was used for model testing. Regarding the total electrical energy loss data, we have 7200 data points. Combined with the corresponding traction energy consumption, photo loss, and line loss data, the collected dataset has certain representativeness and can be used to evaluate the performance and robustness of the model.
Based on the data’s dimensionality and scale, the initial parameter settings for the encoder-decoder architecture in the prediction model were established as follows: the hidden layer dimension is set to 24, while the internal layer dimension is set to 12. In order to more fully fit the complex subway electricity consumption data, we set the number of training epochs to 100 and the base learning rate to 0.0005. Specifically, at the beginning of the training, we set the number of warm-up epochs to 5, with the base learning rate during warm-up being 5 × 10−7. We adopt a cosine annealing learning rate decay strategy and set the minimum learning rate to 5 × 10−6. In addition, we set the weight decay to 0.05 and the batch size during training to 64. Our model was trained and tested on an NVIDIA GeForce RTX 3060 graphics card with 12 GB of video memory (Nvidia Corporation, Santa Clara, CA, USA). The operating environment was Python 3.13 and PyTorch 2.0.1.
This study adopts MAE and MSE as the core evaluation metrics. These two indicators reflect prediction accuracy from different perspectives. MAE measures the average absolute distances, providing an intuitive understanding of the prediction error magnitude; MSE, by squaring the errors, amplifies the impact of larger deviations, making it more sensitive to outliers. Mathematically, smaller values of both metrics indicate a better fit and thus reflect stronger predictive capabilities of the model.
The definitions of the parameters used in the formulas are as follows: represents the mean level of absolute errors across all samples, while denotes the expected value of the squared prediction errors. The variable m refers to the total number of samples in the test dataset; a is an index used to iterate over each sample; denotes the actual observed value of the a-th sample, typically obtained from experimental measurements or authoritative data sources; and represents the model’s predicted value for the a-th sample.
4.2. Results
Table 1 presents a subset of experimental results obtained with a time step of 30 and a prediction horizon of 10. Compared to several state-of-the-art methods, the proposed MTMM model demonstrates superior predictive accuracy, achieving an MSE of 0.0321 and an MAE of 0.1338. The results show that MTMM effectively captures the periodic patterns and trend evolutions in typical energy sequences while maintaining low prediction errors across multiple time intervals. This further confirms the model’s capability to learn long-term dependencies and its potential to deliver high-precision results in practical forecasting tasks.

Table 1.
Comparison with other state-of-art methods. The downward arrow indicates that lower MSE and MAE values are better. Blue indicates the best performance.
The various types of energy consumption in the subway system are generated by the same underlying infrastructure and are thus inherently correlated. Relying solely on univariate prediction of total energy consumption may lead to insufficient accuracy. Therefore, in this study, total energy consumption is selected as the target variable, while traction energy, power, lighting and other energy consumption, and line loss are used as covariates. These four types of energy consumption sequences are simultaneously input into the model to predict the trend of total energy consumption. Table 2 presents the results of both univariate and multivariate prediction. It can be observed that multivariate prediction yields higher accuracy than univariate prediction, indicating that leveraging the correlations among different energy consumption types can effectively enhance the model’s predictive performance.

Table 2.
Comparison with multivariate and univariate prediction. The downward arrow indicates that lower MSE and MAE values are better. Blue indicates the best performance.
In practical applications of prediction algorithms, the required prediction length is not fixed. Each input to the prediction model consists of multiple time steps of data. Specifically, given a time series of length z, it is divided into c subsequences of length p, where p denotes the predefined time step size. For each subsequence, the last q time steps are used as the output, while the first time steps are used as the input, forming multiple input–output pairs. This process can be viewed as a sliding window mechanism, where predictions at various temporal resolutions can be achieved by adjusting the size and stride of the window. By varying the size of the input and output, MTMM is able to capture richer temporal features, thereby improving its generalization ability. This approach is particularly effective for handling long time series, as it reduces computational cost without compromising prediction performance
The MTMM prediction performance under different time step sizes and prediction lengths are summarized in Table 3. “Time Step” refers to predicting the subsequent power consumption by combining the variation patterns of 20 data samples during prediction. It can be observed that, when the time step size is fixed, the prediction accuracy decreases as the prediction length increases. Conversely, when the prediction length is fixed, increasing the time step size leads to improved prediction accuracy. The model consistently demonstrates robust predictive performance across various time step and prediction length configurations, indicating strong generalization capability. The parameters of various models are as shown in Table 4.

Table 3.
Performance comparison with different prediction lengths and time steps.

Table 4.
The parameters of various models.
The number of attention heads has a significant impact, particularly in terms of prediction accuracy, model size, and inference speed. If the amount of heads is too low, the model’s performance is limited, potentially leading to increased prediction errors. Conversely, setting too many heads may enhance the model’s representational capacity but also substantially increases the total number of parameters. Moreover, excessive model complexity can lead to overfitting, negatively affecting predictive performance. To explore an appropriate configuration for this hyperparameter, an ablation study on the number of attention heads was conducted (see Figure 6). The experimental results indicate that a total of five heads is the most optimal. Therefore, the proposed MTMM model adopts a five-head self-attention structure to balance prediction accuracy and computational efficiency. In the dataset collected for Guangzhou Metro Line 16, we conducted a comparative analysis of the prediction results in Figure 7 between the ground-truth labels, the MTM-LSTM model, and our proposed MTMM model. In the visualization, the blue curve represents the ground truth, the red curve corresponds to the predictions of MTM-LSTM, and the green curve denotes the predictions of our MTMM model. It is important to note that the performance metrics in this study were calculated based on normalized energy consumption values and reflect the average performance across all metro lines. As such, localized prediction deviations may occur at certain points in the visualization of an individual metro line. In terms of overall fitting accuracy, the proposed MTMM model demonstrates superior performance compared to existing state-of-the-art approaches.
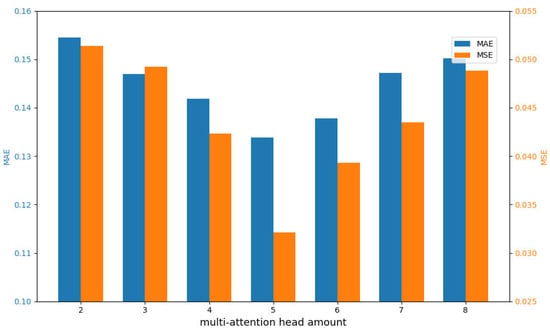
Figure 6.
Comparison based on various attention head amounts.
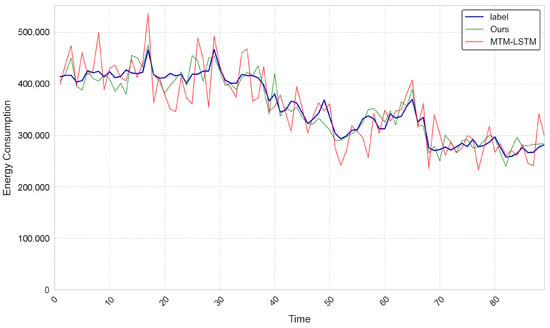
Figure 7.
An illustration of the label, MMTM, and MTM-LSTM energy consumption prediction.
As illustrated in Figure 8, the comparison of MSE and MAE trends during training between MTMM and existing models demonstrates three significant advantages of our approach: its faster convergence speed, greater stability throughout the training process, and superior performance on both evaluation metrics.
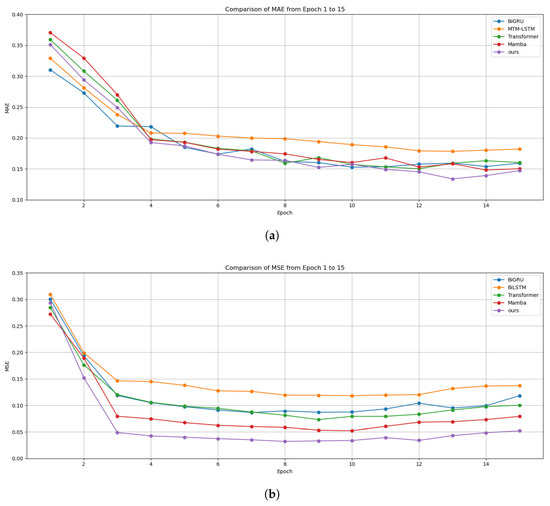
Figure 8.
Illustration of valuation metric trends of our proposed MTMM and other methods: (a) comparison of MAE during training process; (b) comparison of MSE during training process.
4.3. Discussion
We have built a large dataset for subway power consumption prediction which includes 16 subway lines in Guangzhou. These lines cover most areas of Guangzhou, with data from subway stations located near sports venues, large commercial districts, and tourist attractions. The data is characterized by high complexity and diversity. When training on such a dataset, some classical methods like LSTM and GRU show low prediction accuracy in terms of MAE and MSE metrics due to their insufficient ability to fit sequence features. These methods fail to effectively model features in such complex data. In contrast, our method, which combines the Transformer and Mamba structures, can efficiently model global features with linear time complexity. This hybrid structure optimizes the diversity and completeness of feature extraction, enhances the model’s ability to fit complex data, and thereby improves the accuracy of subway power consumption prediction. Moreover, in the comparative experiments between multivariate prediction and univariate prediction using this hybrid structure model, it outperformed existing models, demonstrating certain generalization ability and advancement.
5. Conclusions
With the continuous expansion of urban rail transit systems and the increasing emphasis on energy conservation, emission reduction, and sustainable urban development, accurately forecasting metro energy consumption has become a key research focus in modern urban intelligent management. However, traditional statistical methods fall short in addressing the nonlinear and dynamically fluctuating nature of metro energy data. Meanwhile, existing machine learning and deep learning approaches often struggle to meet the dual demands of predictive performance and computational efficiency in the complex scenarios encountered in real-world metro systems, due to their limited capacity to model temporal dependencies or their high computational cost.
To address these challenges, this study proposes an innovative hybrid prediction model named MTMM. This model combines the strength of the Transformer architecture with the computational efficiency and responsiveness of the Mamba framework. The multi-head attention mechanism in the Transformer component allows the model to fully exploit deep feature patterns in the data, while the Mamba component utilizes a selective state space modeling strategy that reduces computational burden and enhances adaptability to diverse input signals. Additionally, MTMM incorporates a variety of energy consumption sub-features—including traction energy, lighting energy, and line losses—leveraging the intrinsic relationships among them to further improve prediction accuracy and robustness.
A comprehensive set of experiments was conducted using real operational data from the Guangzhou Metro system. The results demonstrate that MTMM outperforms existing mainstream deep learning methods in terms of two key evaluation metrics—MAE and MSE—showcasing superior predictive performance. Specifically, compared with the latest MTM-LSTM model, our MTMM model achieves lower values in terms of MSE and MAE—0.0609 and 0.0446, respectively. Moreover, the model maintains strong generalization and stability across different time granularities and forecasting horizons. These findings confirm the effectiveness and practical potential of MTMM in intelligent metro energy prediction and management. In practical applications, our MTMM needs to pay attention to adjusting the “Time Step” for training and testing to fit data of varying complexities and improve the model’s prediction accuracy. In future work, we need to further consider external variables such as weather conditions and holidays to enhance the generalization ability of the model.
The abbreviations used in this article are as follows:
- IEA: International Energy Agency
- ARFIMA: Fractional ARIMA
- LSSVMs: Least Squares Support Vector Machines
- SVR: Support Vector Regression
- RFR: Random Forest Regression
- CEEMDAN: Complete Ensemble Empirical Mode Decomposition with Adaptive Noise
- ANN: Artificial Neural Network
- MARS: Multivariate Adaptive Regression Splines
- MTMM: Hybrid Mamba–Transformer Metro Energy Consumption Prediction Model
- FFN: Feedforward Neural Network
- SSMs: State Space Modeling
- S6: Selective State Space
- MAE: Mean Absolute Error
- MSE: Mean Squared Error
Author Contributions
Conceptualization, L.L., Z.C. and F.F.; methodology, J.W., Q.F. and Z.Z.; software, Q.F., Z.Z. and R.Z.; validation, J.W., F.F. and R.Z.; formal analysis, Z.C., Z.Z. and R.Z.; investigation, L.L., J.W. and Z.Z.; resources, Z.C., F.F. and R.Z.; data curation, J.W., F.F. and R.Z.; writing—original draft preparation, L.L., Z.Z. and R.Z.; writing—review and editing, Z.C., Z.Z. and R.Z.; visualization, J.W., F.F. and R.Z.; supervision, L.L., Q.F. and R.Z.; project administration, Z.C., Q.F. and R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 62203479), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2022A1515110891), and the Key Scientific Research Projects of China Association of Metros (No. CAMET-KY-202205).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
Authors Liheng Long, Zhiyao Chen and Junqian Wu were employed by the company Guangzhou Metro Design & Research Institute Co., Ltd, Guangdong, China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Han, D.; Wu, S. The capitalization and urbanization effect of subway stations: A network centrality perspective. Transp. Res. Part A Policy Pract. 2023, 176, 103815. [Google Scholar] [CrossRef]
- Su, W.; Li, X.; Zhang, Y.; Zhang, Q.; Wang, T.; Magdziarczyk, M.; Smolinski, A. High-speed rail, technological improvement, and carbon emission efficiency. Transp. Res. Part D Transp. Environ. 2025, 142, 104685. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, N.; Li, M.; Xu, Z.; Wu, D.; Hillmansen, S.; Tsolakis, A.; Blacktop, K.; Roberts, C. A techno-economic analysis of ammonia-fuelled powertrain systems for rail freight. Transp. Res. Part D Transp. Environ. 2023, 119, 103739. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, W.; Liu, Y.; Chen, H.; Skibniewski, M.J. Long-term equilibrium relationship analysis and energy-saving measures of metro energy consumption and its influencing factors based on cointegration theory and an ARDL model. Energy 2023, 263 Pt D, 125965. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T.; Wang, X. Hourly energy consumption characteristics of metro rail transit: Train traction versus station operation. Energy Built Environ. 2023, 4, 568–575. [Google Scholar] [CrossRef]
- Li, H.; Fu, W.; Zhang, H.; Liu, W.; Sun, S.; Zhang, T. Spatio-temporal graph hierarchical learning framework for metro passenger flow prediction across stations and lines. Knowl.-Based Syst. 2025, 311, 113132. [Google Scholar] [CrossRef]
- Kong, G.; Hu, S.; Yang, Q. Uncertainty method and sensitivity analysis for assessment of energy consumption of underground metro station. Sustain. Cities Soc. 2023, 92, 104504. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, Y.; Xia, W.; Cai, W.; Liud, H. Energy Consumption Optimization through Prediction Models in Buildings using Deep Belief Networks and a modified version of Big Bang-Big Crunch Theory. Build. Environ. 2025, 279, 112973. [Google Scholar] [CrossRef]
- Singh, S.K.; Das, A.K.; Singh, S.R.; Racherla, V. Prediction of rail-wheel contact parameters for a metro coach using machine learning. Expert Syst. Appl. 2023, 215, 119343. [Google Scholar] [CrossRef]
- Domala, V.; Kim, T. Application of Empirical Mode Decomposition and Hodrick Prescot filter for the prediction single step and multistep significant wave height with LSTM. Ocean Eng. 2023, 285 Pt 1, 115229. [Google Scholar] [CrossRef]
- Cao, W.; Yu, J.; Chao, M.; Wang, J.; Yang, S.; Zhou, M.; Wang, M. Short-term energy consumption prediction method for educational buildings based on model integration. Energy 2023, 283, 128580. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Huang, S.; Huang, H. AMFFNet: Adaptive Multi-Scale Feature Fusion Network for Urban Image Semantic Segmentation. Electronics 2025, 14, 2344. [Google Scholar] [CrossRef]
- Gao, Z.; Yang, N.; Huang, P.; Xu, W.; Tan, W.; Wu, Z. Self-Calibrating STAP Algorithm for Dictionary Dimensionality Reduction Based on Sparse Bayesian Learning. Electronics 2025, 14, 2350. [Google Scholar] [CrossRef]
- Kao, H.-Y.; Su, L.-Y.; Huang, S.-H.; Cheng, W.-K. A Neural Network Compiler for Efficient Data Storage Optimization in ReRAM-Based DNN Accelerators. Electronics 2025, 14, 2352. [Google Scholar] [CrossRef]
- Fonseca, G.; Marques, G.; Santos, P.A.; Jesus, R. Real-Time Mobile Application for Translating Portuguese Sign Language to Text Using Machine Learning. Electronics 2025, 14, 2351. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.; Yu, J.; Huang, H.; Zhang, R.; Xu, X.; Sheng, B.; Yan, H. DSDformer: An Innovative Transformer-Mamba Framework for Robust High-Precision Driver Distraction Identification. arXiv 2024, arXiv:2409.05587. [Google Scholar]
- Liu, P.; Zhao, J. Part-Attention-Based Pseudo-Label Refinement Reciprocal Compact Loss for Unsupervised Cattle Face Recognition. Electronics 2025, 14, 2343. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, J.; Huang, H.; Chen, J.; Hu, H.; Zhang, R. RNBformer: A High-Performance Roadside Noise Barriers Recognition Algorithm. In Proceedings of the 2024 3rd Asia Conference on Algorithms, Computing and Machine Learning, Shanghai, China, 22–24 March 2024. [Google Scholar]
- Zhao, Y.; Chen, J.; Zhang, Z.; Zhang, R. BA-Net: Bridge Attention for Deep Convolutional Neural Networks. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23 October 2022; pp. 297–312. [Google Scholar]
- Zhang, R.; Zou, R.; Zhao, Y.; Zhang, Z.; Chen, J.; Cao, Y.; Hu, C.; Song, H. BA-Net: Bridge Attention in Deep Neural Networks. Expert Syst. Appl. 2025, 292, 128525. [Google Scholar] [CrossRef]
- Cristino, T.M.; Neto, A.F.; Wurtz, F.; Delinchant, B. The evolution of knowledge and trends within the building energy efficiency field of knowledge. Energies 2022, 15, 691. [Google Scholar] [CrossRef]
- Zhang, L.; Wen, J.; Li, Y.; Chen, J.; Ye, Y.; Fu, Y.; Livingood, W. A review of machine learning in building load prediction. Appl. Energy 2021, 285, 116452. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Ye, Y.; Zuo, W.; Wang, G. A comprehensive review of energy-related data for US commercial buildings. Energy Build. 2019, 186, 126–137. [Google Scholar] [CrossRef]
- Baldacci, L.; Golfarelli, M.; Lombardi, D.; Sami, F. Natural gas consumption forecasting for anomaly detection. Expert Syst. Appl. 2016, 62, 190–201. [Google Scholar] [CrossRef]
- Bilgili, M.; Sahin, B.; Yasar, A.; Simsek, E. Electric energy demands of Turkey in residential and industrial sectors. Renew. Sustain. Energy Rev. 2012, 16, 404–414. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q. Forecasting natural gas demand in China: Logistic modelling analysis. Int. J. Electr. Power Energy Syst. 2016, 77, 25–32. [Google Scholar] [CrossRef]
- Soldo, B.; Potočnik, P.; Šimunović, G.; Šarić, T.; Govekar, E. Improving the residential natural gas consumption forecasting models by using solar radiation. Energy Build. 2014, 69, 498–506. [Google Scholar] [CrossRef]
- Yuan, X.; Tan, Q.; Lei, X.; Yuan, Y.; Wu, X. Wind power prediction using hybrid autoregressive fractionally integrated moving average and least square support vector machine. Energy 2017, 129, 122–137. [Google Scholar] [CrossRef]
- Fang, T.; Lahdelma, R. Evaluation of a multiple linear regression model and SARIMA model in forecasting heat demand for district heating system. Appl. Energy 2016, 179, 544–552. [Google Scholar] [CrossRef]
- Divina, F.; García Torres, M.; Goméz Vela, F.A.; Vázquez Noguera, J.L. A comparative study of time series forecasting methods for short term electric energy consumption prediction in smart buildings. Energies 2019, 12, 1934. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, P.; Chu, Y.; Li, W.; Wu, Y.; Ni, L.; Bao, Y.; Wang, K. Short-term electrical load forecasting using the Support Vector Regression (SVR) model to calculate the demand response baseline for office buildings. Appl. Energy 2017, 195, 659–670. [Google Scholar] [CrossRef]
- Bogomolov, A.; Lepri, B.; Larcher, R.; Antonelli, F.; Pianesi, F.; Pentland, A. Energy consumption prediction using people dynamics derived from cellular network data. EPJ Data Sci. 2016, 5, 1–15. [Google Scholar] [CrossRef]
- Ronao, C.A.; Cho, S.B. Anomalous query access detection in RBAC-administered databases with random forest and PCA. Inf. Sci. 2016, 369, 238–250. [Google Scholar] [CrossRef]
- Karijadi, I.; Chou, S.Y. A hybrid RF-LSTM based on CEEMDAN for improving the accuracy of building energy consumption prediction. Energy Build. 2022, 259, 111908. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Zhang, J.; Mao, S.; Yang, L.; Ma, W.; Li, S.; Gao, Z. Physics-Informed Deep Learning for Traffic State Estimation Based on the Traffic Flow Model and Computational Graph Method. Inf. Fusion 2024, 101, 101971. [Google Scholar] [CrossRef]
- Zhang, J.; Mao, S.; Zhang, S.; Yin, J.; Yang, L.; Gao, Z. EF-Former for Short-Term Passenger Flow Prediction During Large-Scale Events in Urban Rail Transit Systems. Inf. Fusion 2025, 117, 102916. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, J.; Yang, L.; Han, K.; Yang, X.; Gao, Z. Spatial–temporal multi-task learning for short-term passenger inflow and outflow prediction on holidays in urban rail transit systems. Transportation 2025. [Google Scholar] [CrossRef]
- Fernandes, T.; Magalhães, J.P.; Alves, W. Cybersecurity in Smart Railways: Exploring Risks, Vulnerabilities and Mitigation in the Data Communication Services. Green Energy Intell. Transp. 2025, 4, 100305. [Google Scholar] [CrossRef]
- Ray, S.; Kasturi, K.; Nayak, M.R. Multi-Objective Electric Vehicle Charge Scheduling for Photovoltaic and Battery Energy Storage Based Electric Vehicle Charging Stations in Distribution Network. Green Energy Intell. Transp. 2025, 4, 100296. [Google Scholar] [CrossRef]
- Cicek, D.; Kantarci, B.; Schillo, S. A Comparative Review of User Acceptance Factors for Drones and Sidewalk Robots in Autonomous Last Mile Delivery. Green Energy Intell. Transp. 2025, 4, 100310. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Li, Y.; Wang, J.; Dang, Z. Forecasting wind speed using empirical mode decomposition and Elman neural network. Appl. Soft Comput. 2014, 23, 452–459. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, J.; Zhang, N.; Dong, F.; Wang, M.; Li, X. A hybrid model of commercial building cooling load prediction based on the improved NCHHO-FENN algorithm. J. Build. Eng. 2023, 78, 107660. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Lin, Z. Short-term prediction of building sub-item energy consumption based on the CEEMDAN-BiLSTM method. Front. Energy Res. 2022, 10, 908544. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient transformers: A survey. ACM Comput. Surv. 2022, 55, 1–28. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Wan, H.; Li, X.; Cong, G. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting. IEEE Trans. Knowl. Data Eng. 2021, 34, 5415–5428. [Google Scholar] [CrossRef]
- Xu, M.; Dai, W.; Liu, C.; Gao, X.; Lin, W.; Qi, G.; Xiong, H. Spatial-temporal transformer networks for traffic flow forecasting. arXiv 2020, arXiv:2001.02908. [Google Scholar]
- Lei, H.; Guo, Y.; Khan, N. Forecasting energy use and efficiency in transportation: Predictive scenarios from ANN models. Int. J. Hydrogen Energy 2025, 106, 1373–1384. [Google Scholar] [CrossRef]
- Sahraei, M.A.; Duman, H.; Çodur, M.Y.; Eyduran, E. Prediction of transportation energy demand: Multivariate adaptive regression splines. Energy 2021, 224, 120090. [Google Scholar] [CrossRef]
- Hoxha, J.; Çodur, M.Y.; Mustafaraj, E.; Kanj, H.; El Masri, A. Prediction of transportation energy demand in Türkiye using stacking ensemble models: Methodology and comparative analysis. Appl. Energy 2023, 350, 121765. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- He, K.; Yang, Q.; Ji, L.; Zhang, X.; Liu, S. Financial time series forecasting with the deep learning ensemble model. Mathematics 2023, 11, 1054. [Google Scholar] [CrossRef]
- Mohammadi, M.; Jamshidi, S.; Rezvanian, A.; Sadeghi-Niaraki, A. Advanced fusion of MTM-LSTM and MLP models for time series forecasting: An application for forecasting the solar radiation. Meas. Sens. 2024, 33, 101179. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).