Abstract
This study proposes an optimized approach to address the high computational demands and significant GPU memory consumption commonly associated with Transformer-based models. Building upon the HAT framework, a shallow feature extraction module is enhanced to improve local feature representation, thereby achieving a better balance between computational efficiency and model performance. Furthermore, inspired by self-supervised learning (SSL) techniques and incorporating shift operations, the proposed method effectively reduces both the number of parameters and the overall computational load. The resulting ISR-SHA model is trained and evaluated on the DF2K dataset, achieving approximately a 30% reduction in FLOPs and parameter count compared to the original HAT model, with only marginal declines in PSNR (0.02) and SSIM (0.0006). Experimental results confirm that ISR-SHA outperforms most existing super-resolution models in terms of performance while significantly enhancing computational efficiency without compromising output quality.
1. Introduction
Previous image restoration methods have predominantly relied on Convolutional Neural Networks (CNNs) and Generative Adversarial Networks (GANs). CNNs have attracted considerable attention due to their strong feature extraction capabilities, particularly in capturing spatial information within images. By applying multiple layers of convolution and pooling operations, CNNs are able to extract hierarchical representations, making them effective across a wide range of image processing tasks. However, their performance tends to degrade in complex scenes requiring fine-grained detail. Under challenging conditions such as lighting variations, occlusions, and background noise, CNNs often struggle to capture global contextual information, resulting in a noticeable decline in restoration quality. In contrast, Generative Adversarial Networks (GANs) constitute a distinct class of generative models known for their ability to produce high-fidelity synthetic images. Their core mechanism involves a competitive training process between a generator and a discriminator, allowing GANs to learn the underlying data distribution and generate realistic outputs. Despite their impressive image generation performance, GANs suffer from training instability and are prone to mode collapse, limiting their effectiveness in complex image restoration scenarios. With the recent success of Transformer models in natural language processing and related fields, researchers have increasingly investigated their applicability in image processing tasks, particularly in image super-resolution. Transformers are characterized by their self-attention mechanisms, which excel at modeling long-range dependencies within input sequences. This capability offers a significant advantage in image reconstruction, enabling the model to better capture global contextual information. Compared to traditional CNNs, Transformer-based models demonstrate a superior ability to analyze and interpret complex image structures, thereby enhancing restoration performance in visually intricate scenarios.
The primary contribution of this study is the introduction of a Transformer-based super-resolution model, referred to as ISR-SHA. This model leverages shifting operations and hybrid attention techniques to improve image reconstruction efficiency. The central idea of this research is to fully exploit the global perceptual capabilities of Transformers to capture long-range dependencies in images, which is crucial to improving the quality of image reconstruction. Furthermore, to address the high computational demands associated with Transformer models, this study adopts the HAT model as its foundational architecture. It proposes a relatively simple solution to reduce FLOPs (floating-point operations) and the number of parameters without significantly altering the fundamental structure of the Transformer super-resolution model, thereby enhancing its feasibility in practical applications.
During the research process, considering the complexity of deep feature extraction modules, the researchers particularly focused on utilizing shifting operations to achieve a balance between performance and computational cost. Shifting operations serve as an effective technique to enhance the model’s feature capture capabilities without significantly increasing the computational burden. This research direction is not only significant for improving the performance of Transformers in super-resolution tasks but also provides new insights and methods for subsequent studies.
This study used the DF2K dataset for training and validation, with results indicating a significant reduction in both FLOP and parameter counts for ISR-SHA compared to the HAT model. Despite the decrease in computational demands, the model maintains stable performance metrics. Experimental results demonstrate that ISR-SHA continues to surpass the majority of super-resolution models while maintaining its performance levels, even under reduced computational costs that impact practicality, thereby facilitating the further advancement of image processing technologies.
2. Related Work
This chapter provides an overview of essential techniques underlying recent advances in image super-resolution (SR). Deep networks, particularly CNNs, have revolutionized SR by learning mappings between low- and high-quality images, with foundational models like SRCNN leading the way. The Transformer architecture, adapted from natural language processing to computer vision tasks, further enhances SR by capturing complex global interactions, as demonstrated by the Vision Transformer (ViT). Additionally, the Hybrid Attention Transformer (HAT) integrates channel and window-based self-attention to improve both feature extraction and computational efficiency. Finally, techniques like shift operation and ShiftNet are introduced to address computational constraints, especially for resource-limited devices. Together, these components form the basis for understanding and advancing SR techniques.
2.1. Deep Networks for Image SR
Compared to traditional model-based image restoration approaches [1,2,3], learning-based methods, particularly those using CNN, have gained increasing favor due to their exceptional performance. These methods typically learn mappings between low- and high-quality images from extensive datasets. Chao Dong et al. achieved a notable breakthrough in applying deep convolutional neural networks to super-resolution tasks with the introduction of SRCNN (Super-Resolution Convolutional Neural Network) [4]. The core structure of SRCNN involves extracting features from low-quality images, building a non-linear mapping using convolutional layers and activation functions, and reconstructing the mapped features to generate high-quality images. Building upon SRCNN’s fundamental concept, numerous deep networks have since emerged, further enhancing the quality of reconstructed images [5,6,7,8,9].
One prominent example is VDSR (Very Deep Super-Resolution) [6], whose architecture deepens the convolutional layers of SRCNN, thus expanding the receptive field and producing higher quality reconstructions. In addition, many models have adopted more refined convolutional module designs, such as residual blocks [7,10] and dense blocks [11], to improve model performance. A classic model leveraging residual blocks is EDSR (Enhanced Deep Residual Networks for Single Image Super-Resolution) [7], which removes unnecessary modules in conventional residual networks and increases the model parameters, achieving significant performance gains and securing first place in the NTIRE 2017 competition. EDSR further proposes MDSR (Multi-Scale Deep Super-Resolution) [6], a deep super-resolution model designed for multi-scale applications.
To enhance perceptual quality, GANs have also been increasingly applied to super-resolution tasks. A notable example is SRGAN (Super-Resolution Generative Adversarial Network) [10], which produces high-resolution images with realistic textures through a Min–Max process between the generator and the discriminator, coupled with a content loss function. Recently, a series of Transformer-based networks have been introduced, continually advancing the state-of-the-art in super-resolution tasks and showcasing the powerful representational capacity of Transformers.
To further elucidate the mechanisms of super-resolution networks, several studies have proposed analytical and interpretive methods. LAM [12] employs integrated gradients to identify which input pixels contribute the most to the final performance. DDR [13] reveals deep semantic representations within super-resolution networks through dimensionality reduction and visualization of deep features. FAIG [14] aims to discover specific degradation discriminatory filters for blind super-resolution. RDSR [15] uses channel saliency maps to demonstrate how dropout can help prevent co-adaptation in real super-resolution networks. SRGA [16] is focused on evaluating the generalizability of super-resolution methods.
This progression illustrates the dynamic advancements in super-resolution techniques, with CNNs, GANs, and Transformers contributing significant breakthroughs in the field.
2.2. Vision Transformer
The Transformer architecture has recently garnered significant attention in computer vision. Initially designed for neural machine translation, it has since been successfully applied to image classification, object detection, segmentation, and image quality assessment (IQA). A pioneering example in adapting Transformers for image classification is the Vision Transformer (ViT) [17] shown in Figure 1, which leverages the attention mechanism to focus on important regions within images, capturing complex global interactions effectively. Due to its strong performance, Transformers have also been integrated into image restoration tasks.
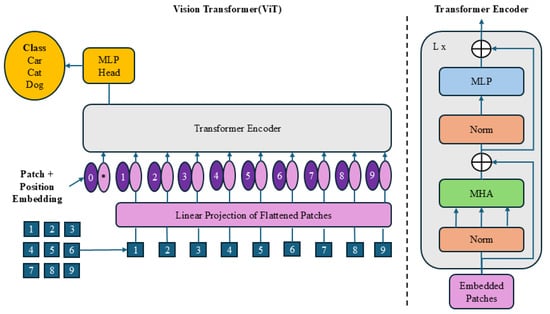
Figure 1.
Vision Transformer architecture.
Recently, Chen et al. introduced IPT [18], a versatile backbone model for multiple image restoration tasks based on the standard Transformer architecture. While IPT demonstrates exceptional performance across tasks, it requires a large parameter count (over 115.5 million parameters) and substantial computational resources, necessitating large-scale datasets such as ImageNet (with over 1 million images) to achieve optimal results. To address computational demands, Cao et al. proposed the VSR-Transformer [19], combining self-attention mechanisms with CNN-based feature extraction to better capture and fuse features for image super-resolution. Notably, many Transformer-based approaches, such as IPT and VSR-Transformer, utilize patch-wise attention, which may not be ideal for image restoration tasks.
In 2021, Liang et al. introduced SwinIR [20], based on the Swin Transformer [21], specifically tailored for image restoration tasks and achieving state-of-the-art results across various restoration applications. The Swin Transformer architecture [21] improves upon the Vision Transformer [17] by utilizing a shifted window-based self-attention mechanism and progressively downsampling image representations. Windowed self-attention is computed on non-overlapping image patches, reducing the complexity of attention calculations from Equation (1) to Equation (2), enabling a more efficient approach to image restoration.
For an image of size and patches of size , when M is fixed, the quadratic computational complexity of the former is reduced to linear complexity. Additionally, learned relative positional biases are incorporated to encode spatial information, calculating similarity for each attention head.
The Swin Transformer V2 [22] further refines the Swin Attention module, optimizing it for better scalability in model capacity and window resolution. Key modifications include replacing pre-normalization with post-normalization, introducing scaled cosine attention instead of dot-product attention and adopting a log-spaced continuous relative positional bias method over the previous parameterized approach. The resulting attention output is defined as follows:
In this setup, represent the query, key, and value matrices, respectively. The relative positional bias is calculated with respect to absolute positional embeddings and obtained by re-indexing the positional offsets. Here, is a learnable scalar parameter.
2.3. Hybrid Attention Transformer
The Hybrid Attention Transformer (HAT) for Image Restoration effectively combines Channel Attention and Window-Based Self-Attention to enhance both feature refinement and computational efficiency. This approach leverages the strengths of each attention type to restore images by emphasizing relevant features while maintaining a manageable computational load.
2.3.1. Channel Attention
Channel Attention is designed to dynamically recalibrate feature responses along the channel dimension, which allows the model to prioritize informative channels. Given an input feature map , where H, W, and C represent the height, width, and number of channels, Channel Attention typically applies a combination of global pooling and fully connected layers. The recalibration can be mathematically expressed as follows:
where and are learnable weight matrices, denotes the sigmoid function, and ⊙ represents element-wise multiplication. The global pooling condenses spatial information, allowing the model to focus on essential channel features, enhancing feature selectivity for image details and textures critical for restoration tasks.
2.3.2. Window-Based Self-Attention
Window-Based Self-Attention divides an image into smaller, non-overlapping windows, applying self-attention locally within each window rather than across the entire image. This approach reduces the computational complexity of standard self-attention, making it more efficient for high-resolution images. If we denote each window as where is the window size, then the attention within a window is computed as follows:
where , , and represent the query, key, and value matrices within the window, respectively, and is the dimensionality of the keys. By limiting attention to localized regions, Window-Based Self-Attention reduces computational complexity from to , making it scalable while retaining spatial correlations within each window.
2.3.3. The Hybrid Mechanism
The HAT model integrates Channel Attention and Window-Based Self-Attention to combine the strengths of both. Formally, the Hybrid Attention in HAT can be represented as follows:
This combined approach ensures that each spatial region receives focused attention within windows, while the model remains sensitive to the channel-wise information, enhancing its ability to preserve fine details and textures. Consequently, HAT provides both global context and localized detail handling, crucial for high-quality image restoration without excessive computational demands.
2.4. Shift Operation
Convolutional neural networks (CNNs) have become ubiquitous in computer vision tasks, including image classification, object detection, face recognition, and style transfer. These tasks enable various emerging mobile applications and Internet of Things (IoT) devices. However, such devices face significant memory constraints and limitations on the size of over-the-air (OTA) updates, typically ranging from 100 to 150 MB. These restrictions impose limits on the size of CNNs employed in these applications, making it essential to reduce model size while maintaining accuracy.
CNNs mainly rely on spatial convolutions with kernel sizes of 3 × 3 or larger to aggregate spatial information within images. However, these spatial convolutions are computationally and memory-intensive, with quadratic increases in computation and model size as kernel size grows. For example, in the VGG-16 model [23], 3 × 3 convolutions account for 15 million parameters, while the first fully connected layer (fc1 layer), essentially a 7 × 7 convolution, comprises over 102 million parameters.
Several strategies have been implemented to reduce the size of spatial convolutions. ResNet [24] utilizes a bottleneck module, placing two 1 × 1 convolutions before and after a 3 × 3 convolution to reduce input and output channels. Despite this, 3 × 3 convolution layers still account for approximately 50% of all parameters in ResNet models with bottleneck modules. SqueezeNet [25] adopts a fire module, concatenating the outputs of 3 × 3 and 1 × 1 convolutions along the channel dimension.
Recent architectures, such as ResNext [26], MobileNet [27], and Xception [28], employ group convolutions and depth-wise separable convolutions as alternatives to standard spatial convolutions. While depth-wise separable convolutions (in Figure 2) theoretically reduce computation, their practical implementation is challenging due to their low arithmetic intensity (FLOPs-to-memory access ratio), limiting efficient hardware utilization. ShuffleNet [29] (in Figure 3) combines depth-wise separable convolutions, pointwise convolution, and channel-wise shuffling, further reducing parameters and complexity. Inspired by separable convolutions, it freezes spatial convolutions, learning only pointwise convolutions. This reduces the number of learnable parameters without decreasing FLOPs or model size.
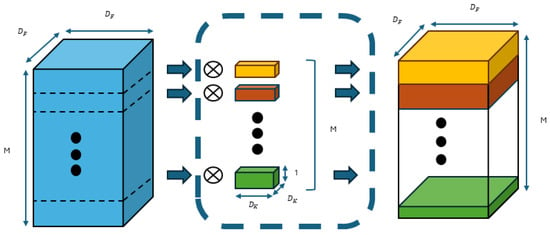
Figure 2.
Depth-wise separable convolutions architecture.
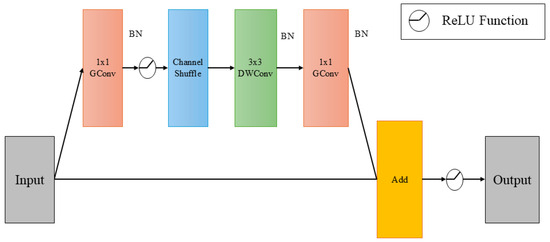
Figure 3.
ShuffleNet architecture.
ShiftNet
To address these issues, ShiftNet [30] was introduced, characterized by zero parameters and zero FLOPs, making it more feasible for constrained devices. The shift operation can be seen as a special case of depth-wise convolution, where each convolution kernel contains only one non-zero value (set to 1), while all others remain 0 (as detailed in Figure 4 and Figure 5). For example, with a rightward shift, only the yellow point is set to 1, and after convolution, the yellow point’s value in the input feature map shifts to the central position of the output feature map. This is followed by pointwise convolution to further integrate inter-channel information. The core concept is that, while the shift operation alone cannot learn new features or produce distinctive features, the channel domain serves as a hierarchical extension of spatial information. By applying shift operations in various directions, spatial information can be blended, enabling the subsequent pointwise convolution to learn richer image features. Moreover, because each shift applies only per channel, each convolution kernel has only possibilities, significantly reducing complexity to achieve zero parameters and zero FLOPs. Building upon this foundation, various shift operation methods have been explored, such as sparse shift operations [31], shift operations for deep neural routes [32], and multiplication-free shift operations [33].
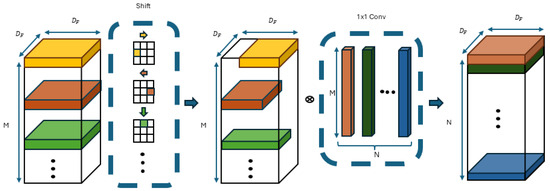
Figure 4.
ShiftNet operation flow.
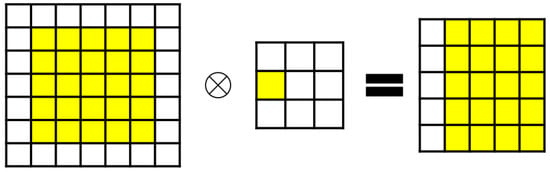
Figure 5.
ShiftNet displacement calculation method.
The standard shift operation, also known as group shift, randomly groups shift directions. For a channel count c, channels are divided into groups, with each group assigned a unique shift direction, where represents the kernel size. The standard shift operation formula is defined as Equation (4):
In this context, I and O represent the input and output feature maps, respectively. The index c denotes the channel, while i and j specify the spatial location within the feature map. Here, and indicate the horizontal and vertical displacements assigned to the c-th input feature map. The number of parameters generated by x and y corresponds to the number of channels in the input feature map, which is almost negligible compared to the parameters generated by convolutional layers. Therefore, the shift operation essentially achieves nearly zero parameters and zero FLOPs.
The formulas for calculating and are as follows:
Despite its advantages, the group shift operation has some limitations. For example, each shift amount is determined by rounding down to the nearest integer and is uniformly distributed, making it non-learnable. The kernel size for each shift operation is also determined through extensive trial and error, rather than through optimization within the model. Additionally, the group shift requires the use of pointwise convolutions to ensure order invariance, which may not be optimal for all tasks. This distribution approach may not effectively adapt to the specific requirements of different tasks.
3. Implementation
This experimental method proposes the ISR-SHA image super-resolution model to verify the effectiveness of using shift operations and hybrid attention mechanisms in reducing model parameters and improving training efficiency.
3.1. ISR-SHA
The model architecture, as shown in Figure 6, is divided into three modules: a shallow feature extraction module, a deep feature extraction module, and a high-quality image reconstruction module. This design is commonly adopted in current Transformer-based super-resolution models. Specifically, for a given low-resolution (LR) image input , a multi-scale feature fusion structure is first used to extract shallow features , where and C represent the number of input and intermediate feature channels, respectively.
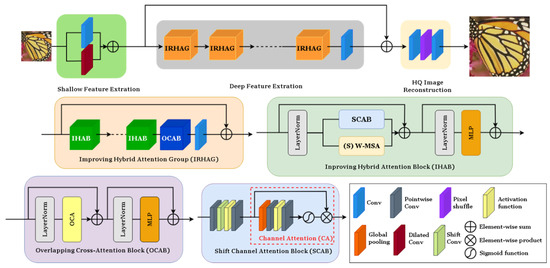
Figure 6.
ShiftNet operation flow.
Then, a series of Integrated Residual Hybrid Attention Groups (IRHAG) and a 3 × 3 convolution layer are applied to perform deep feature extraction. A global residual connection is subsequently added to fuse the shallow features and the deep features , and the high-resolution output is reconstructed through the reconstruction module.
As illustrated in Figure 6, each IRHAG contains multiple Integrated Hybrid Attention Blocks (IHAB), an Overlapping Cross Attention Block (OCAB), and a 3 × 3 convolution layer with residual connections. In the IHAB, a Spatial Channel Attention Block (SCAB) is combined with (Shifted) Window Multi-Head Self-Attention ((S)W-MSA), endowing the model with robust representation capabilities. For the reconstruction module, pixel-shuffle is employed to upsample and fuse features. Finally, an L1 loss is simply used to optimize network parameters.
In this study, the HAT model is used as the base framework and is improved to reduce the model FLOPs and the amount of parameters while maintaining the performance. Unlike the previous modifications, the main focus of the feature extraction is on the shallow feature extraction module rather than the deep feature extraction module. For the deep feature module, only shift operations and some minor architectural adjustments are performed to reduce the FLOPs and parameter counts.
3.2. Shallow Feature Extraction Module
Given the objective of this study to minimize computational costs, we implement a shifting operation within the deep feature extraction module. Nevertheless, it is essential to recognize that the primary function of this module is to capture global information from the input images. Consequently, applying shifting operations may result in the loss of critical global information, which could adversely affect performance. To address this potential loss, we propose modifications to the design of the shallow feature extraction module. Specifically, we introduce a multi-scale feature fusion architecture aimed at maximizing the receptive field during the extraction of shallow features, thereby compensating for the information loss incurred by the shifting operation; this is illustrated in Figure 7.
Figure 7.
Shallow feature extraction model.
For a given low-quality image (where H, W, and denote the height, width, and number of input channels of the image, respectively), we employ both a 3 × 3 convolution and a dilated convolution to facilitate multi-scale feature fusion and extract shallow features and as follows:
where C represents the number of feature channels. The utilization of dilated convolution enables the attainment of an expanded receptive field while maintaining a comparable number of FLOPs and parameters to those of standard convolution. Both standard and dilated convolutions are particularly adept at early-stage visual processing, facilitating enhanced optimization stability and superior results. Moreover, they provide a straightforward mechanism for mapping the input image into a higher-dimensional feature space.
Dilated Convolution is characterized as a convolution operation that fundamentally differs from standard convolution; in standard convolution, each parameter within the convolution kernel interacts multiplicatively with adjacent pixels in the input image, followed by summation to produce the output feature map. In contrast, dilated convolution incorporates additional gaps between the parameters of the convolution kernel; these gaps are fixed intervals situated between the centers of the convolution kernel and are referred to as the dilation rate. A notable feature of dilated convolution is its capacity to enlarge the receptive field without augmenting the number of parameters or computational burden, thereby allowing each output pixel to correspond to an expansive area of the input image. The receptive field of a standard 3 × 3 convolution is 9, whereas a 3 × 3 dilated convolution with a dilation rate of 2 yields a receptive field of 25, all while the parameter count remains at merely 36% of that of a standard 5 × 5 convolution.
3.3. Deep Feature Extraction Module
The shallow feature is subsequently passed into the deep feature extraction module to obtain the deep features and is represented as follows:
The overall architecture is inspired by the Hierarchical Attention Transformer (HAT) framework, wherein the deep feature extraction module comprises multiple Iterative Residual Hierarchical Attention Groups (IRHAGs), formulated as follows:
Here, and represent the IRHAG and standard convolution operations, respectively. The final convolution layer serves to consolidate the information from the IRHAGs, facilitating subsequent processing steps.
The IRHAG is composed of multiple Interleaved Hierarchical Attention Blocks (IHABs) and a single Overlapping Cross Attention Block (OCAB). Within each IHAB, a Shifting Channel Attention Block (SCAB) is integrated following the first LayerNorm layer of the standard Swin Transformer block, operating in parallel with the Shifted Window Multi-Head Self-Attention (SW-MSA). After adding residual connections, the output is further processed through another LayerNorm and a Multi-Layer Perceptron (MLP), culminating in the output of the IHAB denoted as Y; the process is as follows:
In this context, and represent intermediate features, while denotes the Multi-Layer Perceptron. The SCAB module captures global information across channels, while the SW-MSA enables the modeling of long-range dependencies, collectively enhancing the model’s performance.
The Shifting Channel Attention Block comprises two pointwise convolutions, a learnable shifting operation, a GELU activation function, and a channel attention module. Initially, the number of input channels is reduced by a constant factor to decrease computational costs. For an input feature with C channels, the first pointwise convolution reduces the output feature’s channel count to . The active shifting operation further diminishes computational load, followed by a second pointwise convolution that restores the feature to C channels as illustrated in Figure 8. Finally, a standard channel attention module is employed to adaptively scale the channel features. Experimental results demonstrate that this approach can reduce FLOPs and parameter counts by approximately 30%.
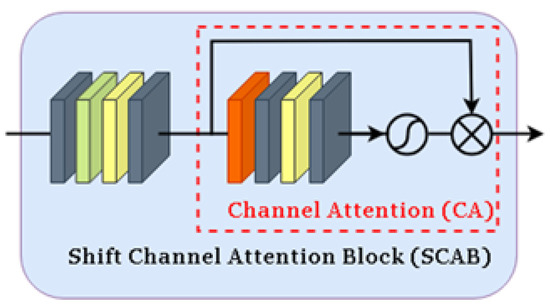
Figure 8.
Shift channel attention block.
Compared to traditional group shifts, the active shifting method offers several advantages. First, the displacement amount in active shifting is learnable, eliminating the need for manual allocation. Secondly, active shifting is independent of the kernel size, meaning that changes to the kernel size do not affect the shifting outcome. Additionally, it does not require pointwise convolutions to maintain permutation invariance. The formulation of the active shifting operation is as follows:
By making the displacement parameters x and y differentiable, the original integer constraints are relaxed to real numbers, transforming the shifting operation into a bilinear interpolation form, which allows for adaptive optimization of x and y. Here, represents the set of the four nearest points defined as , so can be denoted as follows:
3.4. High Quality Image Reconstruction Module
The shallow features and deep features are aggregated to reconstruct a high-quality image , expressed mathematically as follows:
In this equation, denotes the reconstruction module function. The primary role of the shallow features is to capture low-frequency information of the image, whereas the deep features focus on restoring high-frequency information. By integrating both low-frequency and high-frequency information, the model’s performance is significantly enhanced.
4. Results
This chapter presents a comprehensive evaluation of the proposed ISR-SHA model’s performance and computational efficiency. Model validation is conducted using PSNR and SSIM as key metrics to assess image quality, complemented by FLOPs and parameter count to measure computational demands. The DF2K training dataset, along with the Set5 and Set14 validation sets, provide a robust foundation for comparison across models, including SwinIR and HAT. Performance benchmarks highlight ISR-SHA’s significant reduction in computational cost with minimal compromise in image quality, as confirmed by comparative analysis and ablation studies. Additionally, the ablation experiments emphasize the importance of multi-scale feature fusion in preserving model performance. Collectively, these results demonstrate ISR-SHA’s effective balance between high performance and reduced computational complexity, affirming its superiority over traditional SR methods.
4.1. Model Validation
In the model validation process, this study uses Peak Signal-to-Noise Ratio (PSNR) [34,35,36] and Structural Similarity Index Measure (SSIM) [37,38] as primary evaluation metrics. PSNR is used mainly to assess the quality of generated images by calculating the mean squared error (MSE) between generated and real images, thus providing a quantitative score for the fidelity of the image. SSIM, on the other hand, focuses on comparing the brightness, contrast, and structural attributes of images, more closely aligning with human visual perception. The SSIM score is computed through statistical measures such as standard deviation and variance. Additionally, given that the aim of this study is to maintain high PSNR and SSIM scores while reducing computational cost, we evaluate the model by calculating the number of floating-point operations per second (FLOPs) and parameter count. These measurements help determine whether the target goals have been achieved.
4.2. Datasets
In this study, we used the same settings for the training parameters, including the learning rate and the number of iterations, for all the models compared. The comparison includes the following methods: SwinIR: This is a widely recognized super-resolution modeling method that comprises three modules: shallow feature extraction, deep feature extraction, and image reconstruction. HAT: This model represents the most advanced approach to super-resolution, supporting both ×2 and ×4 upscaling. Our study builds on the improvements made to the HAT architecture. The training dataset used in this investigation is DF2K, which combines the DIV2K dataset, which contains 800 clean 2K images, with the Flickr2K dataset, which contains 2,650 noise-laden real-world 2K images. Incorporation of the DF2K dataset significantly improves the utility of the model. For validation, we utilize the commonly used Set5 and Set14 datasets, consisting of 5 and 14 small-sized images, respectively.
4.3. Compare with ISR-SHA
Table 1 presents the performance of the proposed ISR-SHA model compared to other methods on the Set5 and Set14 datasets. It is evident from the table that the ISR-SHA model effectively reduces computational costs while maintaining high model performance. The calculations for FLOPs (measured in GFLOPs, where 1 GFLOP FLOPs) and the number of parameters (expressed in millions) were performed using an input image with three channels and dimensions of pixels.

Table 1.
Performance comparison of different methods on Set5 and Set14 datasets.
As indicated in Table 1, the ISR-SHA model reduces FLOPs by approximately 6.3 billion operations (about a 30% reduction) compared to HAT. Furthermore, it decreases the number of parameters by approximately 6.3 million (also about a 30% reduction).
In terms of PSNR and SSIM metrics, ISR-SHA exhibits only a minor decrease in performance relative to HAT. For the Set5 dataset, the PSNR decreases by approximately 0.02, and the SSIM drops by 0.0008. Similarly, for the Set14 dataset, the PSNR experiences a decrease of around 0.02, while the SSIM decreases by 0.0006. In general, the ISR-SHA model maintains performance levels significantly superior to those of SwinIR and other methods, achieving a balance between performance retention and reduced computational costs compared to HAT.
Figure 9 and Figure 10 illustrate the visual results of the ISR-SHA model compared to other methods. As shown in the figures, ISR-SHA is capable of generating superior image details relative to alternative approaches, particularly when compared to traditional methods such as EDSR. EDSR, which employs residual blocks for super-resolution, demonstrates significantly lower computational costs than Transformer-based super-resolution methods. However, the high-quality images produced by EDSR appear markedly more blurred than those generated by ISR-SHA, and the differences in detail are readily apparent to the naked eye. Additional examples and visual comparisons can be found in Appendix A.

Figure 9.
Set5 valid result.
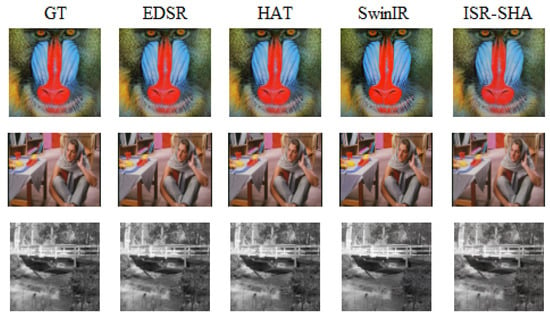
Figure 10.
Set14 valid result.
4.4. Other Methods and References
In this experiment, we used the same experimental setup, including the experimental data and environment, to extract the best individual models for comparison with the proposed method. The methods being compared are as follows:
- EDSR [7]: A deep CNN-based method that improves image quality by removing batch normalization layers and deepening the network structure.
- SwinIR [20]: Built on Swin Transformer, it uses local and global attention to capture fine details across the entire image.
- HAT [39]: Combines local and global attention to enrich image features, ideal for high-magnification tasks that need clear, high-quality results.
4.5. Ablation Experiment
Table 2 and Table 3 present the results of the ablation experiment for the ISR-SHA model. From the data, it is evident that when only the shifting operation is applied without the incorporation of multi-scale feature fusion, both PSNR and SSIM decrease by approximately 0.05 to 0.06 and 0.0007, respectively. This indicates that the inclusion of multi-scale feature fusion is essential for maintaining performance. Furthermore, since the modifications are made within the shallow feature extraction module, the increase in FLOPs and parameter counts is negligible. In summary, the ISR-SHA model effectively combines the shifting operation with multi-scale feature fusion, resulting in reduced computational costs while preserving its performance metrics.

Table 2.
Comparison of shift operation and multi-scale feature fusion on Set5.

Table 3.
Comparison of shift operation and multi-scale feature fusion on Set14.
Based on the experimental results, we conclude that ISR-SHA effectively meets the objectives of this study by maintaining high PSNR and SSIM values while achieving approximately 30% reductions in both FLOPs and parameter counts. Furthermore, the performance of ISR-SHA continues to surpass that of other traditional super-resolution methods.
In summary, this paper presents enhancements to the HAT architecture by modifying the shallow feature extraction module to increase feature diversity while simultaneously reducing the computational burden of the deep feature extraction module. This dual approach enables the model to achieve the desired performance levels with a significantly lower computational cost.
5. Conclusions and Future Work
This study proposes a super-resolution model based on HAT that effectively reduces computational costs while maintaining model performance. Using dilated convolutions, the model enhances the receptive field of shallow feature extraction, compensating for the loss of detail that occurs during shifting operations in the deep feature extraction module. Furthermore, the implementation of an active shifting operation in the shifting channel attention block, combined with pointwise convolutions, significantly reduces computational costs.
Experimental results demonstrate that the proposed method retains the expected performance level of HAT, outperforming most other super-resolution models while achieving approximately 30% reductions in both FLOPs and parameter counts. As illustrated, the images reconstructed by ISR-SHA exhibit superior detail recovery compared to other methods.
However, the ISA-SHA model still presents opportunities for further improvement. For example, utilizing more effective techniques for shallow feature extraction could enhance performance metrics. Furthermore, exploring various methods to further reduce model size would contribute to its practical applicability.
Author Contributions
Conceptualization, H.-M.T., W.-M.T. and J.-W.L.; methodology, H.-M.T., W.-M.T. and J.-W.L.; software, W.-M.T. and J.-W.L.; validation, H.-M.T., W.-M T. and J.-W.L.; formal analysis, H.-M.T., W.-M.T. and J.-W.L.; writing—original draft preparation, H.-M.T., W.-M.T., G.-L.T. and J.-W.L.; writing—review and editing, G.-L.T., J.-W.L. and H.-T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Yu-Sheng Technology (YSTI), Taichung, Taiwan, under grant Super-Resolution Imaging for Shoe Manufacturing: An Industry-Academia Project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Additional Figures
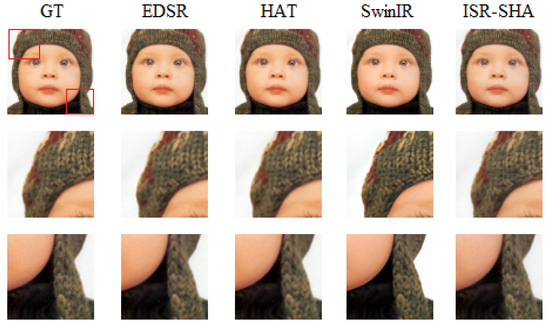
Figure A1.
Set5 baby crop result. The red boxes in the GT image indicate the regions that are enlarged below for comparison.

Figure A2.
Set5 bird crop result. The red boxes in the GT image indicate the regions that are enlarged below for comparison.

Figure A3.
Set5 butterfly crop result. The red boxes in the GT image indicate the regions that are enlarged below for comparison.

Figure A4.
Set14 bolt crop result. The red boxes in the GT image indicate the regions that are enlarged below for comparison.

Figure A5.
Set14 human crop result. The red boxes in the GT image indicate the regions that are enlarged below for comparison.
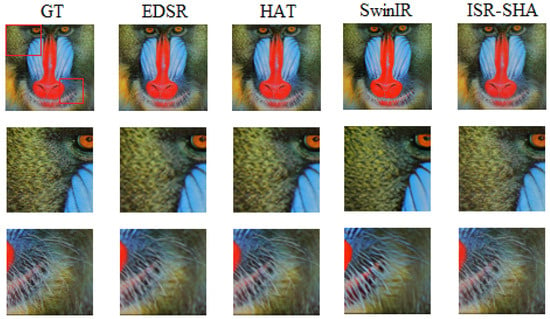
Figure A6.
Set14 baboon crop result. The red boxes in the GT image indicate the regions that are enlarged below for comparison.
References
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern. Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning Texture Transformer Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 5790–5799. [Google Scholar] [CrossRef]
- Gu, S.; Sang, N.; Ma, F. Fast image super resolution via local regression. In Proceedings of the IEEE/CVF International Conference on Pattern Recognition, Tsukuba, Japan, 11–15 November 2012; pp. 3128–03131. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. arXiv 2015, arXiv:1501.00092. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. arXiv 2016, arXiv:1608.00367. [Google Scholar] [CrossRef]
- Lima, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Computer Vision—European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 184–199. [Google Scholar] [CrossRef]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-Order Attention Network for Single Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11057–11066. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef]
- Gu, J.; Dong, C. Interpreting Super-Resolution Networks with Local Attribution Maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9195–9204. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, A.; Gu, J.; Zhang, Z.; Wu, W.; Qiao, Y.; Dong, C. Discovering Distinctive ‘Semantics’ in Super-Resolution Networks. arXiv 2022, arXiv:2108.00406. [Google Scholar] [CrossRef]
- Xie, L.; Wang, X.; Dong, C.; Qi, Z.; Shan, Y. Finding Discriminative Filters for Specific Degradations in Blind Super-Resolution. Adv. Neural Inf. Process. Syst. 2021, 34, 51–61. [Google Scholar]
- Kong, X.; Liu, X.; Gu, J.; Qiao, Y.; Dong, C. Reflash Dropout in Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5992–6002. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, H.; Gu, J.; Qiao, Y.; Dong, C. Evaluating the Generalization Ability of Super-Resolution Networks. arXiv 2023, arXiv:2205.07019. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-Trained Image Processing Transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12294–12305. [Google Scholar] [CrossRef]
- Cao, J.; Li, Y.; Zhang, K.; Gool, L.V. Video Super-Resolution Transformer. arXiv 2023, arXiv:2106.06847. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Gool, L.V.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 9992–10002. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, H.; Lin, Y.; Yao, Z.; Xie, Z.; Wei, Y.; Ning, J.; Cao, Y.; Zhang, Z.; Dong, L.; et al. Swin Transformer V2: Scaling Up Capacity and Resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11999–12009. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Simonyan, K.; Zisserman, A. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5987–5995. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- He, Y.; Liu, X.; Zhong, H.; Ma, Y. AddressNet: Shift-Based Primitives for Efficient Convolutional Neural Networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 7–11 January 2019; pp. 1213–1222. [Google Scholar] [CrossRef]
- Wu, B.; Wan, A.; Yue, X.; Jin, P.; Zhao, S.; Golmant, N.; Gholaminejad, A.; Gonzalez, J.; Keutzer, K. Shift: A Zero FLOP, Zero Parameter Alternative to Spatial Convolutions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9127–9135. [Google Scholar] [CrossRef]
- Chen, W.; Xie, D.; Zhanga, Y.; Pu, S. All You Need Is a Few Shifts: Designing Efficient Convolutional Neural Networks for Image Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7234–7243. [Google Scholar] [CrossRef]
- Elhoushi, M.; Chen, Z.; Shafiq, F.; Tian, Y.H.; Li, J.Y. DeepShift: Towards Multiplication-Less Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Nashville, TN, USA, 19–25 June 2021; pp. 2359–2368. [Google Scholar] [CrossRef]
- Jeon, Y.; Kim, J. Constructing Fast Network through Deconstruction of Convolution. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, Canada, 2–8 December 2018. [Google Scholar]
- Salomon, D. Data Compression: The Complete Reference, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Lv, M.; Song, S.; Jia, Z.; Li, L.; Ma, H. Multi-Focus Image Fusion Based on Dual-Channel Rybak Neural Network and Consistency Verification in NSCT Domain. Fractal Fract. 2025, 9, 432. [Google Scholar] [CrossRef]
- Li, L.; Song, S.; Lv, M.; Jia, Z.; Ma, H. Multi-Focus Image Fusion Based on Fractal Dimension and Parameter Adaptive Unit-Linking Dual-Channel PCNN in Curvelet Transform Domain. Fractal Fract. 2025, 9, 157. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Sun, Y.; Hu, X.; Zhang, N.; Feng, H.; Li, Z.; Wang, Y. Multi-Attitude Hybrid Network for Remote Sensing Hyperspectral Images Super-Resolution. Remote Sens. 2025, 17, 1947. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhang, W.; Kong, X.; Qiao, Y.; Zhou, J.; Dong, C. HAT: Hybrid Attention Transformer for Image Restoration. arXiv 2023, arXiv:2309.05239. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).