Improved Rectangular Extension of Steinmetz Equation Including Small and Large Excitation Signals with DC Bias
Abstract
1. Introduction
2. Review of RESE Based Loss Models
3. Review of Small- and Large-Signal Core Resistance Calculation Methodologies
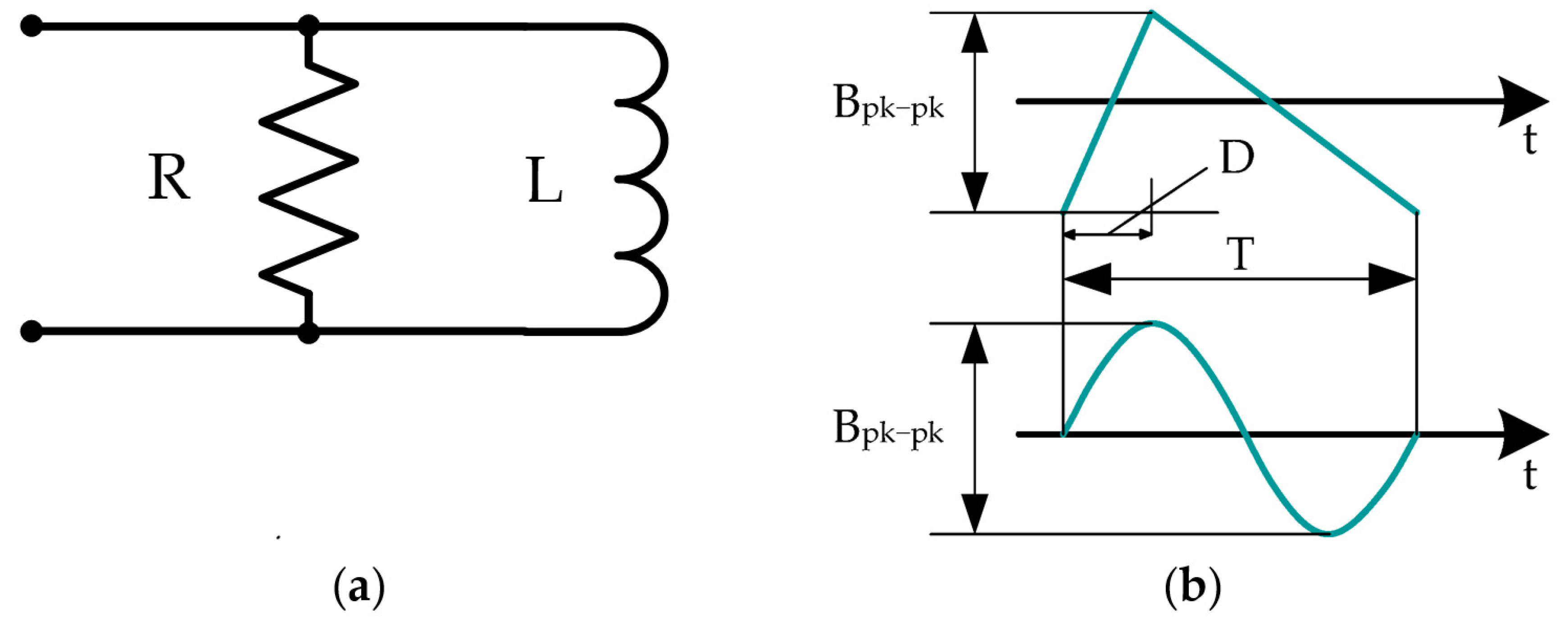
3.1. Small-Signal Core Resistance
3.2. Large-Signal Core Resistance
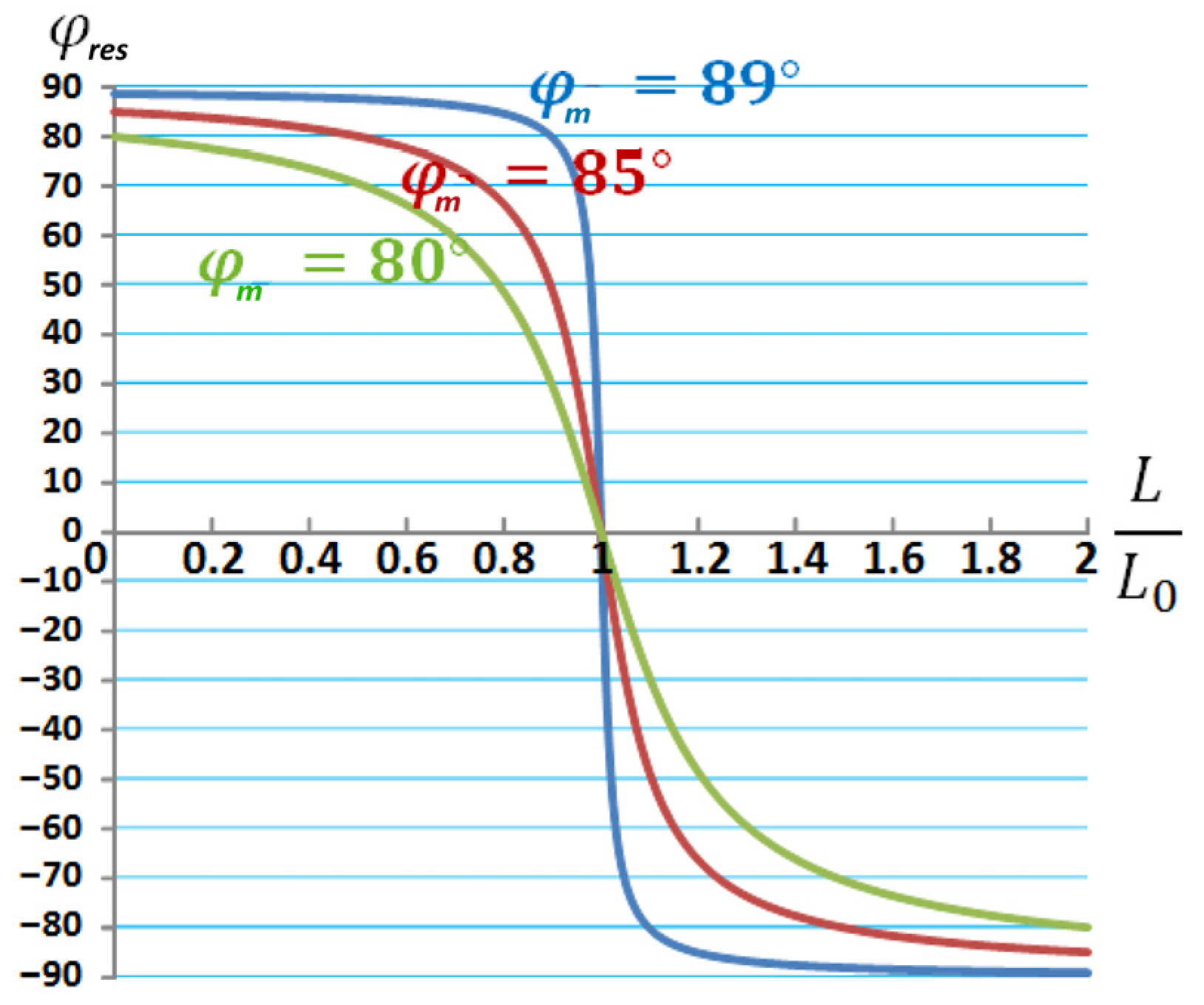
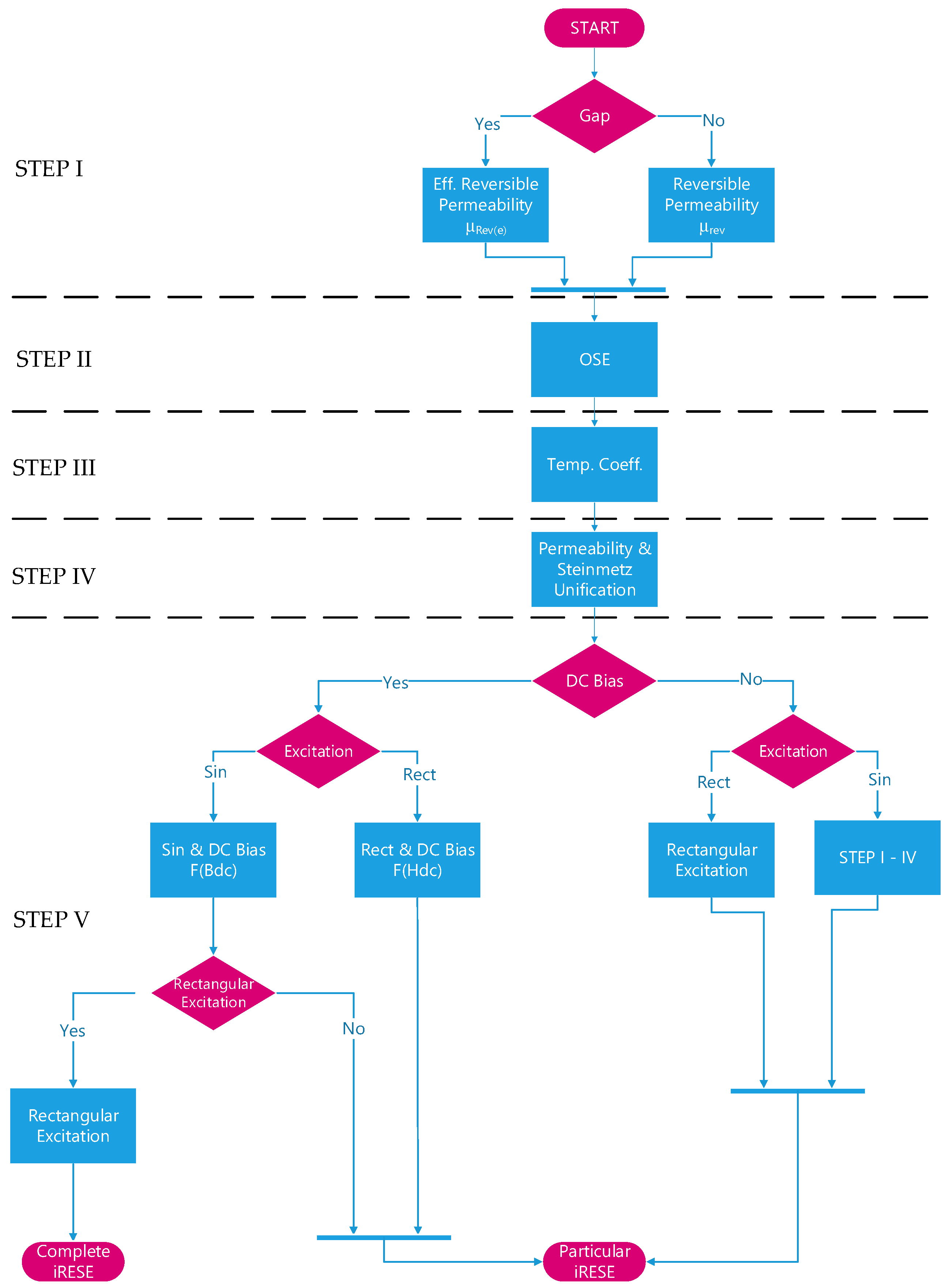
4. Proposed Core Loss Calculation Methodology
- 1.
- If there is a sinusoidal excitation and a DC bias, then the Equation (40) becomes:
- 2.
- If the rectangular excitation takes place, the corresponding relationship can be added to Equation (41), giving:
- 3.
- If there is a rectangular excitation without a DC bias, the Equation (40) changes as follows:
- 4.
- If rectangular excitation comes together with a DC bias, the DC bias is added to rectangular core loss with the assumption that the duty ratio of the signals’ equals . Because a complex relationship exists between B and H near the core saturation region the DC magnetization function to be added is rather a function of than as in Equations (41)–(42), yielding:
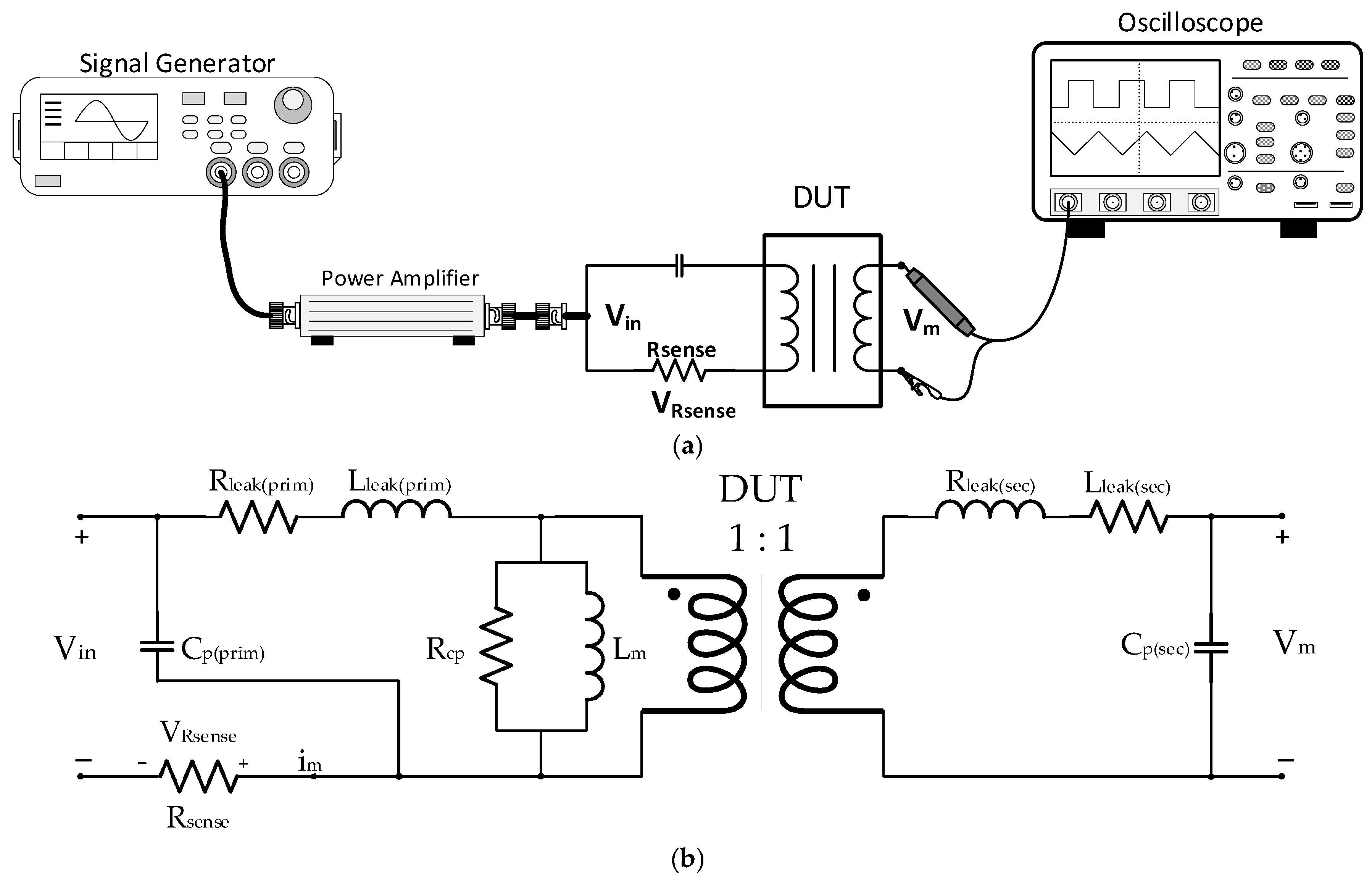
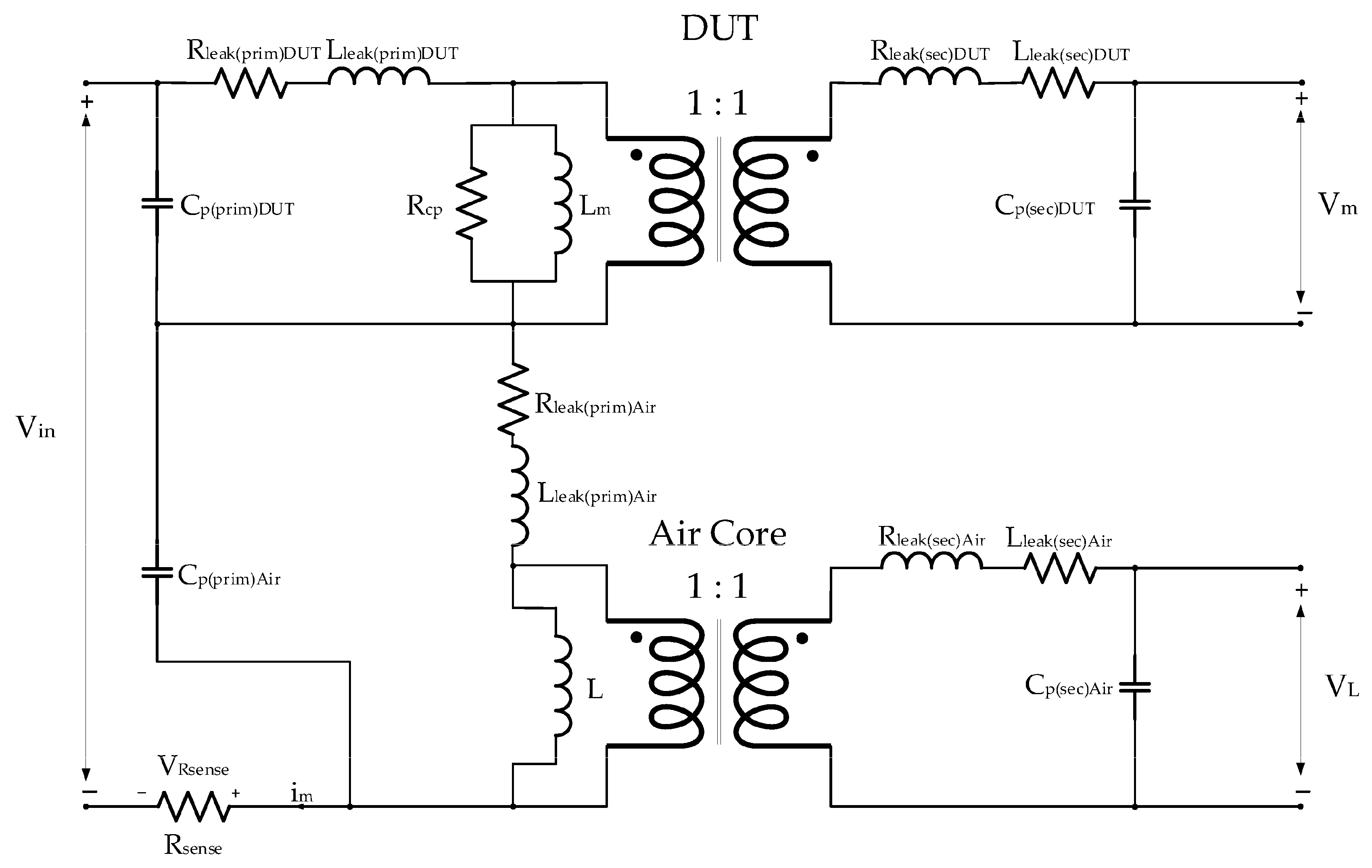
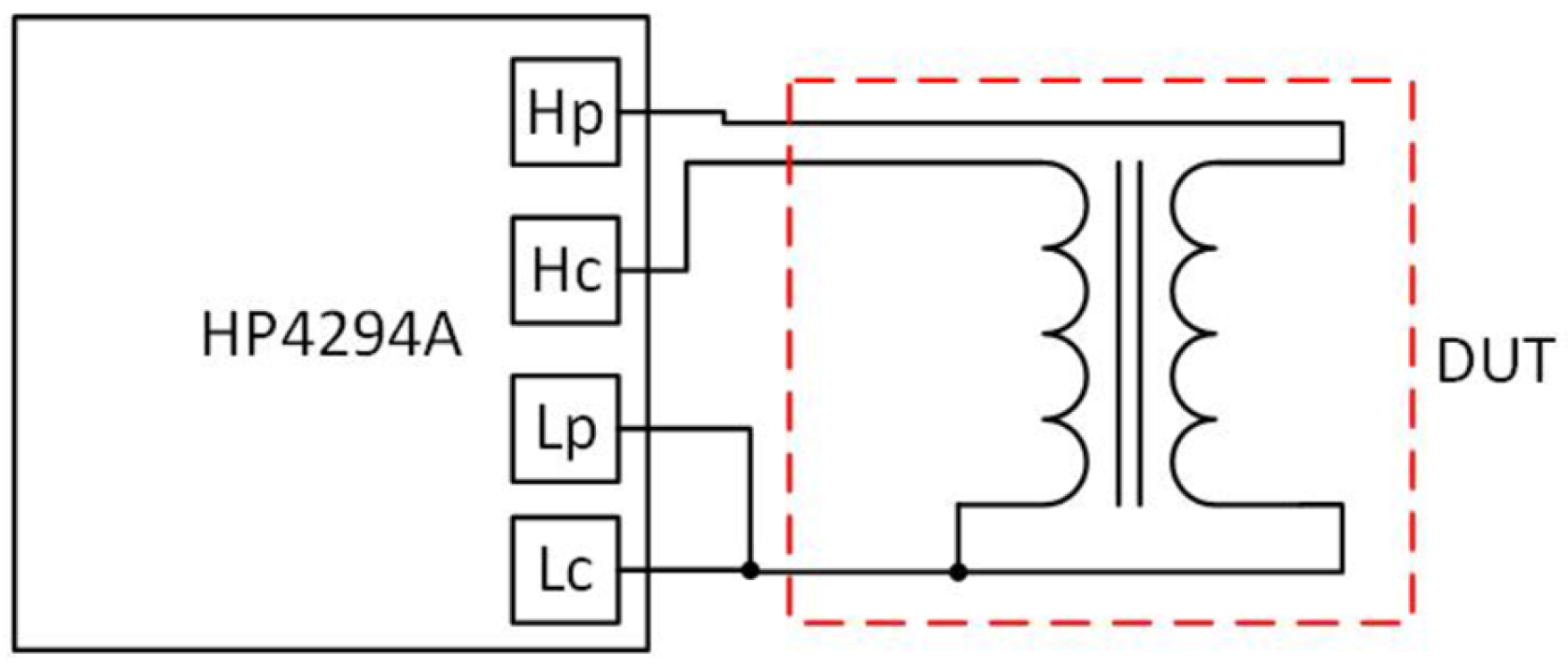
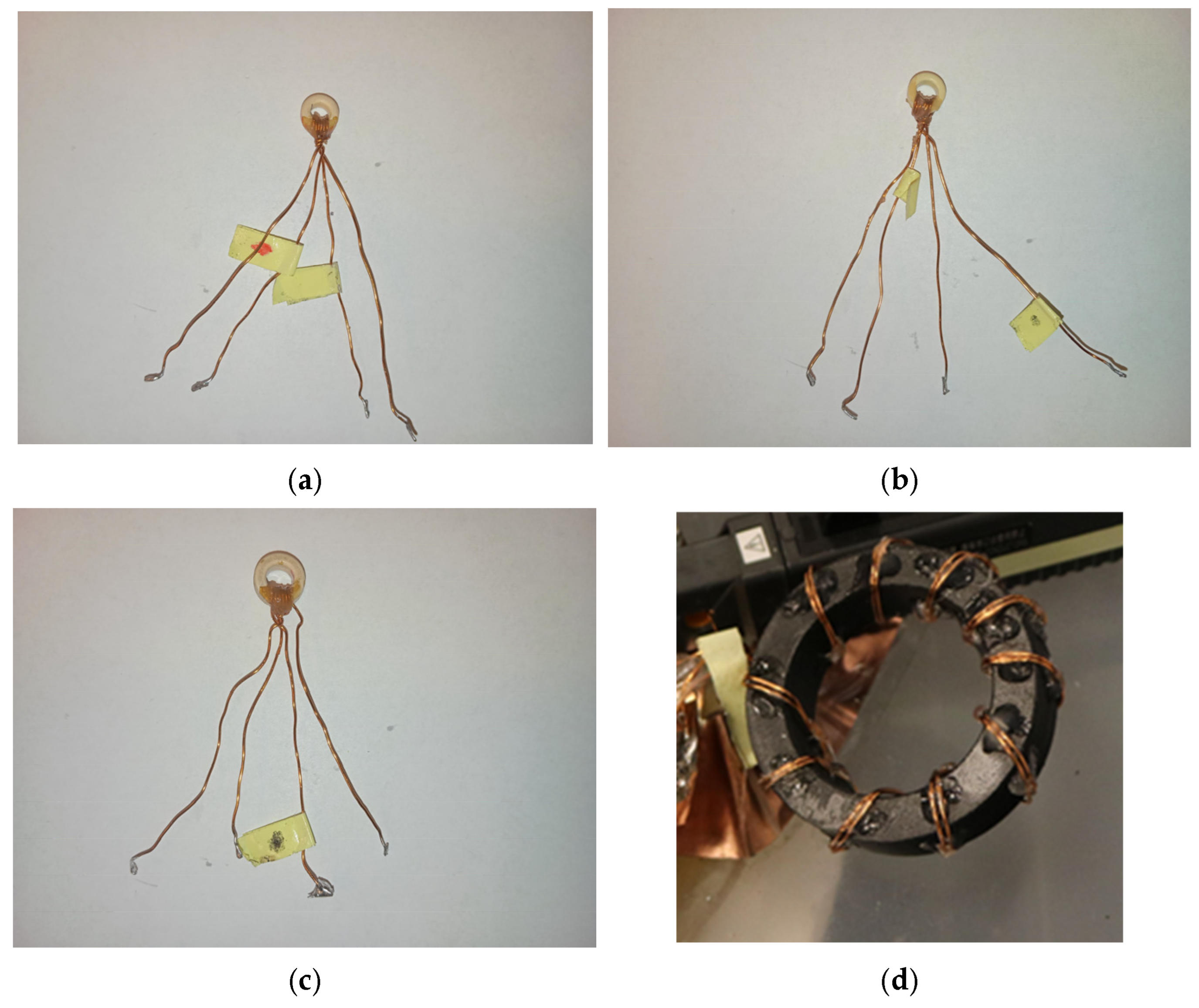
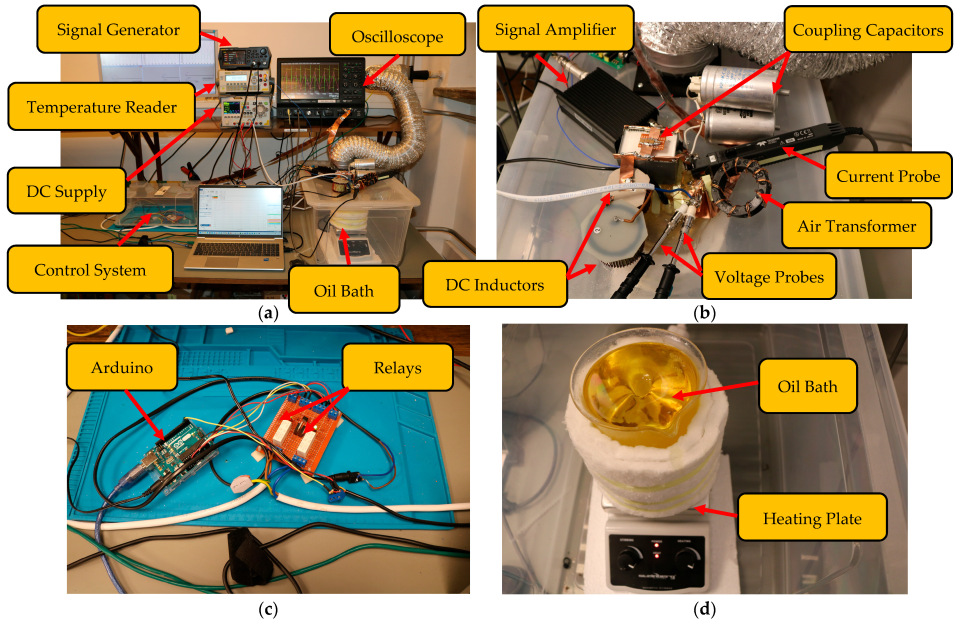
5. Test-Bench Measurement and Verification
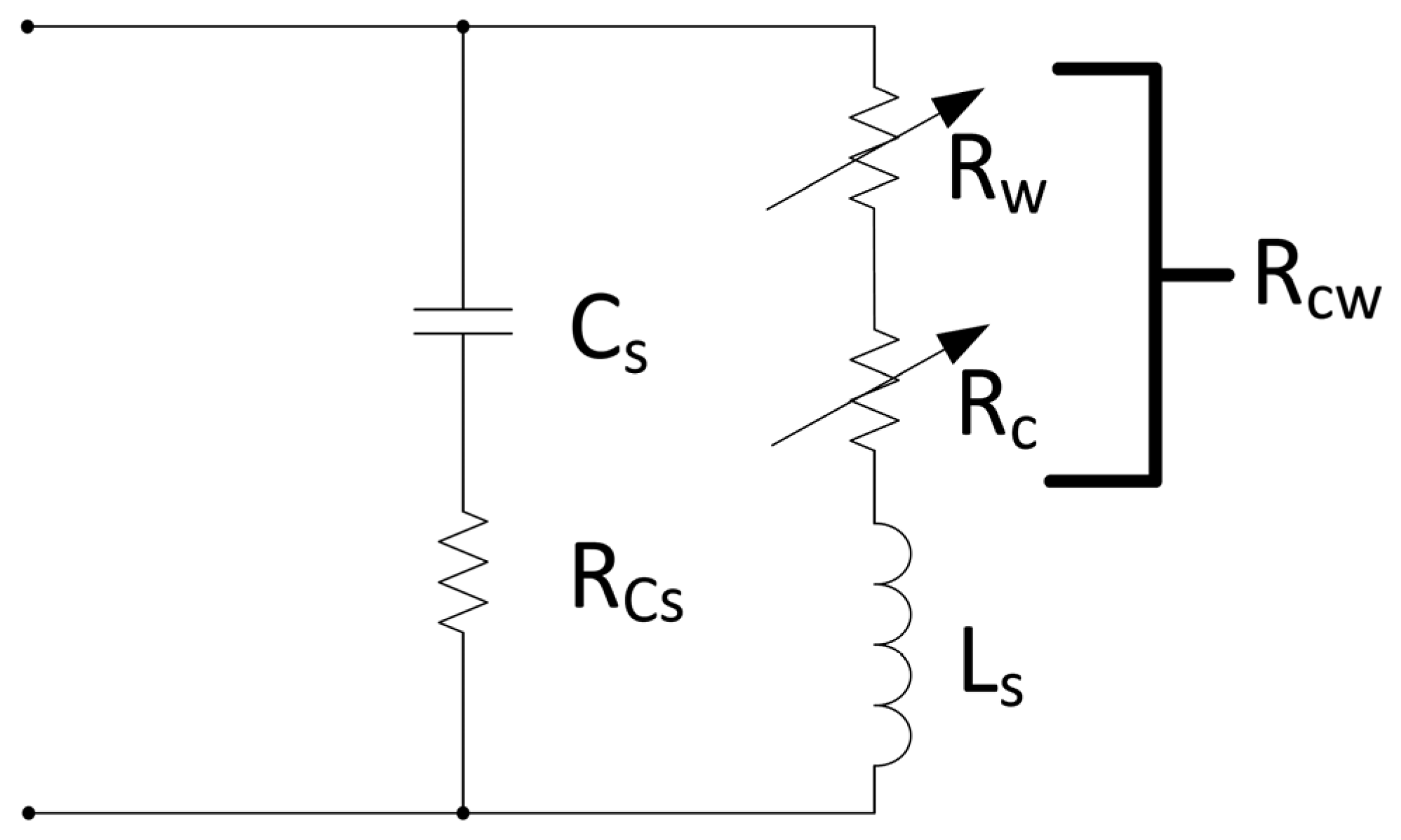
5.1. Reversible Permeability Measurement
5.2. Original Steinmetz Equation Coefficients
5.3. Unified Small and Large-Signal Core Loss Model
5.4. Rectangular and Sinusoidal Excitations with a DC Bias
5.4.1. Sinusoidal Excitation with DC Bias Characteristics—STEP V.1.
5.4.2. Rectangular Excitation with a DC Bias Characteristics—STEP V.2.
5.4.3. Rectangular Excitation Without a DC Bias—STEP V.3.
5.4.4. Rectangular Excitation with a DC Bias Characteristics—STEP V.4.
6. Error Analysis
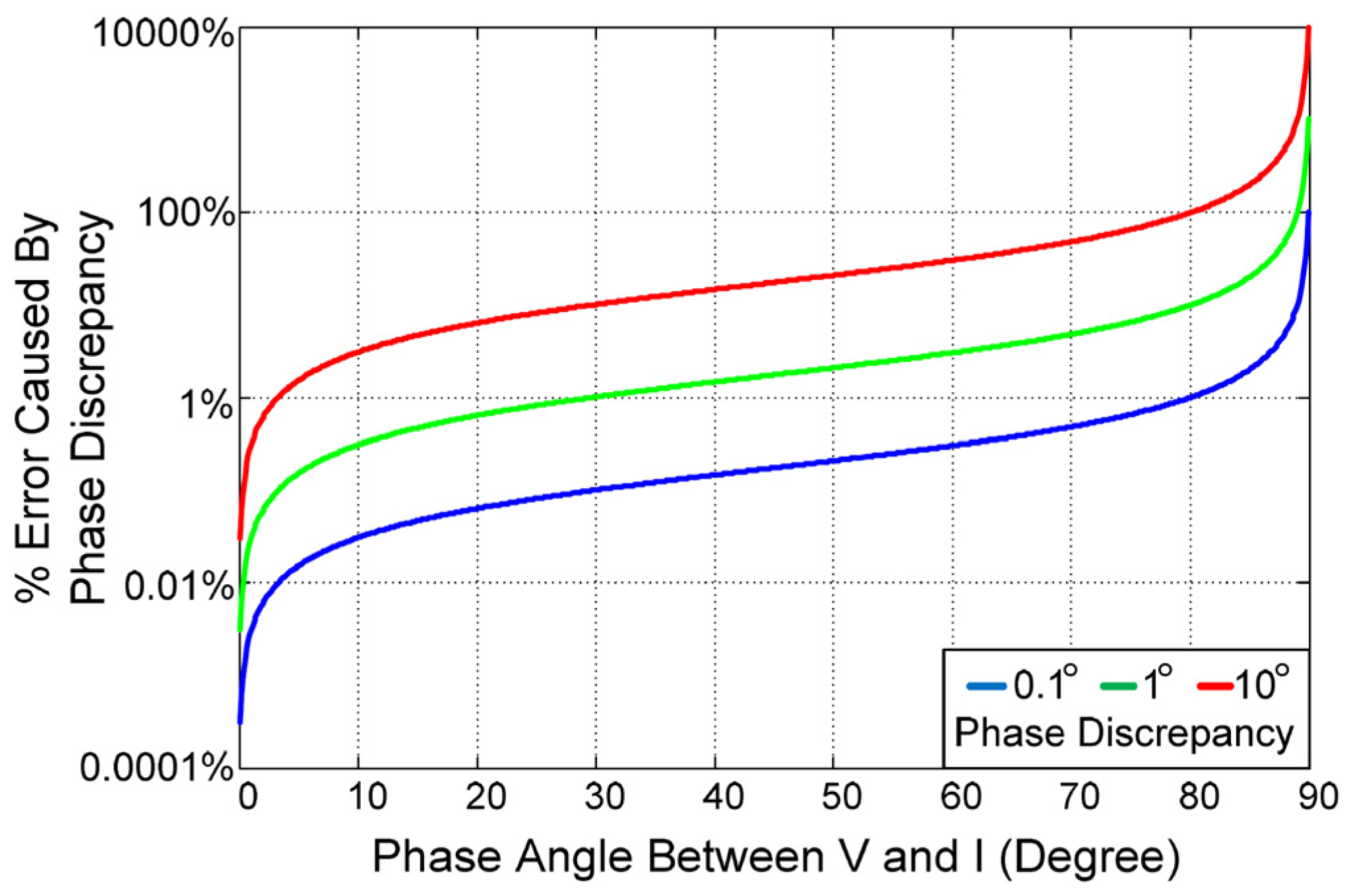
6.1. Oscilloscope Measurement Errors
6.2. Bm Estimation Errors
6.3. Temperature Estimation Errors
6.4. Fitting Errors
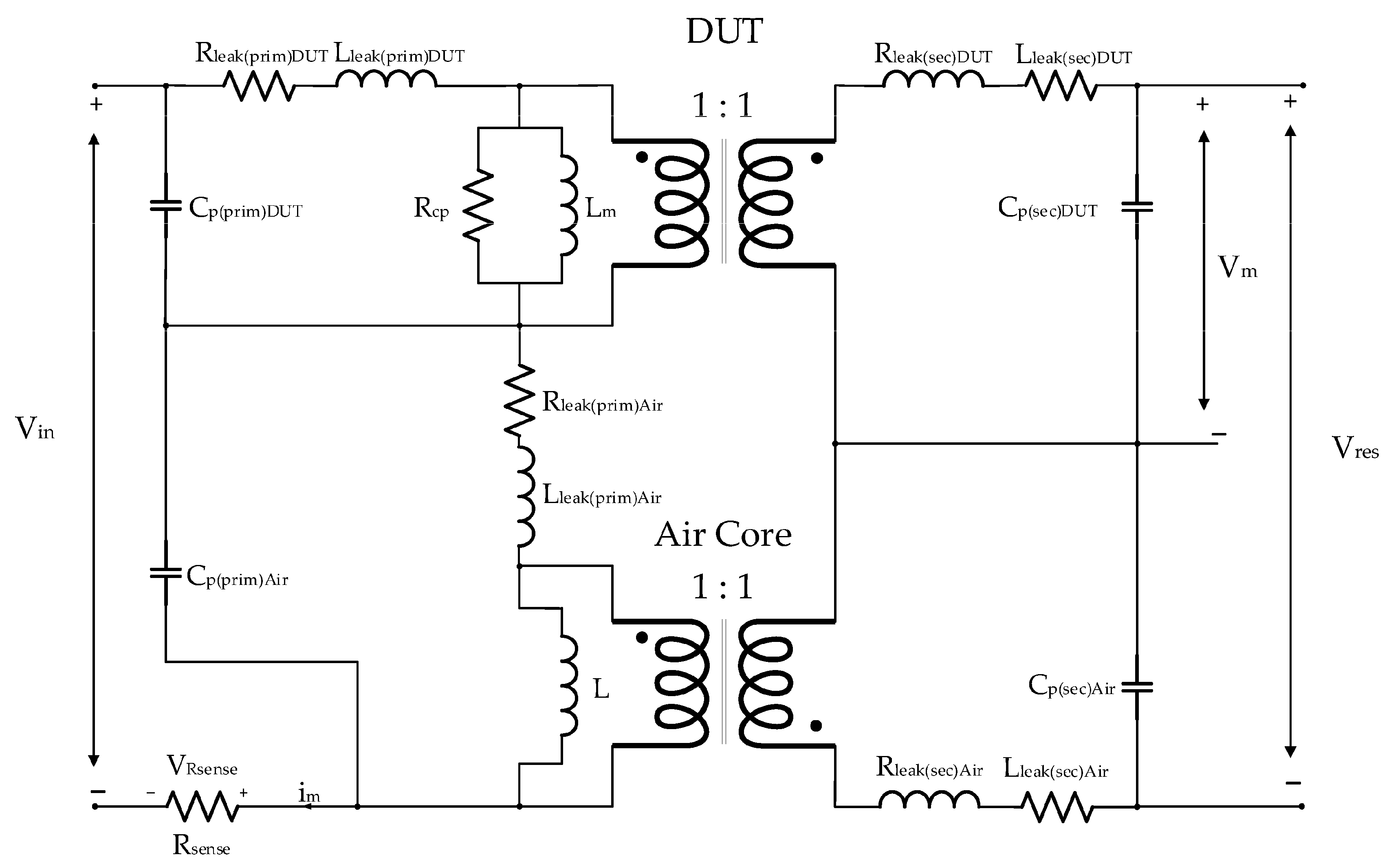
6.5. Error Caused by Parasitic Components
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steinmetz, C.P. On the law of hysteresis. Trans. AIEE 1892, IX, 1–64. [Google Scholar] [CrossRef]
- Reinert, J.; Brockmeyer, A.; De Doncker, R.W.A.A. Calculations of losses in ferro- and ferrimagnetic materials based on the modified Steinmetz equation. IEEE Trans. Ind. Appl. 2001, 37, 1055–1061. [Google Scholar] [CrossRef]
- Li, J.; Abdallah, T.; Sullivan, C.R. Improved calculation of core loss with non-sinusoidal waveforms. In Proceedings of the IEEE Industry Applications Conference, 36th IAS Annual Meeting, Chicago, IL, USA, 30 September–4 October 2001. [Google Scholar] [CrossRef]
- Venkatachalam, K.; Sullivan, C.R.; Abdallah, T.; Tacca, H. Accurate prediction of ferrite core loss with non-sinusoidal waveforms using only Steinmetz parameters. In Proceedings of the IEEE Workshop on Computers in Power Electronics, Mayaguez, Puerto Rico, 3–4 June 2002. [Google Scholar] [CrossRef]
- Shen, W.; Wang, F.; Boroyevich, D.; Tipton, C.W. Loss characterization and calculation of nanocrystalline cores for high-frequency magnetics applications. In Proceedings of the 22nd Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 25 February–1 March 2007. [Google Scholar] [CrossRef]
- Muhlethaler, J.; Biela, J.; Kolar, J.W.; Ecklebe, A. Improved core-loss calculation for magnetic components employed in power electronic systems. IEEE Trans. Power Electr. 2012, 27, 964–973. [Google Scholar] [CrossRef]
- Mu, M.; Lee, F.C. A new core loss model for rectangular AC voltages. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014. [Google Scholar] [CrossRef]
- Barg, S.; Ammous, K.; Mejbri, H.; Ammous, A. An improved empirical formulation for magnetic core losses estimation under non-sinusoidal induction. IEEE Trans. Power Electr. 2017, 32, 2146–2154. [Google Scholar] [CrossRef]
- Do Nascimento, V.C.; Sudhoff, S.D. Continuous time formulation for magnetic relaxation using the Steinmetz equation. IEEE Trans. Energy Conv. 2018, 33, 1098–1107. [Google Scholar] [CrossRef]
- Stenglein, E.; Durbaum, T. Core loss model for arbitrary excitations with DC bias covering a wide frequency range. IEEE Trans. Magn. 2021, 57, 6302110. [Google Scholar] [CrossRef]
- Mu, M. High Frequency Magnetic Core Loss Study. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2013. Available online: https://vtechworks.lib.vt.edu/server/api/core/bitstreams/fe64b26f-f365-48ad-a360-131f9ebabe5e/content (accessed on 15 May 2025).
- Sanusi, B.N.; Zambach, M.; Frandsen, C.; Beleggia, M.; Jorgensen, A.M.; Ouyang, Z. Investigation and modeling of DC bias impact on core losses at high frequencies. IEEE Trans. Power Electr. 2023, 38, 7444–7458. [Google Scholar] [CrossRef]
- Rasekh, N.; Wang, J.; Yuan, X. A new method for offline compensation of phase discrepancy in measuring the core loss with rectangular voltage. IEEE Open J. Ind. Electr. Soc. 2021, 2, 302–314. [Google Scholar] [CrossRef]
- Hou, D.; Mu, M.; Lee, F.C.; Li, Q. New high-frequency core loss measurement method with partial cancellation concept. IEEE Trans. Power Electr. 2017, 32, 2987–2994. [Google Scholar] [CrossRef]
- Dong Tan, F.; Vollin, J.L.; Cuk, S.M. A practical approach for magnetic core-loss characterization. IEEE Trans. Power Electr. 1995, 10, 124–130. [Google Scholar] [CrossRef]
- Mu, M.; Li, Q.; Gilham, D.; Lee, F.C.; Ngo, K.D.T. New core loss measurement method for high frequency magnetic materials. In Proceeding of the IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010. [Google Scholar] [CrossRef]
- Mu, M.; Lee, F.C.; Li, Q.; Gilham, D.; Ngo, K.D.T. A high frequency core loss measurement method for arbitrary excitations. In Proceedings of the 26th Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Forth Worth, TX, USA, 6–11 March 2011. [Google Scholar] [CrossRef]
- Foo, B.X.; Stein, A.L.F.; Sullivan, C.R. A step-by-step guide to extracting winding resistance from an impedance measurement. In Proceeding of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. High-Frequency Magnetic Components, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2014. [Google Scholar] [CrossRef]
- IEC 62044-2; Cores Made of Soft Magnetic Materials—Measuring Methods—Part 2: Magnetic Properties at Low Excitation Level. IEC: Geneva, Switzerland, 2005.
- Szczerba, P.; Ligenza, S.; Worek, C. Measurement and calculation techniques of complex permeability applied to Mn-Zn ferrites based on iterative approximation curve fitting and modified equivalent inductor model. Electronics 2023, 12, 4002. [Google Scholar] [CrossRef]
- Yang, K.; Lu, J.; Ding, M.; Zhao, J.; Ma, D.; Li, Y.; Xing, B.; Han, B.; Fang, J. Improved measurement of the low-frequency complex permeability of ferrite annulus for low-noise magnetic shielding. IEEE Access 2019, 7, 126059–126065. [Google Scholar] [CrossRef]
- Coilcraft. The Fundamentals of Power Inductors. Available online: https://www.coilcraft.com/getmedia/bec1987d-3725-4d3a-a655-d3a9227abcad/Coilcraft-eBook_Power_Inductors.pdf (accessed on 1 March 2025).
- Tarafdar-Hagh, M.; Hasanlouei, N.; Muttaqi, K.; Taghizad-Tavana, K.; Nojavan, S.; Abdi, M. Application of saturated core transformer as inrush current limiter. E-Prime—Adv. Electr. Eng. Electr. Ener. 2024, 9, 100677. [Google Scholar] [CrossRef]
- Esguerra, M. Computation of minor hysteresis loops from measured major loops. J. Magn. Magn. Mater. 1996, 157–158, 366–368. [Google Scholar] [CrossRef]
- Esguerra, M. Modelling hysteresis loops of soft ferrite materials. In Proceedings of the International Conference on Ferrites ICF8, Kyoto, Japan, 18–21 September 2000; Available online: https://www.researchgate.net/publication/235425828_Modeling_Hystesis_loops_of_Soft_Ferrite_Materials (accessed on 3 March 2025).
- Esguerra, M.; Rottner, M.; Goswani, S. Calculating major hysteresis loops from DC-biased permeability. In Proceedings of the International Conference on Ferrites ICF9, San Francisco, CA, USA, 23–27 August 2004; Available online: https://www.researchgate.net/publication/235426048_CALCULATING_MAJOR_HYSTERESIS_LOOPS_FROM_DC-BIASED_PERMEABILITY (accessed on 3 March 2025).
- Esguerra, M. Waveform dependent AC-losses of power ferrites by hysteresis loop modeling. J. Phys. IV 1997, 7, C1-109–C1-110. [Google Scholar] [CrossRef]
- Esguerra, M. DC-Bias Specifications for Gapped Ferrite Cores. Power Electronics Technology. October 2003. Available online: https://www.researchgate.net/publication/235425888_DC-Bias_Specifications_of_gapped_ferrites (accessed on 3 March 2025).
- Moree, G.; Leijon, M. Review of hysteresis models for magnetic materials. Electronics 2023, 16, 3908. [Google Scholar] [CrossRef]
- Hodgdon, M.L. Mathematical theory and calculations of magnetic hysteresis curves. IEEE Tran. Magn. 1988, 24, 3120–3122. [Google Scholar] [CrossRef]
- Hodgdon, M.L. Application of a theory of ferromagnetic hysteresis. IEEE Tran. Magn. 1988, 24, 218–221. [Google Scholar] [CrossRef]
- Ridely, R.; Nace, A. Modeling Ferrite Core Losses. Switching Power Magazine. 2006. Available online: http://ridleyengineering.com/images/phocadownload/7%20modeling%20ferrite%20core%20losses.pdf (accessed on 9 September 2023).
- TDK Electronics. Ferrite Magnetic Design Tool. Available online: https://www.tdk-electronics.tdk.com/en/180490/design-support/design-tools/ferrite-magnetic-design-tool (accessed on 10 June 2025).


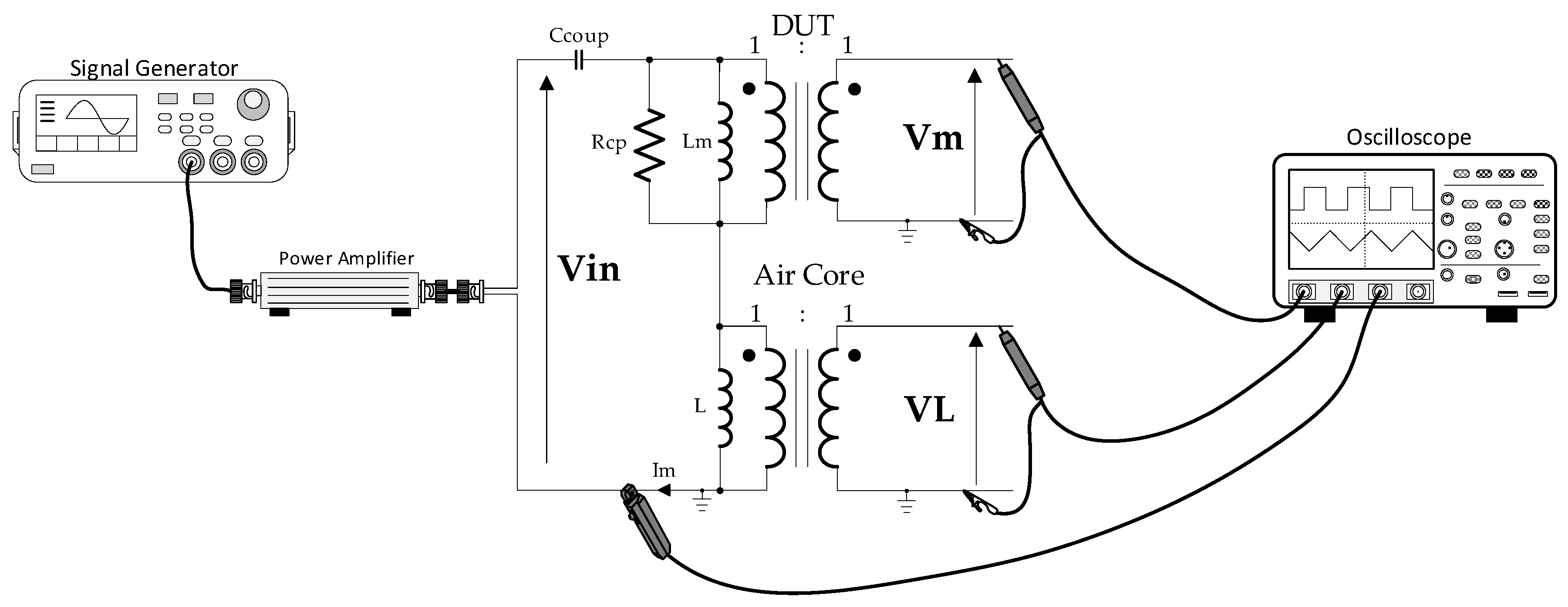
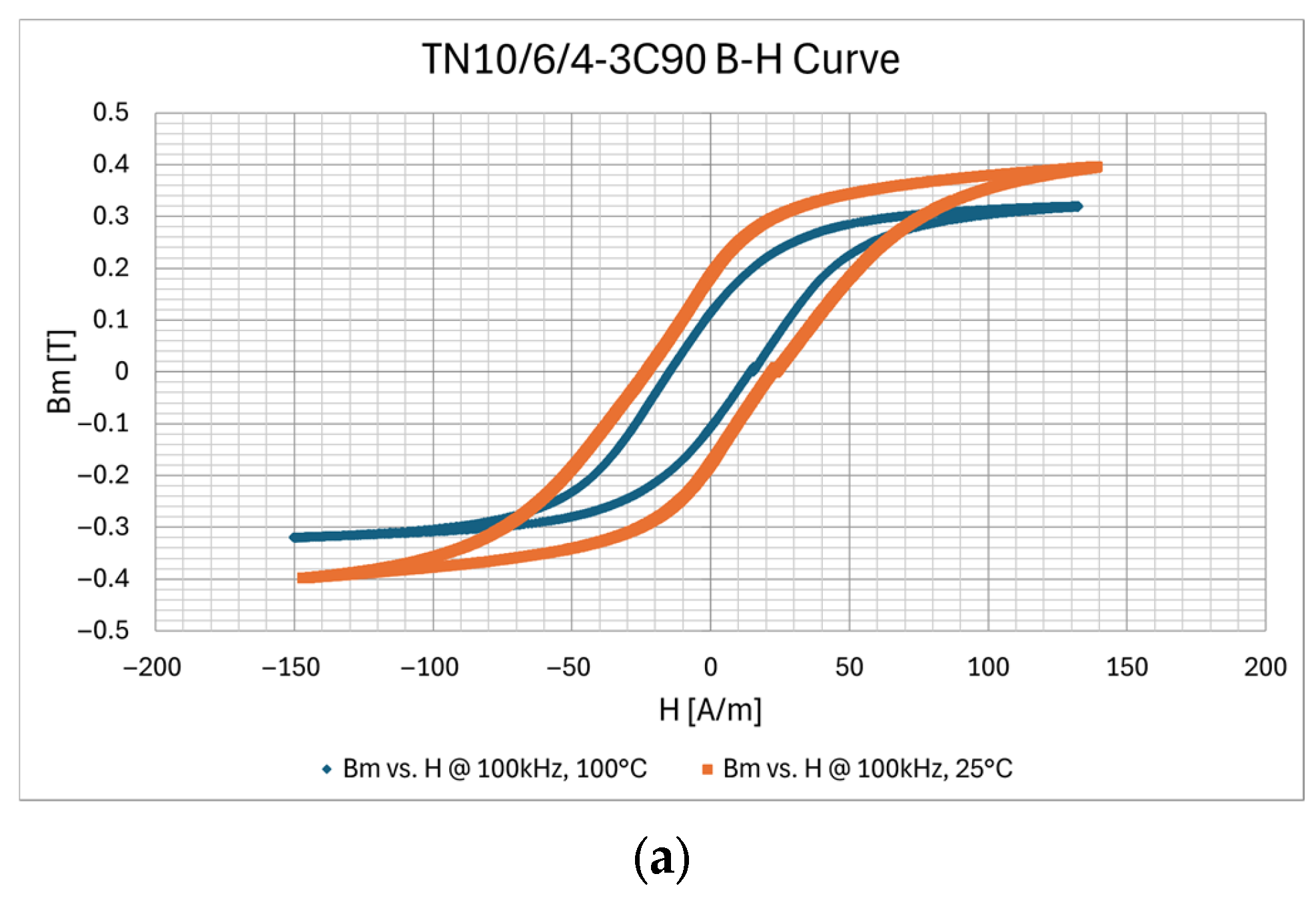
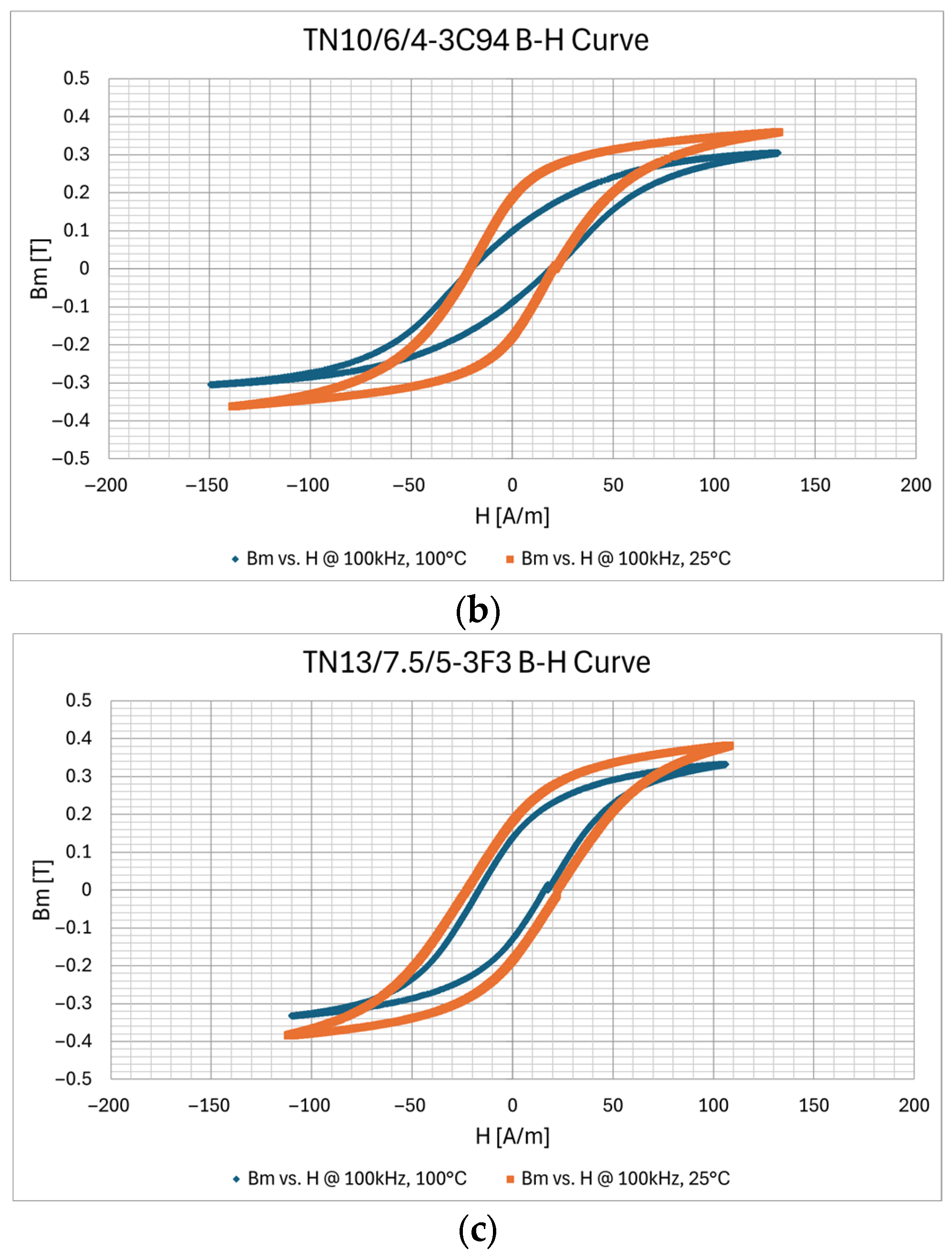
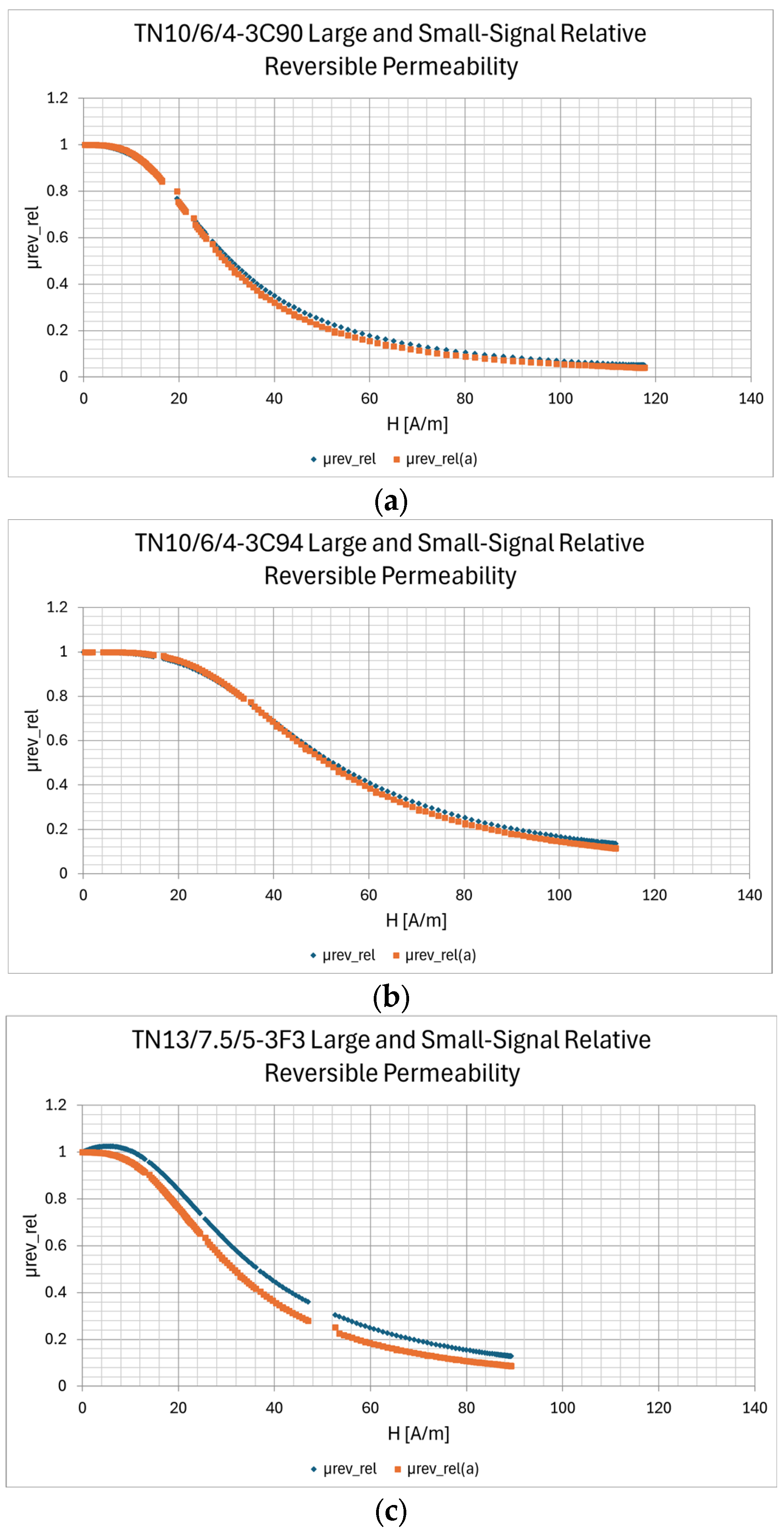

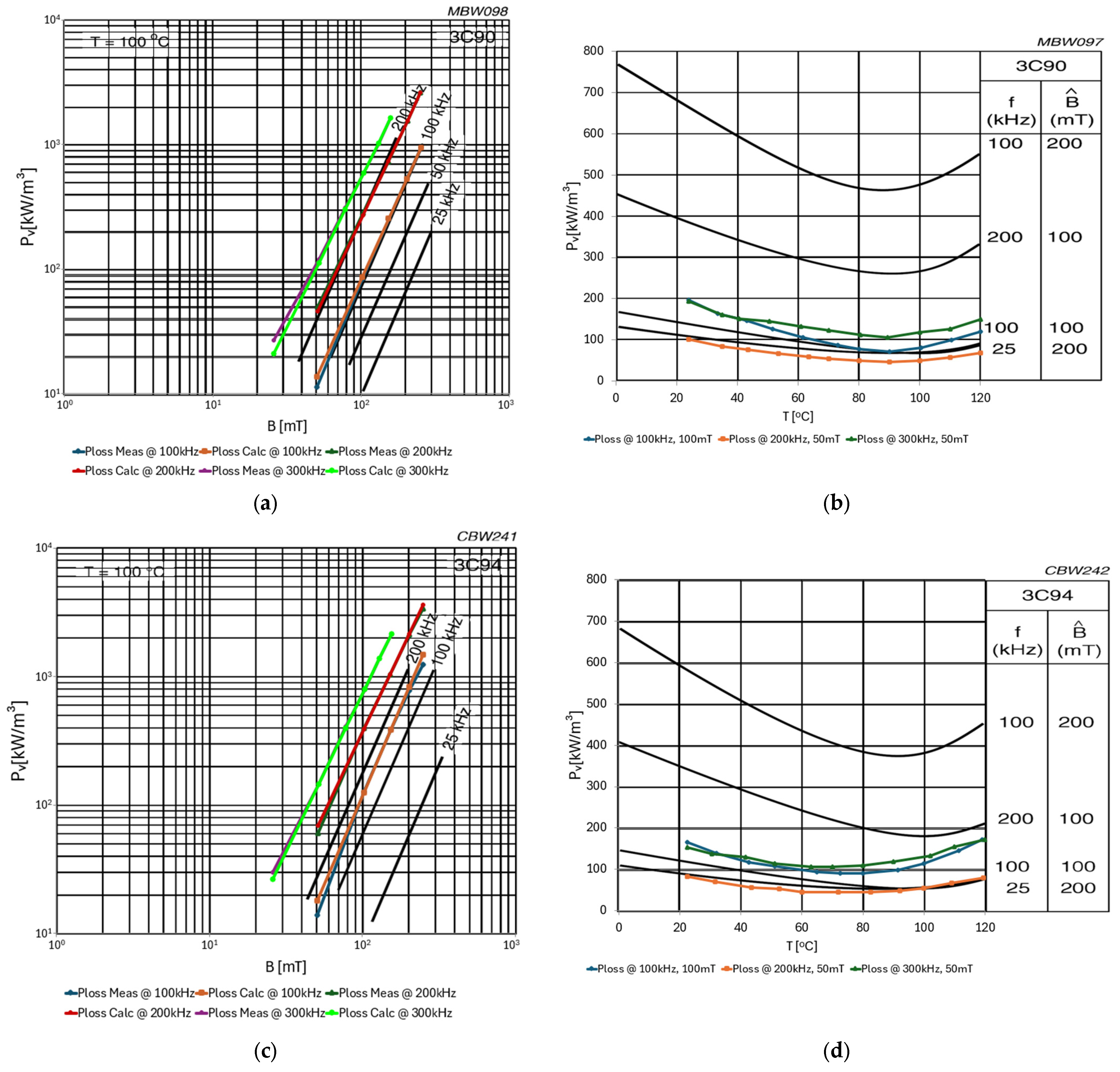
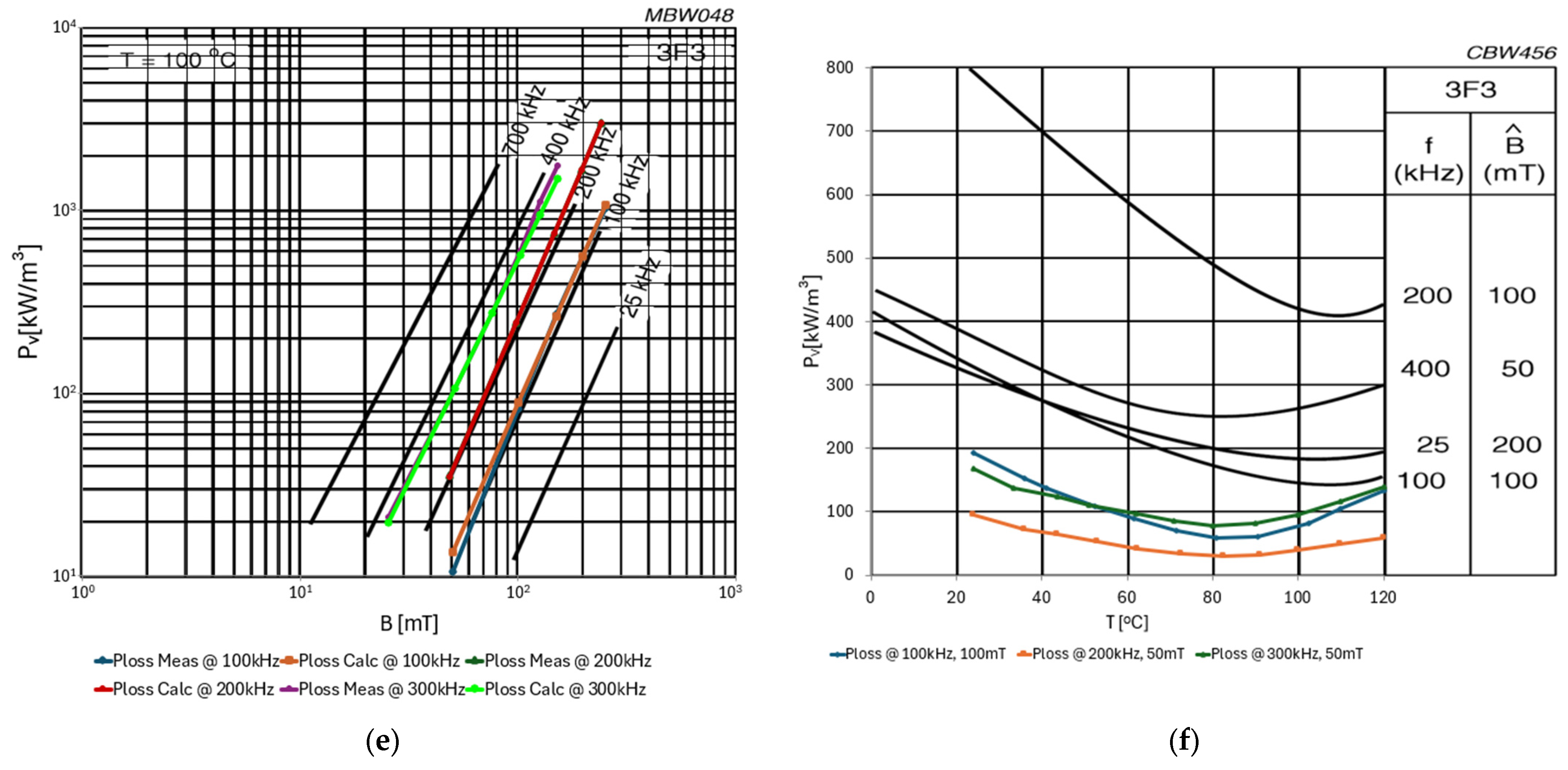
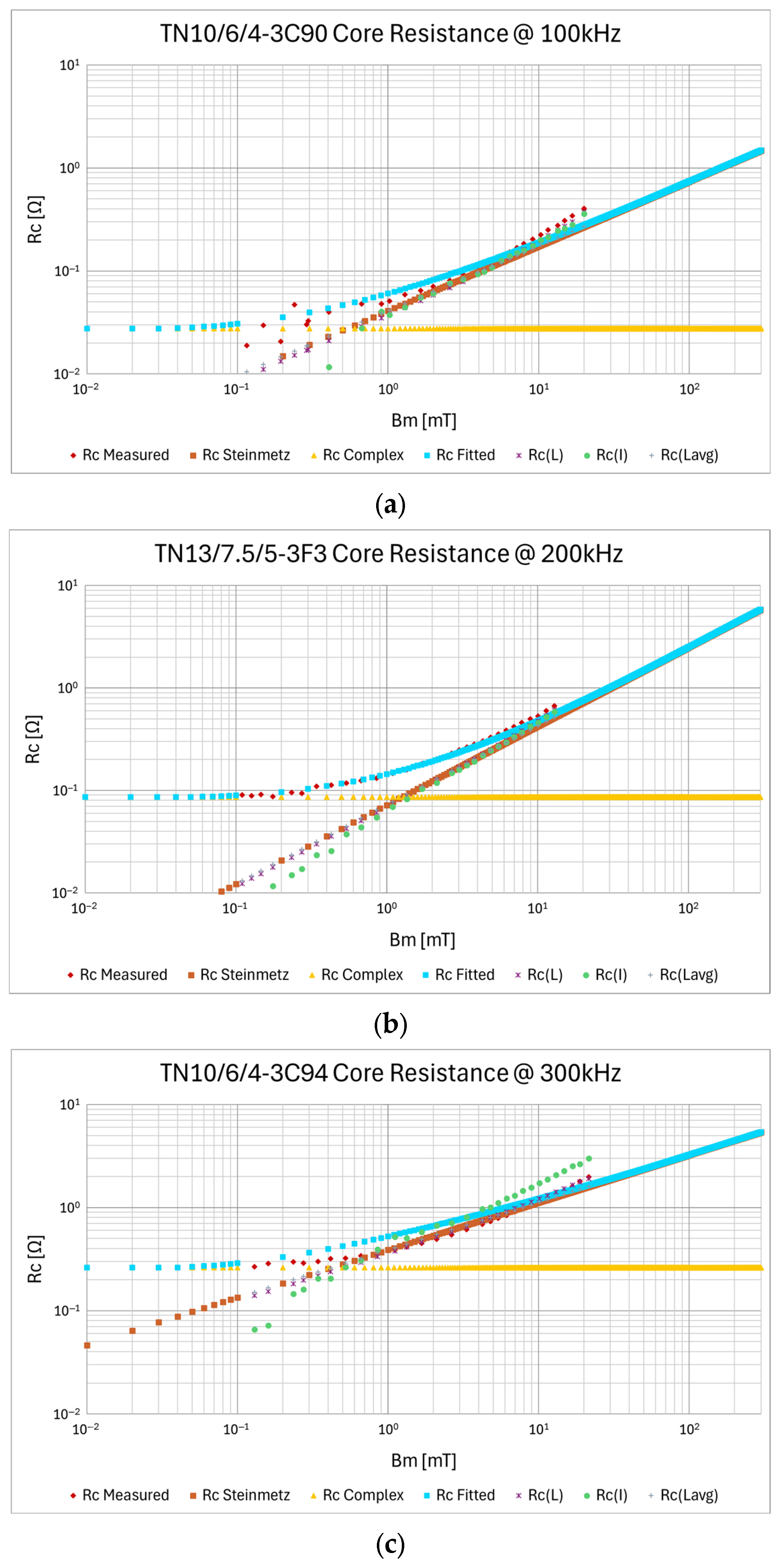
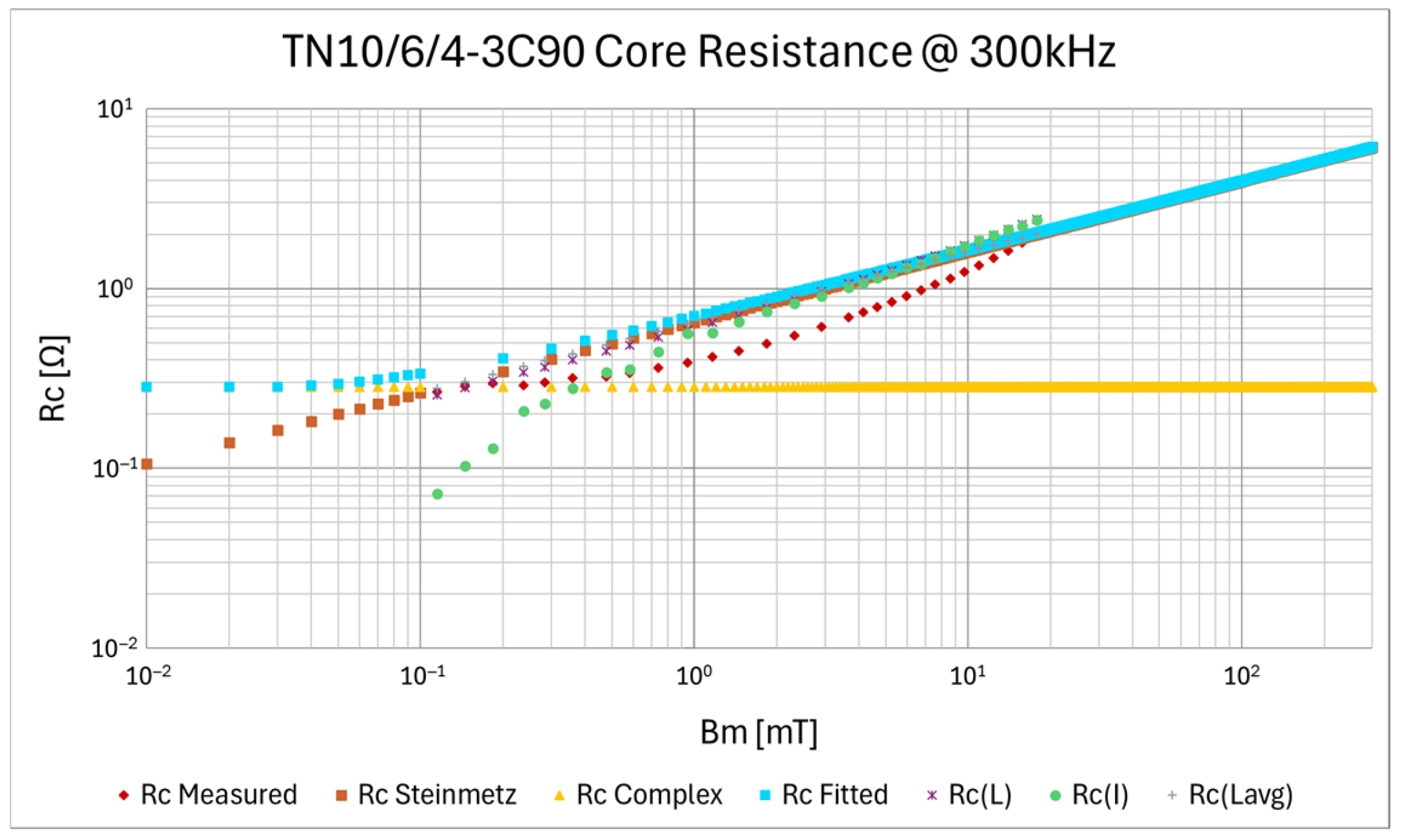
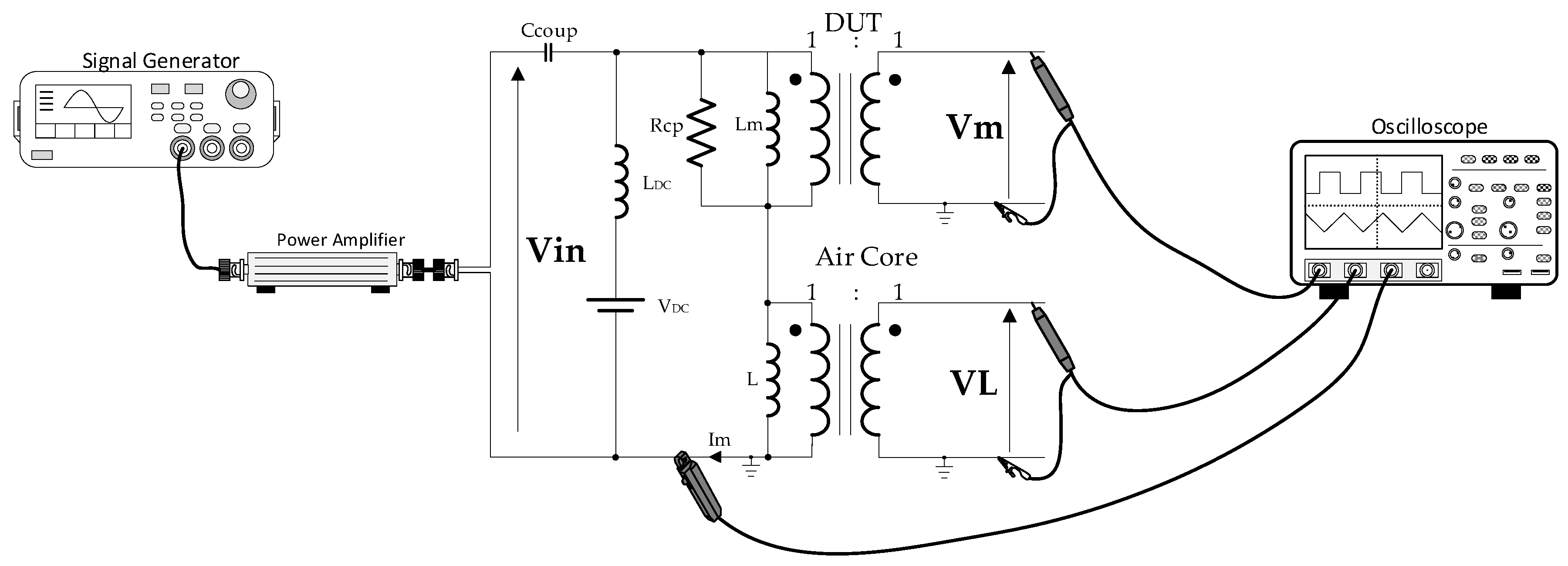


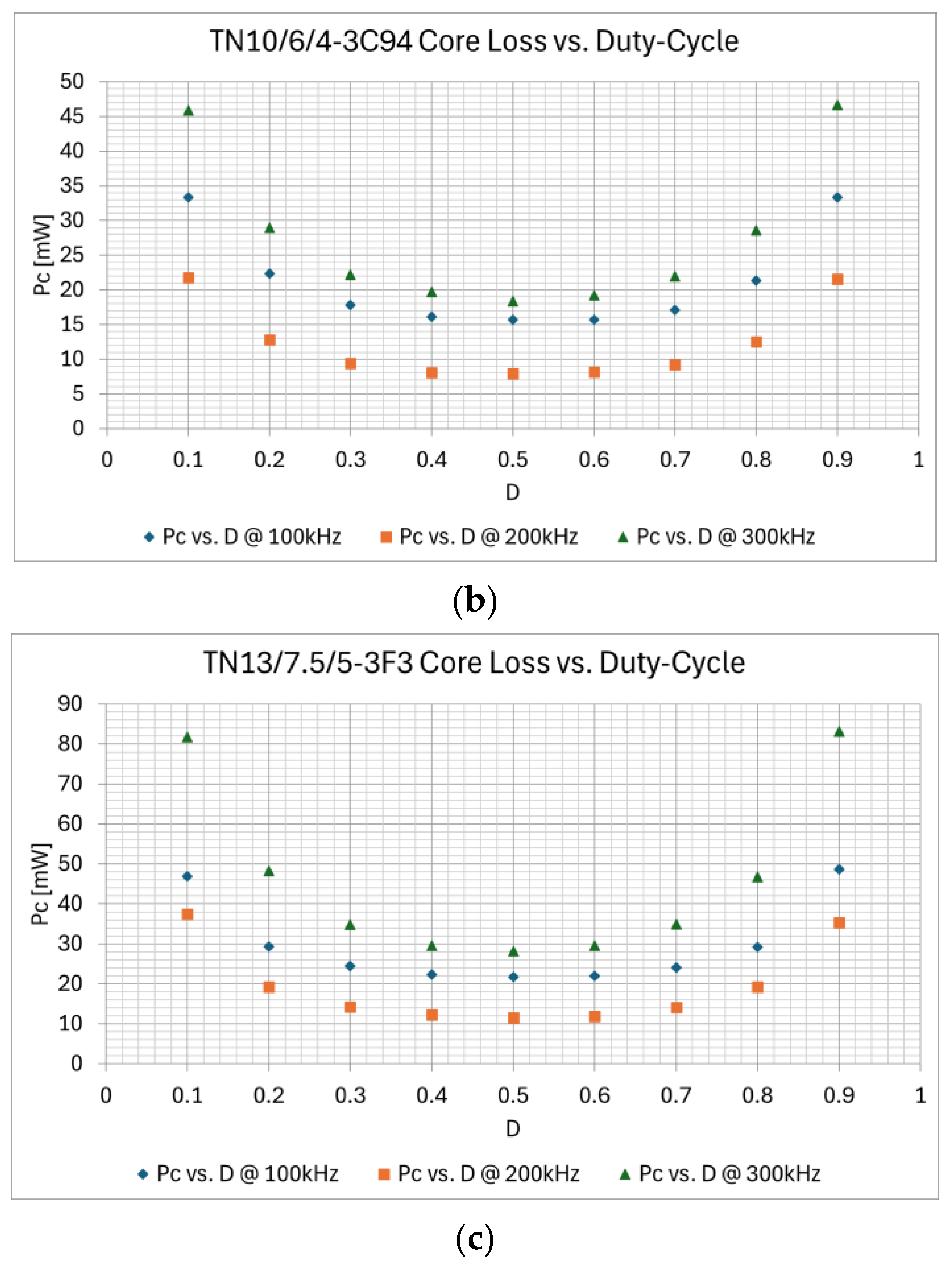
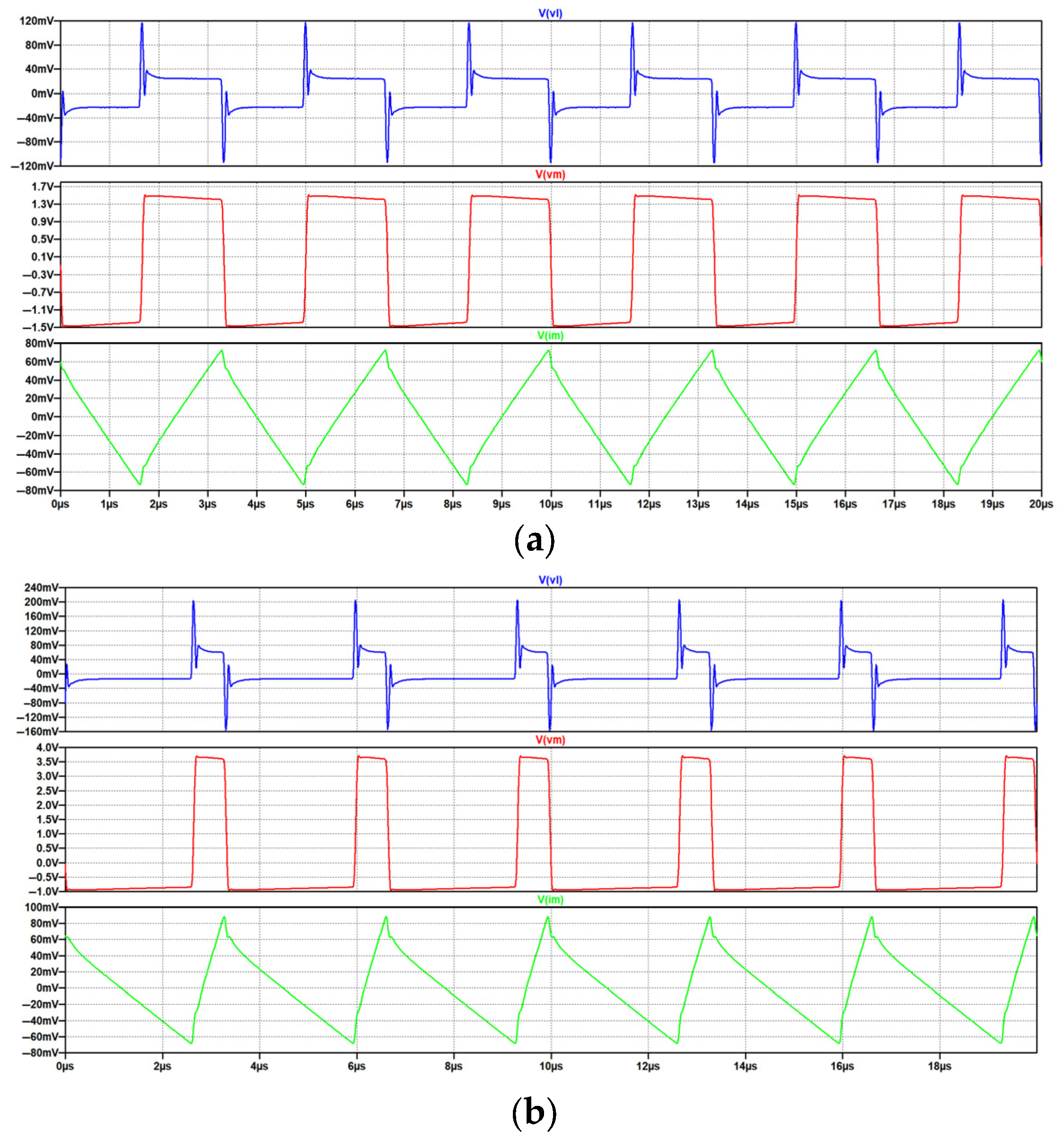



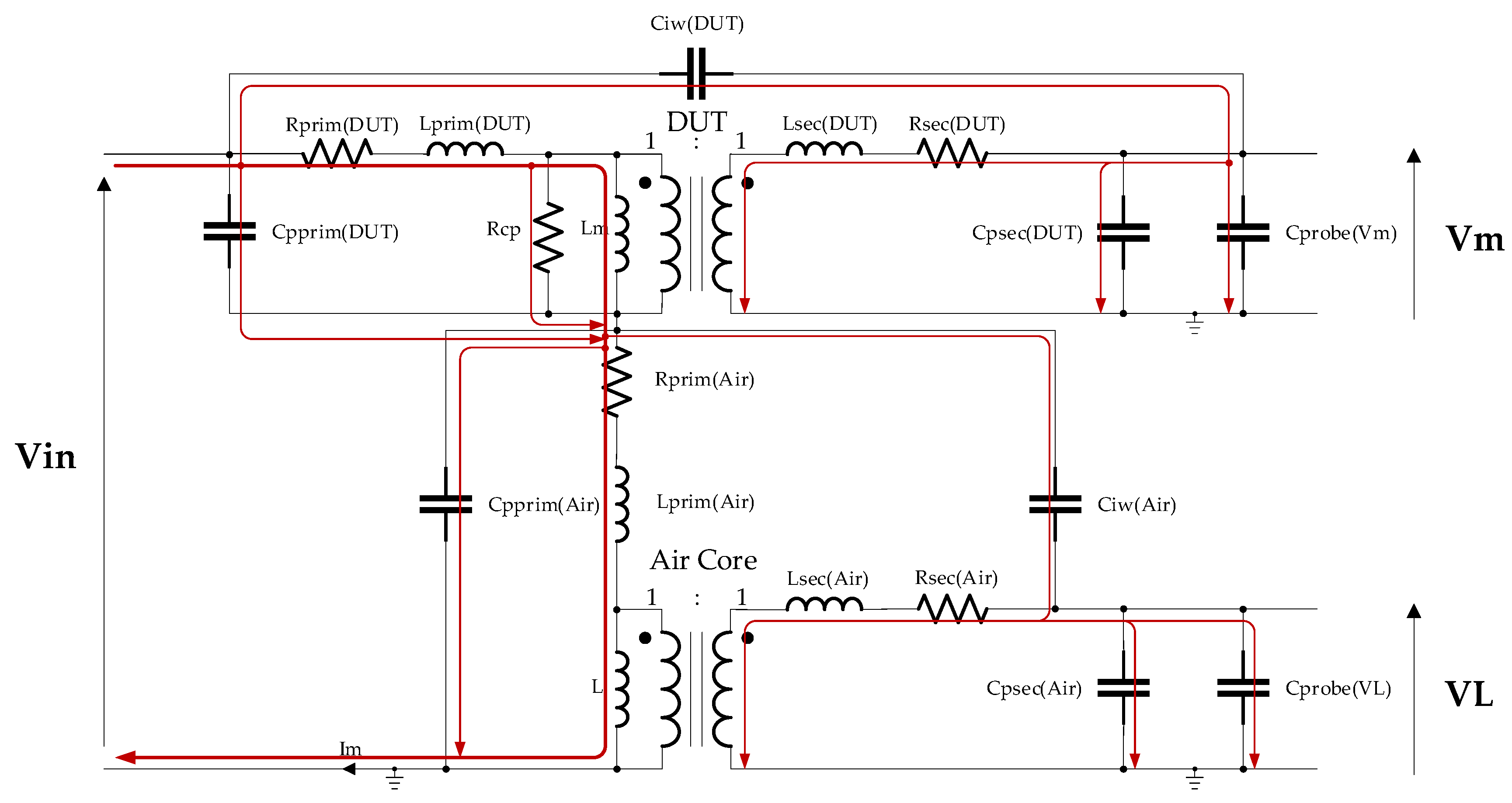
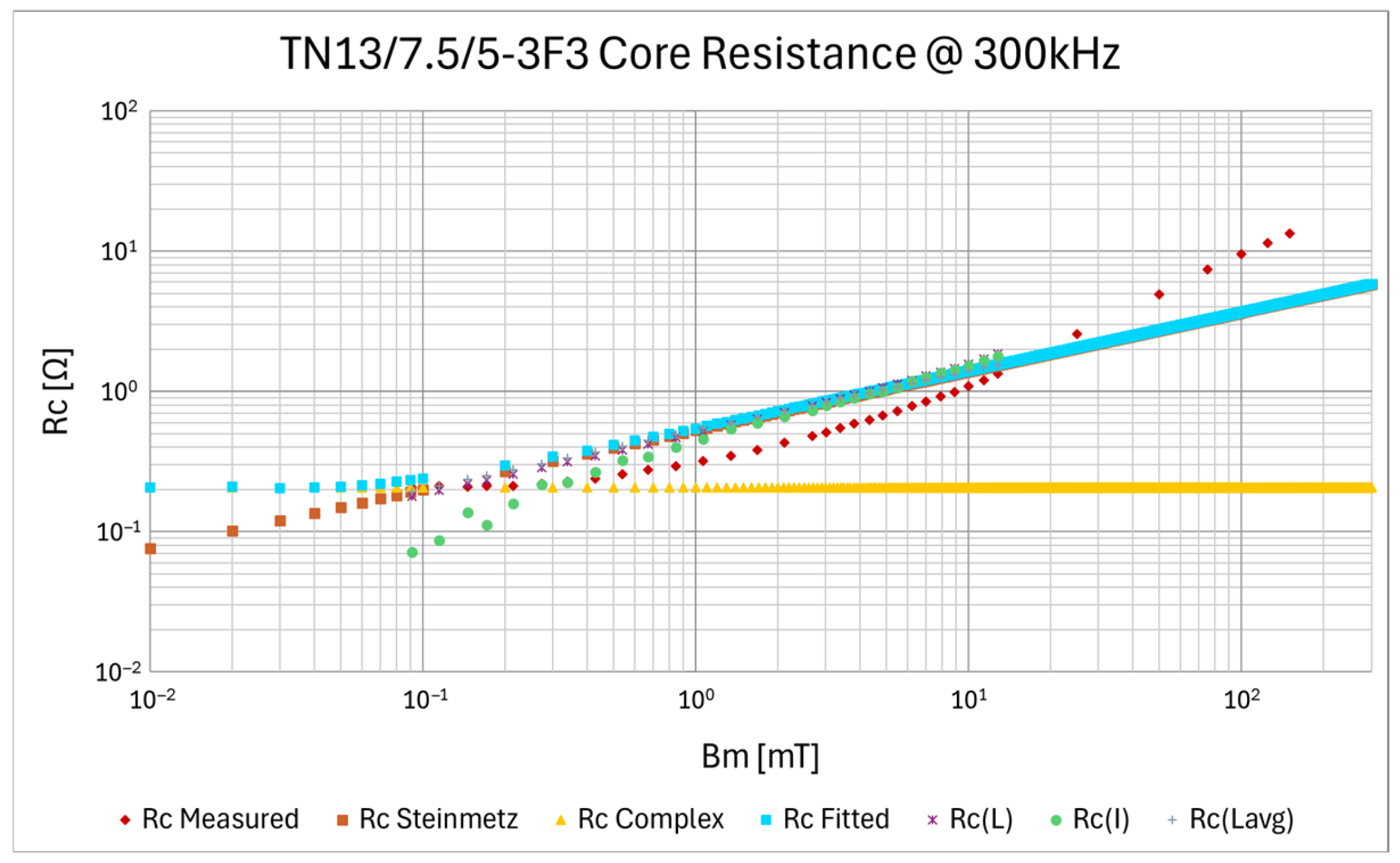
| Description | Core | Material | N | Lprim [μH] | Lsec [μH] | Lleak_prim [nH] | Lleak_sec [nH] | Rleak_prim [mΩ] | Rleak_sec [mΩ] | Cinter_wind [pF] | Rcp [Ω] | fres [MHz] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | TN10/6/4 | 3C90 | 3 | 8.184 | 8.058 | 239.665 | 238.684 | 23.727 | 17.093 | 14.751 | 107.427 | 16.492 |
| Sample 2 | TN10/6/4 | 3C94 | 3 | 9.719 | 9.751 | 249.976 | 236.226 | 13.048 | 12.855 | 12.903 | 111.939 | 11.543 |
| Sample 3 | TN13/7.5/5 | 3F3 | 3 | 9.736 | 9.620 | 172.545 | 183.281 | 11.306 | 10.078 | 12.454 | 128.580 | 8.201 |
| Air Trafo | TN58/18/9 | Air | 10 | 0.476 | 0.476 | 395.626 | 371.912 | 24.617 | 29.967 | 25.676 | - | 100 |
| Description | Core | Material | N | Lprim [μH] | Lsec [μH] | Lleak_prim [nH] | Lleak_sec [nH] | Rleak_prim [mΩ] | Rleak_sec [mΩ] | Cinter_wind [pF] | Rcp [Ω] | fres [MHz] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | TN10/6/4 | 3C90 | 3 | 18.376 | 18.307 | 189.042 | 191.497 | 21.881 | 22.56 | 78.647 | 150.708 | 4.800 |
| Sample 2 | TN10/6/4 | 3C94 | 3 | 11.708 | 11.288 | 182.671 | 199.912 | 23.270 | 21.437 | 95.059 | 148.843 | 7.368 |
| Sample 3 | TN13/7.5/5 | 3F3 | 3 | 17.931 | 17.878 | 196.525 | 171.681 | 26.126 | 24.991 | 27.125 | 171.068 | 4.722 |
| Air Trafo | TN58/18/9 | Air | 10 | - | - | - | - | - | - | - | - | - |
| Description | a | Bsat [T] | |||
|---|---|---|---|---|---|
| Sample 1 | 5627 | 2120 | 3.48 | 10.05 | 0.48 |
| Sample 2 | 7236 | 2639 | 1.84 | 9.06 | 0.46 |
| Sample 3 | 6464 | 1963 | 2.83 | 12.84 | 0.51 |
| Description | a | Bsat [T] | |||
|---|---|---|---|---|---|
| Sample 1 | 6778 | 5070 | 3.22 | 2.56 | 0.36 |
| Sample 2 | 4187 | 3235 | 3.73 | 2.69 | 0.37 |
| Sample 3 | 6939 | 3975 | 2.89 | 4.86 | 0.41 |
| Description | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 100 | 0.791 | 1.529 | 2.629 | −2.45 × 10−9 | 8.91 × 10−7 | −1.20 × 10−4 | 0.0076 | −0.25586 | 5.515 |
| 200 | 0.904 | 1.504 | 2.525 | −1.94 × 10−9 | 7.29 × 10−7 | −1.02 × 10−4 | 0.0068 | −0.23982 | 5.322 | |
| 300 | 0.970 | 1.485 | 2.393 | −2.18 × 10−9 | 8.40 × 10−7 | −1.21 × 10−4 | 0.0083 | −0.27899 | 5.234 |
| Description | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample 2 | 100 | 0.848 | 1.581 | 2.761 | −6.01 × 10−10 | 2.30 × 10−7 | −3.20 × 10−5 | 0.00227 | −0.09287 | 2.644 |
| 200 | 0.810 | 1.540 | 2.508 | −5.91 × 10−10 | 2.11 × 10−7 | −2.80 × 10−5 | 0.00195 | −0.0823 | 2.418 | |
| 300 | 0.838 | 1.533 | 2.461 | −3.49 × 10−10 | 1.06 × 10−7 | −1.09 × 10−5 | 6.01 × 10−4 | −0.02716 | 1.553 |
| Description | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample 3 | 100 | 0.811 | 1.547 | 2.704 | −2.51 × 10−9 | 8.77 × 10−7 | −1.12 × 10−4 | 0.00681 | −0.22914 | 5.049 |
| 200 | 0.709 | 1.571 | 2.769 | −2.54 × 10−9 | 8.87 × 10−7 | −1.15 × 10−4 | 0.00729 | −0.25979 | 5.875 | |
| 300 | 0.826 | 1.503 | 2.421 | −2.27 × 10−9 | 8.18 × 10−7 | −1.10 × 10−4 | 0.00703 | −0.23142 | 4.443 |
| Description | Sample 1 | Sample 2 | Sample 3 | |
|---|---|---|---|---|
| 100 | 7.497 | 8.672 | 8.365 | |
| 200 | 7.454 | 8.741 | 8.467 | |
| 300 | 7.623 | 7.622 | 8.749 |
| Description | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 100 | −725.08 | 1025.98 | −609.21 | 197.11 | −37.45 | 4.17 | −0.25239 | 0.00638 | 2.22 × 10−8 | −1.70 × 10−13 |
| 200 | −733.34 | 1020.17 | −595.92 | 189.24 | −35.24 | 3.84 | −0.22725 | 0.00561 | 1.43 × 10−7 | −8.50 × 10−13 | |
| 300 | −599.28 | 847.12 | −503.48 | 162.89 | −30.94 | 3.45 | −0.20846 | 0.00527 | 2.47 × 10−7 | −1.19 × 10−12 |
| Description | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample 2 | 100 | −631.83 | 879.29 | −513.85 | 163.25 | −30.42 | 3.32 | −0.1964 | 0.00486 | 2.55 × 10−8 | −1.69 × 10−13 |
| 200 | −733.34 | 1020.17 | −595.93 | 189.24 | −35.24 | 3.84 | −0.22725 | 0.00561 | 1.43 × 10−7 | −8.50 × 10−13 | |
| 300 | −1708.83 | 2414.73 | −1434.67 | 464.00 | −88.12 | 9.82 | −0.59329 | 0.015 | 1.67 × 10−7 | −8.71 × 10−13 |
| Description | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample 3 | 100 | −249.76 | 351.26 | −207.63 | 66.79 | −12.61 | 1.39 | −0.08386 | 0.00211 | 2.78 × 10−8 | −1.66 × 10−13 |
| 200 | −587.67 | 829.69 | −492.48 | 159.12 | −30.19 | 3.36 | −0.2028 | 0.00512 | 1.55 × 10−8 | −9.35 × 10−14 | |
| 300 | −206.99 | 287.063 | −167.11 | 52.86 | −9.80 | 1.06 | −0.06253 | 0.00153 | 2.63 × 10−7 | −1.42 × 10−12 |
| Description | ||||||
|---|---|---|---|---|---|---|
| Sample 1 | 100 | −370.118 | 199.123 | −5.470 | −2.5174 | 1.0098 |
| 200 | −186.883 | 232.729 | −10.233 | −4.0389 | 0.9487 | |
| 300 | 99.271 | 66.133 | −3.080 | −2.4056 | 0.9731 |
| Description | ||||||
|---|---|---|---|---|---|---|
| Sample 2 | 100 | 684.753 | −354.010 | 78.725 | −6.8433 | 1.0029 |
| 200 | 150.945 | 83.041 | 25.125 | −8.408 | 1.0161 | |
| 300 | −148.965 | 80.326 | 7.861 | −3.3445 | 0.9999 |
| Description | ||||||
|---|---|---|---|---|---|---|
| Sample 3 | 100 | −449.625 | 188.253 | 1.674 | −0.7833 | 1.0291 |
| 200 | −1136.548 | 667.751 | −71.603 | −0.4124 | 0.9818 | |
| 300 | −224.727 | 179.503 | −12.493 | −1.4470 | 1.0019 |
| Description | |||
|---|---|---|---|
| Sample 1 | 100 | 0.8465 | 0.8512 |
| 200 | 0.9226 | 0.9771 | |
| 300 | 0.8205 | 0.9794 | |
| Sample 2 | 100 | 0.7525 | 0.8510 |
| 200 | 0.9847 | 0.9209 | |
| 300 | 0.8751 | 0.9401 | |
| Sample 3 | 100 | 0.7947 | 0.9028 |
| 200 | 1.1165 | 1.0270 | |
| 300 | 1.0206 | 1.0089 |
| Description | |||
|---|---|---|---|
| Sample 1 | 100 | 0.8465 | 0.8596 |
| 200 | 0.9226 | 0.9271 | |
| 300 | 0.8205 | 0.9531 | |
| Sample 2 | 100 | 0.752 | 0.8535 |
| 200 | 0.9847 | 0.9365 | |
| 300 | 0.8751 | 0.9401 | |
| Sample 3 | 100 | 0.7947 | 0.9028 |
| 200 | 1.1165 | 1.0270 | |
| 300 | 1.0206 | 1.0109 |
| Description | ||||||
|---|---|---|---|---|---|---|
| Sample 1 | 100 | 1.15 × 10−6 | −0.0001627 | 0.007439 | −0.08603 | 1.0606 |
| 200 | 1.15 × 10−6 | −0.0001679 | 0.008528 | −0.11997 | 1.1115 | |
| 300 | 6.07 × 10−8 | −0.0000184 | 0.001820 | −0.03518 | 1.0186 |
| Description | ||||||
|---|---|---|---|---|---|---|
| Sample 2 | 100 | 1.00 × 10−6 | −0.0001296 | 0.0056645 | −0.08053 | 1.1350 |
| 200 | 1.00 × 10−6 | −0.0001325 | 0.0064732 | −0.10974 | 1.1437 | |
| 300 | −1.72 × 10−8 | 2.94 × 10−8 | 0.0004832 | −0.02038 | 1.0186 |
| Description | ||||||
|---|---|---|---|---|---|---|
| Sample 3 | 100 | 1.15 × 10−6 | −0.0001478 | 0.0062136 | −0.05208 | 1.0729 |
| 200 | 1.15 × 10−6 | −0.0001458 | 0.0074738 | −0.12003 | 1.1337 | |
| 300 | 6.07 × 10−8 | −0.0000214 | 0.0018027 | −0.02333 | 1.0186 |
| Description | Lprim [μH] | Lsec [μH] | Lleak_prim [nH] | Lleak_sec [nH] | Rleak_prim [mΩ] | Rleak_sec [mΩ] | Cinter_wind [pF] | Rcp [Ω] | fres [MHz] |
|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 18.568 | 18.548 | 182.694 | 184.247 | 25.784 | 26.471 | 24.220 | 70.4 | 4.800 |
| Sample 2 | 11.841 | 11.414 | 175.229 | 189.403 | 27.772 | 25.497 | 18.526 | 47.1658 | 7.368 |
| Sample 3 | 18.216 | 18.140 | 188.149 | 166.297 | 31.611 | 29.845 | 20.270 | 72.87 | 4.722 |
| Air Trafo | 0.487 | 0.489 | 314.881 | 304.308 | 42.556 | 39.001 | 25.388 | - | 100 |
| Description | Lprim [μH] | Lsec [μH] | Lleak_prim [nH] | Lleak_sec [nH] | Rleak_prim [mΩ] | Rleak_sec [mΩ] | Cinter_wind [pF] | Rcp [Ω] | fres [MHz] |
|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 18.262 | 18.288 | 179.118 | 180.666 | 33.078 | 33.402 | 23.667 | 126.6 | 4.800 |
| Sample 2 | 12.002 | 11.640 | 170.801 | 185.170 | 35.615 | 33.457 | 17.789 | 111.7 | 7.368 |
| Sample 3 | 18.910 | 18.825 | 183.873 | 161.853 | 39.330 | 37.527 | 19.977 | 177.4 | 4.722 |
| Air Trafo | 0.479 | 0.482 | 303.155 | 293.115 | 55.424 | 59.593 | 25.370 | - | 100 |
| Description | Lprim [μH] | Lsec [μH] | Lleak_prim [nH] | Lleak_sec [nH] | Rleak_prim [mΩ] | Rleak_sec [mΩ] | Cinter_wind [pF] | Rcp [Ω] | fres [MHz] |
|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | 17.519 | 17.548 | 176.027 | 177.572 | 40.202 | 40.539 | 23.436 | 120.1 | 4.800 |
| Sample 2 | 11.867 | 11.532 | 167.261 | 181.697 | 43.284 | 41.182 | 17.572 | 109.4 | 7.368 |
| Sample 3 | 19.089 | 18.991 | 181.120 | 159.157 | 46.980 | 44.943 | 19.873 | 171.4 | 4.722 |
| Air Trafo | 0.474 | 0.477 | 295.656 | 285.495 | 70.129 | 75.881 | 25.262 | - | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szczerba, P.; Worek, C. Improved Rectangular Extension of Steinmetz Equation Including Small and Large Excitation Signals with DC Bias. Electronics 2025, 14, 2883. https://doi.org/10.3390/electronics14142883
Szczerba P, Worek C. Improved Rectangular Extension of Steinmetz Equation Including Small and Large Excitation Signals with DC Bias. Electronics. 2025; 14(14):2883. https://doi.org/10.3390/electronics14142883
Chicago/Turabian StyleSzczerba, Piotr, and Cezary Worek. 2025. "Improved Rectangular Extension of Steinmetz Equation Including Small and Large Excitation Signals with DC Bias" Electronics 14, no. 14: 2883. https://doi.org/10.3390/electronics14142883
APA StyleSzczerba, P., & Worek, C. (2025). Improved Rectangular Extension of Steinmetz Equation Including Small and Large Excitation Signals with DC Bias. Electronics, 14(14), 2883. https://doi.org/10.3390/electronics14142883






