Optimization and Verification of Acquisition Time Method Based on a Data-Driven Model for Laser Inter-Satellite Links

Abstract

High-speed communication can be achieved using laser inter-satellite links. However, laser terminals are highly sensitive to environmental conditions, which can lead to link disconnections. Therefore, an acquisition method capable of determining pointing errors is essential. In this study, a fast space–time fusion acquisition method was developed. This method establishes the relationship between satellite position, capture time, and azimuth and elevation angles. The performance of the proposed acquisition time optimization method was verified in a practical engineering application. Experimental results show that the pointing error was reduced by five times, the acquisition rate increased by 40%, the acquisition speed improved by 300 times, and multiple interference factors were effectively addressed.

1. Introduction

Laser inter-satellite links (L-ISLs) have the potential to significantly enhance communication rates—by several orders of magnitude—and reduce interference between multiple laser communication terminals due to their narrow beam divergence [1,2,3,4,5,6,7]. As a result, L-ISLs have attracted considerable attention and have been deployed in satellite constellations such as EDRS in Europe and Starlink in the United States [8,9,10,11].

However, adjacent satellites that need to communicate are usually far apart, making it challenging to establish laser communication links. To establish laser communication links, the pointing error corresponding to the recovery time and tracking error, which in turn corresponds to the link stability, are needed to be eliminated. Traditionally, the error, a scanning method based on a pointing, acquisition, and tracking (PAT) system is required [12,13,14,15]. The speed of the acquisition process determines how quickly communication services can be initiated and how rapidly they can be restored after a disconnection.

During the acquisition process, scanning within the uncertainty cone is typically performed using a scanning function [16,17,18,19]. Among various scanning functions, spiral scanning offers smoother changes in azimuth and elevation. Because equal linear velocity scanning outperforms equal angular velocity scanning in terms of success rate, an equal linear velocity spiral scanning function was adopted. To further accelerate the acquisition process, parameters such as divergence angle, overlap factor, angular velocity, and linear velocity were optimized, and several novel scanning strategies were developed [20,21,22,23]. However, these adjustments were typically made under specific conditions, such as mechanical vibrations or thermal deformation. Given the multiple factors that can affect L-ISL performance, comprehensive adjustments are required.

To achieve this, neural network methods can be employed. Neural networks are capable of approximating the pointing error function in L-ISLs and predicting relationships between pointing errors and satellite status parameters, accounting for multiple influencing factors. Among various architectures, feedforward neural networks (FNNs) are particularly suitable due to their simplicity, faster training, higher accuracy, and ease of deployment on laser terminals [24,25,26,27].

In this paper, a novel scanning method based on an FNN is proposed. To improve data consistency, filter algorithm is used in the first place. Since orbital parameters are more readily available than information related to mechanical vibration or thermal deformation, the relationship between orbital parameters and the pointing azimuth and elevation angles was established. To evaluate performance, the speed and success rate of the original acquisition process, the traditionally adjusted acquisition process, and the FNN-enhanced acquisition process were compared.

To validate the proposed method, the predicted results were analyzed against on-orbit telemetry data. Experimental results demonstrated that the FNN-based acquisition process achieved more than a 300-fold improvement in speed and an 8-fold increase in success rate compared to the original process.

2. Basic Theory and Principle

2.1. Acquisition Process

The acquisition process of the L-ISL is designed to accurately determine the position of the counter laser terminal. This process is facilitated by a pointing, acquisition, and tracking (PAT) system, as illustrated in Figure 1. The PAT system consists of a coarse pointing assembly (CPA), fine pointing assembly (FPA), pointing ahead assembly (PAA), dichroic mirror (DM), fast steering mirror (FSM), and polarizing beam splitter (PBS). The CPA and FPA work together to track the position of the counter laser terminal in real time, while the PAA predicts its position in advance. The azimuth and elevation angles for the PAA are typically calculated based on the relative velocity of the counter satellite.

The movements of the CPA and FPA were controlled using a coarse–fine composite control (CFCC) system, as shown in Figure 2. In this system, the movements of the CPA and FPA are simulated using the transfer function and decoupled with a decoupling function, which is usually established based on the system error. Measurement and vibration errors were introduced into the CPA module to ensure the accuracy of the simulation.

The azimuth and elevation were analyzed by introducing measurement and vibration errors into the CFCC system, as shown in Figure 3. We observed a slight difference before and after the transfer function in the CFCC system.

In the acquisition process, the computation of azimuth and elevation in the CFCC system includes a counterposition calculation step, scanning in the uncertainty cone step, and a coordinate transformation step. The counterposition calculation is typically performed using an orbital recursive algorithm. The scanning step was based on an equal linear velocity spiral scanning function. The coordinate transformation step shown in Figure 4 was used to transform the pointing vector of the counter laser terminal in J2000 coordinates to the coordinate system with the laser terminal as the origin. The coordinate system with the laser terminal as its origin is referred to as the laser terminal coordinate system.

2.2. Feedforward Neural Networks

In satellites, the azimuth and elevation of the laser terminal are influenced by mechanical vibrations, thermal deformation, coaxial errors, installation errors, servo errors, and other factors. The azimuth and elevation must be adjusted to maintain laser link stability. In this study, the adjustment was realized using an FNN Model, the architecture of which is shown in Figure 5. The green, blue and yellow represents input layer, hidden layer and output layer, separately. The adjustment of the azimuth and elevation was defined as the pointing error in the azimuth and elevation. The inputs of the FNN model include the local and target J2000 coordinate and velocities in the x, y, z direction, as well as the azimuth, pitch, yaw angles of the satellite platform, and CPA theoretical angle. The outputs are the pointing errors in azimuth and elevation. There isan activation function and a standard neuron structure between the input and output.

In the FNN modeling process, more than 1 × 10⁵ sample sets were used. Of these, 70% of the data were used as the training set, 15% as the test set, and the remaining 15% as the validation set. The choice of optimization method significantly affects the speed of the FNN modeling process. Several optimization methods are compared in

Table 1. Comparison of MSE between multiple optimization methods.

Optimization Method	Iterative Steps	MSE
Adam	200	4551.5825
Adamax	200	7025.6172
AdamW	200	1374.5110
Adagrad	200	20,831.5346
RMSprop	200	9259.3991
Adadelta	200	17,830.1423

. During modeling, the learning rate was set to 0.01, and performance evaluation was based on the mean square error (MSE). The minibatch size is settled as 100. Among the methods tested, the Adaptive Moment Estimation (AdamW) optimizer demonstrated the best performance, achieving the lowest MSE.

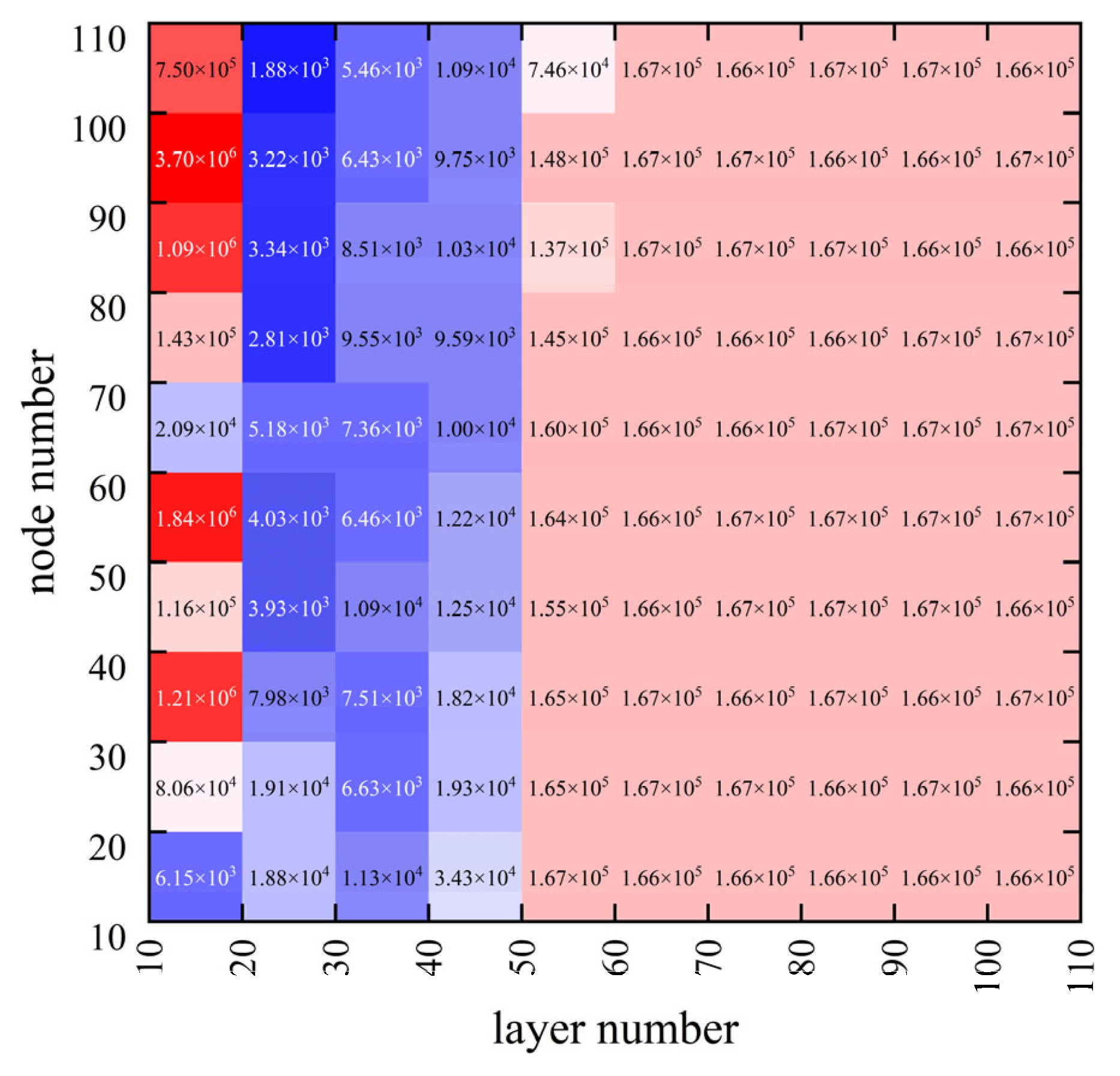
To improve the performance and avoid overfitting, the MSEs of multiple FNN Models were evaluated at different numbers of hidden layer nodes and layers. The results of this analysis are presented in Figure 6. The FNN Model showed higher performance when the hidden layer was set to 70 nodes and 20 layers.

Activation functions can introduce nonlinear transformations to enhance the expression of the FNN and improve its performance of the FNN Model. To obtain the appropriate activation functions, activation functions including PReLU, sigmoid, and tanh were compared, as shown in

Table 2. Comparison of MSE between multiple activation functions.

Activation Function	Iterative Steps	MSE (μrad2)
ReLu	200	1602.0095
Leaky ReLU	200	1905.9974
PReLu	200	1374.5110
RReLu	200	2234.6063
Sigmoid	200	166,471.11
Tanh	200	166,175.66

. We can observe that the PReLU function exhibits higher performance with a smaller MSE.

3. Implementation

All computations in this section were performed using Python 3.9.19 with the NumPy 1.26.4, SciPy 1.13.1, and PyTorch 2.4 packages. To ensure experimental reproducibility, the random seed was set to 0. In the scanning method, the divergence angle was set to 70 μrad.

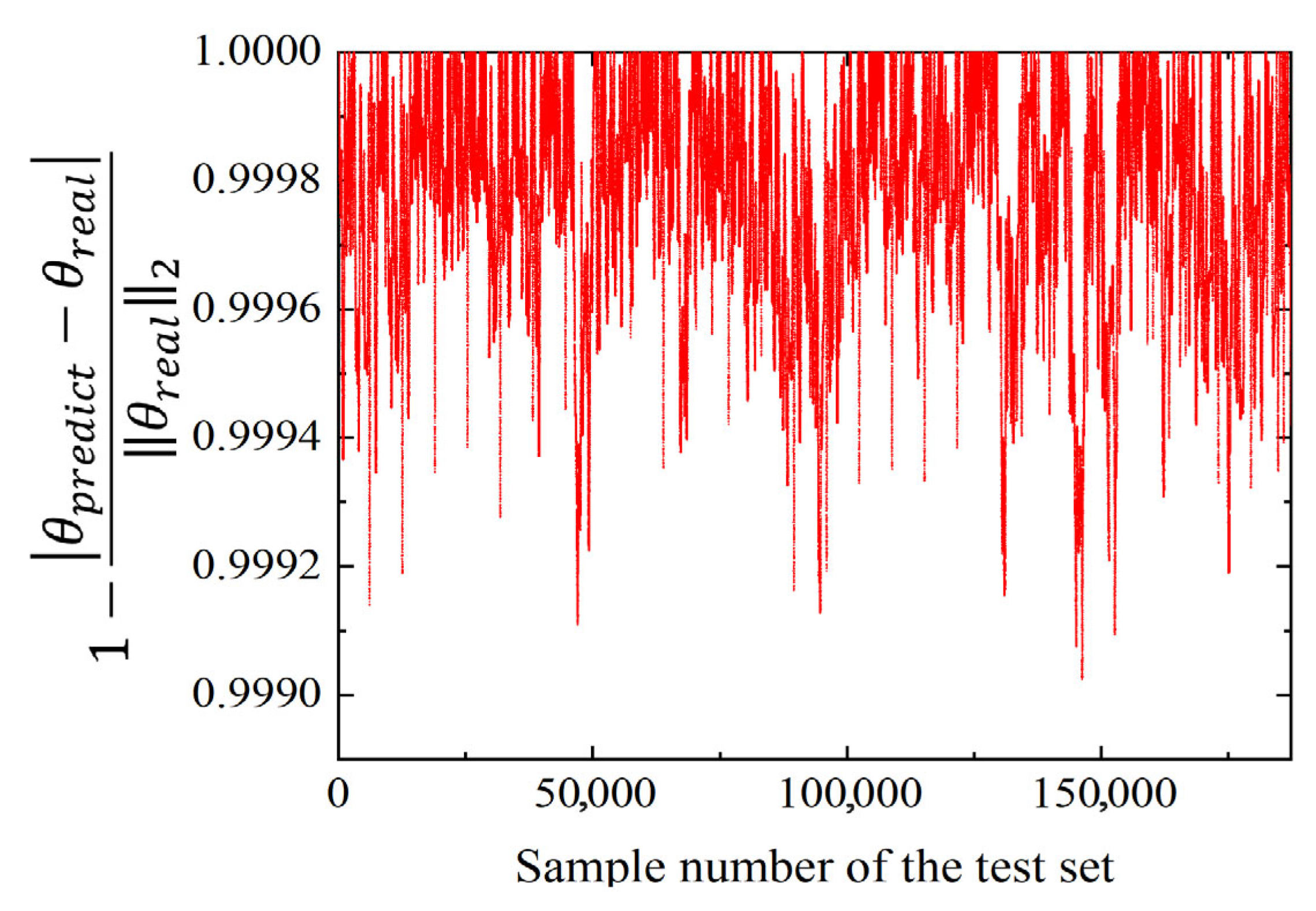
The FNN model converged within 200 steps, achieving a mean square error (MSE) of 0.117 μrad. The accuracy of the FNN Model is illustrated in Figure 7, where θ_predict denotes the predicted values and θ_real represents the corresponding test set sample data. As shown, the prediction accuracy of the FNN Model exceeded 99.9%.

The predicted errors of the FNN Model are presented in Figure 8. We can observe that most of the predicted errors in azimuth are between −60 μrad and 100 μrad while the predicted errors in elevation are between −30 μrad and 60 μrad. Compared with the original pointing errors, the adjusted pointing errors were reduced by an order of magnitude.

The trajectory of the scanning step, obtained by combining the pointing error predicted by the FNN Model with an equal linear velocity spiral scanning function, is shown in Figure 9. The uncertainty cone is at 0.6 mrad while the whole pointing error is below 1 mrad. In order to show the original and adjusted scanning trajectory curves clearly, a smaller coordinate axis range is set in Figure 9.

4. Experimental Verification

To verify the accuracy of the Model, the predicted results were compared with telemetry data, which were obtained during the bidirectional stable laser communication of an L-ISL based on on-orbit commercial satellites.

4.1. Precision of the FNN Model

The predicted results and real pointing errors obtained from the actual telemetry data are shown in Figure 10. The Pearson correlation coefficients between the predicted results and actual telemetry data were 99.85% and 98.42%.

Based on the above analysis and discussion, the error distribution of the calculated pointing error using the proposed algorithm is shown in Figure 11. As can be seen from Figure 11, the median calculation error of the elevation, azimuth, and combined pointing error is 2.0448 μrad, 13.1691 μrad, and −9.3123 μrad, respectively, while 75% of the error is within 50 μrad. Since the field of view is 600 μrad, the pointing error can meet the requirement.

4.2. Success Rate of the Acquisition Process

As pointing errors can be predicted, the acquisition process has greater potential to improve its success rate. To verify this improvement, a single step of the proposed acquisition process was compared with the traditional acquisition method using actual telemetry data, as described in Figure 12. The results show that the novel acquisition process achieves a success rate of over 90% within an uncertainty cone of 100 µrad—an improvement that is eight times higher than that of the traditional acquisition process.

Considering that the acquisition process took 5 min, the success rates of both methods are shown in Figure 13. The success rate of the novel acquisition process is higher than that of the traditional acquisition process when the uncertainty cone is below 3 mrad.

4.3. Speed of the Acquisition Process

To verify the speed of the acquisition process, the time required to achieve different success rates was analyzed using telemetry data, as shown in Figure 14. We can observe that the novel acquisition process can achieve a 90% success rate in 0.1 s, while the traditional acquisition process needs 32 s. Therefore, the acquisition process was accelerated by more than 300 times.

5. Discussion

To evaluate the effectiveness of the FNN Model at different frequencies induced by temperature and vibration, the pointing errors were analyzed using Fourier coordinates. Because the pointing error is influenced by multiple factors, its amplitude in the Fourier domain is smaller than in the time domain. As shown in Figure 15a,b, the FNN Model demonstrates better performance in reducing elevation errors compared to azimuth errors. This is attributed to the larger initial pointing errors in the azimuth direction, which provide greater potential for optimization. Additionally, Figure 15c,d show that the original pointing error exhibited a periodicity of 27 s, whereas the adjusted pointing error no longer displays this periodic behavior. This phenomenon may be related to the specific settings of the laser terminal on the satellite.

6. Conclusions

This paper proposes a novel acquisition process that leverages a FNN Model to establish the relationship between satellite orbital parameters and pointing errors in both azimuth and elevation. To evaluate the performance of the FNN Model, the predicted results were compared with on-orbit telemetry data. By integrating the predicted pointing errors with a spiral scanning function, the acquisition process was accelerated by more than 300 times, while the success rate increased by a factor of 8. The FNN Model proved effective in scenarios involving multiple influencing factors. Moreover, the potential of reinforcement learning and the feasibility of achieving full automation warrant further investigation.