Dual-Branch Spatio-Temporal-Frequency Fusion Convolutional Network with Transformer for EEG-Based Motor Imagery Classification
Abstract
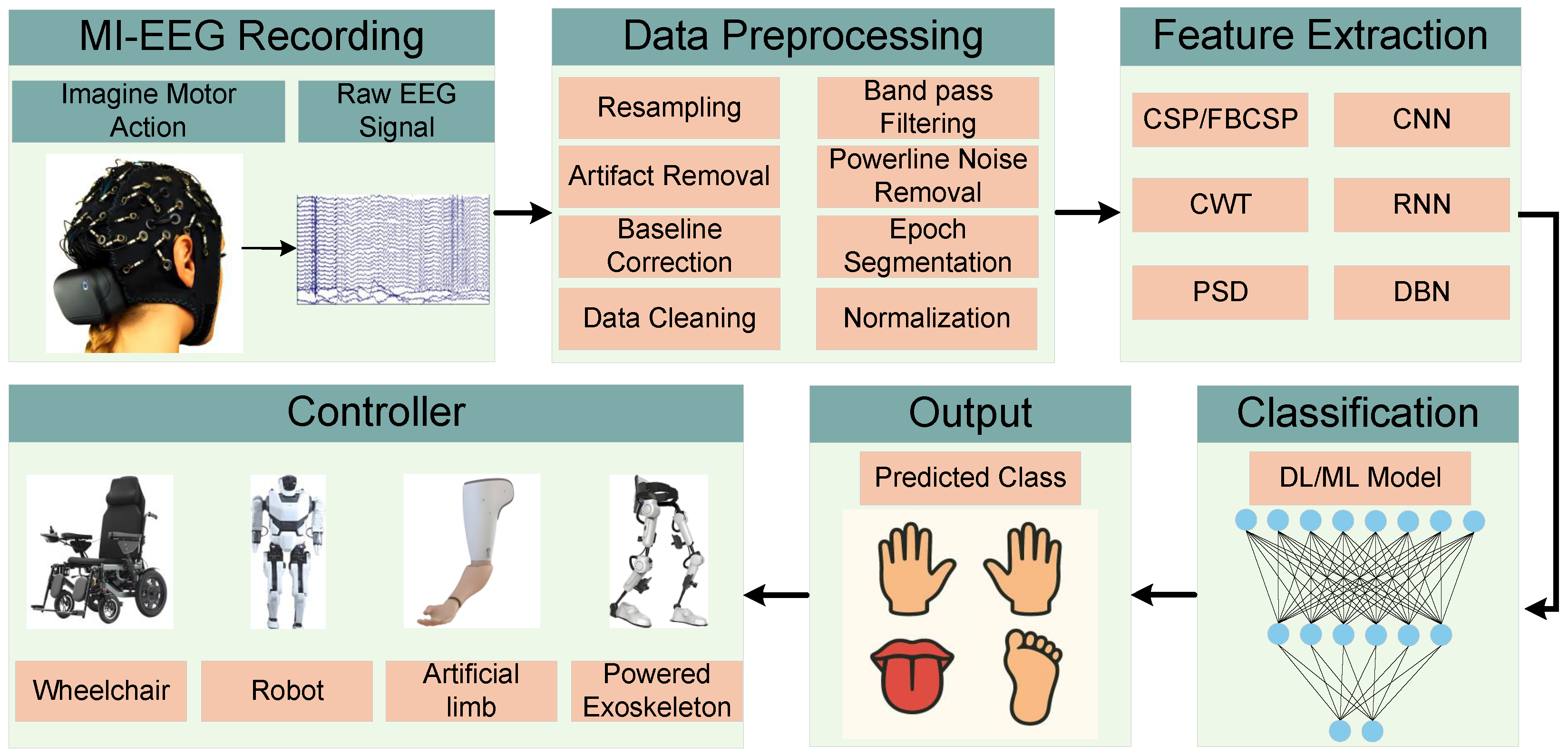
1. Introduction
- A Transformer-based multi-domain feature learning framework was proposed, which is capable of extracting global contextual information and long-term dependencies from various feature domains, enhancing the model’s overall perception of multi-dimensional signal features.
- A parallel frequency domain feature extraction module was constructed. This module integrates the FFT with a self-designed multi-scale frequency convolution to effectively mine spectral features, and it further consolidates global frequency domain information through a multi-head self-attention mechanism.
- Deep fusion of spatiotemporal and frequency domain features were achieved, and efficient classification was performed using a fully connected layer, which significantly enhances the model’s discriminative performance. Experimental results demonstrate superior performance on the BCI Competition IV-2a and IV-2b datasets.
2. Literature Review
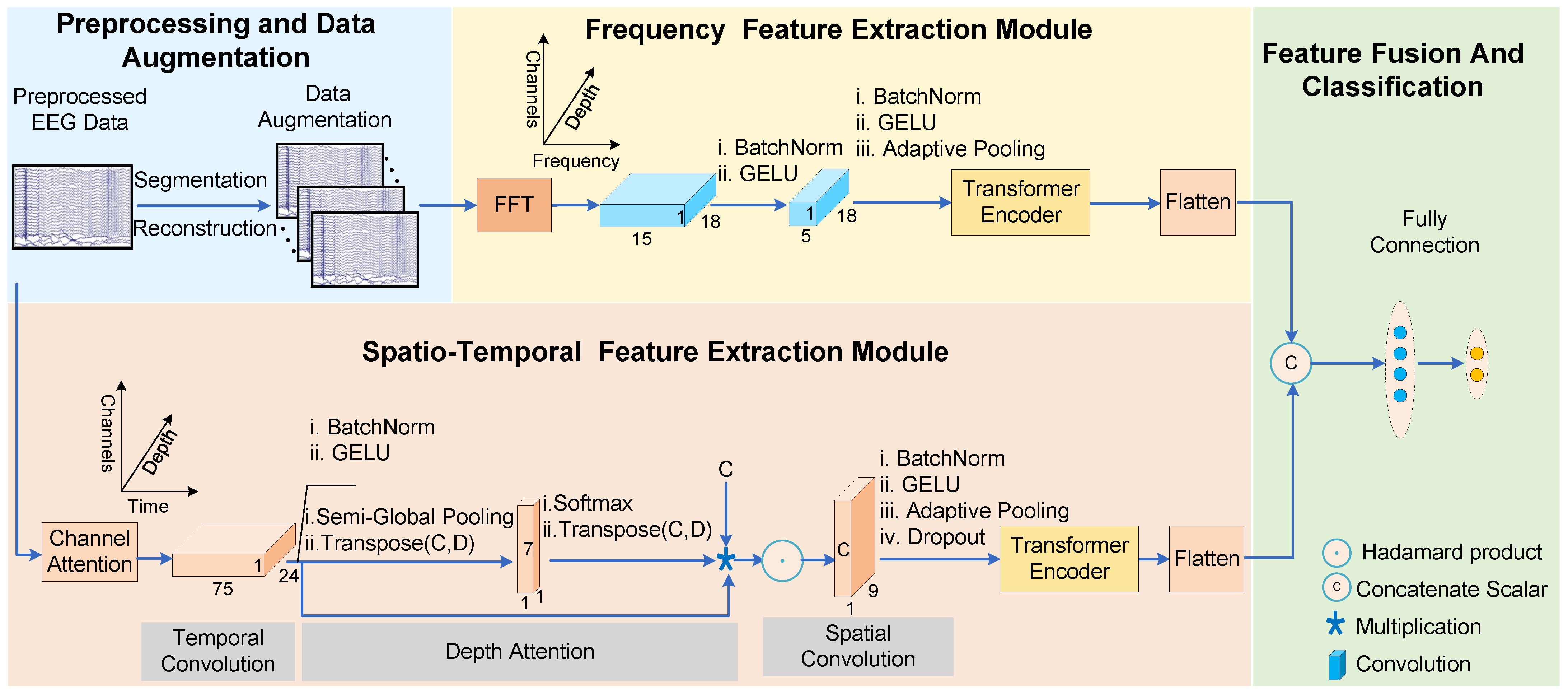
3. Methods
3.1. Preprocessing and Data Augmentation
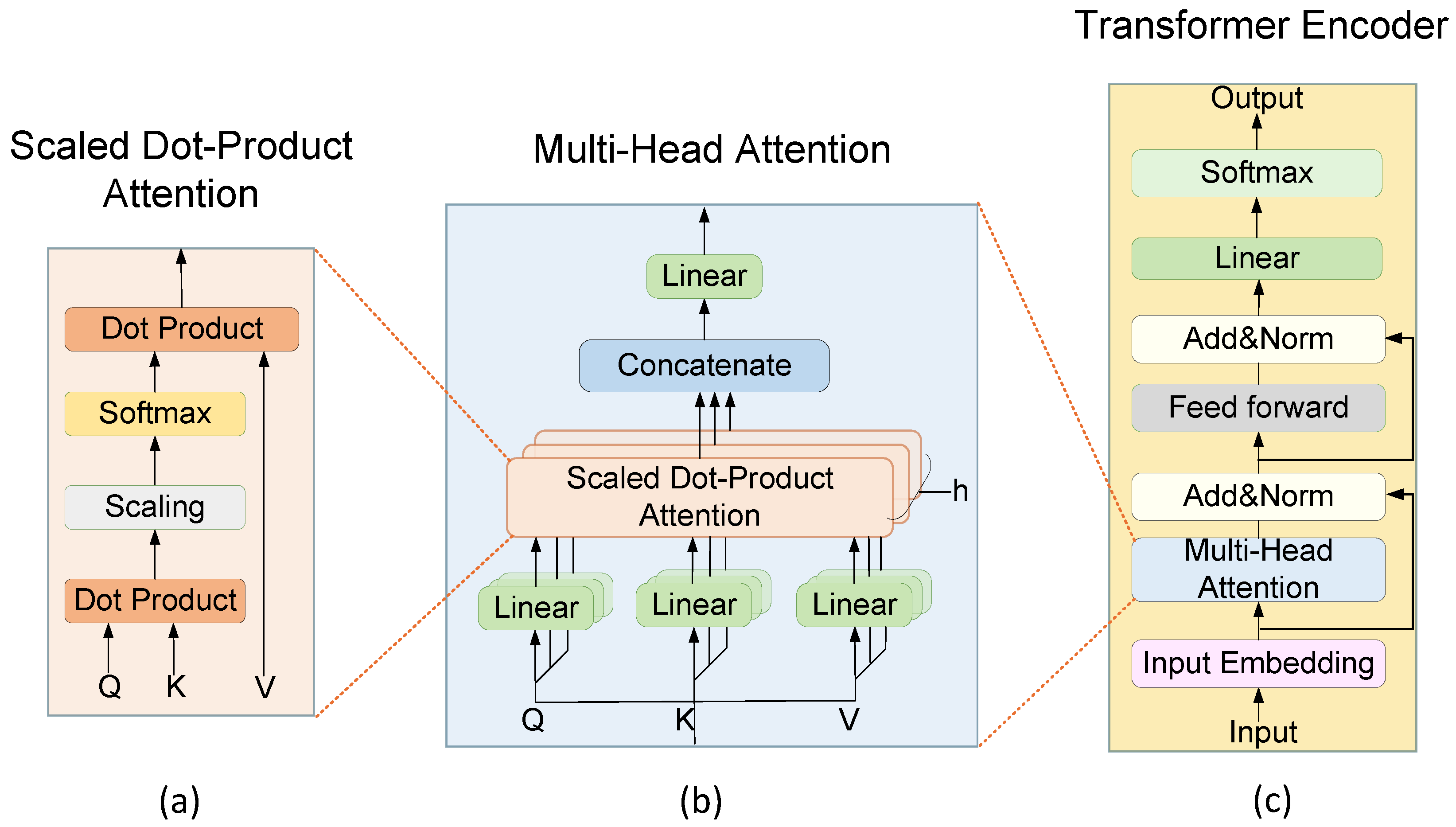
3.2. Transformer Encoder
3.3. Spatiotemporal Feature Extraction Module
3.4. Frequency Feature Extraction Module
3.5. Feature Fusion and Classification
4. Experiment and Result
4.1. Experiment Settings
4.2. Comparison of Classification Results
4.3. Ablation Study
4.4. Training Progress
4.5. Detailed Classification Analysis
4.6. Evalution of Parameter Selection
5. Discussion
5.1. Analysis of Model Complexity
5.2. EEG Signal Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Graimann, B.; Allison, B.; Pfurtscheller, G. Brain-Computer Interfaces: A Gentle Introduction. In Brain-Computer Interfaces: Revolutionizing Human-Computer Interaction; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–27. [Google Scholar] [CrossRef]
- Padfield, N.; Zabalza, J.; Zhao, H.; Masero, V.; Ren, J. EEG-Based Brain-Computer Interfaces Using Motor-Imagery: Techniques and Challenges. Sensors 2019, 19, 1423. [Google Scholar] [CrossRef] [PubMed]
- Freiwald, W.A.; Kreiter, A.K.; Singer, W. Synchronization and assembly formation in the visual cortex. Prog. Brain Res. 2001, 130, 111–140. [Google Scholar] [CrossRef] [PubMed]
- Jeon, Y.; Nam, C.S.; Kim, Y.J.; Whang, M.C. Event-related (De) synchronization (ERD/ERS) during motor imagery tasks: Implications for brain–computer interfaces. Int. J. Ind. Ergon. 2011, 41, 428–436. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Li, W.; Zhang, S.; Lv, P.; Yin, Y. Effects of motor imagery based brain-computer interface on upper limb function and attention in stroke patients with hemiplegia: A randomized controlled trial. BMC Neurol. 2023, 23, 136. [Google Scholar] [CrossRef]
- Alam, M.N.; Ibrahimy, M.I.; Motakabber, S. Feature Extraction of EEG signal by Power Spectral Density for Motor Imagery Based BCI. In Proceedings of the 2021 8th International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 22–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 234–237. [Google Scholar] [CrossRef]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Muller, K.R. Optimizing Spatial filters for Robust EEG Single-Trial Analysis. IEEE Signal Process. Mag. 2007, 25, 41–56. [Google Scholar] [CrossRef]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter Bank Common Spatial Pattern (FBCSP) in Brain-Computer Interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2390–2397. [Google Scholar] [CrossRef]
- Sakhavi, S.; Guan, C.; Yan, S. Learning Temporal Information for Brain-Computer Interface Using Convolutional Neural Networks. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 5619–5629. [Google Scholar] [CrossRef]
- Bouallegue, G.; Djemal, R.; Alshebeili, S.; Aldhalaan, H. A Dynamic Filtering DF-RNN Deep-Learning-Based Approach for EEG-Based Neurological Disorders Diagnosis. IEEE Access 2020, 8, 206992–207007. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, H.; Wang, J.; Li, D.; Fang, X. Recognition of EEG Signal Motor Imagery Intention Based on Deep Multi-View Feature Learning. Sensors 2020, 20, 3496. [Google Scholar] [CrossRef]
- Saibene, A.; Ghaemi, H.; Dagdevir, E. Deep learning in motor imagery EEG signal decoding: A Systematic Review. Neurocomputing 2024, 610, 128577. [Google Scholar] [CrossRef]
- Schirrmeister, R.; Springenberg, J.; Fiederer, L.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Chen, X.; Teng, X.; Chen, H.; Pan, Y.; Geyer, P. Toward reliable signals decoding for electroencephalogram: A benchmark study to EEGNeX. Biomed. Signal Process. Control 2024, 87, 105475. [Google Scholar] [CrossRef]
- Miao, Z.; Zhao, M.; Zhang, X.; Ming, D. LMDA-Net: A lightweight multi-dimensional attention network for general EEG-based brain-computer interfaces and interpretability. NeuroImage 2023, 276, 120209. [Google Scholar] [CrossRef] [PubMed]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M. Physics-Informed Attention Temporal Convolutional Network for EEG-Based Motor Imagery Classification. IEEE Trans. Ind. Inform. 2022, 19, 2249–2258. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q.; Liu, B.; Gao, X. EEG Conformer: Convolutional Transformer for EEG Decoding and Visualization. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 31, 710–719. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, X.; Zhang, B.; Xiao, S.; Weng, S. CTNet: A convolutional transformer network for EEG-based motor imagery classification. Sci. Rep. 2024, 14, 20237. [Google Scholar] [CrossRef]
- Zhao, D.; Tang, F.; Si, B. and Feng, X. Learning joint space–time–frequency features for EEG decoding on small labeled data. Neural Netw. 2019, 114, 67–77. [Google Scholar] [CrossRef]
- Ke, S.; Yang, B.; Qin, Y.; Rong, F.; Zhang, J.; Zheng, Y. FACT-Net: A Frequency Adapter CNN With Temporal-Periodicity Inception for Fast and Accurate MI-EEG Decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 4131–4142. [Google Scholar] [CrossRef]
- Cao, J.; Li, G.; Shen, J.; Dai, C. IFBCLNet: Spatio-temporal frequency feature extraction-based MI-EEG classification convolutional network. Biomed. Signal Process. Control 2024, 92, 106092. [Google Scholar] [CrossRef]
- Altuwaijri, G.A.; Muhammad, G.; Altaheri, H.; Alsulaiman, M. A Multi-Branch Convolutional Neural Network with Squeeze-and-Excitation Attention Blocks for EEG-Based Motor Imagery Signals Classification. Diagnostics 2022, 12, 995. [Google Scholar] [CrossRef]
- Chunduri, V.; Aoudni, Y.; Khan, S.; Aziz, A.; Rizwan, A.; Deb, N.; Keshta, I.; Soni, M. Multi-scale spatiotemporal attention network for neuron based motor imagery EEG classification. J. Neurosci. Methods 2024, 406, 110128. [Google Scholar] [CrossRef]
- Chen, W.; Luo, Y.; Wang, J. Three-branch Temporal-Spatial Convolutional Transformer for Motor Imagery EEG Classification. IEEE Access 2024, 12, 79754–79764. [Google Scholar] [CrossRef]
- Zhou, K.; Haimudula, A.; Tang, W. Dual-Branch Convolution Network With Efficient Channel Attention for EEG-Based Motor Imagery Classification. IEEE Access 2024, 12, 74930–74943. [Google Scholar] [CrossRef]
- Zhi, H.; Yu, Z.; Yu, T.; Gu, Z.; Yang, J. A Multi-Domain Convolutional Neural Network for EEG-Based Motor Imagery Decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 3988–3998. [Google Scholar] [CrossRef]
- Cai, Z.; Luo, T.; Cao, X. Multi-branch spatial-temporal-spectral convolutional neural networks for multi-task motor imagery EEG classification. Biomed. Signal Process. Control 2024, 93, 106156. [Google Scholar] [CrossRef]
- Brunner, C.; Leeb, R.; Müller-Putz, G.; Schlögl, A.; Pfurtscheller, G. BCI Competition 2008–Graz data set A. Inst. Knowl. Discov. (Lab. Brain-Comput. Interfaces) Graz Univ. Technol. 2008, 16, 1. [Google Scholar]
- Leeb, R.; Brunner, C.; Müller-Putz, G.; Schlögl, A.; Pfurtscheller, G. BCI Competition 2008–Graz data set B. Graz Univ. Technol. Austria 2008, 16, 1–6. [Google Scholar]
- He, H.; Wu, D. Transfer Learning for Brain–Computer Interfaces: A Euclidean Space Data Alignment Approach. IEEE Trans. Biomed. Eng. 2019, 67, 399–410. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Chen, W.; Pei, Z.; Zhang, Y. and Chen, J. Attention-based convolutional neural network with multi-modal temporal information fusion for motor imagery EEG decoding. Comput. Biol. Med. 2024, 175, 108504. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Zhu, W. TMSA-Net: A novel attention mechanism for improved motor imagery EEG signal processing. Biomed. Signal Process. Control 2025, 102, 107189. [Google Scholar] [CrossRef]
- Wang, J.; Yao, L.; Wang, Y. IFNet: An Interactive Frequency Convolutional Neural Network for Enhancing Motor Imagery Decoding From EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1900–1911. [Google Scholar] [CrossRef]
- Lotte, F. Signal Processing Approaches to Minimize or Suppress Calibration Time in Oscillatory Activity-Based Brain–Computer Interfaces. Proc. IEEE 2015, 103, 871–890. [Google Scholar] [CrossRef]
- Samiee, K.; Kovacs, P.; Gabbouj, M. Epileptic Seizure Classification of EEG Time-Series Using Rational Discrete Short-Time Fourier Transform. IEEE Trans. Biomed. Eng. 2014, 62, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Fixing Weight Decay Regularization in Adam. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Mane, R.; Chew, E.; Chua, K.; Ang, K.K.; Robinson, N.; Vinod, A.P.; Lee, S.W.; Guan, C. FBCNet: A Multi-view Convolutional Neural Network for Brain-Computer Interface. arXiv 2021, arXiv:2104.01233. [Google Scholar] [CrossRef]








| Dataset | Subjects | Channels | Trials | Classes | Sampling Rate (Hz) | Trial Duration (s) |
|---|---|---|---|---|---|---|
| BCI-IV-2a | 9 | 22 | 576 | 4 | 250 | 4 |
| BCI-IV-2b | 9 | 3 | 720 | 2 | 250 | 4 |
| Methods | A01 | A02 | A03 | A04 | A05 | A06 | A07 | A08 | A09 | Average | Std | Kappa |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EEGNet | 85.10 | 64.24 | 84.72 | 68.40 | 60.42 | 57.64 | 84.38 | 83.33 | 86.11 | 74.93 | 11.99 | 0.66 |
| FBCNet | 83.53 | 57.64 | 85.76 | 78.27 | 73.81 | 56.25 | 84.13 | 82.64 | 82.99 | 76.11 | 11.45 | 0.69 |
| Conformer | 86.73 | 60.12 | 94.25 | 77.38 | 59.87 | 67.45 | 91.69 | 89.01 | 87.56 | 79.34 | 13.62 | 0.72 |
| LMDA-Net | 87.15 | 68.44 | 92.01 | 76.74 | 66.54 | 61.46 | 92.36 | 85.07 | 86.11 | 79.54 | 11.61 | 0.63 |
| ATCNet | 85.21 | 63.89 | 92.70 | 76.98 | 79.72 | 67.33 | 89.12 | 85.45 | 82.67 | 80.34 | 9.60 | 0.73 |
| TMSA-Net | 86.75 | 63.48 | 95.92 | 83.16 | 79.28 | 66.89 | 92.47 | 89.35 | 84.79 | 82.45 | 10.99 | 0.76 |
| Ours | 89.58 | 69.89 | 93.06 | 82.99 | 74.10 | 67.71 | 94.10 | 89.89 | 86.81 | 83.13 | 10.09 | 0.78 |
| Methods | B01 | B02 | B03 | B04 | B05 | B06 | B07 | B08 | B09 | Average | Std | Kappa |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EEGNet | 75.00 | 62.50 | 60.42 | 98.33 | 80.00 | 88.33 | 85.00 | 93.33 | 90.83 | 81.53 | 13.32 | 0.72 |
| FBCNet | 79.42 | 56.83 | 61.27 | 96.15 | 92.49 | 86.12 | 81.90 | 91.37 | 88.95 | 81.61 | 13.84 | 0.64 |
| ATCNet | 72.85 | 62.10 | 86.42 | 95.10 | 92.50 | 89.91 | 90.25 | 95.80 | 89.92 | 86.09 | 11.26 | 0.73 |
| LMDA-Net | 82.58 | 62.78 | 74.80 | 99.60 | 95.52 | 92.33 | 90.43 | 95.89 | 93.69 | 87.51 | 11.98 | 0.73 |
| Conformer | 78.43 | 71.92 | 84.17 | 96.84 | 96.55 | 88.62 | 91.78 | 93.41 | 91.66 | 88.15 | 8.46 | 0.76 |
| TMSA-Net | 82.17 | 70.58 | 87.25 | 97.82 | 97.95 | 90.11 | 93.04 | 94.17 | 86.95 | 88.89 | 8.63 | 0.77 |
| Ours | 83.83 | 68.56 | 78.77 | 99.80 | 95.76 | 94.89 | 92.56 | 96.68 | 94.97 | 89.54 | 10.31 | 0.78 |
| Method | Accuracy (%) | Traing Time (s) | Inference Time (ms) |
|---|---|---|---|
| Ours | 83.13 | 1.19 | 0.479 |
| Ours-w/o FFE | 80.19 | 1.03 | 0.476 |
| Ours-w/o FFE + encoder(STFE) | 79.54 | 0.87 | 0.472 |
| Ours-w/o STFE | 60.81 | 0.61 | 0.465 |
| Ours-w/o STFE + encoder(FFE) | 58.79 | 0.53 | 0.486 |
| Ours-w/o Augmentation | 75.49 | 0.79 | 0.531 |
| Ours-w/o encoder(STFE) | 79.84 | 1.11 | 0.524 |
| Ours-w/o encoder(FFE) | 78.61 | 1.17 | 0.542 |
| Ours-w/o encoder(STFE+FFE) | 75.87 | 0.88 | 0.476 |
| Method | Accuracy (%) | Traing Time (s) | Inference Time (ms) |
|---|---|---|---|
| Ours | 89.54 | 0.83 | 0.243 |
| Ours-w/o FFE | 88.22 | 0.54 | 0.206 |
| Ours-w/o FFE + encoder(STFE) | 87.51 | 0.22 | 0.125 |
| Ours-w/o STFE | 71.47 | 0.3 | 0.163 |
| Ours-w/o STFE + encoder(FFE) | 68.58 | 0.16 | 0.144 |
| Ours-w/o Augmentation | 80.97 | 0.54 | 0.178 |
| Ours-w/o encoder(STFE) | 82.73 | 0.4 | 0.131 |
| Ours-w/o encoder(FFE) | 78.75 | 0.48 | 0.163 |
| Ours-w/o encoder(STFE+FFE) | 79.89 | 0.2 | 0.1 |
| Method | Parameters | Flops | Accuracy (%) |
|---|---|---|---|
| Ours | 29.5 k | 66.33 M | 83.13 |
| EEGNet | 3.91 k | 13.25 M | 74.93 |
| Conformer | 156.56 k | 71.35 M | 79.34 |
| L MDANet | 5.4 k | 64.87 M | 79.54 |
| T MSANet | 20.9 k | 33 M | 82.45 |
| ATCNet | 113.73 k | 29.79 M | 80.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Zhou, Z.; Zhang, Z.; Yuan, W. Dual-Branch Spatio-Temporal-Frequency Fusion Convolutional Network with Transformer for EEG-Based Motor Imagery Classification. Electronics 2025, 14, 2853. https://doi.org/10.3390/electronics14142853
Hu H, Zhou Z, Zhang Z, Yuan W. Dual-Branch Spatio-Temporal-Frequency Fusion Convolutional Network with Transformer for EEG-Based Motor Imagery Classification. Electronics. 2025; 14(14):2853. https://doi.org/10.3390/electronics14142853
Chicago/Turabian StyleHu, Hao, Zhiyong Zhou, Zihan Zhang, and Wenyu Yuan. 2025. "Dual-Branch Spatio-Temporal-Frequency Fusion Convolutional Network with Transformer for EEG-Based Motor Imagery Classification" Electronics 14, no. 14: 2853. https://doi.org/10.3390/electronics14142853
APA StyleHu, H., Zhou, Z., Zhang, Z., & Yuan, W. (2025). Dual-Branch Spatio-Temporal-Frequency Fusion Convolutional Network with Transformer for EEG-Based Motor Imagery Classification. Electronics, 14(14), 2853. https://doi.org/10.3390/electronics14142853





