Cascaded Quasi-Resonant Extended State Observer-Based Deadbeat Predictive Current Control Strategy for PMSM
Abstract
1. Introduction
2. Mathematical Model of the PMSM Considering Disturbance
3. Proposed CQRESO-Based DPCC Strategy
3.1. Principles of the CQRESO
3.2. CQRESO-Based DPCC Strategy
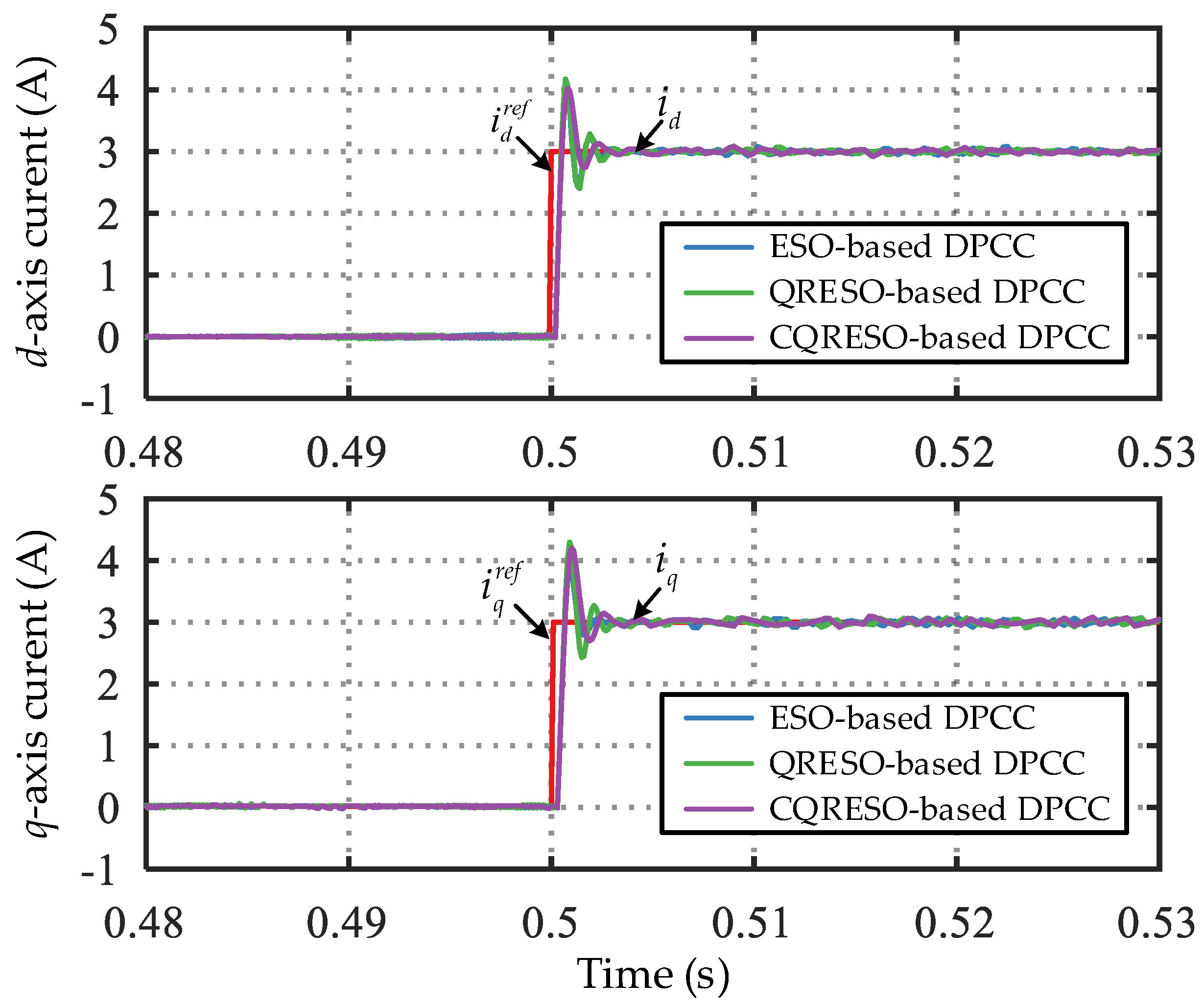
4. Simulation Results
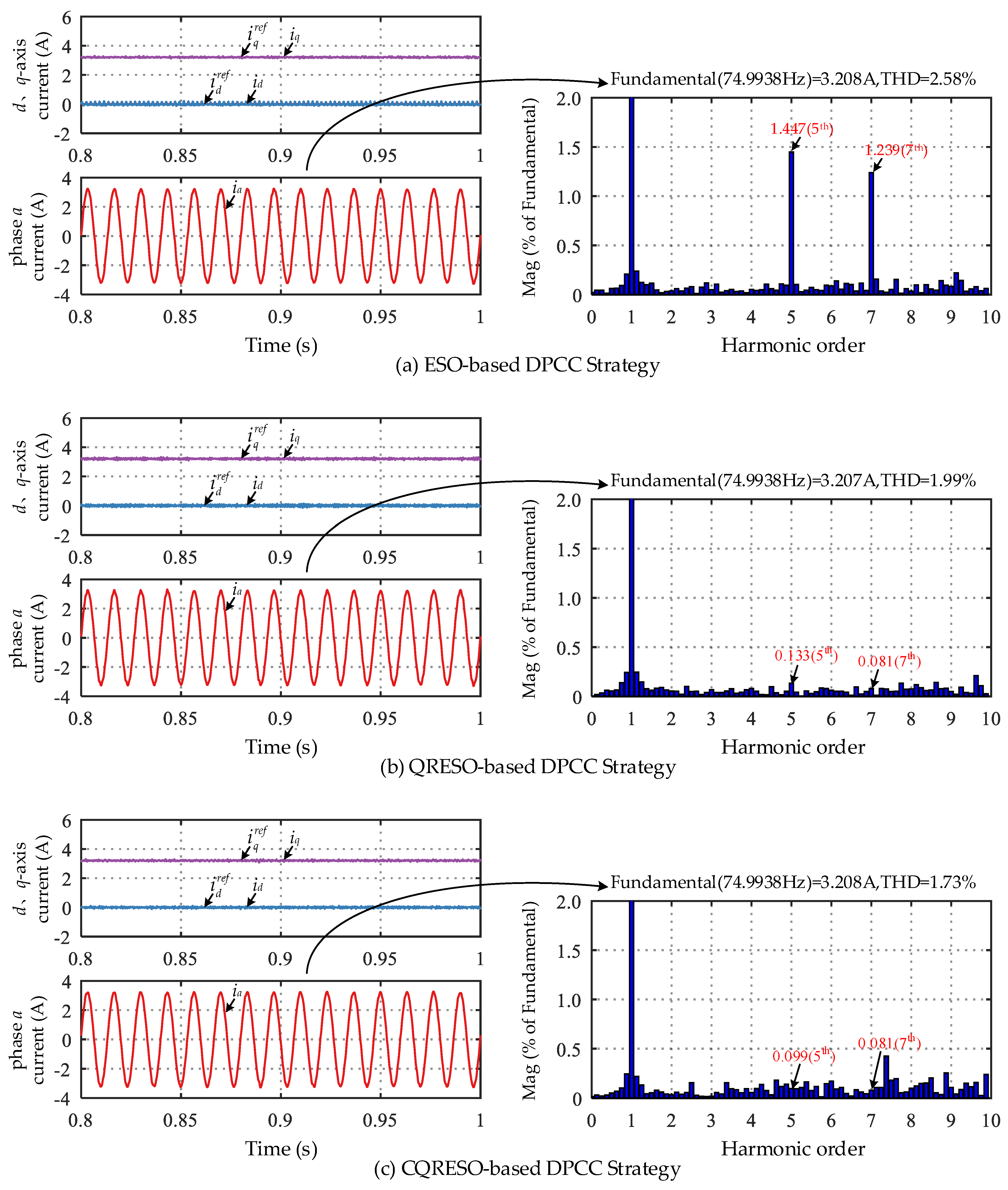
4.1. Steady-State Performance
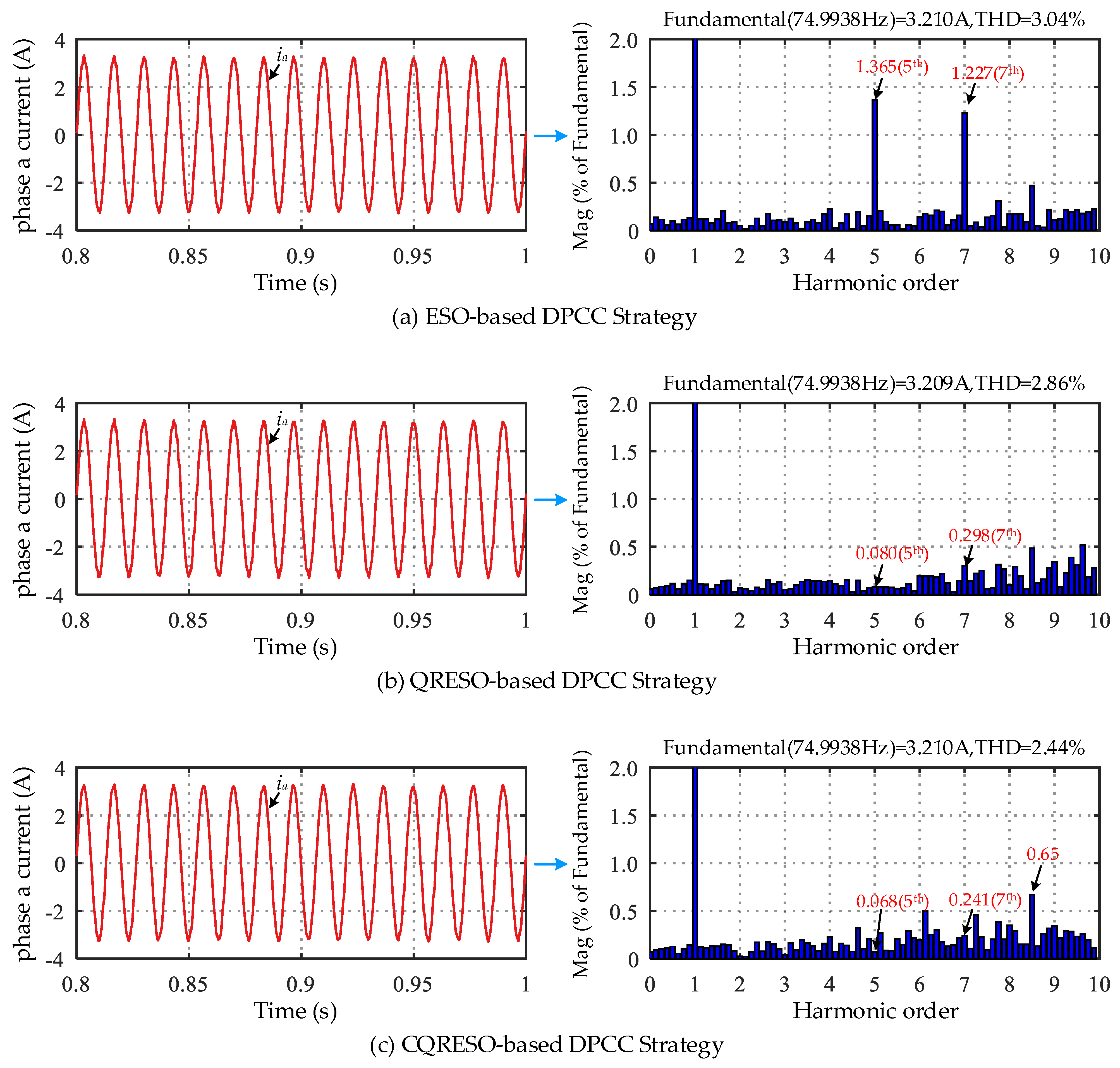
4.2. Robust Performance Comparison Under Parameter Changes
4.3. Noise Sensitivity Performance Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sarlioglu, B.; T Morris, C. More electric aircraft: Review, challenges, and opportunities for commercial transport aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Yao, Y.; Yu, L.; Yan, Y. Electric power system and key technologies of more electric aircraft. J. Nanjing Univ. Aeronaut. Astronaut. 2022, 54, 969–984. [Google Scholar]
- Guan, L.; Lian, W. Review on electro-hydrostatic actuation technology of aircraft flight control system. Meas. Control Technol. 2022, 41, 1–11. [Google Scholar]
- Liu, C.; Luo, G.; Tu, W. Survey on active disturbance rejection control of permanent magnet synchronous motor for aviation electro-mechanical actuator. Meas. Control Technol. 2021, 4, 12–24. [Google Scholar]
- Zhang, Y.; Wang, F.; Yin, Z.; Bai, C.; Wang, G.; Liu, J. A rotor position and speed estimation method using an improved linear extended state observer for IPMSM sensorless drives. IEEE Trans. Power Electron. 2021, 36, 14062–14073. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, R.; Chen, Z.; Tu, W.; Zhang, S.; Ralph, K. A novel nonlinear modeling method for permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2016, 63, 6490–6498. [Google Scholar] [CrossRef]
- Yuang, X.; Zuo, Y.; Fan, Y.; Christopher, H.T.; Lee, C.H. Model-free predictive current control of SPMSM drives using extended state observer. IEEE Trans. Ind. Electron. 2022, 63, 6540–6550. [Google Scholar] [CrossRef]
- Gao, F.; Bozhko, S.; Costabeber, A.; Asher, G.; Wheeler, P. Control design and voltage stability analysis of a droop-controlled electrical power system for more electric aircraft. IEEE Trans. Ind. Electron. 2017, 64, 9271–9281. [Google Scholar] [CrossRef]
- Lang, X.; Yang, T.; Bai, G.; Bozhko, S.; Wheeler, P. Active disturbance rejection control of dc-bus voltages within a high-speed aircraft electric starter/generator system. IEEE Trans. Transp. Electrif. 2022, 8, 4229–4241. [Google Scholar] [CrossRef]
- Lang, X.; Yang, T.; Li, C.; Enalou, H.B.; Bozhko, S.; Wheeler, P. A dual-channel-enhanced power generation architecture with back-to-back converter for MEA application. IEEE Trans. Ind. Appl. 2020, 56, 3006–3019. [Google Scholar] [CrossRef]
- Guo, F.; Yang, T.; Bozhko, S.; Wheeler, P. Active modulation strategy for capacitor voltage balancing of three-level neutral-point-clamped converters in high-speed drives. IEEE Trans. Ind. Electron. 2022, 69, 2276–2287. [Google Scholar] [CrossRef]
- Cao, H.; Deng, Y.; Zuo, Y.; Li, H.; Wang, J.; Liu, X.; Lee, C.H.T. Improved adrc with a cascade extended stated observer based on quasi-generalized integrator for PMSM current disturbances attenuation. IEEE Trans. Transp. Electrif. 2024, 10, 2145–2157. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-free predictive current control of PMSM drives based on extended state observer using ultralocal model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Wu, S.; Shi, J.; Li, Z. Research on deadbeat predictive current control of PMSM based on ESO. Electr. Drive 2021, 51, 22–28. [Google Scholar]
- Ke, D.; Wang, F.; Yu, X.; Davari, S.A.; Kennel, R. Predictive error model based enhanced observer for PMSM deadbeat control systems. IEEE Trans. Ind. Electron. 2024, 71, 2242–2252. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Adaptive active disturbance rejection control for uncertain current ripples suppression for PMSM drives. IEEE Trans. Ind. Electron. 2023, 71, 2320–2331. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, X.; Liu, C.; Zhang, H.; Luo, G. Research on current decoupling and harmonic suppression strategy of permanent magnet synchronous motor based on proportional resonance type adrc. Proceeding CSEE 2022, 42, 9062–9071. [Google Scholar]
- Xu, J.; Wang, T.; Jia, P. Quasi-resonant active disturbance rejection control for current harmonics suppression of permanent magnet synchronous motor. Proceeding CSEE 2023, 42, 2450–2459. [Google Scholar]
- Yang, X.; Hu, H.; Hu, H.; Liu, Y.; He, Z. A quasi-resonant extended state observer-based predictive current control strategy for three-phase PWM rectifier. IEEE Trans. Ind. Electron. 2022, 69, 13910–13917. [Google Scholar] [CrossRef]
- Guo, B.; Bacha, S.; Alamir, M.; Hably, A.; Boudinet, C. Generalized integrator-extended state observer with applications to grid-connected converters in the presence of disturbances. IEEE Trans. Control. Syst. Technol. 2021, 29, 744–755. [Google Scholar] [CrossRef]
- Wasng, G.; Liu, R.; Zhao, N.; Ding, D.; Xu, D. Enhanced linear ADRC strategy for HF pulse voltage signal injection-based sensorless IPMSM drives. IEEE Trans. Power Electron. 2019, 34, 514–525. [Google Scholar] [CrossRef]
- Xie, H.; Hu, C.; Lu, M.; Liu, X.; Huang, S. Reseach on speed control strategy for permanent magnet linear synchronous motor based on cascaded linear-nonlinear active disturbance rejection controller. Proceeding CSEE 2024, 15, 6158–6168. [Google Scholar]
- Han, J. Active Disturbance Rejection Control Technique: The Technique for Estimating and Compensating the Uncertainties; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Hang, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar]
- Gao, Z. Scaling and bandwidth parameterization based on control tuning. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 4989–4996. [Google Scholar]
- Zhu, B. Introduction to Active Disturbance Rejection Control; Beihang University Press: Beijing, China, 2017. [Google Scholar]



| Parameter | Symbol | Value |
|---|---|---|
| Rated speed | ωN | 1500 rpm |
| Stator resistance | Rs0 | 2.25 Ω |
| D-axis inductance | Ld0 | 15 mH |
| Q-axis inductance | Lq0 | 15 mH |
| Number of pole pairs | Pn | 3 |
| Rated torque | TN | 7 N∙m |
| Flux linkage | ψf | 0.249 Wb |
| Total inertia | J | 0.0123 kg∙m2 |
| DC side voltage of inverter | Udc | 270 V |
| Control Strategy | THD of ia | 5th Harmonic Mag (% of Fundamental) | 7th Harmonic Mag (% of Fundamental) |
|---|---|---|---|
| ESO-based DPCC | 2.58% | 1.447 | 1.239 |
| QRESO-based DPCC | 1.99% | 0.133 | 0.081 |
| CQRESO-based DPCC | 1.73% | 0.099 | 0.081 |
| Control Strategy | THD of ia | 5th Harmonic Mag (% of Fundamental) | 7th Harmonic Mag (% of Fundamental) |
|---|---|---|---|
| ESO-based DPCC | 3.04% | 1.365 | 1.227 |
| QRESO-based DPCC | 2.86% | 0.080 | 0.298 |
| CQRESO-based DPCC | 2.44% | 0.068 | 0.241 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, X.; Zhang, Y.; Hu, T. Cascaded Quasi-Resonant Extended State Observer-Based Deadbeat Predictive Current Control Strategy for PMSM. Electronics 2025, 14, 2782. https://doi.org/10.3390/electronics14142782
Liu Y, Yang X, Zhang Y, Hu T. Cascaded Quasi-Resonant Extended State Observer-Based Deadbeat Predictive Current Control Strategy for PMSM. Electronics. 2025; 14(14):2782. https://doi.org/10.3390/electronics14142782
Chicago/Turabian StyleLiu, Yang, Xiaowei Yang, Yongqiang Zhang, and Tao Hu. 2025. "Cascaded Quasi-Resonant Extended State Observer-Based Deadbeat Predictive Current Control Strategy for PMSM" Electronics 14, no. 14: 2782. https://doi.org/10.3390/electronics14142782
APA StyleLiu, Y., Yang, X., Zhang, Y., & Hu, T. (2025). Cascaded Quasi-Resonant Extended State Observer-Based Deadbeat Predictive Current Control Strategy for PMSM. Electronics, 14(14), 2782. https://doi.org/10.3390/electronics14142782





